Numerical Study of Cavitation Characteristics through Butterfly Valve under Different Regulation Conditions
Abstract
1. Introduction
2. Numerical Method
2.1. Governing Equation
2.2. Turbulence Model
2.3. Cavitation Model
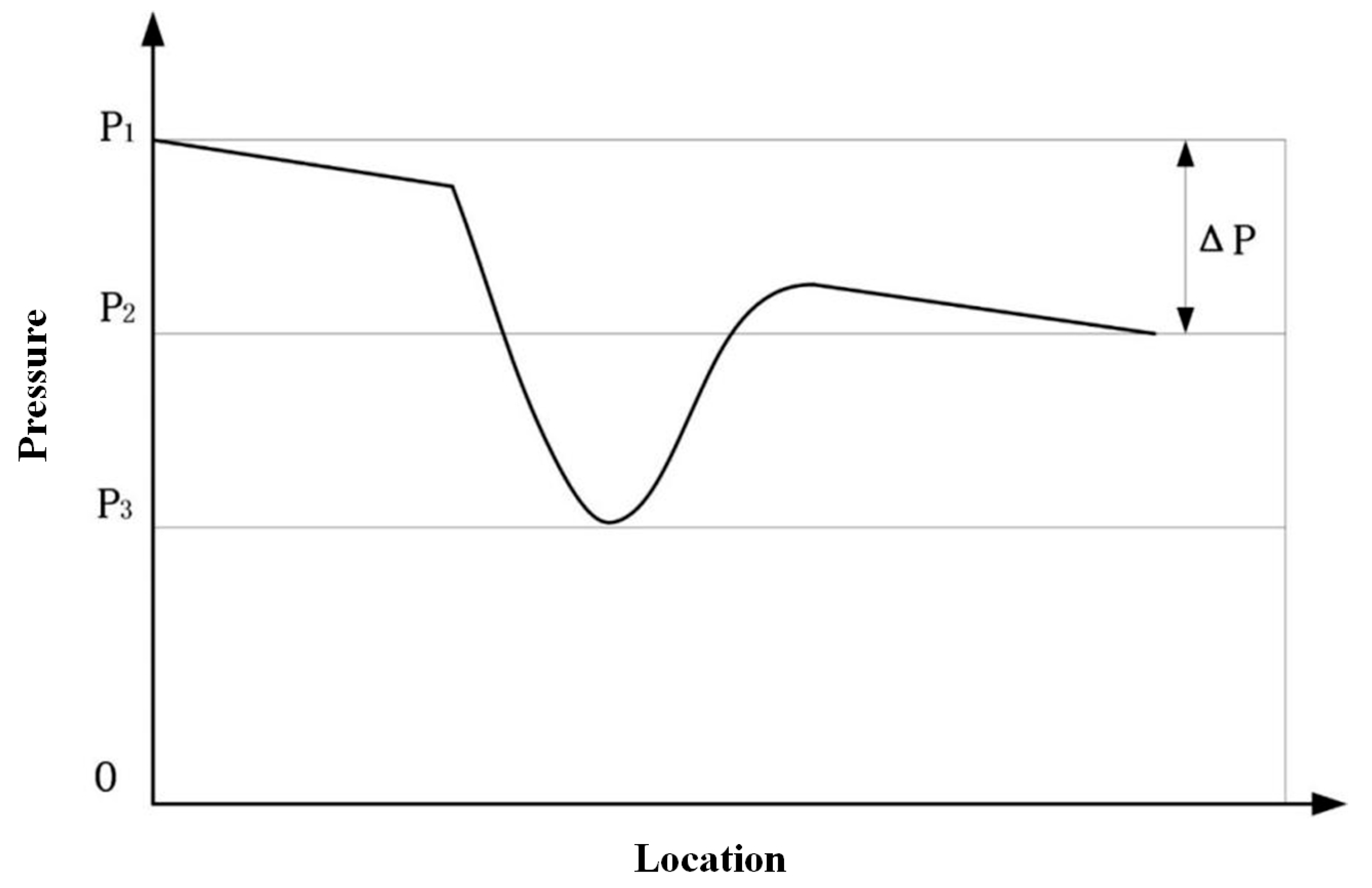
2.4. Flow Coefficient and Cavitation Coefficient
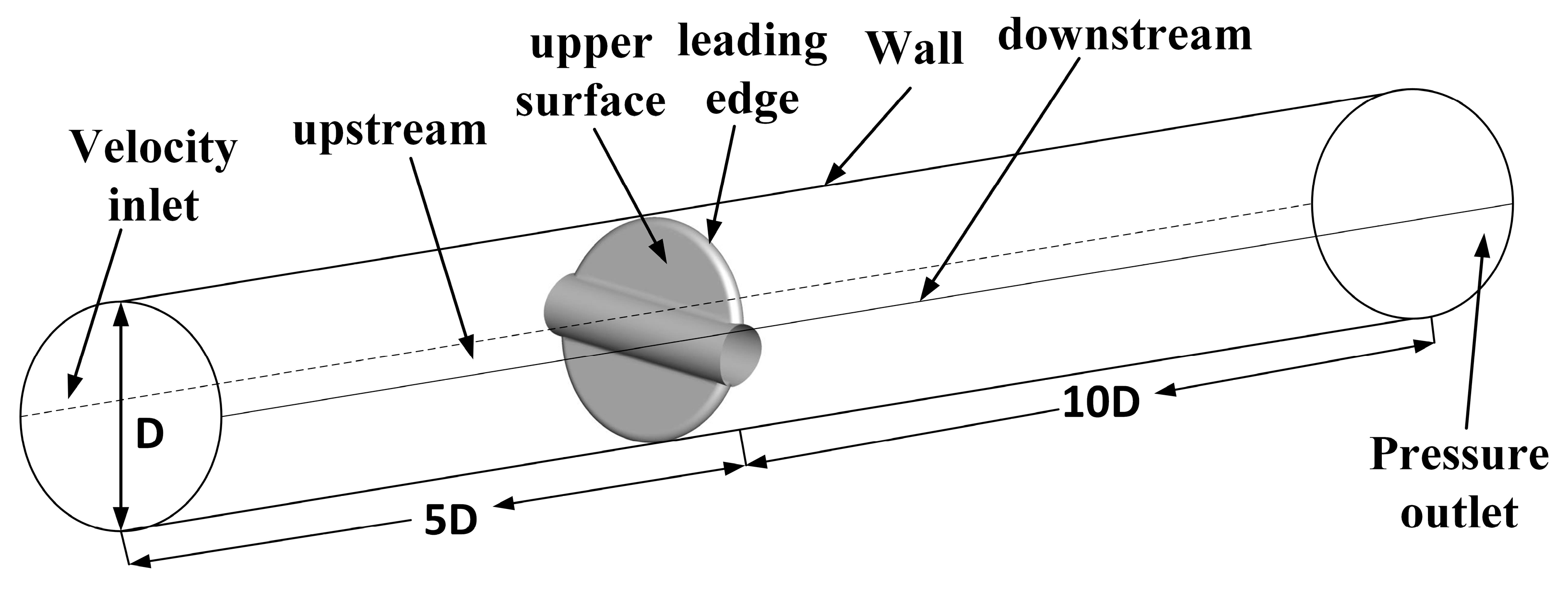
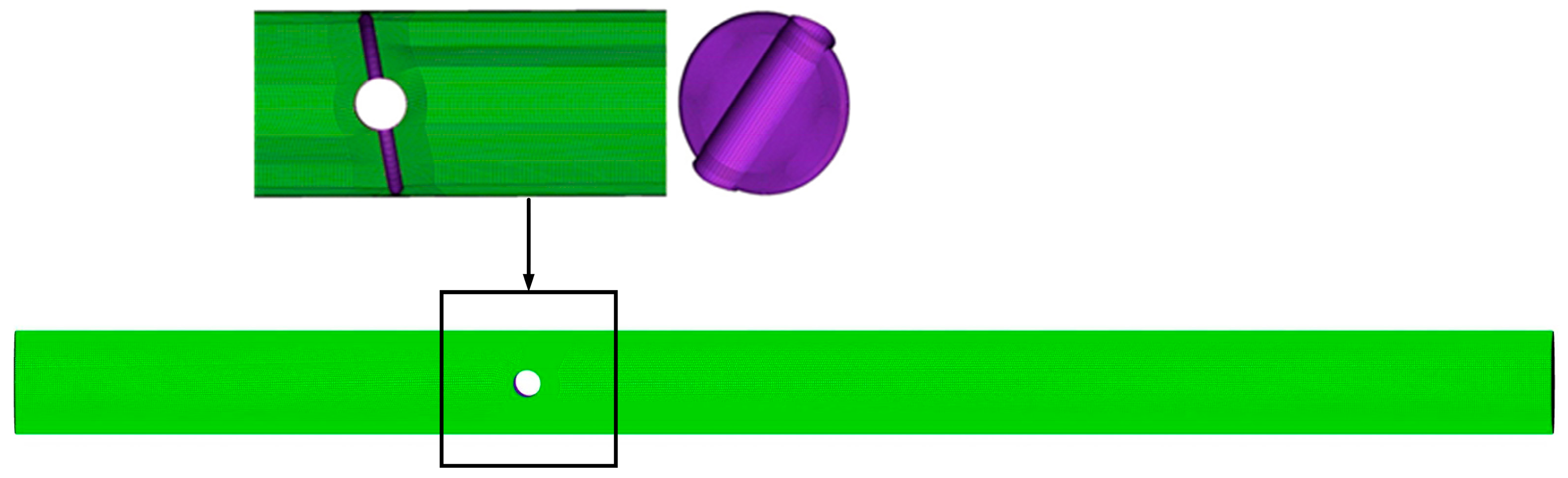
2.5. Computational Domain and Boundary Conditions
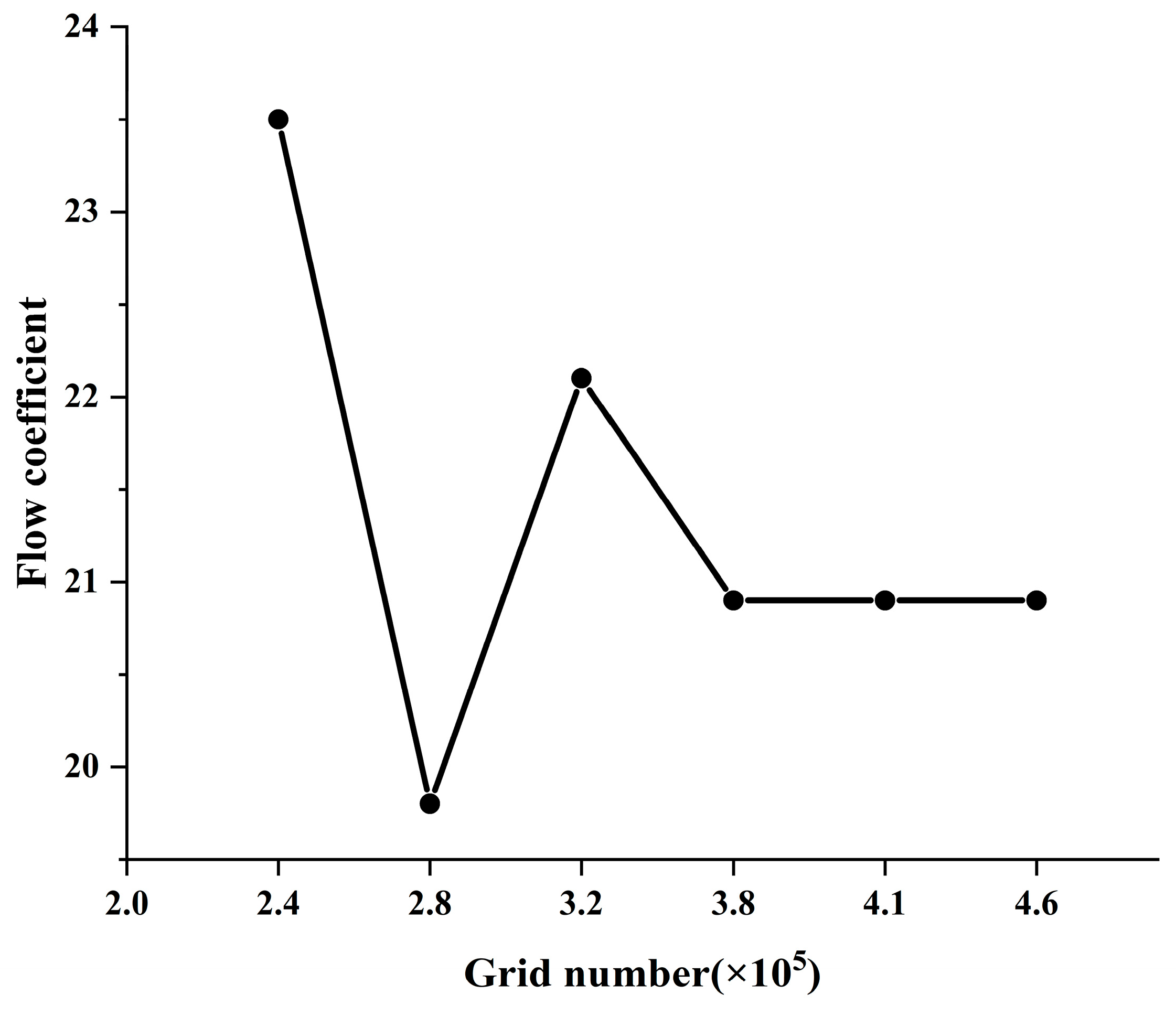
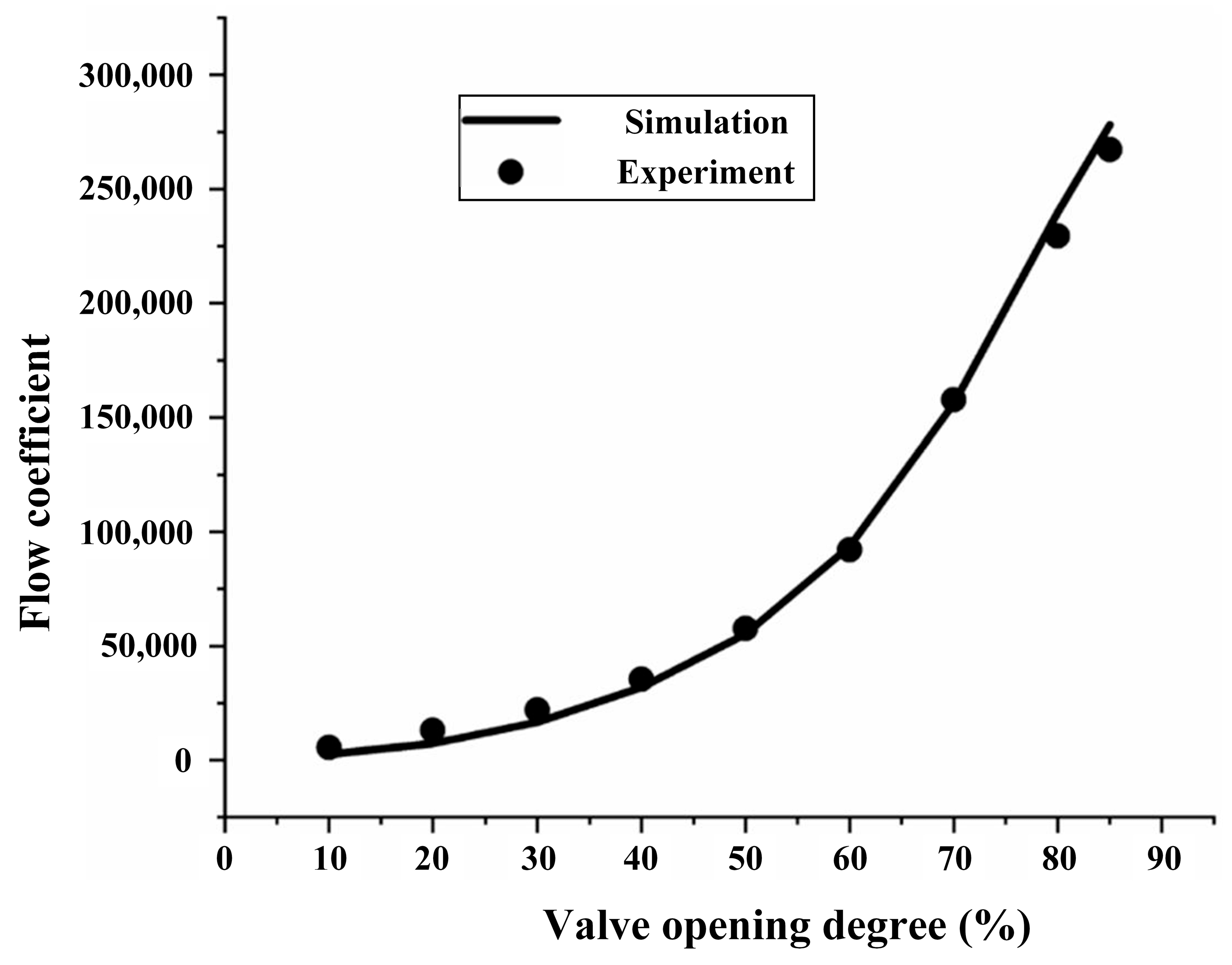
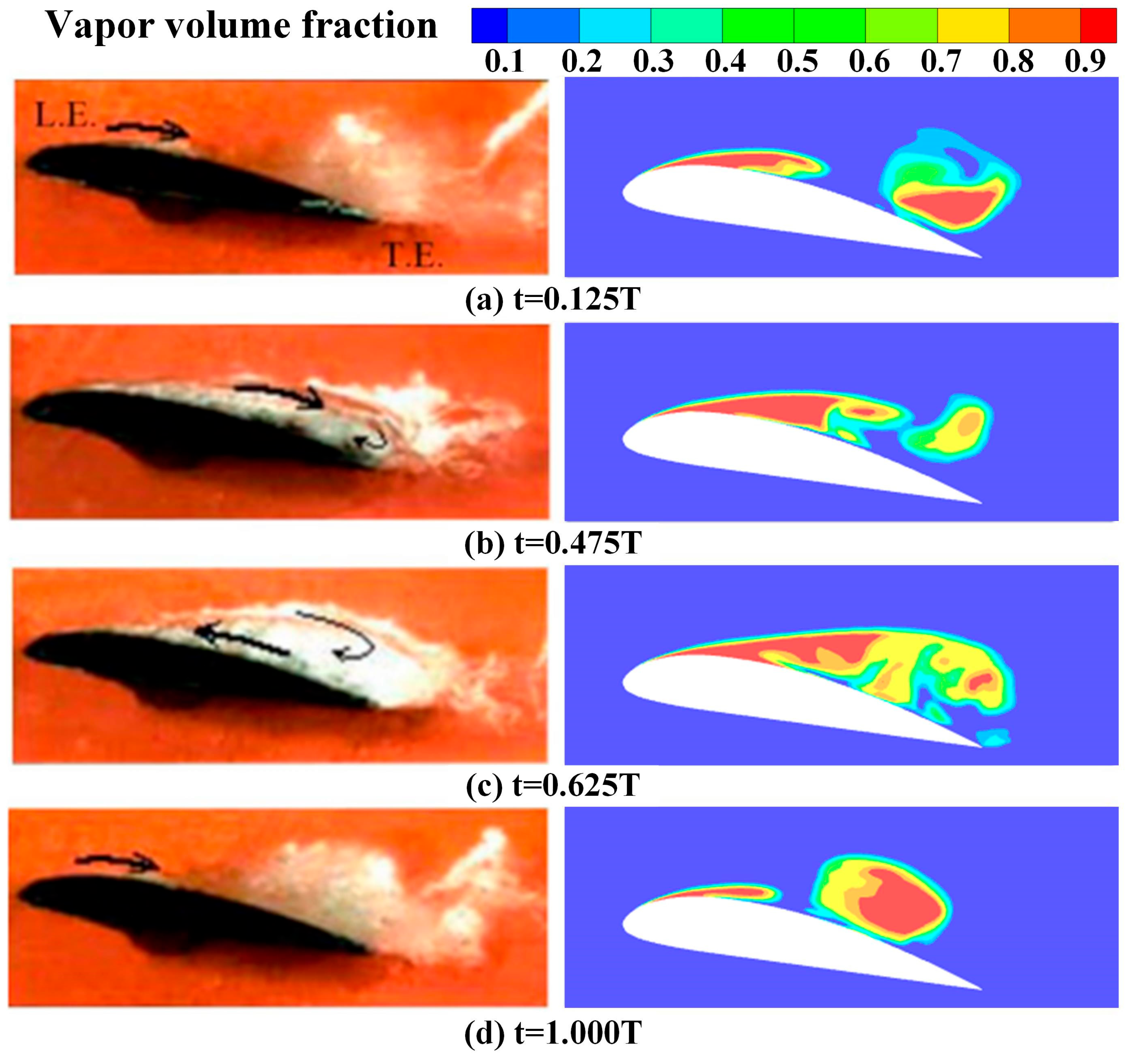
2.6. Verification of the Numerical Method
3. Results and Discussion
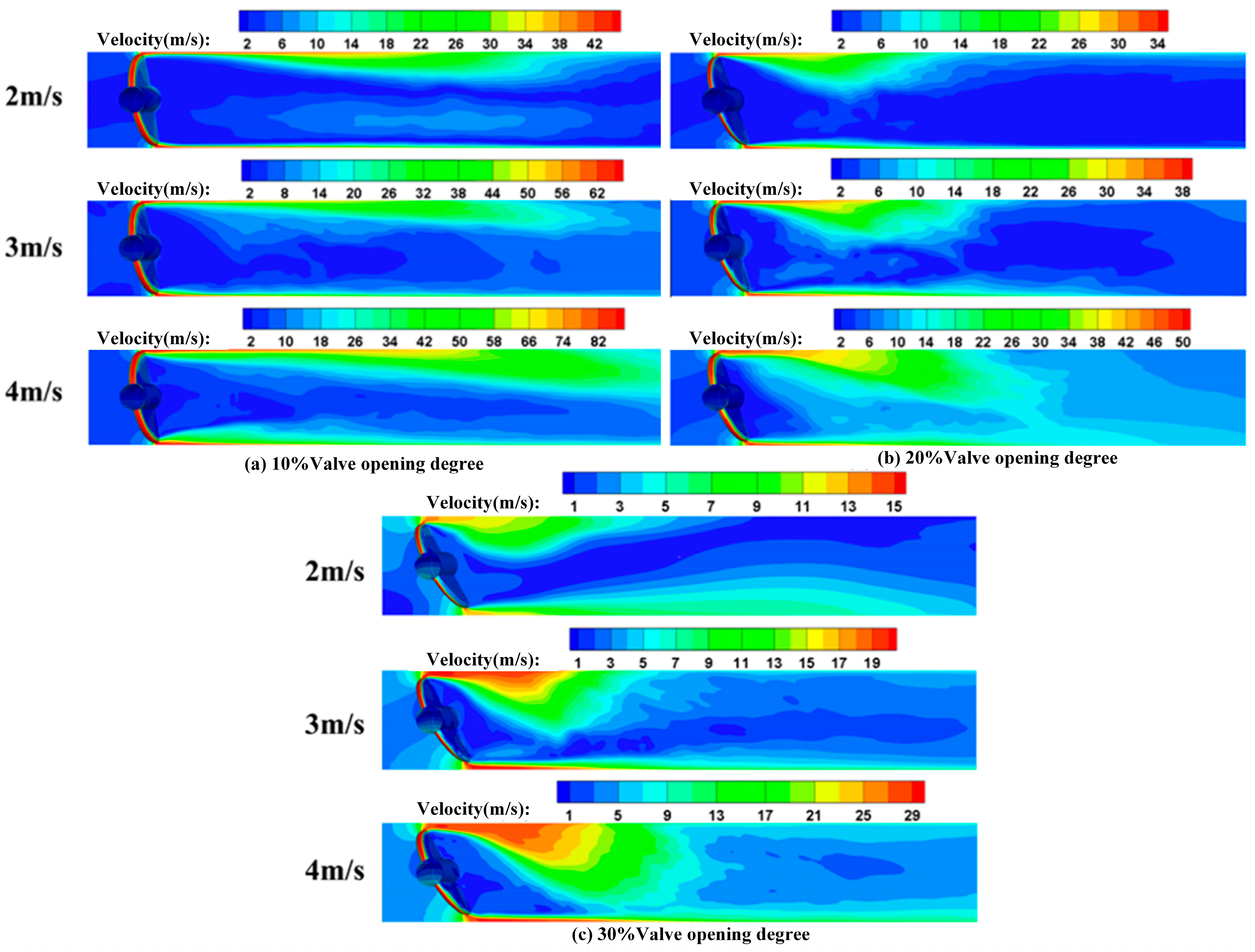
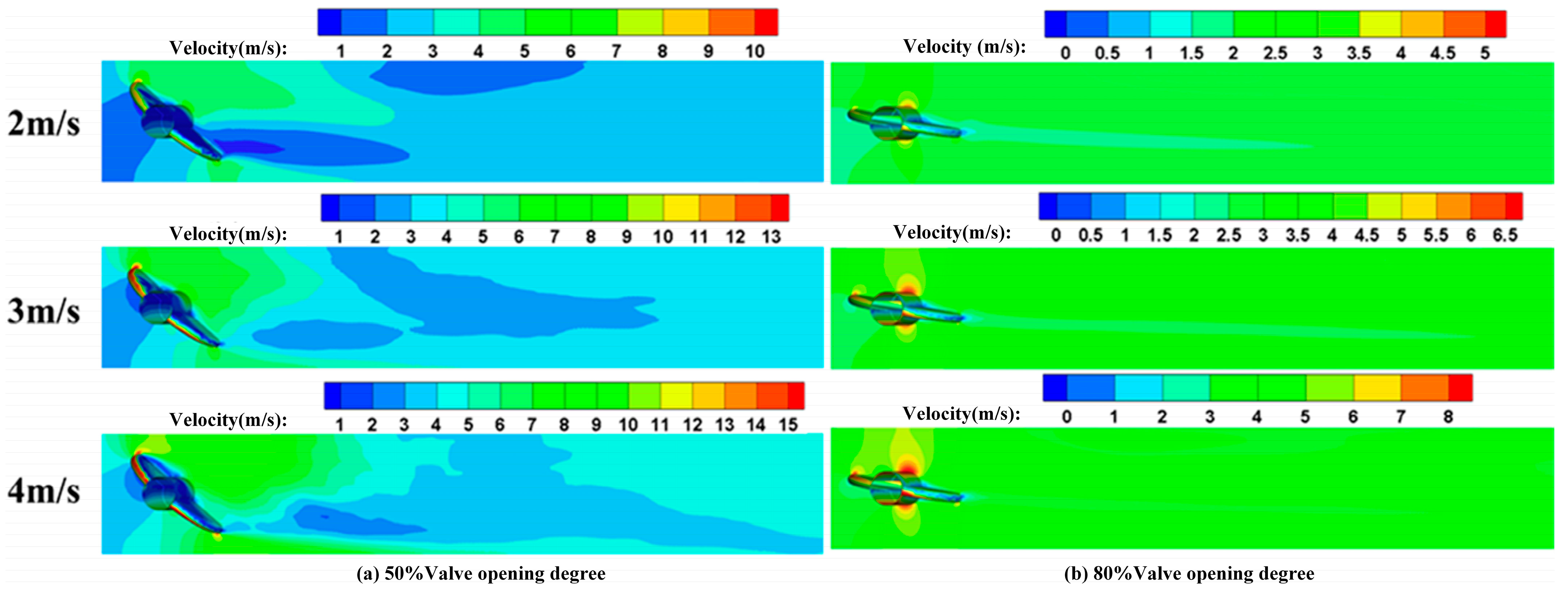
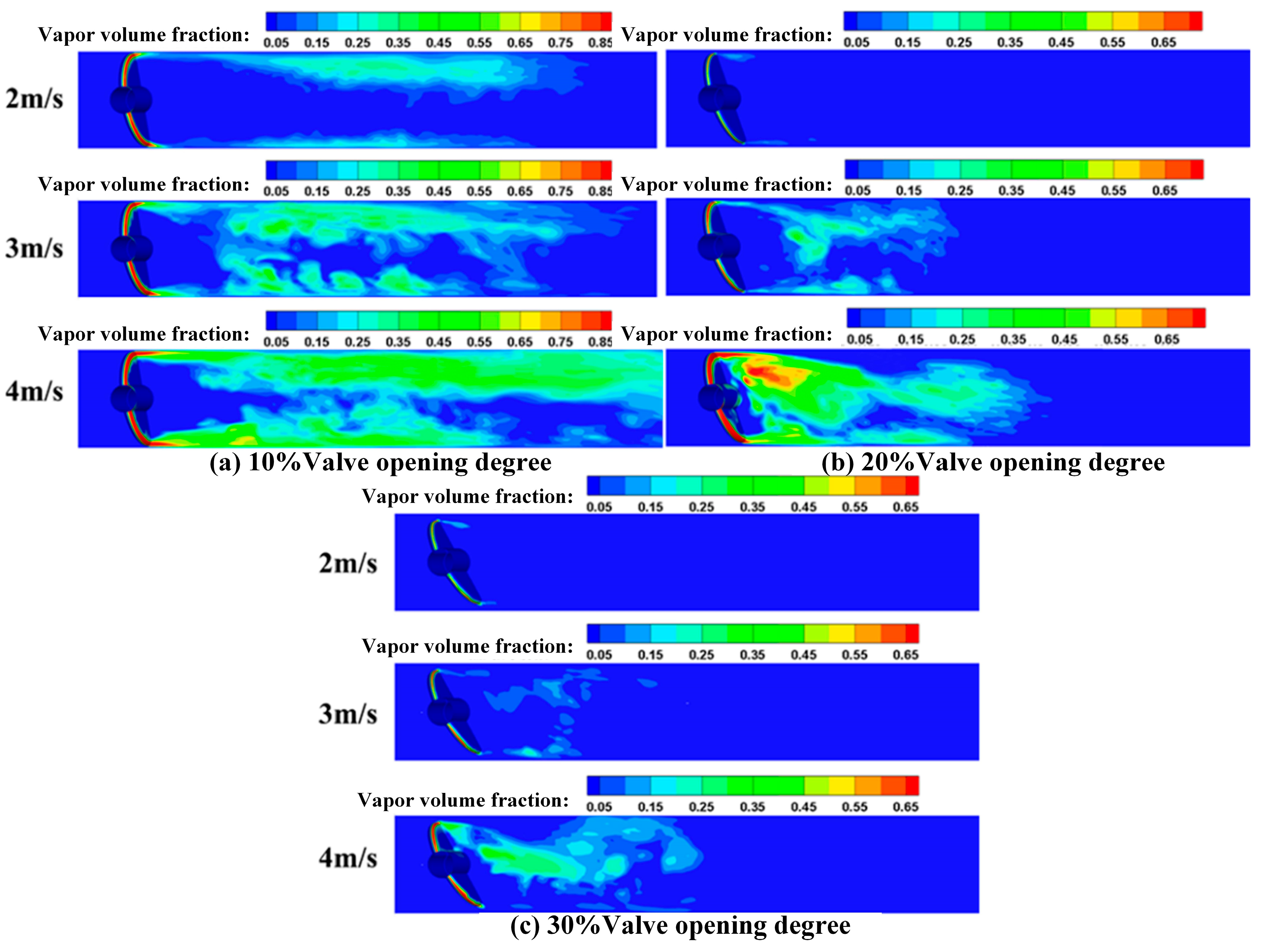
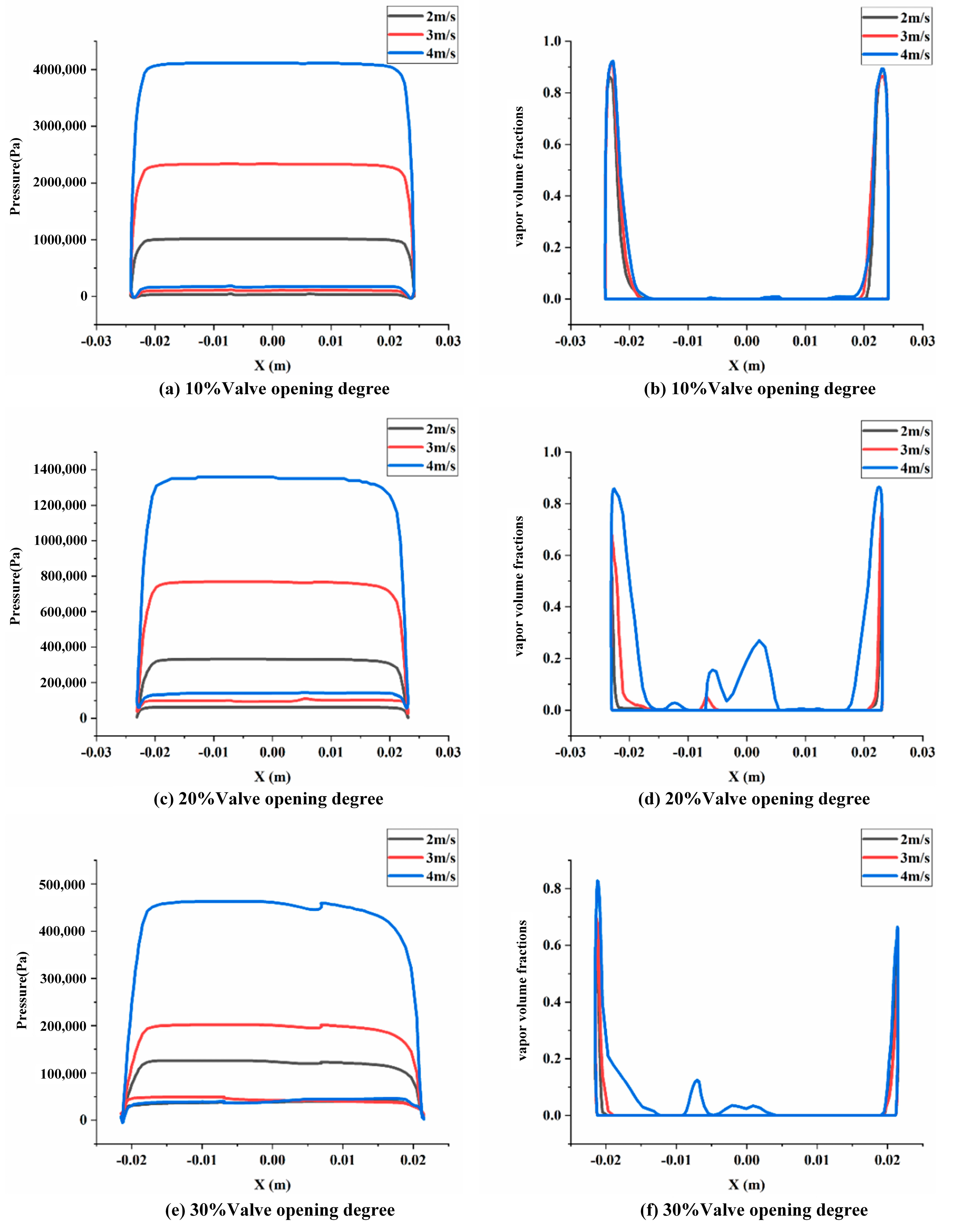
3.1. Cavitation Flow Field
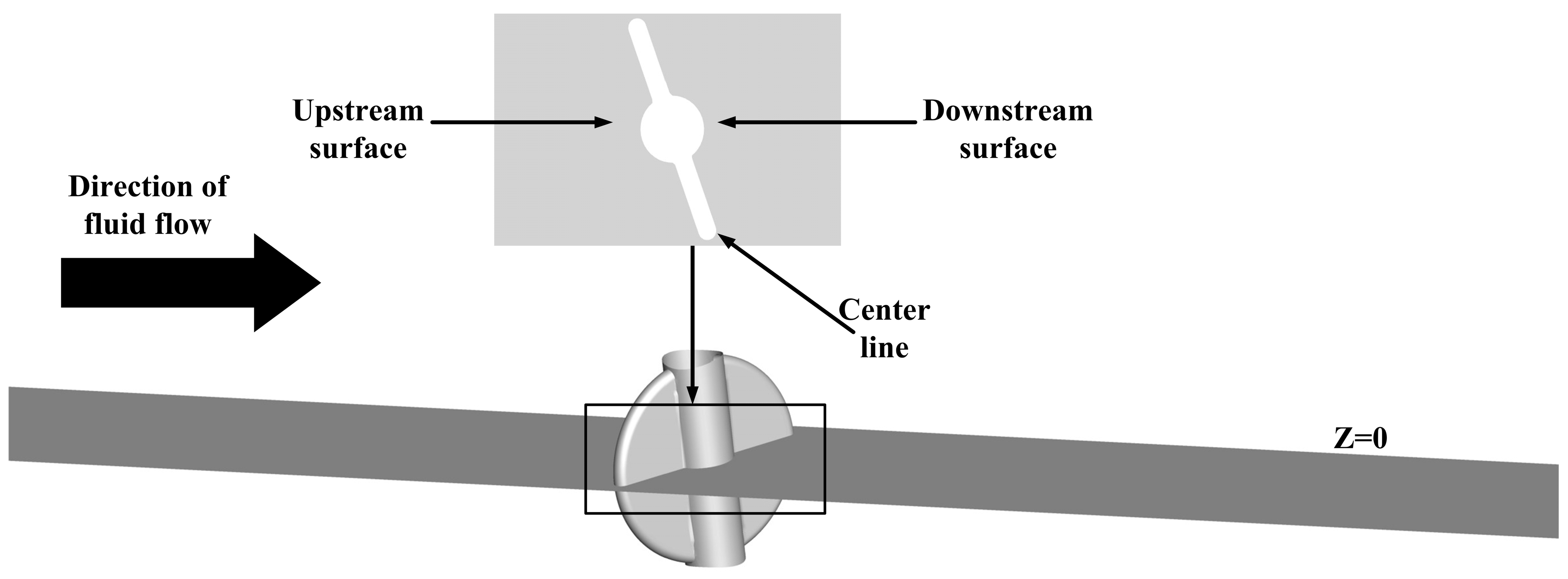
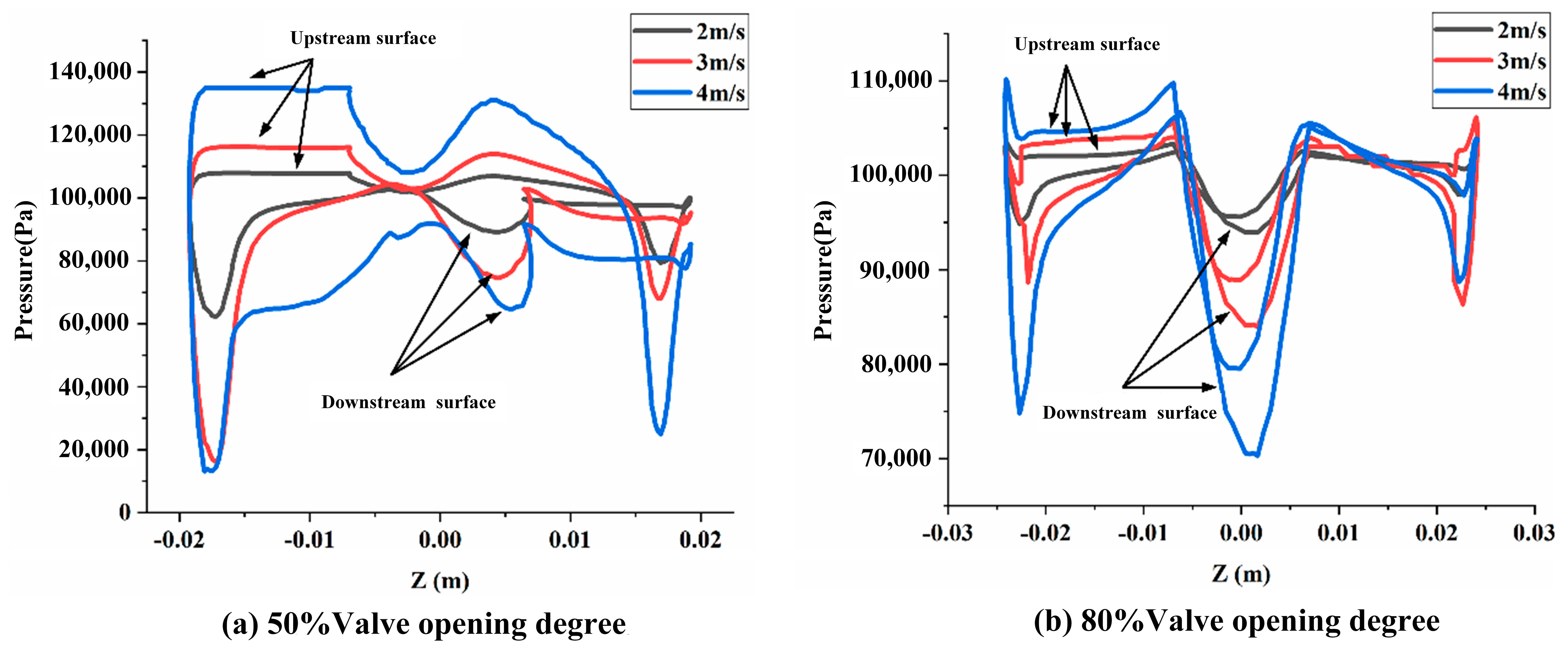
3.2. Interaction between Cavitation and Wall
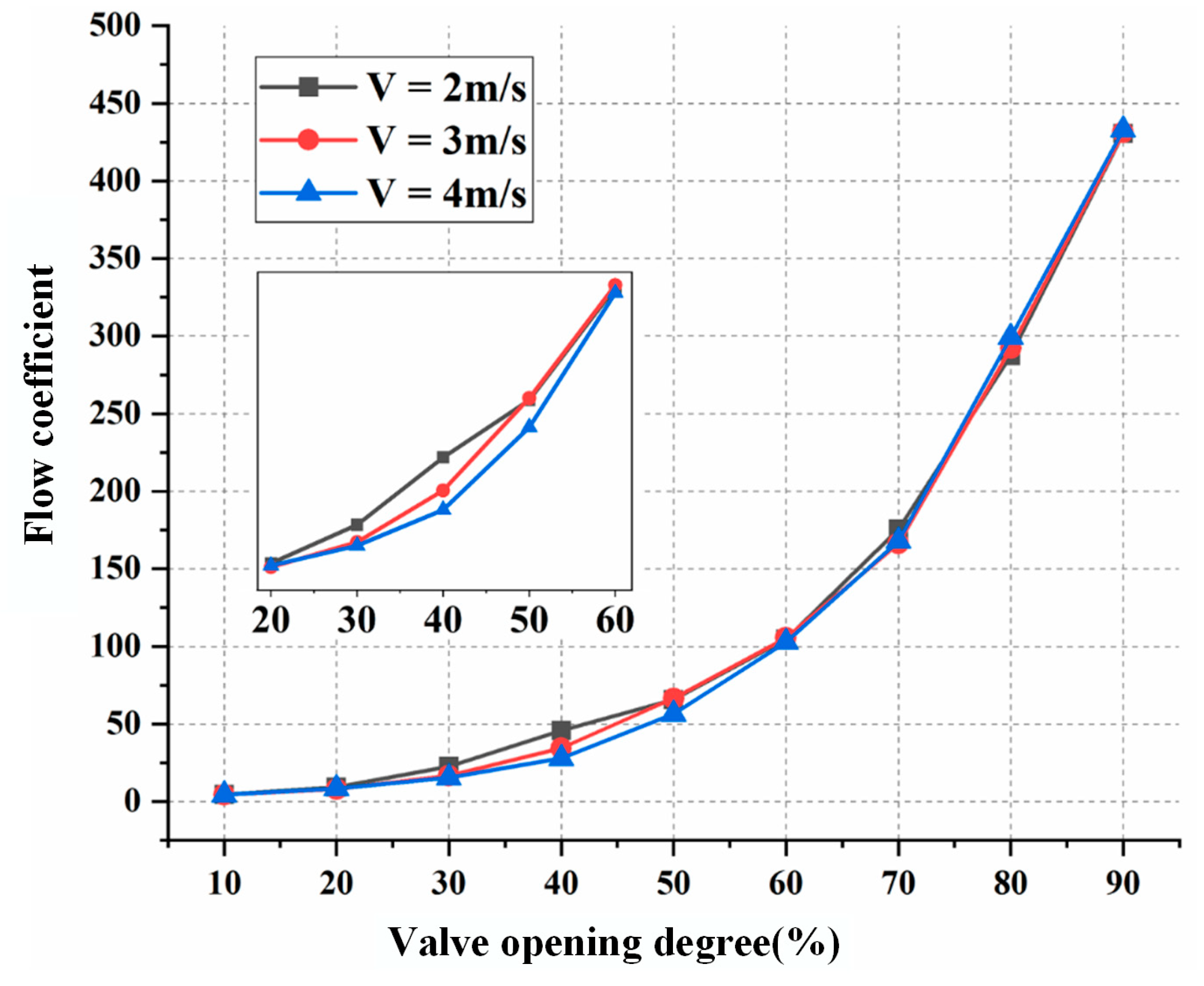
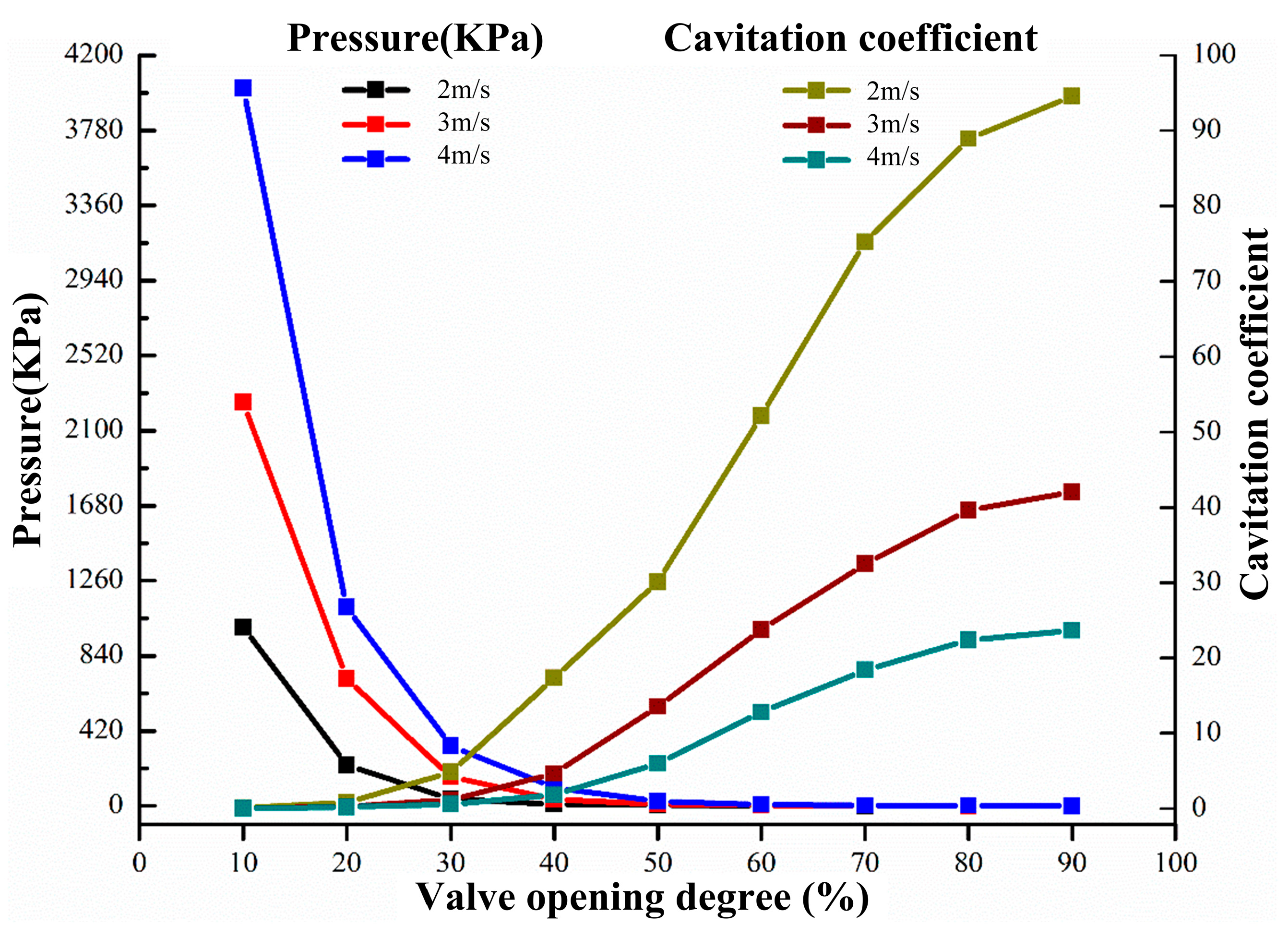
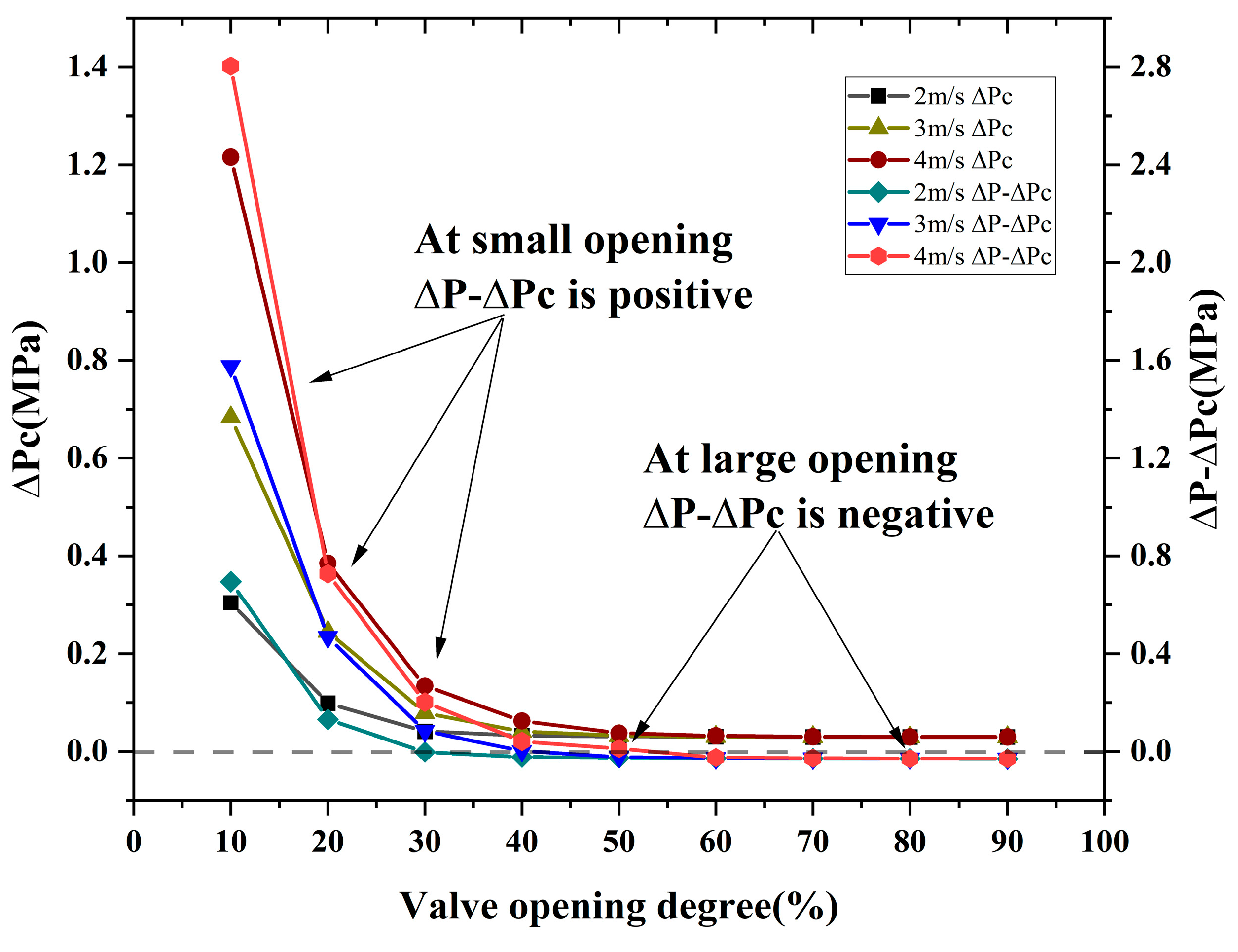
3.3. Correlation between Cavitation and Valve Performance
4. Conclusions
- (1)
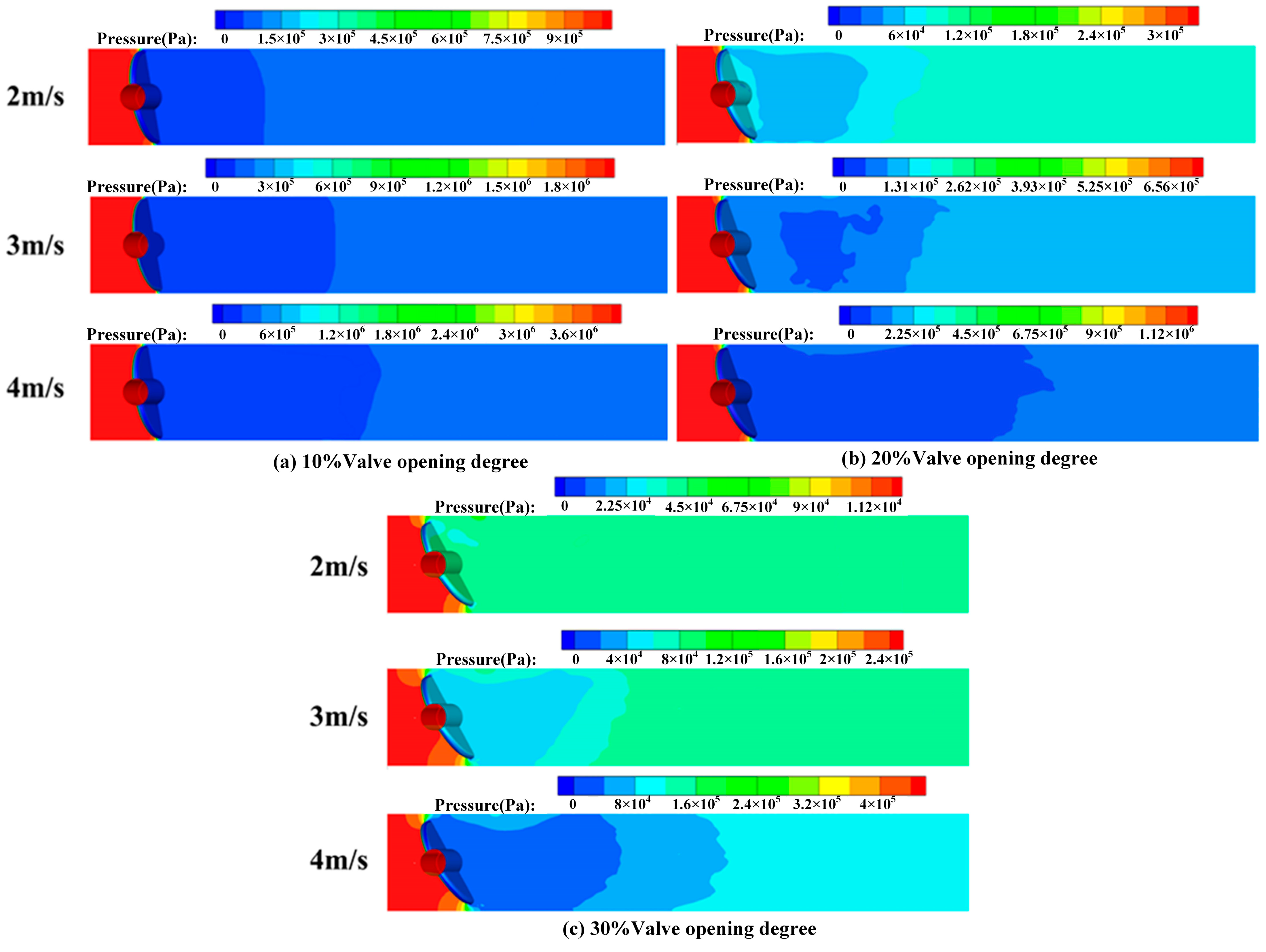
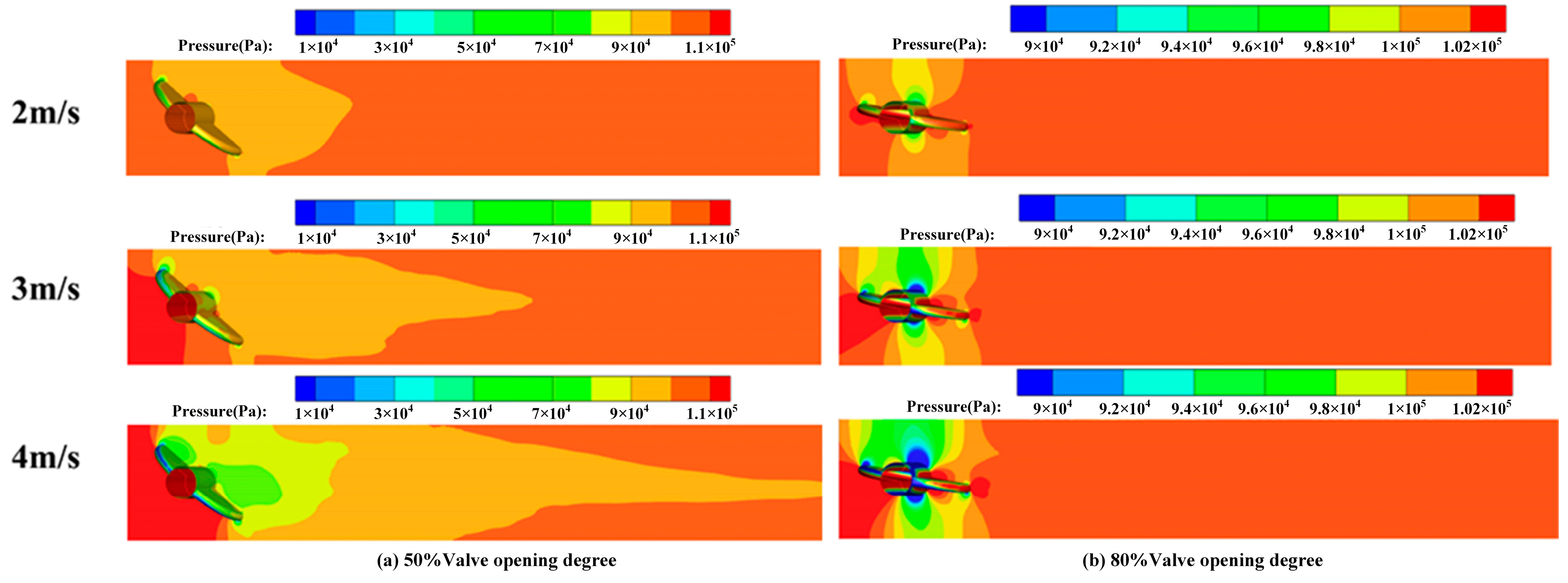
- The valve opening degree and inlet velocity have great effects on the cavitation generated in a butterfly valve. With the decrease in the valve opening degree and the increase in the inlet velocity, the vapor volume fraction increases. At smaller valve opening degrees, stronger high-speed jets and larger low-pressure areas are observed behind the valve plate, which are the main reasons that cavitation is induced in a butterfly valve. Cavitation tends to interact with the valve plate, primarily occurring at the rear end and shaft of the valve. As the valve opening degree increases, the interaction between cavitation and the valve plate becomes less obvious. However, the vapor volume fraction on the solid wall surface of the valve plate increases, with the highest vapor volume fraction occurring at the edge of the valve plate. As the velocity increases, the vapor volume also becomes wider. In addition, cavitation is always attached to the leading edge of the butterfly valve. This indicates that the inhibition of cavitation can be well improved by optimizing the structure of the leading edge of the valve plate.
- (2)
- Cavitation has an obvious influence on the operation performance of butterfly valves. With the increase in vapor volume, the flow coefficient gradually decreases. At smaller valve opening degrees, smaller cavitation numbers and a larger vapor volume are observed, and the flow coefficients are relatively smaller. In addition, the flow-blocking pressure difference is higher, which means most flow is blocked due to the existence of cavitation. As the inlet velocity increases under the same valve opening degree, the vapor volume becomes larger, and the flow coefficients become smaller, indicating that the operation performance of the butterfly valve becomes weaker. When the valve opening degree is larger than 50%, the flow coefficients are the same as those obtained at different inlet velocities because no cavitation is generated in the butterfly valve. As the valve opening degree increases, the flow coefficients gradually increase, and the flow capacity across the valve plate improves. In addition, the blocking effect becomes less obvious. Thus, it is suggested that under practical operating conditions, butterfly valves can work at relatively large valve opening degrees with high cavitation numbers. This condition can inhibit the generation of cavitation and raise the operation performance of butterfly valves.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Volume fraction | |
| Specific heat of water (J/(kg·K)) | |
| Diameter (m) | |
| Vaporization coefficient | |
| Condensation coefficient | |
| Force (N) | |
| Fluid specific gravity (m/s2) | |
| Velocity gradient tensor (1/s) | |
| Flow coefficient | |
| Mixing length of subgrid scale (m) | |
| Cavitation bubble density (kg/m3) | |
| Pressure (Pa) | |
| Mean pressure (Pa) | |
| Import and export pressure difference (Pa) | |
| Volume flow rate (m3/h) | |
| Radius (m) | |
| Reynolds number | |
| Strain-rate tensor (1/s) | |
| Components of the strain-rate tensor (1/s) | |
| Magnitude of the strain-rate tensor (1/s) | |
| Time (s) | |
| Velocity component (m/s) | |
| Mean velocities (m/s) | |
| Volume (m³) | |
| Flow velocity (m/s) | |
| Spatial coordinate component (m) | |
| Kinematic viscosity (m2/s) | |
| Cavitation coefficient | |
| Turbulent viscosity (Pa·s) | |
| Density (kg/m3) | |
| Reynolds stresses (Pa) | |
| Subscripts | |
| Cavitation bubbles | |
| -direction vector | |
| -direction vector | |
| -direction vector | |
| Liquid phase | |
| Mixture | |
| Vapor phase | |
| Inlet | |
| Outlet | |
References
- Wu, P.F.; Bai, L.X.; Lin, W.J. On the definition of cavitation intensity. Ultrason. Sonochem. 2020, 67, 105141. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, A.; Razaghian, A.H.; Tootian, A.; Seif, M.S. An experimental investigation of hydrodynamic performance, cavitation, and noise of a normal skew B-series marine propeller in the cavitation tunnel. Ocean Eng. 2021, 238, 109739. [Google Scholar] [CrossRef]
- Wang, Y.; Qing, Z.H. The flow field analysis and structure optimization of large diameter butterfly valve. Am. J. Mech. Ind. Eng. 2020, 5, 59–63. [Google Scholar]
- Rastogi, M.; Mueller, A.; Ben Haha, M.; Scrivener, K.L. The role of cavitation in drying cementitious materials. Cem. Concr. Res. 2022, 154, 106710. [Google Scholar] [CrossRef]
- Sarc, A.; Stepisnik-Perdih, T.; Petkovsek, M.; Dular, M. The issue of cavitation number value in studies of water treatment by hydrodynamic cavitation. Ultrason. Sonochem. 2017, 34, 51–59. [Google Scholar] [CrossRef]
- Dan, G.; Jiaxi, Y.; Lining, G. Review of the cavitation mechanism and prevention or enhancement. Mod. Phys. Lett. B 2022, 36, 8. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L. Collapsing characteristics of gas-bearing cavitation bubble. Res. Prog. Hydrodyn. Part B 2019, 31, 66–75. [Google Scholar] [CrossRef]
- Zhan, G.; Wang, W.X.; Bing, W. The effects of nanoscale nuclei on cavitation. J. Fluent Mech. 2021, 911, 20. [Google Scholar]
- Zhang, J. Flow characteristics of a hydraulic cone-throttle valve during cavitation. Ind. Lubr. Tribol. 2019, 71, 1186–1193. [Google Scholar] [CrossRef]
- Podnar, A.; Hocevar, M.; Novak, L. Analysis of Bulb Turbine Hydrofoil Cavitation. Appl. Sci. 2021, 11, 2639. [Google Scholar] [CrossRef]
- Wu, W.R.; Qiu, B.H.; Tian, G.T.; Liao, X.N.; Wang, T. CFD-Based Cavitation Research and Structure Optimization of Relief Valve for Noise Reduction. IEEE Access 2022, 10, 66356–66373. [Google Scholar] [CrossRef]
- Liu, J.B.; Liu, Z.M.; Wu, J.C.; Gu, X.L. Numerical Study on Cavitation Flow Characteristics in Diesel Fuel Injector Control Valve. Int. J. Automot. Technol. 2022, 23, 881–897. [Google Scholar] [CrossRef]
- Ren, R.; Su, T.X.; Ma, F.K.; Wu, X.J.; Xu, C.L.; Zhao, X. Study of the influence laws of the flow and cavitation characteristics in an injector control valve. Energy Sci. Eng. 2022, 10, 932–950. [Google Scholar] [CrossRef]
- Duan, A.Q.; Wang, C.; Xu, J.; Gao, S.Q.; Liu, X.F.; Jin, H.Z.; Ou, G.F. Experiment and numerical simulation investigation on cavitation evolution and damage in the throttling section of pressure reducing valve. Energy Sci. Eng. 2022, 10, 2348–2366. [Google Scholar] [CrossRef]
- Habibnejad, D.; Akbarzadeh, P.; Salavatipour, A.; Gheshmipour, V. Cavitation reduction in the globe valve using oblique perforated cages: A numerical investigation. Flow Meas. Instrum. 2022, 83, 102110. [Google Scholar] [CrossRef]
- Zhou, X.; Zhi, X.Q.; Gao, X.; Chen, H.; Zhu, S.L.; Wang, K.; Qiu, L.M.; Zhang, X.B. Cavitation evolution and damage by liquid nitrogen in a globe valve. J. Zhejiang Univ. Part A Appl. Phys. Eng. 2022, 23, 101–117. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Z.M.; Xu, H.C.; Li, J.L. Effects of throttling structures on cavitation flow and circumferential uniformity in a control valve. Eng. Fail. Anal. 2022, 134, 106025. [Google Scholar] [CrossRef]
- Hao, Q.H.; Wu, W.R.; Tian, G.T. Study on reducing both flow force and cavitation in poppet valves. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 11160–11179. [Google Scholar] [CrossRef]
- Wei, A.B.; Gao, R.G.; Zhang, W.; Wang, S.H.; Zhou, R.; Zhang, X.B. Computational fluid dynamics analysis on flow-induced vibration of a cryogenic poppet valve in consideration of cavitation effect. J. Zhejiang Univ. Part A Appl. Phys. Eng. 2022, 23, 83–100. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Z.Y.; Wu, K.X.; Ou, Y.Q.; Kim, H.D.; Lin, Z. Effect of the opening of a butterfly valve on the dynamic evolution of cavitation. J. Mech. Sci. Technol. 2022, 36, 3457–3467. [Google Scholar] [CrossRef]
- Sun, X.; You, W.B.; Xuan, X.X.; Ji, L.; Xu, X.T.; Wang, G.C.; Zhao, S.; Boczkaj, G.; Yoon, J.Y.; Chen, S.Y. Effect of the cavitation generation unit structure on the performance of an advanced hydrodynamic cavitation reactor for process intensifications. Chem. Eng. J. 2021, 412, 128600. [Google Scholar] [CrossRef]
- Baran, G.; Catana, I.; Magheti, I.; Safta, C.A.; Savu, M. Controlling the cavitation phenomenon of evolution on a butterfly valve. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012100. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, J.G.; Qian, J.H. Numerical analysis of cavitation erosion and particle erosion in butterfly valve. Eng. Fail. 2017, 80, 312–324. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Du, Y.X.; Liu, J.Q.; Sun, Y.R.; Yao, Z.F.; Zhong, Q. Experimental and numerical investigations of the collapse of a laser-induced cavitation bubble near a solid wall. Res. Prog. Hydrodyn. Part B 2022, 34, 189–199. [Google Scholar] [CrossRef]
- Kapranova, A.B.; Lebedev, A.E.; Gudanov, I.S.; Meltzer, A.M. Simulation of Cavitation Emerging When Throttling a Fluid Flow in a Butterfly Control Valve. J. Mech. Sci. Technol. 2022, 58, 473–482. [Google Scholar] [CrossRef]
- Maklakov, D. On the direction of the re-entrant jet and the limiting cavity flow configureurations. J. Fluent Mech. 2005, 936, 30. [Google Scholar] [CrossRef]
- Song, X.G.; Park, Y.C. Numerical Analysis of Butterfly Valve-Prediction of Flow Coefficient and Hydrodynamic Torque Coefficient. Lect. Notes Eng. Comput. Sci. 2007, 2167, 1. [Google Scholar]
- Ghahramani, E.; Arabnejad, M.H.; Bensow, R.E. Realizability improvements to a hybrid mixture-bubble model for simulation of cavitating flows. Comput. Fluids 2018, 174, 135–143. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive Equations. Mon. Weather. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow 2004, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]
- Sun, X.; Kim, H.S.; Yang, S.D.; Kim, C.K.; Yoon, J.Y. Numerical investigation of the effect of surface roughness on the flow coefficient of an eccentric butterfly valve. J. Mech. Sci. Technol. 2017, 31, 2839–2848. [Google Scholar] [CrossRef]
- Lopez Quesada, G.; Tatsios, G.; Valougeorgis, D.; Rojas-Cardenas, M.; Baldas, L.; Barrot, C.; Colin, S. Thermally driven pumps and diodes in multistage assemblies consisting of microchannels with converging, diverging and uniform rectangular cross sections. Microfluid. Nanofluidics 2020, 24, 54. [Google Scholar] [CrossRef]
- Long, Y.; Long, X.P.; Ji, B.; Xing, T. Verification and validation of Large Eddy Simulation of attached cavitating flow around a Clark-Y hydrofoil. Int. J. Multiph. Flow 2019, 115, 93–107. [Google Scholar] [CrossRef]
- Sun, X.; Yang, Z.; Wei, X.S.; Tao, Y.; Boczkaj, G.; Yoon, J.Y.; Xuan, X.X.; Chen, S.Y. Multi-objective Optimization of the Cavitation Generation Unit Structure of an Advanced Rotational Hydrodynamic Cavitation Reactor. Ultrason. Sonochem. 2021, 80, 105771. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Value |
|---|---|
| Pipe diameter (mm) | 50 |
| Valve opening degree (%) | 10, 20, 30, 50, 80 |
| Velocity inlet (m/s) | 2, 3, 4 |
| Pressure outlet (Pa) | 101,325 |
| Openings Degree | 2 m/s | 3 m/s | 4 m/s |
|---|---|---|---|
| 10% | 833,845.03 | 2,265,957.61 | 4,021,751.72 |
| 20% | 323,608.78 | 724,987.59 | 1,272,218.81 |
| 30% | 117,440.53 | 206,866.85 | 444,751.03 |
| 50% | 105,690.52 | 110,871.28 | 117,850.51 |
| 80% | 101,511.01 | 101,619.41 | 102,138.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Hu, R.; Yin, D.; Chen, D.; Zhou, H.; Lin, Z. Numerical Study of Cavitation Characteristics through Butterfly Valve under Different Regulation Conditions. Processes 2024, 12, 686. https://doi.org/10.3390/pr12040686
Zhang G, Hu R, Yin D, Chen D, Zhou H, Lin Z. Numerical Study of Cavitation Characteristics through Butterfly Valve under Different Regulation Conditions. Processes. 2024; 12(4):686. https://doi.org/10.3390/pr12040686
Chicago/Turabian StyleZhang, Guang, Runhua Hu, Dapeng Yin, Desheng Chen, Haolin Zhou, and Zhe Lin. 2024. "Numerical Study of Cavitation Characteristics through Butterfly Valve under Different Regulation Conditions" Processes 12, no. 4: 686. https://doi.org/10.3390/pr12040686
APA StyleZhang, G., Hu, R., Yin, D., Chen, D., Zhou, H., & Lin, Z. (2024). Numerical Study of Cavitation Characteristics through Butterfly Valve under Different Regulation Conditions. Processes, 12(4), 686. https://doi.org/10.3390/pr12040686






