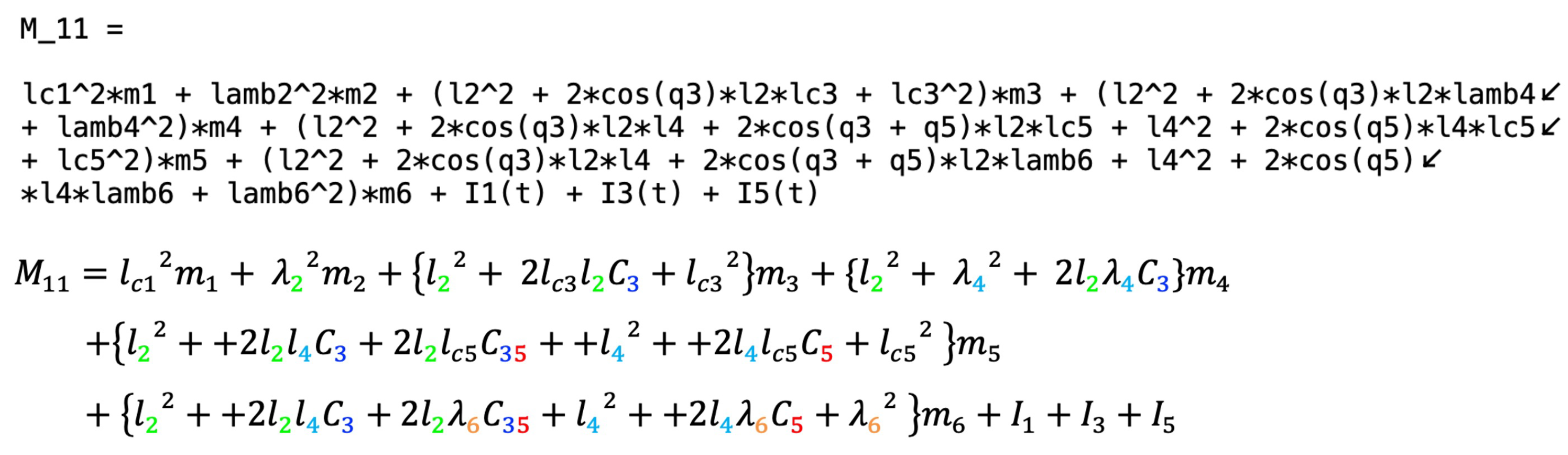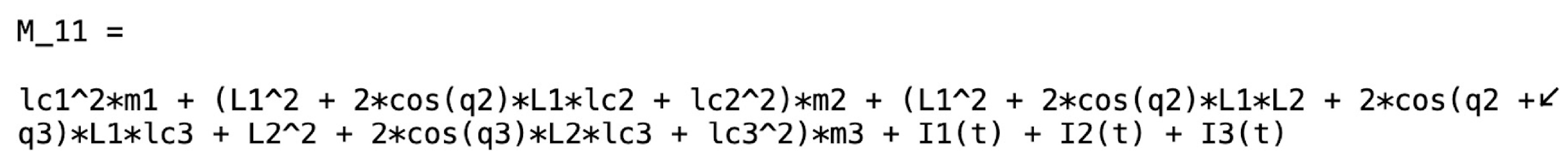Automated Symbolic Processes for Dynamic Modeling of Redundant Manipulator Robots

Abstract

In this study, groundbreaking software has been developed to automate the generation of equations of motion for manipulator robots with varying configurations and degrees of freedom (DoF). The implementation of three algorithms rooted in the Lagrange–Euler (L-E) formulation is achieved through the utilization of .m files in MATLAB R2020a software.This results in the derivation of a symbolic dynamic model for industrial manipulator robots. To comprehend the unique features and advantages of the developed software, dynamic simulations are conducted for two 6- and 9-DoF redundant manipulator robots as well as for a 3-DoF non-redundant manipulator robot equipped with prismatic and rotational joints, which is used to simplify the dynamic equations of the redundant prototypes. Notably, for the 6-DoF manipulator robot, model predictive control (MPC) is employed using insights gained from the dynamic model. This enables optimal control by predicting the future evolution of state variables: specifically, the values of the robot’s joint variables. The software is executed to model the dynamics of different types of robots, and the CPU time for a MacBook Pro with a 3 GHz Dual-Core Intel Core i7 processor is less than a minute. Ultimately, the theoretical findings are validated through response graphs and performance indicators of the MPC, affirming the accurate functionality of the developed software. The significance of this work lies in the automation of motion equation generation for manipulator robots, paving the way for enhanced control strategies and facilitating advancements in the field of robotics.

1. Introduction

Manipulator robots are complex mechanisms, and their mathematical modeling has always been a crucial aspect, especially when considering dynamic phenomena. In recent decades, dynamic modeling of classical industrial manipulator robots has been the subject of unprecedented attention [1] because it is critical for mechanical design and is of paramount importance for controller simulation and implementation [2,3]. This area of study has not only focused on robotic arms but also on other types of robot morphologies, such as wheeled mobile robots [4], space robots [5], submarine robots [6], flexible robots [7], and parallel manipulator robots [8].

Deep understanding of the dynamic characteristics of a manipulator robot is fundamental for practical robot applications. Many of these applications require, for example, effective trajectory tracking capacities that—to improve their performance—should consider a dynamic model of a manipulator robot [9,10,11]. Knowledge and modeling of a manipulator robot’s dynamics are crucial for the optimal performance of its control strategies (based on the robot model), such as inverse dynamic control, calculated torque control, and model predictive control [12,13,14]. An effective dynamic model together with a robust controller not only allow for the optimal design of the trajectory planning scheme but also for the safe and accurate maneuvering of the manipulator robot when getting close to the grip point of an object [15,16]. Controllers that consider the dynamic behavior of manipulator robots are faster, more dexterous, and more efficient as well as smoother in tracking than static controllers [17]. Knowing the dynamics can guide both the design and construction of robot systems, including the selection of their actuators and transmission components to initiate motion. Particularly, dynamic equations play an important role in real-time control applications, as they help determine the forces/torques necessary to generate the desired trajectories (position, velocity, and acceleration) [18].

MPC controllers are a promising candidate for handling constraints and enhancing system robustness. However, the convergence of the system cannot be assured in the face of the uncertainty of the modeling procedure, which significantly influences the execution of the MPC. Several current works have included a robot manipulator model in the construction of this type of controller; however, they have had to incorporate adaptive mechanisms to the controller mainly due to imprecise models or external disturbances. For example, in [19], a sliding-mode-based MPC with an auxiliary controller based on a node-adaptive neural network is constructed to dynamically compensate for nonlinear uncertain dynamics and to enhance the trajectory tracking of a robotic manipulator with state constraints. Similar work was carried out in [20], wherein a linear extended-state observer (LESO)-based MPC was proposed for high-precision trajectory tracking of space robotic manipulators. Particularly, the LESO was designed to minimize the impact of the inaccuracies in the dynamic model. In [21], the impact of external noise and imprecise models on the system performance is eliminated through a radial basis function neural network (RBFNN) integrated into a Lyapunov-based MPC (LMPC) strategy for dual-arm manipulators. Therefore, in these types of model-based control strategies, it is crucial to have accurate dynamic models in order to improve system performance and/or to avoid adding components from other control methods.

Usually, equations of motion are described in the 3D Euclidean space, which rapidly produces a great quantity of equations for connected body systems. Due to the need to design and implement systems that operate in real-time, especially in terms of controllers, the robotics community has focused on the computational efficiency problem. In the literature, several Information Technology (IT) programs for modeling the dynamics of robots with different capacities and properties have been proposed, and most of them are based on numerical calculations (instead of symbolic calculations) [22]. The concept “symbolic” is used in robotics when the dynamics of manipulator robots are described by symbolic expressions using symbolic variables that do not have numerical values. A symbolic calculation program is more powerful than a numerical one, since, from a design perspective, a symbolic representation is easier to analyze when verifying, for example, the influence of parameters such as mass or length of the links in the model [23]. In general, the execution of a simulation based on a symbolic (exact) model is faster than that based on a numerical model. In addition, from a research point of view, symbolic programming allows for using some special control approaches that are impossible to address through a numerical model [24].

Specifically, to generate the dynamic equations of a manipulator robot in symbolic form, simulation programs are used, which include algebraic systems and advanced algorithms that minimize computational costs and reorganize calculations in a smart way. Dynamic methods can be mainly divided into two types: explicit and recursive. These procedures include the recursive Lagrange method, the generalized D’Alembert principle, the Kane method, the recursive Newton–Euler algorithm (RNEA), and the Lagrange–Euler formulation (L-E) [25,26,27].

More than four decades ago, researchers started to focus on developing software to generate the dynamic representation of manipulator robots. In [28], an open source program is presented—namely, Dynamic Models of Industrial Robots (DYMIR)—which uses the Lagrangian formulation, kinematic description, and some characteristics of a system based on the LISt Processor (LISP) to perform the symbolic calculation of dynamic models with up to 12 degrees of freedom (DoF). Another computer program based on LISP and the C language, the Algebraic Robot Modeler (ARM), was implemented to generate the model’s components in a symbolic form—namely, the inertial, centripetal, Coriolis, and gravitational parts of a Lagrangian dynamic model—using a special Q matrix formulation [29]. Additionally, the Robotic Toolbox for MATLAB provides numerical calculations of inverse dynamics employing the Newton–Euler recursive formula. In its library, this program only includes PUMA (Programmable Universal Manipulation Arm) and Stanford industrial manipulator robots as examples [30].

During recent decades, the MATLAB software has enabled the implementation of the Planar Manipulators Toolbox program for modeling and simulating the dynamics of planar manipulator robots with n-DoF and which include only rotary joints. Using this program, dynamic equations are obtained from the Lagrange–Euler formulation [31]. In addition, other computer programs have been created for robot systems, but these were conceived to adequately study the dynamics of serial manipulator robots, and their use is limited by the number of DoF of the robot [32,33]. Recently, some works have incorporated the use of computer programs for the automatic generation of kinematic and dynamic models. Among these, the Hybrid Robot Dynamics (HyRoDyn) software stands out; its application in the dynamic modeling of series–parallel hybrid robots is based on previous knowledge of the modeling of submechanisms that are already available in its library [34]. In turn, the MATLAB software allows for obtaining, in a symbolic form, a dynamic model of two collaborative robots: Kinova Gen2 and Kuka LWR4+ with 7-DoF; for these two types of robots, users should input the Denavit–Hartenberg (D-H) parameters and the vector parameters of the robots into a script .m file [35]. Additionally, a Unified Robot Description Format (URDF) file created in the SolidWorks software allows for calculating dynamic models of non-conventional robot configurations of n-DoF. However, continuously modeling new configurations in computer-assisted design (CAD) software is not time efficient [36].

Based on the aforementioned research, it is inferred that most authors propose a numerical solution (instead of a symbolic one) to solve the dynamic problem of manipulator robots. Existing software programs that do focus on generating symbolic models have several strengths (already highlighted above) but also some weaknesses, such as limitations to the maximum number of DoF and/or omission of the robot’s prismatic joints, slow response time of the program for displaying the desired dynamic models, limited library of available robots, and a request for input information that sometimes is not intuitive and which implies more interaction time with the user. Currently, all programs that have been designed have one or more of these weaknesses. The motivation for this research is to create software that eliminates all the above shortcomings and, additionally, facilitates the construction of mathematical models, optimizes the implementation of simulators, and ensures the correct operation of control systems. Thanks to the creation of this software, errors inherent in the manipulation of complex dynamic equations are avoided, and more reliable dynamic models are obtained in real-time. The main contributions of this article are listed below.

• In Section 3, novel software for the automatic generation of robot dynamic models in a symbolic form is developed, specifically for n-DoF industrial manipulator robots with varying configurations. Section 4 presents examples of manipulator robot dynamics generated by the program, particularly for the 3-, 6-, and 9-DoF robot arms that have been calculated manually in Section 2. The dynamics of a 3-DoF non-redundant manipulator robot equipped with prismatic and rotational joints are used to simplify the equations of the redundant prototypes;
• In Section 4, an intuitive graphical user interface (GUI) in MATLAB is written. Through this interface, the user can select the joint variables (rotational or prismatic) and interactively change the manipulator robot model using editing boxes. The combination of rotational and prismatic joints generates an infinite number of manipulator robot configurations.
• In Section 5, an MPC-based control strategy for the 6-DoF redundant manipulator robot is proposed. This controller and the generated dynamic model are implemented in the MATLAB/Simulink environment to conduct dynamic simulations and to validate the theoretical results. Finally, the correct operation, characteristics, and ease-of-use of the software are confirmed.

2. Dynamics of Robotic Manipulators

The dynamic equations of an n-DoF manipulator robot are derived based on the Lagrange–Euler formulation. The standard form (matrix–vector) of the dynamics is presented in Equation (1) [37,38,39]:

$$\mathbf{M}\left(\mathbf{p}\right)\ddot{\mathbf{p}}+\mathbf{C}(\mathbf{p},\dot{\mathbf{p}})\dot{\mathbf{p}}+\mathbf{g}\left(\mathbf{p}\right)+\mathbf{f}\left(\dot{\mathbf{p}}\right)+{\mathit{\tau }}_0=\mathit{\tau }$$

(1)

where $\mathbf{p},\ddot{\mathbf{p}},\ddot{\mathbf{p}}\in {\mathbb{R}}^n$ are the generalized position, velocity, and acceleration vectors, respectively; $\mathbf{M}\in {\mathbb{R}}^{n\times n}$ is the symmetric positive-definite inertia (generalized mass) matrix; $\mathbf{C}\in {\mathbb{R}}^{n\times n}$ is the damping, Coriolis, and centripetal forces matrix; $\mathbf{g}\in {\mathbb{R}}^n$ is the gravitational forces vector; $\mathbf{f}\in {\mathbb{R}}^n$ is the friction forces vector; ${\mathit{\tau }}_{\mathbf{0}}$$\in {\mathbb{R}}^n$ is the external disturbances and uncertainties vector of the system parameters; and $\mathit{\tau }$$\in {\mathbb{R}}^n$ is the control input vector (consisting of forces and torques exerted by the actuators).

As a result of the rotational and linear motion of the joints of a manipulator robot, additional forces known as Coriolis and centripetal forces are generated. These forces represent the $jk$-th element that forms the matrix $\mathbf{C}(\mathbf{p},\dot{\mathbf{p}})$ and are calculated through Equation (2) [40]:

$$C_{jk}(\mathbf{p},\dot{\mathbf{p}})=\sum _{i=1}^n{C}_{ij}^k\left(\mathbf{p}\right)\dot{p_i}$$

(2)

where $\dot{p_i}$ is the i-th component of the generalized velocity vector, and $C_{ij}^k\left(\mathbf{p}\right)$ are the Christoffel symbols (coefficients) of the first kind described by Equation (3) [41]:

$$C_{ij}^k\left(\mathbf{p}\right)=\frac{1}{2}\left(\frac{\partial M_{ki}}{\partial p_j}+\frac{\partial M_{kj}}{\partial p_i}-\frac{\partial M_{ij}}{\partial p_k}\right)$$

(3)

where $M_{ij}\left(\mathbf{p}\right)$ is the $ij$-th element from the mass matrix $\mathbf{M}\left(\mathbf{p}\right)$, and $p_i$ is the i-th component of the generalized position vector. Using Equations (2) and (3), the damping, centripetal, and Coriolis forces vector $\mathbf{c}(\mathbf{p},\dot{\mathbf{p}})$ presented in Equation (4) is obtained.

$$\mathbf{c}(\mathbf{p},\dot{\mathbf{p}})=\mathbf{C}(\mathbf{p},\dot{\mathbf{p}})\dot{\mathbf{p}}=\left[c_{i{1}_{(n-DoF)}}\right]$$

(4)

where $c_{i{1}_{(n-DoF)}}$ is the $i1$-th component of the $\mathbf{c}(\mathbf{p},\dot{\mathbf{p}})$ vector corresponding to an n-DoF robot, with $i=1,\dots ,n$.

The gravity force $g_j\left(\mathbf{p}\right)$ on the j-th robot joint (component of the vector $\mathbf{g}\left(\mathbf{p}\right)$) is obtained through Equation (5) [42]:

$$g_j\left(\mathbf{p}\right)=\sum _{i=1}^n{m}_i{\mathbf{g}}_r^{\mathrm{T}}·{\mathbf{J}}_{vij}$$

(5)

where ${\mathbf{J}}_{vij}$ is the vector of the j-th column of the Jacobian matrix for linear speed ${\mathbf{J}}_{vi}$ corresponding to the i-th link of the manipulator robot, and ${\mathbf{g}}_r$, defined in Equation (6), corresponds to gravitational acceleration:

$${\mathbf{g}}_r={\left[00g\right]}^{\mathrm{T}}$$

(6)

The vector of friction forces $\mathbf{f}\left(\dot{\mathbf{p}}\right)$ of the manipulator robot is given by Equation (7):

$$\mathbf{f}\left(\dot{\mathbf{p}}\right)=\left[F_{vi}\right]\dot{\mathbf{p}}$$

(7)

where $F_{vi}$ are the friction coefficients of the manipulator robot’s joints, with $i=1,\dots ,n$.

A dynamic model of the actuators is not considered in the modeling process nor in the simulations below.

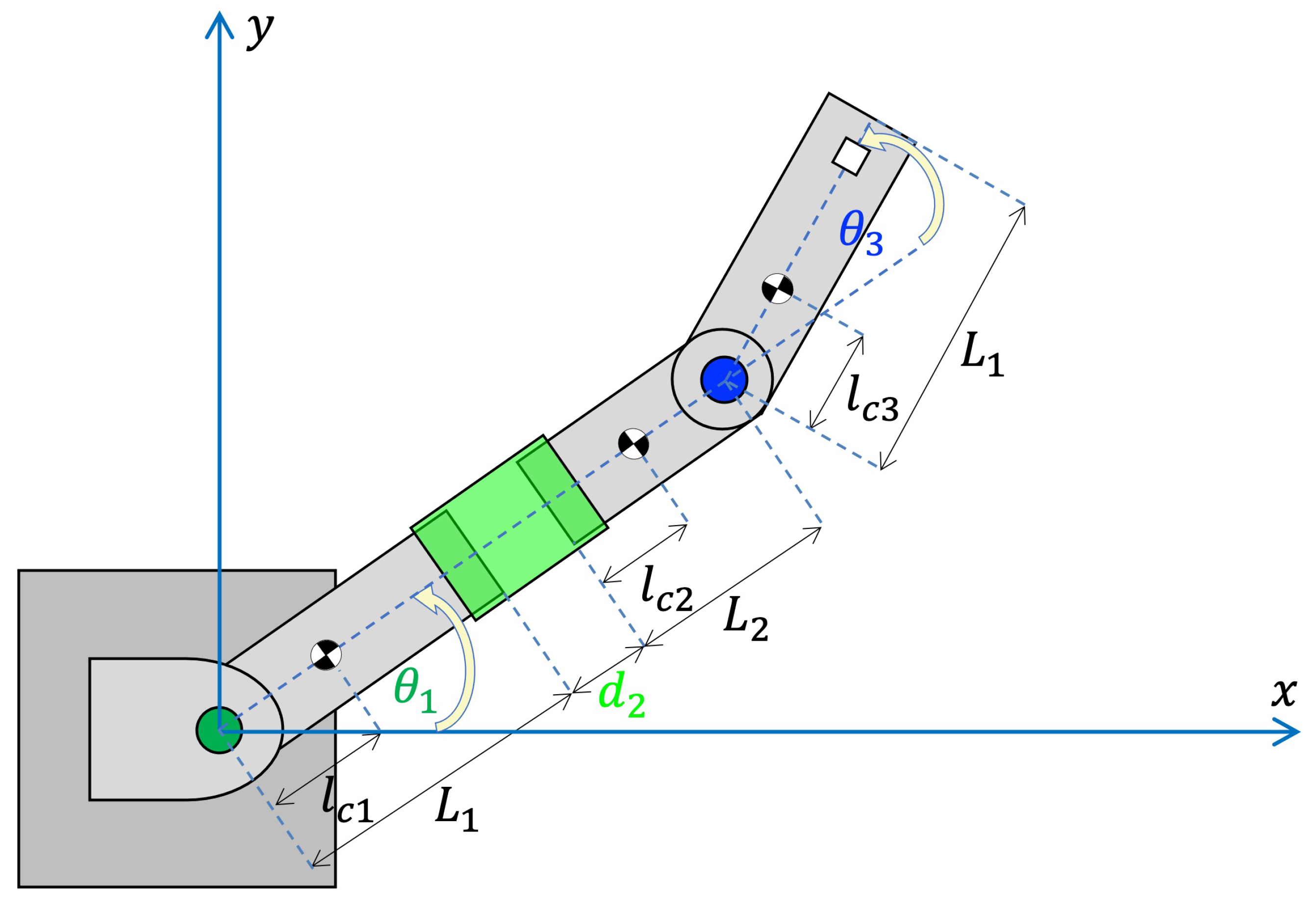
2.1. Description and Dynamic Modeling of a 3-DoF Planar Manipulator Robot

Figure 1 shows the structure of a 3-DoF planar manipulator robot with an RPR (Rotational–Prismatic–Rotational) configuration. The robot has two articulated arms composed of two links that rotate in the x−y plane and one link that translates (moves linearly) in the same plane to create a 2D serial rigid-link manipulator. The first rotational joint ${\theta }_1$, assembles the fixed base and the first arm; the second prismatic joint $d_2$, between links 1 and 2, elongates/shrinks the first arm; and the third rotational joint ${\theta }_3$, between links 2 and 3, assembles both arms. For motion control, the dynamic equations of the mechanism are conveniently described by the Lagrange–Euler formulation represented in the joint-space form. Vectors $\mathbf{f}\left(\dot{\mathbf{p}}\right)$ and ${\mathit{\tau }}_{\mathbf{0}}$ are not considered in the modeling process of this planar robot.

where $L_1$ is the length of the first and third link; $L_2$ is the length of the second link; and $l_{ci}$ is the length from the origin of link i to its centroid of $i=1,2,3$ mass.

The elements of the mass matrix, $\mathbf{M}\left(\mathbf{p}\right)$ are:

$$M_{{11}_{(3-DoF)}}=I_1+I_3+m_1{l_{c1}}^2+m_2{{\lambda }_2}^2+m_3[{l_2}^2+{l_{c3}}^2+2l_2{l}_{c3}{c}_3]$$

(8)

$$\begin{array}{c}{M}_{{12}_{(3-DoF)}}=M_{{21}_{(3-DoF)}}=M_{{23}_{(3-DoF)}}=M_{{32}_{(3-DoF)}}=-m_3{l}_{c3}{s}_3\hfill \end{array}$$

(9)

$$\begin{array}{c}{M}_{{13}_{(3-DoF)}}=M_{{31}_{(3-DoF)}}=I_3+m_3[{l_{c3}}^2+l_2{l}_{c3}{c}_3]\hfill \end{array}$$

(10)

$$\begin{array}{c}{M}_{{22}_{(3-DoF)}}=m_2+m_3\hfill \end{array}$$

(11)

$$\begin{array}{c}{M}_{{33}_{(3-DoF)}}=I_3+m_3{l_{c3}}^2\hfill \end{array}$$

(12)

The elements of the Coriolis–centripetal forces matrix $\mathbf{C}(\mathbf{p},\dot{\mathbf{p}})$ are:

$$C_{{11}_{(3-DoF)}}=[m_2{\lambda }_2+m_3(l_2+l_{c3}{c}_3)]\dot{d_2}-m_3\left[l_{c3}{l}_2{s}_3\right]{\dot{\theta }}_3$$

(13)

$$C_{{12}_{(3-DoF)}}=[m_2{\lambda }_2+m_3(l_2+l_{c3}{c}_3)]{\dot{\theta }}_1$$

(14)

$$C_{{13}_{(3-DoF)}}=-m_3\left[l_{c3}{l}_2{s}_3\right]({\dot{\theta }}_1+{\dot{\theta }}_3)$$

(15)

$$C_{{21}_{(3-DoF)}}=-[m_2{\lambda }_2+m_3(l_2+l_{c3}{c}_3)]\dot{{\theta }_1}-m_3\left[l_{c3}{c}_3\right]\dot{{\theta }_3}$$

(16)

$$C_{{22}_{(3-DoF)}}=C_{{33}_{(3-DoF)}}=0$$

(17)

$$C_{{23}_{(3-DoF)}}=-m_3{l}_{c3}{c}_3(\dot{{\theta }_1}+\dot{{\theta }_3})$$

(18)

$$C_{{31}_{(3-DoF)}}=m_3\left[l_2{l}_{c3}{s}_3\right]\dot{{\theta }_1}+m_3\left[l_{c3}{c}_3\right]\dot{d_2}$$

(19)

$$C_{{32}_{(3-DoF)}}=m_3\left[l_{c3}{c}_3\right]\dot{{\theta }_1}$$

(20)

Considering that gravitational acceleration acts in the negative direction of the y-axis, i.e., ${\mathbf{g}}_r={[0-g]}^{\mathrm{T}}$, the components of the gravity forces vector are:

$$g_1=m_{1}g{l}_{c1}{c}_1+m_{2}g{\lambda }_2{c}_1+m_{3}g(l_{c3}+l_2)c_{13}$$

(21)

$$g_2=(m_2+m_3)g{s}_1$$

(22)

$$g_3=m_{3}g{l}_{c3}{c}_{13}$$

(23)

with $c_1=cos\left({\theta }_1\right)$, $c_3=cos\left({\theta }_3\right)$, $s_1=sin\left({\theta }_1\right)$, $s_3=sin\left({\theta }_3\right)$, $c_{13}=cos({\theta }_1+{\theta }_3)$, ${\lambda }_2=L_1+d_2+l_{c2}$, and $l_2=L_1+d_2+L_2$; where $l_2$ is the length of the first arm (m); $m_i$ is the i-th link mass (kg), $i=1,2,3$; and $I_j$ is the j-th link inertia moment with respect to the first z-axis of its joint (kg· m²), $j=1,3$.

2.2. Description and Dynamic Modeling of a 6-DoF Planar Manipulator Robot

As a second example, a 6-DoF planar manipulator robot with an RPRPRP (Rotational–Prismatic–Rotational–Prismatic–Rotational–Prismatic) configuration is considered. Figure 2 shows a 9-DoF non-planar manipulator robot, for which only the first 6-DoF were included in the dynamic model after neglecting the degrees of freedom in the robot’s end-effector. The robot has three articulated arms composed of six links in total that rotate and translate in the same plane x−y. Rotational and prismatic joints are responsible for assembling and elongating/shrinking the robot’s arms, respectively.

The dynamic model for the RPRPRP mechanism inherits the RPR robot dynamics model derived from Section 2.1. For the sake of space and conciseness, the mass matrix $\mathbf{M}$($\mathbf{p}$), Coriolis–centripetal matrix terms in $\mathbf{C}$($\mathbf{p}$,$\dot{\mathbf{p}}$), as well as the gravity matrix $\mathbf{g}$($\mathbf{p}$) as derived by the authors for the 6-DoF robot dynamics are stored at https://dynamics.6-DoF.robot for reference.

2.3. Description and Dynamic Modeling of a 9-DoF Non-Planar Manipulator Robot

As a third example, a 9-DoF non-planar manipulator robot with an RPRPRPPRR (Rotational–Prismatic–Rotational–Prismatic–Rotational–Prismatic-Prismatic–Rotational– Rotational) configuration is considered, as shown in Figure 2. The robot has four arms in total, with six links that rotate/translate in the x−y plane and three links out-of-plane to create a 3D rigid-link redundant manipulator. The seventh prismatic joint, $d_7$, between links 6 and 7, elongates/shrinks the fourth robot arm, and the last two rotational joints, ${\theta }_8$ and ${\theta }_9$, position the end-effector in x−y−z space in a pitch–roll way. The dynamic model for the RPRPRPPRR mechanism inherits the RPRPRP robot dynamics model derived from Section 2.2.

The elements of the mass matrix $\mathbf{M}\left(\mathbf{p}\right)$, the components of the Coriolis–centripetal forces vector $\mathbf{c}(\mathbf{p},\dot{\mathbf{p}})$, and the components of the gravity forces vector $\mathbf{g}$($\mathbf{p}$) of the 9-DoF manipulator robot are presented in extenso in Appendix A. All these calculations (Equations (8) and (A40))will be conducted manually to validate the correct operation of the proposed software for planar, non-planar, and multiple-DoF manipulator robots.

Figure 2. Diagram of a pitch–roll type 9-DoF non-planar manipulator robot considering the location of the centroids.

Figure 2. Diagram of a pitch–roll type 9-DoF non-planar manipulator robot considering the location of the centroids.

where $L_j$ is the length of link j (m), $j=7,8,9$; and $l_{ci}$ is the length from the origin of link i to its centroid of $i=1,2,3,4,5,6,7,8,9$ mass (m).

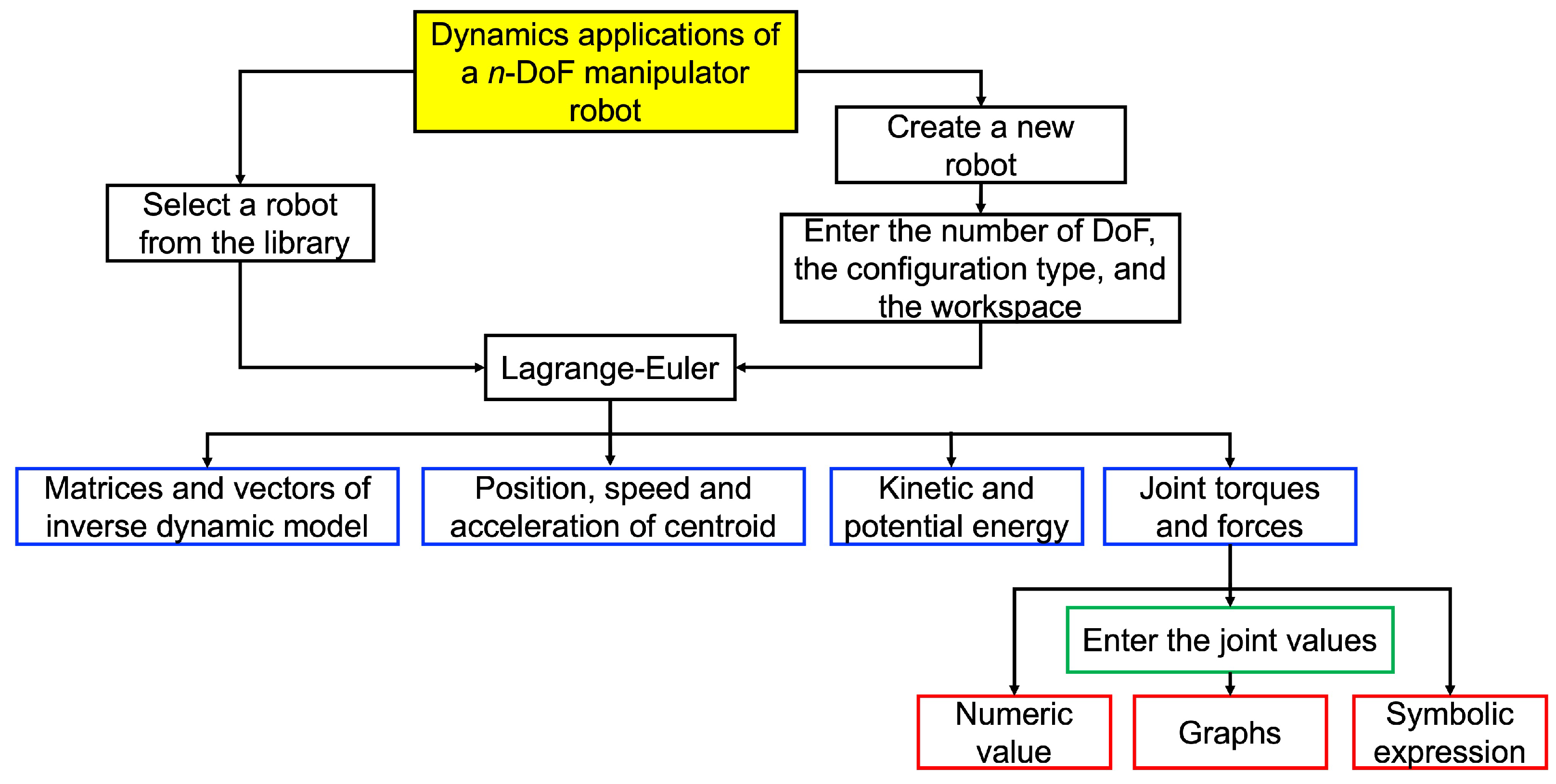
3. Description of the Designed Software

To conduct the identification of the dynamic model of an n-DoF redundant manipulator robot, the designed software is composed of three algorithms.

3.1. First Algorithm

The first algorithm conducts the symbolic calculation of speed, acceleration, kinetic energy, and potential energy of each robot link. To this end, using a GUI, the program file (script) energy.m is executed, which requests the user to enter the following robot specifications in the command window of MATLAB:

• Number of degrees-of-freedom;
• Type of configuration;
• Location of links in the workspace.

For the location of links in the workspace, the Cartesian plane (x−y, x−z, or y−z) on which the robot link is placed at rest should be specified. In case the point is not specified on the Cartesian plane, it is assumed by default that the robot is planar and that all its links are located in the x−y plane. With the specifications already entered, the first algorithm states, in a symbolic form, the scalar and vector variables in the workspace of MATLAB and searches for the centroid positions, from which kinetic and potential energy are obtained and saved in the workspace as energy.mat. Then, the software notifies the user that energy.mat has been successfully created and asks the user whether he/she authorizes the execution of the energy_opt.m script. If the user denies permission, the loop is repeated. Otherwise, energy_opt.m uses an algorithm to refine the symbology of this part of the robot’s dynamic model and saves the response as energy_opt.mat. In this way, the first algorithm—summarized in Algorithm 1—ends its execution successfully.

Algorithm 1 Calculate the energy of the system

Require:  Number of degrees of freedom of the manipulator robot $\left(n\right)$, configuration type $(R,P)$, and location of links in the workspace $(2D,3D)$ Ensure:  Velocity ($\mathbf{v}$), acceleration ($\mathbf{a}$), and the kinetic and potential energy of the robotic system (K,U) 1: $syms$ scalar variables and functions 2: $c=c_1=p\left(1\right)=p\left(2\right)=0;p\left(3\right)=L$▹ Initial condition of the position of the center of gravity 3: for  $i=1,2,\dots ,n$  do 4:     if type_of_robot = 2D then 5:         $link\left(i\right)=Y$ 6:     else[type_of_robot = 3D] 7:         $link\left(i\right)=input\left(YorN\right)$ 8:     end if 9: end for 10: for  $i=1,2,\dots ,n$  do 11:     if $joint\left(i\right)=R$ then 12:         if $link\left(i\right)=Y$ then 13:            ${\mathbf{p}}_i=[p\left(1\right)+l_{ci}cos(c+{\theta }_i),p\left(2\right)+l_{ci}sin(c+{\theta }_i),p\left(3\right)]$ 14:         else[$link\left(i\right)=N$] 15:            $c_1=c_1+p_i$ 16:            ${\mathbf{p}}_i=[p\left(1\right)+l_{ci}sin\left(c_1\right)sin\left(c\right),p\left(2\right)-l_{ci}sin\left(c_1\right)cos\left(c\right),p\left(3\right)]$ 17:         end if 18:         if $i\ge 2$ ∧ $joint(i-1)=P$ ∧ $link\left(i\right)=N$ then 19:            $subs({\mathbf{p}}_i,[l_{c(i-1)},L],[L_2,L-l_{ci}cos\left(c_1\right)])$ 20:         else if $i\ge 2$ ∧ $joint(i-1)=R$ ∧ $link\left(i\right)=N$ then 21:            $subs({\mathbf{p}}_i,[l_{c(i-1)},L],[L_1+L_2,L-l_{ci}cos\left(c_1\right)])$ 22:         else if $i\ge 2$ ∧ $joint(i-1)=R$ then 23:            $subs({\mathbf{p}}_i,l_{c(i-1)},L_1+L_2)$ 24:         else if $i\ge 2$ then 25:            $subs({\mathbf{p}}_i,l_{c(i-1)},L_2)$ 26:         end if 27:     else[$joint\left(i\right)=P$] 28:         if $i=1$ ∧ $joint\left(1\right)=P$ then 29:            ${\mathbf{p}}_i=[p\left(1\right)+L_1+d_i+l_{ci},p\left(2\right),p\left(3\right)]$ 30:         else 31:            ${\mathbf{p}}_i=[p\left(1\right),p\left(2\right),p\left(3\right)]$ 32:         end if 33:         if $i\ge 2$ ∧ $joint(i-1)=P$ ∧ $link\left(i\right)=N$ then 34:            $subs({\mathbf{p}}_i,[l_{c(i-1)},L],[L_2,L-l_{ci}-L_1-d_i])$ 35:         else if $i\ge 2$ ∧ $joint(i-1)=R$ ∧ $link\left(i\right)=N$ then 36:            $subs({\mathbf{p}}_i,[l_{c(i-1)},L],[L_1+L_2,L-l_{ci}-L_1-d_i])$ 37:         else if $i\ge 2$ ∧ $joint(i-1)=R$ then 38:            $subs({\mathbf{p}}_i,l_{c(i-1)},L_1+l_{ci}+d_i)$ 39:         else if $i\ge 2$ then 40:            $subs({\mathbf{p}}_i,l_{c(i-1)},L_1+L_2+l_{ci}+d_i)$ 41:         end if 42:         ${\mathbf{v}}_i=velocity\_vector\left({\mathbf{p}}_i\right)$; ${\mathbf{a}}_i=acceleration\_vector\left({\mathbf{v}}_i\right)$; $K_i=kinetic\_energy(m_i,I_i,{\mathbf{v}}_i)$; $U_i=potential\_energy(m_i,{\mathbf{p}}_i,\mathbf{g})$ 43:     end if 44: end for

In the algorithm, ${\mathbf{p}}_i$ is the i-th link centroid position, and $\mathbf{g}$ is the gravitational acceleration vector. The velocity_vector(), acceleration_vector(), kinetic_energy(), and potential_energy() functions compute the centroid velocity, centroid acceleration, kinetic energy, and potential energy, respectively, of link i. These equations are described based on the Lagrange–Euler formulation and the MATLAB functions ‘syms’ and ‘subs’, which create and convert, respectively, the symbolic variables and functions.

3.2. Second Algorithm

The second algorithm develops the equations of motion of the manipulator robot. To this end, the generalized_forces.m script should be executed, as it loads the information from the energy_opt.mat file. Then, this algorithm calculates the Lagrangian from the energies obtained through the first algorithm and uses it to calculate the generalized forces applied to the robot’s joints. Once the script’s execution is over, data from the .m file are automatically stored as a .mat file, i.e., the symbolic expressions of torques and forces necessary to move the system are saved in the force_torque.mat file. In this way, the second algorithm—summarized in Algorithm 2—ends its execution successfully.

Algorithm 2 Calculate the robot’s equations of motion

Require:  Kinetic and potential energy of the robotic system $(K,U)$ Ensure:  Vector of generalized forces applied at the robot joints $\left(\tau \right)$ 1: $L_S=lagrangian(K,U)$ 2: $L=lagrangian\_time\left(L_S\right)$ 3: for  $i=1,2,\dots ,n$  do 4:     $D{L}_i=derivative\_l\left(L\right)$ 5:     $D{T}_i=convert\left(D{L}_i\right)$ 6:     $DD{T}_i=derivative\_dt\left(D{T}_i\right)$ 7:     $R{T}_i=remove\_time\left(DD{T}_i\right)$ 8:     $T_i=derivative\_ls\left(L_S\right)$ 9:     ${\tau }_i=generalized\_forces(R{T}_i,T_i)$ 10: end for

In the algorithm, lagrangian() computes the Lagrangian of the system, lagrangian_time() defines the elements of $L_S$ and the joint angle/displacement vector as a function of time, derivative_l() derives L with respect to the i-th joint speed, convert() converts the elements of the derivative of $L_i$ as a function of time, derivative_dt() derives $D{T}_i$ with respect to time, remove_time() temporarily removes the time variable from $DD{T}_i$, derivative_ls() derives $L_S$ with respect to the generalized coordinate $q_i$ of the vector q, and generalized_forces() computes the force/torque applied to the i-th robot joint.

3.3. Third Algorithm

The third algorithm is formed by four loops that—from the second algorithm—extract the most relevant terms of the inverse dynamic model of the robot. To this end, the user executes the dynamic.m script, after which the energy_opt.mat and force_torque.mat files are loaded from the first and second algorithm, respectively. Then, the third algorithm notifies the user that dynamic.mat has been successfully created and asks the user whether he/she wants to execute the terms.m script; if the request is denied, the loop is repeated. Otherwise, the terms.m script optimizes the dynamic model and saves the results as terms.mat. This file contains the symbolic forms of the elements in the mass matrix and the elements in the Coriolis–centripetal forces matrix. Additionally, the third algorithm saves the components of the gravity forces vector of non-planar manipulator robots. In this way, the software notifies the user of the output, and the third algorithm—summarized in Algorithm 3—ends its execution successfully.

Algorithm 3 Calculate the terms of the generalized forces vector

Require:  Vector of the generalized forces applied at the robot joints ($\tau$) Ensure:  Elements of the inertia matrix ($\mathbf{M}$), elements of the centrifugal and Coriolis forces matrix ($\mathbf{C}$), and components of the gravitational forces vector ($\mathbf{g}$) 1: for  $i=1,2,\dots ,n$  do 2:     for $j=1,2,\dots ,n$ do 3:         $M_{ij}=inertia\_matrix\_element\left({\tau }_i\right)$ 4:     end for 5: end for 6: for  $k=1,2,\dots ,n$  do 7:     for $j=1,2,\dots ,n$ do 8:         for $i=1,2,\dots ,n$ do 9:            $C_{ijk}=christoffel\_coefficients(M_{kj},M_{ki},M_{ij})$ 10:         end for 11:     end for 12: end for 13: for  $i=1,2,\dots ,n$  do 14:     for $j=1,2,\dots ,n$ do 15:         $C_{ij}=cc\_matrix\_element(C_{ijk},\dot{\mathbf{p}})$ 16:     end for 17: end for 18: for  $i=1,2,\dots ,n$  do 19:     $g_i=gf\_vector\_component\left(U\right)$ 20: end for

In the algorithm, inertia_matrix_element() derives ${\tau }_i$ with respect to the acceleration ${\ddot{q}}_j$; christoffel_coefficients() computes the Christoffel coefficients; matrix_element() computes the elements of the centrifugal and Coriolis forces matrix; and GF_vector_component() derives U with respect to the generalized coordinate $q_i$ of the vector q.

The flowchart in Figure 3 summarizes the structure and working principle of the three algorithms.

4. Graphic User Interface

The designed GUI provides intuitive access to the simulations as well as an interactive and real-time view of manipulator robot modeling. In the main GUI box, users can create different types of robots capable of maneuvering their grippers both in the Cartesian plane x−y and the Cartesian space x−y−z along with searching for the robot dynamics by selecting one of the following options:

• Dynamics of a robot from the library;
• Dynamics of a new robot prototype.

The first option provides access to a library that includes dynamic models of some well-known robots, including PUMA, Stanford, SCARA (Selective Compliance Articulated Robot Arm), and planar manipulator robots. The second option allows for obtaining the dynamic model of a new robot type created by the user, who should specify the number of degrees of freedom, the type of configuration, and the workspace. These three statements (five maximum) are entered into the command window of MATLAB once the software is executed and requests the input. Specifically, to indicate the robot’s DoF (input 1), a number must be entered at the command line; to set up the type of robot (input 2), the characters R and/or P should be typed, as they denote rotational and prismatic joints, respectively; while for the workspace (input 3), the initial location of each link in space should be indicated through the statement 2D or 3D. If the input is 2D, the software computes the complete robot dynamics and confirms that it is a planar prototype that starts to operate from the x−y plane with its links resting on the positive semi-axis x, whereas if the input is 3D, the software confirms that the robot is non-planar and immediately requests additional information (inputs 4 and 5) to define the initial position of each link. For example, for a 2-DoF non-planar robot, if the first combination of inputs is 3D and Y (input 4), then the first link is positioned in the x−y plane, whereas if the second combination of inputs is 3D and N, the second link is positioned in the x−z or y−z plane depending on what the user specifies (input 5). The general description and organization of the GUI is illustrated in Figure 4.

Figure 5 shows a sub-window of the GUI, which displays the applications of the robot dynamics that can be accessed. These include the elements of the mass matrix (M); the elements of the damping, Coriolis, and centripetal forces matrix (C); the components of the gravity forces vector (G), positions (P), velocities (V), and accelerations (A) of the center of gravity (centroid); and the kinetic energies (K) and potential energies (U) of the robot links. Additionally, the toolbox allows for the monitoring of the generalized forces acting on each manipulator robot joint in a numerical, graphic, or symbolic form. For example, with the ‘Symbolic’ icon, the symbolic equations of the torques and forces are displayed in a GUI static text box. To improve readability, these expressions can be shown in code or plain-text format.

To better illustrate the qualities of the software, robots with 3-DoF, 6-DoF, and 9-DoF are presented in Section 2. In the particular case of the 6-DoF manipulator robot, its mass and Coriolis–centripetal forces matrices are composed of 36 elements, while the gravity forces vector has six components. By clicking on the corresponding icon on the menu in Figure 5, any matrix or vector forming the inverse dynamic model can be obtained along with other applications. Figure 6, Figure 7 and Figure 8 show some of the equations that the software generates as code.

5. Results

To validate the dynamic model, the manual calculations (Equations (8) and (A40)) are compared with the results of this software (Figure 6, Figure 7 and Figure 8). It is confirmed that the program completely solves the problem of direct and inverse dynamics of manipulator robots. A proof of the model matching in the case of the 6-DoF manipulator robot is shown in Figure 9.

The software is executed to generate the dynamics for different types of robots, and the CPU time for a MacBook Pro with a 3 GHz Dual-Core Intel Core i7 processor is between 15 and 35 s for a symbolic-model-based approach and between 25 and 60 s for a numerical-model-based approach. Additionally, dynamic simulations are conducted using the MATLAB/Simulink software to test the performance of the constructed 6-DoF manipulator robot model considering the dynamic parameters described in

Table 1. Parameters for 6-DoF redundant manipulator robot [43].

Links 1, 3, 5	Links 2, 4, 6	Units
$m_1=m_3=m_5=0.4822$	$m_2=m_4=m_6=0.65$	(kg)
$L_1=0.093$	$L_2=0.067$	(m)
$l_{c1}=l_{c3}=l_{c5}=0.0317$	$l_{c2}=l_{c4}=l_{c6}=0.0105$	(m)
$I_1=I_3=I_5=0.0058$	–	(kg· m2)
$F_{v1}=F_{v3}=F_{v5}=0.01313$	$F_{v2}=F_{v4}=F_{v6}=0.01208$	(N· m· s/rad)

.

Figure 9. Comparison between the results obtained by the program (top) and those calculated manually (bottom).

Figure 9. Comparison between the results obtained by the program (top) and those calculated manually (bottom).

In the table, $F_{vi}$ is the motor’s viscous friction, $i=1,2,3,4,5,6$.

In this specific simulation, the desired angles of the robot’s rotational joints are ${\theta }_1=0.5$ (rad), ${\theta }_3=0.7$ (rad), and ${\theta }_5=1$ (rad); the lengths of the prismatic joints are $d_2=0.2$ (m), $d_4=0.1$ (m) and $d_6=0.15$ (m); and the simulation time is preset to $3.5$ s.

Model predictive control (MPC)-based controllers for each DoF of the robot were also developed; these require knowing the dynamic model of the robot. Predictive control is a technique in which an explicit model is required for the prediction of the output of the process. Future values of the manipulated variables are predicted by optimizing the reduction of the difference between the current and desired trajectory. MPC-based control is described by Equation (24):

$$J=\sum _{j=n_1}^{n_2}{(q_r(t+j)-q(t+j))}^2+\rho \sum _{j=1}^{n_u}{(u^{\prime }(t+j-1)-u^{\prime }(t+j-2))}^2$$

(24)

where $n_1$ is the prediction horizon, $n_2$ is the cost horizon, $n_u$ is the control horizon, $u^{\prime }\left(t\right)$ is the tentative control signal at instant t, $q_r$ is the desired response, q is the network model response, and $\rho$ is the controller weighting factor. The values $n_1,n_2$, and $n_u$ assist with evaluation of the control increments, while the factor $\rho$ determines the contribution that the sum of the squares of the control increments has on the performance index.

Figure 10 shows the control scheme of the simulator for the 6-DoF robot.

where $m{v}_i$ is the i-th manipulated variable (torque or force); $m{o}_i$ is the i-th measured output (angle or displacement); ${\tau }_i$ is the i-th generalized force applied over the robot’s joints; ${\theta }_{ir}$ is the i-th reference joint position; and ${\theta }_i$, $\dot{{\theta }_i}$, $\ddot{{\theta }_i}$ are the i-th actual joint position, speed, and acceleration, respectively, with $i=1,2,3,4,5,6$.

The best performance of the controllers was obtained considering the following values: sample time = 0.08, $n_1=150$, $n_2=200$, $n_u=2$, $\rho =0.5$, state estimation = faster, and closed-loop performance = moderately aggressive. These parameters were empirically tuned using the MPC Toolbox of the MATLAB/Simulink software. Additionally, saturation blocks were incorporated to limit the extreme values of the generalized forces exerted on the robot joints.

Table 2. Lower and upper saturation block values.

Saturation	Lower Limit	Upper Limit
$1.2$	$-3$	3
$3.4$	$-2$	2
$5.6$	$-1$	1

shows the lower and upper limits of the saturators installed at the output of each MPC controller.

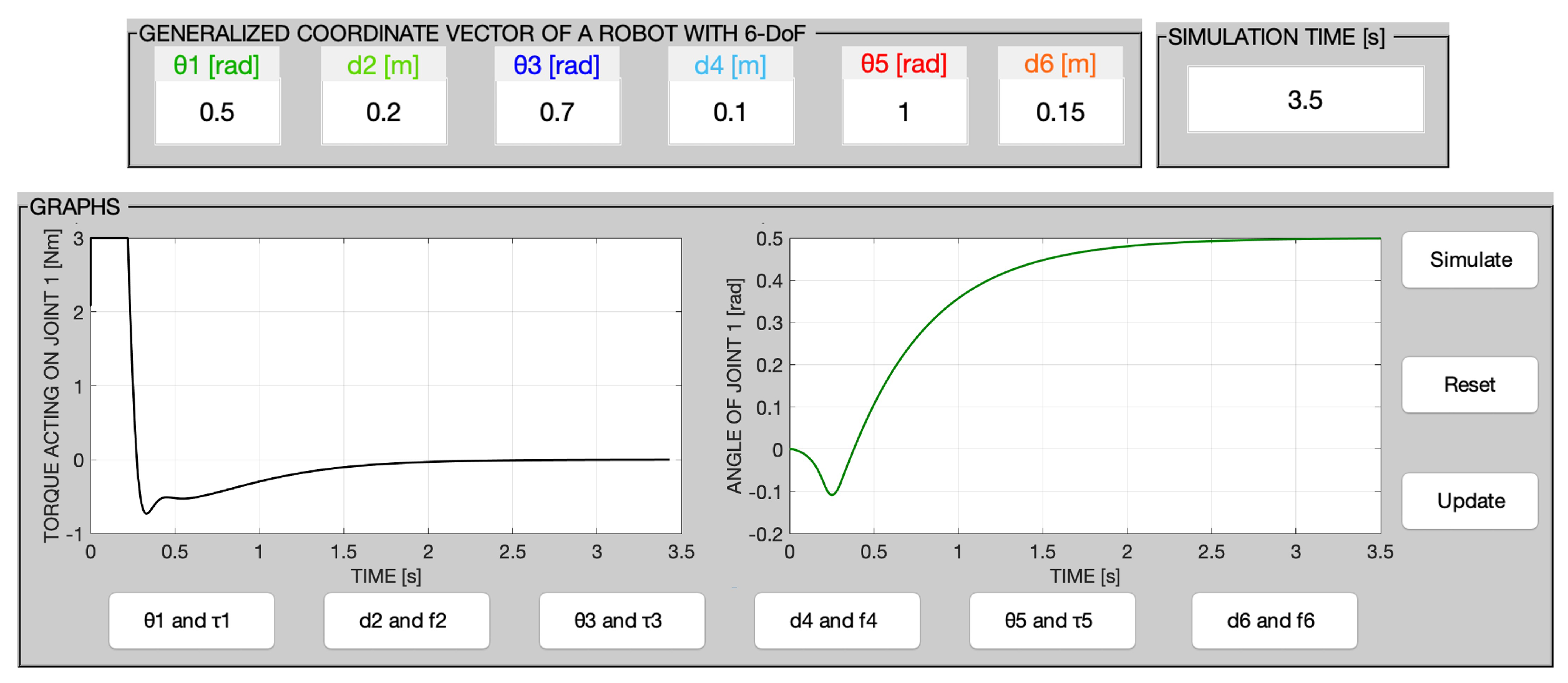
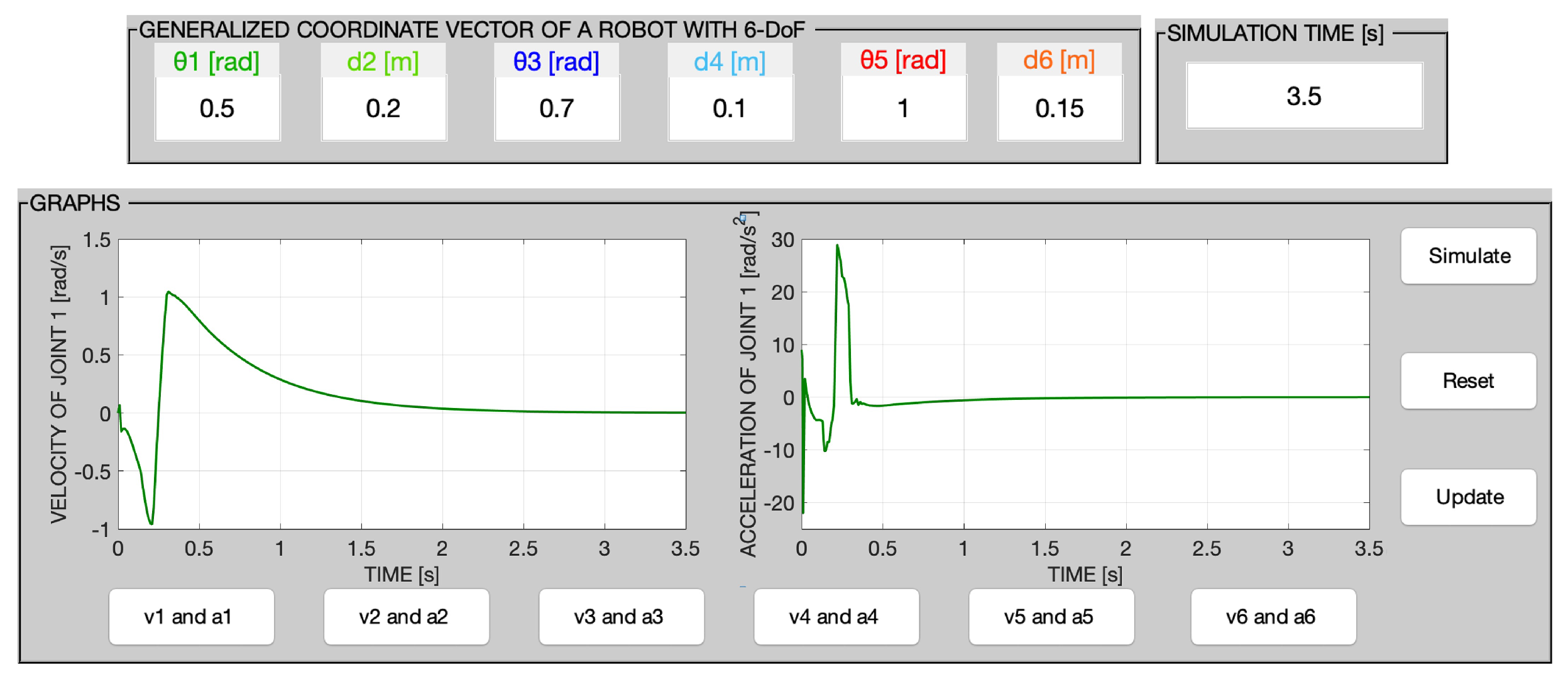
To monitor the instant numerical values or the graphics of the control signal, the icons ‘Numeric’ and ‘Graphs’, respectively, in Figure 5 are selected. Specifically, for a view of the control signal graphics, the value of each joint needs to have been previously entered in the editable box. In general, by clicking the icons ‘Simulate’ and ‘$\theta$ and $\tau$’ (or ‘d and f’) in Figure 11,the graphs of the generalized forces and motion of the 6-DoF redundant manipulator robot joints can be seen. Additionally, graphs of the velocities and accelerations of the robot joints can be displayed by pushing the ‘Simulate’ and ‘v and a’ buttons, as shown in Figure 12.

By clicking on the ’Reset’ icon, shown in Figure 11 and Figure 12, the information saved in the editable boxes is erased, and in turn, the screen graphics are cleared, allowing for entering the new desired joint values. In addition, by clicking on the ‘Update’ icon, the user returns to the main menu of the GUI and is able to change the current configuration of the robot and to specify new desired values and parameters for subsequent simulations.

The performance of the MPC controller is also evaluated from the following performance indicators: residual mean square (RMS), which measures the variability of the residuals (the differences between the desired and actual joint positions of the robot); residual standard deviation (RSD), which explains the deviation of the series; and index of agreement (IA), which provides the trends between two series to be compared. Equations (25)–(27) detail the expressions to calculate these indicators:

$$\mathrm{RMS}=\sqrt{\frac{1}{c}\sum _{i=1}^c{(p_i-p{d}_i)}^2}$$

(25)

$$\mathrm{RSD}=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^c{(p_i-p{d}_i)}^2}{{\sum }_{i=1}^c{p}_i^2}}}$$

(26)

$$\mathrm{IA}=1-{\displaystyle \frac{{\sum }_{i=1}^c{(p_i-p{d}_i)}^2}{{\sum }_{i=1}^c\left(\right|p_i^{\prime }|-|p{d}_i^{\prime }{\left|\right)}^2}}$$

(27)

with $|p_i^{\prime }|=p_i-p_m$, $|p{d}_i^{\prime }|=p{d}_i-p_m$, where c is the total number of observed data; $p_i$ is the i-th current joint value; $p{d}_i$ is the i-th desired joint value; and $p_m$ is the mean joint value.

Table 3. Joint error indexes of MPC-based controllers.

	Performance	Rotary	Prismatic	Rotary	Prismatic	Rotary	Prismatic
	Indicator	Joint 1	Joint 2	Joint 3	Joint 4	Joint 5	Joint 6
MPC-based controllers	RMS	0.1391	0.0405	0.1169	0.0205	0.2083	0.0304
	RSD	0.2964	0.2136	0.1716	0.2150	0.2226	0.2141
	IA	0.9742	0.9873	0.9922	0.9872	0.9860	0.9872

shows the results of the joint error indicators calculated considering $c=1008$ in 10 s of simulation. In particular, the results reveal good performance of the proposed controller since the RMS and RSD indices have values close to zero, while the IA indicator has values close to unity.

6. Conclusions

This work presented the development of software that automatically generates the equations of motion of industrial manipulator robots with any configuration type and number of DoF. The designed algorithms are based on the Lagrange–Euler formulation and allow for obtaining the dynamics of robotic manipulators formed by inflexible bodies (links) interconnected through n rotation and/or translation joints. To enter both the manipulator robot parameters and the desired values for their joints, a GUI was developed, which provides intuitive access to the simulation as well as an interactive and real-time view of the robots. This software is a powerful tool not only for modeling robotic arms but also for the design of diverse control systems. As an example, software simulations were conducted to generate the dynamics of a 3-DoF non-redundant manipulator robot and two 6- and 9-DoF redundant manipulator robots that included prismatic and rotational joints. The software, running on a MacBook Pro with a 3 GHz Dual-Core Intel Core i7 processor, takes less than a minute to model the symbolic dynamics of different robotic arms. Specifically, a model of the 3-DoF non-redundant manipulator robot was constructed to simplify the equations of motion of the redundant robots. In the case of the 6-DoF robot, MPC was performed based on the previous knowledge of its dynamic model, thanks to which optimal control to predict the future evolution of its state variables was achieved, i.e., the values of the joint variables of the robot. It was confirmed that manual calculations of the dynamic models of these three types of robots match the results of the software. Thus, the developed software is validated, as it correctly solves the direct and inverse dynamics problems of manipulator robots.

In future research work, it is contemplated to build other relevant mathematical models—for example, direct and inverse kinematics models—by taking advantage of the ideas of this study. In addition, it is desired to expand the gallery of robots available in the software library, possibly by incorporating mobile, flexible, and spatial robots. The large amount of information requested by the program before displaying the dynamic models is an aspect that is also being considered for the future. Addressing the latter would improve the efficiency of this work by ensuring that the interaction between the software and user is minimal and that any person in general is able to manipulate this type of program.