Study on Length–Diameter Ratio of Axial–Radial Flux Hybrid Excitation Machine
Abstract
1. Introduction
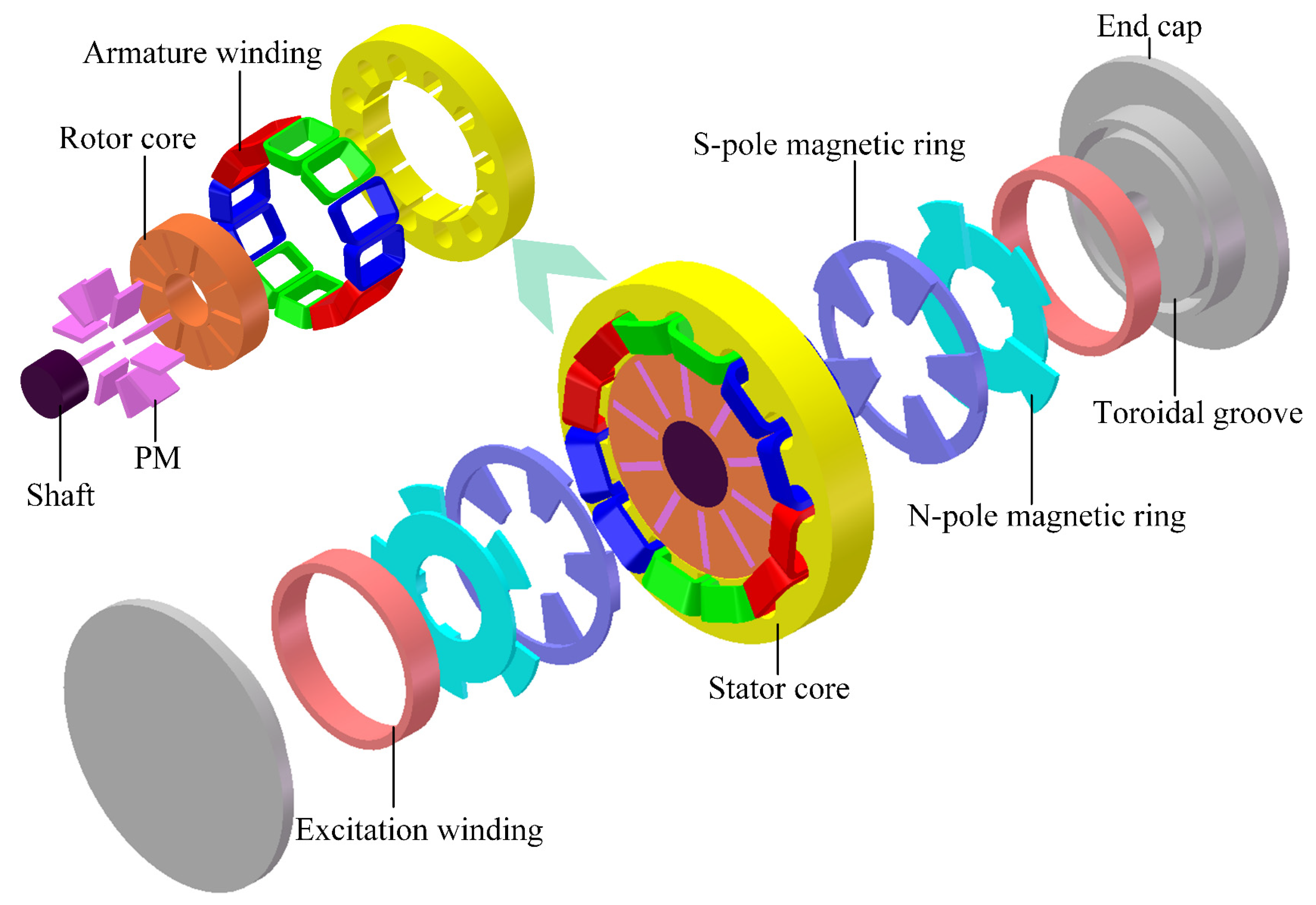
2. Structure and Operation Principle of ARFHEM
2.1. Structure of ARFHEM
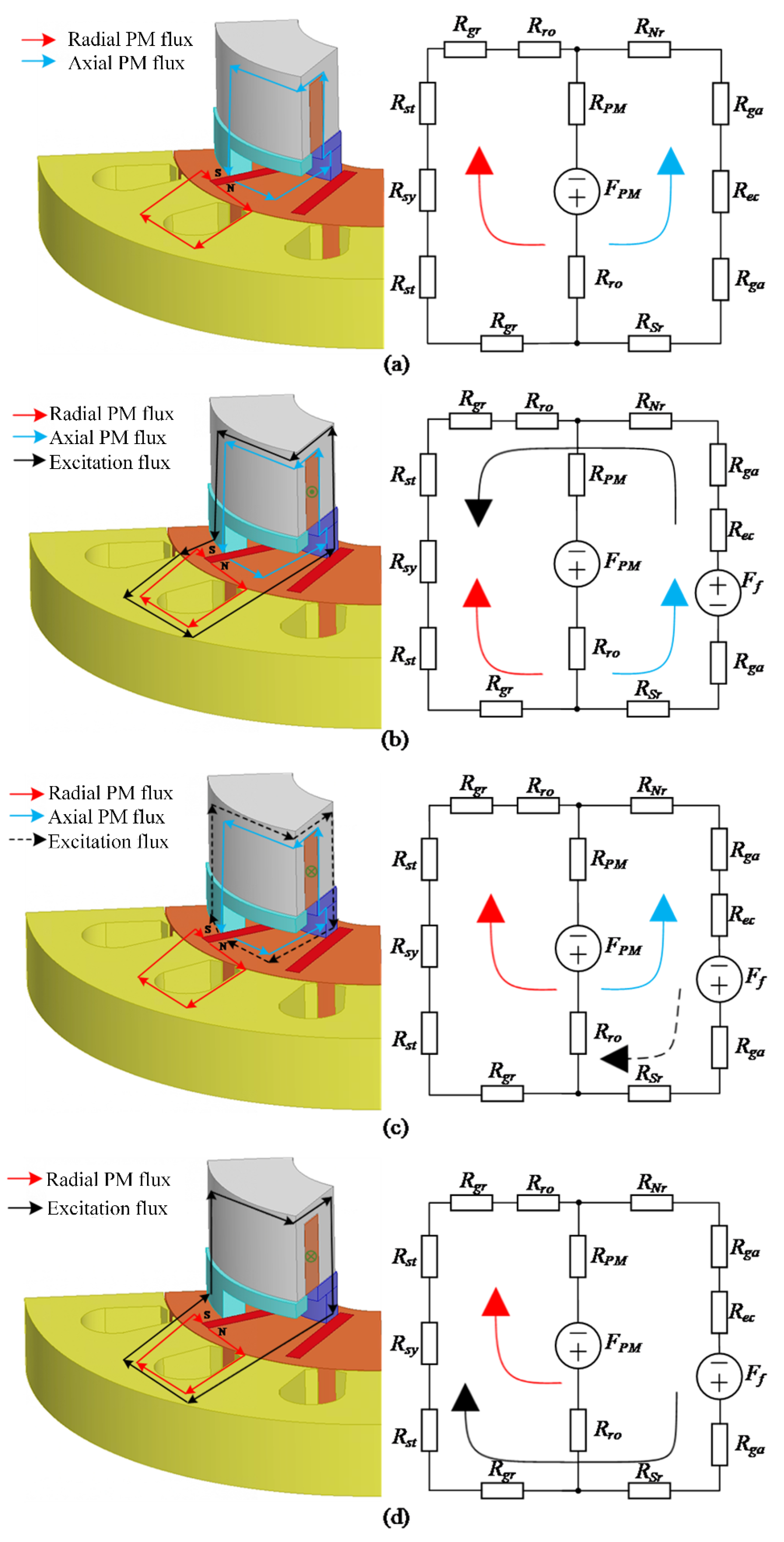
2.2. Operating Principle
3. Analysis of LDR Selection
3.1. Analysis of Constraints of Bypass Effect
3.2. Analysis of Constraint Conditions in the Selection of LDR
4. Influence of Different LDRs on Electromagnetic Properties
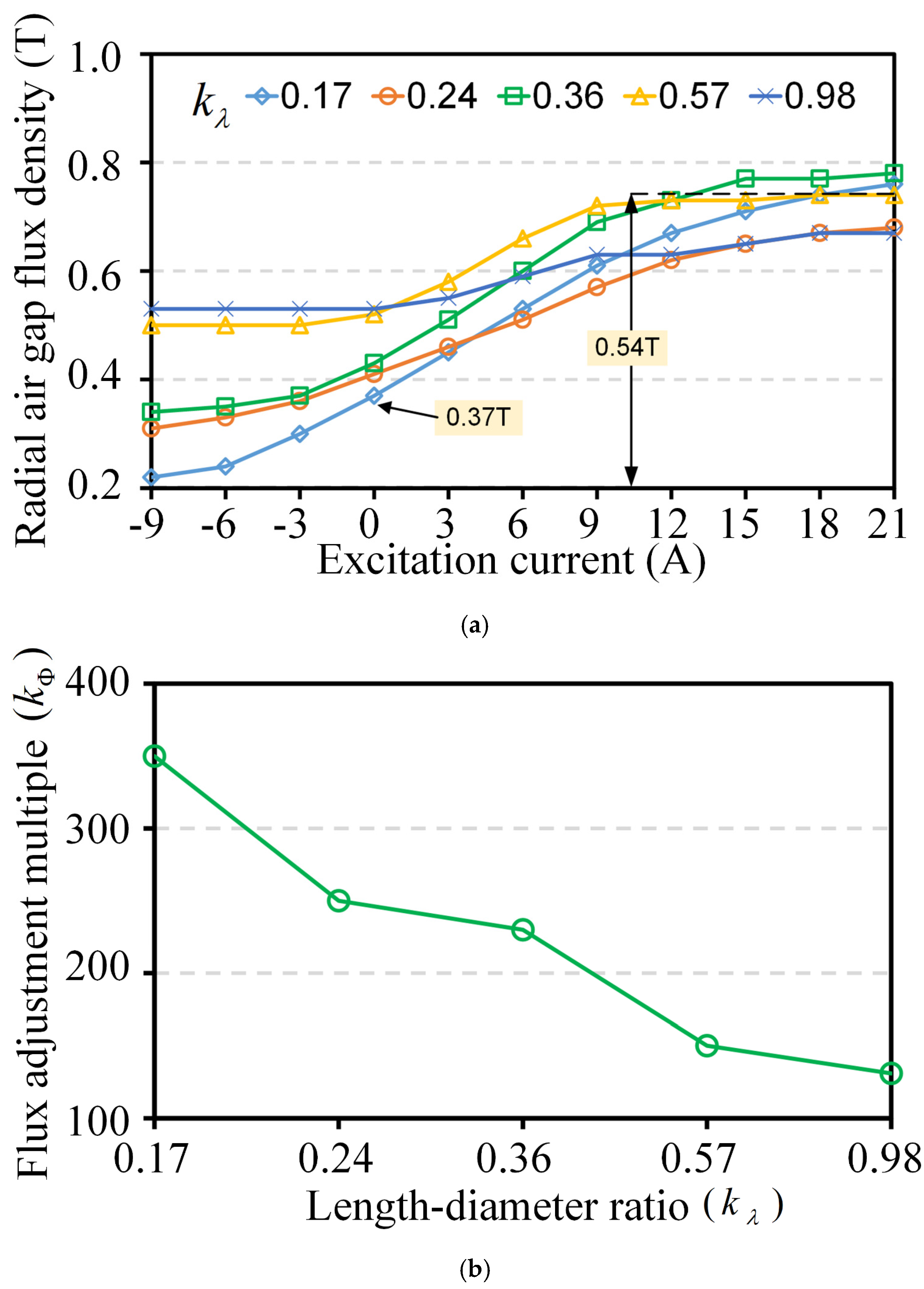
4.1. Influence on the Flux Regulation Properties
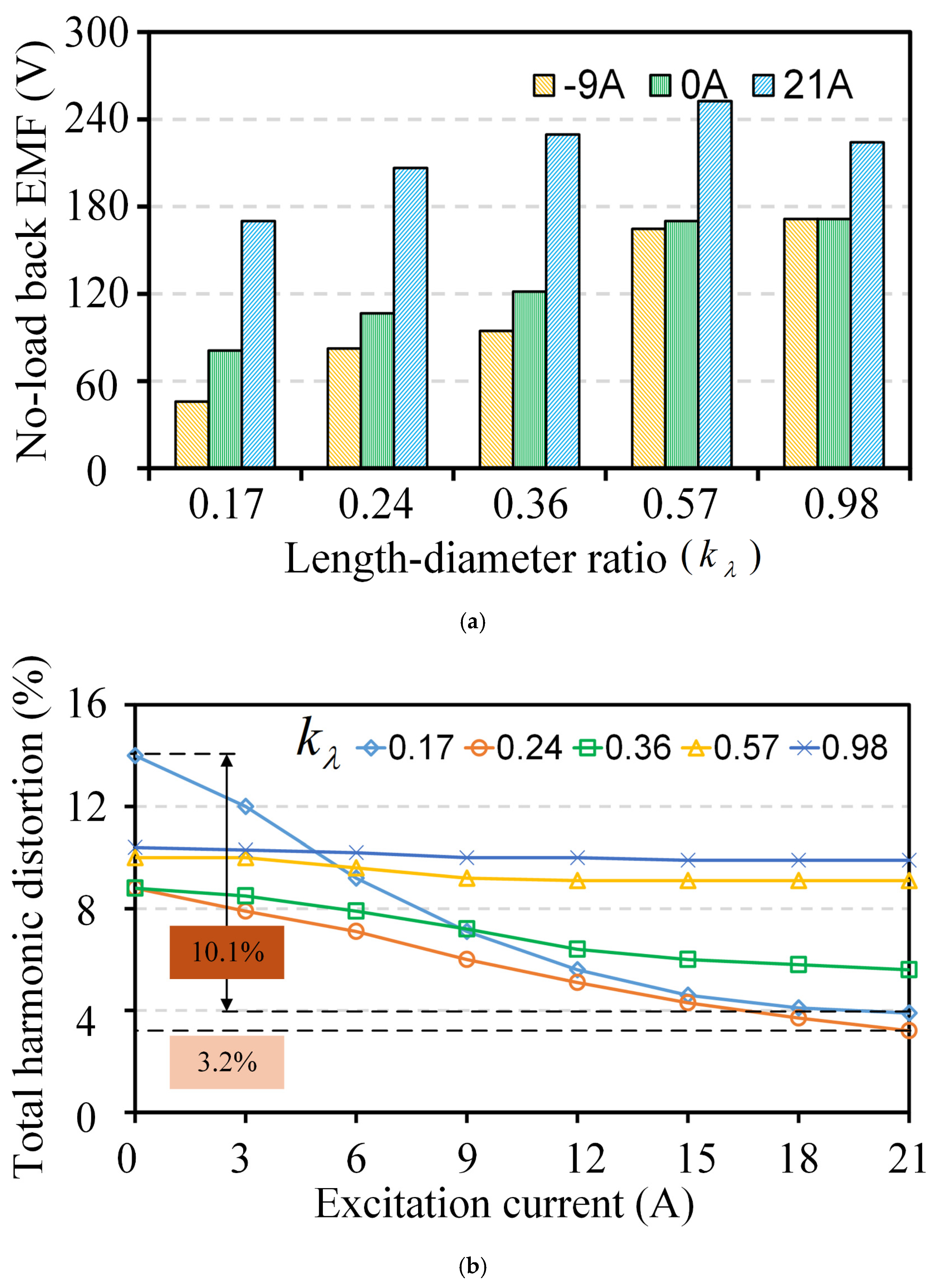
4.2. Influence on No-Load Back EMF and Harmonics
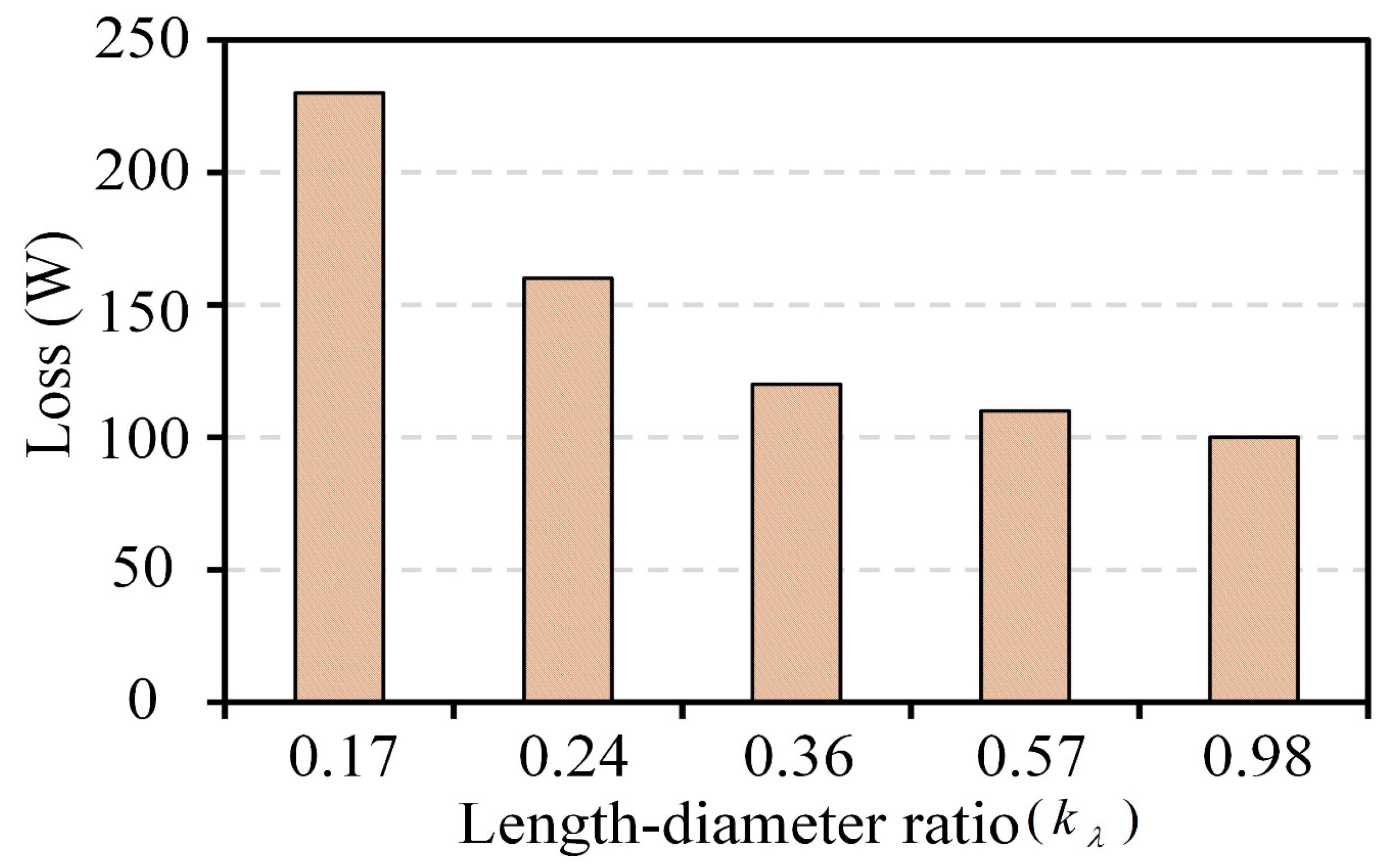
4.3. Influence on Output Torque and Loss
5. Experimental Validation
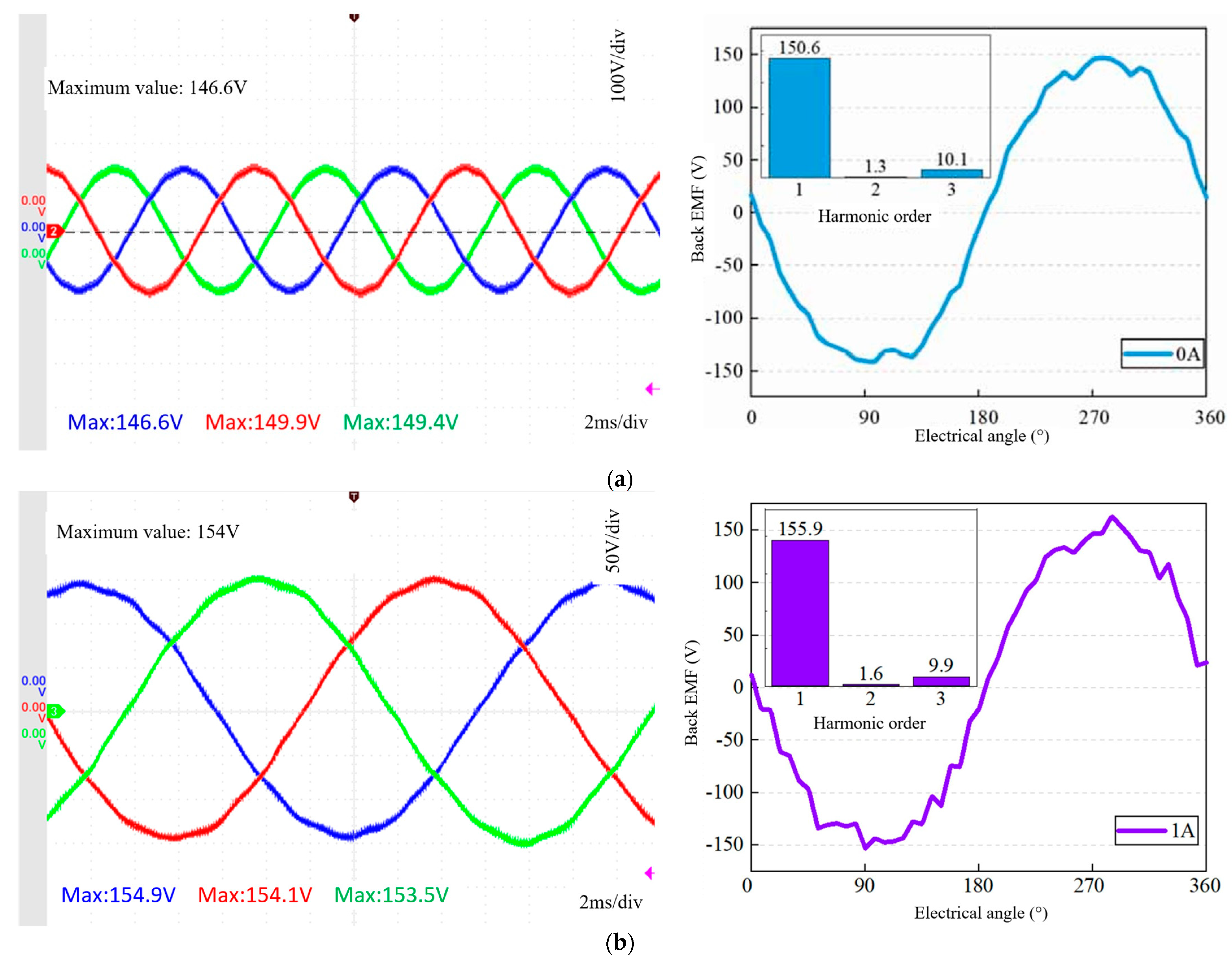
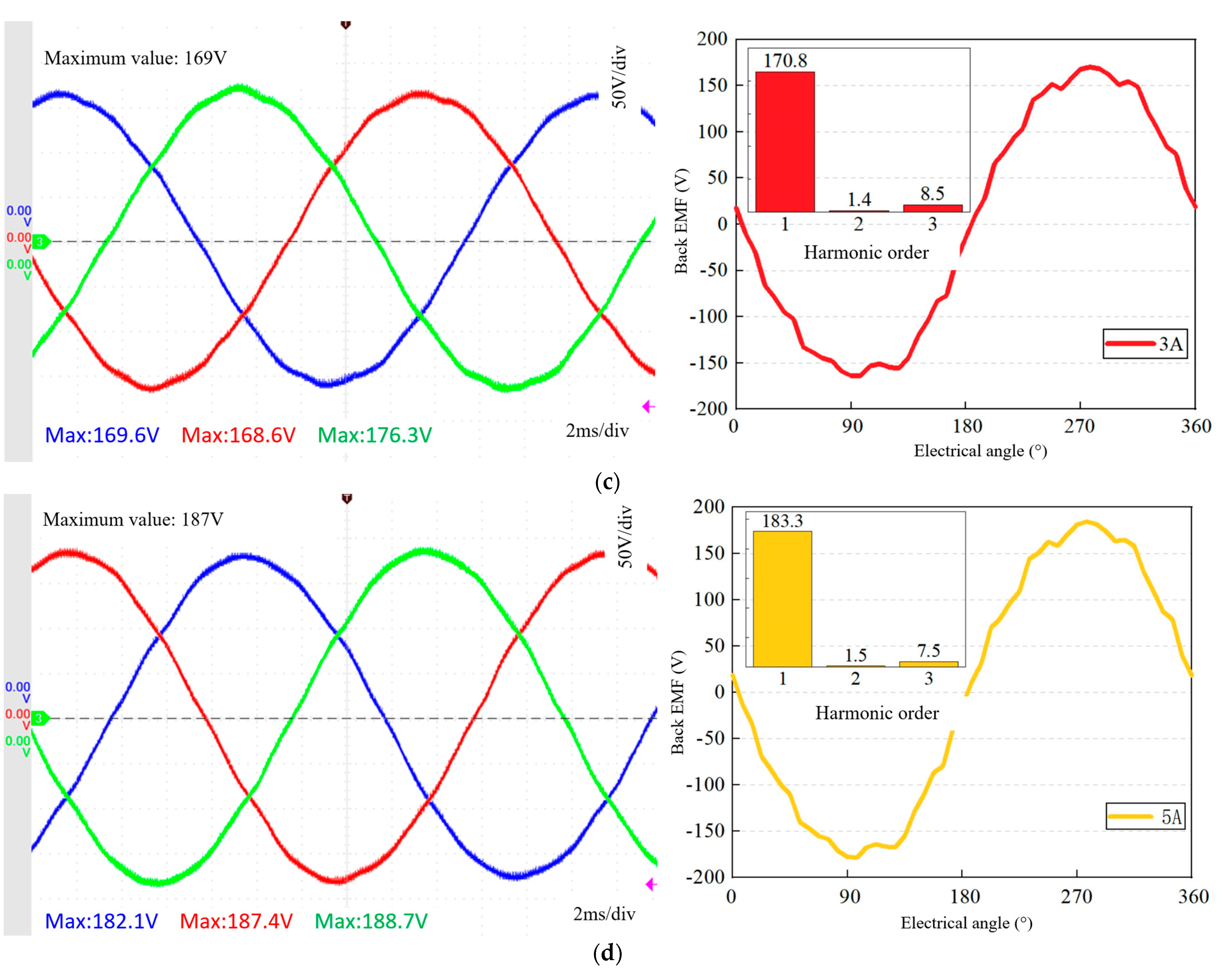
5.1. No-Load Experiment
5.2. Flux Regulation Experiment
6. Conclusions
- (1)
- The air-gap flux regulation ratio with the LDR of 0.17 is about 350%, while the air-gap flux regulation ratio with the LDR of 0.98 is about 130%. The results show that the air-gap flux adjustment ratio decreases significantly with the increase in LDR, and the ability of air gap magnetic field regulation becomes worse.
- (2)
- The THD of the back EMF decreases with the increase in the excitation current, mainly because the positive current increases the DC component of the back EMF. When the excitation current is 21 A, the THD of the motor with the LDR of 0.24 is the lowest, at 3.2%. The THD of the back EMF of the motor with the LDRs of 0.57 and 0.98 has little change.
- (3)
- When the excitation current is 0 A, the output torque of the motor increases with the increase in the LDR. Different from PMSM, after the introduction of excitation current, the output torque of the motor increases with the increase in excitation current, and the ability of improving output torque is independent of the LDR, and the value of improved output torque does not exceed 15 Nm. The loss in the motor decreases sharply with the increase in LDR.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Wang, Z.; He, M.; Zhou, Q.; Liu, X.; Meng, X. Fault-Tolerant control of dual three-phase PMSM drives with minimized copper loss. IEEE Trans. Power Electron. 2021, 36, 12938–12953. [Google Scholar] [CrossRef]
- Chen, Y.; Zang, B.; Wang, H.; Liu, H.; Li, H. Composite PM rotor design and alternating flux density harmonic component analysis of a 200 kW high-speed PMSM used in FESS. IEEE Trans. Ind. Appl. 2023, 59, 1469–1480. [Google Scholar] [CrossRef]
- Liu, S.; Song, Z.; Liu, Y.; Chen, Y.; Liu, C. Flux-Weakening controller design of dual three-phase PMSM drive system with copper loss minimization. IEEE Trans. Power Electron. 2023, 38, 2351–2363. [Google Scholar] [CrossRef]
- Wu, L.; Lyu, Z. Harmonic injection-based torque ripple reduction of PMSM with improved DC-link voltage utilization. IEEE Trans. Power Electron. 2023, 38, 7976–7981. [Google Scholar] [CrossRef]
- Formentini, A.; Trentin, A.; Marchesoni, M.; Zanchetta, P.; Wheeler, P. Speed finite control set model predictive control of a PMSM fed by matrix converter. IEEE Trans. Ind. Electron. 2015, 62, 6786–6796. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhu, C.; Jin, X.; Shi, W.; Zhao, R. Hybrid space vector modulation strategy for torque ripple minimization in three-phase four-switch inverter-fed PMSM drives. IEEE Trans. Ind. Electron. 2017, 64, 2122–2134. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.; Li, C.; Liu, C. Design and analysis of a new six-phase fault-tolerant hybrid-excitation motor for electric vehicles. IEEE Trans. Magn. 2015, 51, 8700504. [Google Scholar] [CrossRef]
- Sulaiman, E.; Kosaka, T.; Matsui, N. High power density design of 6-slot–8-pole hybrid excitation flux switching machine for hybrid electric vehicles. IEEE Trans. Magn. 2011, 47, 4453–4456. [Google Scholar] [CrossRef]
- Michieletto, D.; Cinti, L.; Bianchi, N. Hybrid excitation PM synchronous motors: Part II—Finite element analysis. IEEE Trans. Energy Convers. 2022, 37, 495–504. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Li, J. A HESM-based variable frequency AC starter-generator system for aircraft applications. IEEE Trans. Energy Convers. 2018, 33, 1998–2006. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, S.; Dai, J.; Yan, Y. Investigation of hybrid excitation synchronous machines with axial auxiliary air-gaps and non-uniform air-gaps. IEEE Trans. Ind. Appl. 2014, 50, 1729–1737. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Z.; Wang, C.; Geng, W.; Wang, H. Electromagnetic performance analysis of a new hybrid excitation synchronous machine for electric vehicle applications. IEEE Trans. Magn. 2018, 54, 8204804. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Z.; Geng, W.; Li, J. A simplified finite-element model of hybrid excitation synchronous machines with radial/axial flux paths via magnetic equivalent circuit. IEEE Trans. Magn. 2017, 53, 7403004. [Google Scholar] [CrossRef]
- Yang, Q.; Zhao, C.; Zhang, W. Theoretical and experimental analysis of electromagnetic force waves for rotor magnetic shunt hybrid excitation synchronous motor. IEEE Sens. J. 2024, 24, 22511–22522. [Google Scholar] [CrossRef]
- Huang, M.; Lin, H.; Yunkai, H.; Jin, P.; Guo, Y. Fuzzy control for flux weakening of hybrid exciting synchronous motor based on particle swarm optimization algorithm. IEEE Trans. Magn. 2012, 48, 2989–2992. [Google Scholar] [CrossRef]
- Geng, W.; Zhang, Z.; Jiang, K.; Yan, Y. A new parallel hybrid excitation machine: Permanent-magnet/variable-reluctance machine with bidirectional field-regulating capability. IEEE Trans. Ind. Electron. 2015, 62, 1372–1381. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, B.; Chen, Z.; Yan, Y. Comparison of flux regulation ability of the hybrid excitation doubly salient machines. IEEE Trans. Ind. Electron. 2014, 61, 3155–3166. [Google Scholar] [CrossRef]
- Tao, M.; Xiaoguang, L.; Wei, X. Optimization Design of Excitation Source Parameters and Magnetic Field Regulation Characteristics Analysis for Parallel Dual-Rotor Hybrid Self-Excited Motor. Electr. Mach. Control. Appl. 2024, 51, 67–75. [Google Scholar]
- Xu, L.; Wang, S.; Wang, J.; Li, S. Influence investigation of rotor pole numbers on flux adjustment capability in hybrid excited switched flux permanent magnet machines. Electr. Mach. Control. 2020, 24, 19–26. [Google Scholar]
- Wu, S.; Wang, Y.; Tong, W. Design and analysis of new modular stator hybrid excitation synchronous motor. CES Trans. Electr. Mach. Syst. 2022, 6, 188–194. [Google Scholar] [CrossRef]
- Jiang, T.; Xu, L.; Ji, J.; Zhu, X. A new partitioned stator hybrid excitation machine with internal magnetic ring. IEEE Trans. Magn. 2022, 58, 8105706. [Google Scholar] [CrossRef]
- Wang, X.; Fan, Y.; Chen, Q.; Wu, Z. Magnetic circuit feature investigation of a radial-axial brushless hybrid excitation machine for electric vehicles. IEEE Trans. Transp. Electrif. 2023, 9, 382–393. [Google Scholar] [CrossRef]
- Yildiriz, E.; Gulec, M.; Aydin, M. An innovative dual-rotor axial-gap f lux-switching permanent-magnet machine topology with hybrid excita tion. IEEE Trans. Magn. 2018, 54, 8107705. [Google Scholar] [CrossRef]




| LDR | 0.98 | 0.57 | 0.36 | 0.24 | 0.17 |
|---|---|---|---|---|---|
| (mm) | 190 | 210 | 230 | 250 | 270 |
| (mm) | 100 | 120 | 140 | 160 | 180 |
| (mm) | 100 | 68.4 | 50 | 38.28 | 30.25 |
| Parameters | Value | Parameters (mm) | Value |
|---|---|---|---|
| Rated voltage (V) | 150 | Axial air-gap length | 0.5 |
| Rated frequency (Hz) | 41.66 | Stator outside diameter | 230 |
| Number of poles | 10 | Rotor outside diameter | 139.3 |
| Number of slots | 12 | Stator core length | 50 |
| Armature winding turns | 150 | Main air-gap length | 0.35 |
| Excitation winding turn | 300 | PM length | 40 |
| Number of parallel branches Material of PM | 1 N35 | PM breadth LDR | 5 0.24 |
| Speed (r/min) | Experiment (V) | Simulation (V) |
|---|---|---|
| 250 | 76.56 | 77.62 |
| 500 | 149.9 | 151.3 |
| 750 | 216.5 | 217.7 |
| 1000 | 283.2 | 284.5 |
| Excitation Current (A) | Experiment (V) | Simulation (V) |
|---|---|---|
| 0 | 149.4 | 151.3 |
| 1 | 154.1 | 155.5 |
| 3 | 169.6 | 171.5 |
| 5 | 187.4 | 188.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Xia, J.; Wu, Q.; Gao, W.; Qiu, H. Study on Length–Diameter Ratio of Axial–Radial Flux Hybrid Excitation Machine. Processes 2024, 12, 2942. https://doi.org/10.3390/pr12122942
Guo M, Xia J, Wu Q, Gao W, Qiu H. Study on Length–Diameter Ratio of Axial–Radial Flux Hybrid Excitation Machine. Processes. 2024; 12(12):2942. https://doi.org/10.3390/pr12122942
Chicago/Turabian StyleGuo, Mingyu, Jiakuan Xia, Qimin Wu, Wenhao Gao, and Hongbo Qiu. 2024. "Study on Length–Diameter Ratio of Axial–Radial Flux Hybrid Excitation Machine" Processes 12, no. 12: 2942. https://doi.org/10.3390/pr12122942
APA StyleGuo, M., Xia, J., Wu, Q., Gao, W., & Qiu, H. (2024). Study on Length–Diameter Ratio of Axial–Radial Flux Hybrid Excitation Machine. Processes, 12(12), 2942. https://doi.org/10.3390/pr12122942




