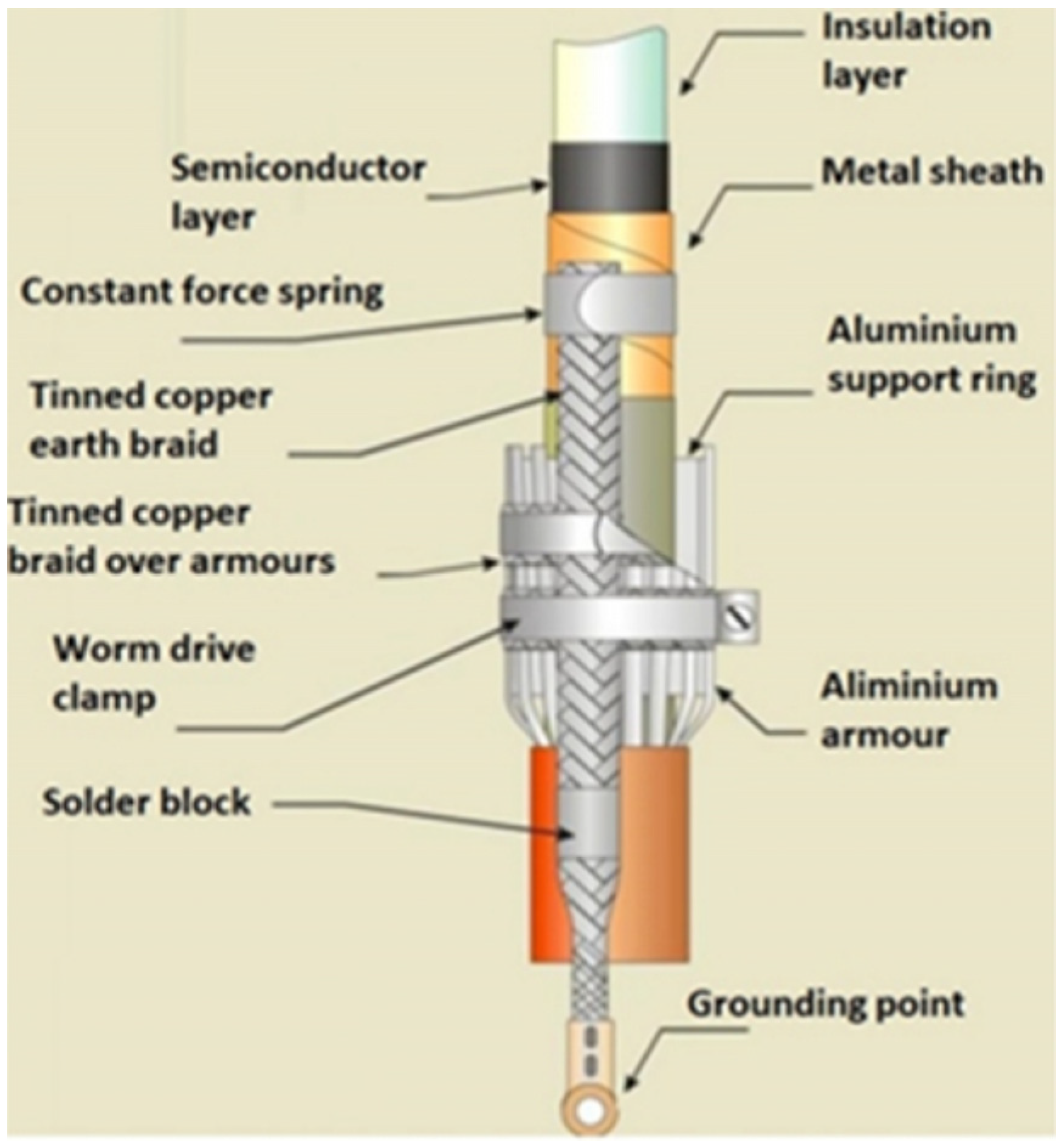
Figure 1.
A high-voltage cable.
Figure 1.
A high-voltage cable.
Figure 2.
The cable configurations.
Figure 2.
The cable configurations.
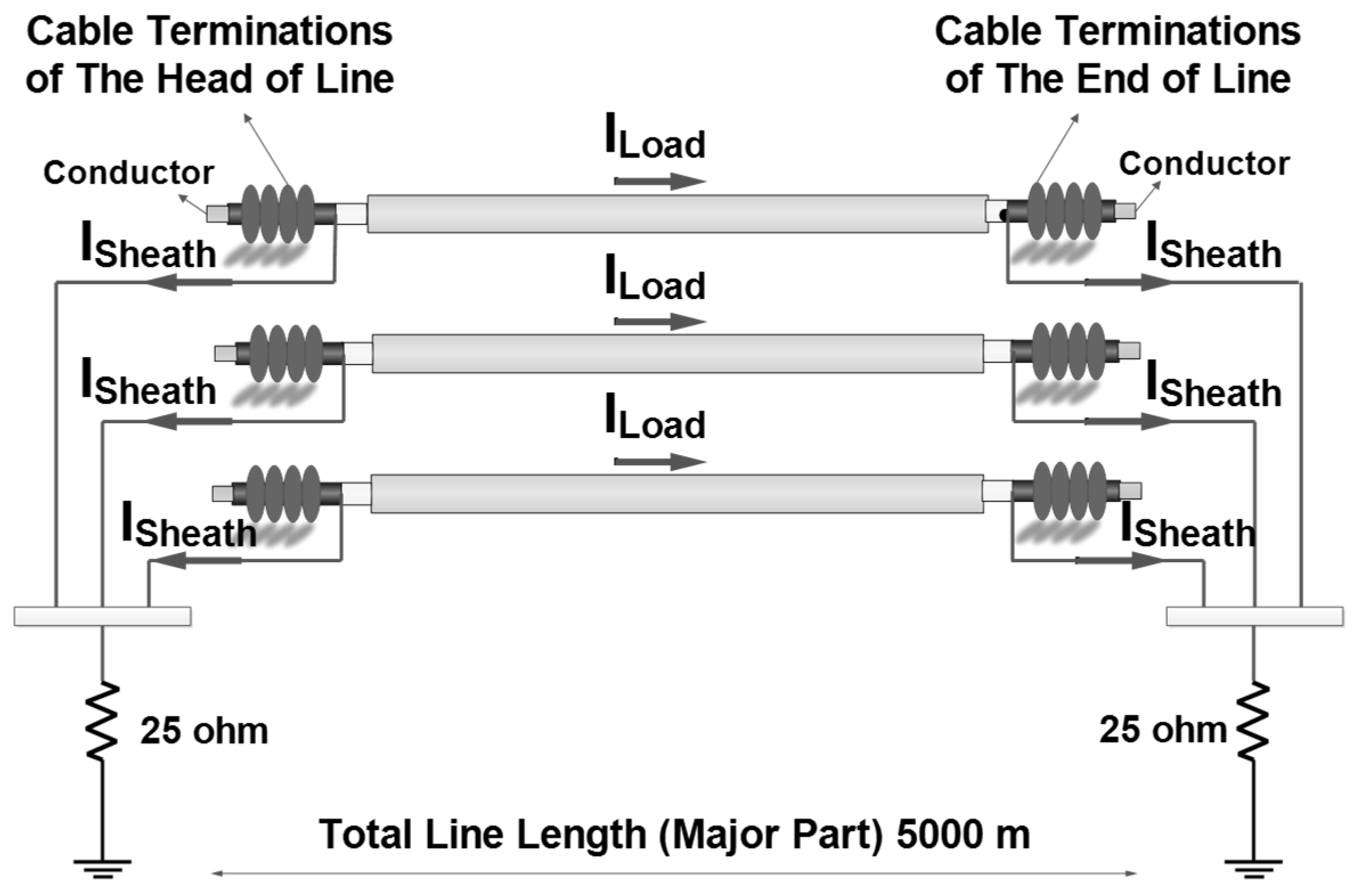
Figure 3.
The zero sequence path in a high-voltage power cable line.
Figure 3.
The zero sequence path in a high-voltage power cable line.
Figure 5.
The Pareto front.
Figure 5.
The Pareto front.
Figure 6.
Hybrid ANN algorithm.
Figure 6.
Hybrid ANN algorithm.
Figure 7.
The input matrix for training.
Figure 7.
The input matrix for training.
Figure 8.
The output matrices for training.
Figure 8.
The output matrices for training.
Figure 9.
The input matrix for prediction.
Figure 9.
The input matrix for prediction.
Figure 10.
The prediction process of MV in the optimum minor part detection algorithm.
Figure 10.
The prediction process of MV in the optimum minor part detection algorithm.
Figure 11.
The optimum minor part detection algorithm with the MV.
Figure 11.
The optimum minor part detection algorithm with the MV.
Figure 12.
The Pareto front and Pareto points.
Figure 12.
The Pareto front and Pareto points.
Figure 13.
The new input matrix for the prediction of MC and MHC.
Figure 13.
The new input matrix for the prediction of MC and MHC.
Figure 14.
The prediction process for the MC of each Pareto point.
Figure 14.
The prediction process for the MC of each Pareto point.
Figure 15.
The prediction process for the MHC of each Pareto point.
Figure 15.
The prediction process for the MHC of each Pareto point.
Figure 16.
Solid bonding.
Figure 16.
Solid bonding.
Figure 17.
The Pareto front and the Pareto points for Case 1.
Figure 17.
The Pareto front and the Pareto points for Case 1.
Figure 18.
The Pareto front and the Pareto points for Case 2.
Figure 18.
The Pareto front and the Pareto points for Case 2.
Figure 19.
The Pareto front and the Pareto points for Case 3.
Figure 19.
The Pareto front and the Pareto points for Case 3.
Figure 20.
The Pareto front and the Pareto points for Case 4.
Figure 20.
The Pareto front and the Pareto points for Case 4.
Figure 21.
The Pareto front and the Pareto points for Case 5.
Figure 21.
The Pareto front and the Pareto points for Case 5.
Figure 22.
The Pareto front and the Pareto points for Case 6.
Figure 22.
The Pareto front and the Pareto points for Case 6.
Figure 23.
The Pareto front and the Pareto points for Case 7.
Figure 23.
The Pareto front and the Pareto points for Case 7.
Figure 24.
The Pareto front and the Pareto points for Case 8.
Figure 24.
The Pareto front and the Pareto points for Case 8.
Figure 25.
The Pareto front and the Pareto points for Case 9.
Figure 25.
The Pareto front and the Pareto points for Case 9.
Table 1.
SC and the cable temperature.
Table 1.
SC and the cable temperature.
| SC (A) | 0 | 10 | 20 | 30 | 40 |
|---|
| CT (°C) | 43.1 | 54.4 | 74.2 | 119.0 | 184.1 |
Table 2.
Current, voltage and harmonic distortion rates of a high-voltage line.
Table 2.
Current, voltage and harmonic distortion rates of a high-voltage line.
| | Line Current (A) | Line Voltage (kV) | THDI (%) | THDV (%) |
|---|
| L1 | 485 | 24.7 | 3.97 | 4.20 |
| L2 | 485 | 24.7 | 5.44 | 5.30 |
| L3 | 455 | 24.7 | 3.18 | 3.04 |
Table 3.
Comparison of grounding methods.
Table 3.
Comparison of grounding methods.
| The Bonding Method | The Sheath Current | The Sheath Voltage | Harmonic Distortion |
|---|
| Single point bonding | not taken into account | above touch voltage limit | not taken into account |
| Solid bonding | taken into account | under touch voltage limit | not taken into account |
| Cross Bonding | taken into account | above touch voltage limit | not taken into account |
| SSBLR | taken into account | under touch voltage limit | taken into account |
Table 4.
The results of the solid bonding method.
Table 4.
The results of the solid bonding method.
| The Head of Line Cable Terminations Values | The End of Line Cable Terminations Values |
|---|
| Parameters | Phases | Phases |
| L1 | L2 | L3 | L1 | L2 | L3 |
| MV (V) | 798 | 822 | 647 | 786 | 793 | 630 |
| MC (A) | 181 | 179 | 173 | 176 | 175 | 169 |
| MHC (%) | 5.87 | 4.75 | 3.47 | 5.89 | 5.01 | 3.45 |
Table 5.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 1.
Table 5.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 1.
| Point | L (m) | Rg1 (ohm) | Rg2 (ohm) | Lg1 (H) | Lg2 (H) |
|---|
| A | 198 | 12.49 | 9 | 0.0086 | 0.0014 |
| B | 201 | 22 | 4 | 0.0084 | 0.0051 |
| C | 184 | 23.16 | 19 | 0.0073 | 0.0048 |
| D | 188 | 6 | 23.29 | 0.0071 | 0.0059 |
| E | 209 | 12.2 | 4.21 | 0.00325 | 0.0014 |
| F | 204 | 25 | 4 | 0.0043 | 0.0038 |
| G | 202 | 10 | 12 | 0.0058 | 0.0051 |
| H | 183 | 11 | 19 | 0.0081 | 0.0082 |
Table 6.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 2.
Table 6.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 2.
| Point | L (m) | Rg1 (ohm) | Rg2 (ohm) | Lg1 (H) | Lg2 (H) |
|---|
| A | 234 | 11.8 | 9.66 | 0.0092 | 0.0062 |
| B | 224 | 7.32 | 1.66 | 0.0099 | 0.0078 |
| C | 243 | 13.46 | 23.08 | 0.0091 | 0.0071 |
| D | 218 | 14.46 | 3.27 | 0.0088 | 0.00751 |
Table 7.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 3.
Table 7.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 3.
| Label | L (m) | Rg1 (ohm) | Rg2 (ohm) | Lg1 (H) | Lg2(H) |
|---|
| A | 201 | 21.5 | 18.48 | 0.0088 | 0.0029 |
| B | 206 | 11.77 | 3.73 | 0.007 | 0.0026 |
| C | 202 | 18.71 | 15.36 | 0.0082 | 0.0052 |
| D | 201 | 11.33 | 12.29 | 0.0083 | 0.0057 |
| E | 207 | 4.31 | 10.03 | 0.0059 | 0.0039 |
| F | 182 | 14.81 | 9.23 | 0.011 | 0.0102 |
| G | 200 | 14.18 | 12.18 | 0.0035 | 0.0018 |
Table 8.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 4.
Table 8.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 4.
| Point | L (m) | Rg1 (ohm) | Rg2 (ohm) | Lg1 (H) | Lg2 (H) |
|---|
| A | 194 | 7.25 | 9.31 | 0.0059 | 0.0096 |
| B | 211 | 7.94 | 12 | 0.0086 | 0.0055 |
Table 9.
The optimum minor part parameter values of dominant the Pareto points on the Pareto front for Case 5.
Table 9.
The optimum minor part parameter values of dominant the Pareto points on the Pareto front for Case 5.
| Point | L (m) | Rg1 (ohm) | Rg2 (ohm) | Lg1 (H) | Lg2 (H) |
|---|
| A | 213 | 3.55 | 13.36 | 0.0072 | 0.0095 |
| B | 219 | 13.62 | 3.28 | 0.0048 | 0.0096 |
Table 10.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 6.
Table 10.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 6.
| Label | L (m) | Rg1 (ohm) | Rg2 (ohm) | Lg1 (H) | Lg2 (H) |
|---|
| A | 211 | 10.64 | 10.10 | 0.0073 | 0.0067 |
| B | 207 | 6.43 | 12.39 | 0.0046 | 0.0070 |
| C | 202 | 6.49 | 2.75 | 0.0044 | 0.0016 |
Table 11.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 7.
Table 11.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 7.
| Point | L (m) | Rg1 (ohm) | Rg2 (ohm) | Lg1 (H) | Lg2 (H) |
|---|
| A | 204 | 2.10959 | 17.65897 | 0.00904 | 0.00720 |
| B | 206 | 10.68774 | 14 | 0.00936 | 0.00816 |
| C | 208 | 21.67438 | 9.763249 | 0.00113 | 0.00708 |
Table 12.
The optimum minor part parameter values of dominant Pareto points on the Pareto front for Case 8.
Table 12.
The optimum minor part parameter values of dominant Pareto points on the Pareto front for Case 8.
| Point | L (m) | Rg1 (ohm) | Rg2 (ohm) | Lg1 (H) | Lg2 (H) |
|---|
| A | 212 | 14.77 | 8.63 | 0.0051 | 0.0033 |
| B | 219 | 23.01 | 16.03 | 0.0063 | 0.0072 |
| C | 226 | 17.05 | 5.14 | 0.0015 | 0.0084 |
| D | 236 | 24.21 | 13.37 | 0.0095 | 0.0025 |
| E | 249 | 21.90 | 6.23 | 0.0086 | 0.0030 |
Table 13.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 9.
Table 13.
The optimum minor part parameter values of the dominant Pareto points on the Pareto front for Case 9.
| Point | L (m) | Rg1 (ohm) | Rg2 (ohm) | Lg1 (H) | Lg2 (H) |
|---|
| A | 175 | 5.12 | 14.20 | 0.0093 | 0.0095 |
| B | 185 | 9.80 | 10.85 | 0.0055 | 0.0038 |
| C | 189 | 9.79 | 10.85 | 0.0054 | 0.0040 |
| D | 191 | 14.29 | 11.47 | 0.0039 | 0.0057 |
| E | 192 | 14.10 | 11.43 | 0.0040 | 0.0058 |
| F | 191 | 11.44 | 8.17 | 0.0059 | 0.0073 |
Table 14.
The simulation results for the Pareto front solution in Case 1.
Table 14.
The simulation results for the Pareto front solution in Case 1.
| Values | A | B | C | D | E | F | G | H |
|---|
| | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL |
|---|
| MV1 (V) | 91 | 16 | 68 | 42 | 59 | 40 | 55 | 48 | 74 | 32 | 58 | 51 | 43 | 40 | 36 | 40 |
| MV2 (V) | 96 | 18 | 73 | 44 | 63 | 43 | 57 | 52 | 79 | 34 | 62 | 53 | 45 | 42 | 38 | 42 |
| MV3 (V) | 77 | 10 | 54 | 36 | 49 | 30 | 48 | 36 | 59 | 26 | 44 | 45 | 33 | 29 | 29 | 28 |
| MC1 (A) | 33 | 33 | 25 | 25 | 25 | 26 | 24 | 25 | 69 | 69 | 41 | 41 | 22 | 23 | 14 | 14 |
| MC2 (A) | 32 | 32 | 24 | 24 | 24 | 25 | 23 | 24 | 66 | 67 | 39 | 40 | 21 | 22 | 13 | 13 |
| MC3 (A) | 30 | 30 | 23 | 23 | 24 | 24 | 23 | 23 | 63 | 63 | 38 | 38 | 20 | 21 | 13 | 13 |
| MHC1 (%) | 2.80 | 2.87 | 2.82 | 2.90 | 2.88 | 2.95 | 2.81 | 2.89 | 2.70 | 2.73 | 2.77 | 2.82 | 2.50 | 2.61 | 2.51 | 2.97 |
| MHCI2 (%) | 3.54 | 3.57 | 3.46 | 3.50 | 3.40 | 3.44 | 3.45 | 3.50 | 3.84 | 3.85 | 3.60 | 3.63 | 3.63 | 3.69 | 3.46 | 3.55 |
| MHCI3 (%) | 5.27 | 5.31 | 5.27 | 5.33 | 5.29 | 5.34 | 5.23 | 5.29 | 5.45 | 5.47 | 5.27 | 5.30 | 5.01 | 5.08 | 4.98 | 5.08 |
Table 15.
The simulation results for the Pareto front solution in Case 2.
Table 15.
The simulation results for the Pareto front solution in Case 2.
| Values | A | B | C | D |
|---|
| | HL | EL | HL | EL | HL | EL | HL | EL |
|---|
| MV1 (V) | 74 | 52 | 74 | 59 | 73 | 59 | 65 | 56 |
| MV2 (V) | 79 | 56 | 80 | 63 | 76 | 65 | 69 | 59 |
| MV3 (V) | 62 | 42 | 58 | 51 | 62 | 47 | 50 | 48 |
| MC1 (A) | 25 | 26 | 23 | 24 | 25 | 25 | 23 | 23 |
| MC2 (A) | 24 | 25 | 22 | 22 | 24 | 24 | 22 | 22 |
| MC3 (A) | 23 | 24 | 21 | 22 | 23 | 24 | 21 | 21 |
| MHC1 (%) | 2.85 | 2.94 | 2.80 | 2.89 | 2.81 | 2.91 | 2.78 | 2.87 |
| MHC2 (%) | 3.42 | 3.48 | 3.40 | 3.47 | 3.45 | 3.50 | 3.39 | 3.45 |
| MHC3 (%) | 5.38 | 5.44 | 5.24 | 5.32 | 5.23 | 5.30 | 5.15 | 5.22 |
Table 16.
The simulation results for the Pareto front solution in Case 3.
Table 16.
The simulation results for the Pareto front solution in Case 3.
| Values | A | B | C | D | E | F | G |
|---|
| | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL |
|---|
| MV1 (V) | 81 | 28 | 80 | 30 | 66 | 44 | 64 | 45 | 66 | 45 | 52 | 49 | 51 | 27 |
| MV2 (V) | 86 | 31 | 85 | 32 | 70 | 47 | 68 | 49 | 69 | 50 | 55 | 53 | 54 | 29 |
| MV3 (V) | 68 | 21 | 66 | 25 | 55 | 35 | 54 | 36 | 57 | 34 | 42 | 41 | 39 | 19 |
| MC1 (A) | 29 | 29 | 36 | 36 | 25 | 26 | 24 | 24 | 35 | 35 | 15 | 15 | 43 | 44 |
| MC2 (A) | 28 | 28 | 34 | 34 | 24 | 25 | 23 | 23 | 33 | 34 | 12 | 14 | 42 | 42 |
| MC3 (A) | 27 | 27 | 33 | 33 | 23 | 24 | 22 | 23 | 32 | 33 | 14 | 14 | 39 | 39 |
| MHC1 (%) | 2.81 | 2.89 | 2.79 | 2.85 | 2.81 | 2.89 | 2.81 | 2.90 | 2.78 | 2.84 | 2.82 | 2.94 | 2.46 | 2.52 |
| MHC2 (%) | 3.50 | 3.54 | 3.55 | 3.59 | 3.46 | 3.51 | 3.45 | 3.50 | 3.54 | 3.58 | 3.44 | 3.42 | 3.88 | 3.91 |
| MHC3 (%) | 5.27 | 5.32 | 5.28 | 5.32 | 5.24 | 5.30 | 5.27 | 5.33 | 5.27 | 5.31 | 5.20 | 5.29 | 5.06 | 5.10 |
Table 17.
The simulation results for the Pareto front solution in Case 4.
Table 17.
The simulation results for the Pareto front solution in Case 4.
| Values | A | B |
|---|
| | HL | EL | HL | EL |
|---|
| MV1 (V) | 40 | 66 | 69 | 46 |
| MV2 (V) | 42 | 71 | 72 | 50 |
| MV3 (V) | 32 | 55 | 59 | 36 |
| MC1 (A) | 21 | 21 | 25 | 26 |
| MC2 (A) | 20 | 20 | 24 | 24 |
| MC3 (A) | 20 | 20 | 23 | 224 |
| MHC1 (%) | 2.8 | 2.89 | 2.80 | 2.88 |
| MHC2 (%) | 3.41 | 3.46 | 3.43 | 3.48 |
| MHC3 (%) | 5.23 | 5.30 | 5.22 | 5.28 |
Table 18.
The simulation results for the Pareto front solution in Case 5.
Table 18.
The simulation results for the Pareto front solution in Case 5.
| Values | A | B |
|---|
| | HL | EL | HL | EL |
|---|
| MV1 | 49 | 68 | 41 | 80 |
| MV2 | 51 | 74 | 44 | 84 |
| MV3 | 42 | 53 | 28 | 70 |
| MC1 | 22 | 22 | 25 | 26 |
| MC2 | 20 | 21 | 24 | 24 |
| MC3 | 20 | 20 | 23 | 24 |
| MHC1 | 2.80 | 2.89 | 2.75 | 2.84 |
| MHC2 | 3.41 | 3.46 | 3.41 | 3.46 |
| MHC3 | 5.24 | 5.31 | 5.14 | 5.20 |
Table 19.
The simulation results for the Pareto front solution in Case 6.
Table 19.
The simulation results for the Pareto front solution in Case 6.
| Values | A | B | D |
|---|
| | HL | EL | HL | EL | HL | EL |
|---|
| MV1 (V) | 59 | 56 | 44 | 68 | 77 | 28 |
| MV2 (V) | 62 | 60 | 47 | 73 | 82 | 30 |
| MV3 (V) | 48 | 46 | 37 | 55 | 63 | 23 |
| MC1 (A) | 25 | 25 | 29 | 30 | 54 | 54 |
| MC2 (A) | 24 | 24 | 28 | 28 | 52 | 52 |
| MC3 (A) | 23 | 24 | 27 | 27 | 50 | 50 |
| MHC1 (%) | 2.79 | 2.87 | 2.79 | 2.86 | 2.73 | 2.77 |
| MHC2 (%) | 3.43 | 3.48 | 3.49 | 3.52 | 3.71 | 3.73 |
| MHC3 (%) | 5.21 | 5.27 | 5.25 | 5.30 | 5.30 | 5.33 |
Table 20.
The simulation results for the Pareto front solution in Case 7.
Table 20.
The simulation results for the Pareto front solution in Case 7.
| Values | A | B | C |
|---|
| | HL | EL | HL | EL | HL | EL |
|---|
| MV1 (V) | 45 | 40 | 44 | 42 | 17 | 94 |
| MV2 (V) | 46 | 43 | 43 | 47 | 19 | 99 |
| MV3 (V) | 38 | 25 | 32 | 33 | 7 | 83 |
| MC1 (A) | 15 | 16 | 14 | 14 | 41 | 42 |
| MC2 (A) | 15 | 15 | 13 | 13 | 40 | 40 |
| MC3 (A) | 14 | 14 | 12 | 13 | 38 | 38 |
| MHC1 (%) | 2.50 | 2.67 | 2.50 | 2.67 | 3.06 | 2.16 |
| MHC2 (%) | 3.53 | 3.62 | 3.44 | 3.55 | 3.77 | 3.81 |
| MHC3 (%) | 5.01 | 5.11 | 4.98 | 5.09 | 4.52 | 4.58 |
Table 21.
The simulation results for the Pareto front solution in Case 8.
Table 21.
The simulation results for the Pareto front solution in Case 8.
| Values | A | B | C | D | E |
|---|
| | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL |
|---|
| MV1 (V) | 51 | 34 | 55 | 64 | 21 | 101 | 99 | 27 | 99 | 35 |
| MV2 (V) | 54 | 36 | 59 | 68 | 23 | 106 | 106 | 30 | 105 | 38 |
| MV3 (V) | 38 | 26 | 44 | 54 | 9 | 89 | 84 | 21 | 80 | 29 |
| MC1 (A) | 20 | 30 | 27 | 27 | 37 | 38 | 33 | 33 | 36 | 36 |
| MC2 (A) | 29 | 29 | 26 | 26 | 36 | 36 | 31 | 32 | 34 | 34 |
| MC3 (A) | 27 | 27 | 25 | 25 | 34 | 35 | 30 | 30 | 33 | 33 |
| MHC1 (%) | 2.50 | 2.58 | 2.07 | 2.16 | 2.75 | 2.81 | 2.80 | 2.88 | 2.79 | 2.86 |
| MHC2 (%) | 3.71 | 3.76 | 3.62 | 3.69 | 3.55 | 3.58 | 3.51 | 3.55 | 3.55 | 3.59 |
| MHC3 (%) | 5.00 | 5.06 | 4.41 | 4.51 | 5.27 | 5.32 | 5.22 | 5.28 | 5.27 | 5.32 |
Table 22.
The simulation results for the Pareto front solution in Case 9.
Table 22.
The simulation results for the Pareto front solution in Case 9.
| Values | A | B | C | D | E | F |
|---|
| | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL |
|---|
| MV1 (V) | 47 | 50 | 58 | 42 | 43 | 34 | 31 | 47 | 42 | 62 | 47 | 58 |
| MV2 (V) | 49 | 55 | 62 | 45 | 45 | 36 | 33 | 49 | 45 | 65 | 49 | 62 |
| MV3 (V) | 40 | 39 | 49 | 33 | 34 | 24 | 22 | 36 | 31 | 52 | 34 | 49 |
| MC1 (A) | 16 | 16 | 33 | 33 | 24 | 25 | 24 | 24 | 33 | 33 | 24 | 25 |
| MC2 (A) | 15 | 15 | 31 | 32 | 23 | 20 | 23 | 23 | 31 | 31 | 23 | 24 |
| MC3 (A) | 15 | 15 | 31 | 31 | 22 | 22 | 22 | 22 | 30 | 30 | 23 | 23 |
| MHC1 (%) | 2.8 | 7.2 | 2.8 | 2.8 | 2.5 | 2.5 | 2.5 | 2.6 | 2.8 | 2.8 | 2.8 | 2.9 |
| MHC2 (%) | 3.3 | 5.3 | 3.5 | 3.5 | 3.6 | 3.5 | 3.6 | 3.7 | 3.5 | 3.5 | 3.4 | 3.5 |
| MHC3 (%) | 5.2 | 5.8 | 5.2 | 5.3 | 5.0 | 5.0 | 5.0 | 5.1 | 5.3 | 5.3 | 5.2 | 5.3 |
Table 23.
The dominant Pareto points in each of the cases.
Table 23.
The dominant Pareto points in each of the cases.
| The Case | DPP | PM-OM | L (m) | Rg1 (ohm) | Rg2 (ohm) | Lg1 (H) | Lg2 (H) |
|---|
| The Case 1 | H | ENN, GA | 183 | 11 | 19 | 0.0081 | 0.0082 |
| The Case 2 | D | ENN, PSO | 218 | 14.46 | 3.27 | 0.0088 | 0.00751 |
| The Case 3 | F | ENN, GSA | 182 | 14.81 | 9.23 | 0.011 | 0.0102 |
| The Case 6 | A | MGR, GSA | 211 | 10.64 | 10.10 | 0.0073 | 0.0067 |
| The Case 7 | B | H-GA, GA | 206 | 10.68774 | 14 | 0.00936 | 0.00816 |
| The Case 8 | B | H-GA, PSO | 219 | 23.01 | 16.03 | 0.0063 | 0.0072 |
| The Case 9 | A | H-GA, GSA | 175 | 5.12 | 14.20 | 0.0093 | 0.0095 |
Table 24.
The simulation results for the dominant Pareto points.
Table 24.
The simulation results for the dominant Pareto points.
| Values | ENN, GA | ENN, PSO | ENN, GSA | MGR, GSA | H-GA, GA | H-GA, PSO | H-GA, GSA |
|---|
| | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL | HL | EL |
|---|
| MV1 (V) | 36 | 40 | 65 | 56 | 52 | 49 | 59 | 56 | 44 | 42 | 55 | 64 | 47 | 50 |
| MV2 (V) | 38 | 42 | 69 | 59 | 55 | 53 | 62 | 60 | 43 | 47 | 59 | 68 | 49 | 55 |
| MV3 (V) | 29 | 28 | 50 | 48 | 42 | 41 | 48 | 46 | 32 | 33 | 44 | 54 | 40 | 39 |
| MC1 (A) | 14 | 14 | 23 | 23 | 15 | 15 | 25 | 25 | 14 | 14 | 27 | 27 | 16 | 16 |
| MC2 (A) | 13 | 13 | 22 | 22 | 12 | 14 | 24 | 24 | 13 | 13 | 26 | 26 | 15 | 15 |
| MC3 (A) | 13 | 13 | 21 | 21 | 14 | 14 | 23 | 24 | 12 | 13 | 25 | 25 | 15 | 15 |
| MHC1 (%) | 2.51 | 2.97 | 2.78 | 2.87 | 2.82 | 2.94 | 2.79 | 2.87 | 2.50 | 2.67 | 2.07 | 2.16 | 2.81 | 7.17 |
| MHC2 (%) | 3.46 | 3.55 | 3.39 | 3.45 | 3.44 | 3.42 | 3.43 | 3.48 | 3.44 | 3.55 | 3.62 | 3.69 | 3.37 | 5.30 |
| MHC3 (%) | 4.98 | 5.08 | 5.15 | 5.22 | 5.20 | 5.29 | 5.21 | 5.27 | 4.98 | 5.09 | 4.41 | 4.51 | 5.22 | 5.83 |