Preload Multi-Objective Optimization Method for Ultrasonic Motors Based on NSGA-II

Abstract

The preload has a significant impact on the output performance of ultrasonic motors. To achieve optimal output from the ultrasonic motor, this paper proposes a novel multi-objective optimization method for preload, utilizing the Non-dominated Sorting Genetic Algorithm II (NSGA-II) to solve the problem of determining the optimal preload. Firstly, a platform for preload adjustment and testing is established to conduct experimental tests on the motor’s characteristics. Based on the experimental data, the influence of preload on the motor’s output performance is analyzed. Secondly, linear regression models are established for three performance indicators: no-load speed, stall torque, and output efficiency with respect to preload, and the objective functions are fitted accordingly. Finally, the NSGA-II algorithm is used for multi-objective optimization with three objectives to obtain the Pareto front and determine the optimal preload for the ultrasonic motor. Simulation and experimental results show that after preload optimization, the no-load speed increased by 4.93%, stall torque increased by 26.10%, and output efficiency increased by 11.28%. Compared to existing optimization methods, this approach has lower computational complexity and better optimization performance, ensuring higher optimization accuracy and precision. The preload optimization method based on NSGA-II can improve the performance of ultrasonic motors in practical applications.

1. Introduction

Ultrasonic motors are characterized by their small size, high precision, noiseless operation, and resistance to magnetic interference, making them widely used in applications such as medical robotics [1,2,3,4], aerospace [5,6,7], and precision instruments [8,9,10]. They have significant potential and prospects in the field of miniature motors. The traveling-wave rotary ultrasonic motor converts electrical energy into mechanical energy through the inverse piezoelectric effect and ultrasonic vibration of piezoelectric ceramics. Specifically, when a high-frequency alternating voltage is applied, the piezoelectric ceramics expand or contract in response to the voltage, generating ultrasonic vibrations. These vibrations are transformed into a traveling wave through the friction between the stator and rotor, which drives the rotor’s motion. The friction between the stator and rotor needs to be regulated by applying a preload. The magnitude of the preload directly determines the motor’s frictional drive efficiency and mechanical characteristics. Preload plays a critical role in the performance of the motor and is one of the fundamental characteristics of ultrasonic motors. Therefore, researchers worldwide have conducted a series of studies on preload.

Mashimo, T. [11] designed a preload mechanism based on a miniature spiral spring, using both axial and longitudinal preload mechanisms to improve the motor’s angular velocity, torque, and efficiency. Kazumi, T. [12] proposed a preload mechanism by embedding the stator of the ultrasonic motor into a movable slider, applying internal mechanical preload within the motor, and eliminating the need for external preload mechanisms, thus achieving miniaturization of the motor. Niu, R. K. [13] designed an electromagnetic clutch-type self-adjusting preload mechanism, which, when assembled on the ultrasonic motor, significantly improves the motor’s output efficiency compared to traditional ultrasonic motors. Li, B. [14] introduced a new three-degree-of-freedom spherical ultrasonic motor preload mechanism, where the interaction between the stator coil and permanent magnetic poles on the spherical rotor generates preload through an electromagnetic force. The above studies mainly focus on structural improvements to the ultrasonic motor to apply the desired preload. However, they often neglect the analysis of the characteristics of different preloads and are relatively complex, making them difficult to implement. Therefore, a method to optimize and adjust the preload based on the relationship between the output characteristics of the ultrasonic motor and the preload would address the problem of determining the optimal preload at its core.

Wang, H. X. [15] established a dynamic model of the ultrasonic motor to analyze the impact of preload on motor performance. By adjusting the preload according to the actual load, the motor’s output efficiency was improved, though the output characteristics of the motor are not limited to this. Chen, N. [16] analyzed the effect of preload on several key performance indicators of the ultrasonic motor and proposed optimization criteria for the preload under different operating conditions, determining its optimal range. However, the exact optimal preload value could not be determined. Sun, H. Y. [17] used the Analytic Hierarchy Process (AHP) to analyze four performance indicators of the ultrasonic motor and obtain the optimal preload. AHP is a multi-objective decision-making method that decomposes objectives into several levels for qualitative and quantitative analysis. However, AHP has some subjectivity when determining weights, and the process of building the hierarchy and comparison matrix may be influenced by subjective factors, which may not ensure the accuracy of the multi-objective optimization results or make them acceptable to all decision-makers.

The field of multi-objective optimization currently includes methods such as the Multi-Objective Evolutionary Algorithm based on Decomposition (MOEAD), Multi-Objective Particle Swarm Optimization (MOPSO), and Non-dominated Sorting Genetic Algorithm II (NSGA-II). MOEAD is a multi-objective optimization algorithm based on decomposition, which breaks a multi-objective problem into several single-objective sub-problems and uses evolutionary algorithms to optimize them simultaneously, thus finding the Pareto front. However, compared to other algorithms, MOEAD has a more complex theory and is more difficult to implement. MOPSO is an extension of Particle Swarm Optimization (PSO) for multi-objective problems. It uses a swarm intelligence algorithm to solve multi-objective problems. When dealing with a larger number of objectives, MOPSO also faces issues of high computational complexity and is prone to getting stuck in local optima. NSGA-II can significantly improve computational speed while ensuring optimization accuracy and precision, making it widely applied to solving multi-objective optimization problems. Wang, X. X. [18] applied the NSGA-II algorithm to optimize the transmission system parameters of hybrid electric vehicles, reducing fuel consumption while improving engine efficiency, resulting in enhanced economic performance and driving capabilities of the hybrid vehicle. Wang, X. H. [19] proposed a multi-objective optimization model for the production process in metal mines based on the NSGA-II algorithm. After optimization, both profit and resource utilization were improved, achieving a balance between economic benefits and resource efficiency. Modrak, V. [20] used the NSGA-II and MOPSO algorithms in the wire electrical discharge machining process of Al-Mg-MoS₂, evaluating the effects of current, pulse on-time, and gap voltage on the cut width and surface roughness. Liu, W. [21] introduced an improved NSGA-II algorithm for solving distributed generation planning problems, achieving higher economic benefits and safer voltage levels. These studies demonstrate the feasibility of NSGA-II in bi-objective optimization. For the ultrasonic motor, which focuses on three core indicators—no-load speed, stall torque, and output efficiency—this paper extends the NSGA-II algorithm to a three-objective optimization framework.

In summary, to ensure the motor operates at optimal performance, this paper addresses the issues of low accuracy and suboptimal results in existing ultrasonic motor preload optimization methods. Instead of relying on structural design improvements, the paper analyzes the mapping relationship between output characteristics and preload. It establishes linear regression models for no-load speed, stall torque, and output efficiency as functions of preload, fitting the objective functions accordingly. The NSGA-II algorithm is then used to simultaneously optimize the three objective functions, obtaining the Pareto front. Finally, sorting is applied to determine the optimal solution, thereby identifying the optimal preload for the ultrasonic motor. The technology roadmap of this paper is shown in Figure 1, which includes three progressive levels: the left part represents the experimental equipment and method, the middle part illustrates the linear regression prediction models for the objective functions, and the right part covers algorithm simulations and result analysis.

2. Experimental Equipment and Method

2.1. Experimental Equipment

The schematic diagram of the ultrasonic motor preload adjustment and testing platform is shown in Figure 2. The platform consists of three main modules: the drive and input measuring module, the preload application and adjustment module, and the load and output measuring module.

The drive and input measuring module includes an ultrasonic motor driver and a digital oscilloscope. The driver is used to drive the ultrasonic motor and control the driving frequency, while the oscilloscope is used to measure input voltage and other related data.

The preload application and adjustment module include a servo-electric cylinder driver, a servo-electric cylinder, a pressure transducer, and a digital display instrument. The servo-electric cylinder driver drives and controls the motion of the electric cylinder to apply and adjust the preload to the ultrasonic motor. The pressure transducer and digital display instrument are used to transmit and display the applied preload value.

The load and output measuring module includes a torque sensor, a magnetic powder brake, a tension controller, and a data acquisition unit. The tension controller adjusts the magnetic powder brake to provide a load for the ultrasonic motor. The torque sensor, connected to a PC via the data acquisition unit, collects the motor’s output speed and torque signals in real-time.

The experimental equipment for the ultrasonic motor preload adjustment and testing platform is shown in Figure 3.

2.2. Experimental Method

The no-load speed, stall torque, and output efficiency directly determine the output performance of the ultrasonic motor and are the core indicators reflecting the motor’s performance. As preload is adjusted, the motor’s output characteristics will inevitably change. Both excessive and insufficient preload can adversely affect the motor’s performance. Therefore, there must be a relationship between preload and output characteristics. Therefore, this paper uses the no-load speed, stall torque, and output efficiency as evaluation metrics for the motor’s performance under different preloads, aiming to determine the optimal preload for the ultrasonic motor.

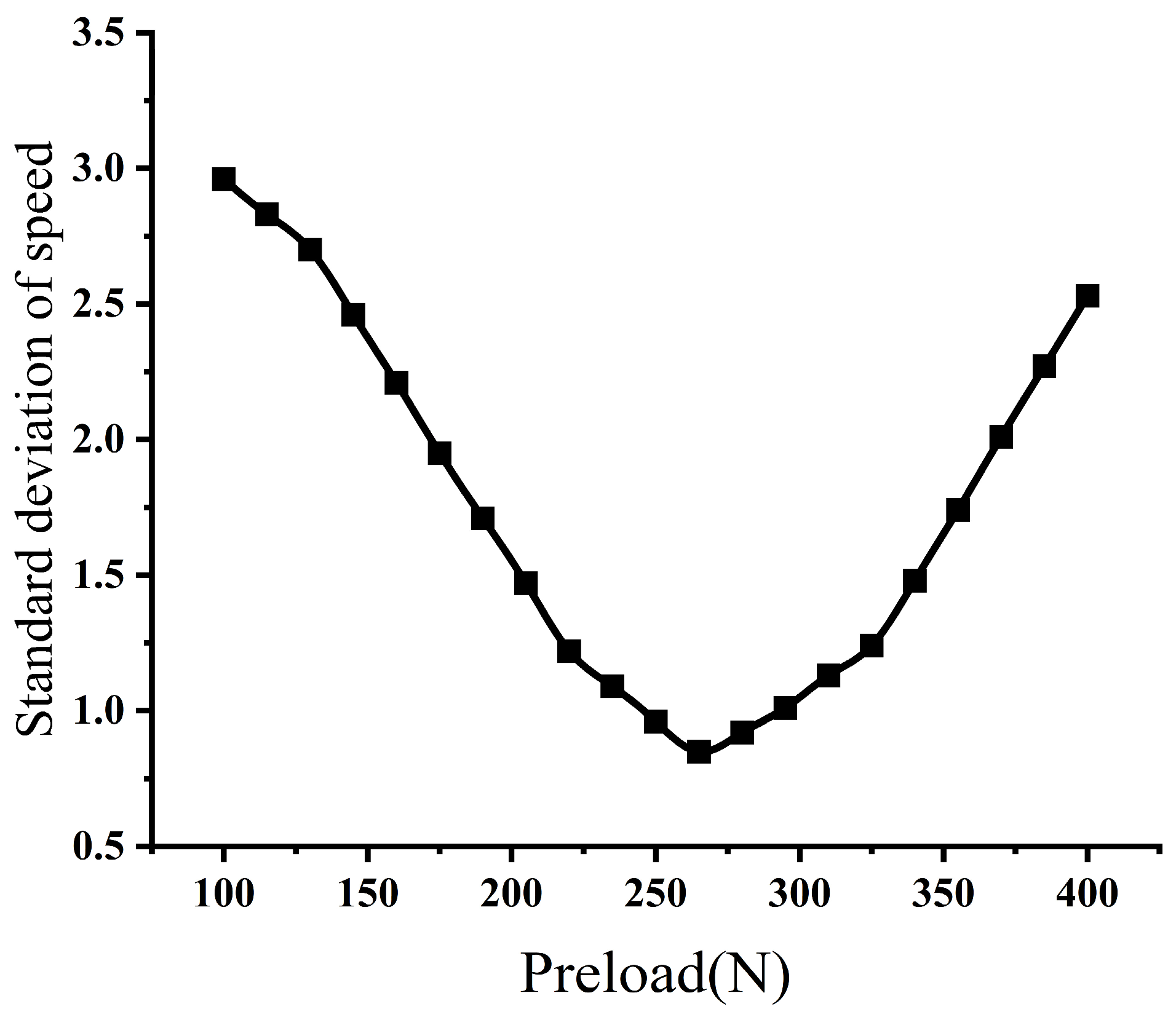
Additionally, references [16,17] have also included the standard deviation of speed as one of the evaluation indicators to reflect the speed stability of the ultrasonic motor. In this paper, the standard deviation of speed under different preloads is tested using the ultrasonic motor preload adjustment and testing platform, as shown in Figure 4. The results meet the motor’s requirements for speed stability. Pursuing an excessively low standard deviation in speed can negatively affect the optimization of other performance indicators, so the standard deviation of speed is not considered one of the evaluation metrics in this paper.

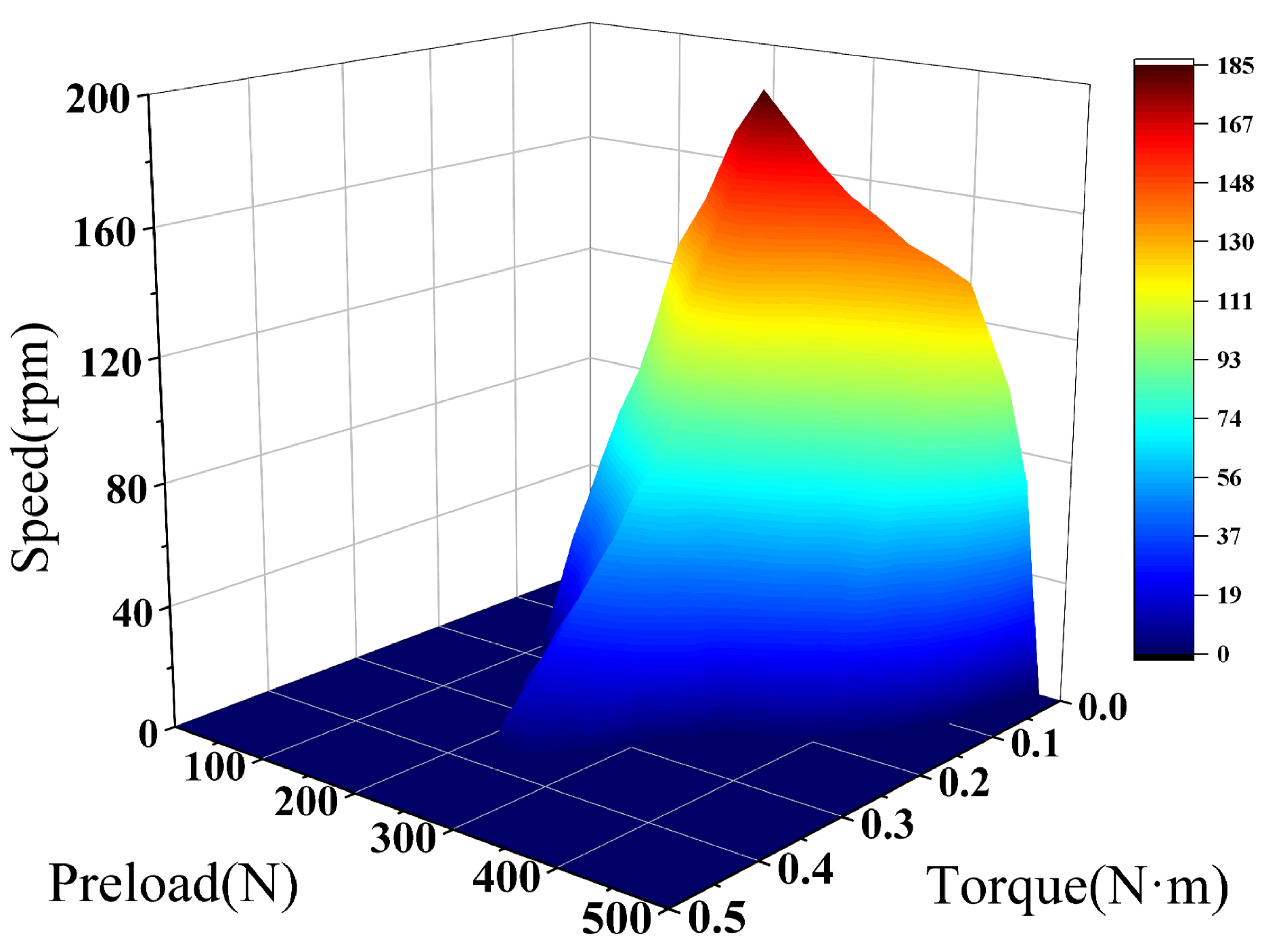
Experiments are conducted at an ambient temperature of 25 °C using an ultrasonic motor with a stator diameter of 60 mm. Meanwhile, experiments are conducted within a preload range of 100 N to 400 N, with a 15 N increment for each group, to test the motor’s input and output characteristics as the load increases. Through the ultrasonic motor preload adjustment and testing platform, the output speed and torque of the motor under different preloads and varying load torques are tested. Experimental data are used to determine the no-load speed and stall torque. Additionally, by testing the output power, input voltage, and input current during the load increase, the motor’s maximum efficiency at different preloads is calculated. The motor’s output speed and power with load torque under different preloads are shown in Figure 5 and Figure 6.

As observed, the motor’s output speed consistently decreases as the load torque increases until a stall occurs. Furthermore, at the same load torque, the motor’s output speed initially increases and then decreases as preload increases. Additionally, at a given preload, the motor’s output power increases and then decreases with the increase in load torque. Similarly, at a given load torque, the motor’s output power shows an initial increase followed by a decrease.

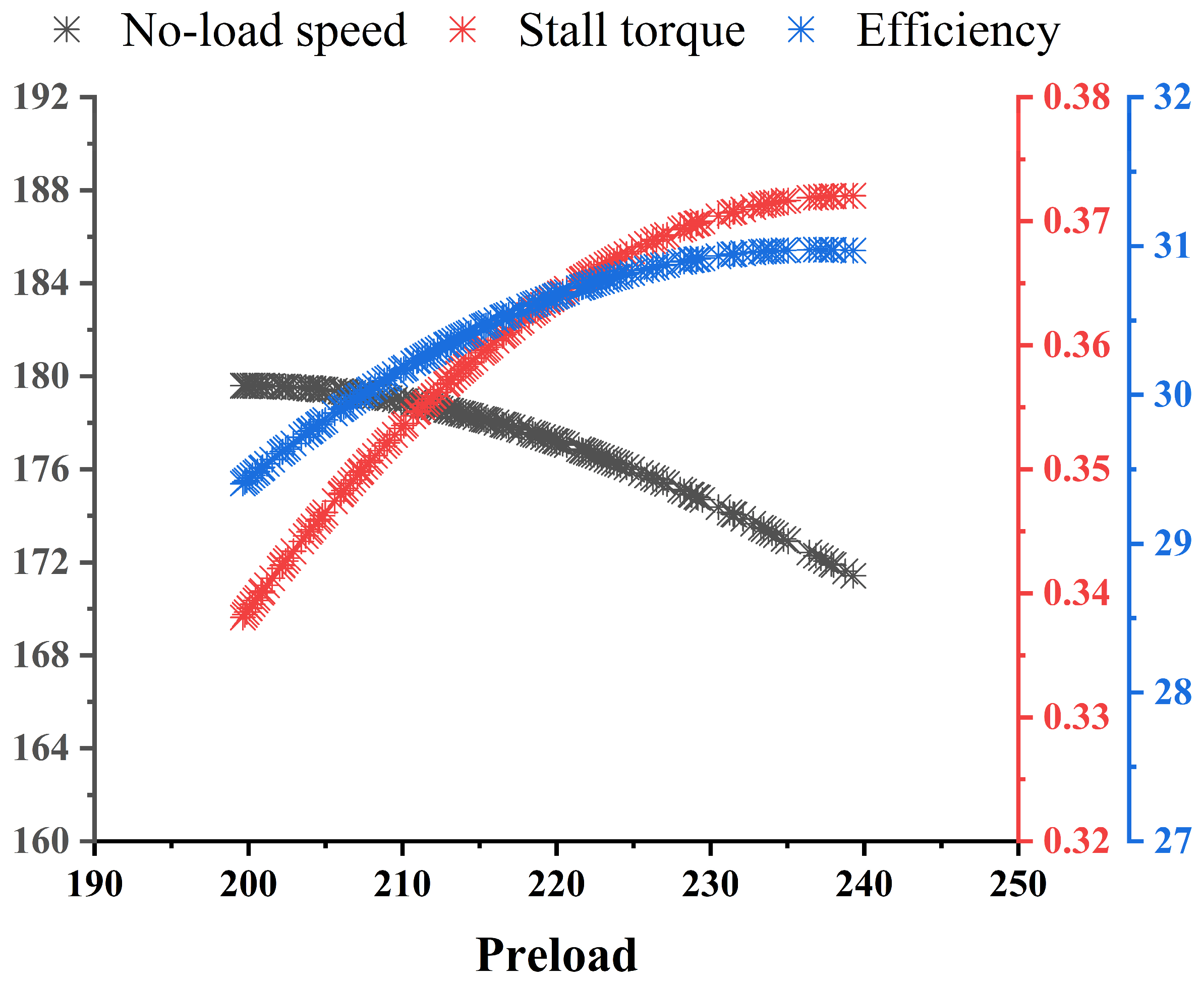
Meanwhile, the no-load speed, stall torque, and output efficiency of the ultrasonic motor under different preloads are summarized in Figure 7.

Based on the analysis of experimental data, it is clear that there is a relationship between the ultrasonic motor’s no-load speed, stall torque, output efficiency and the preload in this range. However, this relationship is neither purely positive nor negative. The optimal preload values for each of these characteristics differ. Therefore, the optimization of the optimal preload is essentially a multi-objective optimization problem.

3. NSGA-II Algorithm

NSGA-II, as an improved multi-objective optimization algorithm, introduces a fast non-dominated sorting algorithm, which greatly reduces computational complexity. It incorporates a crowding distance and crowding distance comparison operator, which evaluates the superiority of individuals by calculating crowding distance. This allows individuals in the quasi pareto front to be spread evenly across the entire pareto front, ensuring population diversity. The elitist strategy ensures that the best individuals are retained in the population, preventing the loss of optimal individuals, thus improving the accuracy and precision of the algorithm [22]. Therefore, this paper applies NSGA-II for multi-objective optimization of the preload in ultrasonic motors. The algorithm flow diagram of NSGA-II is shown in Figure 8.

3.1. Fast Non-Dominated Sorting

Let $P$ be a population containing $N$ individuals. For two individuals $x_i$ and $x_j$, if their objective functions $f\left(x_i\right)$, $f\left(x_j\right)$ satisfy:

$$\forall k\in \left\{1,2,\cdots n\right\},f_k\left(x_i\right)\le f_k\left(x_j\right)$$

(1)

and

$$\exists l\in \left\{1,2,\cdots n\right\},f_l\left(x_i\right)\le f_l\left(x_j\right)$$

(2)

then $x_i$ dominates $x_j$. Based on the domination and non-domination relationships between individuals, the non-dominated individuals form the first front of the population. This process is repeated until the entire population is divided into layers.

Fast non-dominated sorting builds a tree-like structure of dominance relationships, efficiently assigning solutions to different front layers. Furthermore, during population selection and updating, the algorithm only requires local comparisons between solutions, avoiding redundant global calculations and improving overall computational efficiency.

3.2. Crowding Distance Calculation

Crowding distance is used to analyze the density of individuals in the current non-dominated layer. Individuals with a larger crowding distance are more sparsely distributed within that layer and have a higher probability of being selected.

For each non-dominated layer, the individuals are sorted based on their objective values. The boundary individuals in the sorted list are assigned an infinite crowding distance:

$$d_1^k=d_n^k=\infty$$

(3)

For non-boundary individuals, the crowding distance is calculated as:

$$d_i^k={\displaystyle \frac{f_k\left(x_{i+1}\right)-f_k\left(x_{i-1}\right)}{f_k^{max}-f_k^{min}}}$$

(4)

where $f_k^{max}$ and $f_k^{min}$ represent the maximum and minimum values of the objective function in the non-dominated layer.

Simply put, the greater the difference in objective values between an individual and others, the higher its crowding distance. This means there are fewer individuals around it, offering a larger search space and helping avoid local optima.

3.3. Elitist Strategy

For the number $t$ generation of parent population $P_t$, selection, crossover, and mutation are performed to obtain the offspring population $Q_t$. The parent and offspring populations are then merged to form a combined population $R_t$ of size $2N$:

$$R_t=P_t\cup Q_t$$

(5)

The merged population $R_t$ undergoes non-dominated sorting, obtaining non-dominated layers, and crowding distance is calculated. The top $N$ individuals are selected to form the new generation population $P_{t+1}$.

The elitism strategy combines the parent and offspring populations to compete for the next generation. This ensures that good individuals from the parent generation are carried over, and the best individuals are not lost during the genetic and mutation processes.

3.4. Crossover and Mutation

Simulated Binary Crossover (SBX) is employed. Two parent individuals $x_1$ and $x_2$ are selected, and a uniformly distributed random number $u\in \left[0,\right.\left.1\right)$ is generated to calculate $\beta$:

$$\beta =\left\{\begin{array}{c}{\left(2u\right)}^{{\displaystyle \frac{1}{n_e+1}}}, if u\le 0.5\\ {\left({\displaystyle \frac{1}{2-2u}}\right)}^{{\displaystyle \frac{1}{n_e+1}}}, if u>0.5\end{array}\right.$$

(6)

where $n_e$ is the crossover distribution index. The offspring individuals $c_1$ and $c_2$ are then generated as:

$$\begin{array}{c}{c}_1=0.5\left(\left(1+\beta \right)x_1+\left(1-\beta \right)x_2\right)\\ c_2=0.5\left(\left(1-\beta \right)x_1+\left(1+\beta \right)x_2\right)\end{array}$$

(7)

For each offspring individual $c_i$, a uniformly distributed random number $u\in \left[0,\right.\left.1\right)$ is generated, and mutation is performed:

$$\delta =\left\{\begin{array}{c}{\left(2u\right)}^{{\displaystyle \frac{1}{n_f+1}}}-1, if u<0.5\\ 1-{\left({\displaystyle \frac{1}{2-2u}}\right)}^{{\displaystyle \frac{1}{n_f+1}}}, if u\ge 0.5\end{array}\right.$$

(8)

where $n_f$ is the mutation distribution index, $c_i$ are generated as:

$$c_i=c_i+\delta \left(c_i^{max}-c_i^{min}\right)$$

(9)

4. Multi-Objective Optimization

4.1. Objective Function Construction

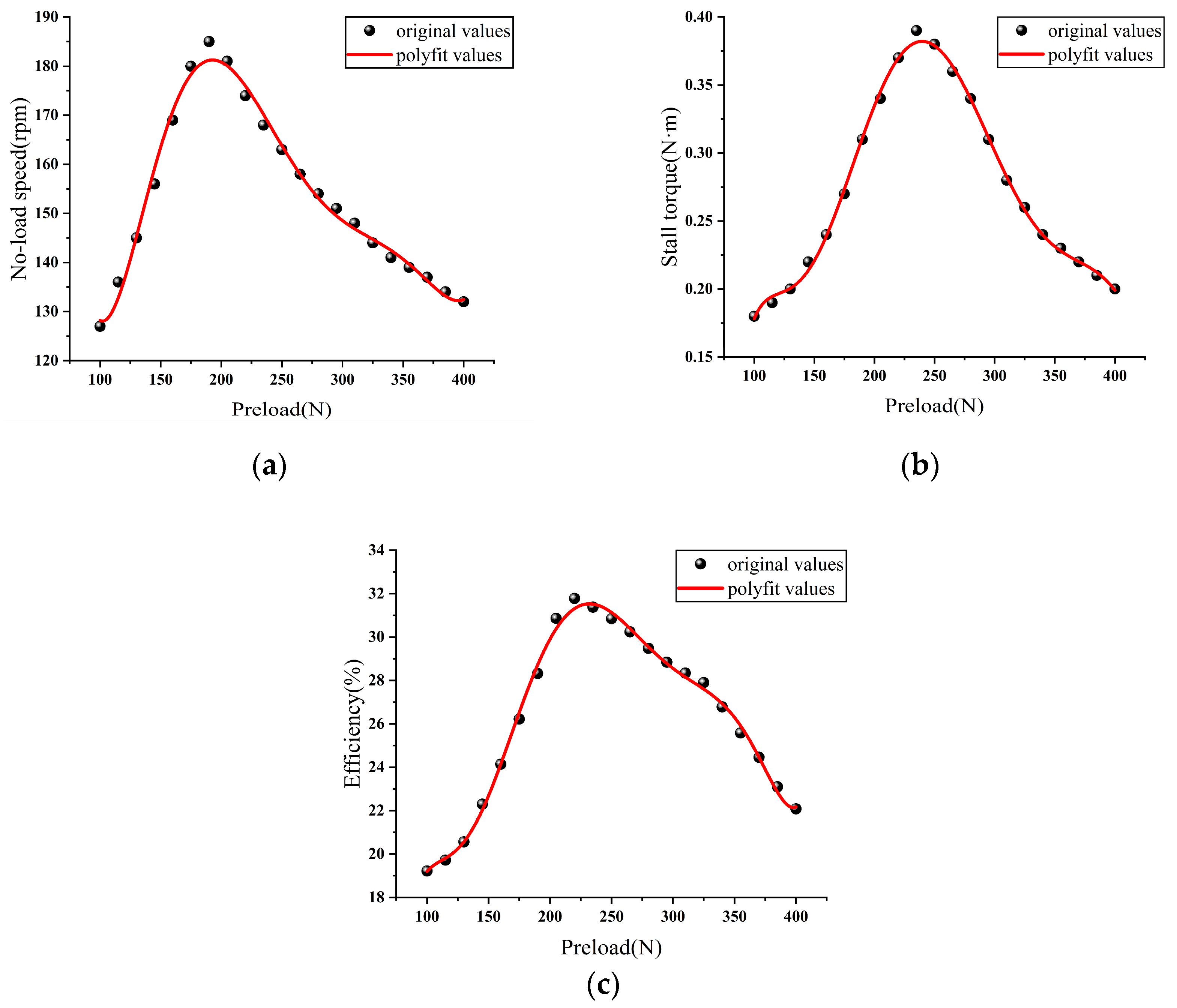
Before performing multi-objective optimization using the NSGA-II algorithm, it is necessary to establish the functional relationships between the parameters and the objectives. In this paper, a linear regression model is used to construct the objective functions. Preload is taken as the parameter, and no-load speed, stall torque, and output efficiency are the objectives. The mapping relationships between no-load speed, stall torque, output efficiency, and preload are established, and the objective functions are fitted accordingly.

The fitting models for no-load speed, stall torque, and output efficiency in relation to preload are shown in Figure 9.

The R-squared values of the fitting curves are 0.990, 0.997, and 0.996, respectively, indicating a good fit. The objective functions are thus successfully established.

4.2. Algorithm Optimization

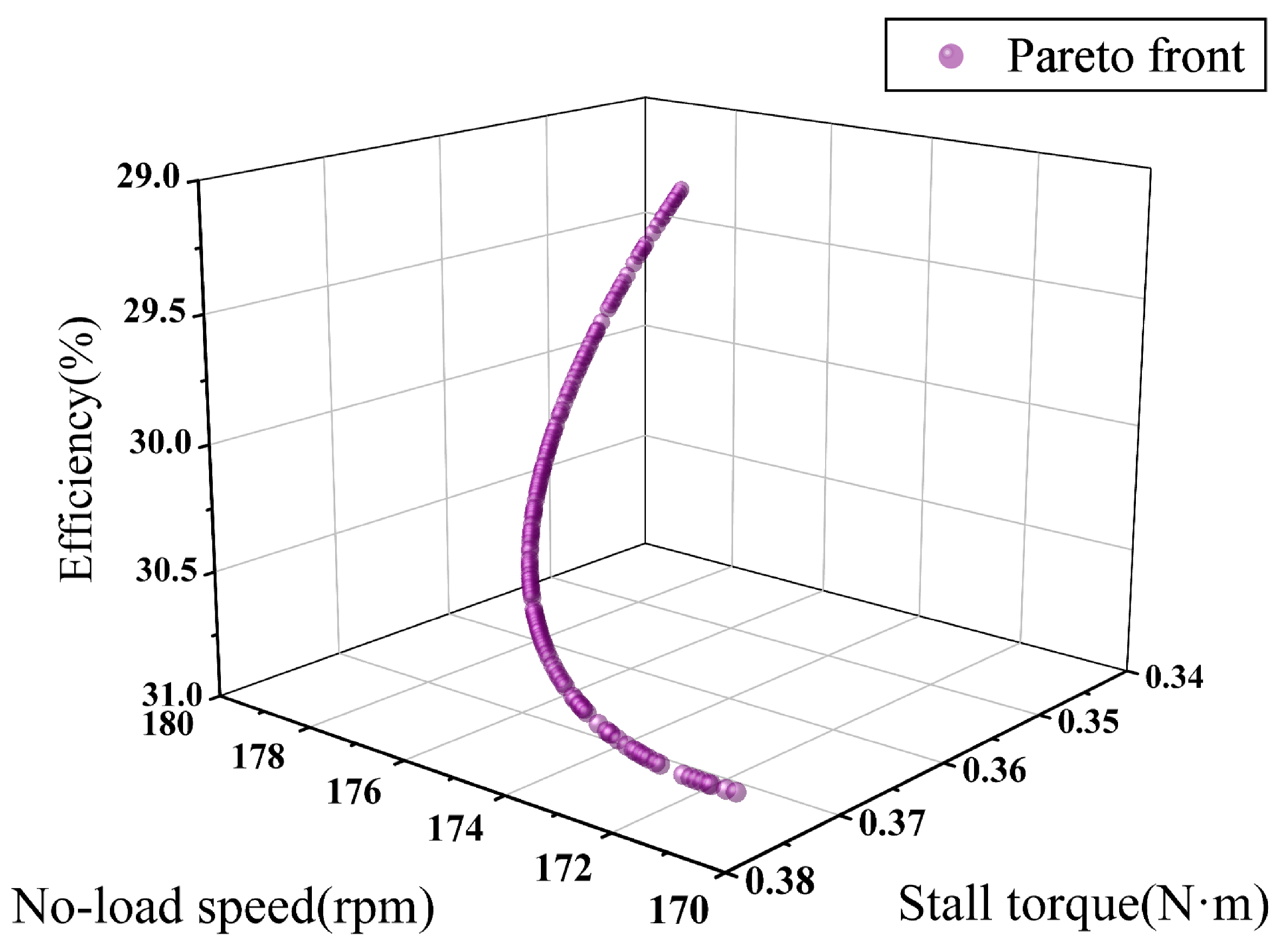
The parameters for the NSGA-II algorithm are set as follows: crossover probability is 0.85, population size is 150, maximum number of iterations is 500, and fitness function deviation is 0.01. The algorithm is run in MATLAB R2021b to maximize all three objective functions. The optimized Pareto front is shown in Figure 10, and the corresponding preloads of the Pareto front are shown in Figure 11. The top 10 ranked individuals in the Pareto front and their corresponding preloads are listed in

Table 1. Top 10 ranked individuals in the Pareto front.

Preload (N)	No-Load Speed (rpm)	Stall Torque (N·m)	Output Efficiency (%)
236.9	172.3	0.372	30.98
237.4	172.1	0.372	30.98
238.6	171.7	0.372	30.97
239.3	171.4	0.372	30.97
213.2	178.5	0.357	30.35
211.9	178.7	0.356	30.28
206.2	179.3	0.348	29.92
200.8	179.6	0.340	29.51
200.0	179.6	0.339	29.44
199.6	179.6	0.338	29.40

.

It can be seen that the optimal preload range for the motor is between 200 N and 240 N. Furthermore, the individual ranked first in the Pareto front is the optimal solution for the multi-objective optimization, with the optimal preload being 236.9 N. The corresponding no-load speed is 172.3 rpm, the stall torque is 0.372 N·m, and the output efficiency is 30.98%.

Additionally, the computational complexity and simulation speed of several optimization algorithms are compared. With a population size of 150, the simulation runtime of the MOEAD algorithm exceeds 40 s, is around 20 s for the MOPSO algorithm, and less than 10 s for the NSGA-II algorithm. Therefore, the NSGA-II algorithm features lower computational complexity, faster computation, and easier implementation, making it more suitable for ultrasonic motor preload optimization.

4.3. Optimization Results and Validation

The ultrasonic motor used in this study has a fixed and non-adjustable original preload. By constructing the preload application and adjustment module, the preload of the motor is adjusted. After optimization using the NSGA-II algorithm, the motor’s performance improvements are shown in

Table 2. Motor performance comparison before and after optimization.

Index	No-Load Speed (rpm)	Stall Torque (N·m)	Output Efficiency (%)
Original preload	164.2	0.295	27.84
Optimized preload	172.3	0.372	30.98
Absolute value	+8.1	+0.077	+3.14
Percentage	+4.93%	+26.10%	+11.28%

.

After preload optimization, the friction between the stator and rotor is in an optimal state. The efficiency of converting the ultrasonic vibrations from the piezoelectric ceramics into a traveling wave is greatly improved. The experimental results show that all three major performance indicators of the motor have significant improvements. As can be seen, the absolute value of the no-load speed increased by 8.1 rpm, a 4.93% improvement. The stall torque increased by 0.077 N·m, a 26.10% improvement. The output efficiency increased by 3.14%, an 11.28% improvement.

Additionally, the AHP used in reference [17] neglects the no-load speed of the motor while aiming for an excessively low standard deviation in speed. A comparison between the preload optimization method based on NSGA-II and the AHP is shown in

Table 3. Comparison between NSGA-II and AHP.

Optimization Method	Preload (N)	No-Load Speed (rpm)	Stall Torque (N·m)	Output Efficiency (%)
AHP	310	−5.5%	+20.7%	+15.3%
NSGA-II	236.9	+4.93%	+26.10%	+11.28%

. It can be seen that the preload optimization method proposed in this paper provides better optimization results for the no-load speed and stall torque of the motor, leading to superior motor performance.

To verify the accuracy of the optimization algorithm, experimental tests were conducted on the preload adjustment and testing platform. The preload of the ultrasonic motor was adjusted to 236.9 N. The no-load speed, stall torque, and output efficiency at the optimal preload were measured as 167.2 rpm, 0.388 N·m, and 29.93%, respectively. The errors between N·m, the algorithm-optimized values, and the testing values were 3.05%, 4.12%, and 3.51%, as shown in

Table 4. Comparison between optimized values and testing values.

Preload: 236.9 N	No-Load Speed (rpm)	Stall Torque (N·m)	Output Efficiency (%)
Optimized values	172.3	0.372	30.98
Testing values	167.2	0.388	29.93
Error	3.05%	4.12%	3.51%

. It can be seen that the errors between the optimized values and the testing values are small, indicating that the optimization method has good accuracy and meets the expected requirements.

Through the analysis of experimental results and experimental verification, after preload optimization using the NSGA-II algorithm, the performance indicators of the ultrasonic motor, including no-load speed, stall torque, and output efficiency, all show varying degrees of improvement. Compared to other methods, the optimization effect is better, with higher optimization accuracy and precision.

5. Conclusions

To solve the problem of determining the optimal preload for ultrasonic motors, this paper proposes a preload optimization method based on NSGA-II, performing multi-objective optimization of the motor’s key performance indicators. Both simulation and experimental results show that this method can determine the optimal preload for the motor, achieving the best output performance.

• Through experimental testing of the motor’s characteristics, the relationship between preload and motor performance was analyzed. A linear regression model was used to establish predictive models for the no-load speed, stall torque, and output efficiency as functions of the preload. The goodness of fit is satisfactory, making these models suitable as objective functions for multi-objective optimization.
• After optimizing the preload using the NSGA-II algorithm, the no-load speed improved by 4.93%, the stall torque increased by 26.10%, and the output efficiency rose by 11.28%. Compared to existing optimization methods, this method yields better optimization results, allowing the motor to achieve its best performance. Furthermore, the errors between the optimized values and testing values for the three performance indicators are 3.05%, 4.12%, and 3.51%, respectively, meeting the accuracy requirements.
• In the field of ultrasonic motors, existing preload optimization methods typically either fail to determine the exact optimal preload value, cannot guarantee optimization accuracy and precision, or are complex and difficult to implement. The preload optimization method based on NSGA-II proposed in this paper has low computational complexity, is easy to implement, and offers good optimization effects and accuracy. Therefore, the NSGA-II-based preload optimization method can enhance the performance of ultrasonic motors in reality applications. It can meet the higher demands for motor speed, torque, and efficiency in various operating conditions, making it more aligned with practical needs.