Observer Design for State and Parameter Estimation for Two-Time-Scale Nonlinear Systems
Abstract
1. Introduction
2. Preliminaries
3. Main Results
3.1. Model Reduction
3.2. Observer Design
4. Examples
4.1. Numerical System
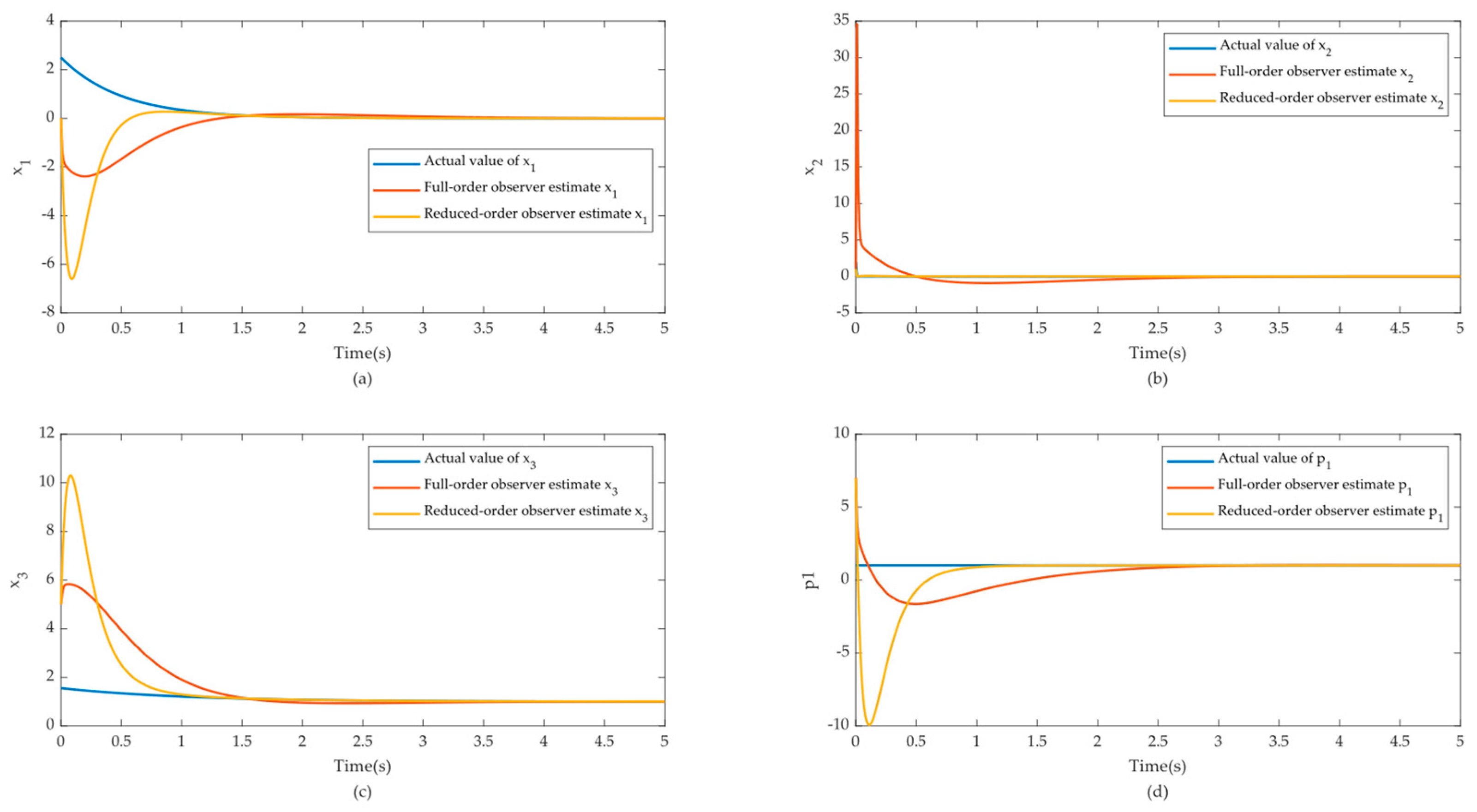
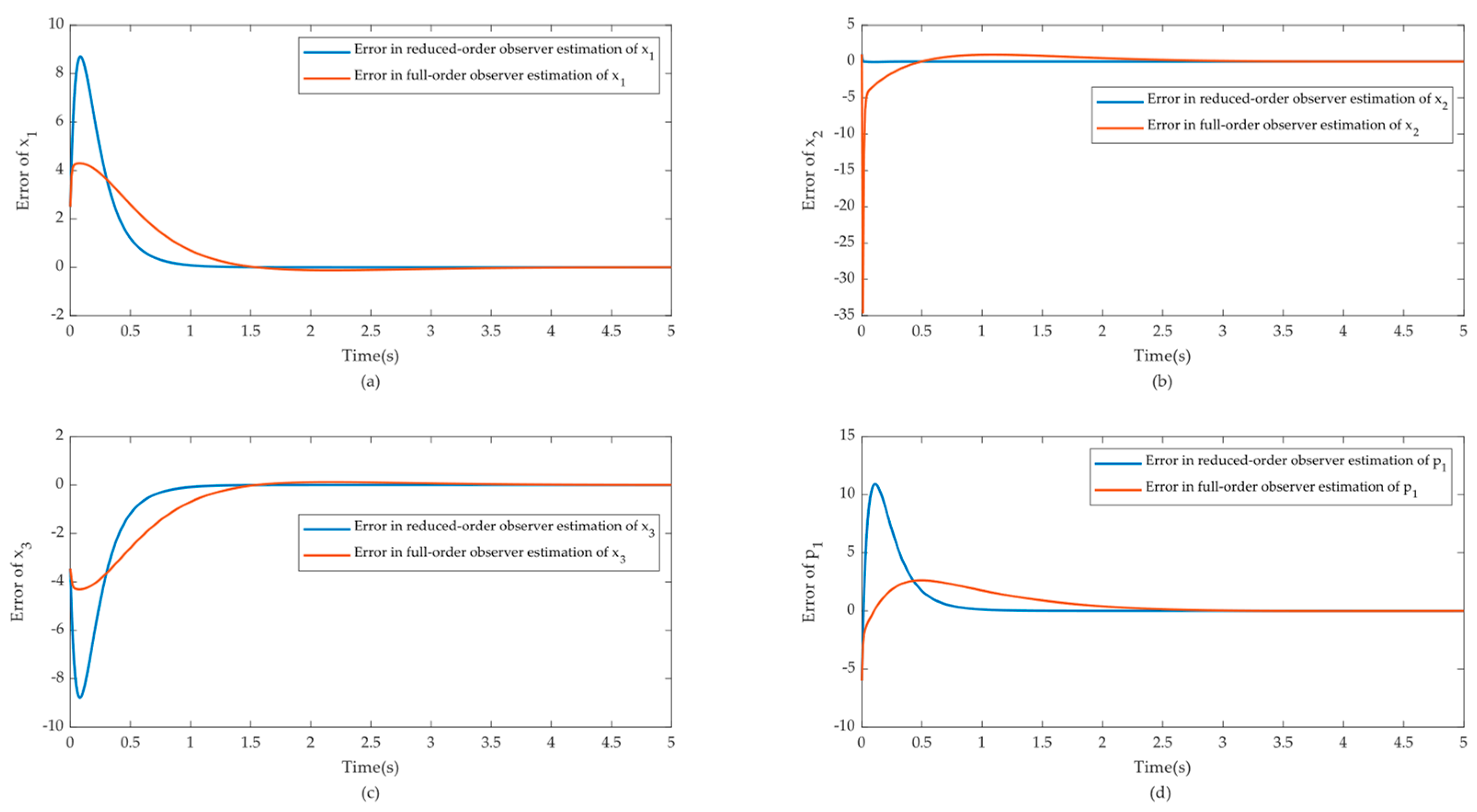
4.1.1. Observer Design Based on the Original System
4.1.2. Observer Design Based on the Reduced-Order System
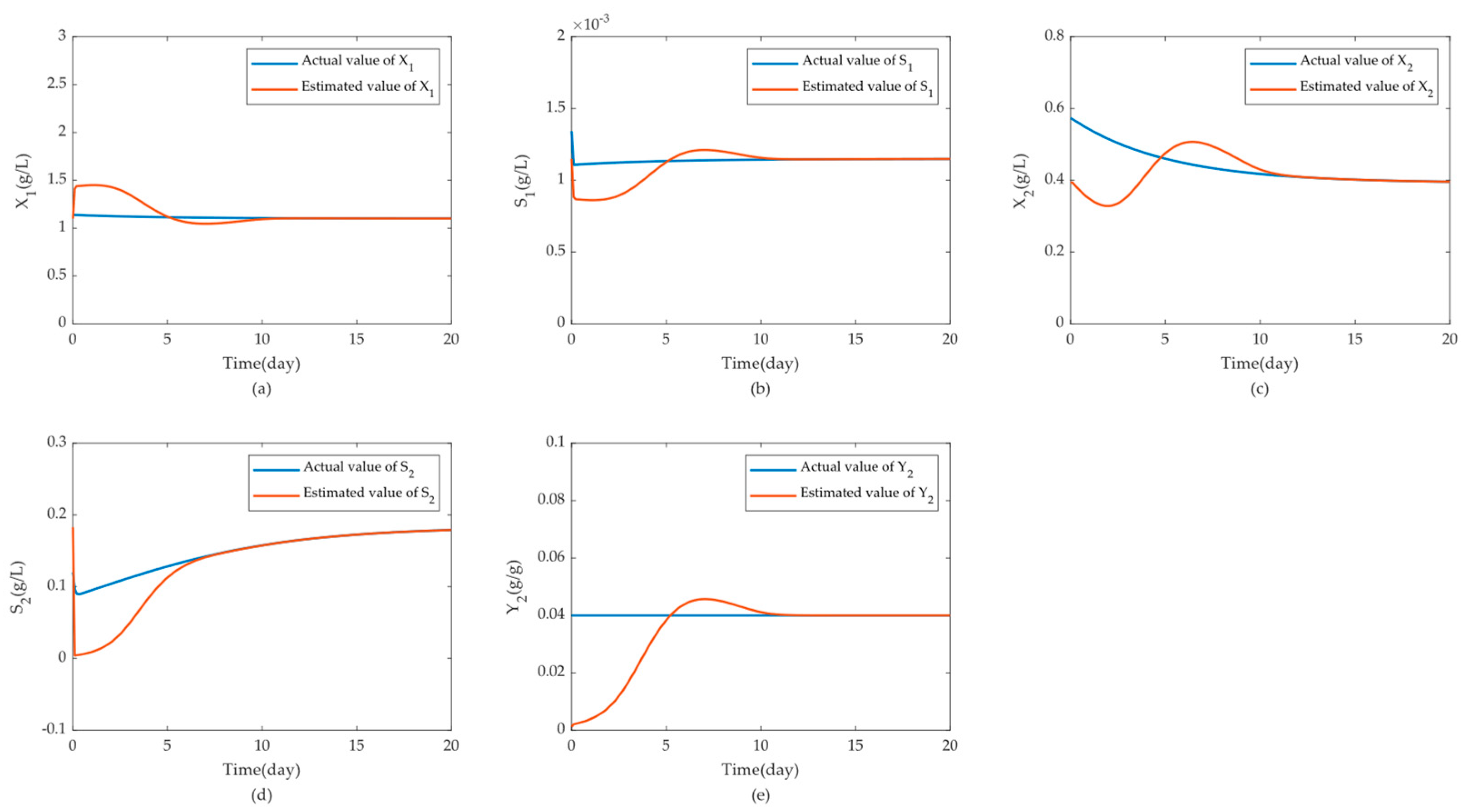
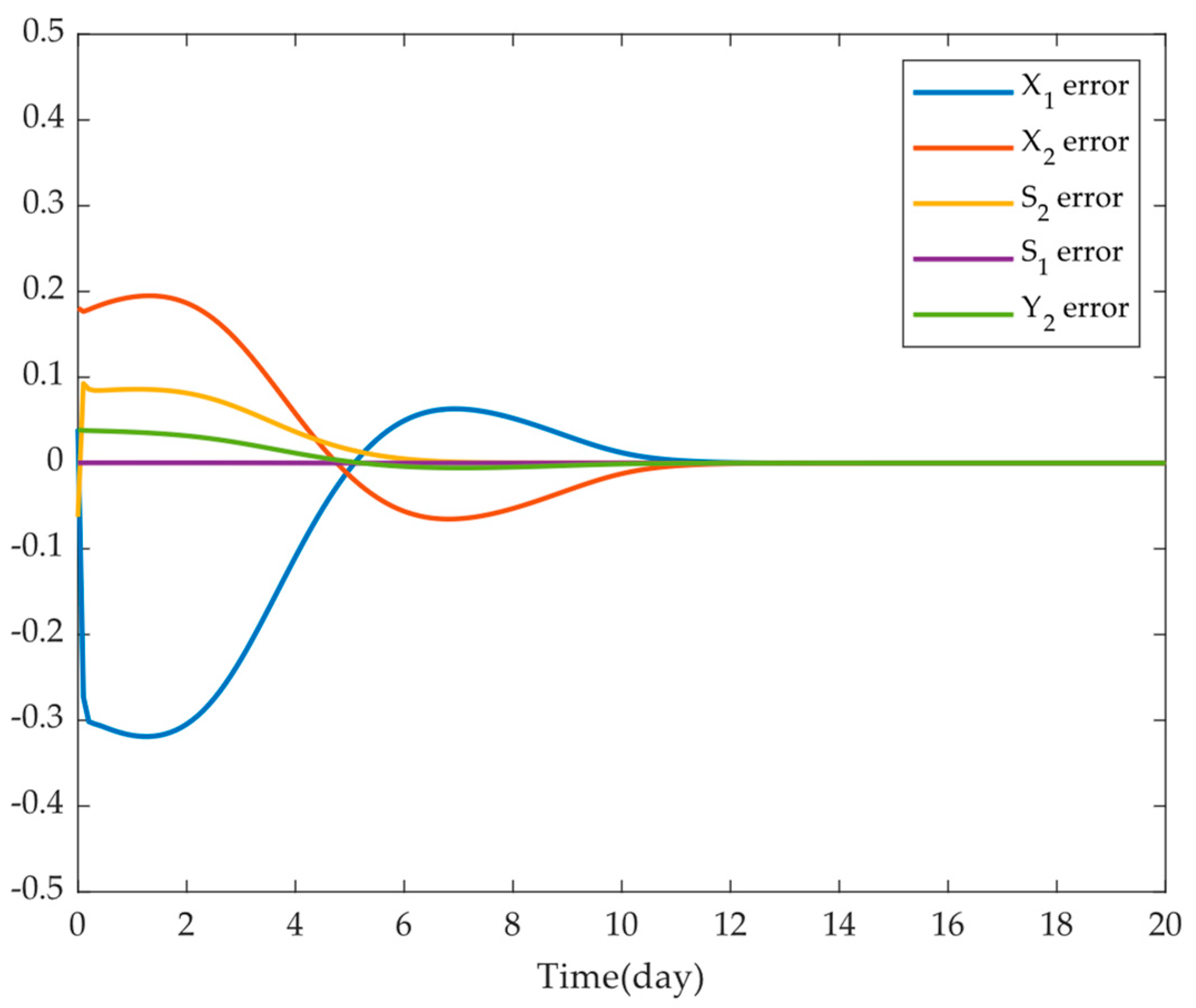
4.2. Anaerobic Digestion System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bernard, P.; Andrieu, V.; Astolfi, D. Observer design for continuous-time dynamical systems. Annu. Rev. Control 2022, 53, 224–248. [Google Scholar] [CrossRef]
- Ding, F. Least squares parameter estimation and multi-innovation least squares methods for linear fitting problems from noisy data. J. Comput. Appl. Math. 2023, 426, 115107. [Google Scholar] [CrossRef]
- Lathrop, P.M.; Duan, Z.; Ling, C.; Elabd, Y.A.; Kravaris, C. Modeling and observer-based monitoring of RAFT homopolymerization reactions. Processes 2019, 7, 768. [Google Scholar] [CrossRef]
- Corigliano, A.; Mariani, S. Parameter identification in explicit structural dynamics: Performance of the extended Kalman filter. Comput. Methods Appl. Mech. Eng. 2004, 193, 3807–3835. [Google Scholar] [CrossRef]
- Wang, C.; Wang, S.; Zhou, J.; Qiao, J.; Yang, X.; Xie, Y. A novel back propagation neural network-dual extended Kalman filter method for state-of-charge and state-of-health co-estimation of lithium-ion batteries based on limited memory least square algorithm. J. Energy Storage 2023, 59, 106563. [Google Scholar] [CrossRef]
- Sheikholeslam, S. Observer-based parameter identifiers for nonlinear systems with parameter dependencies. IEEE Trans. Autom. Control 1995, 40, 382–387. [Google Scholar] [CrossRef]
- Zhu, M.; Wen, Y.; Sun, W.; Lei, T. Extended state observer-based parameter identification of Nomoto model for autonomous vessels. Chin. J. Ship Res. 2023, 18, 75–85. [Google Scholar]
- Patelski, R.; Pazderski, D. Novel adaptive extended state observer for dynamic parameter identification with asymptotic convergence. Energies 2022, 15, 3602. [Google Scholar] [CrossRef]
- Marzougui, S.; Bedoui, S.; Atitallah, A.; Abderrahim, K. Parameter and state estimation of nonlinear fractional-order model using Luenberger observer. Circuits Syst. Signal Process. 2022, 41, 5366–5391. [Google Scholar] [CrossRef]
- Cecilia, A.; Costa-Castello, R. Addressing the relative degree restriction in nonlinear adaptive observers: A high-gain observer approach. J. Frankl. Inst. 2022, 359, 3857–3882. [Google Scholar] [CrossRef]
- Yildiz, R.; Demir, R.; Barut, M. Online estimations for electrical and mechanical parameters of the induction motor by extended Kalman filter. Trans. Inst. Meas. Control 2023, 45, 2725–2738. [Google Scholar] [CrossRef]
- Yin, X.; Bo, S.; Liu, J.; Huang, B. Consensus-based approach for parameter and state estimation of agro-hydrological systems. AIChE J. 2021, 67, e17096. [Google Scholar] [CrossRef]
- Backi, C.J.; Gravdahl, J.T.; Skogestad, S. Combined state and parameter estimation for not fully observable dynamic systems. IFAC J. Syst. Control 2020, 13, 100103. [Google Scholar] [CrossRef]
- Afri, C.; Andrieu, V.; Bako, L.; Dufour, P. State and parameter estimation: A nonlinear Luenberger observer approach. IEEE Trans. Autom. Control 2016, 62, 973–980. [Google Scholar] [CrossRef]
- Liu, J.; Gnanasekar, A.; Zhang, Y.; Bo, S.; Liu, J.; Hu, J.; Zou, T. Simultaneous state and parameter estimation: The role of sensitivity analysis. Ind. Eng. Chem. Res. 2021, 60, 2971–2982. [Google Scholar] [CrossRef]
- Yin, X.; Liu, J. Distributed moving horizon state estimation of two-time-scale nonlinear systems. Automatica 2017, 79, 152–161. [Google Scholar] [CrossRef]
- Duan, Z.; Kravaris, C. Nonlinear observer design for two-time-scale systems. AIChE J. 2020, 66, e16956. [Google Scholar] [CrossRef]
- Yoo, H.; Gajic, Z. New designs of linear observers and observer-based controllers for singularly perturbed linear systems. IEEE Trans. Autom. Control 2018, 63, 3904–3911. [Google Scholar] [CrossRef]
- Eilertsen, J.; Schnell, S.; Walcher, S. Rigorous estimates for the quasi-steady state approximation of the Michaelis–Menten reaction mechanism at low enzyme concentrations. Nonlinear Anal. Real World Appl. 2024, 78, 104088. [Google Scholar] [CrossRef]
- Petrov, N.K. On the method of quasi-steady-state approximation. Mendeleev Commun. 2023, 33, 103–106. [Google Scholar] [CrossRef]
- Patsatzis, D.G.; Goussis, D.A. Algorithmic criteria for the validity of quasi-steady state and partial equilibrium models: The Michaelis–Menten reaction mechanism. J. Math. Biol. 2023, 87, 27. [Google Scholar] [CrossRef]
- Rao, S.; van der Schaft, A.; Jayawardhana, B. A graph-theoretical approach for the analysis and model reduction of complex-balanced chemical reaction networks. J. Math. Chem. 2013, 51, 2401–2422. [Google Scholar] [CrossRef]
- Li, M.; Wang, R.Q.; Jia, G. Efficient dimension reduction and surrogate-based sensitivity analysis for expensive models with high-dimensional outputs. Reliab. Eng. Syst. Saf. 2020, 195, 106725. [Google Scholar] [CrossRef]
- Hasan, B.M.S.; Abdulazeez, A.M. A review of principal component analysis algorithm for dimensionality reduction. J. Soft Comput. Data Min. 2021, 2, 20–30. [Google Scholar]
- Tan, X.; Li, C.; Liu, D.; Wang, H.; Lu, X.; Zhu, Z.; Xu, R. Stability analysis and singular perturbation model reduction of DFIG-based variable-speed pumped storage unit adopting the fast speed control strategy. J. Energy Storage 2024, 87, 111340. [Google Scholar] [CrossRef]
- Duan, Z.; Wilms, T.; Neubauer, P.; Kravaris, C.; Bournazou, M.N.C. Model reduction of aerobic bioprocess models for efficient simulation. Chem. Eng. Sci. 2020, 217, 115512. [Google Scholar] [CrossRef]
- Mereles, A.; Alves, D.S.; Cavalca, K.L. Model reduction of rotor-foundation systems using the approximate invariant manifold method. Nonlinear Dyn. 2023, 111, 10743–10768. [Google Scholar] [CrossRef]
- Jain, S.; Haller, G. How to compute invariant manifolds and their reduced dynamics in high-dimensional finite element models. Nonlinear Dyn. 2022, 107, 1417–1450. [Google Scholar] [CrossRef]
- Hooshmand, H.; Fateh, M. Voltage control of flexible-joint robot manipulators using singular perturbation technique for model order reduction. J. Electr. Comput. Eng. Innov. 2022, 10, 123–142. [Google Scholar]
- Farza, M.; Ménard, T.; Ltaief, A.; Maatoug, T.; M’Saad, M.; Koubaa, Y. Extended high gain observer design for state and parameter estimation. In Proceedings of the 2015 4th International Conference on Systems and Control (ICSC), Sousse, Tunisia, 28–30 April 2015; pp. 345–350. [Google Scholar]
- Kazantzis, N.; Kravaris, C.; Syrou, L. A new model reduction method for nonlinear dynamical systems. Nonlinear Dyn. 2010, 59, 183–194. [Google Scholar] [CrossRef]
- Brandon, J. Introduction to applied nonlinear dynamical systems and chaos. Math. Gaz. 1991, 75, 255. [Google Scholar] [CrossRef]
- Stamatelatou, K.; Syrou, L.; Kravaris, C.; Lyberatos, G. An invariant manifold approach for CSTR model reduction in the presence of multi-step biochemical reaction schemes. Application to anaerobic digestion. Chem. Eng. J. 2009, 150, 462–475. [Google Scholar] [CrossRef]
- Woodbury, D.P. Accounting for Parameter Uncertainty in Reduced-Order Static and Dynamic Systems; Texas A&M University: College Station, TX, USA, 2011. [Google Scholar]
- Villaverde, A.F. Observability and structural identifiability of nonlinear biological systems. Complexity 2019, 2019, 8497093. [Google Scholar] [CrossRef]
- Byrnes, C.I.; Pandian, S.V. Exponential observer design. In Nonlinear Control Systems Design 1992; Elsevier: Amsterdam, The Netherlands, 1993; pp. 215–218. [Google Scholar]
- Kazantzis, N.; Kravaris, C. Nonlinear observer design using Lyapunov’s auxiliary theorem. Syst. Control Lett. 1998, 34, 241–247. [Google Scholar] [CrossRef]
- Kravaris, C.; Hahn, J.; Chu, Y. Advances and selected recent developments in state and parameter estimation. Comput. Chem. Eng. 2013, 51, 111–123. [Google Scholar] [CrossRef]
- Ram, N.R.; Nikhil, G.N. Assessment of microbial consortiums and their metabolic patterns during the bioconversion of food waste. Biomass Convers. Biorefinery 2023, 1–14. [Google Scholar] [CrossRef]
- Nabaterega, R.; Kumar, V.; Khoei, S.; Eskicioglu, C. A review on two-stage anaerobic digestion options for optimizing municipal wastewater sludge treatment process. J. Environ. Chem. Eng. 2021, 9, 105502. [Google Scholar] [CrossRef]
- Cárdenas, D.C.L.; Bournazou, M.N.C.; Barz, T.; Neubauer, P. Parameter Estimation, Ill-Conditioning and Identifiability Analysis of the Anaerobic Digestion Model No 1 (adm1) for Biogas Production. In Proceedings of the 2016 SIAM Annual Meeting, Boston, MA, USA, 11-15 July 2016. [Google Scholar]
- Kazantzis, N. Singular PDEs and the problem of finding invariant manifolds for nonlinear dynamical systems. Phys. Lett. A 2000, 272, 257–263. [Google Scholar] [CrossRef]

| Parameters | Implication | Value | Unit |
|---|---|---|---|
| Organic substrates concentration in feed | |||
| Dilution rate | |||
| Acid-producing bacteria yield coefficients | |||
| Methanogenic bacteria yield coefficients | |||
| Stoichiometric coefficients for the conversion of organic substrates to volatile fatty acids | |||
| Maximum growth rate of acid-producing bacteria | |||
| Maximum growth rate of methanogenic bacteria | |||
| Saturation factor of acid producing bacteria | |||
| Saturation factor of methanogenic bacteria | |||
| Inhibition factor of volatile fatty acids |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Z.; Duan, Z. Observer Design for State and Parameter Estimation for Two-Time-Scale Nonlinear Systems. Processes 2024, 12, 2875. https://doi.org/10.3390/pr12122875
Xiao Z, Duan Z. Observer Design for State and Parameter Estimation for Two-Time-Scale Nonlinear Systems. Processes. 2024; 12(12):2875. https://doi.org/10.3390/pr12122875
Chicago/Turabian StyleXiao, Zhenyu, and Zhaoyang Duan. 2024. "Observer Design for State and Parameter Estimation for Two-Time-Scale Nonlinear Systems" Processes 12, no. 12: 2875. https://doi.org/10.3390/pr12122875
APA StyleXiao, Z., & Duan, Z. (2024). Observer Design for State and Parameter Estimation for Two-Time-Scale Nonlinear Systems. Processes, 12(12), 2875. https://doi.org/10.3390/pr12122875








