Investigation of a Cogeneration System Combining a Solid Oxide Fuel Cell and the Organic Rankine Cycle: Parametric Analysis and Multi-Objective Optimization
Abstract
1. Introduction
2. Methodology
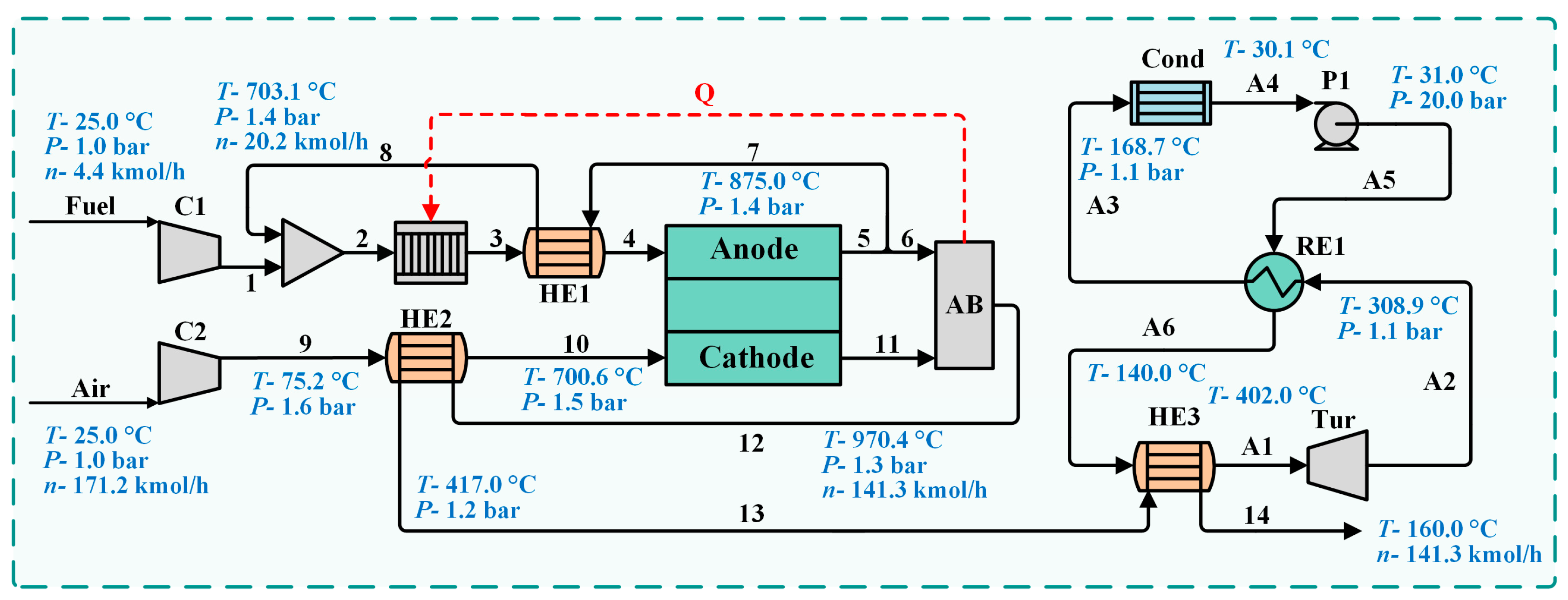
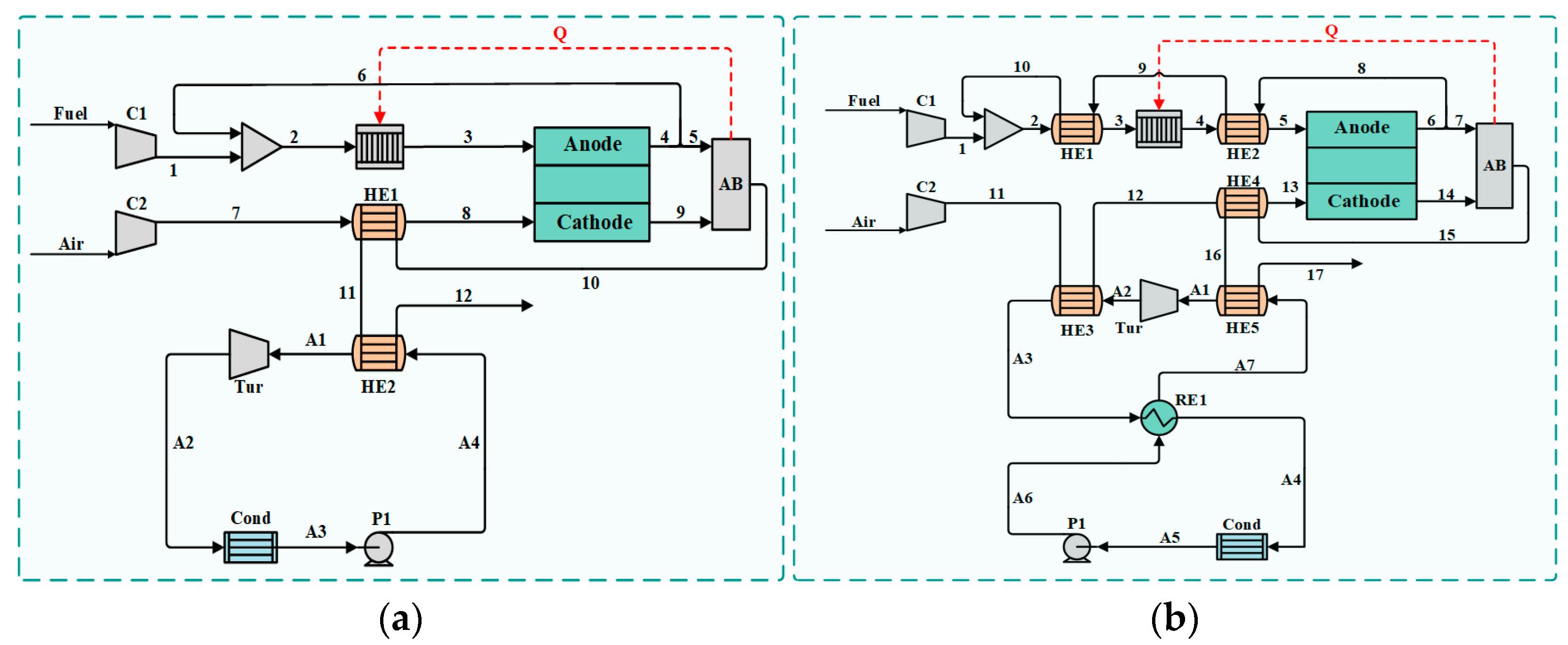
2.1. System Description
2.2. Simulation Models
- (1)
- Basic assumptions
- (2)
- Pre-reformer reactor model
- (3)
- SOFC stack model
- (4)
- ORC subsystem
2.3. Performance Indicators
- (1)
- Energy performance indicators
- (2)
- Exergy performance indicators
- (3)
- Economic performance indicators
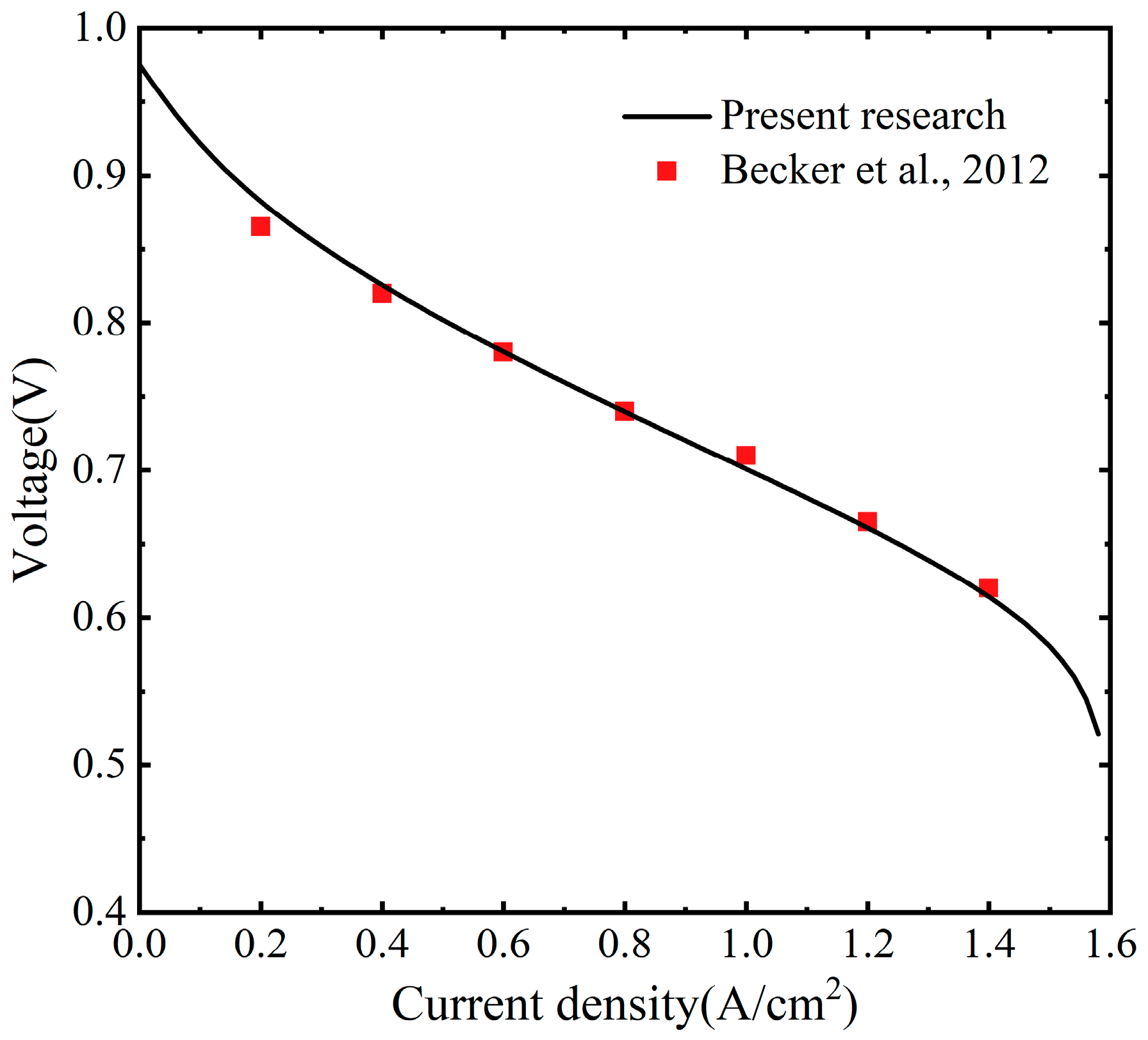
2.4. Model Verification
3. Parametric and Performance Analyses
3.1. Current Density
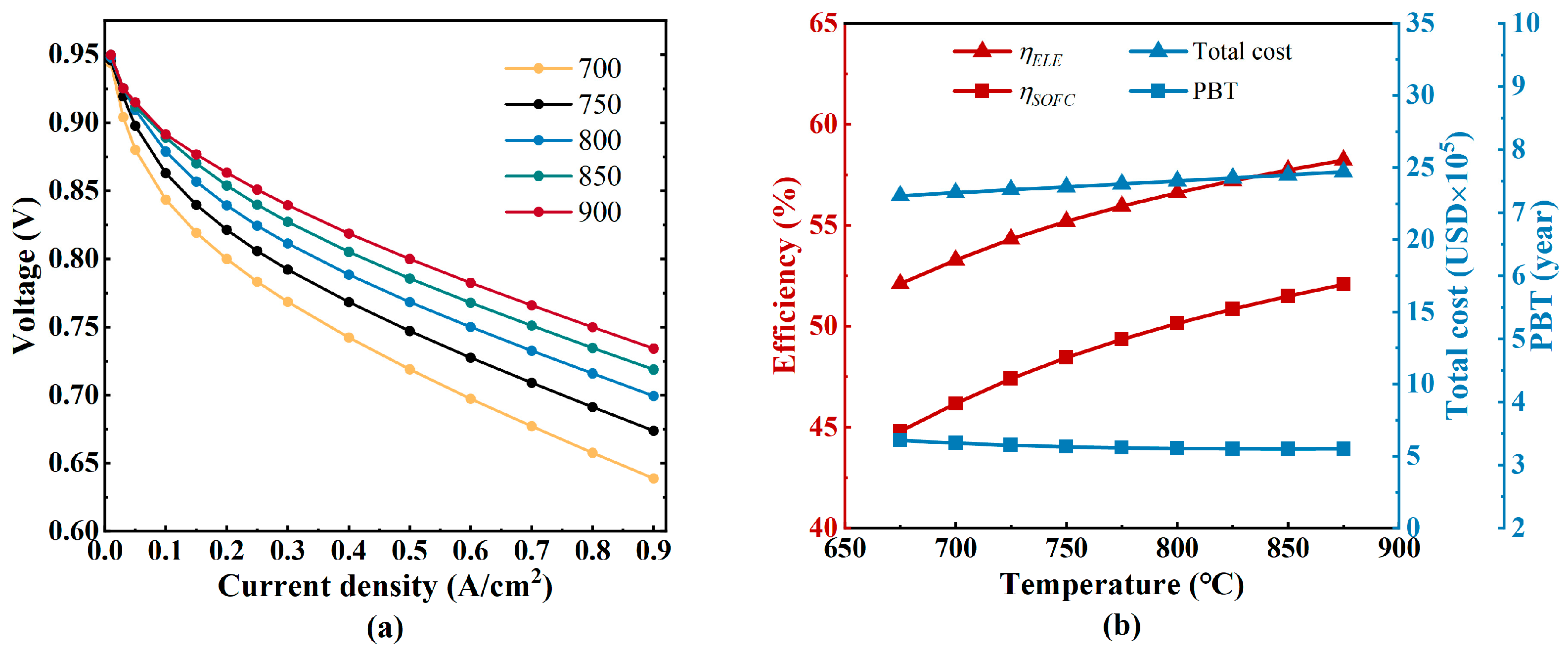
3.2. Average Stack Temperature
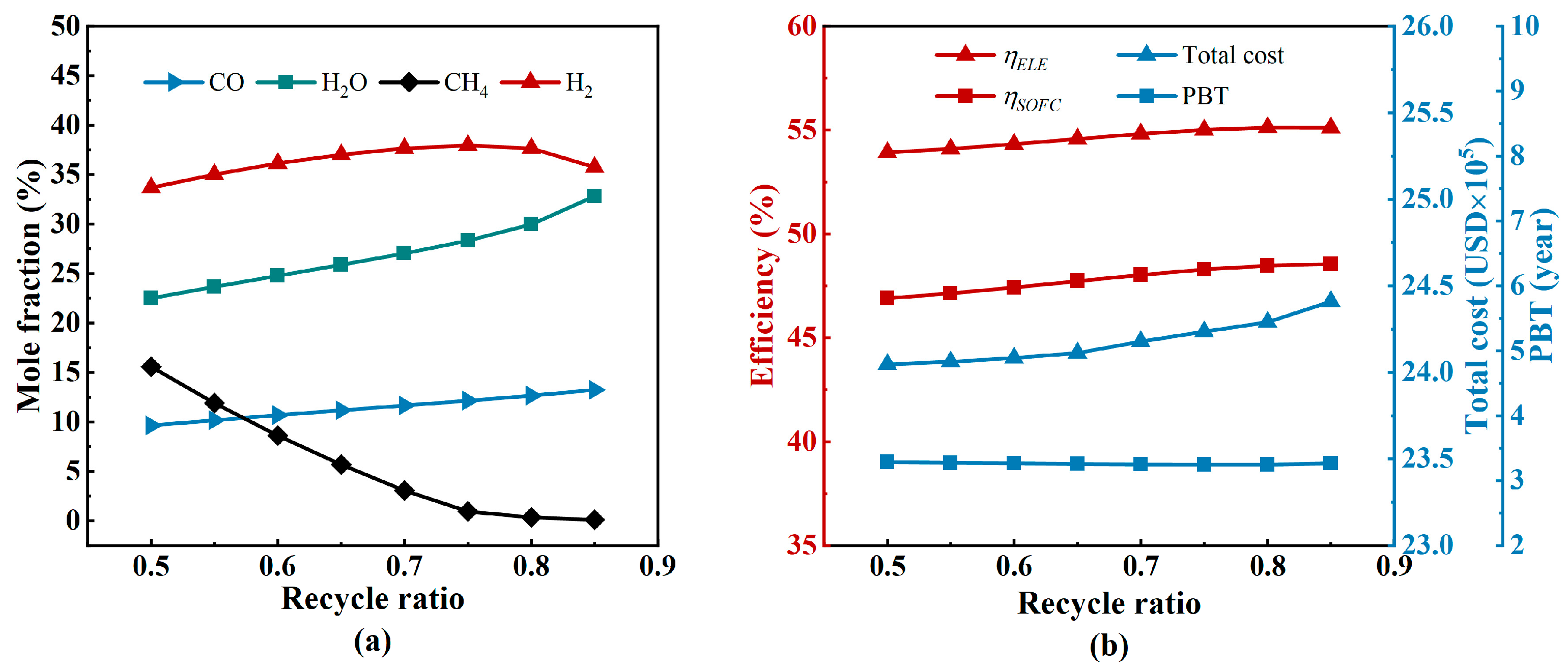
3.3. Anode Recycle Ratio
3.4. System Performance
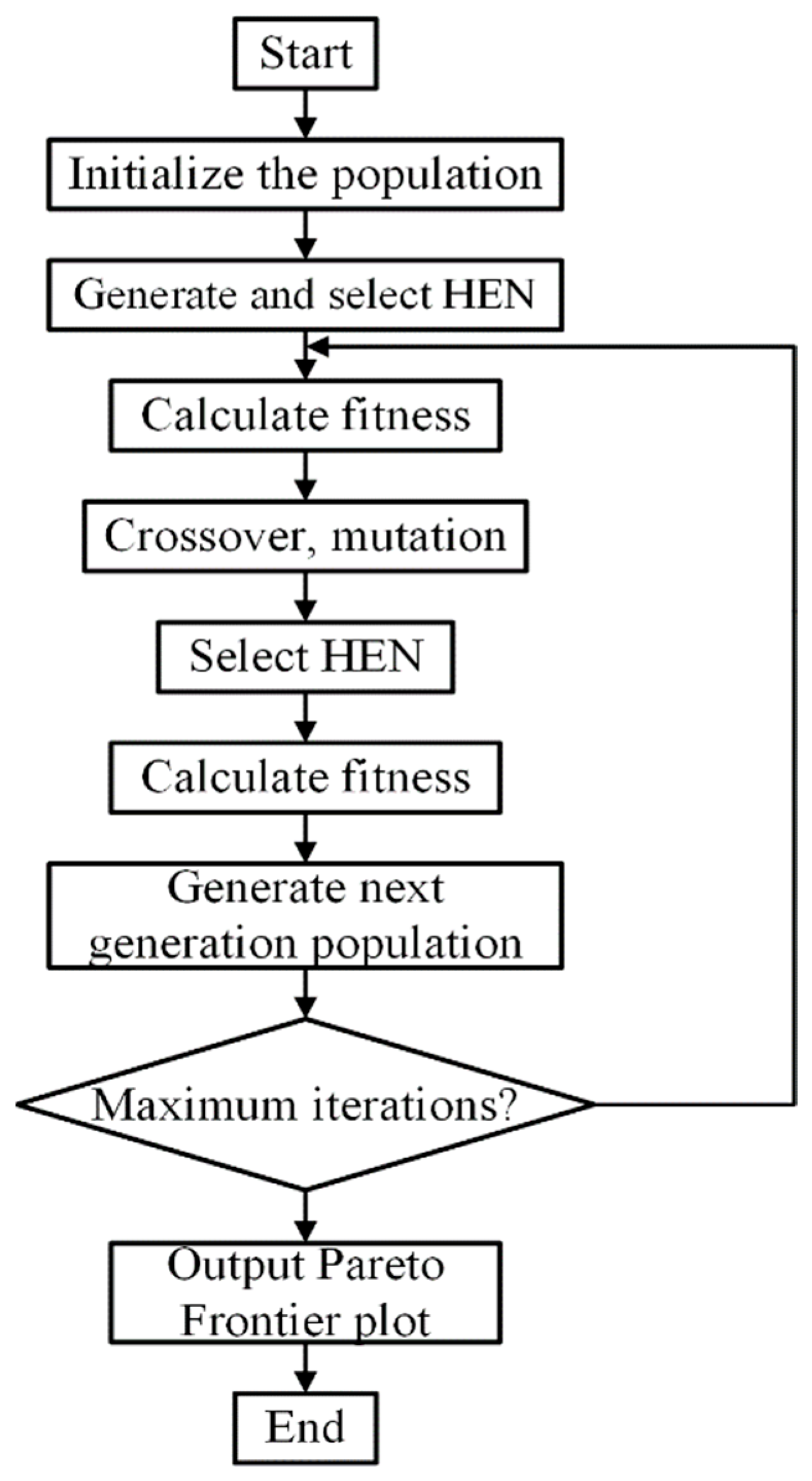
4. System Optimization
4.1. Optimization Model
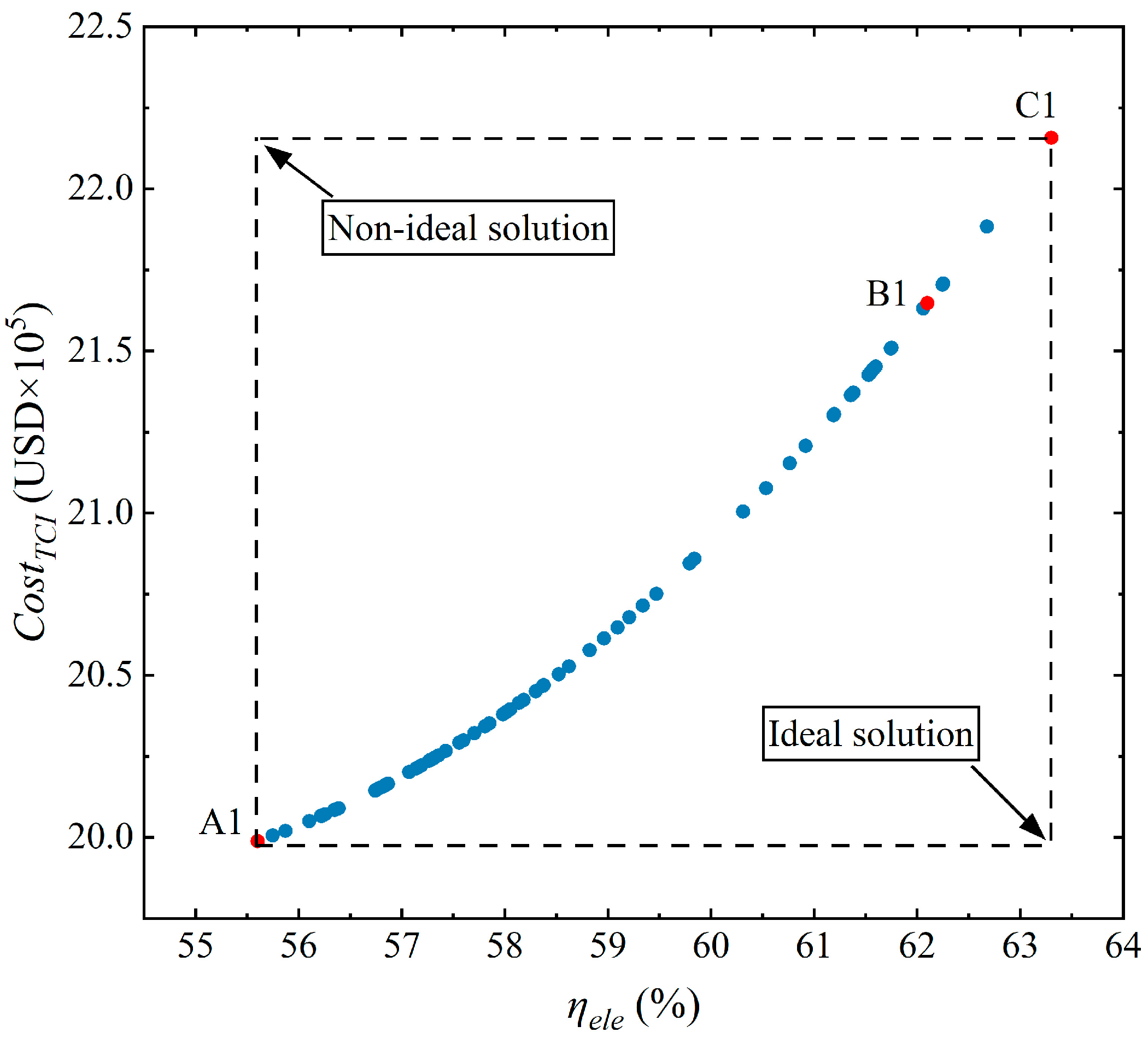
4.2. Optimization Results of Case 1 (ηele-CostTCI)
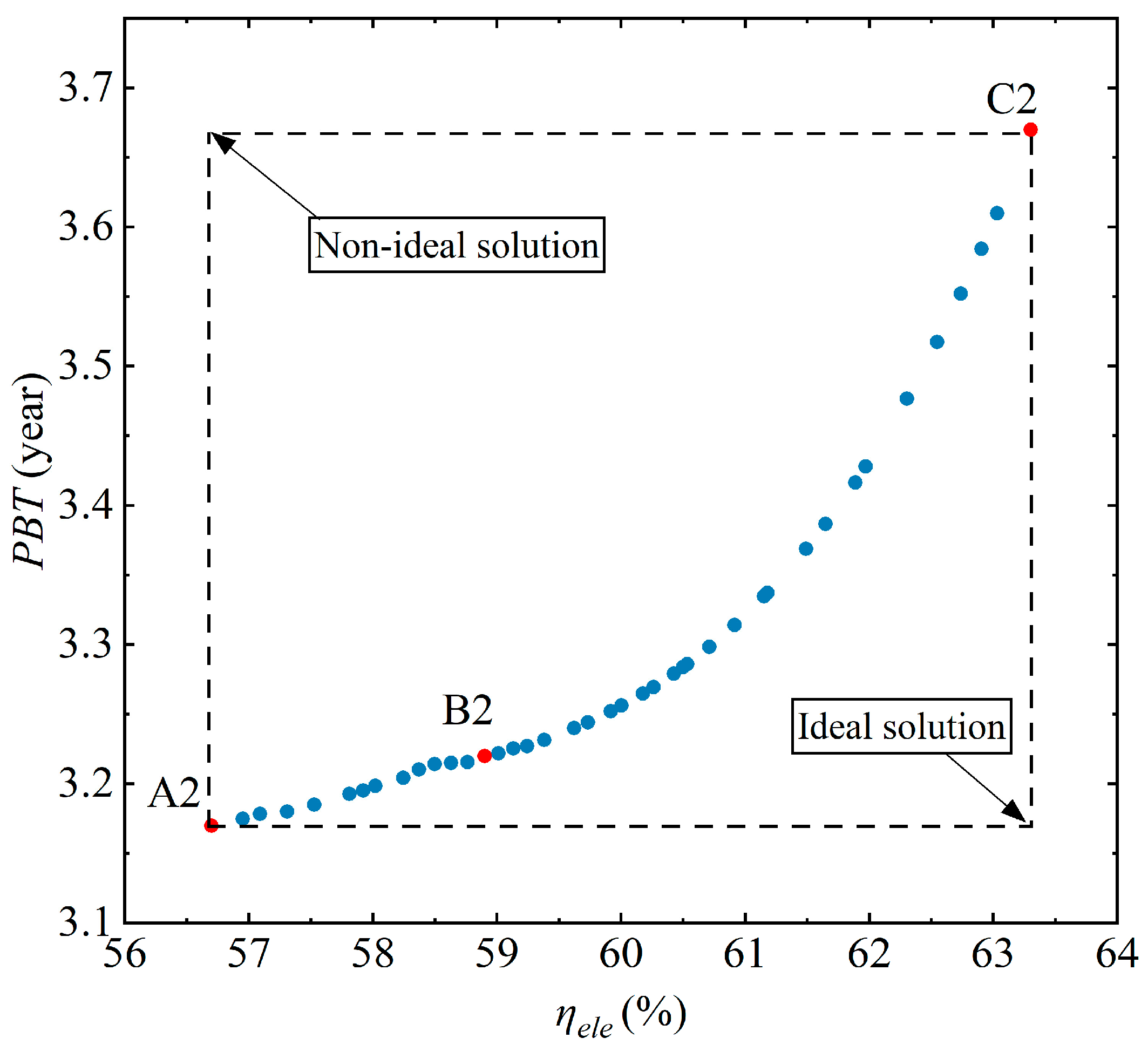
4.3. Optimization Results of Case2 (ηele-PBT)
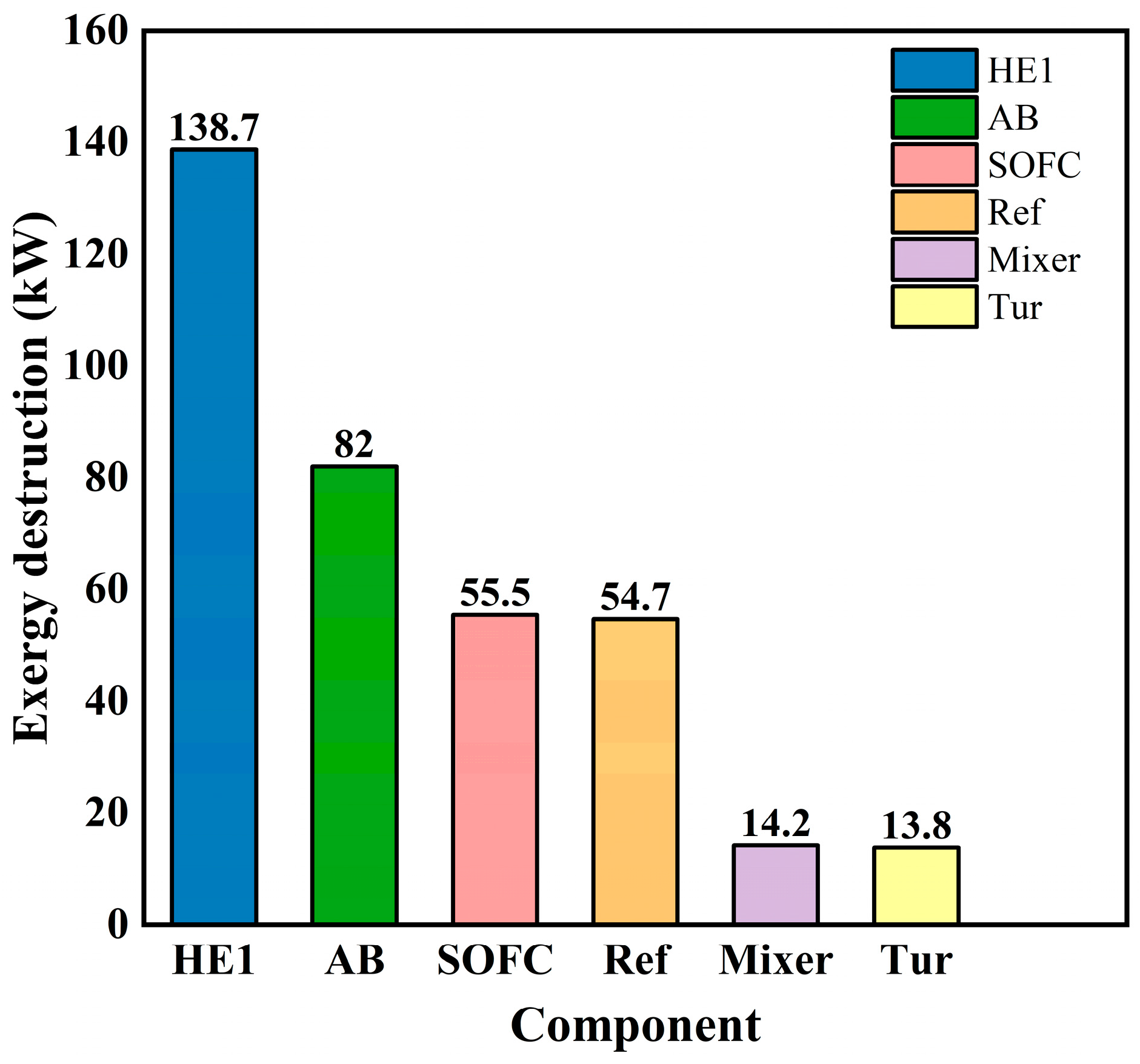
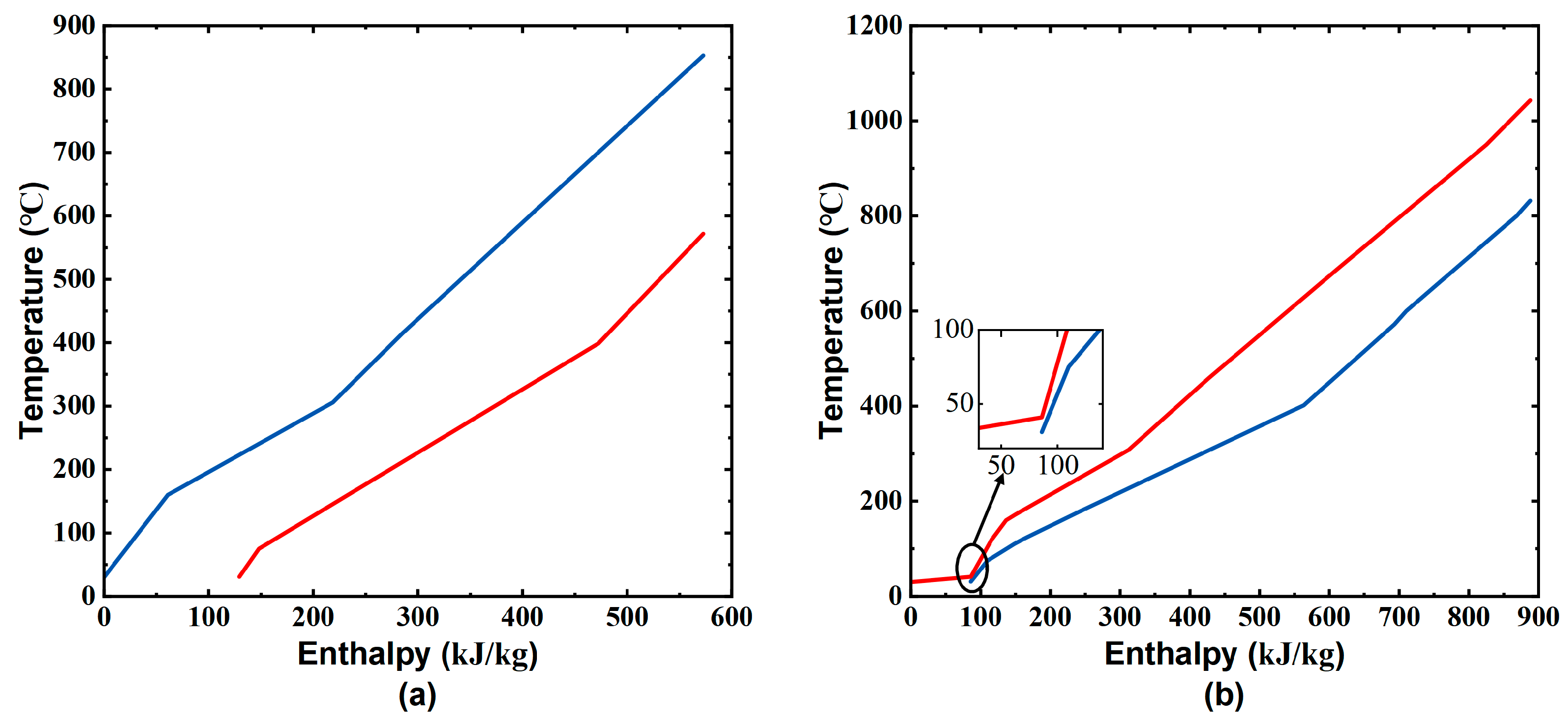
4.4. Optimization Results of Heat Exchange Network
5. Conclusions
- (1)
- The variations in current density and stack temperature lead to an imbalance between efficiency and economy. The current density is recommended to be between 0.3 A/cm2 and 0.9 A/cm2. The operating temperature of the SOFC stack should be limited between 675 °C and 875 °C. A lower recycle ratio would improve the risk of carbon accumulation, and a higher recycle ratio would reduce the efficiency and increase the total cost, so the recycle ratio of this system is recommended to be within 0.5–0.8.
- (2)
- Under initial conditions, the system net power efficiency, investment cost, and payback period are 56.6%, USD 2,408,256, and 3.27 years, respectively. In the case 1 (ηele-CostTCI) optimization, the cost and the electrical efficiency of the optimal point are USD 2,164,742 and 62.1%. In the case 2 (ηele-PBT) optimization, the PBT and the electrical efficiency of B2 are 3.22 years and 58.9%.
- (3)
- Comparing the two configurations of the heat exchange network for the lowest-cost purpose and highest-efficiency purpose, the former requires only two heat exchangers, while the latter requires five heat exchangers. The heat exchange network optimization reduces the consumption of cold utilities by 43 kW.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| AB | Afterburner |
| COND | Condenser |
| COP | Coefficient of performance |
| HE | Humidity efficiency/heat exchanger |
| KC | Karina cycle |
| LHV | Lower heating value |
| ORC | Organic Rankine cycle |
| RE | Recycle heat exchange |
| REF | Reformer |
| STCR | Steam-to-carbon ratio |
| SOFC | Solid oxide fuel cell |
| TUR | Turbine |
| TOPSIS | Technique for Order Preference by Similarity to an Ideal Solution |
| Symbols | |
| A | Area |
| F | Faraday’s constant |
| G | Gibbs free energy |
| h | Specific enthalpy |
| i | Current density |
| I | Current |
| L | Length |
| n | Molar flow rate |
| P | Power/pressure |
| T | Temperature |
| Ua | Air utilization factor |
| Uf | Fuel utilization factor |
| V | Voltage |
| Vact | Activation loss |
| Vcon | Concentration loss |
| VN | Nernst voltage |
| Vohm | Ohmic loss |
| Greek letters | |
| γ | Pre-exponential coefficient |
| η | Efficiency |
| Subscripts | |
| an | Anode |
| avg | Average |
| ca | Cathode |
| ele | Electricity |
| p | Pump |
| T | Turbine |
Appendix A
| Systems | Block type | Block ID | Description |
|---|---|---|---|
| SOFC subsystem | RGibbs | Ref | Simulate methane reforming process |
| RGibbs | anode | Simulate the electrochemical reaction process | |
| Sep | cathode | Simulate oxygen ion transport | |
| RStoic | Burner | Simulate combustion reaction | |
| Compr | Comp1 | Increase the pressure of the fuel | |
| Compr | Comp2 | Increase the pressure of the air | |
| Heater | HE1 | Preheated air | |
| Heater | HE2 | Preheated air | |
| Mixer | Mix | Mix the stream | |
| ORC subsystem | Compr | Tur | Convert the energy into mechanical work |
| Heater | HE3 | Heat recovery | |
| Heater | RE1 | Heat the working fluid | |
| Heater | Cond1 | Condense the working fluid | |
| Pump | P1 | Increase the pressure of the working fluid |
| Components | Cost (USD) | Year | CEPCI |
|---|---|---|---|
| SOFC stack | 2002 | 395.6 | |
| SOFC auxiliaries | 2002 | 395.6 | |
| SOFC inverter | 2002 | 395.6 | |
| Afterburner | 1994 | 368.1 | |
| Compressor | 2003 | 402.3 | |
| Vale | 2001 | 394.3 | |
| Pump | 2001 | 394.3 | |
| Turbine | 2001 | 394.3 | |
| Preheater | 2005 | 468.2 | |
| Heat exchanger | 2000 | 394.1 | |
| Condenser | 2005 | 468.2 |
| Stream | Temperature (°C) | Pressure (bar) | Mole Flow (kmol/h) | Mole Fraction (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N2 | O2 | CO2 | CO | H2O | CH4 | H2 | ||||
| Fuel | 25.0 | 1.0 | 4.4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Air | 25.0 | 1.0. | 171.2 | 79.0 | 21.0 | 0.0 | 0 | 0 | 0 | 0 |
| 1 | 64.7 | 1.6 | 4.5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2 | 562.8 | 1.6 | 24.7 | 0 | 0 | 19.4 | 7.8 | 40.5 | 18.2 | 14.0 |
| 3 | 600.0 | 1.5 | 28.7 | 0 | 0 | 19.8 | 10.7 | 24.8 | 8.6 | 36.1 |
| 4 | 725.0 | 1.5 | 28.7 | 0 | 0 | 19.8 | 10.7 | 24.8 | 8.6 | 36.1 |
| 5 | 875.0 | 1.4 | 33.7 | 0 | 0 | 23.8 | 9.6 | 49.6 | 0 | 17.1 |
| 6 | 875.0 | 1.4 | 13.5 | 0 | 0 | 23.8 | 9.6 | 49.6 | 0 | 17.1 |
| 7 | 875.0 | 1.4 | 20.2 | 0 | 0 | 23.8 | 9.6 | 49.6 | 0 | 17.1 |
| 8 | 703.1 | 1.4 | 20.2 | 0 | 0 | 23.8 | 9.6 | 49.6 | 0 | 17.1 |
| 9 | 75.2 | 1.6 | 136.9 | 0.79 | 0.21 | 0 | 0 | 0 | 0 | 0 |
| 10 | 700.6 | 1.5 | 136.9 | 0.79 | 0.21 | 0 | 0 | 0 | 0 | 0 |
| 11 | 875.0 | 1.4 | 129.8 | 83.4 | 16.6 | 0 | 0 | 0 | 0 | 0 |
| 12 | 970.4 | 1.3 | 141.3 | 76.5 | 14.0 | 3.2 | 0 | 6.4 | 0 | 0 |
| 13 | 417.0 | 1.2 | 141.3 | 76.5 | 14.0 | 3.2 | 0 | 6.4 | 0 | 0 |
| 14 | 160.0 | 1.4 | 141.3 | 76.5 | 14.0 | 3.2 | 0 | 6.4 | 0 | 0 |
| Stream | Temperature (°C) | Pressure (bar) | Mole Flow (kmol/h) | R123 Mole Fraction (%) |
|---|---|---|---|---|
| A1 | 402.0 | 20.0 | 20.86 | 100 |
| A2 | 308.9 | 1.1 | 20.86 | 100 |
| A3 | 168.7 | 1.1 | 20.86 | 100 |
| A4 | 30.1 | 1.1 | 20.86 | 100 |
| A5 | 31.0 | 20.0 | 20.86 | 100 |
| A6 | 140.0 | 20.0 | 20.86 | 100 |
References
- Wang, L.; Guo, W.; Zhang, Z.; Wang, F.; Yuan, J. Performance analysis and optimization of syngas composition for reversible solid oxide fuel cells in dual-mode operation based on extreme learning machine. J. Power Sources 2024, 614, 234982. [Google Scholar] [CrossRef]
- Vengatesan, S.; Jayakumar, A.; Sadasivuni, K.K. FCEV vs. BEV—A short overview on identifying the key contributors to af-fordable & clean energy (SDG-7). Energy Strategy Rev. 2024, 53, 101380. [Google Scholar] [CrossRef]
- Song, M.; Zhuang, Y.; Zhang, L.; Li, W.; Du, J.; Shen, S. Thermodynamic performance assessment of SOFC-RC-KC system for multiple waste heat recovery. Energy Convers. Manag. 2021, 245, 114579. [Google Scholar] [CrossRef]
- Song, M.; Zhuang, Y.; Zhang, L.; Wang, C.; Du, J.; Shen, S. Advanced exergy analysis for the solid oxide fuel cell system combined with a kinetic-based modeling pre-reformer. Energy Convers. Manag. 2021, 245, 114560. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, S.; Huang, X.; Luo, X.; Tu, Z. 4E analysis and multiobjective optimization of a PEMFC-based CCHP system with dehumidification. Energy Convers. Manag. 2021, 248, 114789. [Google Scholar] [CrossRef]
- Tu, B.; Wen, H.; Yin, Y.; Zhang, F.; Su, X.; Cui, D.; Cheng, M. Thermodynamic analysis and experimental study of electrode reactions and open circuit voltages for methane-fuelled SOFC. Int. J. Hydrog. Energy 2020, 45, 34069–34079. [Google Scholar] [CrossRef]
- Abbasi, H.R.; Pourrahmani, H.; Chitgar, N.; Van herle, J. Thermodynamic analysis of a tri-generation system using SOFC and HDH desalination unit. Int. J. Hydrog. Energy 2021, 72, 1204–1215. [Google Scholar] [CrossRef]
- Singh, M.; Zappa, D.; Comini, E. Solid oxide fuel cell: Decade of progress, future perspectives and challenges. Int. J. Hydrog. Energy 2021, 46, 27643–27674. [Google Scholar] [CrossRef]
- Ding, A.; Sun, H.; Zhang, S.; Dai, X.; Pan, Y.; Zhang, X.; Rahman, E.; Guo, J. Thermodynamic analysis and parameter optimization of a hybrid system based on SOFC and graphene-collector thermionic energy converter. Energy Convers. Manag. 2023, 291, 117327. [Google Scholar] [CrossRef]
- Li, C.; Wang, Z.; Liu, H.; Guo, F.; Li, C.; Xiu, X.; Wang, C.; Qin, J.; Wei, L. Exergetic and exergoeconomic evaluation of an SOFC-Engine-ORC hybrid power generation system with methanol for ship application. Fuel 2024, 357, 129944. [Google Scholar] [CrossRef]
- Zhu, P.; Wu, Z.; Guo, L.; Yao, J.; Dai, M.; Ren, J.; Kurko, S.; Yan, H.; Yang, F.; Zhang, Z. Achieving high-efficiency conversion and poly-generation of cooling, heating, and power based on biomass-fueled SOFC hybrid system: Performance assessment and multi-objective optimization. Energy Convers. Manag. 2021, 240, 114245. [Google Scholar] [CrossRef]
- Gholamian, E.; Zare, V. A comparative thermodynamic investigation with environmental analysis of SOFC waste heat to power conversion employing Kalina and Organic Rankine Cycles. Energy Convers. Manag. 2016, 117, 150–161. [Google Scholar] [CrossRef]
- Zeng, R.; Guo, B.; Zhang, X.; Li, H.; Zhang, G. Study on thermodynamic performance of SOFC-CCHP system integrating ORC and double-effect ARC. Energy Convers. Manag. 2021, 242, 114326. [Google Scholar] [CrossRef]
- You, H.; Han, J.; Liu, Y.; Chen, C.; Ge, Y. 4E analysis and multi-objective optimization of a micro poly-generation system based on SOFC/MGT/MED and organic steam ejector refrigerator. Energy 2020, 206, 118122. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, Y.; Bucknall, R. Optimised MOPSO with the grey relationship analysis for the multi-criteria objective energy dispatch of a novel SOFC-solar hybrid CCHP residential system in the UK. Energy Convers. Manag. 2021, 243, 114406. [Google Scholar] [CrossRef]
- Liang, W.; Yu, Z.; Liu, W.; Ji, S. Investigation of a novel near-zero emission poly-generation system based on biomass gasification and SOFC: A thermodynamic and exergoeconomic evaluation. Energy 2023, 282, 128822. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, X.; Wang, J.; Guan, Z.; Wang, Z.; Zhang, Y.; Wu, W.; Wang, X. Performance analysis and multi-objective optimization for a hybrid system based on solid oxide fuel cell and supercritical CO2 Brayton cycle with energetic and ecological objective approaches. Appl. Therm. Eng. 2023, 221, 119871. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Z.; Wang, D.; Li, G.; Xu, G. Energy, exergetic and economic analysis and multi-objective optimization of atmospheric and pressurized SOFC based trigeneration systems. Energy Convers. Manag. 2021, 239, 114183. [Google Scholar] [CrossRef]
- Forootan, M.M.; Ahmadi, A. Machine learning-based optimization and 4E analysis of renewable-based polygeneration system by integration of GT-SRC-ORC-SOFC-PEME-MED-RO using multi-objective grey wolf optimization algorithm and neural networks. Renew. Sustain. Energy Rev. 2024, 200, 114616. [Google Scholar] [CrossRef]
- Abedinia, O.; Shakibi, H.; Shokri, A.; Sobhani, B.; Sobhani, B.; Yari, M.; Bagheri, M. Optimization of a syngas-fueled SOFC-based multigeneration system: Enhanced performance with biomass and gasification agent selection. Renew. Sustain. Energy Rev. 2024, 199, 114460. [Google Scholar] [CrossRef]
- Oliva, D.G.; Francesconi, J.A.; Mussati, M.C.; Aguirre, P.A. Ethanol and glycerin processor systems coupled to solid oxide fuel cells (SOFCs). Optimal operation and heat exchangers network synthesis. Int. J. Hydrog. Energy 2013, 38, 7140–7158. [Google Scholar] [CrossRef]
- Fei, Z.; Yang, H.; Du, L.; Guerrero, J.M.; Meng, K.; Li, Z. Two-Stage Coordinated Operation of A Green Multi-Energy Ship Microgrid With Underwater Radiated Noise by Distributed Stochastic Approach. IEEE Trans. Smart Grid 2024, 1. [Google Scholar] [CrossRef]
- Xu, Y.; Lei, Y.; Xu, C.; Chen, Y.; Tan, Q.; Ye, S.; Li, J.; Huang, W. Multi-objective optimization of a solid oxide fuel cell-based integrated system to select the optimal closed thermodynamic cycle and heat coupling scheme simultaneously. Int. J. Hydrog. Energy 2021, 46, 31828–31853. [Google Scholar] [CrossRef]
- Lei, Y.; Ye, S.; Xu, Y.; Kong, C.; Xu, C.; Chen, Y.; Huang, W.; Xiao, H. Multi-objective optimization and algorithm improvement on thermal coupling of SOFC-GT-ORC integrated system. Comput. Chem. Eng. 2022, 164, 107903. [Google Scholar] [CrossRef]
- Xuan Wang, R.H. Comparison and analysis of heat exchange and offgas recycle strategies in tri-reforming-SOFC system. Int. J. Hydrog. Energy 2023, 48, 34069–34079. [Google Scholar] [CrossRef]
- Huber, D.; Birkelbach, F.; Hofmann, R. Unlocking the potential of synthetic fuel production: Coupled optimization of heat exchanger network and operating parameters of a 1 MW power-to-liquid plant. Chem. Eng. Sci. 2024, 284, 119506. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, L.; Tera, I.; Liu, G. Multi-objective optimization of heat exchanger network with disturbances based on graph theory and decoupling. Chem. Eng. Sci. 2024, 287, 119763. [Google Scholar] [CrossRef]
- Doherty, W.; Reynolds, A.; Kennedy, D. Computer simulation of a biomass gasification-solid oxide fuel cell power system using Aspen Plus. Energy 2010, 35, 4545–4555. [Google Scholar] [CrossRef]
- Anderson, T.; Vijay, P.; Tade, M.O. An adaptable steady state Aspen Hysys model for the methane fuelled solid oxide fuel cell. Chem. Eng. Res. Des. 2014, 92, 295–307. [Google Scholar] [CrossRef]
- Wu, Z.; Tan, P.; Chen, B.; Cai, W.; Chen, M.; Xu, X.; Zhang, Z.; Ni, M. Dynamic modeling and operation strategy of an NG-fueled SOFC-WGS-TSA-PEMFC hybrid energy conversion system for fuel cell vehicle by using MATLAB/SIMULINK. Energy 2019, 175, 567–579. [Google Scholar] [CrossRef]
- Alsarraf, J.; Alnaqi, A.A.; Al-Rashed, A.A.A.A. Thermodynamic modeling and exergy investigation of a hydrogen-based integrated system consisting of SOFC and CO2 capture option. Int. J. Hydrog. Energy 2022, 47, 26654–26664. [Google Scholar] [CrossRef]
- Diglio, G.; Hanak, D.P.; Bareschino, P.; Pepe, F.; Montagnaro, F.; Manovic, V. Modelling of sorption-enhanced steam methane reforming in a fixed bed reactor network integrated with fuel cell. Appl. Energy 2018, 210, 1–15. [Google Scholar] [CrossRef]
- Becker, W.L.; Braun, R.J.; Penev, M.; Melaina, M. Design and technoeconomic performance analysis of a 1MW solid oxide fuel cell polygeneration system for combined production of heat, hydrogen, and power. J. Power Sources 2012, 200, 34–44. [Google Scholar] [CrossRef]
- Huang, Y.; Turan, A. Mechanical equilibrium operation integrated modelling of hybrid SOFC–GT systems: Design analyses and off-design optimization. Energy 2020, 208, 118334. [Google Scholar] [CrossRef]
- Yang, S.; Jin, Z.; Ji, F.; Deng, C.; Liu, Z. Proposal and analysis of a combined cooling, heating, and power system with humidity control based on solid oxide fuel cell. Energy 2023, 284, 129233. [Google Scholar] [CrossRef]
- Pirkandi, J.; Ghassemi, M.; Hamedi, M.H.; Mohammadi, R. Electrochemical and thermodynamic modeling of a CHP system using tubular solid oxide fuel cell (SOFC-CHP). J. Clean. Prod. 2012, 29–30, 151–162. [Google Scholar] [CrossRef]
- Ma, L.; Ru, X.; Wang, J.; Lin, Z. System model and performance analysis of a solid oxide fuel cell system self-humidified with anode off-gas recycling. Int. J. Hydrog. Energy 2024, 57, 1164–1173. [Google Scholar] [CrossRef]
- Sinha, A.A.; Saini, G.; Sanjay; Shukla, A.K.; Ansari, M.Z.; Dwivedi, G.; Choudhary, T. A novel comparison of energy-exergy, and sustainability analysis for biomass-fueled solid oxide fuel cell integrated gas turbine hybrid configuration. Energy Convers. Manag. 2023, 283, 116923. [Google Scholar] [CrossRef]
- Wei, S.; Ni, S.; Ma, W.; Du, Z.; Lu, P. Exergy analysis and parameters optimization for zero-carbon/low-carbon fuels on SOFC-engine hybrid system. Fuel 2024, 364, 131076. [Google Scholar] [CrossRef]
- Meng, N.; Li, T.; Jia, Y.; Qin, H.; Liu, Q.; Zhao, W.; Lei, G. Techno-economic performance comparison of enhanced geothermal system with typical cycle configurations for combined heating and power. Energy Convers. Manag. 2020, 205, 112409. [Google Scholar] [CrossRef]
- Zhao, Z.; Shi, X.; Zhang, M.; Ouyang, T. Multi-scale assessment and multi-objective optimization of a novel solid oxide fuel cell hybrid power system fed by bio-syngas. J. Power Sources 2022, 524, 231047. [Google Scholar] [CrossRef]
- Comidy, L.J.F.; Staples, M.D.; Barrett, S.R.H. Technical, economic, and environmental assessment of liquid fuel production on aircraft carriers. Appl. Energy 2019, 256, 113810. [Google Scholar] [CrossRef]
- Su, Z.; Ouyang, T.; Chen, J.; Xu, P.; Tan, J.; Chen, N.; Huang, H. Green and efficient configuration of integrated waste heat and cold energy recovery for marine natural gas/diesel dual-fuel engine. Energy Convers. Manag. 2020, 209, 112650. [Google Scholar] [CrossRef]
- Chitgar, N.; Emadi, M.A.; Chitsaz, A.; Rosen, M.A. Investigation of a novel multigeneration system driven by a SOFC for electricity and fresh water production. Energy Convers. Manag. 2019, 196, 296–310. [Google Scholar] [CrossRef]
- Ouyang, T.; Zhao, Z.; Lu, J.; Su, Z.; Li, J.; Huang, H. Waste heat cascade utilisation of solid oxide fuel cell for marine applications. J. Clean. Prod. 2020, 275, 124133. [Google Scholar] [CrossRef]
- Xia, W.; Ren, Z.; Li, H.; Pan, Z. A data-driven probabilistic evaluation method of hydrogen fuel cell vehicles hosting capacity for integrated hydrogen-electricity network. Appl. Energy 2024, 376, 123895. [Google Scholar] [CrossRef]
- Yan, Z.; He, A.; Hara, S.; Shikazono, N. Modeling of solid oxide fuel cell (SOFC) electrodes from fabrication to operation: Microstructure optimization via artificial neural networks and multi-objective genetic algorithms. Energy Convers. Manag. 2019, 198, 111916. [Google Scholar] [CrossRef]
- Xie, N.; Liu, Z.; Luo, Z.; Ren, J.; Deng, C.; Yang, S. Multi-objective optimization and life cycle assessment of an integrated system combining LiBr/H2O absorption chiller and Kalina cycle. Energy Convers. Manag. 2020, 225, 113448. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Ncell | 2054 |
| Acell (cm2) | 625 |
| γa (A/m2) | 7 × 109 |
| γc (A/m2) | 7 × 109 |
| E0 (V) | E0 = 1.2723–2.7645 × 10−4 × T |
| ASRohm (Ωcm2) | 0.04 |
| Ean (J/mol) | 110,000 |
| Eca (J/mol) | 160,000 |
| Tair (°C) | 25 |
| Tfuel (°C) | 25 |
| Tatm (°C) | 25 |
| Patm (bar) | 1 |
| Uf/Ua | 0.85/0.2 |
| PSOFC (bar) | 1.1 |
| Cost | Equation |
|---|---|
| Fixed investment cost Costfix | Costfix |
| Maintenance cost Costmaint | Costmaint = 0.1 Costfix |
| Contingency cost Costcont | Costcont = 0.198 Costfix |
| Fuel cost Costfuel | Costfuel |
| Total depreciation cost CostTDC | CostTDC = Costfix + Costmaint + Costcont + Costfuel |
| Startup cost Coststart | Coststart = 0.1 CostTDC |
| Total cost of the system CostTCI | CostTCI = CostTDC + Coststart |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Current density i (A/m2) | 6000 | Single-cell voltage Vcell (V) | 0.75 |
| SOFC stack power WSOFC (kW) | 566 | Turbine power WTur (kW) | 65 |
| SOFC electrical efficiency (%) | 50.1 | System electrical efficiency ηele (%) | 56.6 |
| Item | Value | Percentage |
|---|---|---|
| Fixed investment cost Costfix (USD) | 593,377.5 | 24.6% |
| Maintenance cost Costmaint (USD) | 59,337.75 | 2.5% |
| Contingency cost Costcont (USD) | 117,488.7 | 4.9% |
| Fuel cost Costfuel (USD) | 1,419,120 | 58.9% |
| Total depreciation cost CostTDC (USD) | 2,189,324 | 90.9% |
| Startup cost Coststart (USD) | 218,932.4 | 9.1% |
| Total cost of the system CostTCI (USD) | 2,408,256 | 100% |
| Payback Time PBT (Year) | 3.27 | - |
| Decision Variables | Value Range | Unit |
|---|---|---|
| Current density | 0.3–0.9 | A/cm2 |
| Average stack temperature | 675–750 | °C |
| Anode recycle ratio | 0.5–0.8 | - |
| Algorithm Parameters | Values |
|---|---|
| Population size | 100 |
| Number of variables | 3 |
| Crossover ratio | 80% |
| Proportion of variation | 20% |
| Maximum number of iterations | 100 |
| Unit | A1 | B1 | C1 | |
|---|---|---|---|---|
| Current density | A/cm2 | 0.3 | 0.3 | 0.3 |
| Stack temperature (average) | °C | 677 | 843 | 875 |
| Anode recycle ratio | - | 0.51 | 0.60 | 0.78 |
| ηele | % | 55.6 | 62.1 | 63.3 |
| CostTCI | USD | 1,998,885 | 2,164,742 | 2,215,737 |
| PBT | Year | 3.58 | 3.57 | 3.67 |
| Unit | A2 | B2 | C2 | |
|---|---|---|---|---|
| Current density | A/cm2 | 0.8 | 0.57 | 0.3 |
| Stack temperature (average) | °C | 850 | 850 | 875 |
| Anode recycle ratio | - | 0.65 | 0.62 | 0.78 |
| ηele | % | 56.7 | 58.9 | 63.3 |
| PBT | Year | 3.17 | 3.22 | 3.67 |
| CostTCI | USD | 3,136,668 | 2,363,673 | 2,215,737 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Liang, A.; Jin, Z.; Xie, N. Investigation of a Cogeneration System Combining a Solid Oxide Fuel Cell and the Organic Rankine Cycle: Parametric Analysis and Multi-Objective Optimization. Processes 2024, 12, 2873. https://doi.org/10.3390/pr12122873
Yang S, Liang A, Jin Z, Xie N. Investigation of a Cogeneration System Combining a Solid Oxide Fuel Cell and the Organic Rankine Cycle: Parametric Analysis and Multi-Objective Optimization. Processes. 2024; 12(12):2873. https://doi.org/10.3390/pr12122873
Chicago/Turabian StyleYang, Sheng, Anman Liang, Zhengpeng Jin, and Nan Xie. 2024. "Investigation of a Cogeneration System Combining a Solid Oxide Fuel Cell and the Organic Rankine Cycle: Parametric Analysis and Multi-Objective Optimization" Processes 12, no. 12: 2873. https://doi.org/10.3390/pr12122873
APA StyleYang, S., Liang, A., Jin, Z., & Xie, N. (2024). Investigation of a Cogeneration System Combining a Solid Oxide Fuel Cell and the Organic Rankine Cycle: Parametric Analysis and Multi-Objective Optimization. Processes, 12(12), 2873. https://doi.org/10.3390/pr12122873








