Study of the Transient Heat Transfer of a Single-U-Tube Ground Heat Exchanger by Integrating a Forward-Difference Numerical Scheme with an Analytical Technique
Abstract
1. Introduction
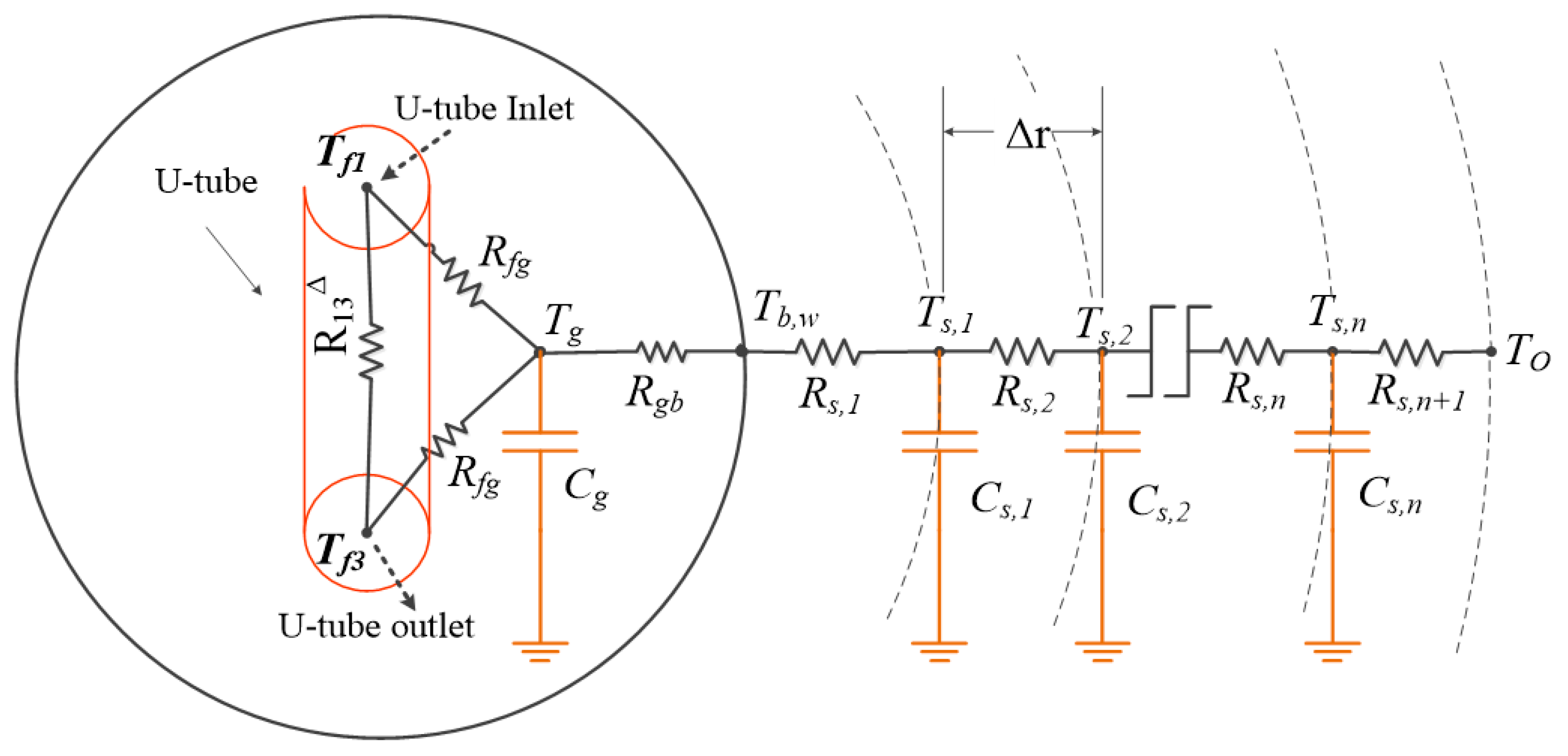
2. Mathematical Modeling
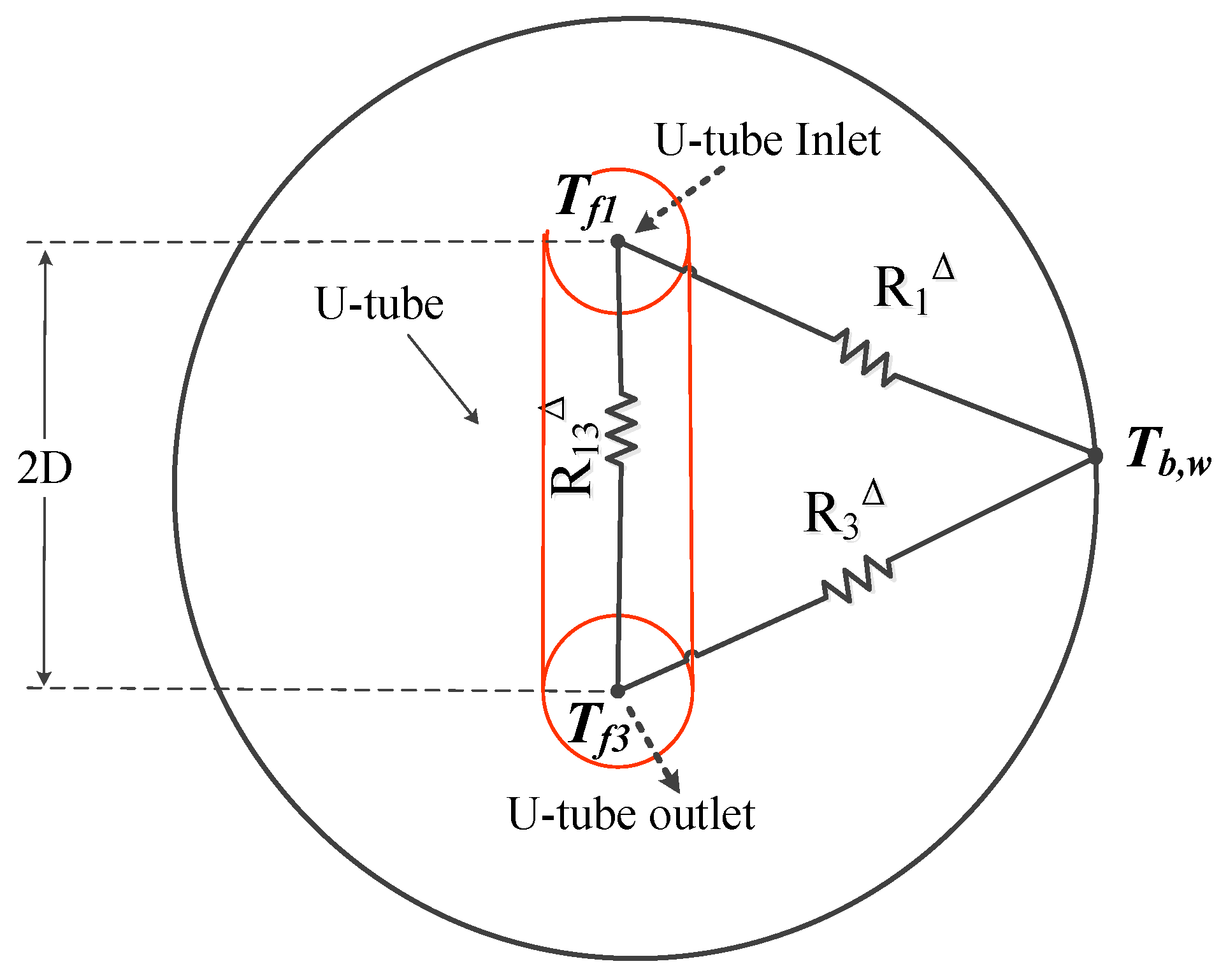
2.1. Analytical Modeling
2.2. Numerical Modeling
2.3. Coupling the Analytical and Numerical Method
2.4. Energy Storage
2.5. Model Adaptation to Varying Boundary Conditions
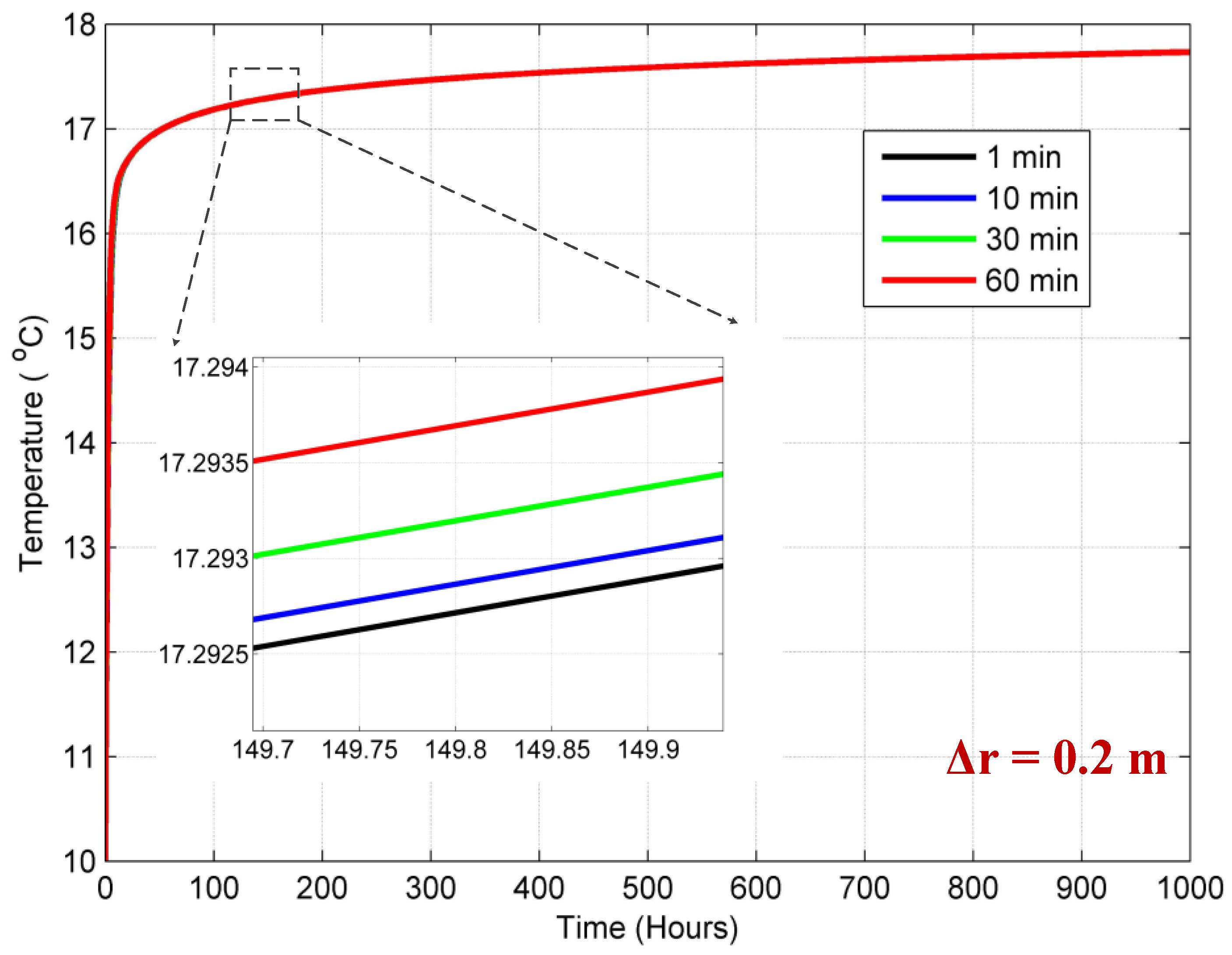
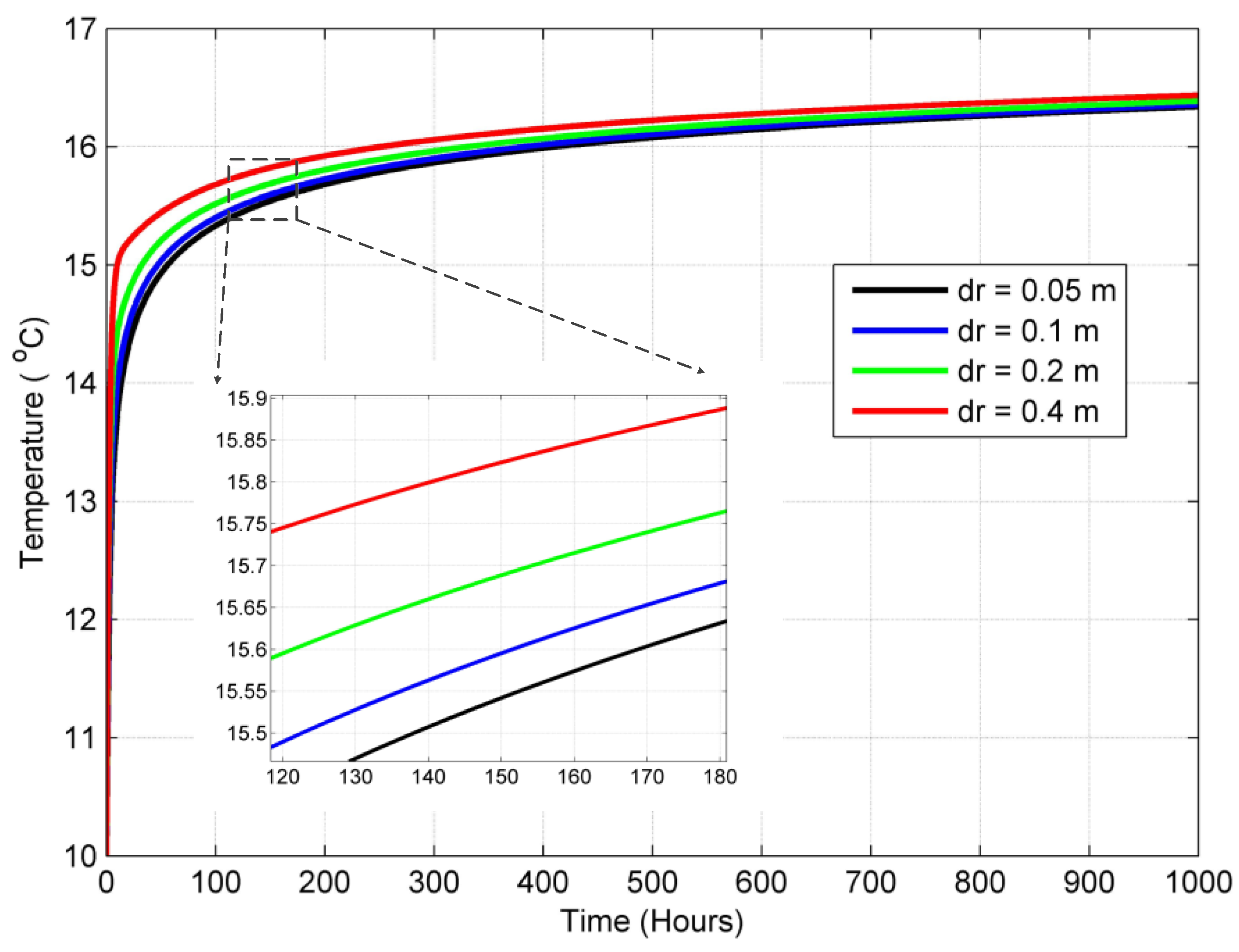
3. Mesh and Time Step Sensitivity
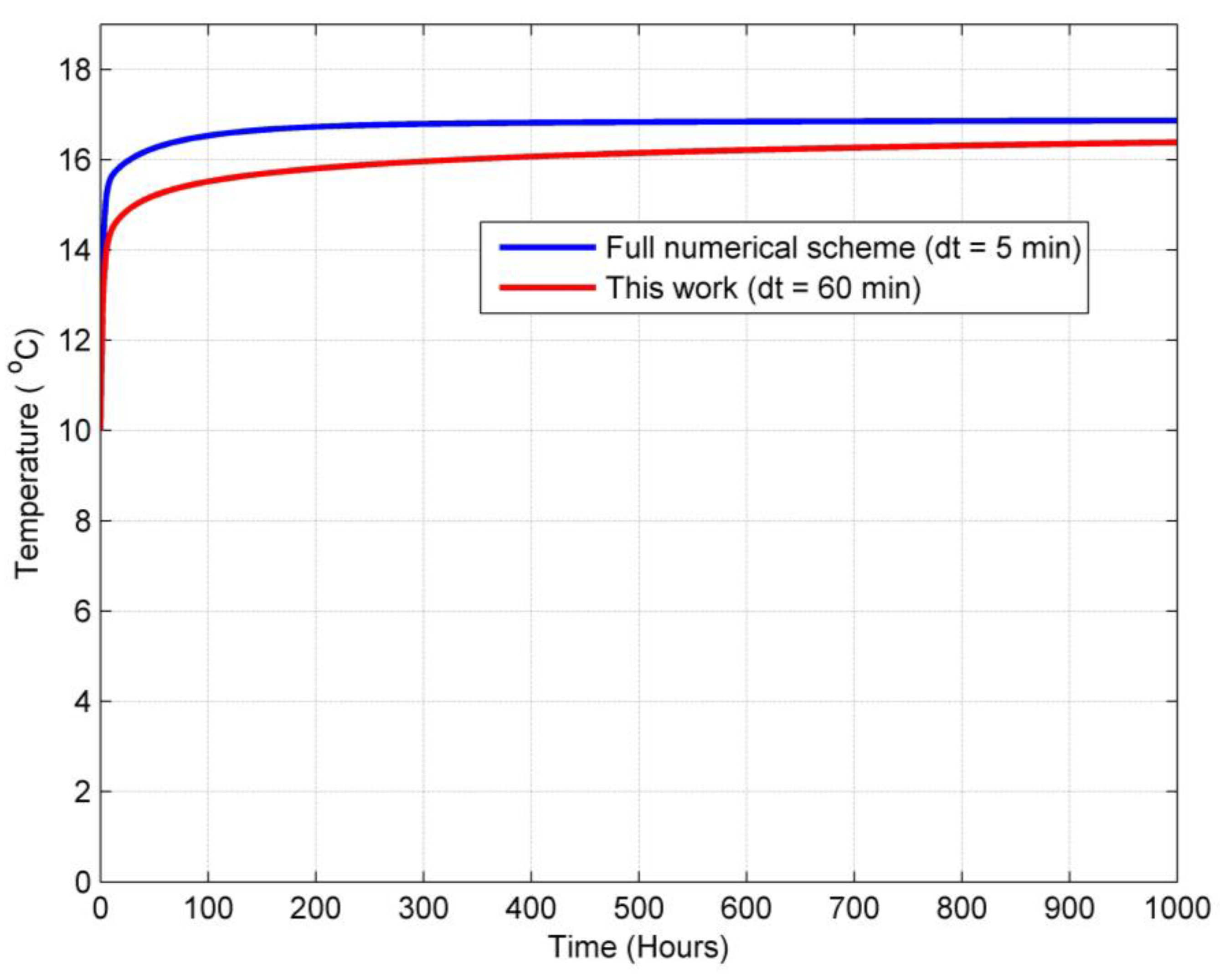
4. Validation and Comparison with Other Methods
5. Results and Discussion
6. Conclusions
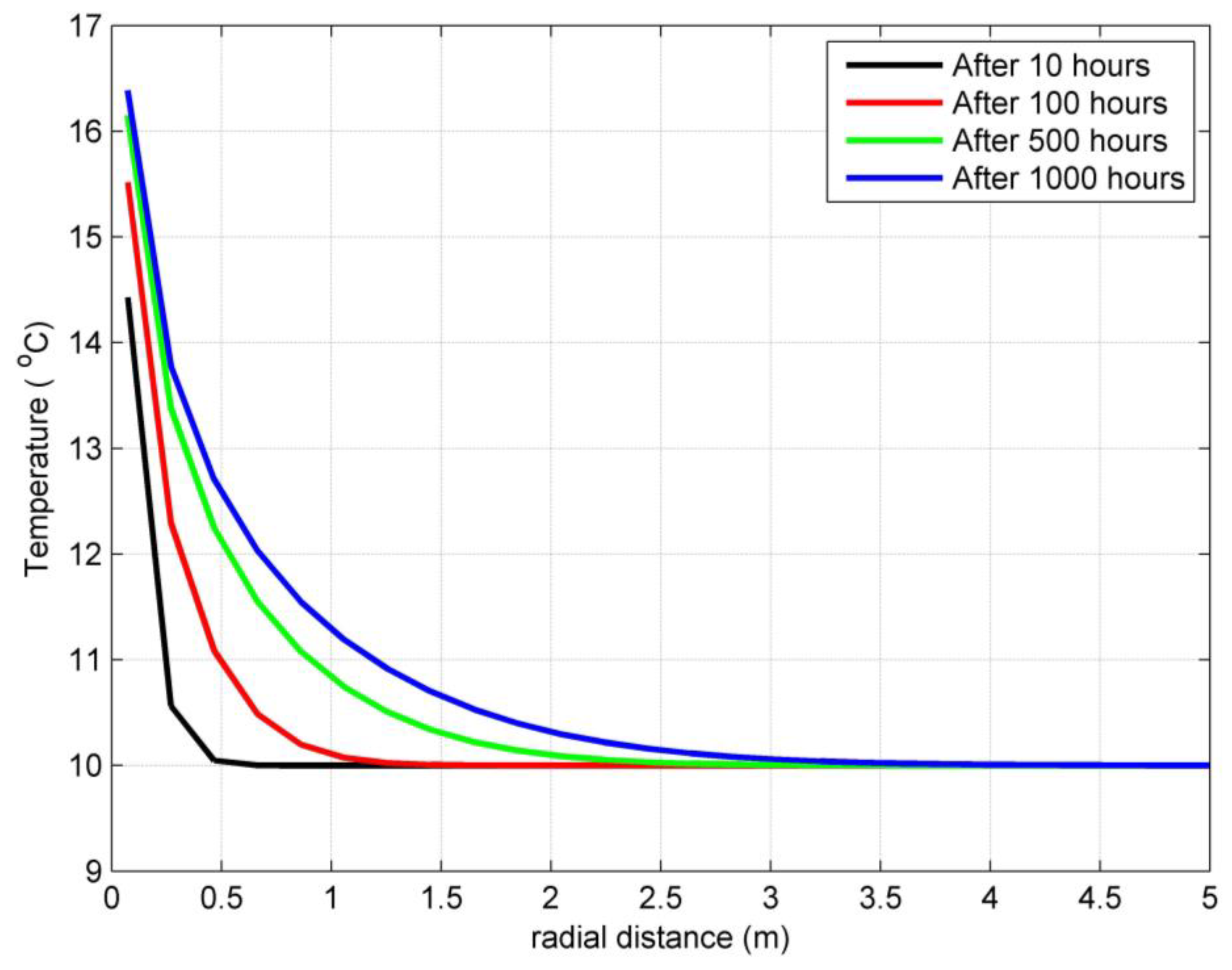
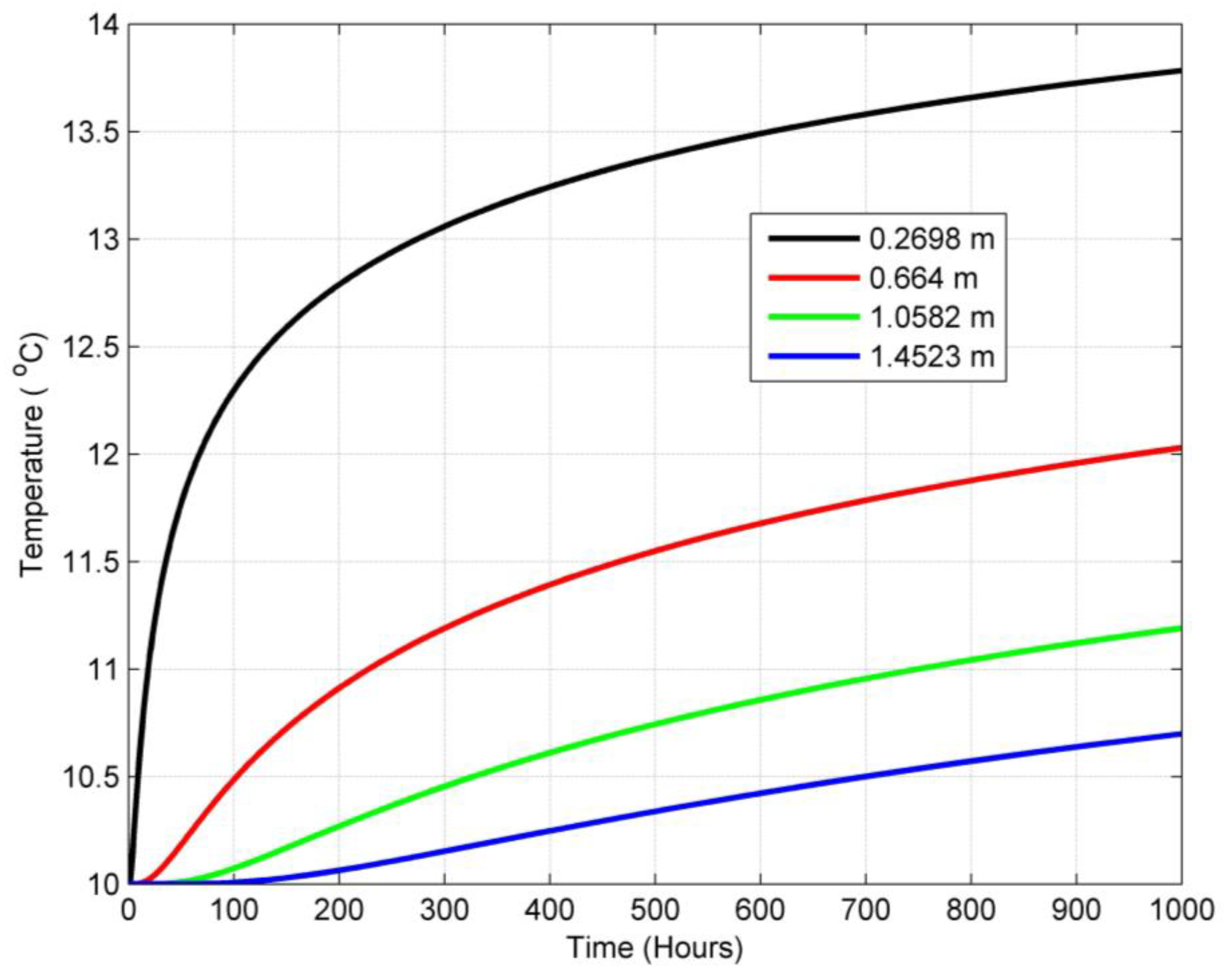
- Considering the radial temperature change of the soil material, the temperature decreases exponentially outward along the radial direction. This is because heat is transferred from the hotter fluid in the U-tube to the soil nodes radially in the outward direction.
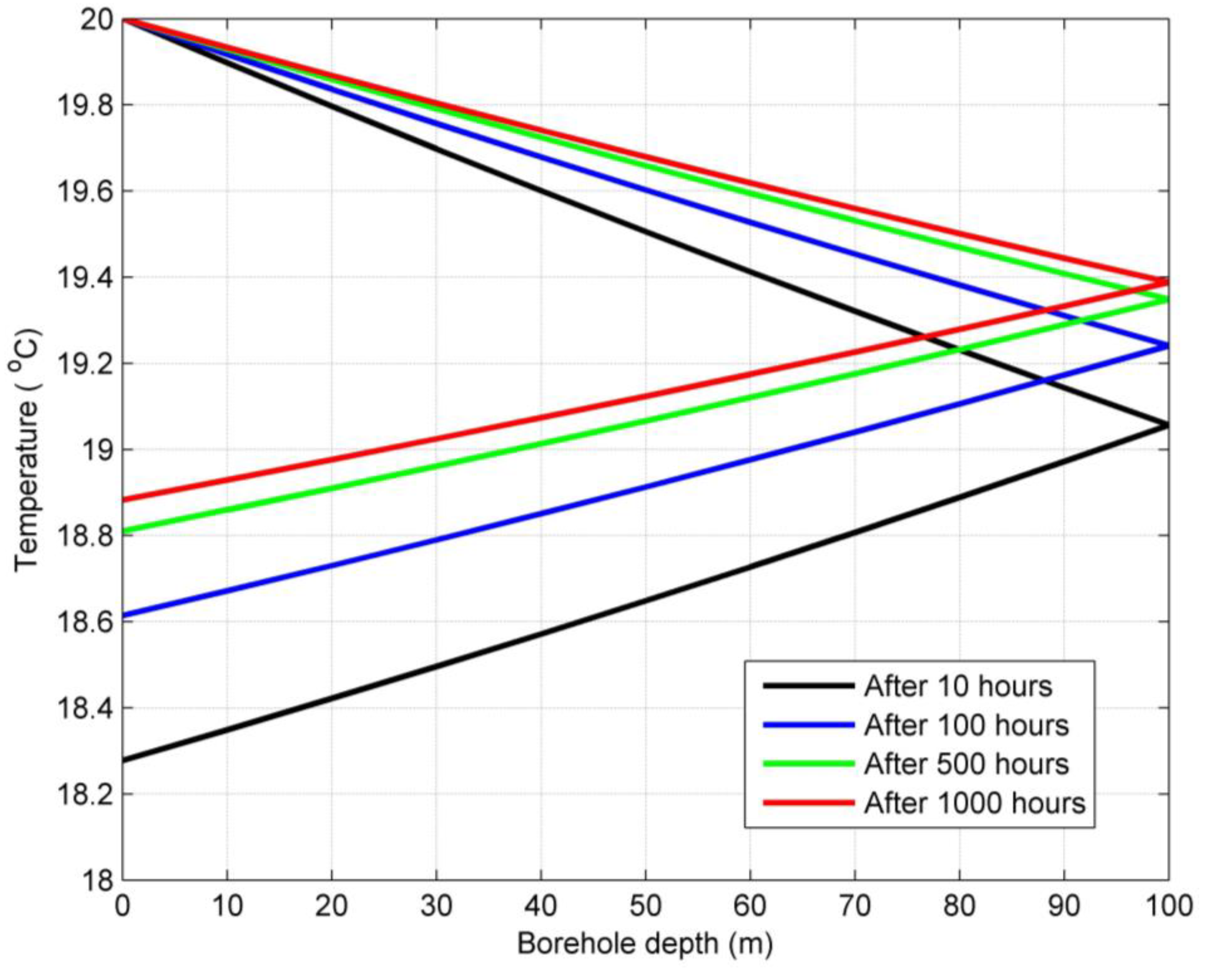
- The temperature of the grout is higher than that of the borehole wall, as the position of the borehole wall is located in the outward direction of the grout node.
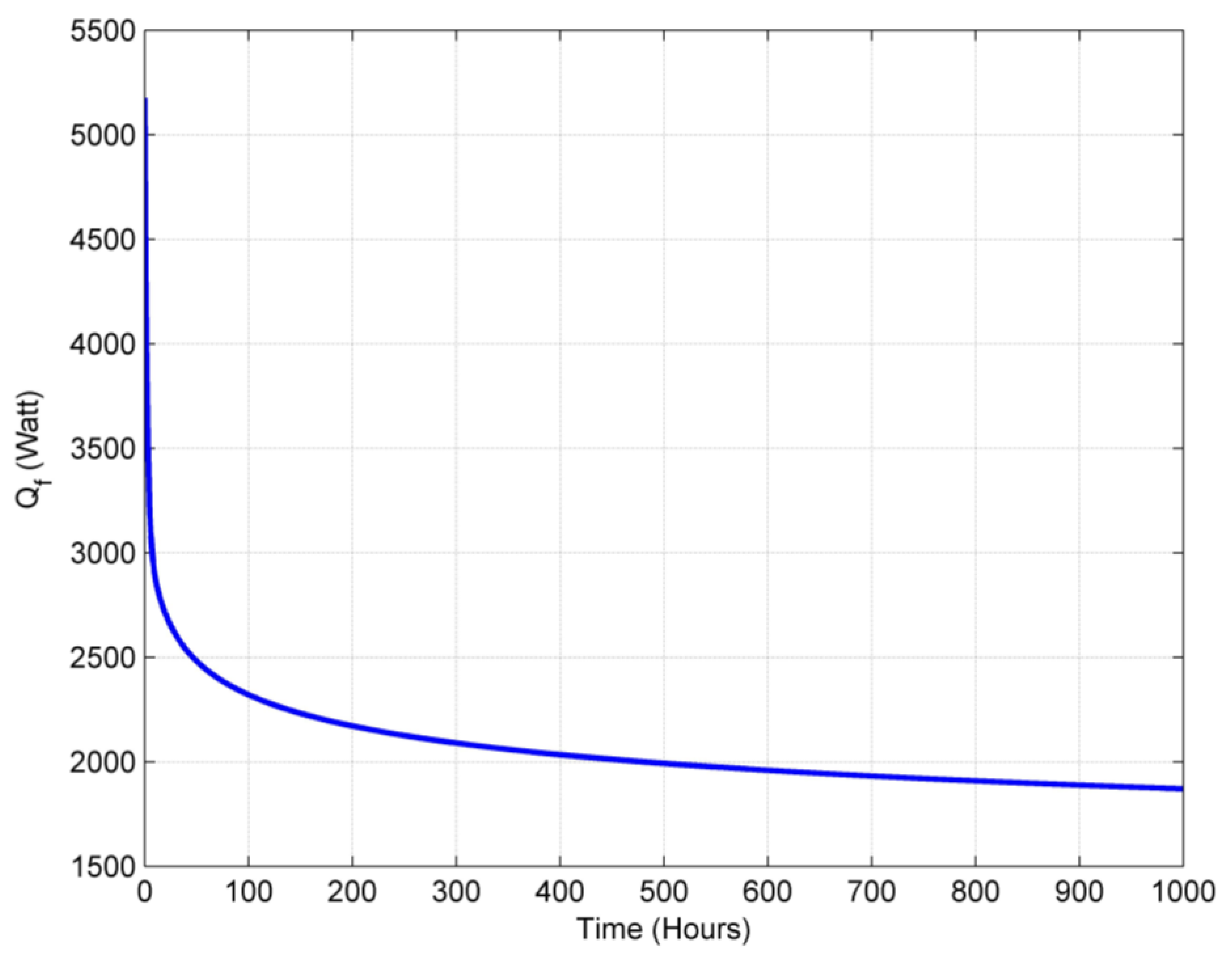
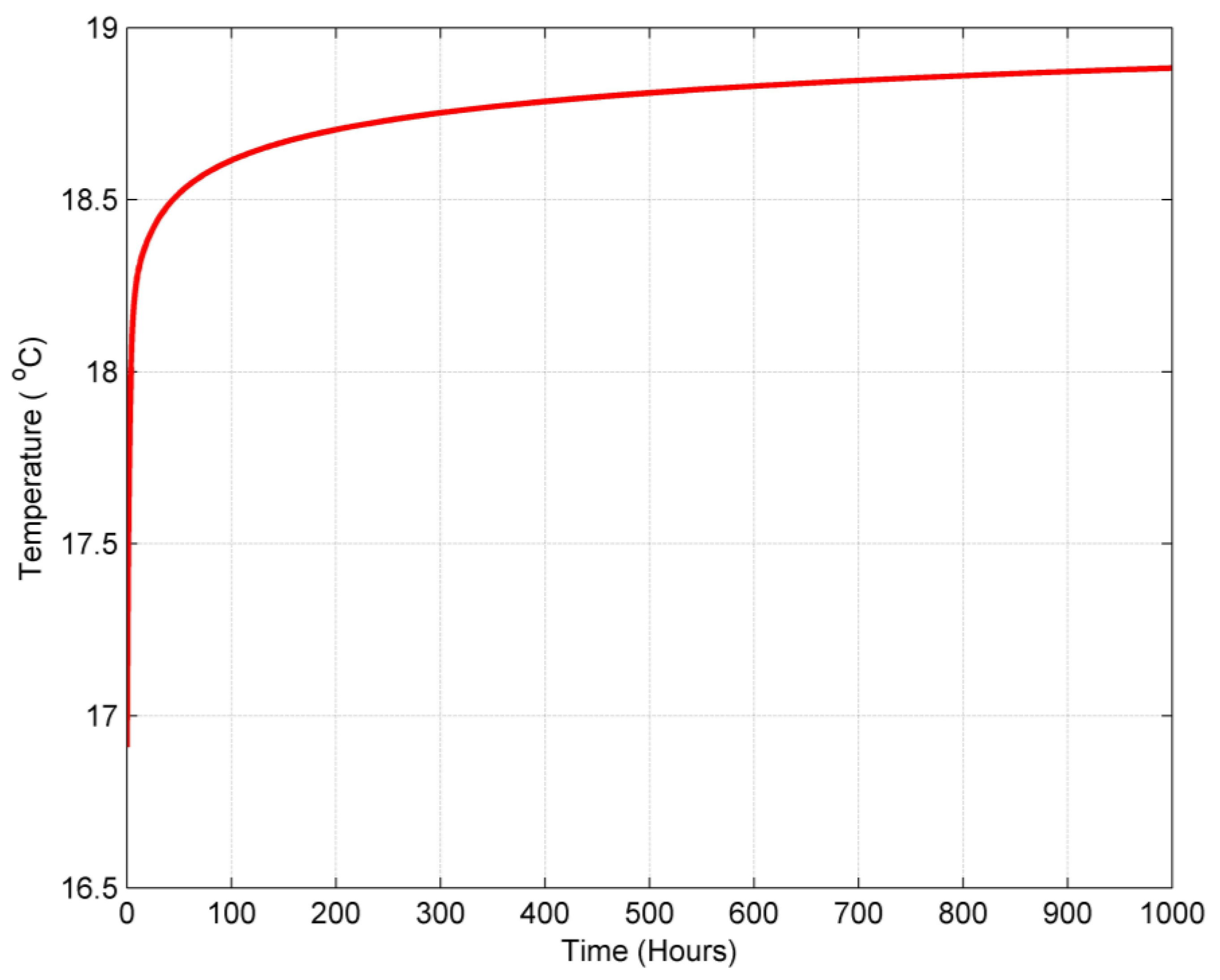
- The heat transfer between the streaming fluid and the surrounding grout and soil materials decreases exponentially with time as the temperature difference between the inlet fluid temperature and the grout temperature decreases with time, while the temperature of the grout is elevated with the heating process.
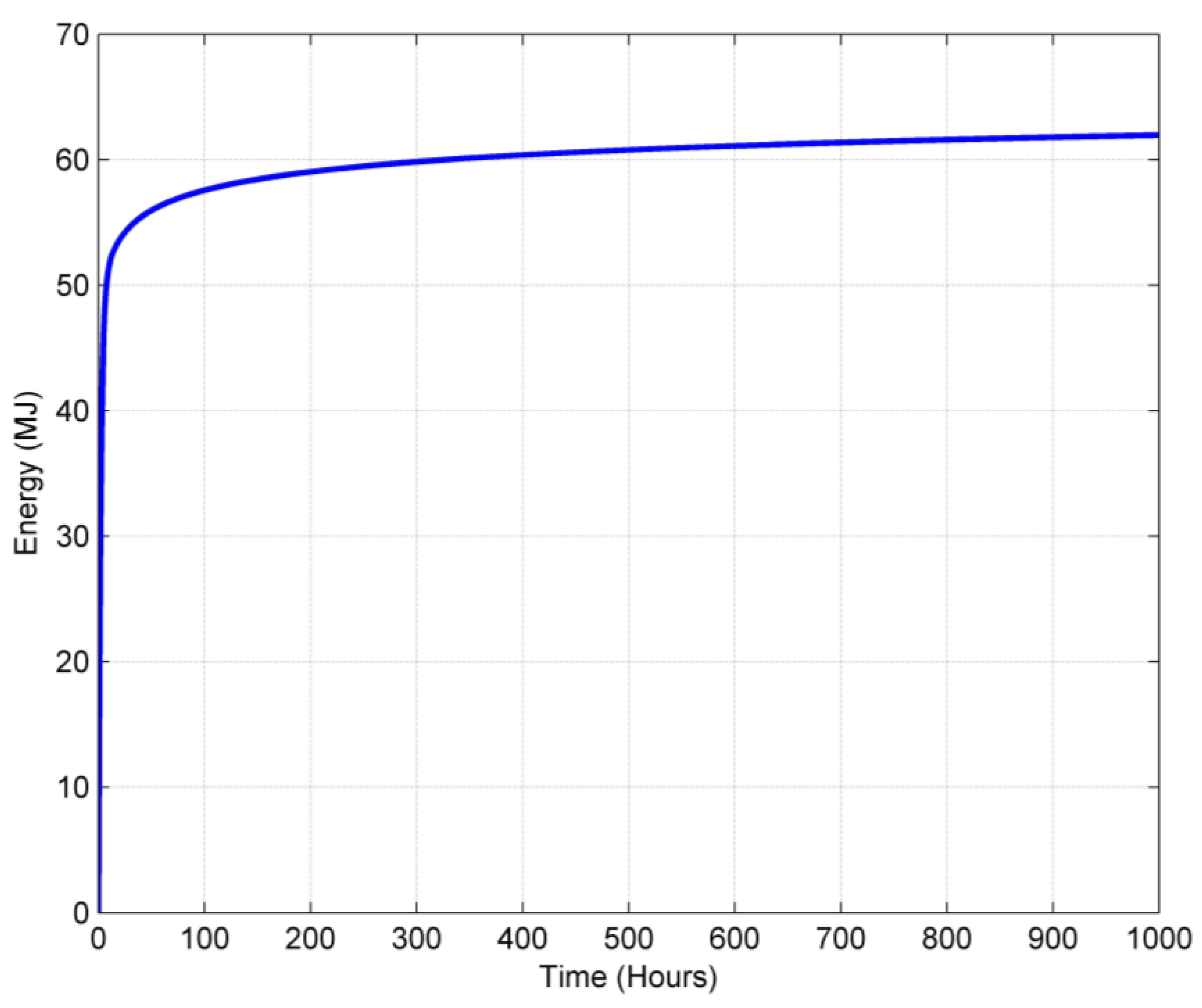
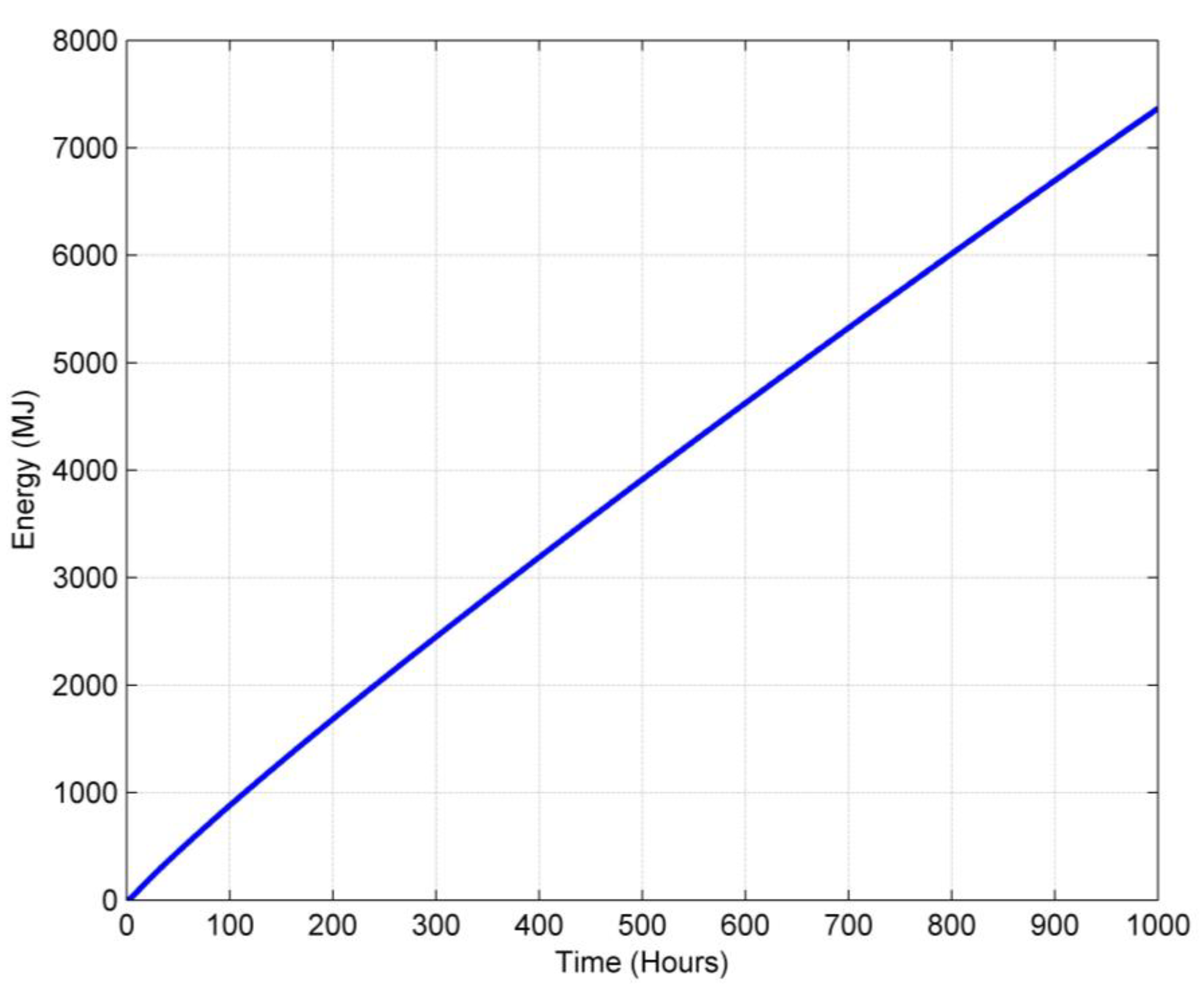
- The energy storage of the grout material inside the borehole is only about 62 MJ, while the energy storage of the soil material outside the borehole reaches 7366 MJ after 1000 h of operation.
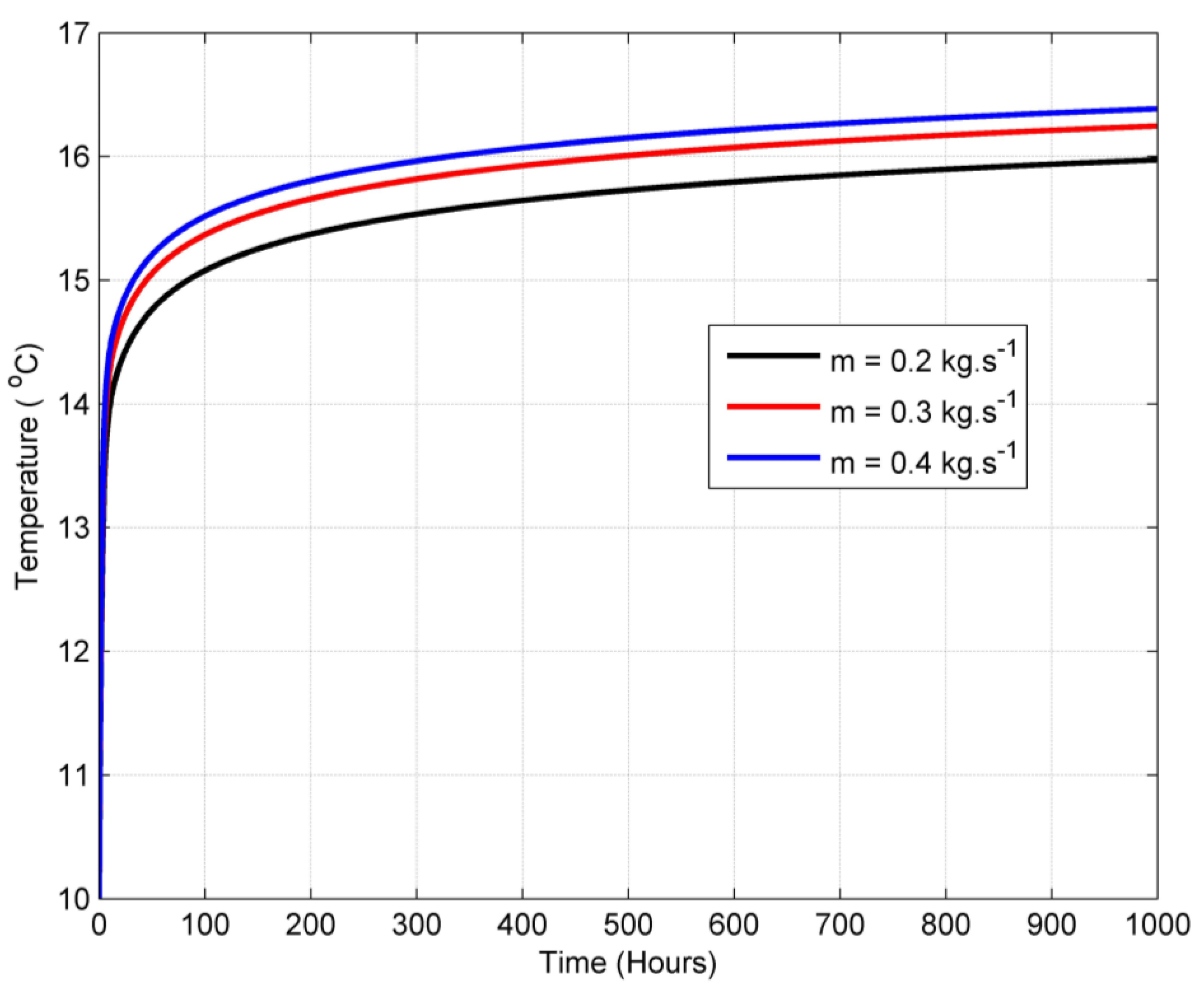
- The heat transfer performance of the ground heat exchanger increases with the mass flow rate.
- The suggested model is insignificantly sensitive to the change in time step. The sensitivity of the model is investigated with the grout temperature. There is only about a 0.001 °C difference as the time step changes from 1 min to 60 min.
- There is a small sensitivity in the model to the radial mesh size. The change in the borehole wall temperature can reach as high as 0.9 °C for a change in mesh size from 0.05 m to 0.2 m. The change in the borehole wall temperature can reach as high as 0.5 °C for a change in mesh size from 0.2 m to 0.4 m.
- The suggested method is numerically efficient and stable compared to a full numerical scheme, and the solution can even converge for a large time step of 150 min.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Specific heat of the fluid in the U-tube | |
| Thermal capacitance of the grout | |
| Thermal capacitance of the ith soil node | |
| Half-shank spacing according to Figure 2 | |
| Thermal energy stored by the grout | |
| Thermal energy stored by the soil | |
| Convective coefficient of the fluid in the pipe | |
| Thermal conductivity of the grout inside the borehole | |
| Thermal conductivity of the pipe | |
| Thermal conductivity of the soil outside of the borehole | |
| Mass flow rate of the fluid in the U-tube | |
| Prandtl number of the fluid inside the U-tube | |
| Heat transfer rate from the fluid to the grout node | |
| Thermal resistance between the fluid in the U-tube and borehole wall per unit length | |
| Thermal resistance between the grout and the borehole wall per unit length | |
| U-tube pipe’s wall thermal resistance per unit length | |
| Thermal resistance of the ith soil node | |
| Reynolds number of the fluid inside the U-tube | |
| Radius of borehole | |
| Inner radius of U-tube pipe | |
| Outer radius of U-tube pipe | |
| Time | |
| Temperature of the borehole wall | |
| Inlet fluid temperature | |
| Temperature of the fluid in the down-running tube | |
| Temperature of the fluid in the up-running tube | |
| Temperature of the grout node | |
| Undisturbed ground temperature | |
| Temperature of the ith soil node | |
| Axial coordinate | |
| Non-dimensional axial coordinate | |
| Greek Symbols | |
| Δ | Change in |
| Non-dimensional temperature in the down-running tube | |
| Non-dimensional temperature in the up-running tube | |
References
- Ma, J.; Wang, H.; Li, Y.; Ren, J.; Sun, H.; Du, S.; Wen, H. Heating and storage of medium-deep borehole heat exchangers: Analysis of operational characteristics via an optimized analytical solution model. J. Energy Storage 2024, 90, 111760. [Google Scholar] [CrossRef]
- Sharifishourabi, M.; Dincer, I.; Mohany, A. A novel trigeneration energy system with two modes of operation for thermal energy storage and hydrogen production. Energy 2024, 304, 132121. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Alsulami, R.A.; Aljinaidi, A.A.; Alazwari, M.A.; Eltaher, M.A.; Almitani, K.H.; Alnefaie, K.A.; Rawa, M.J.H.; Abusorrah, A.M.; Sindi, H.F.; et al. Numerical investigation of molten salt/SiO2 nano-fluid in the solar power plant cycle and examining different arrangements of shell and tube heat exchangers and plate heat exchangers in these cycles. J. Taiwan Inst. Chem. Eng. 2021, 124, 1–8. [Google Scholar] [CrossRef]
- Yao, B.; Salehi, A.; Baghoolizadeh, M.; Khairy, Y.; Baghaei, S. Multi-objective optimization of office egg shadings using NSGA-II to save energy consumption and enhance thermal and visual comfort. Int. Commun. Heat Mass Transf. 2024, 157, 107697. [Google Scholar] [CrossRef]
- Lu, Q.; Xie, P.; Lin, Y.; Liu, Y.; Yang, Y.; Lin, X. Hierarchical Power System Scheduling and Energy Storage Planning Method Considering Heavy Load Rate. Processes 2024, 12, 2725. [Google Scholar] [CrossRef]
- Skrzyniarz, M.; Morel, S.; Rzącki, J. Prediction of Chemical Composition of Gas Combustion Products from Thermal Waste Conversion. Processes 2024, 12, 2728. [Google Scholar] [CrossRef]
- Zhou, J.; Li, R.; Li, Y.; Shi, L. Aggregation Modeling for Integrated Energy Systems Based on Chance-Constrained Optimization. Processes 2024, 12, 2672. [Google Scholar] [CrossRef]
- Eletri, H.; Salilih, E.M.; Hamed, M.; Fellah, A. Performance analysis of a hybrid solar-driven cooler for refrigerator vehicle. Int. J. Refrig. 2023, 153, 281–295. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Nguyen, T.N.; Ramadan, Z.; Park, C.W. Comparative study on thermal performance of two graphite fin thermal energy storages based on experiment, simulation, and artificial neural network. Int. Commun. Heat Mass Transf. 2024, 156, 107645. [Google Scholar] [CrossRef]
- Weng, T.; Zhang, G.; Wang, H.; Qi, M.; Qvist, S.; Zhang, Y. The impact of coal to nuclear on regional energy system. Energy 2024, 302, 131765. [Google Scholar] [CrossRef]
- Bakhshi, N.; Rashidi, S.; Rafee, R. Vertical coaxial ground heat exchangers with teeth and grooves on their outer pipes; a hydrothermal investigation. Appl. Therm. Eng. 2024, 243, 122570. [Google Scholar] [CrossRef]
- Giertl, T.; Vitázek, I.; Gaduš, J.; Kollárik, R.; Przydatek, G. Thermochemical Conversion of Biomass into 2nd Generation Biofuel. Processes 2024, 12, 2658. [Google Scholar] [CrossRef]
- Abdelhalim, A.M.; Meana-Fernández, A.; Suarez-Ramon, I. Integration of Thermal Solar Power in an Existing Combined Cycle for a Reduction in Carbon Emissions and the Maximization of Cycle Efficiency. Processes 2024, 12, 2557. [Google Scholar] [CrossRef]
- Jia, T.; Chen, H.; Zeng, X.; Zhu, Y.; Qin, H. Mitigating Risk and Emissions in Power Systems: A Two-Stage Robust Dispatch Model with Carbon Trading. Processes 2024, 12, 2497. [Google Scholar] [CrossRef]
- Žirgulis, G.; Javadi, H.; Chaudhari, O.A.; Ghafar, A.N.; Fontana, P.; Sanner, B.; Urchueguía, J.F.; Badenes, B.; Castell, J.M.C.; Shuster, M. Temperature evolution around four laboratory-scale borehole heat exchangers grouted with phase change materials subjected to heating–cooling cycles: An experimental study. J. Energy Storage 2023, 74, 109302. [Google Scholar] [CrossRef]
- Garau, M.; Torsæter, B.N. A methodology for optimal placement of energy hubs with electric vehicle charging stations and renewable generation. Energy 2024, 304, 132068. [Google Scholar] [CrossRef]
- Moreno-Leiva, S.; Haas, J.; Nowak, W.; Kracht, W.; Eltrop, L.; Breyer, C. Flexible copper: Exploring capacity-based energy demand flexibility in the industry. Energy 2024, 305, 132147. [Google Scholar] [CrossRef]
- Saeidi, R.; Karimi, A.; Noorollahi, Y. The novel designs for increasing heat transfer in ground heat exchangers to improve geothermal heat pump efficiency. Geothermics 2024, 116, 102844. [Google Scholar] [CrossRef]
- Cao, W.; Yu, J.; Xu, M. Optimization Scheduling of Virtual Power Plants Considering Source-Load Coordinated Operation and Wind–Solar Uncertainty. Processes 2024, 12, 11. [Google Scholar] [CrossRef]
- Salahodjaev, R.; Sadikov, A. Examining the Nexus Between Renewable Energy, CO2 Emissions, and Economic Factors: Implications for Countries Marked by High Rates of Coronary Heart Disease. Energies 2024, 17, 6057. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Salilih, E.M.; Alsulami, R.A.; Rawa, M.J.H.; Aljinaidi, A.A.; Alazwari, M.A.; Eltaher, M.A.; Almitani, K.H.; Abulkhair, H.A.; Alnefaie, K.A.; et al. The effects of incident solar radiation on the collector efficiency using coolant hybrid nanofluid via simulation of solar tower system with the parallel heat exchangers. J. Taiwan Inst. Chem. Eng. 2021, 124, 106–115. [Google Scholar] [CrossRef]
- Huang, S.; Li, Y.; Shi, X.; Bai, W.; Huang, Y.; Hong, Y.; Liu, X.; Ma, H.; Li, P.; Xu, M.; et al. The Role of Underground Salt Caverns in Renewable Energy Peaking: A Review. Energies 2024, 17, 6005. [Google Scholar] [CrossRef]
- Clemens, T.; Hunyadi-Gall, M.; Lunzer, A.; Arekhov, V.; Datler, M.; Gauer, A. Wind–Photovoltaic–Electrolyzer-Underground Hydrogen Storage System for Cost-Effective Seasonal Energy Storage. Energies 2024, 17, 5696. [Google Scholar] [CrossRef]
- Fan, M.; Cao, S.; Lu, S. Optimal allocation of multiple energy storage in the integrated energy system of a coastal nearly zero energy community considering energy storage priorities. J. Energy Storage 2024, 87, 111323. [Google Scholar] [CrossRef]
- Zhu, S.; Li, X.; Li, Y.; Sun, H.; Kang, X. Thermo-Mechanically Coupled Settlement and Temperature Response of a Composite Foundation in Complex Geological Conditions for Molten Salt Tank in Tower Solar Plants. Processes 2024, 12, 2602. [Google Scholar] [CrossRef]
- Zhao, C.; Duan, Q.; Lu, J.; Wang, H.; Sha, G.; Jia, J.; Zhou, Q. Coordinated Optimization Method for Distributed Energy Storage and Dynamic Reconfiguration to Enhance the Economy and Reliability of Distribution Network. Energies 2024, 17, 6040. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, X.; Zou, S.; Xu, X.; Tu, Y.; Tian, Y.; Ke, Z. Enhancing the phase change material based shell-tube thermal energy storage units with unique hybrid fins. Int. Commun. Heat Mass Transf. 2024, 157, 107763. [Google Scholar] [CrossRef]
- Szajding, A.; Kuta, M.; Cebo-Rudnicka, A.; Rywotycki, M. Analysis of work of a thermal energy storage with a phase change material (PCM) charged with electric heaters from a photovoltaic installation. Int. Commun. Heat Mass Transf. 2023, 140, 106547. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z.; Nie, C.; Li, Y. Design of combinational fins for a vertical shell-tube latent heat thermal energy storage unit. Int. Commun. Heat Mass Transf. 2023, 146, 106921. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Salilih, E.M. A case study in the field of sustainability energy: Transient heat transfer analysis of an ice thermal storage system with boiling heat transfer process for air-conditioning application. Energy Rep. 2022, 8, 1034–1045. [Google Scholar] [CrossRef]
- Pokhrel, S.; Amiri, L.; Poncet, S.; Ghoreishi-Madiseh, S.A. Reduced order 1 + 3D numerical model for evaluating the performance of solar borehole thermal energy storage systems. J. Energy Storage 2023, 66, 107503. [Google Scholar] [CrossRef]
- Uribe, D.; Vera, S.; Perino, M. Development and validation of a numerical heat transfer model for PCM glazing: Integration to EnergyPlus for office building energy performance applications. J. Energy Storage 2024, 91, 112121. [Google Scholar] [CrossRef]
- Vahidhosseini, S.M.; Rashidi, S.; Hsu, S.; Yan, W.; Rashidi, A. Integration of solar thermal collectors and heat pumps with thermal energy storage systems for building energy demand reduction: A comprehensive review. J. Energy Storage 2024, 95, 112568. [Google Scholar] [CrossRef]
- Kim, Y.; Dinh, H.; Kang, G.; Hoang, D. Performance evaluation of a novel horizontal ground heat exchanger: Coil-column system. J. Build. Eng. 2023, 76, 107180. [Google Scholar] [CrossRef]
- Meana-Fernández, A.; Suárez-López, M.J.; Blanco, E.; Prieto, J.; García, D. Experimental heating and cooling curves of the ground for temporary energy storage applications. J. Energy Storage 2024, 94, 112419. [Google Scholar] [CrossRef]
- Deng, Z.; Nian, Y.; Liu, Q.; Cheng, W. Numerical analysis of borehole heat exchanger using a single shape-stabilized phase change material in heating and cooling seasons. J. Energy Storage 2023, 70, 107897. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, C.; Cai, C.; Lu, X.; Liu, D. Comparative analysis of ground thermal conductivity and thermal resistance of borehole heat exchanger in different geological layered sequence. J. Build. Eng. 2024, 84, 108541. [Google Scholar] [CrossRef]
- Rajeh, T.; Al-Kbodi, B.H.; Li, Y.; Zhao, J.; Zhang, Y. Modeling and techno-economic comparison of two types of coaxial with double U-tube ground heat exchangers. Appl. Therm. Eng. 2023, 225, 120221. [Google Scholar] [CrossRef]
- Xu, Y.; Zeng, Z.; Sun, D. Experimental and numerical investigation on heat transfer characteristics of vertical ground heat exchangers in karst areas. Energy Build. 2022, 275, 112481. [Google Scholar] [CrossRef]
- Lein, R.; Fujii, H.; Ikeda, R.; Bina, S.M.; Harada, R.; Kosukegawa, H. Optimization of double layered horizontal directional drilled ground heat exchangers by water injection into the borehole. Geothermics 2024, 118, 102913. [Google Scholar] [CrossRef]
- Shoji, Y.; Katsura, T.; Nagano, K. Improvement of accuracy with uncertainty quantification in the simulation of a ground heat exchanger by combining model prediction and observation. Geothermics 2023, 107, 102611. [Google Scholar] [CrossRef]
- Ahmadfard, M.; Bernier, M. Simulation of borehole thermal energy storage (BTES) systems using simplified methods. J. Energy Storage 2023, 73, 109240. [Google Scholar] [CrossRef]
- Hosseinnia, S.M.; Sorin, M. Numerical approach for sizing vertical ground heat exchangers based on constant design load and desired outlet temperature. J. Build. Eng. 2022, 48, 103932. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Y.; Luo, J.; Zheng, J.; Cheng, Y. Numerical study on heat transfer and flow characteristics of coaxial geothermal heat exchangers with helical finned inner tubes. J. Build. Eng. 2023, 65, 105752. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, G.; Liu, W.V. A new semi-analytical solution addressing varying heat transfer rates for U-shaped vertical borehole heat exchangers in multilayered ground. Energy 2023, 274, 127373. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, J.; Liu, W.V. A novel solution for vertical borehole heat exchangers in multilayered ground with Robin boundary condition. Appl. Therm. Eng. 2024, 255, 123923. [Google Scholar] [CrossRef]
- Shen, J.; Zhou, C.; Luo, Y.; Tian, Z.; Zhang, S.; Fan, J.; Ling, Z. Comprehensive thermal performance analysis and optimization study on U-type deep borehole ground source heat pump systems based on a new analytical model. Energy 2023, 274, 127367. [Google Scholar] [CrossRef]
- Chen, W.; Zhou, C.; Huang, X.; Luo, H.; Luo, Y.; Cheng, N.; Tian, Z.; Zhang, S.; Fan, J.; Zhang, L. Study on thermal radius and capacity of multiple deep borehole heat exchangers: Analytical solution, algorithm and application based on Response Factor Matrix method (RFM). Energy 2024, 296, 131132. [Google Scholar] [CrossRef]
- Extremera-Jiménez, J.; Yousif, C.; Casanova-Peláez, P.J.; Cruz-Peragón, F. Fast segregation of thermal response functions in short-term for vertical ground heat exchangers. Appl. Therm. Eng. 2024, 246, 122849. [Google Scholar] [CrossRef]
- Li, M.; Tan, Y.; Wu, Y.; Wang, Q.; Li, Y. New algorithm for estimating parameters from interrupted thermal response tests of ground heat exchangers. Appl. Therm. Eng. 2024, 239, 122088. [Google Scholar] [CrossRef]
- Kerme, E.D.; Fung, A.S. Heat transfer simulation, analysis and performance study of single U-tube borehole heat exchanger. Renew. Energy 2020, 145, 1430–1448. [Google Scholar] [CrossRef]
- Kerme, E.D.; Fung, A.S. Transient heat transfer simulation, analysis and thermal performance study of double U-tube borehole heat exchanger based on numerical heat transfer model. Appl. Therm. Eng. 2020, 173, 115189. [Google Scholar] [CrossRef]
- Salilih, E.M.; Abu-Hamdeh, N.H.; Khoshaim, A.; Almasri, R.A.; Sajadi, S.M.; Karimipour, A. Thermal systems energy optimization employing two independent circuits of double vertical ground U-tube with PCM as the backfill material for building. J. Build. Eng. 2022, 56, 104752. [Google Scholar] [CrossRef]
- Salilih, E.M.; Abu-Hamdeh, N.H.; Oztop, H.F. Analysis of double U-tube ground heat exchanger for renewable energy applications with two-region simulation model by combining analytical and numerical techniques. Int. Commun. Heat Mass Transf. 2021, 123, 105144. [Google Scholar] [CrossRef]
- Zeng, H.; Diao, N.; Fang, Z. Heat transfer analysis of boreholes in vertical ground heat exchangers. Int. J. Heat Mass Transf. 2003, 46, 4467–4481. [Google Scholar] [CrossRef]
- Biglarian, H.; Abbaspour, M.; Saidi, M.H. A numerical model for transient simulation of borehole heat exchangers. Renew. Energy 2017, 104, 224–237. [Google Scholar] [CrossRef]
- Hu, P.; Yu, Z.; Zhu, N.; Lei, F.; Yuan, X. Performance study of a ground heat exchanger based on the multipole theory heat transfer model. Energy Build. 2013, 65, 231–241. [Google Scholar] [CrossRef]
- Yang, W.; Shi, M.; Liu, G.; Chen, Z. A two-region simulation model of vertical u-tube ground heat exchanger and its experimental verification. Appl. Energy 2009, 86, 2005–2012. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Salilih Elias, M. Numerical modelling of a parallel flow heat exchanger with two-phase heat transfer process. Int. Commun. Heat. Mass Transf. 2021, 120, 105005. [Google Scholar] [CrossRef]
- Minaei, A.; Maerefat, M. Thermal resistance capacity model for short-term borehole heat exchanger simulation with non-stiff ordinary differential equations. Geothermics 2017, 70, 260–270. [Google Scholar] [CrossRef]
- Lamarche, L.; Kajl, S.; Beauchamp, B. A review of methods to evaluate borehole thermal resistances in geothermal heat-pump systems. Geothermics 2010, 39, 187–200. [Google Scholar] [CrossRef]





| Inlet condition | |
| Intersection of the down-running and up-running tubes |
| Parameter | Value |
|---|---|
| 100 m | |
| 72.7 mm | |
| 16 mm | |
| D | 36.7 mm |
| 0.013 m | |
| 1.5 W·m−1·K−1 | |
| 1.0 W·m−1·K−1 | |
| 2650 kg·m−3 | |
| 2650 kg·m−3 | |
| 2016 J·kg−1·K−1 | |
| 2016 J·kg−1·K−1 | |
| 4187 J·kg−1·K−1 | |
| 20.0 °C | |
| 10.0 °C | |
| Initial temperatures of grout, soil, and borehole wall | 10.0 °C |
| Parameters | Value |
|---|---|
| (time step) | 3600 s |
| (mesh size of the soil outside of the borehole) | 0.2 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salilih, E.M.; Kerme, E.D.; Fung, A.S.; Leong, W.H.; Leon-Salas, W.D. Study of the Transient Heat Transfer of a Single-U-Tube Ground Heat Exchanger by Integrating a Forward-Difference Numerical Scheme with an Analytical Technique. Processes 2024, 12, 2867. https://doi.org/10.3390/pr12122867
Salilih EM, Kerme ED, Fung AS, Leong WH, Leon-Salas WD. Study of the Transient Heat Transfer of a Single-U-Tube Ground Heat Exchanger by Integrating a Forward-Difference Numerical Scheme with an Analytical Technique. Processes. 2024; 12(12):2867. https://doi.org/10.3390/pr12122867
Chicago/Turabian StyleSalilih, Elias M., Esa Dube Kerme, Alan S. Fung, Wey H. Leong, and Walter D. Leon-Salas. 2024. "Study of the Transient Heat Transfer of a Single-U-Tube Ground Heat Exchanger by Integrating a Forward-Difference Numerical Scheme with an Analytical Technique" Processes 12, no. 12: 2867. https://doi.org/10.3390/pr12122867
APA StyleSalilih, E. M., Kerme, E. D., Fung, A. S., Leong, W. H., & Leon-Salas, W. D. (2024). Study of the Transient Heat Transfer of a Single-U-Tube Ground Heat Exchanger by Integrating a Forward-Difference Numerical Scheme with an Analytical Technique. Processes, 12(12), 2867. https://doi.org/10.3390/pr12122867







