Abstract
The separation of high-purity hydrogen from mixed gasses using dense metallic alloy membranes is essential for advancing a hydrogen-based economy. Palladium-based membranes exhibit outstanding catalytic activity and theoretically infinite hydrogen selectivity, but their high cost and limited performance in contaminant-rich environments restrict their widespread use. This study addresses these limitations by exploring strategies to develop cost-effective, high-performance alternatives. Key challenges include the vast compositional design space, lack of systematic design principles, and the slow pace of traditional material development. This review emphasizes the potential of high-throughput and combinatorial techniques, such as composition-spread alloy films and the statistical design of experiments (DoE), combined with machine learning and materials informatics, to accelerate the discovery, optimization, and characterization of palladium-based membranes. These approaches reduce development time and costs while improving efficiency. Focusing on critical properties such as surface catalytic activity, resistance to chemical and physical stresses, and the incorporation of low-cost base metals, this study introduces domain-specific descriptors to address data scarcity and improve material screening. By integrating computational and experimental methods, future research can identify hidden material correlations and expedite the rational design of next-generation hydrogen separation membranes.
1. Introduction
Transitioning to clean energy is one of the most effective solutions to mitigate carbon-induced climate change and remains central to global sustainable development efforts []. At the heart of this transition are low-carbon energy vectors, designed to store and transport energy with minimal environmental impact throughout their lifecycle [,]. Among these, green hydrogen has emerged as a key player in facilitating the shift toward a carbon-neutral energy infrastructure. Hydrogen’s appeal is driven by several factors: it is the most abundant element in the universe, constituting 75% of its mass, and its unique properties make it ideal for energy applications. As the lightest chemical element, with a gaseous H₂ density of 0.00082 g/cm3 at the standard atmospheric pressure and 20 °C, hydrogen offers significant advantages for energy storage and transportation []. Additionally, the conversion of hydrogen’s chemical energy to electricity or heat is entirely carbon-free at the point of use. With an energy-to-weight ratio of 143 MJ/kg based on the higher heating value (HHV) and 120 MJ/kg on the lower heating value (LHV), hydrogen outperforms other non-nuclear energy sources [,,].
However, hydrogen usage depends on its purity, which varies depending on the production method and downstream purification processes. A life cycle assessment shows that hydrogen can achieve near carbon neutrality when supported by power-to-hydrogen systems or carbon capture, utilization, and storage (CCUS) technologies []. Given its status as a priority energy carrier in distributed energy systems, hydrogen is considered a critical element of a decarbonized, sustainable energy future [,].
Although hydrogen gas does occur naturally—such as in Bourakebougou, Mali []—most hydrogen in use today is produced synthetically. Synthetic hydrogen, therefore, will continue to predominate until strategies to harness natural hydrogen sources become techno-economically viable. This predominance arises from various challenges associated with geological hydrogen, including infrastructure, exploration, extraction, environmental and safety considerations, as well as storage and transportation.
Current production methods are often classified using a color-coded system based on their carbon footprint. For example, black hydrogen is produced from coal without carbon capture, while gray hydrogen comes from natural gas without CCUS. Low-carbon hydrogen includes green hydrogen, produced from renewable energy, blue hydrogen from fossil fuels with CCUS, and aqua hydrogen, similar to blue hydrogen but without carbon emissions [,]. Despite a future shift toward green hydrogen, in 2023, two-thirds of the 97 Mt of global hydrogen production came from unabated natural gas, and one-fifth from unabated coal, contributing to 75–95% of the 920 Mt CO₂ emissions associated with global hydrogen production [].
Hydrogen’s demand spans industries such as agriculture and food, chemicals (e.g., methanol production), healthcare, transportation, energy, manufacturing, and nuclear fusion [,,]. However, hydrogen purity requirements vary significantly by application. For instance, ultra-pure hydrogen is critical in contaminant-sensitive industries like polymer electrolyte membrane fuel cell vehicles (PEMFCVs) and microelectronics, where purity levels of ≥99.7% (ISO 14687:2019 standard []) and 99.9999%, respectively, are required [,,]. Meeting these purity standards is challenging due to the impurities typically found in crude hydrogen produced from fossil fuels. These mixtures contain carbon oxides (CO, CO2), O2, H2O, N2, NOx, NH3, SOx, volatile organic compounds (VOCs), sulfur compounds, and metals, among others. Thus, high-purity hydrogen production requires two critical downstream processes: separation, followed by further purification or upgrading to meet industrial standards.
Hydrogen separation and recovery is a well-established industry that uses adsorption, cryogenic, and membrane separation techniques. Pressure swing adsorption (PSA) accounted for over 85% of global hydrogen production in 2009 due to its techno-economic feasibility, with applications ranging from small to large-scale plants, achieving purity levels as high as 99.9999 vol.% [,]. However, PSA is less suited to small-scale production due to high initial investment and operational costs []. Cryogenic separation, while offering superior recovery rates, is the most capital- and cost-intensive method []. Given the rising importance of distributed energy systems—where energy conversion units are located near consumers—membrane technology provides a modular solution with lower investment and maintenance costs []. While polymer membranes dominate due to lower costs and mild operation conditions, metallic membranes offer superior hydrogen permselectivity at high temperatures [,], making them valuable in contaminant-sensitive applications like fuel cells [,].
Despite over 60 years of development, metallic membranes have seen limited application outside niche sectors like microelectronics and nuclear fusion []. The slow adoption is due to the high cost of palladium and other precious metals, combined with insufficient mechanical strength and resistance to chemical poisoning. Efforts have been made to explore multicomponent Pd-based alloys, body-centered cubic (BCC) refractory metal alloys, and amorphous alloys [,,]. However, Pd-based membranes have demonstrated limited long-term resistance to hydrogen sulfide poisoning. BCC refractory metal alloys, while promising, lack the native catalytic surface properties required for effective hydrogen dissociation unless coated with noble metals. Furthermore, amorphous alloys, being metastable, face the risk of crystallizing at high temperatures, restricting their use to lower temperature applications where hydrogen permeation rates are slower and hydrogen embrittlement-induced membrane destruction is a potential threat [,,,]. While computational chemistry based on density functional theory has been employed to screen new alloys, much of the work relies on trial and error, informed guesswork, and past literature. Density functional theory (DFT) approaches become prohibitive in substitutionally disordered systems with more than three components [,], and experimental trials are resource-intensive and prone to failure []. The challenge remains to develop fast, robust methods for rational metallic membrane design.
Recent advances in heterogeneous catalysis and materials science have increasingly used combinatorial and high-throughput techniques, along with data-driven methods, to reveal hidden insights and establish structure–property–performance relationships [,]. A key driver of this shift is Material Informatics (MI)—a term coined by J. R. Rodgers in 2003 []—which has revolutionized materials research by enabling rapid screening and optimization through artificial intelligence, data analytics, and computational methods. Despite its success in catalysis and material design, material informatics remains underutilized in metallic membrane development.
Building on these insights, this review presents selected case studies where combinatorial and high-throughput techniques have significantly advanced research on Pd-based membranes for hydrogen separation. Additionally, it offers a forward-looking perspective on leveraging material informatics to accelerate metallic membrane development. Although the literature on applying material informatics to metallic membrane design is currently scarce, we project how this approach could expedite the design of Pd-based membranes. This includes guidelines for applying machine learning to high-throughput screening and a proposed set of feature descriptors to guide future research in this rapidly evolving field. To ensure completeness, an overview of the three main industrial hydrogen separation methods is given.
2. General Overview of Main Hydrogen Separation Technologies
Industrially applied methods in hydrogen gas separation can be broadly categorized into adsorption-based techniques, cryogenic separation, and membrane diffusion-driven processes [,,,,,,,].
Pressure Swing Adsorption (PSA) is the leading industrial hydrogen separation method, operating through a cyclic process that selectively adsorbs impurities from hydrogen-rich feed gas onto porous materials like zeolites, activated carbons, silica, and alumina gel at high pressure (10–40 bar) and ambient temperature (290–310 K) [,,,,,,]. Impurities are released during regeneration by reducing the pressure (1–3 bar), allowing the adsorbent to be reused []. PSA is effective for feed gasses containing 60–90 mol% hydrogen, producing ultra-pure hydrogen—99.9% purity for ammonia synthesis and >99.9999% purity with <1 ppm CO, CO₂, and CH₄ for semiconductor applications [,]. Recovery rates typically reach 80%, with advanced systems like Honeywell UOP’s Polybed™ PSA achieving over 90% recovery and handling high throughputs of up to 265,000 Nm3/h []. PSA is resilient to impurities such as COx, hydrocarbons, H₂S, and water, unlike dense metallic membranes, and recent advancements have improved its compactness and cost-efficiency. However, it faces challenges, including high energy demands, inefficiency with feed gasses containing less than 90% hydrogen, and impracticality for small-scale applications [,]. Low-hydrogen feeds require larger units to manage impurity loads, further increasing system size and complexity [,].
Cryogenic separation is the second most common method for gas separation, utilizing partial condensation in distillation column cascades to exploit vapor pressure differences at cryogenic temperatures and high pressures [,]. This process separates lighter components with higher vapor pressures and lower boiling points from heavier components and is also used in hydrogen isotope separation for nuclear fusion systems []. While cryogenic separation achieves lower hydrogen purities (95–98%) than PSA, it offers higher productivity and facilitates hydrogen liquefaction, making it well-suited for large industrial applications but impractical for smaller scales, such as hydrogen fuel station purification [,]. Its major drawbacks include high energy consumption, significant costs due to extreme operating conditions, and safety risks associated with the flammability and toxicity of cryogenic fluids [,,,].
Membrane separation is widely studied for hydrogen purification due to its modularity, low cost, and suitability for small to medium-scale operations compared to PSA and cryogenic methods [,,,,]. The most commonly used membranes are polymers, ceramics porous carbons, and dense metallic membranes. The latter group offers an advantage in high-temperature environments and can achieve infinite permselectivity, unlike dense organic polymers [,,]. A comparative study showed that Pd-based membrane-assisted hydrogen separation (0.50 kWh/kg energy, 28.4% exergy efficiency) is more energy-efficient than cryogenic-assisted methods (2.01 kWh/kg energy, 14.7% exergy efficiency), though the latter has achieved higher purity and recovery rates, highlighting a trade-off between efficiency and output quality [].
Table 1 compares the three main hydrogen separation technologies—PSA, cryogenic distillation, and membrane separation—based on feed gas requirements, product purity, yield, operating conditions, recovery capacity, product pressure, and costs. While compression or liquefaction costs may apply for storage or transport, membranes generally provide a favorable trade-off in purity and cost.

Table 1.
Comparison of Hydrogen Purification Techniques [].
3. Market Outlook and Future Potential of Membrane Technologies
As of 2023, the global membrane gas separation market was valued at $1.4 billion, with polymer membranes dominating at 73.3% across sectors []. Gas separation-specific membranes made up 10.53% of the overall market, with polyimide and polyaramids leading due to their chemical resistance, high thermal stability, and superior gas separation capabilities. Other materials such as polysulfone and cellulose acetate are also widely used []. The global hydrogen separation membrane market was valued at USD 194.6 million in 2023, is projected to reach USD 298 million by 2030, and is growing at a CAGR of 6.3% []. Inorganic membranes (ceramics and metal oxides) accounted for 20.3% of the market, while metallic membranes made up 6.68%. This segment is expected to grow at a CAGR of 6.7% from 2024 to 2030 []. Market growth in hydrogen separation is driven by decarbonization efforts, increased demand for clean energy, energy efficiency, and cost-effectiveness, as well as the modularity of membranes, which suit medium- and small-scale applications. Although metallic membranes, such as those used in hydrogen diffusers, can achieve ultra-pure hydrogen (up to 8N purity), they require a pure feed (≥a volume fraction of 99.5%) to avoid corrosion, poisoning, and mechanical issues under high temperature and pressure conditions [,]. Additionally, the high cost and limited availability of certain metals, influenced by geopolitical factors, pose challenges. The characteristics of the most reported hydrogen permselective membranes are summarized in Table 2.

Table 2.
Hydrogen selective membrane main types [,,].
4. Dense Metallic Membranes
Hydrogen purification technologies are crucial for the hydrogen economy, with a focus on medium-scale production units rather than large-scale facilities. Membranes, especially dense metallic ones, offer a promising, cost-effective solution. When defect-free, dense metallic membranes can achieve infinite hydrogen permselectivity, producing impurity-free gas and outperforming conventional methods in recovery rates [,]. Metallic membranes have been extensively researched, with around 10,000 related articles indexed by 2013 []. This research builds on early discoveries, including Deville and Troost’s work on hydrogen permeability through platinum (1863) and Graham’s 1866 study on palladium’s hydrogen absorption [,,]. The first commercial Pd-based membranes (Pd–25%Ag) were introduced in the 1960s, leading to ongoing research on palladium alloys and silver-, gold-free palladium-lean membranes using Group IVB, VB, and VIB alloys as alternatives [,,].
4.1. Applications of Dense Metallic Membranes
Dense metallic membranes (Pd, Pt, Ni, and elements from groups IIIB to VB) are key for providing ultrapure hydrogen (9N, 99.9999999%) with minimal energy consumption in various applications [,,,]. These include:
Commercial-Scale Production of Ultrapure Hydrogen: Used as key components in hydrogen diffusers, with or without heated getters, for ultra-pure hydrogen supply in microelectronics.
Hydrogen Isotope Separation: Palladium alloys are employed in catalyzed isotopic exchange for tritium and deuterium recovery in fusion fuel cycles (tokamak systems) [,,,,].
Gas Sensing: Utilized In Sensitive Detection Systems [].
Permeable Catalyst Applications: Palladium-based membranes can catalyze hydrogenation reactions by allowing hydrogen dosing through the membrane’s high-pressure side and catalyzed hydrogenation reaction on the low-pressure surface enabling reactions such as dienes conversion to olefins, which aids sustainable polymer upgrading [,,].
Process Intensification: Integrated into catalytic membrane reactors to improve energy efficiency in hydrogenation, dehydrogenation, and related reactions [,,,,,,,]. These membranes optimize hydrogen production in systems like steam methane reforming and coal gasification.
Ammonia Synthesis: Group V hydrogen permselective membranes (e.g., niobium-based) have enabled ammonia synthesis under milder conditions (0.8 atm, 500 °C), achieving a synthesis rate of 6 × 10⁻⁹ mol·cm⁻2·s⁻1 [], compared to the energy-intensive Haber-Bosch process (200 atm, 400–450 °C).
Electrochemical Palladium Membrane Reactors (ePMRs): In ePMRs, Pd-based membranes separate the electrochemical chamber from the hydrogenation chamber, utilizing water as the hydrogen source, eliminating the need for pure H₂ gas, and mitigating the competitive hydrogen evolution reaction (HER) [,,].
Hydrogen Storage and Catalysis: Palladium-based hydrides are explored for hydrogen storage and catalytic applications, including hydrogen evolution reactions and superconductivity [,,].
Despite their potential, metallic alloy membranes face limitations that hinder broader industrial adoption, resulting in a smaller market share compared to polymeric and other inorganic membranes.
4.2. Problems with Pure Palladium Membranes
Pure palladium membranes face several challenges that limit their widespread application. These include:
High Cost and Supply Uncertainty: Palladium, along with platinum and rhodium, is costly and scarce due to its low price-to-crustal abundance ratio, as shown in Figure 1.
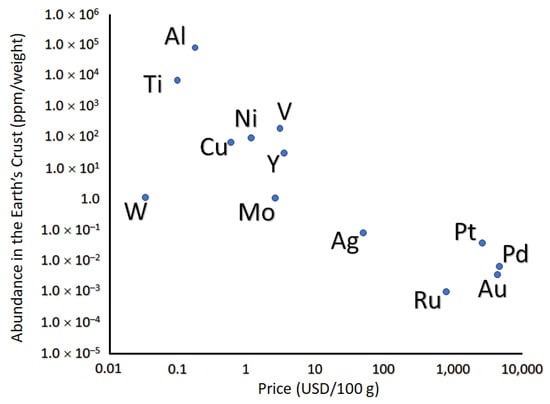
Figure 1.
Abundance and cost of the most used metals for the fabrication of Pd-based membranes (Each price is referred to 2019. Price of titanium is based on TiO2 with a minimum purity of 95%; price of yttrium is based on yttrium metal with minimum purity 99.9%; price of vanadium is based on the vanadium pentoxide). Reproduced with permission from [], Progress in Energy and Combustion Science; published by Elsevier, 2020.
Hydrogen Embrittlement in Palladium: Hydrogen absorption in palladium (Pd) below critical conditions (Tc = 298 °C, Pc = 2 MPa) causes the formation of two hydride phases: the hydrogen-lean α-PdH and the hydrogen-rich β-PdH, both in a face-centered cubic FCC structure but with different lattice parameters [,]. As hydrogen is absorbed, the Pd lattice parameter expands from 3.889 Å to 3.894 Å at H/Pd ≈ 0.015, reaching the maximum solubility in the α-PdH phase. At higher hydrogen uptakes, the β-PdH phase nucleates and grows, with the lattice parameter increasing to 4.025 Å at H/Pd ≈ 0.6, and up to 4.04 Å at H/Pd = 0.70 as a result of ~70% of the octahedral sites occupied []. The coexistence of α- and β-PdH results in a ΔVβ-α/Vα = 10% irreversible volume expansion, leading to mechanical degradation, including a loss of ductility and increased brittleness, known as hydrogen embrittlement. This issue arises even under controlled temperature cycling in inert gas environments. The critical temperature for the α → β phase transition is reduced by alloying Pd with transition metals [].
Poisoning in Sulfur Environments: In environments with H2S concentrations >100 ppm, a dense tetrapalladium sulfide Pd4S layer forms on palladium membranes, reducing hydrogen permeance to 1/20th of pure Pd [,,]. Pd4S can eventually cover the entire membrane, causing “corrosive decay” []. Despite its presence, pure Pd retains hydrogen dissociation activity, indicating that Pd4S impedes H2 diffusion []. Pd4S formation follows the reaction:
8Pd(s) + S2(g) ⇌ 2Pd4S(s) ΔGf° (J) = −368,790 + 168.2 T (K)
At lower temperatures (623–908 K), Pd4S is favored due to its lowest Gibbs free energy. Additionally, Pd4S can form via:
4Pd + H2S ⇄ Pd4S + H2, ΔG = −71.613 kJ/mol.
Pd4S crystallizes in a tetragonal structure with larger lattice parameters () than pure Pd (~3.89Å), causing stress cracking and sulfur propagation [,]. Below 100 ppm H2S, poisoning may occur through chemisorptive dissociation of H2S, forming Pd-S covalent bonds, and leading to the decomposition of sulfur adatoms that physically block hydrogen dissociation sites or possibly weaken Pd catalytic properties by withdrawing electron density from Pd in the surface vicinity [,], as shown in the reactions (3)–(5) []:
where X* denotes an adsorbed species, and * an unoccupied surface site.
H2S + * ⇌ H2S*
H2S* + * ⇌ HS* + H*
HS* + * ⇌ S* + H*
Poisoning in CO environments: CO inhibits H2 permeation through Pd membranes at temperatures <250 °C (for 50% CO in H2) or <400 °C [,], mainly through reversible blocking of Pd surface sites. CO’s effect is negligible at higher temperatures (>250 °C or 400 °C), where CO adsorption and Pd site blocking becomes reversible [,]. At higher temperatures, CO can react with Pd to form a metastable Pd-C phase leading to a more deleterious effect than the reversible Pd site-blocking mechanism, although Pd-C has been shown to suppress β-PdH formation []. The Pd-C forming reaction involves carbon deposition and diffusion through the Pd lattice, expanding the lattice parameter. The formation of Pd-C phases is promoted by reactions like Boudouard’s (2CO ⇌ C + CO2 (6)) and methanation (CO + 3H2 ⇌ CH4 + H2O (7)) []. In summary, CO poisoning mechanisms include adsorptive site-blocking, carbon deposition, the formation of bulk Pd1−xCx phases [], and the formation of surface-adsorbed methylene species (CH2*) possibly accompanied by gas-phase CH4 molecules exacerbating with lower temperatures and leading to cumulative site-blocking effects [,]. Further readings on the mechanism of poisoning of Pd-based membranes can be found at [].
4.3. Challenges Associated with Pd–Alloy Membranes
Pd-based alloy membranes face challenges such as corrosion under harsh conditions, poisoning, hydrogen embrittlement during thermal cycling, mechanical integrity loss over time, and the high cost and uncertainty supply of platinum group metals [,,,,]. Early membranes in the 1960s used Pd–Ag alloys to address β-hydride nucleation and prevent dimensional expansion in pure Pd membranes. Despite recent advances like applying electric fields to reduce sulfur poisoning, alloying remains the preferred approach for improving membrane performance [,].
Five Key Considerations for Hydrogen Separation Membranes [].
Hydrogen Permeability and Phase Stability: Membranes must resist α→β phase transformation during operation (400–600 °C). Alloys should be designed to avoid hydride formation by closing α-β miscibility gaps at room temperature [].
Thickness–Durability Tradeoff: Thinner membranes improve hydrogen flux and possibly reduce material costs but compromise strength under high-pressure gradients.
Membrane Holder Design: Composite membranes must balance mechanical strength, thermal and chemical stability, and cost-effectiveness.
Membrane Assembly Architecture: Use-case-oriented membrane configurations—tube, folded-foil, or plane-foil—should maximize separation efficiency, productivity, and recovery rate.
Start-up/Shutdown Optimization: Proper operating protocols can enhance performance and extend membrane lifespan.
Considering Intrinsic Properties Specifically of The Dense Metallic Membrane: Membranes should exhibit high hydrogen permeability, corrosion resistance, and mechanical stability at operating conditions (preferably high tensile strength and low Young’s modulus or high elasticity). They must feature low dilatation during hydrogen saturation, small coefficients of thermal expansion, and be easily fabricated into thin foils or tubing [,]. Economically, widespread adoption depends on cost competitiveness and durability compared to alternative technologies.
4.4. Intricacies in Dense Membrane Alloys Development
Single-element transition metal membranes (IIIB–VB, Pd) lack long-term stability in hydrogen environments due to hydride phase formation, causing miscibility gaps, volume expansion (ΔV/V0 >> 0), and structural changes, as seen in their PCT diagrams (Figure 2) []. These issues necessitate material modifications for hydrogen transport applications. Table 3 summarizes the hydrogen dissolution properties of commonly used metals.
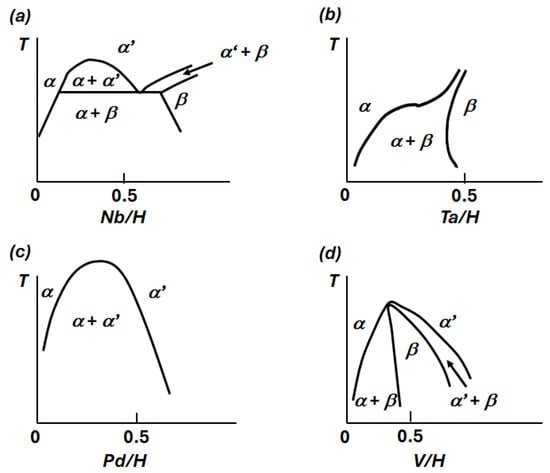
Figure 2.
Schematic representations of phase diagrams for Group VB and Pd metal–hydrogen systems showing miscibility gaps at low to moderate hydrogen concentrations: (a) Nb–H, (b) Ta–H, (c) Pd–H, (d) V–H. Reproduced with permission from [], Electronic structure and properties of hydrogen in metals; published by Springer Nature, 1983.

Table 3.
Fundamental properties of pure metals for hydrogen separation. Taken from [].
4.4.1. Pd–Cu Series
The Pd–Cu binary series offers alloys with distinct hydrogen transport properties, notably Pd60-40 wt.% Cu (Pd47.3–52.7 at.% Cu), an ordered BCC (CsCl-type) structure referred to as B2 structure, exhibiting high hydrogen permeability (comparable to pure Pd at 450–475 °C), superior tensile strength, lower thermal expansivity, and resistance to hydrogen embrittlement due to reduced hydrogen solubility. However, its permeability drops sharply above 500 °C due to a hydrogen-accelerated B2 → FCC + BCC phase transition (Figure 3) [,]. B2 Pd–Cu resists β-hydride nucleation but is less resistant to sulfur poisoning than disordered FCC Pd–Cu, which has lower hydrogen permeability [,]. Density functional theory attributes the lower hydrogen permeability in FCC Pd–Cu compared to BCC Pd–Cu to hydrogen’s diffusion barrier: lower for BCC Pd–Cu (0.016 eV with the interstitial diffusion following a Tet-to-Tet path) than FCC Pd–Cu (0.346 eV with the interstitial diffusion following an Oct-to-Tet path), where interstitial hydrogen clustering impedes diffusion in FCC alloys []. FCC Pd–Cu permeance (908–1173 K) is about 1/10th of pure Pd and depends on synthesis methods for H2S resistance [,]. Figure 3 depicts the hydrogen permeability of Pd60-40 wt.% Cu as a function of the temperature.
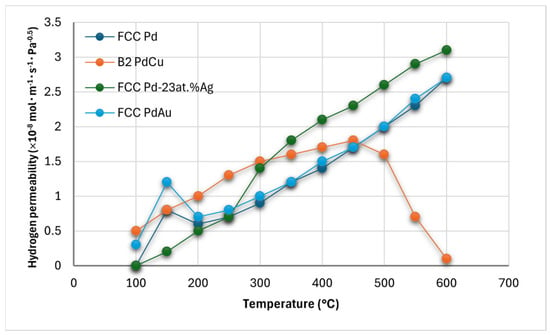
Figure 3.
Pure hydrogen permeability in pure FCC Pd (dark blue), FCC Pd–Ag (green), FCC Pd–Au (light-blue), B2 Pd–Cu (orange). Up to ~450° Pd–40wt.%Cu exists in B2 structure, between 450 °C and 550 °C the mixed B2 + FCC exits, and at T > 550 °C a continuous FCC region occurs [].
4.4.2. Pd–Ag Series
The Pd–Ag system, with an optimal composition of Pd-23–25 at.% Ag, has the highest hydrogen permeability in the FCC Pd–Ag series, surpassing pure Pd by 1.7 times at 350 °C [], and offers good hydrogen embrittlement resistance (Figure 3). However, Pd-23 at.% Ag is more susceptible to poisoning by sulfur and carbon compounds than Pd–Cu alloys, making it more suitable for purifiers than separators [,]. Exposure of Pd-25 at.% Ag to a 10 ppm H2S in a 80%H2-concentrated feed causes a rapid flux decline, with Ag5Pd10S5 formation after ~3 days []. Even with sulfur cleanup systems, Pd–Ag membranes risk irreparable poisoning []. Segregation phenomena have also been observed in Pd-25% Ag foils during hydrogen absorption [,,,].
4.4.3. Pd–Au Series
The Pd–Au series, with optimal composition Pd-8–10 at.% Au offers higher chemical stability and superior hydrogen permeability in CO and H2S-rich environments compared to Pd, Pd–Ag, and Pd–Cu alloys [,,]. McKinley found Pd-40 wt.% Au to have higher permeability than Pd–Cu or Pd–Ag when exposed to 4 ppm H2S, though it only achieves less than 50% of pure Pd’s permeability in pure H2 conditions (Figure 3) [,,]. Gold’s high cost is a drawback in Pd–Au alloys.
4.4.4. Pd–Rare-Earth Series
In the Pd–Rare-Earth series, adding to Pd elements like Y, Ce, Gd, Tm, Lu, and Sm in 8.8, 5.75, 8.0, 4.5, 7.70, and 2.6–11.0 at.%, respectively, increases hydrogen permeability compared to pure Pd and Pd-25 at.% Ag due to enhanced high-temperature hydrogen solubility gradients [,,,,]. These alloys also exhibit improved mechanical strength, though solid solution hardening and large lattice expansion compared to pure Pd can impede their mechanical stability. Pd-8.8 wt.% Y, for example, has higher permeability than Pd-25 wt.% Ag but is harder to be worked into thin foils by cold rolling due to several intermediate strain relief annealing requirements []. As a consequence, they are required to be hydrogenated before rolling []. Hydrogen permeability of many binary Pd alloys with solute concentrations equal to 4 at.%, 8 at.%, or 25 at.t% has been studied by Shirasaki and coworkers, and their result is shown in Figure 4 [].
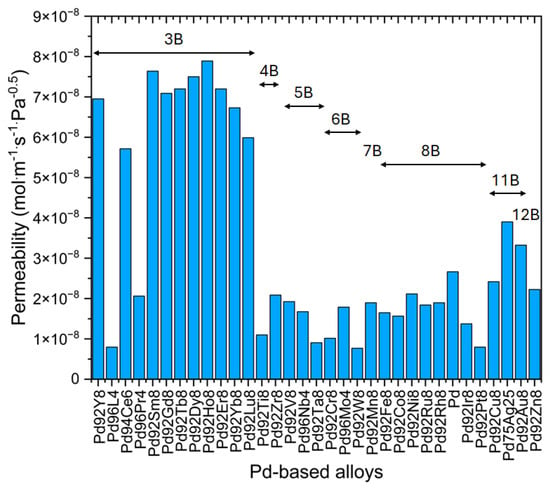
Figure 4.
Hydrogen permeability of various Pd–metal binary alloy membranes PdxM(100−x) ((100–x) represents the atomic concentration of the solute metal) at 873 K, where the metal M’s Group in the Periodic Table of Elements is depicted. The letter B in the figure represents a Group in the Periodic Table of Elements and the preceding roman numeral assigned before B is based on the American Group labelling scheme. Readapted from [].
4.4.5. Refractory Metals Alloys
Refractory metals of Groups VB-VIB transition metals, e.g., tantalum, vanadium, and niobium exhibit hydrogen permeability an order of magnitude higher than pure palladium but are poor catalysts for molecular hydrogen dissociation. To prevent passivation by surface oxidation and enhance dissociative adsorption and recombinative desorption, these metals require surface coating at their entry-terminal layer with more active metals, e.g., palladium [,,].
When designing Pd-based membrane materials, key factors include the maximum solubility of alloying elements in palladium, eliminating the α/β miscibility gap, and optimizing hydrogen permeability, chemical stability, and mechanical resistance. Recent studies suggest that introducing short-range ordered phases improves hydrogen permeability [], and using less expensive dopants as alternatives to silver enhances economic viability []. However, the search for optimal binary or ternary alloys remains complex and resource-intensive due to the large number of potential alloy combinations that need to be synthesized and evaluated.
5. Methods in Palladium Membranes Research
5.1. Mechanism of Mass Transfer in Metallic Membranes
In this review, palladium is deliberately selected as the prototype for metallic membranes, with mechanistic insights applicable to palladium inferred to similar materials. Amongst the variability of theories used to describe light interstitials diffusion, e.g., hydrogen in a host metal crystal lattice, Kehr [] suggested four temperature-dependent possible diffusion mechanisms depicted in Figure 5 below. A summary of each mechanism can be consulted in reference [].
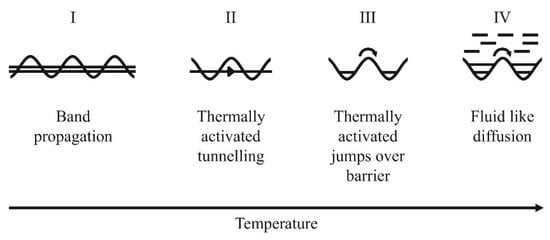
Figure 5.
Kehr’s suggested temperature-dependent diffusion models of light interstitials such as hydrogen in host metal lattice. Reproduced with permission from [], Renewable and Sustainable Energy Reviews; published by Elsevier, 2015.
Specifically, the thermally activated jumps over barrier mechanism commonly applies to hydrogen diffusion in defect-free dense metallic membranes in a gaseous environment and is considered in this review. In such a case, a higher activation energy is required to surmount the barrier, making this process dominant at elevated temperatures.
The accepted model of this mechanism (given below) can be attributed to []. Consecutively, when a mixture of gas is to be separated using a Pd-based membrane, from the higher partial pressure side to the lower partial pressure side the solution–diffusion mechanism can be summarized as follows [,,]:
S1: transport of molecular H2(g),f from the bulk gas—the feed gas f—onto the gas layer surrounding the surface Sf, where Sf refers to the membrane’s surface incident to the high-pressure gas flow.
S2 (dissociative adsorption): H2(g),f diatomic molecules are adsorbed at favorable surface sites disseminated on Sf and are catalytically dissociated into H adatoms denoted as H.Sf.
S3 (surface-to-subsurface): hydrogen adatoms H.Sf are absorbed from the adsorbed state into the metal subsurface, occupying thermodynamically favorable interstitial sites M located in the subsurface crystal lattice as H·Mf,
S4 (bulk diffusion): the interstitial H solutes then diffuse across the membrane’s bulk crystal lattice via activated hops with subsequent transition states,
S5 (bulk-to-surface): upon reaching close to the low-pressure side of the membrane referred to as permeate surface Sp, the interstitial H atoms H.Mp egress from the bulk metal onto Sp forming adsorbed HSp species,
S6 (recombinative desorption): pairs of hydrogen atoms species adsorbed on the permeate surface H.Sp associatively desorb as H2(g) molecules,
S7: newly recombined diatomic H2(g),p gas transport away from the low-pressure surface.
Microkinetic modeling is one of the three main approaches for studying reaction kinetics, alongside the Anderson–Schulz–Flory (ASF) distribution and the lumped kinetic model []. Unlike the lumped kinetic model, which primarily focuses on overall reactant conversion—often using empirical power-law expressions that can oversimplify or overcomplicate the reaction details—microkinetic modeling integrates the fundamental surface chemistry of catalytic reactions []. This method is particularly well-suited for investigating reactions involving surface phenomena, as it allows for the identification of key reaction intermediates and the determination of rate-limiting elementary steps. Such insights are crucial for optimizing the performance of membranes and catalysts []. From this perspective, the stepwise diffusion of hydrogen through metals can be described using a detailed sequence of elementary reactions (6)–(11) [].
S2: H2(g),f + 2Sf ⇌ 2H.Sf
S3: H.Sf + Mf ⇌ H.Mf + Sf
S4: H.Mf + Mp ⇌ H.Mp + Mf
S5: H.Mp + Sp ⇌ H.Sp + Mp
S6: 2H.Sp ⇌ H2(g),p + 2Sp
H2(g),f ⇌ H2(g),p
In the previous description, S represents a surface, and M is a metal active site. Note that the S1 is not represented because no reaction happens in that step.
In the case of composite alloy membranes, i.e., supported dense metal membranes, mass transfer through the support layers involving Knudsen, Poiseuille, and ordinary diffusion have to be accounted, when applicable [].
A graphical illustration of the general mechanisms described above is given in Figure 6.
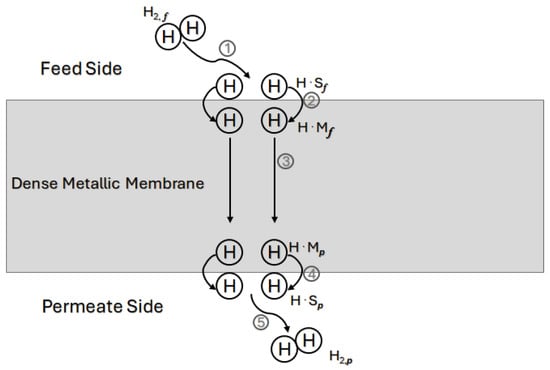
Figure 6.
Schematic of hydrogen-selective diffusion through dense metallic alloy membrane. (1) and (2) external diffusion from the feed gas and dissociative adsorption at the surface metal site followed by transport from the surface to the subsurface, (3) diffusion in the bulk lattice from the subsurface close to the high-pressure side to the subsurface close to the low-pressure side. (4) and (5) the H atoms egress and reassociate followed by desorption in the purified bulk gas. Reproduced with permission from [], Journal of Membrane Science; published by Elsevier, 2013.
Although the dissolution and diffusion mechanisms involved in hydrogen permeation are activated processes, it has been argued that hydrogen surface adsorption is not activation-dependent, provided the Pd surface is perfectly clean [].
To develop robust, domain-specific machine learning feature descriptors—one of the primary goals of this paper—it is essential to gain an in-depth understanding of the hydrogen mass transfer mechanism across membranes. Predicting target properties, such as hydrogen permeability, requires more than simply using the physicochemical properties explicitly present in the mathematical flux expression; indirect and less apparent properties can often serve as even more powerful descriptors. Guided by this rationale, the following sections focus on the experimental determination of the direct properties that describe hydrogen diffusion across dense metallic membranes.
Equation of Diffusion, Richardson Formula, and Siverts’ Law
In the solution–diffusion mechanism, hydrogen diffuses in atomic form through the membrane []. The key physical quantity used to describe hydrogen mass transfer through a dense metallic membrane is the permeation flux J. The latter can be defined as the quantity of hydrogen diffusing through a perpendicular unit cross-sectional area per unit of time []. Fick’s laws of diffusion can model hydrogen mass flow across a dense metal matrix. When one-dimensional and steady-state diffusion are assumed, as is common in practical membrane studies, the mathematical expression is referred to as Fick’s first law, which expression is shown in Equation (12):
where JH represents atomic hydrogen permeation flux, D the coordinate and concentration-independent diffusivity or diffusion coefficient of hydrogen across the medium, the concentration gradient or driving force along the diffusion direction, x. The concentration gradient is assigned a negative sign to indicate that mass flow occurs down the concentration gradient. Strictly speaking, the driving force dC/dx represents the gradient of the chemical potential dμ/dx. As the equilibrium described in Equation (13):
establishes between gaseous molecular hydrogen with pressure and dissolved hydrogen atoms, the chemical potential is expressed as in Equation (14):
where the standard designation (°) indicates 1 bar pressure of , μH refers to H dissolved in the solid phase, is the equilibrium .
By considering the equilibrium in Equation (13) above, one can relate the flux of H to the flux of H2 and integrate Fick’s first law (12) over x = 0 and x = l and keep the concentration difference as ΔCH for the moment being. This gives Equation (15):
where is the thickness of the membrane.
The rate-limiting step for the permeation process can be either surface phenomena or bulk diffusion or a combination of these phenomena thereof [,,], depending on various factors, e.g., the membrane thickness, the presence of defects, membrane surface cleanliness, etc. When the rate-determining step is the transport of hydrogen in the metal matrix (bulk diffusion), surface reactions are considered to be very fast, and the equilibrium reaction above (13) holds. In that case, the equilibrium constant K is:
where is the activity of dissolved hydrogen. For small concentrations (ideal solution), i.e., dilute phase, can be substituted for its concentration, which is conveniently expressed as the dissolved hydrogen-to-metal ratio (H/M), atom ratio r:
Expression (17) is Henry’s law of ideal solubility for a dissociating gas and, for the solution of diatomic gasses that dissolve dissociatively in metals, it is referred to as Sieverts’ law and Ks is Sieverts’ constant. It is remarkable that CH = r, hence combining these equations yields Richardson’s equation defined in Equation (18) as:
where and represent diatomic hydrogen gas partial pressure at the feed and permeate side, respectively. In Equation (18), the quantity:
corresponds to the hydrogen permeability of the membrane.
ϕ has been found to experimentally vary exponentially with the temperature in an Arrhenius-type relationship, thus can be expressed as (19):
where ϕ0 is the pre-exponential factor and Eϕ is the activation energy. It has been suggested that Eϕ < 30 kJ/mol indicates that surface phenomena—such as dissociative adsorption and recombinative desorption of H2—do not significantly contribute to the permeation process, as these surface reactions typically require higher activation energies, ranging from 54 to 146 kJ/mol []. Consequently, designing membranes with lower activation energies for hydrogen permeation, within the operating range, is of critical importance for enhancing performance.
Regularly, there are deviations from ideality (Sievert’s law), and the extended Richardson’s equation is used (20):
where holds for the pressure exponent, a dimensionless number such that 0.5 ≤ n ≤ 1.
Since dissolution and diffusion are activated processes, the solubility constant and diffusivity coefficient have been described by Arrhenius-type relationships (21) and (22), such that:
and
where D0 and K0 are the preexponential factors in the diffusivity and solubility, respectively, and ED and Es their activation energy, respectively. One can easily infer that (23):
Eϕ = ED + ES
A useful alternative to the permeability, where the thickness fluctuates is the permeance defined in Equation (24) as the permeability divided by the thickness:
The steps for the establishment of the previous equations have been discussed in the previous literature [,].
5.2. Experimental Determination of Flux and Permeability
The performance of dense metal membranes is primarily evaluated by their pure hydrogen permeability, selectivity toward hydrogen over other gasses, and long-term durability, specifically, the ability to maintain optimal permeability, selectivity, and mechanical integrity over time. Additionally, the U.S. Department of Energy (DOE) technical targets serve as a benchmark for assessing the viability of metal membranes in hydrogen separation applications (Table 4). The first step in evaluating a dense metallic membrane is to measure its pure hydrogen permeation flux. When only hydrogen permeation is measured during testing, it is referred to as a single-gas permeation test, which assesses the membrane’s performance under pure hydrogen conditions.

Table 4.
U.S. DOE Hydrogen Separation Performance Targets.
5.2.1. Single Gas Permeation Test
Various methods exist to measure the hydrogen permeation flux in single gas permeation testing. The main components of a typical single gas permeation setup are the pure hydrogen and inert gas, e.g., nitrogen gas tanks, mass flow controllers, and if applicable, a soap film flowmeter for permeate gas flow measurements at small flow rates. Digital and manual bubble meters or soap film flow meters are relatively cheap for usage compared to mass flow controllers in pure hydrogen gas testing. The soap film meter directly measures the time taken for the moving front of a soap film to pass through a defined volume at atmospheric pressure, thereby providing the corresponding rate. It is particularly well-suited for measuring small flow rates; however, when a flow tube with a fixed small diameter and length is used, the main design constraint of the flow meter lies in its ability to generate a single coherent soap bubble.
If a flat membrane is taken as an example, the flux is defined as the quantity of hydrogen gas permeating the membrane’s active surface unit area per unit of time. By translating this definition into a Formula (25):
In most recent membrane literature, Quantity can be an extensive parameter such as the volume [L−3] or number of moles. A is the membrane’s active area or the area exposed to incident gas flow.
Since Fick’s First Law and extended Richardson’s equation (given above (20)) are applied, it is recommended that flux values be reported once steady-state conditions are achieved. Establishing this regime can take up to approximately 24 h in some cases []. Monitoring gas permeation over time or observing pressure increases in a calibrated volume on the permeate side of a pre-vacuumed system are commonly used techniques for identifying the steady-state regime. This approach forms the basis of the time-lag method, which is useful for directly determining the diffusion coefficient and indirectly obtaining the solubility constant [,].
From the previous Equation (20), the permeability can be derived as follows:
The permeability is a measure of the gas flux permeated through the membrane at a given partial-pressure difference []. The permeability derived from the above equality is given in Quantity∙[L−1∙T−1∙P−n]. For single gas permeation tests, authors sometimes apply either vacuum on the permeate side in which case can be taken as null, or if the permeate side is left at atmospheric pressure the ≈ 100kPa (depending on geographical localization) has to be taken.
The product of hydrogen flux and membrane thickness is often referred to as specific permeability []. While flux is dependent on membrane thickness, specific permeability is not, as it normalizes the thickness effect. This makes specific permeability a useful parameter for comparing hydrogen permeation fluxes across membranes of varying thicknesses within the same alloy system. Russian researchers have measured the specific hydrogen permeability of metallic membranes by calculating the permeability based on the time required to fill a calibrated volume with permeated hydrogen [,,,].
The determination of the pressure exponent n may give hints on the rate-limiting steps in the permeation process. Oftentimes, the trustworthy value of the pressure exponent n is found by regressing using the least mean-square method the relation from Equation (20) in the straight-line part of the root square function, where the n ∈ [0.5, 1]. The actual value of n is obtained from the regression line with the highest correlation coefficient R2. This value is then compared to 0.5 to predict the rate-limiting step. If n is close to 0.5, the rate-limiting step is bulk diffusion (agreement with Sieverts’ law), and if n considerably deviates from 0.5, other phenomena can be assumed to gain in importance. Regularly, thick Pd-based membranes are found to have n = 0.5 and ultrathin-film membranes can deviate. In their modeling study, ref. [] concluded that bulk diffusion is expected to be the rate-limiting step for pure Pd membrane with thickness down to ~1 μm at temperatures above ∼300 °C, provided that external mass transfer resistance is absent. Care should be taken not to assume n = 0.5 or 1 based on the thickness (inconsistent nature of the rate-limiting step) because several factors other than the thickness (e.g., surface segregation) can cause the mass transfer to deviate from Sieverts’ law. For example, a value of n higher than 1 has been reported in the case of Pd/Ag alloy membranes of thickness 0.5–1.2 μm []. This conclusion is well-known in the literature. Lundin et al. described a method of determining n using a non-linear regression technique consisting of minimizing the sum of the residuals given by the linear regression []. This leads to a curve with a local minimum at one specific pressure dependence indicating the probable value of n, instead of a straight line like in the LMSE method, which will be biased at low n values. Determining whether bulk diffusion or surface phenomena is the rate-limiting step using the parameter n remains a topic of debate in the literature [].
5.2.2. Mixture Gas Tests
Important quality features of palladium membranes or membranes, in general, are the selectivity α, the separation factor SF, and the hydrogen recovery factor HRF [,,]. A common quality parameter characterization technique utilizes an H2/N2 gas mixture to determine hydrogen-to-nitrogen selectivity and separation factor of the membrane. In that case, the H2/N2 separation factor defines how well are H2 components separated compared to N2 components. The as-defined selectivity and separation factor can be inferred for any hydrogen-impurity pair present in the system. The hydrogen recovery factor HRF also represents a critical parameter both in terms of operation and in terms of cost []. The above-mentioned parameters are summarized in Table 5.

Table 5.
Quality parameters for dense metallic membrane separation efficiency.
6. Combinatorial and High-Throughput Experimental Methods in Metallic Membrane Development
Despite the considerable number of investigations geared toward the design and improvement of dense metallic membranes, very few novel alloy compositions have been developed to a wide commercial scale since the first commercialization of palladium–silver membranes in the 1960s. The high cost of precious metals required aligns with their application in advanced fields, such as the fusion fuel cycle []. Outside fusion technology, Pd-based membranes have found only niche applications in fields where high purity of hydrogen is in demand. Tokyo Gas has employed palladium-rare-earth metal-based alloys with much higher permeability and mechanical strength than Pd–Ag in their membrane reformer with world-class performance [].
Although the 17 elements (scandium, yttrium, and the lanthanides) forming the rare-earth (RE) family are relatively abundant, obtaining high-purity RE metals at the desired quantity for making profitable commercial-scale membranes will render the final price onerous. Instead, membranes incorporating base metals might offer a cost-effective advantage. Since, the higher permeability of Pd–RE alloy membranes, e.g., Pd–Y, Pd–Gd, is attributed to some extent (but not only) to the increase in H solubility due to an expansion in lattice parameter compared to pure palladium (), alloying with base metals will contract the lattice parameter () compared to pure Pd, thus H solubility will be lowered and will cause little to negative benefit in gain in permeability compared to pure palladium. Expanding the compositional complexity from binary to higher-order systems (ternary, quaternary, and beyond) through the strategic incorporation of base metals offers a promising avenue to simultaneously enhance membrane robustness and hydrogen permeability. Consequently, developing efficient high-throughput screening methodologies becomes crucial for navigating the vast compositional landscape of these complex alloy systems.
High-throughput techniques operate on two distinct levels: primary screening for the systematic discovery of promising material candidates, and secondary screening for the precise optimization of their compositions []. While the field of dense metallic membranes has seen limited application of combinatorial and high-throughput methodologies, several pioneering efforts warrant careful consideration. This section examines selected case studies of high-throughput experimental approaches in dense metallic membrane development.
6.1. Definition
The terms combinatorial and high-throughput require clarification in the context of materials science. Maier et al. defined combinatorial as “experiments in which groups or elements of different materials or components of a recipe, such as solvents, additives, or other components, are combined” []. In dense metal membrane discovery, this approach involves systematically varying both the types and concentrations of metal components in the membrane’s effective layer. High-throughput methods, on the other hand, focus on the rapid, parallel synthesis, processing, and characterization of large numbers of samples. This includes systematic variation in composition, the number of elements in the alloy, and other parameters, coupled with integrated data recording and analysis systems. While distinct, combinatorial, and high-throughput approaches are often used synergistically in advanced materials research []. In the upcoming discussion, various use cases in the acceleration of dense membrane discovery and optimization are summarized.
6.2. Compositional Spread Methods
Combinatorial and high-throughput material screening is often based on the preparation of composition spread alloy thin films (CSAF) libraries. These libraries consist of multicomponent materials such as alloys, AxByC1−x−y deposited in such a way that there is a lateral gradient in their local composition []. CSAFs contain continuous composition distributions of binary or higher-order alloys on a single compact substrate. These can span entire composition spaces or focus on composition subspaces of interest. CSAF were originally developed in the 1950s for the determination of alloy phase diagrams []. An example of CSAF prepared using a physical vapor deposition apparatus combining a rotatable shadow mask technique is shown in Figure 7.
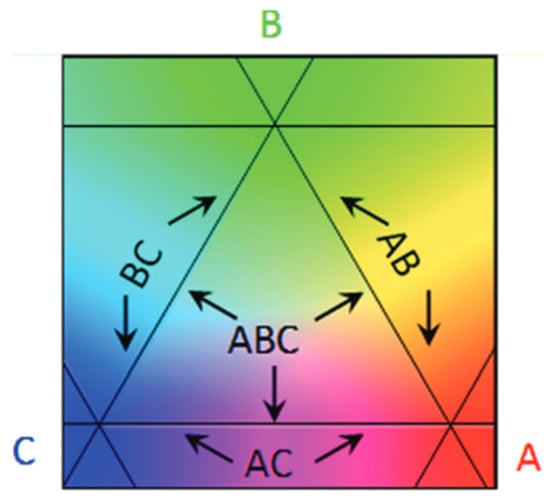
Figure 7.
Schematic representation of a CSAF generated by the rotatable shadow mask RSM-CSAF deposition tool with regions containing the entire ternary alloy composition space, AxByC1−x−y (x = 0 → 1, y = 0 → 1 − x), all three binary alloys AxB1−x, AxC1−x, and BxC1−x (x = 0 → 1) and all three pure compositions. A, B, and C are the pure metal components of the ternary system. Reproduced with permission from [], Journal of Vacuum Science & Technology A; published by American Vacuum Society, 2012.
Various methods can be used to create these libraries. One method uses co-deposition from several sources operating simultaneously to produce a mixed film, where no mask is required and the concentration of the component depends on its distance from the source []. A second group uses binary masks or moving edge masks to first deposit components layer-by-layer, with tunable thickness followed by treatment to induce solid-state diffusion of the deposited components []. When spatially resolved methods are used to characterize their composition and functional properties, CSAF libraries allow rapid determination of composition–property relationships across broad, continuous regions of alloy composition space.
In a study, Lewis et al. reported a combinatorial and high-throughput screening workflow for discovering and optimizing sulfur and carbon-resistant ternary Pd-based ternary alloy membranes []. Before that report, no other has been found in the open English-based literature with such in-depth endeavors for metal membrane development. Given, Pd–Cu, Pd–Ag, and Pd–Au, the goal was to screen a third element capable of reinforcing the final alloy resistance against S/C poisoning, while possessing a high pure H2 permeability and being easily processable in thin film. The sequential procedure adopted is as follows: (1) creation of compositional spread alloys thin films (CSAF) using a four-gun magnetron co-sputtering deposition on silicon wafer substrates; (2) simulated synthetic coal gas exposure of the CSAFs to grossly evaluate resistance to poisoning; (3) visual characterization of the wafers by phasing out all tarnished zone upon S/C interaction and retaining still shining spot as sweet spots; (4) rigorous characterization of the sweet spots using Raman spectroscopy based on the intensity band of potential S–S and M–S bonds; (5) Syntheses of the hits (six composition) using electroless plating technique and/or magnetron sputtering thereof; (6) Measurement of the hydrogen-transport properties of the prepared membranes (the hits) in pure H2 and simulated syngas environment. A description of the custom sputtering apparatus can be found in the reference [], and our adaptation of the general methodology is depicted in Figure 8 and Figure 9, based on the author’s descriptions. The authors also evaluated the reproducibility of the synthesis methods. Despite the characterization of the sweet spots deposited on the silicon wafer by Raman spectroscopy has been reported to be rather fastidious, the rapidity of identification of hits after primary screening is impressive. The study could be improved using: a) a high-throughput permeation testing system. Aware of that limitation, the authors suggested hydrogenography as a high-throughput testing technique. Finally, out of many elements screened Pd–Ag–Au and Pd–Zr–Au (the leads) were the top-performing compositions. In this one-of-a-kind research in dense membrane development, co-sputtering was adopted as the technique for preparing continuous composition spreads. Many examples of the application of this technique in combinatorial material development have been given on the fly by []. Based on the authors’ description, the following graphics were created to summarize the workflow.
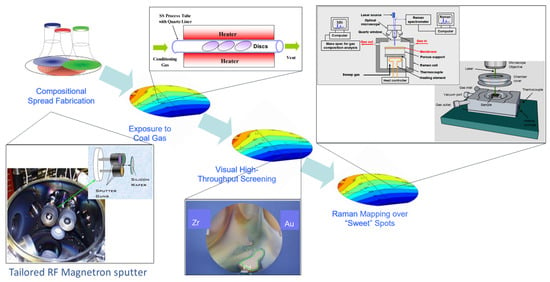
Figure 8.
Combinatorial palladium-based ternary alloys development for membrane application. The green circle shows a Pd-based sweet spot of the CSAF which is not tarnished upon sulfur exposure i.e., a promising sulfur-resistant alloy candidate. Readapted from [].
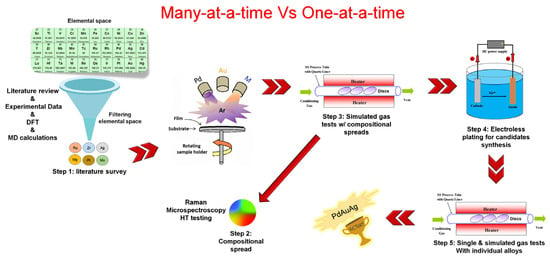
Figure 9.
General approach to screen ternary Pd-based thin film for hydrogen separation application. Proposed based on description from [].
6.3. Thin Film Libraries with Discrete Concentration
In an attempt to contribute to the shift from the one-at-a-time experimentation paradigm, which still dominates the metal membrane development field, refs. [,,,] engineered a combinatorial and high-throughput technique to screen BCC Nb–Pd–Ti, FCC Pd–Ag–Ti, and FCC Pd–Ag–Ni system of ternary alloys over a broad compositional domain. Unlike the previous description, where the deposition was a composition spread [], herein 21 glass discs arranged to form a triangular shape were used to prepare ternary thin film alloy libraries with discrete concentrations utilizing a magnetron sputtering apparatus tunable in co-deposition or sequential deposition modes (Figure 10).
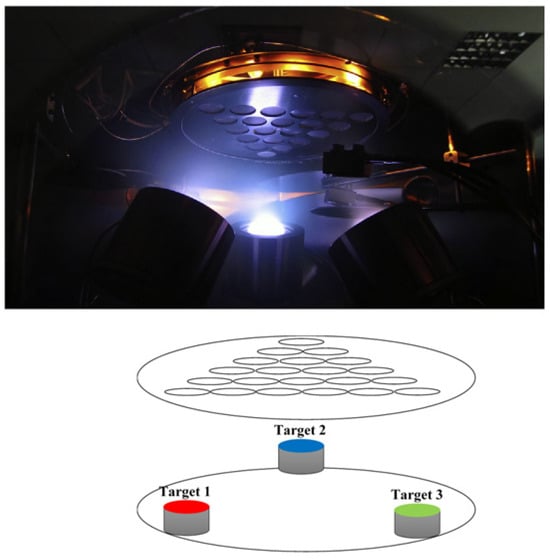
Figure 10.
Schematic illustration of the combinatorial sputter deposition setup for thin-film membrane synthesis. The triangular configuration of magnetron sputter sources and corresponding substrate array enables the simultaneous fabrication of 21 compositionally distinct membrane specimens. Each position in the substrate array yields a unique compositional point within the ternary phase space. Taken from [,].
The electrical resistivity of alloys upon hydrogen permeation is known to increase. Therefore, the physical parameter used for the high-throughput screening procedure was the reactivity index, which the authors defined as “the ratio of resistivity under hydrogen to that under argon in the same conditions” []. Based on those criteria, the higher the resistivity the higher the reactivity index (>>1), thus the higher the potential of the alloy to be nominated a hit. Three alloys Pd–Ag–Ni were identified as hits and were all synthesized by arc-melting with subsequent roll milling, following which they were tested in single gas H2 tests, and an alloy with 55%Pd content was identified as the most promising. Later on, the same group [] conducted a study to screen other alloys incorporating base metals, such as, viz. Pd–Mn–Ag and Pd–Co–Ni using a similar approach. Quickly, it was concluded that Pd–Co–Ni was ineffective and only Pd–Mn–Ag was promising.
Although the protocol described here may necessitate high initial investing costs, the methodology adopted appears highly reproducible. In that work, the pace at which new promising metal membrane materials were screened was impressive. The validation of electrical resistance measurements as a reliable high-throughput screening technique remains incomplete, as membrane performance was evaluated only in pure hydrogen streams rather than industrially relevant gas mixtures.
6.4. Composition Spread Using E-Beam
The Gellman Group at Carnegie Mellon University, USA, developed a novel rotating shadow mask composition spread alloy films (CSAFs) library preparation apparatus that allows the co-deposition of up to four metal elements using an electron beam physical vapor deposition system []. The apparatus was used to perform the high-throughput screening studies of sulfur uptake in the Pd–Cu–Au series in an annealed PdxCuyAu100−x−y CSAF in order to discover corrosion-resistant alloys satisfying the formula PdxCuyAu100−x−y. The screening consists of exposing the CSAF to 100 ppm H2S in H2 at 673 K for 24 h after which surface sulfur is mapped using spatially resolved XPS. This apparatus allows Tarditi et al. [] to establish a structure–property relationship, i.e., sulfur intake as a function of alloy composition. Based on that study, ternary alloys with a low sulfur intake having at least 40 at.%Pd (to allow for high H2 permeability) were selected. Figure 11 shows the sulfur content of the CSAF’s surface as a function of alloy composition. Following that primary screening step, nominated candidate alloys have been prepared by sequential electroless plating and individually tested in single gas and mixture gas tests.
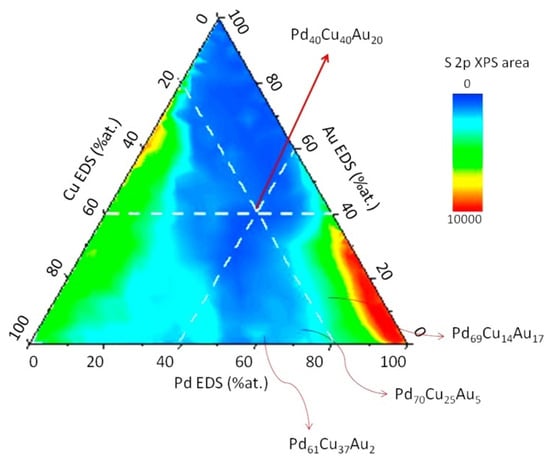
Figure 11.
Surface sulfur enrichment across the CSAFs, quantified via S2p XPS peak intensity. Exposure conditions: 100 ppm H2S in H2 at 400 °C for 24 h. Reproduced with permission from [], Journal of Membrane Science; published by Elsevier, 2015.
The insights drawn from that research are that the ternary alloy with the highest gold content possesses the highest hydrogen permeability and that the poisoning effect of sulfur was reversible (~80% of flux recovery to the initial value) upon reintroduction in pure H2, demonstrating that the discovered alloys are effectively more sulfur-resistant and permeable than pure Pd.
Gellman and coworkers have consistently developed methods for the high throughput study of surface phenomena. Amongst works of interest, one cannot turn a blind eye to the study of surface segregation in alloys of the type CuxPd1−x [], CuxAuyPd1−x−y [], in an attempt to accelerate and parallelize the methods of sample preparation and characterization. In the former, an offset filament tool was developed to co-deposit binary CSAFs of CuxPd1−x (x = 0.05–0.95) via evaporation of metals at high temperatures in ultra-high vacuum (UHV). Spatially resolved XPS and LEISS have enabled the high throughput characterization of surface segregation through composition mapping. The local structure across the CSAFs as given by the Electron Backscatter Diffraction EBSD method was shown to accurately corroborate the phase diagram of Pd–Cu. Bearing in mind that the thermodynamic nature of surface segregation is dependent on the temperature, pressure, and component concentration in the bulk thin films, the authors constructed a Langmuir–McLean thermodynamic model that relates the composition x to the enthalpy and entropy of the segregation of Cu on the outermost layer in a 427 °C–627 °C range. The authors distinguished that Cu preferentially segregates to the topmost layer at each bulk concentration. This constitutes another use case of CSAFs and high-throughput techniques to fuel the structure–property relationship mapping. The authors emphasized that this was the first report of an experimental high-throughput technique for the study of surface segregation in the Pd–Cu system, although the study was restricted to ideal conditions, i.e., vacuum.
Similarly, a recent paper [] used apparatus developed in [] to implement a high-throughput workflow for the study of surface segregation in the entire composition space of CuxAuyPd1−x−y in UHV at 227 °C and 327 °C over 164 different bulk compositions forming the CSAF. The investigators noticed the segregation tendency of Au in the topmost layer, with increasing temperatures in every case, and the depletion of Pd on the surface. Those observations are very important in membrane development. The concentration profile of the rotatable shadow mask-physical vapor deposition generated CSAF is depicted in Figure 12.
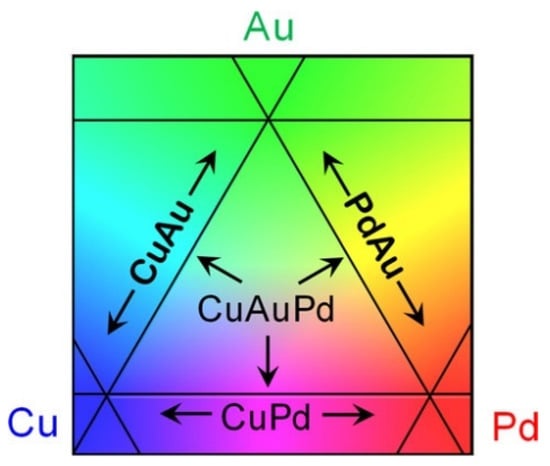
Figure 12.
Schematic representation of a CSAF. Subregions of the Cu–Au–Pd ternary alloy, Cu–Pd, Au–Pd, Cu–Au binary alloys, and pure Pd, Cu, and Au can be found on a single CSAF. The CSAF is deposited as ∼100 nm thick films on a 14 × 14 × 3 mm3 Mo substrate. Reproduced with permission from [], The Journal of Physical Chemistry C; published by American Chemical Society, 2020.
High-throughput methods based on CSAFs and spatially resolved XPS core level shift can also help to demonstrate uncommon properties []. Using a variant of CSAF having both compositions spread in one direction and thickness gradient in another direction, it was demonstrated that for thin film thickness < 6 nm binary alloys of composition CuzPd1−z with 0.35 < z < 0.55 was still in a face-centered cubic phase in conditions where they should have a CsCl B2 type structure in the bulk phase diagram. This phenomenon was referred to as a dimensionally stabilized phase, where at the nanoscale the morphology is determined by both the composition and the thickness of the thin film. The implications of this research are probably of interest in membrane and membrane catalysts. This constitutes an example of composition and phase-thickness relationship definition.
In the previous cases, the resistivity upon hydrogen uptake, intensity band in Raman spectroscopy, spatially resolved XPS, LEIS, and EBSD have been mentioned as high-throughput characterization techniques to analyze various compositions contained in the combinatorial library, either gradient or discrete. In addition, the reversible optical transformations exhibited by rare-earth metals upon hydrogen incorporation provide another powerful platform for high-throughput membrane characterization.
6.5. Hydrogenography
In this part, many use cases of a new kind of high-throughput technique that allows the indirect determination of the hydrogen permeability, viz. hydrogenography will be described.
6.5.1. Principle of Hydrogenography
Yttrium, lanthanum, and other trivalent rare-earth metals, when capped with a catalytic palladium overlayer, undergo a hydrogen-induced metal-to-insulator transition characterized by dramatic optical transformations—a phenomenon known as the switchable mirror effect [,]. In their as-deposited state, hydrogen switchable mirrors are shiny metals, but they become optically transparent when exposed to a hydrogen-rich environment []. This switchable mirror behavior is particularly promising for energy-saving applications, such as enhancing heat insulation in buildings. In particular, metallic YH2 and LaH2 transform into their respective semiconducting trihydride phases, YH3 and LaH3, accompanied by distinct electronic structure changes. As a consequence, the thin film of YHx or LaHx can be transformed rapidly from metal to insulator, from shiny mirror to transparent window (the switchable mirror behavior), simply by changing the surrounding hydrogen gas pressure or an electrolytic cell potential at room temperature []. A detailed review of the switchable mirror effect was provided by Griessen et al. (2004) [].
As a high-throughput combinatorial technique, hydrogenography exploits the characteristic optical response of rare-earth metals to hydrogen absorption, facilitating parallel evaluation of intrinsic permeability across vast compositional libraries under uniform experimental conditions []. The measured permeability is referred to as intrinsic because it only accounts for bulk phenomena. This versatile technique has found widespread applications across hydrogen-related materials research, including: high-throughput screening of hydrogen storage materials []; visualization of hydrogen isotope diffusion dynamics []; determination of important thermodynamic parameters, e.g., enthalpy, and entropy of hydrogen storage in metal hydrides; optimization of hydrogen sensing materials, development of catalytic cap layers hydrogen uptake promoters, development of smart coatings for adaptive solar collectors []; screening of hydrogen sorption catalysts [], combinatorial and high-throughput screening of palladium-based membranes [,,].
6.5.2. Use Case #1: Combinatorial Screening of PdyCu1−y Alloys Membranes
De Man et al. [] reported synthesizing a composition gradient thin film sample of PdyCu1−y alloys using an ultra-high vacuum magnetron sputtering co-deposition system. The composition of the films as determined by Rutherford Backscattering Spectrometry was mapped to contain both the BCC (0.35< y < 0.47), the FCC + BCC 0.47 < y < 0.61 and FCC (y > 0.61) phases, as characterized using XRD. The application of the hydrogenography technique for intrinsic hydrogen permeability measurement consists of using an indicator, viz. a yttrium layer to entirely cover the gradient sample top surface, while the yttrium layer itself is partially coated using a hydrogen dissociating catalyst, viz. palladium allowing the uncoated yttrium surface to be oxidized by air and form an inactivate hydrogen dissociating skin, viz. yttrium oxide Y2O3. If the conditioned sample is sealed in a chamber with an optical window, the color of the non-oxidized yttrium layer directly located under the palladium cap layer will instantaneously start to change and form a moving front bell-curve-type shape upon 105 Pa hydrogen uptake at room temperature due to the penetration of hydrogen into the indicator layer. Even if the membrane material is located under the yttrium layer, one can understand how the phenomena on the yttrium indicator relate to hydrogen diffusion in the membrane. The lateral hydrogen diffusion mainly takes place in the membrane alloy, because the hydrogen diffusion coefficient in the membrane is 105-fold (or more) higher than that in yttrium. Due to the low plateau pressure of YH2 and YH3, the hydrogen lateral diffusion through the Pd–Cu layer will leak back into the yttrium layer to form the yttrium hydride phase [].
By taking photographs at regular intervals of the moving-front using a charge-coupled device (CCD) camera, one can determine the position of the front position xf at the time t and fit a time series xf = (t∙K)0.5 where the K0.5, the slope of the straight line obtained represents the mobility front and is directly related to the intrinsic permeability. This previous procedure represents an embodiment of the application of hydrogenography. A photograph of the optical response of the membrane–yttrium indicator assembly is depicted in Figure 13.
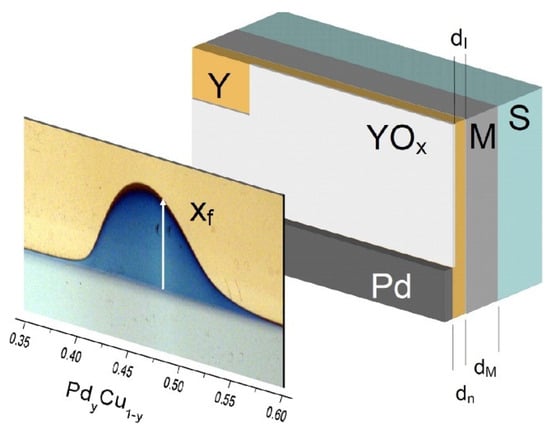
Figure 13.
Spatially resolved hydrogen permeation visualization in a compositional gradient PdyCu1−y membrane. Surface-view photograph after hydrogen exposure (105 Pa, room temperature, 48 h) showing lateral diffusion with maximum front displacement xf = 7.2 mm. The membrane architecture consists of a PdyCu1−y gradient film (M) fabricated via an ultra-high vacuum magnetron co-sputtering on a Ti-modified Si substrate (S), overlaid with a 60 nm yttrium indicator layer (Y), and partially capped with a Pd catalyst. The hydrogen transport pathway involves dissociation at the Pd surface, through-thickness diffusion across the membrane, and subsequent chromatic transformation of the yttrium layer from reflective to blue. A protective yttrium oxide layer (YOx) prevents direct hydrogen uptake by the indicator. Reproduced with permission from [], Journal of Membrane Science; published by Elsevier, 2013.
By applying hydrogenography, the permeability values of hundreds of PdyCu1−y alloys were determined. It was shown that permeability is a function of the composition. Most importantly, the technique clearly distinguished Pd0.47Cu0.53 (at.%), the popular BCC Pd-40 wt.%Cu attributed with the largest hydrogen permeability at 623 K in the Pd–Cu series, even though the authors experimented with room temperature, which they attributed to the fact that permeability of hydrogen in the Pd–Cu family is weakly dependent on temperature compared to diffusivity. Because, the permeability values considered were intrinsic, i.e., entirely neglecting surface phenomena, the value determined at room temperature for Pd0.47Cu0.53 was k = 1.2 × 10−8 mol/m/s/Pa0.5 and was a little higher than the extrapolated value determined by density functional theory [].
In an attempt to generalize, the authors extended the technique to Pd–Cu–Mo, Pd–Cu–Ti, and Pd–Cu–Ta composition gradient samples and demonstrated that it is easier to apply for ternary systems. This work constitutes a powerful demonstration of the hydrogenography technique coupled with compositional gradient samples that can advance membrane research within hours instead of relying on serendipity for a long period.
6.5.3. Use Case #2: High-Throughput Determination of Hydrogen Permeability in Pd–Cu Alloy Membranes
A more recent application of the hydrogenography technique has been documented by Westerwaal et al. []. The goal was to build a structure–property relationship, viz. Pd–Cu series microstructure-intrinsic permeability relationship. A composition gradient sample deposition technique and analysis similar to that described by de Man et al. (2013) in use case #1 [], for determining lateral intrinsic permeation was employed, but with varying substrate temperatures. Using this approach, Westerwaal et al. measured hydrogen permeability as a function of alloy composition and correlated the results with the low-temperature phase diagram of Pd–Cu []. The schematic representation of the experimental setup is depicted in Figure 14. The palladium hydrogen dissociating catalyst cap layers had either dots or quadrilateral shapes. Quickly, the technique identified FCC + BCC Pd48Cu58 as the alloy with the highest hydrogen intrinsic permeability within the composition gradient. Alloys of FCC and BCC structure were found to possess much lower permeability than mixed FCC + BCC. This is unusual in bulk Pd–Cu as a comparison with experimental knowledge. Therefore, by comparing to data from the literature, the authors remarked that other phenomena might occur, and they concluded that diffusion occurs mainly via heterogeneous grain boundaries []. Although a difference is found between the result and those from the literature, this constitutes a formidable opportunity to study phenomena that would have been fastidious in normal routine.
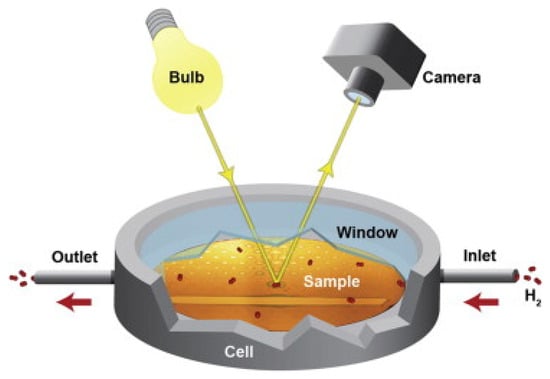
Figure 14.
Schematic of the optical hydrogen migration measurement setup. The configuration comprises: (i) a light source, (ii) a CCD camera, and (iii) a hydrogenation cell housing the assembled gradient diffusion sample. The sample is a composition gradient sample prepared by magnetron co-sputtering. The sample was assembled with the yttrium cover and dot-shaped palladium cap layer. The cell, connected to a gas handling system for controlled hydrogen supply and venting, is positioned 40 cm below both the illumination source and the camera. Reproduced with permission from [], International Journal of Hydrogen Energy; published by Elsevier, 2015.
In an earlier attempt, the same authors combined the hydrogenography technique and the cluster expansion method—a statistical thermodynamic method—to implement a high-throughput screening routine of Pd–alloys membranes (in the Pd–Cu series) with critical temperature below room temperature, and it was demonstrated that such a method can reveal fundamental insights where thermodynamic data are inexistent [].
While hydrogenography efficiently maps composition–property relationships through parallel screening of compositional gradients, it cannot identify optimal operating conditions for promising membrane candidates. The traditional one-factor-at-a-time optimization approach commonly used in membrane development is time-consuming and may overlook complex parameter interactions. Statistical Design of Experiments (DoE) methodologies offer a more systematic route to membrane optimization, enabling efficient parameter space exploration with minimal experimental iterations.
6.6. Design of Experiments
Rational statistical methods, particularly Design of Experiments (DoE), have a long-standing history in the design and optimization of chemicals, materials, and processes. Statistical experimental design approaches offer fundamental advantages over trial-and-error and one-factor-at-a-time (OFAT) methodologies, as they: (i) maximize the knowledge-to-experiment ratio, (ii) provide precise factor effect estimations, (iii) enable systematic quantification of parameter interactions, and (iv) explore broader parameter spaces []. The statistical design of experiments constitutes a mandatory part of the modern combinatorial material cycle [], and can also intervene in process optimization. This section summarizes a few recent use cases of design of experiments in dense metallic membrane development relevant to the scope of this paper.
6.6.1. Use Case #1: Hybrid Statistical-Observational Screening of Appropriate Support Surface Parameters for Reproducible Electroless-Plating Deposition of Pd–Base Alloys Membranes
A critical challenge in scaling electroless-plated composite metallic membranes to industrial applications lies in the selection of support materials compatible with standard stainless steel reactors []. While ceramic supports offer ideal characteristics for electroless palladium deposition—notably controlled surface roughness and optimized pore architecture—their industrial implementation is hindered by challenges in sealing, module integration, and chemical resistance. Metallic supports, while offering an alternative substrate platform, present inherent surface challenges that necessitate pre-treatment protocols before successful electroless plating deposition. The challenge was to study which suitable target surface parameters can be reproducibly and repeatably achieved by surface pre-treatment to permit electroless plating to be successfully realized for metallic supports.
Gallucci’s group [], proposed a solving scheme for this problem for highly rough Hastelloy X (nickel–chromium–iron–molybdenum alloy) supports with large pore diameter, using a hybrid observational (solid state support surface characterization)-statistical approach, i.e., a sequential approach composed of: surface pretreatment–surface parameters characterization–design of experiments–analysis of variance (ANOVA). Analysis of variance (ANOVA) is a statistical technique used to analyze the differences between two or more means []. As a result, threshold values of average surface roughness < 0.8 μm, average profile height < 7 μm, and in-pore leveling < 6 μm were identified as the target surface parameters for pretreatment reproducibility.
In the previous application, a statistical experimental design approach was used to optimize the surface properties of membrane support materials. Similarly, DoE can be applied to study the effect of process conditions on membrane efficiency. This approach is demonstrated in the second use case.
6.6.2. Use Case #2: Mixed Taguchi Design-Machine Learning Analyses of Hydrogen Permeation in Pd Membranes
Recently, Chen et al. 2024 [], reported a combination of the Taguchi method of experimental design, analysis of variances (ANOVA), artificial neural network, and classification models (support vector machine SVM, decision trees (coarse tree, medium tree, and fine tree), ensemble models herein boosted and bagged models), to study the effect of three factors viz., the feed gas composition (H2/H2O/CO2), the vacuum pressure, and the retentate side total pressure on hydrogen gas permeation flux across electroless plating deposited Pd membranes and obtained H2 purity (Figure 15). The research question was how to optimize the operating conditions to obtain the maximum H2 flux. Each factor was attributed to four levels. The Taguchi method utilizes a set of orthogonal arrays to examine numerous variables with as few experiments as possible, which is more effective than traditional design methods. It contributes to minimizing the number of experimental runs required to efficiently evaluate the influences of the system’s parameters’ effects by designing an orthogonal array and the resultant signal-to-noise (S/N) ratios [,,]. An L16 orthogonal array and the larger-the-better S/N ratio were adopted to analyze the objective function and predict the optimal combination of the factors. The previous L16 orthogonal array (with three replication tests = 16) created for the Taguchi approach was used as a dataset for a Levenberg–Marquardt ANN modeling (with a tan-sigmoid activation function) with each factor’s relative importance analyzed using the Gasson method, which comprises one input layer of the three factors, one hidden layer of fifteen neurons, and one output target—the H2 permeation flux. Despite this dataset can be thought to be rather small for ANN modeling; it was argued that the statistical robustness provided by the orthogonal array (broader coverage of the sampling space) makes the dataset a very good quality one, precluding the need for extensive data. The ANN used (Figure 16) presented high accuracy as given by the R2 at each step (training, testing, validation) always higher than 0.96, with a relative error of 2.1% between the predicted and the experimental data. The analysis of ANN results using the Garson method to determine factors’ relative importance ranked in order feed composition > retentate-side total pressure > vacuum pressure as given by their RI, representing a formidable agreement with Taguchi’s analysis. Among the classification models used to yield categorical predictions—that is “low” (>95%) or “high” (>95%) hydrogen purity, the ensemble methods gave better accuracy as given by the confusion matrix, for the prediction of the true class of the purity 85.7%, surely because they used combined classifier prediction to yield a more definitive classification. It was shown that the effect of input variables on the purity can be ranked from the highest to the lowest as feed gas mixture > retentate-side total pressure > vacuum pressure, as given by the ensemble models feature importance examination.
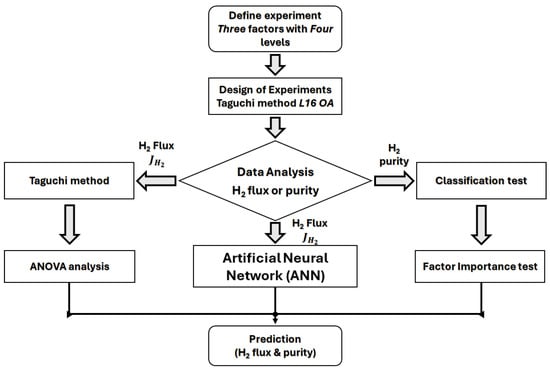
Figure 15.
General methodology of a hybrid DoE-Machine Learning workflow for separation target parameters optimization and prediction. Reproduced with permission from [], International Journal of Hydrogen Energy; published by Elsevier, 2024.
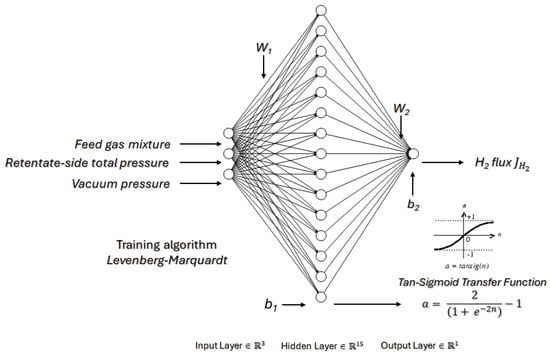
Figure 16.
Architecture of the ANN is composed of three layers: (i) a three-neurons input layer, (ii) a fifteen-neurons hidden layer, and (iii) a single-neuron output layer. Reproduced with permission from [], International Journal of Hydrogen Energy; published by Elsevier, 2024.
This study demonstrated the power of integrated statistical approaches: using only 16 strategically designed experiments, the combination of Design of Experiments (DoE), statistical analysis, and machine learning algorithms provided comprehensive insights into membrane separation optimization. Since data collection, data quality, and dataset size are among the most pivotal aspects in applied machine learning [,], using a Taguchi-constructed experimental design to supply high quality data to the machine learning algorithm can be adopted to accelerate various studies in membrane development. This efficient methodology represents a significant advancement over traditional one-factor-at-a-time approaches for optimizing metallic membrane separation processes.
The classification analysis using the SVM, DT, and ensemble models aimed at predicting the purity of the hydrogen obtained after separation, knowing that hydrogen purity data have been obtained when performing the previous L16 ×3 experiments, in addition to the flux using a GC. As a result, the authors always found a positive effect of vacuum on hydrogen flux, but with minimal effect, i.e., ~+2.5% with vacuum compared to without vacuum, the inhibition effect of CO2 is higher than that in H2O, which authors attributed to reverse water–gas shift (CO2 + H2 ⇆ CO + H2O); transmembrane pressure showed a negative effect on hydrogen purity, which the authors attributed to increased permeability of impurities with the driving force. Binary mixtures showed more threat to H2 purity out of membrane than ternary mixtures, which authors attributed to adsorption competition between H2O and CO2. There was a good agreement between the Taguchi prediction, i.e., flux is predicted to be maximum with H2/H2O, 3 atm total pressure, and 45 kPa vacuum pressure, and the importance of the ranked factor was given by ANOVA analysis as given by F-value and p-value statistics.
In addition to the previous references, other works reported a mix of statistical-machine learning approach, e.g., Taguchi method, response surface methodology, multivariate adaptative regression splines, and supervised learning approach [,].
6.7. Microreactors and Micromembrane Reactors
Although the metals of group IV–V have been demonstrated to be more permeable to hydrogen than palladium, the latter stands out because of its intrinsic active catalytic surface for hydrogen dissociation [,,]. The effect of introducing a solute metal in palladium’s bulk to improve its properties might be deleterious or beneficial for its catalytic activity. Thus, it is of scientific interest to define tools to easily access alloy catalytic activity and establish a composition–catalytic activity relationship.
A glass multichannel microreactor array [], has been used to continuously deliver reactant gasses to 100 isolated regions on a CSAF surface manufactured using an offset-filament evaporative source, as described in []. The microfluidic device is designed to allow the withdrawal of the products from each region for mass spectrometry analysis. The gas layers were produced by stacking multiple flat borosilicate sheets using chemical bonding and annealing and contained micromachined channels for gas flow, with 100 inlets and 100 outlets. The device (Figure 17) was used to measure the catalytic activity at 333K of the CSAF of PdxCuyAu1−x−y deposited on polycrystalline Mo in UHV and at room temperature, for a H2/D2 isotopic exchange elementary reaction (H2 + D2 → HD [], is a well-known reaction to study surface activity in catalysis). The H2/D2 Isotopic exchange reaction is a reaction of industrial importance in Pd–base membrane separation because it can be used to probe the kinetics of dissociative adsorption and associative desorption, thus determining the suitability of a Pd–base membrane for H2 separation []. The composition of the CSAF (10 mm × 10 mm) is determined by spatially resolved XPS, which can give a two-dimensional composition distribution map of each elemental component, and the products of the isotopic exchange reaction were determined using mass spectrometry. A non-linear dependence of the catalytic activity on Pd content was found. By approaching the Cu-rich region, the catalytic activity vanishes, and the activity inhibiting potency of Cu was higher than that of Au. In this study, 100 different alloy compositions’ catalytic activities in H2/D2 isotopic exchange reaction were measured in the strictly same condition making this method improvable and adoptable as a high-throughput catalytic activity screening technique to advance metallic membrane research.
Figure 17.
The design scheme of the 100-channel microreactor array used to deliver (H2 + D2) and withdraw gasses (H2 + D2 + HD) at specific coordinates of PdxCuyAu1−x−y CSAF samples for the evaluation of the catalytic activity in an isotopic exchange reaction. (a) Channels for input and output are etched into flat glass sheets. (b) Ten input layers and ten output layers are alternately stacked and bonded together with cover plates. (c) The side of the microfluidic device containing 100 inputs and 100 outputs is ground and polished to achieve a smooth finish. Reproduced with permission from [], Journal of Catalysis; published by Elsevier, 2013.
6.8. Microkinetics Modeling
Metallic membranes such as palladium-based membranes absorb and permeate hydrogen through the solution–diffusion mechanism, which is best described using the sequential elementary reaction as described in Section 5.1. As part of the solution–diffusion mechanism, surface phenomena require rigorous attention while modeling hydrogen permeation. Microkinetic modeling is the reaction kinetic analysis that attempts to incorporate into the kinetic model the basic surface chemistry involved in the catalytic reaction, with more details than the lumped (or global) kinetic modeling []. Microkinetic modeling is now a powerful tool in heterogenous catalysis thanks to computational advances and has also provided the metallic membrane researcher precious insights to understand complex systems. In this section, two use cases of the application of microkinetic modeling in metallic membrane research are mentioned in brevity.
This study by O’Brien et al. focuses on the catalytic activity (adsorption–desorption) of metallic membranes, excluding hydrogen permeation within the bulk lattice. O’Brien and co-workers investigated the kinetics and energetics of hydrogen adsorption and desorption (absorption not accounted for) on the surface of fixed-bed diced foils of Pd, Cu, and FCC Pd70Cu30, B2 Pd47Cu53, FCC Pd47Cu53 by microkinetic analysis of the H2/D2 isotopic exchange reaction (H2 + D2 → 2H–D, Figure 18) data at near-ambient pressure and 27 °C–627 °C []. The results revealed very insightful information never known before. It was shown that phase structure strongly influences H2–D2 isotopic exchange kinetics.
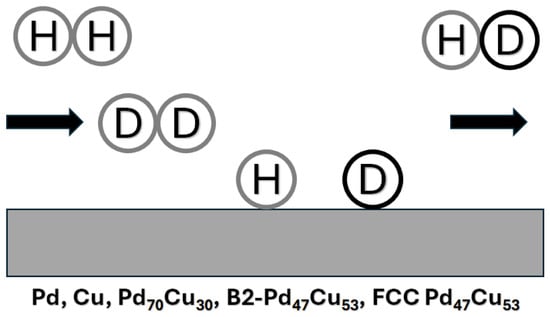
Figure 18.
Schematic of H2–D2 exchange over Pd, Cu single elements, and Pd–Cu alloy membranes for catalytic surface activity study in H2/D2 isotopic exchange reaction. Reproduced with permission from [], The Journal of Physical Chemistry C; published by American Chemical Society, 2011.
In the order, the activation energy barrier of hydrogen dissociative adsorption on the metal surfaces was: Cu (0.54 eV) > β-Pd–H (0.3 eV) > B2 Pd47Cu53 (0.15 eV) > α-Pd–H (0.12 eV) > Pd70Cu30 (0.09 eV) > FCC Pd47Cu53 (0.00 eV). Copper is the least active metal in the H2/D2 exchange because of the large activation energy of dissociative adsorption. Unlike copper whose H2/D2 exchange reaction was limited by H2 adsorption, that of the other metals was limited by HD desorption. The barrier energy for H2 desorption was: FCC Pd47Cu53 (0.46 eV) < Pd70Cu30 (0.52 eV) < β-PdH (0.63 eV) < B2 Pd47Cu53 (0.67 eV)< α-PdH (0.68 eV). This microkinetic treatment of experimental data on H2/D2 exchange on Cu, Pd, and Pd–Cu foils provided insights into why pure copper is not a good catalyst for hydrogenation. Conversely, alloying copper (up to ~50 atom percent) and palladium is favorable to enhance the catalytic activity of Pd toward H2 adsorption. This constitutes an exemplary application of microkinetic analysis to derive practical insights into catalyst and membrane design. In the present paper, the microkinetic analysis was performed on top of the data gathered from laboratory experiments.
Use Case #2: Microkinetic Modeling of Hydrogen Diffusion
In a dexterous and theoretical study, Deveau et al. used microkinetic modeling to generalize Sieverts’ model of the solution–diffusion mechanism of hydrogen transport in the Pd membrane, to non-ideal solutions and expand the range of its validity. The attempt took into consideration surface roughness and treated the sequence of elementary reactions (see Figure 6) as a reaction route graph RR graph (based on reaction route theory, graph theory, and Kirchhoff’s laws) so that an analogy between electrical circuits can be made []. Applying the reaction route theory, which was described in [], the RR graphs can be converted into an equivalent circuit allowing a reduction in the model to a three-step problem rather than five. This study constitutes a robust theoretical application of microkinetic modeling in metallic membrane science.
6.9. Non-Relativistic Density Functional Theory and High Throughput Application
Density Functional Theory represents a Quantum Mechanics approach to solving the non-relativistic, time-independent Schrödinger equation (TISE) by considering a single functional of three spatial coordinates—the electron density—rather than 3N coordinates wave functions []. Over the years, first-principles calculations based on density functional theory have been applied to elucidate intricated phenomena related to hydrogen transport in metals, which would have been otherwise inaccessible in experimental work. Hydrogen diffusion and dissolution [,], permeability [], interactions of co-adsorbates (CO, CO2, H2S, N2, CH4, H2O) with membranes [,,], diffusion mechanisms [], surface segregation [], hydrogen embrittlement [], and alloy membrane screening [,,], have all been thoroughly investigated using density functional theory (DFT), with good quantitative agreement with experimental results. DFT has also provided valuable insights, such as explaining why B2 Pd–Cu is more permeable than FCC Pd–Cu, where experimental studies have fallen short []. Most importantly, there are now many instances where density functional theory calculations have been used to screen metallic materials for application in hydrogen separation. In this section, a few use cases of density functional theory for high-throughput screening of metallic membrane materials for hydrogen separation applications are covered. A comprehensive approach to DFT can be retrieved from authoritative books in references [,,,] and article []. High throughput applications of DFT relevant to dense metallic membrane study are thus considered below.
6.9.1. Computational Material Screening Using DFT
The application of density functional theory (DFT) to metallic membranes was pioneered by Sholl and Kamakoti, who developed a theoretical framework to predict macroscopic properties of crystalline metals as hydrogen-selective membranes using plane wave DFT and coarse-grained lattice gas modeling [,,,,,,,,,,,,,,,,,,,,,,,]. Sholl’s group advanced methods incorporating transition state theory, statistical mechanics, Kinetic Monte Carlo (KMC) simulations, Grand Canonical Monte Carlo simulations, Cluster expansion, and ab initio molecular dynamics to study substitutional solid solution membranes, intermetallics [], and amorphous membranes. Their works provide a comprehensive overview of these approaches [,,]. This summary focuses on crystalline membranes, particularly Pd-based membranes, and emphasizes high-throughput applications.
Use Case #1: High-Throughput Screening of Pd96M4 Alloy Membranes
A high-throughput computational material screening using first-principles density functional theory (DFT) was employed to investigate hydrogen permeability in substitutionally disordered FCC binary alloys with a Pd96M4 (at.%) composition, where M represents doping metals. This study covered 50 elements at 327 °C, confirming known Pd-based alloys and discovering new compositions like Pd96Tm4, which exhibited hydrogen permeability 111% higher than Pd and 44% superior to Pd80Ag20 at 773K, with DFT predictions closely matching experimental values. The Vienna Ab initio Simulation Package (VASP) was used for plane-wave DFT calculations with the PW91-GGA exchange-correlation functional (https://www.vasp.at/). Hydrogen solubility and diffusivity in the disordered crystalline structure were determined by analyzing interstitial sites (octahedral and tetrahedral) and transition states. Lattice contraction or expansion upon alloying was identified as a key descriptor of hydrogen permeability [,]. Pd96RE4 alloys, where RE is a rare-earth metal (Y, Gd, Ce, Er, Tb, Dy, etc.), exhibited high solubility due to lattice expansion. Alloys with similar lattice parameters but different solubility were influenced by chemical effects, seen in elements like Lu, Hf, In, Yb, and Na. Some alloys like Pd96Cu4 had higher solubility than Pd, while alloys with Fe showed lower solubility. Despite higher permeability in BCC metals (Nb, V, Ta), FCC-Pd alloys exhibited lower permeability. This DFT-driven screening, validated by experiments, accelerates the discovery of new alloys for hydrogen separation.
Use Case #2: Using Grain Boundary Segregation as a Screening Criterion for Alloy Membrane Screening
This study investigated the computational screening of substitutional alloying elements that can induce grain boundary (GB) segregation in vanadium, acting as a diffusion barrier between vanadium and the Pd-coating layer in vanadium-based membranes. Inter-diffusion between BCC V and Pd occurs mainly through high-diffusivity paths like grain boundaries and dislocations, while hydrogen diffusion is not restricted at typical operating conditions []. Given that yttrium can induce this behavior, the study explores other elements and their optimal concentrations for similar effects.
First-principles calculations based on plane-wave DFT, implemented in VASP with the PAW pseudopotential and PW91-GGA exchange-correlation functional, were used to estimate the binding energy of solute atoms at specific grain boundary sites (Σ3 and Σ9). Elements were evaluated based on the sign (+/−) and magnitude of binding energy, with a positive binding energy indicating cohesive attraction between the solute and the grain boundary. Favorable solutes were selected with binding energy > 0.7 eV, considering GB embrittlement, solute-solute binding, and solute-Pd binding tendencies.
The study found that stronger binding between solute atoms and the GB correlates with larger solute size. A database of over 60 elements (metals and non-metals) was built, examining segregation behavior based on solute size and solute-vacancy binding energy. Although solute concentration was not considered due to computational limitations, the study provides valuable insights for selecting elements to inhibit intermetallic diffusion. This work highlights how DFT can advance membrane technology but leaves unresolved questions about the role of GB embrittlement in membrane failure.
6.10. Machine Learning
In the section on the design of experiments above, artificial neural networks and classification models have been used to predict the hydrogen permeation flux and the level of purity, respectively, based on the operating conditions. It is also useful to mention instances of the application of neural networks to predict membrane properties. This section reports an early use case of artificial neural networks in dense metallic membranes study.
Although the Perceptron learning algorithm—the simplest form of the artificial neural network algorithm—was proposed as early as 1958 [], one of the first reported applications of machine learning to dense metallic membranes (available in the open literature) was carried out in 1995 by Jemma et al. []. In that attempt, the authors studied the effect of Pd–Ag membranes’ hydrogen content and hydrogen permeation temperature on the hydrogen diffusion coefficient obtained from steady-state hydrogen permeation flux measurements. They correlated the non-linear relationship of the solubility constant with the temperature and the pressure using a feed-forward neural network model to fit a dataset of 43 solubility records collected from the literature from 41 °C to 441 °C and 0.051 MPa, 0.101 MPa, and 0.446 MPa. Then, based on experimental measurement of steady-state hydrogen permeation flux, the diffusion coefficient was derived. The architecture of the artificial neural network comports two input nodes, i.e., x1 (normalized temperature) and x2 (normalized pressure); two neurons in its hidden layer represented by equation Sa and Se, each of these neurons taking both x1 and x2 as inputs; and one output layer composed of one neuron and represented by equation Sx. The last neuron takes the output of the two neurons in the hidden layer (after activation) as its input.
The least-square analysis using the conjugate gradient method was the optimization algorithm used to minimize the error function of the neural network. Based on the previous description, one can attempt to propose an architecture for this basic neural network (Figure 19).
Figure 19.
The architecture of the neural network to model the solubility H/M or atomic ratio H/M (n). Modeled after [].
The error of the prediction was 3% on average and 12% at maximum, which constitutes an acceptable agreement between the experimental value and the model prediction. Overall, it was found that the membrane hydrogen diffusivity decreases with increasing hydrogen content in the membrane in the range 423–573 K.
Previously the time-lag method was cited as the most common method for the determination of the diffusion coefficient. The just reviewed study demonstrated that machine learning can be used jointly with experimental data to fully characterize the most fundamental properties of a membrane viz., the diffusion coefficient, and the solubility.
In all the previously examined applications of machine learning in metallic membrane studies, none have dealt with the prediction of membrane properties based on its chemical composition or phase structure. The latter endeavor pertains to the realm of material informatics, which constitutes a priority method in materials development today and is set to become a routine in the future due to an increase in computation power and the fourth industrial revolution powered by artificial intelligence. The perspective section of this paper examines multiple considerations that require researchers’ attention in the future to encourage the massive inception of material informatics in metallic membrane design.
7. Perspective
Materials informatics involves the use of organic or inorganic materials data and data science techniques such as data mining, machine learning, and artificial intelligence, in order to design and optimize materials []. Early attempts at material informatics (although not explicitly referred to as such) have been recorded since the 1990s when authors reported neural networks to predict Ni-based alloys’ mechanical properties based on their chemical composition and temperature [,]. Since the launch of the Material Genome initiative by the US administration in 2011 [,], substantial efforts, with significant contributions from both academia and industry, have been made to support this endeavor. Notwithstanding, many sectors such as solid-state batteries, synthetic polymers, and metal hydrides for hydrogen storage have harnessed its power. However, the dense metallic membrane field has not fully utilized all the capabilities offered.
A data-driven approach for dense metallic membrane materials screening, design, and optimization can harness extensive literature data published over six decades of development. A first step toward this goal is the constitution of a large dataset that can benefit future research. Such datasets should not only take into consideration the composition of the alloys, crystalline or amorphous, or intermetallics but also the presence or absence of support, the thickness, the pressure exponent, the temperature, and the pressure at which measurement of permeation is performed. Attention needs to be paid as well to collecting data in similar conditions. For example, data from a single gas permeation test cannot be used to predict membranes properties under mixed-gas conditions. Most importantly, there should be unit uniformity for fast utilization of the dataset. For example, all the permeability values in the dataset should have a unique unit, e.g., mol∙m−1∙s−1∙Pa−n, and so on for the thickness (e.g., m or μm) and the other parameters. However, one should not neglect the standardization or normalization step required to equally scale the features []. The datasets should be large enough and diverse, e.g., not biased toward a specific series of alloys. Useful reviews with large table summaries of alloys for membrane usage can be found in [,,,]. On the other hand, a systematic comparison of membrane permeability across different thicknesses is not feasible. To address this, the specific permeability, a normalized permeability value, can be utilized []. Alternatively, the permeability ratio of the alloy to that of pure palladium or the primary constituent element may also serve as a useful comparison strategy [].
The meaningful data in the peer-reviewed dense metallic membrane literature are summarized in a textual, tabular form and oftentimes in a graphical form. The manual collection of those data and subsequent annotation is a labor-intensive task and time-consuming []. Since the automatic extraction and annotation of data in material science literature is still imperfect, the constitution of a metallic membrane large dataset would benefit from the use of the state-of-the-art semi-automated annotation workflow combining human-intervention and large-language models (LLM) []. The latter reference reported the use of Google Gemini; however, other LLM will equally provide useful acceleration.
The next step before extracting knowledge from the database is to develop robust machine learning descriptors, features, or input variables. In that case, domain knowledge is key to proper feature inclusion. It was demonstrated that domain knowledge incorporation in feature selection offers advantages in predictive ability in the absence of a large dataset or for data that are not fully representative []. Herein, it is suggested a list of domain knowledge-based features table constituted based on recurrent notice from the literature (Table 6). The list will benefit future improvement. The reader will also find it useful to consult reference [] for descriptors related to lattice parameter expansion and its ratio with the effective valence electron concentration. There also exists composition-based feature vectors (CBFV) and data-driven techniques. The two classes of features have been benchmarked by Murdock et al. []. Popular feature-building packages such as Matminer exist in material informatics []. Matminer does not contain an AI routine, but Automatminer does, i.e., it can perform feature engineering, model selection, hyperparameter tuning, etc. [].
The number of features applicable using Matminer is >100. However, there arises the curse of dimensionality when the features vector exceeds a certain dimension—that is the number of features exceeds a certain threshold (Stergiou et al., 2023 []). For that reason, dimensionality reduction techniques such as PCA (Principal Component Analysis) should be applied for feature selection using, e.g., the elbow method. PCA is a general technique in statistical learning []. On the contrary, SISSO (Sure Independence Screening and Sparsifying Operator) is a feature selection technique specifically designed for material informatics tasks [].

Table 6.
Proposed feature descriptors for machine learning tasks in dense metallic membrane material informatics.
Table 6.
Proposed feature descriptors for machine learning tasks in dense metallic membrane material informatics.
| Descriptors | Definition | Formula | Accessibility | Reference |
|---|---|---|---|---|
| Composition (at.%) | Alloy formula (atomic percentage) | - | Experimental/ historical data | - |
| Thickness (m) | Membrane thickness () | Experimental/ historical data | in text | |
| Temperature (K) | Temperature of measurement T | - | Experimental/ historical data | in text |
| Pressure differential | Difference between in/out partial pressures (Pa) | Experimental/ historical data | in text | |
| Pressure exponent n | H/M ratio (n ≤ 0.5 ≤ 1) | - | Experimental/ historical data | in text |
| Diffusivity (m2∙s −1) | Defined according to Fick’s 1st law | with ED activation energy of diffusion, and the pre-exponential term | Experimental/historical/DFT | [,], in text |
| Solubility S (mol∙m−3∙Pa−0.5) | Defined according to Sieverts’ law | or C = KP0.5 ES activation energy of dissolution and S0 the pre-exponential term | Experimental/historical/DFT | [,,,] |
| Lattice constant (Å) | Size of alloy as derived experimentally from Miller indices or by solving the Kohn–Sham equation. Lattice parameter difference compared to pure Pd’s can also be inferred. | or calculated at 0K using DFT [] | Experimental/historical/DFT | [] |
| Microstructure | Crystal structure | (FCC/BCC/HCP) | Experimental | - |
| Adsorption energy | The energy potential of adsorption on a specific facet | Difference between the total energy of the adsorbates (H2)–metal substrate (M) complex, Eads+subs, and that of the adsorbate and substrate in isolation, Eads(g) and Esubs, respectively: Ea=Eads+subs − Eads(g) + Esubs [] | DFT calculation on surface slab | [,,] |
| Absorption energies (solution energy) | Enthalpy of dissolution reaction in the bulk of the supercell | Eabs = Etot(MH) − Etot(M) − 0.5 EH2 + EZP1(H) − EZP2(H), where ZP referred to the zero point. | DFT calculation in bulk | [] |
| Binding energy | Minimum energy to separate H from the interstitial site in the alloys | DFT calculation in bulk | [,,,] | |
| Cohesive energy | Critical indicator describing the stability of the membrane. It is important in the description of the performance for hydrogen separation membranes | DFT calculations | [] | |
| Activation energy | The potential energy barrier to overcome for solute H transport in the bulk | Eϕ = ED + ES Sum of activation energy of dissolution and diffusion | Experimental/historical/DFT | [,,] |
| d-band center | The variation in the adsorption energy from one TM surface to another correlates the upward shift in this d-band center with respect to the Fermi energy, thus can be referred to as the most prominent descriptors to predict molecule adsorption on surface | DFT calculations (d-band center theory compared to the Fermi level Ed) | [,] | |
| Atomic radius difference (δ) | As per definition | Calculation | [,] | |
| Mixing entropy (ΔS) | As per definition | Calculation | [,] | |
| Mixing enthalpy (ΔH) | As per definition | Calculation | [] | |
| Electronegativity difference (Δχ) | As per definition | with | Calculation | [,] |
| Valence electrons concentration (VEC) | The number of all valence electrons in the alloy per number of atoms | Calculation | [,] | |
| Lattice expansion per unit effective valency electron concentration | ||||
| Melting temperature (Tm) | As per definition | Calculation | [] |
Similarly, not only is the hydrogen permeation flux across the membrane important, but so are mechanical properties, resistance to poisoning, and durability. The optimization of all the target properties simultaneously, i.e., multiobjective optimization can be conflicting, that is some desirable properties are mutually exclusive. In that case, the Pareto front reports the optimal trade-offs between competing objectives [].
Any material informatics task should abide by fixed best practices to allow for transparency and result reproducibility []. Such best practices were suggested in the previous reference. A suggestion list of algorithms commonly used in material informatics can be found in reference [].
An interesting strategy for compositional space screening is active learning. This method allows the effective navigation of the search space iteratively to identify promising candidates for guiding experiments and computations []. This methodology leverages probabilistic modeling and surrogate-based predictions, coupled with a utility function that guides exploration toward regions of high uncertainty in the data space, thereby optimizing the decision-making process under limited information []. Bayesian optimization is an active learning-based iterative approach to global optimization, which is a powerful strategy for heterogeneous catalysts and alloy design. A Multi-Objective Bayesian Optimization (MOBO) strategy to screen probable niobium-based candidates superalloy and BCC high entropy alloys for hydrogen storage has been given by [] and [], respectively. It might be emphasized that these approaches require preliminary strong domain knowledge to parametrize the alloy composition domain to screen, based on knowledge of the phase diagram and past state of the art. This approach enables the development of a dataset of promising alloy candidates that, at least computationally, meet the preliminary defined superalloy criteria, providing valuable guidance for future experimental studies.
Finally, using first-principles calculations and/or calculation of phase diagram (CALPHAD), the potential candidates’ list can be more refined before synthesis and testing in the lab [].
8. Conclusions
Dense metallic membranes for hydrogen separation and purification present a promising pathway toward decentralized hydrogen production and the potential utilization of more cost-effective hydrogen gas in the future. The development of advanced membranes, alongside the optimization of existing ones, is crucial to meet the anticipated surge in demand for pure hydrogen in the coming years. This review has explored the application of high-throughput and combinatorial methods, as well as material informatics, to accelerate research in dense metallic membranes. We have discussed key cases where combinatorial techniques, such as composition-gradient thin films combined with spatially resolved rapid characterization, have enabled efficient screening of binary and ternary alloy candidates.
For these techniques to yield impactful insights, robust data acquisition and analysis pipelines are essential. In light of the data-driven era, we propose initial steps for integrating artificial intelligence into metallic membrane design, with the establishment of comprehensive datasets as a foundational step to bolster material informatics. Such datasets must be extensive, with standardized units and thorough documentation, to facilitate reproducibility and utility in machine learning applications. The integration of domain expertise will also be critical, particularly in the feature engineering stage, where relevant descriptors can guide model accuracy and interpretability. Based on our review, we have compiled a list of commonly used feature descriptors, which will be elaborated on in an upcoming publication. Future research should examine the predictive power of these descriptors and strive to develop even more precise indicators.
Author Contributions
E.K.: conceptualization, methodology, and writing—original draft, M.U.: conceptualization, methodology, and writing and review—original draft, S.B.: review and editing, K.M.: review and editing, J.S.C.: review and editing, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grants from funding agencies in the public, commercial, or not-for-profit sectors.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The first author would like to acknowledge the Japan Ministry of Education, Culture, Sports, Science and Technology (MEXT) financial support for the MEXT Scholarship for graduate studies. In preparing this manuscript, first author used generative AI tools, specifically ChatGPT, to assist in rewriting, rephrasing, and checking the grammar of certain sections. These tools were employed selectively to enhance the clarity and readability of the content, ensuring that the manuscript meets the highest standards of academic communication. All intellectual contributions, research findings, and interpretations remain entirely our own.
Conflicts of Interest
The authors affirm that they do not have any known financial interests or personal relationships that might be perceived as influencing the research presented in this paper.
References
- IPCC. Summary for Policymakers. In Climate Change 2023: Synthesis Report; Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; pp. 1–34. [Google Scholar]
- Usman, M.; Cheng, S.; Cross, J.S. Biomass Feedstocks for Liquid Biofuels Production in Hawaii & Tropical Islands: A Review. Int. J. Renew. Energy Dev. 2022, 11, 111–132. [Google Scholar] [CrossRef]
- Usman, M.; Cheng, S.; Boonyubol, S.; Cross, J.S. From Biomass to Biocrude: Innovations in Hydrothermal Liquefaction and Upgrading. Energy Convers. Manag. 2024, 302, 118093. [Google Scholar] [CrossRef]
- Stopić, S.; Friedrich, B. Formation and Application of Hydrogen in Non-Ferrous Metallurgy. Vojnoteh. Glas. 2023, 71, 783–796. [Google Scholar] [CrossRef]
- Klell, M. Storage of Hydrogen in the Pure Form. In Handbook of Hydrogen Storage: New Materials for Future Energy Storage; Wiley-VCH: Weinheim, Germany, 2010; p. 8. ISBN 978-3-527-32273-2. [Google Scholar]
- Møller, K.T.; Jensen, T.R.; Akiba, E.; Li, H. Hydrogen—A Sustainable Energy Carrier. Prog. Nat. Sci. Mater. Int. 2017, 27, 34–40. [Google Scholar] [CrossRef]
- Zhang, X.; Schwarze, M.; Schomäcker, R.; van de Krol, R.; Abdi, F.F. Life Cycle Net Energy Assessment of Sustainable H2 Production and Hydrogenation of Chemicals in a Coupled Photoelectrochemical Device. Nat. Commun. 2023, 14, 991. [Google Scholar] [CrossRef] [PubMed]
- Nikolaidis, P.; Poullikkas, A. A Comparative Overview of Hydrogen Production Processes. Renew. Sustain. Energy Rev. 2017, 67, 597–611. [Google Scholar] [CrossRef]
- Staffell, I.; Scamman, D.; Abad, A.V.; Balcombe, P.; Dodds, P.E.; Ekins, P.; Shah, N.; Ward, K.R. The Role of Hydrogen and Fuel Cells in the Global Energy System. Energy Environ. Sci. 2019, 12, 463–491. [Google Scholar] [CrossRef]
- US Department of Energy. The Green Hydrogen Report: The 1995 Progress Report of the Secretary of Energy’s Hydrogen Technical Advisory Panel; National Renewable Energy Lab: Golden, CO, USA, 1995; p. DOE/GO--10095-179, 81032. [Google Scholar]
- Maiga, O.; Deville, E.; Laval, J.; Prinzhofer, A.; Diallo, A.B. Characterization of the Spontaneously Recharging Natural Hydrogen Reservoirs of Bourakebougou in Mali. Sci. Rep. 2023, 13, 11876. [Google Scholar] [CrossRef]
- Kusoglu, A. (Re)Defining Clean Hydrogen: From Colors to Emissions. Electrochem. Soc. Interface 2022, 31, 47–52. [Google Scholar] [CrossRef]
- Yu, M.; Wang, K.; Vredenburg, H. Insights into Low-Carbon Hydrogen Production Methods: Green, Blue and Aqua Hydrogen. Int. J. Hydrogen Energy 2021, 46, 21261–21273. [Google Scholar] [CrossRef]
- IEA. Global Hydrogen Review 2024; IEA: Paris, France, 2024. [Google Scholar]
- Sneha, L.; Yalamati, H.P.S.; Srivastava, R. Application of Hydrogen in Various Sectors. In Solar-Driven Green Hydrogen Generation and Storage; Srivastava, R., Chattopadhyay, J., Santos, D.M.F., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 507–524. ISBN 978-0-323-99580-1. [Google Scholar]
- Timofeev, N.; Berseneva, F.; Makarov, V. New Palladium-Based Membrane Alloys for Separation of Gas Mixtures to Generate Ultrapure Hydrogen. Int. J. Hydrogen Energy 1994, 19, 895–898. [Google Scholar] [CrossRef]
- Tosti, S.; Violante, V. Numerical Approach for a Study of the Hydrogen Isotopes Separation by Palladium Alloy Membranes. Fusion Eng. Des. 1998, 43, 93–100. [Google Scholar] [CrossRef]
- ISO 14687:2019; Hydrogen Fuel Quality—Product Specification. International Organization for Standardization (ISO): Geneva, Switzerland, 2019.
- Maxwell, D.S.; Sun, Q.; Rojas, H.; Kendrick, I.; Pavlicek, R.K.; De Castro, E.S.; Aurora, A.; Mukerjee, S. High Purity Hydrogen Separation with HT-PBI Based Electrochemical Pump Operation at 120 °C. J. Electrochem. Soc. 2023, 170, 034510. [Google Scholar] [CrossRef]
- Murugan, A.; De Huu, M.; Bacquart, T.; Van Wijk, J.; Arrhenius, K.; Te Ronde, I.; Hemfrey, D. Measurement Challenges for Hydrogen Vehicles. Int. J. Hydrogen Energy 2019, 44, 19326–19333. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, G.; Zhang, L.; Zhang, S.; Lin, L. Comparison of Hydrogen Specification in National Standards for China. E3S Web Conf. 2019, 118, 03042. [Google Scholar] [CrossRef]
- Shah, M. Linde plc Hydrogen Purification Technologies Overview 2021 ARPA-E Methane Pyrolysis Annual Program Review Virtual Meeting. In Proceedings of the 2021 ARPA-E Methane Pyrolysis Annual Program Review Virtual Meeting, Tonawanda, NY, USA, 12–14 January 2021. [Google Scholar]
- Sircar, S.; Golden, T.C. Pressure Swing Adsorption Technology for Hydrogen Production. In Hydrogen and Syngas Production and Purification Technologies; Liu, K., Song, C., Subramani, V., Eds.; Wiley: Hoboken, NJ, USA, 2009; pp. 414–450. ISBN 978-0-471-71975-5. [Google Scholar]
- Nordio, M.; Wassie, S.A.; Van Sint Annaland, M.; Pacheco Tanaka, D.A.; Viviente Sole, J.L.; Gallucci, F. Techno-Economic Evaluation on a Hybrid Technology for Low Hydrogen Concentration Separation and Purification from Natural Gas Grid. Int. J. Hydrogen Energy 2021, 46, 23417–23435. [Google Scholar] [CrossRef]
- Airproducts; Benson, J.; Celin, A. Recovering Hydrogen—And Profits—From Hydrogen-Rich Offgas. Chem. Eng. Prog. 2018, 114, 55–59. [Google Scholar]
- US EPA. Distributed Generation of Electricity and Its Environmental Impacts. Available online: https://www.epa.gov/energy/distributed-generation-electricity-and-its-environmental-impacts (accessed on 13 October 2024).
- Kim, D.-W.; Park, Y.J.; Moon, J.-W.; Ryi, S.-K.; Park, J.-S. The Effect of Cu Reflow on the Pd–Cu–Ni Ternary Alloy Membrane Fabrication for Infinite Hydrogen Separation. Thin Solid Films 2008, 516, 3036–3044. [Google Scholar] [CrossRef]
- Ryi, S.-K.; Park, J.-S.; Kim, S.-H.; Cho, S.-H.; Hwang, K.-R.; Kim, D.-W.; Kim, H.-G. A New Membrane Module Design with Disc Geometry for the Separation of Hydrogen Using Pd Alloy Membranes. J. Membr. Sci. 2007, 297, 217–225. [Google Scholar] [CrossRef]
- Bang, G.; Moon, D.-K.; Kang, J.-H.; Han, Y.-J.; Kim, K.-M.; Lee, C.-H. High-Purity Hydrogen Production via a Water-Gas-Shift Reaction in a Palladium-Copper Catalytic Membrane Reactor Integrated with Pressure Swing Adsorption. Chem. Eng. J. 2021, 411, 128473. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Xu, H.; Xiong, G. Integrated One-Step PEMFC-Grade Hydrogen Production From Liquid Hydrocarbons Using Pd Membrane Reactor. Ind. Eng. Chem. Res. 2007, 46, 5510–5515. [Google Scholar] [CrossRef]
- Tosti, S.; Pozio, A.; Santucci, A. Membrane Technologies for Hydrogen Separation. Energ. Ambiente E Innov. 2021, 107–111. [Google Scholar] [CrossRef]
- Conde, J.J.; Maroño, M.; Sánchez-Hervás, J.M. Pd-Based Membranes for Hydrogen Separation: Review of Alloying Elements and Their Influence on Membrane Properties. Sep. Purif. Rev. 2017, 46, 152–177. [Google Scholar] [CrossRef]
- Dolan, M.; Dave, N.; Morpeth, L.; Donelson, R.; Liang, D.; Kellam, M.; Song, S. Ni-Based Amorphous Alloy Membranes for Hydrogen Separation at 400 °C. J. Membr. Sci. 2009, 326, 549–555. [Google Scholar] [CrossRef]
- Hao, S.; Sholl, D.S. Rapid Prediction of Hydrogen Permeation through Amorphous Metal Membranes: An Efficient Computational Screening Approach. Energy Environ. Sci 2013, 6, 232–240. [Google Scholar] [CrossRef]
- Cerone, N.; Zito, G.D.; Florio, C.; Fabbiano, L.; Zimbardi, F. Recent Advancements in Pd-Based Membranes for Hydrogen Separation. Energies 2024, 17, 4095. [Google Scholar] [CrossRef]
- Jazani, O.; Elharati, M.A.; Liguori, S. Effects of Porous Supports and Binary Gases on Hydrogen Permeation in Pd–Ag–Y Alloy Membrane. J. Membr. Sci. 2025, 713, 123327. [Google Scholar] [CrossRef]
- Bhalani, D.V.; Lim, B. Hydrogen Separation Membranes: A Material Perspective. Molecules 2024, 29, 4676. [Google Scholar] [CrossRef] [PubMed]
- Kudapa, V.K.; Paliyal, P.S.; Mondal, A.; Mondal, S. A Critical Review of Fabrication Strategies, Separation Techniques, Challenges, and Future Prospects for the Hydrogen Separation Membrane. Fusion Sci. Technol. 2024, 80, 803–825. [Google Scholar] [CrossRef]
- Kang, S.G.; Coulter, K.E.; Gade, S.K.; Way, J.D.; Sholl, D.S. Identifying Metal Alloys with High Hydrogen Permeability Using High Throughput Theory and Experimental Testing. J. Phys. Chem. Lett. 2011, 2, 3040–3044. [Google Scholar] [CrossRef]
- Nicholson, K.M.; Chandrasekhar, N.; Sholl, D.S. Powered by DFT: Screening Methods That Accelerate Materials Development for Hydrogen in Metals Applications. Acc. Chem. Res. 2014, 47, 3275–3283. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.N.; Nhat, T.T.P.; Takimoto, K.; Thakur, A.; Nishimura, S.; Ohyama, J.; Miyazato, I.; Takahashi, L.; Fujima, J.; Takahashi, K.; et al. High-Throughput Experimentation and Catalyst Informatics for Oxidative Coupling of Methane. ACS Catal. 2020, 10, 921–932. [Google Scholar] [CrossRef]
- Schmack, R.; Friedrich, A.; Kondratenko, E.V.; Polte, J.; Werwatz, A.; Kraehnert, R. A Meta-Analysis of Catalytic Literature Data Reveals Property-Performance Correlations for the OCM Reaction. Nat. Commun. 2019, 10, 441. [Google Scholar] [CrossRef] [PubMed]
- Senderowitz, H.; Tropsha, A. Materials Informatics. J. Chem. Inf. Model. 2018, 58, 1313–1314. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.; Fernando, S. Hydrogen Membrane Separation Techniques. Ind. Eng. Chem. Res. 2006, 45, 875–881. [Google Scholar] [CrossRef]
- Ockwig, N.W.; Nenoff, T.M. Membranes for Hydrogen Separation. Chem. Rev. 2007, 107, 4078–4110. [Google Scholar] [CrossRef] [PubMed]
- Lider, A.; Kudiiarov, V.; Kurdyumov, N.; Lyu, J.; Koptsev, M.; Travitzky, N.; Hotza, D. Materials and Techniques for Hydrogen Separation from Methane-Containing Gas Mixtures. Int. J. Hydrog. Energy 2023, 48, 28390–28411. [Google Scholar] [CrossRef]
- Songolzadeh, M.; Soleimani, M.; Takht Ravanchi, M.; Songolzadeh, R. Carbon Dioxide Separation from Flue Gases: A Technological Review Emphasizing Reduction in Greenhouse Gas Emissions. Sci. World J. 2014, 2014, 828131. [Google Scholar] [CrossRef] [PubMed]
- Golmakani, A.; Fatemi, S.; Tamnanloo, J. Investigating PSA, VSA, and TSA Methods in SMR Unit of Refineries for Hydrogen Production with Fuel Cell Specification. Sep. Purif. Technol. 2017, 176, 73–91. [Google Scholar] [CrossRef]
- Rahimpour, H.R.; Nategh, M.; Rahimpour, M.R. Industrial Membranes for Hydrogen Separation. In Hydrogen Production, Separation and Purification for Energy; Basile, A., Dalena, F., Tong, J., Veziroglu, T.N., Eds.; IET Energy Engineering Series; IET: London, UK, 2017; pp. 343–361. ISBN 978-1-78561-101-8. [Google Scholar]
- Rahimpour, M.R.; Samimi, F.; Babapoor, A.; Tohidian, T.; Mohebi, S. Palladium Membranes Applications in Reaction Systems for Hydrogen Separation and Purification: A Review. Chem. Eng. Process. Process Intensif. 2017, 121, 24–49. [Google Scholar] [CrossRef]
- Yon, C.M.; Sherman, J.D. Adsorption, Gas Separation. In Kirk-Othmer Encyclopedia of Chemical Technology; Kirk-Othmer, Ed.; Wiley: Hoboken, NJ, USA, 2003; ISBN 978-0-471-48494-3. [Google Scholar]
- Ruthven, D.M.; Farooq, S.; Knaebel, K.S. Pressure Swing Adsorption; 1. Printing; VCH: New York, NY, USA, 1994; ISBN 978-0-471-18818-6. [Google Scholar]
- Luberti, M.; Ahn, H. Review of Polybed Pressure Swing Adsorption for Hydrogen Purification. Int. J. Hydrogen Energy 2022, 47, 10911–10933. [Google Scholar] [CrossRef]
- Elseviers, W.; Hassett, F.P.; Navarre, J.-L.; Whysall, M. 50 Years of PSA Technology for H2 Purification; UOP LLC: Des Plaines, IL, USA, 2015. [Google Scholar]
- Lee, K.B.; Beaver, M.G.; Caram, H.S.; Sircar, S. Reversible Chemisorbents for Carbon Dioxide and Their Potential Applications. Ind. Eng. Chem. Res. 2008, 47, 8048–8062. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of Gases, with Special Reference to the Evaluation of Surface Area and Pore Size Distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Wiessner, F.G. Basics and Industrial Applications of Pressure Swing Adsorption (PSA), the Modern Way to Separate Gas. Gas Sep. Purif. 1988, 2, 115–119. [Google Scholar] [CrossRef]
- Melaina, M.W.; Antonia, O.; Penev, M. Blending Hydrogen into Natural Gas Pipeline Networks: A Review of Key Issues; Technical Report NREL/TP-5600-51995; IGEM: Cambridge, CA, USA, 2013. [Google Scholar]
- Naquash, A.; Qyyum, M.A.; Chaniago, Y.D.; Riaz, A.; Yehia, F.; Lim, H.; Lee, M. Separation and Purification of Syngas-Derived Hydrogen: A Comparative Evaluation of Membrane- and Cryogenic-Assisted Approaches. Chemosphere 2023, 313, 137420. [Google Scholar] [CrossRef] [PubMed]
- Naquash, A.; Islam, M.; Qyyum, M.A.; Haider, J.; Chaniago, Y.D.; Lim, H.; Lee, M. Membrane and Desublimation Integrated Hydrogen Separation Followed by Liquefaction Process: An Energy, Exergy, and Economic Evaluation. Int. J. Hydrogen Energy 2024, 54, 1295–1306. [Google Scholar] [CrossRef]
- Valenti, G. Separation of Hydrogen Isotopes by Cryogenic Distillation. In Hydrogen Production, Separation and Purification for Energy; Basile, A., Dalena, F., Tong, J., Vezirolu, T.N., Eds.; Institution of Engineering and Technology: London, UK, 2017; pp. 433–456. ISBN 978-1-78561-100-1. [Google Scholar]
- Aasadnia, M.; Mehrpooya, M.; Ghorbani, B. A Novel Integrated Structure for Hydrogen Purification Using the Cryogenic Method. J. Clean. Prod. 2021, 278, 123872. [Google Scholar] [CrossRef]
- Aasadnia, M.; Mehrpooya, M. Large-Scale Liquid Hydrogen Production Methods and Approaches: A Review. Appl. Energy 2018, 212, 57–83. [Google Scholar] [CrossRef]
- Atsonios, K.; Panopoulos, K.D.; Doukelis, A.; Koumanakos, A.K.; Kakaras, E.; Peters, T.A.; van Delft, Y.C. Introduction to Palladium Membrane Technology. In Palladium Membrane Technology for Hydrogen Production, Carbon Capture and Other Applications; Doukelis, A., Panopoulos, K., Koumanakos, A., Kakaras, E., Eds.; Woodhead Publishing Series in Energy; Elsevier: Amsterdam, The Netherlands; WP, Woodhead Publisher: Cambridge, UK, 2015; pp. 1–21. ISBN 978-1-78242-241-9. [Google Scholar]
- Yun, S.; Oyama, S.T. Correlations in Palladium Membranes for Hydrogen Separation: A Review. J. Membr. Sci. 2011, 375, 28–45. [Google Scholar] [CrossRef]
- Moral, G.; Ortiz-Imedio, R.; Ortiz, A.; Gorri, D.; Ortiz, I. Hydrogen Recovery from Coke Oven Gas. Comparative Analysis of Technical Alternatives. Ind. Eng. Chem. Res. 2022, 61, 6106–6124. [Google Scholar] [CrossRef]
- Grand View Research Gas Separation Membrane Market Size, Share Report, 2030. Available online: https://www.grandviewresearch.com/industry-analysis/gas-separation-membrane-market-report (accessed on 19 August 2024).
- Fortune Business Insights Membranes Market Size, Share, Growth: Forecast Report 2032. Available online: https://www.fortunebusinessinsights.com/membranes-market-102982 (accessed on 19 August 2024).
- Japan Pionics. Palladium Alloy Memrane Permeation Hydrogen Gas Purifier; MODEL-VP-DH; Air Water Mechatronics Inc.: Tokyo, Japan, 2023. [Google Scholar]
- Santucci, A.; Tosti, S.; Basile, A. 4—Alternatives to Palladium in Membranes for Hydrogen Separation: Nickel, Niobium and Vanadium Alloys, Ceramic Supports for Metal Alloys and Porous Glass Membranes. In Handbook of Membrane Reactors; Basile, A., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Cambridge, UK, 2013; Volume 1, pp. 183–217. ISBN 978-0-85709-414-8. [Google Scholar]
- Ghasemzadeh, K.; Amiri, T.Y.; Zeynali, R.; Basile, A. Membranes for Hydrogen Separation. In Current Trends and Future Developments on (Bio-) Membranes; Elsevier: Amsterdam, The Netherlands, 2020; pp. 91–134. ISBN 978-0-12-817110-3. [Google Scholar]
- Uemiya, S. State-of-the-Art of Supported Metal Membranes for Gas Separation. Sep. Purif. Methods 1999, 28, 51–85. [Google Scholar] [CrossRef]
- Graham, T. II. On the Occlusion of Hydrogen Gas by Metals. Proc. R. Soc. Lond. 1868, 16, 422–427. [Google Scholar] [CrossRef]
- Grashoff, G.J.; Pilkington, C.E.; Corti, C.W. The Purification of Hydrogen. Platin. Met. Rev. 1983, 27, 157–169. [Google Scholar] [CrossRef]
- Wisniak, J. Thomas Graham: I. Contributions to Thermodynamics, Chemistry, and Occlusion of Gases. Educ. Quím. 2013, 24, 316–325. [Google Scholar] [CrossRef]
- Paglieri, S.N.; Way, J.D. Innovations in Palladium Membrane Research. Sep. Purif. Methods 2002, 31, 1–169. [Google Scholar] [CrossRef]
- Phair, J.W.; Donelson, R. Developments and Design of Novel (Non-Palladium-Based) Metal Membranes for Hydrogen Separation. Ind. Eng. Chem. Res. 2006, 45, 5657–5674. [Google Scholar] [CrossRef]
- Dube, S.; Gorimbo, J.; Moyo, M.; Okoye-Chine, C.G.; Liu, X. Synthesis and Application of Ni-Based Membranes in Hydrogen Separation and Purification Systems: A Review. J. Environ. Chem. Eng. 2023, 11, 109194. [Google Scholar] [CrossRef]
- Aoki, K.; Ogata, Y.; Kusakabe, K.; Morooka, S. Applicability of Palladium Membrane for the Separation of Protium and Deuterium. Int. J. Hydrogen Energy 1998, 23, 325–332. [Google Scholar] [CrossRef]
- Bulubasa, G.; Niculescu, A.; Craciun, M.; Bucur, C.; Ana, G.; Bornea, A. Investigations on Hydrogen Isotope Separation Factor Employing Palladium-Based Solid Metallic Membranes. Fusion Sci. Technol. 2024, 1–5. [Google Scholar] [CrossRef]
- Pati, S.; Jat, R.A.; Anand, N.S.; Derose, D.J.; Karn, K.N.; Mukerjee, S.K.; Parida, S.C. Pd-Ag-Cu Dense Metallic Membrane for Hydrogen Isotope Purification and Recovery at Low Pressures. J. Membr. Sci. 2017, 522, 151–158. [Google Scholar] [CrossRef]
- Shere, L.; Hill, A.K.; Mays, T.J.; Lawless, R.; Brown, R.; Perera, S.P. The next Generation of Low Tritium Hydrogen Isotope Separation Technologies for Future Fusion Power Plants. Int. J. Hydrogen Energy 2024, 55, 319–338. [Google Scholar] [CrossRef]
- Sharma, B.; Myung, J. Pd-Based Ternary Alloys Used for Gas Sensing Applications: A Review. Int. J. Hydrogen Energy 2019, 44, 30499–30510. [Google Scholar] [CrossRef]
- Gryaznov, V.M. Hydrogen Permeable Palladium Membrane Catalysts: An Aid to the Efficient Production of Ultra Pure Chemicals and Pharmaceuticals. Platin. Met. Rev. 1986, 30, 68–72. [Google Scholar] [CrossRef]
- Gryaznov, V.M. Surface Catalytic Properties and Hydrogen Diffusion in Palladium Alloy Membranes. Z. Phys. Chem. 1986, 147, 123–132. [Google Scholar] [CrossRef]
- Shu, J.; Grandjean, B.P.A.; Neste, A.V.; Kaliaguine1, S. Catalytic Palladium-based Membrane Reactors: A Review. Can. J. Chem. Eng. 1991, 69, 1036–1060. [Google Scholar] [CrossRef]
- Basile, A.; Tereschenko, G.F.; Orekhova, N.V.; Ermilova, M.M.; Gallucci, F.; Iulianelli, A. An Experimental Investigation on Methanol Steam Reforming with Oxygen Addition in a Flat Pd-Ag Membrane Reactor. Int. J. Hydrogen Energy 2006, 31, 1615–1622. [Google Scholar] [CrossRef]
- Basov, N.L.; Ermilova, M.M.; Orekhova, N.V.; Yaroslavtsev, A.B. Membrane Catalysis in the Dehydrogenation and Hydrogen Production Processes. Russ. Chem. Rev. 2013, 82, 352–368. [Google Scholar] [CrossRef]
- Dittmeyer, R.; Caro, J. Catalytic Membrane Reactors. In Handbook of Heterogeneous Catalysis; Ertl, G., Knözinger, H., Schüth, F., Weitkamp, J., Eds.; Wiley: Hoboken, NJ, USA, 2008; pp. 2198–2248. ISBN 978-3-527-31241-2. [Google Scholar]
- Gallucci, F.; Fernandez, E.; Corengia, P.; Van Sint Annaland, M. Recent Advances on Membranes and Membrane Reactors for Hydrogen Production. Chem. Eng. Sci. 2013, 92, 40–66. [Google Scholar] [CrossRef]
- Gryaznov, V. Metal Containing Membranes for the Production of Ultrapure Hydrogen and The Recovery of Hydrogen Isotopes. Sep. Purif. Methods 2000, 29, 171–187. [Google Scholar] [CrossRef]
- Gryaznov, V.M. Platinum Metals as Components of Catalyst-Membrane Systems. Platin. Met. Rev. 1992, 36, 70–79. [Google Scholar] [CrossRef]
- Fuerst, T.F. Dense Metallic Membrane Reactor Synthesis of Ammonia at Moderate Conditions and Low Cost. In Proceedings of the NH3 Fuel Conference 2017, Minneapolis, MN, USA, 1–2 November 2017. [Google Scholar]
- Delima, R. Efficient, Carbon-Neutral Hydrogenation Using a Palladium Membrane Reactor. Ph.D. Thesis, University of British Columbia, Kelowna, BC, Canada, 2021. [Google Scholar] [CrossRef]
- Han, G.; Li, G.; Sun, Y. Electrocatalytic Hydrogenation Using Palladium Membrane Reactors. JACS Au 2024, 4, 328–343. [Google Scholar] [CrossRef]
- Jansonius, R.P.; Kurimoto, A.; Marelli, A.M.; Huang, A.; Sherbo, R.S.; Berlinguette, C.P. Hydrogenation without H2 Using a Palladium Membrane Flow Cell. Cell Rep. Phys. Sci. 2020, 1, 100105. [Google Scholar] [CrossRef]
- Das, P.; Lee, Y.-S.; Lee, S.-C.; Bhattacharjee, S. Computational Design of a New Palladium Alloy with Efficient Hydrogen Storage Capacity and Hydrogenation-Dehydrogenation Kinetics. Int. J. Hydrogen Energy 2023, 48, 18795–18803. [Google Scholar] [CrossRef]
- Jia, Y.; Huang, T.-H.; Lin, S.; Guo, L.; Yu, Y.-M.; Wang, J.-H.; Wang, K.-W.; Dai, S. Stable Pd–Cu Hydride Catalyst for Efficient Hydrogen Evolution. Nano Lett. 2022, 22, 1391–1397. [Google Scholar] [CrossRef] [PubMed]
- Kawae, T.; Inagaki, Y.; Wen, S.; Hirota, S.; Itou, D.; Kimura, T. Superconductivity in Palladium Hydride Systems. J. Phys. Soc. Jpn. 2020, 89, 051004. [Google Scholar] [CrossRef]
- Liguori, S.; Kian, K.; Buggy, N.; Anzelmo, B.H.; Wilcox, J. Opportunities and Challenges of Low-Carbon Hydrogen via Metallic Membranes. Prog. Energy Combust. Sci. 2020, 80, 100851. [Google Scholar] [CrossRef]
- Lewis, F.A. The Palladium-Hydrogen System: Part III: Alloy Systems and Hydrogen Permeation. Platin. Met. Rev. 1982, 26, 121–128. [Google Scholar] [CrossRef]
- Jamieson, H.C.; Weatherly, G.C.; Manchester, F.D. The β → α Phase Transformation in Palladium-Hydrogen Alloys. J. Common Met. 1976, 50, 85–102. [Google Scholar] [CrossRef]
- Bosko, M.L.; Dalla Fontana, A.; Tarditi, A.; Cornaglia, L. Advances in Hydrogen Selective Membranes Based on Palladium Ternary Alloys. Int. J. Hydrogen Energy 2021, 46, 15572–15594. [Google Scholar] [CrossRef]
- Morreale, B.D.; Howard, B.H.; Iyoha, O.; Enick, R.M.; Ling, C.; Sholl, D.S. Experimental and Computational Prediction of the Hydrogen Transport Properties of Pd4S. Ind. Eng. Chem. Res. 2007, 46, 6313–6319. [Google Scholar] [CrossRef]
- O’Brien, C.P.; Howard, B.H.; Miller, J.B.; Morreale, B.D.; Gellman, A.J. Inhibition of Hydrogen Transport through Pd and Pd47Cu53 Membranes by H2S at 350 °C. J. Membr. Sci. 2010, 349, 380–384. [Google Scholar] [CrossRef]
- Rivera, D.J.; Muhich, C.L. Preventing H2S Poisoning of Dense Pd Membranes for H2 Purification Using an Electric-Field: An Ab Initio Study. Surf. Sci. 2023, 733, 122303. [Google Scholar] [CrossRef]
- Grønvold, F.; Røst, E. The Crystal Structures of Pd4 Se and Pd4S. Acta Crystallogr. 1962, 15, 11–13. [Google Scholar] [CrossRef]
- Alfonso, D.R. First-Principles Studies of H2S Adsorption and Dissociation on Metal Surfaces. Surf. Sci. 2008, 602, 2758–2768. [Google Scholar] [CrossRef]
- Amano, M.; Nishimura, C.; Komaki, M. Effects of High Concentration CO and CO2 on Hydrogen Permeation through the Palladium Membrane. Mater. Trans. JIM 1990, 31, 404–408. [Google Scholar] [CrossRef]
- Li, H.; Goldbach, A.; Li, W.; Xu, H. PdC Formation in Ultra-Thin Pd Membranes during Separation of H2/CO Mixtures. J. Membr. Sci. 2007, 299, 130–137. [Google Scholar] [CrossRef]
- Ziemecki, S.B.; Jones, G.A.; Swartzfager, D.G.; Harlow, R.L.; Faber, J. Formation of Interstitial Palladium-Carbon Phase by Interaction of Ethylene, Acetylene, and Carbon Monoxide with Palladium. J. Am. Chem. Soc. 1985, 107, 4547–4548. [Google Scholar] [CrossRef]
- O’Brien, C.P.; Dunbar, Z.W.; Lee, I.C. A Spectroscopic Membrane Permeation Cell for In-Situ Infrared-Reflection Absorption Spectroscopic Analysis of Membrane Surfaces and Simultaneous Measurement of Trans-Membrane Gas Permeation Rates. J. Membr. Sci. 2017, 526, 43–51. [Google Scholar] [CrossRef]
- Gao, H.; Lin, Y.S.; Li, Y.; Zhang, B. Chemical Stability and Its Improvement of Palladium-Based Metallic Membranes. Ind. Eng. Chem. Res. 2004, 43, 6920–6930. [Google Scholar] [CrossRef]
- Guo, L.; Wu, Z.; Wang, H.; Yan, H.; Yang, F.; Cheng, G.; Zhang, Z. Efficient Hydrogen Recovery and Purification from Industrial Waste Hydrogen to High-Purity Hydrogen Based on Metal Hydride Powder. Chem. Eng. J. 2023, 455, 140689. [Google Scholar] [CrossRef]
- Mordkovich, V.Z.; Baichtock, Y.K.; Sosna, M.H. The Large Scale Production of Hydrogen from Gas Mixtures: A Use for Ultra Thin Palladium Alloy Membranes. Platinum Metals Rev. 1992, 36, 90–97. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Chen, F.L.; Kinari, Y. Permeability and Diffusivity of Hydrogen through Pd-Y-In(Sn, Pb) Alloy Membranes. J. Alloys Compd. 1994, 205, 205–210. [Google Scholar] [CrossRef]
- Ievlev, V.M.; Burkhanov, G.S.; Roshan, N.R.; Belonogov, E.K.; Maksimenko, A.A.; Dontsov, A.I.; Rudakov, K.E. Structure, Mechanical Properties, and Hydrogen Permeability of Pd-Cu and Pd-Ru Membrane Foils Prepared by Magnetron Sputtering. Russ. Metall. Met. 2012, 2012, 994–1001. [Google Scholar] [CrossRef]
- Hall, C.K. A Review of the Statistical Theory of the Phase-Change Behavior of Hydrogen in Metals. In Electronic Structure and Properties of Hydrogen in Metals; Jena, P., Satterthwaite, C.B., Eds.; Springer US: Boston, MA, USA, 1983; pp. 11–24. ISBN 978-1-4684-7632-3. [Google Scholar]
- Horikawa, D.; Matsumura, T.; Ebisugi, M.; Kubota, S. Hydrogen Permeable Membrane Made of Pdcu Alloy and Hydrogen Purification Method Due to Hydrogen Permeable Membrane. JP Patent JP2023039770A, 9 September 2021. [Google Scholar]
- Warren, J. The Effect of Hydrogen on Palladium-Copper Based Membranes for Hydrogen Purification. Master Thesis, University of Birmingham, Birmingham, UK, 2012. [Google Scholar]
- Guerreiro, B.H.; Martin, M.H.; Roué, L.; Guay, D. Hydrogen Permeability of PdCuAu Membranes Prepared from Mechanically-Alloyed Powders. J. Membr. Sci. 2016, 509, 68–82. [Google Scholar] [CrossRef]
- Kamakoti, P.; Morreale, B.D.; Ciocco, M.V.; Howard, B.H.; Killmeyer, R.P.; Cugini, A.V.; Sholl, D.S. Prediction of Hydrogen Flux Through Sulfur-Tolerant Binary Alloy Membranes. Science 2005, 307, 569–573. [Google Scholar] [CrossRef]
- Wang, T.; Dong, P.; Li, J.; You, Y.-W. The Factors Affecting the Diffusion Properties of Hydrogen in Palladium Copper Alloys: Ab Initio Study. Int. J. Hydrogen Energy 2022, 47, 27579–27589. [Google Scholar] [CrossRef]
- Kulprathipanja, A.; Alptekin, G.; Falconer, J.; Way, J. Pd and Pd–Cu Membranes: Inhibition of H Permeation by HS. J. Membr. Sci. 2005, 254, 49–62. [Google Scholar] [CrossRef]
- Peters, T.A.; Kaleta, T.; Stange, M.; Bredesen, R. Hydrogen Transport through a Selection of Thin Pd-Alloy Membranes: Membrane Stability, H2S Inhibition, and Flux Recovery in Hydrogen and Simulated WGS Mixtures. Catal. Today 2012, 193, 8–19. [Google Scholar] [CrossRef]
- Mundschau, M.V.; Xie, X.; Evenson, C.R.; Sammells, A.F. Dense Inorganic Membranes for Production of Hydrogen from Methane and Coal with Carbon Dioxide Sequestration. Catal. Today 2006, 118, 12–23. [Google Scholar] [CrossRef]
- Coulter, K.E.; Way, J.D.; Gade, S.K.; Chaudhari, S.; Sholl, D.S.; Semidey-Flecha, L. Predicting, Fabricating, and Permeability Testing of Free-Standing Ternary Palladium−Copper−Gold Membranes for Hydrogen Separation. J. Phys. Chem. C 2010, 114, 17173–17180. [Google Scholar] [CrossRef]
- Shu, J.; Bongondo, B.E.W.; Grandjean, B.P.A.; Adnot, A.; Kaliaguine, S. Surface Segregation of PdAg Membranes upon Hydrogen Permeation. Surf. Sci. 1993, 291, 129–138. [Google Scholar] [CrossRef]
- Lai, T.; Lind, M.L. Heat Treatment Driven Surface Segregation in Pd77Ag23 Membranes and the Effect on Hydrogen Permeability. Int. J. Hydrogen Energy 2015, 40, 373–382. [Google Scholar] [CrossRef]
- Easa, J.; Yan, C.; Schneider, W.F.; O’Brien, C.P. CO and C3H6 Poisoning of Hydrogen Permeation across Pd77Ag23 Alloy Membranes: A Comparative Study with Pure Palladium. Chem. Eng. J. 2022, 430, 133080. [Google Scholar] [CrossRef]
- Coulter, K.E.; Way, J.D.; Gade, S.K.; Chaudhari, S.; Alptekin, G.O.; DeVoss, S.J.; Paglieri, S.N.; Pledger, B. Sulfur Tolerant PdAu and PdAuPt Alloy Hydrogen Separation Membranes. J. Membr. Sci. 2012, 405–406, 11–19. [Google Scholar] [CrossRef]
- Mckinley, D.L. Method for Hydrogen Separation and Purification; CRC Press: Boca Raton, FL, USA, 1969. [Google Scholar]
- Gade, S.K.; DeVoss, S.J.; Coulter, K.E.; Paglieri, S.N.; Alptekin, G.O.; Way, J.D. Palladium–Gold Membranes in Mixed Gas Streams with Hydrogen Sulfide: Effect of Alloy Content and Fabrication Technique. J. Membr. Sci. 2011, 378, 35–41. [Google Scholar] [CrossRef]
- Mckinley, D.L. Metal Alloy for Hydrogen Separation and Purification. U.S. Patent 3,350,845, 18 November 1965. [Google Scholar]
- Hughes, D.T.; Harris, I.R. A Comparative Study of Hydrogen Permeabilities and Solubilities in Some Palladium Solid Solution Alloys. J. Common Met. 1978, 61, P9–P21. [Google Scholar] [CrossRef]
- Hughes, D.T.; Harris, I.R. Hydrogen Diffusion Membranes Based on Some Palladium-Rare Earth Solid Solution Alloys. Z. Phys. Chem. 1979, 117, 185–193. [Google Scholar] [CrossRef]
- Kolchugina, N.B.; Gorbunov, S.V.; Roshan, N.R.; Burkhanov, G.S.; Kaminskaya, T.P.; Dormidontov, N.A.; Bakulina, A.S.; Rusinov, D.A. Membrane Pd–7.70 Wt % Lu Alloy for the Preparation and Purification of Hydrogen. Phys. Met. Metallogr. 2021, 122, 54–59. [Google Scholar] [CrossRef]
- Kolchugina, N.B.; Gorbunov, S.V.; Roshan, N.R.; Burkhanov, G.S.; Dormidontov, N.A.; Zheleznyi, M.V.; Bakulina, A.S. Membrane Characteristics of Palladium-Samarium Alloy Foils: Mechanical Properties and Hydrogen Permeability. In Proceedings of the METAL 2020—29th International Conference on Metallurgy and Materials, Conference Proceedings, Brno, Czech Republic, 20–22 May 2020; pp. 1042–1047. [Google Scholar]
- Fletcher, S. Thin Film Palladium—Yttrium Membranes for Hydrogen Separation. Ph.D. Thesis, The University of Birmingham, Birmingham, UK, 2009. [Google Scholar]
- Shirasaki, Y.; Tsuneki, T.; Seki, T.; Yasuda, I.; Sato, T.; Itoh, N. Improvement in Hydrogen Permeability of Palladium Membrane by Alloying with Transition Metals. J. Chem. Eng. Jpn. 2018, 51, 123–125. [Google Scholar] [CrossRef]
- Job, A.L.; Li, C.; Fuerst, T.F.; Douglas Way, J.; Wolden, C.A. Acceleration of Pd-V Intermetallic Diffusion by Hydrogen. J. Alloys Compd. 2024, 972, 172825. [Google Scholar] [CrossRef]
- Suzuki, A.; Yukawa, H.; Nambu, T.; Matsumoto, Y.; Murata, Y. Consistent Description of Hydrogen Permeability through Metal Membrane Based on Hydrogen Chemical Potential. Int. J. Hydrogen Energy 2014, 39, 7919–7924. [Google Scholar] [CrossRef]
- Didenko, L.P.; Sementsova, L.A.; Chizhov, P.E.; Babak, V.N.; Savchenko, V.I. Separation Performance of Foils from Pd—In(6%)—Ru(0.5%), Pd—Ru(6%), and Pd—Ru(10%) Alloys and Influence of CO2, CH4, and Water Vapor on the H2 Flow Rate through the Test Membranes. Russ. Chem. Bull. 2016, 65, 1997–2003. [Google Scholar] [CrossRef]
- Kehr, K.W. Theory of the Diffusion of Hydrogen in Metals. In Hydrogen in Metals I; Alefeld, G., Völkl, J., Eds.; Topics in Applied Physics; Springer: Berlin/Heidelberg, Germany, 1978; Volume 28, pp. 197–226. ISBN 978-3-540-08705-2. [Google Scholar]
- Al-Mufachi, N.A.; Rees, N.V.; Steinberger-Wilkens, R. Hydrogen Selective Membranes: A Review of Palladium-Based Dense Metal Membranes. Renew. Sustain. Energy Rev. 2015, 47, 540–551. [Google Scholar] [CrossRef]
- Wang, J.-S. On the Diffusion of Gases through Metals. Math. Proc. Camb. Philos. Soc. 1936, 32, 657–662. [Google Scholar] [CrossRef]
- Caravella, A.; Barbieri, G.; Drioli, E. Modelling and Simulation of Hydrogen Permeation through Supported Pd-Alloy Membranes with a Multicomponent Approach. Chem. Eng. Sci. 2008, 63, 2149–2160. [Google Scholar] [CrossRef]
- Deveau, N.D.; Ma, Y.H.; Datta, R. Beyond Sieverts’ Law: A Comprehensive Microkinetic Model of Hydrogen Permeation in Dense Metal Membranes. J. Membr. Sci. 2013, 437, 298–311. [Google Scholar] [CrossRef]
- Ward, T.L.; Dao, T. Model of Hydrogen Permeation Behavior in Palladium Membranes. J. Membr. Sci. 1999, 153, 211–231. [Google Scholar] [CrossRef]
- Theampetch, A.; Prapainainar, C.; Tungkamani, S.; Narataruksa, P.; Sornchamni, T.; Árnadóttir, L.; Jovanovic, G.N. Detailed Microkinetic Modelling of Syngas to Hydrocarbons via Fischer Tropsch Synthesis over Cobalt Catalyst. Int. J. Hydrogen Energy 2021, 46, 24721–24741. [Google Scholar] [CrossRef]
- Cortright, R.D.; Dumesic, J.A. Kinetics of Heterogeneous Catalytic Reactions: Analysis of Reaction Schemes. In Advances in Catalysis; Elsevier: Amsterdam, The Netherlands, 2001; Volume 46, pp. 161–264. ISBN 978-0-12-007846-2. [Google Scholar]
- Motagamwala, A.H.; Dumesic, J.A. Microkinetic Modeling: A Tool for Rational Catalyst Design. Chem. Rev. 2021, 121, 1049–1076. [Google Scholar] [CrossRef]
- deRosset, A.J. Diffusion of Hydrogen through Palladium Membranes. Ind. Eng. Chem. 1960, 52, 525–528. [Google Scholar] [CrossRef]
- Kompaniets, T.N.; Kurdyumov, A.A. Surface Processes in Hydrogen Permeation through Metal Membranes. Prog. Surf. Sci. 1984, 17, 75–151. [Google Scholar] [CrossRef]
- Caravella, A.; Scura, F.; Barbieri, G.; Drioli, E. Sieverts Law Empirical Exponent for Pd-Based Membranes: Critical Analysis in Pure H2 Permeation. J. Phys. Chem. B 2010, 114, 6033–6047. [Google Scholar] [CrossRef] [PubMed]
- Gallucci, F. Richardson Law. In Encyclopedia of Membranes; Drioli, E., Giorno, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–2. ISBN 978-3-642-40872-4. [Google Scholar]
- Gallucci, F.; De Falco, M.; Tosti, S.; Marrelli, L.; Basile, A. The Effect of the Hydrogen Flux Pressure and Temperature Dependence Factors on the Membrane Reactor Performances. Int. J. Hydrogen Energy 2007, 32, 4052–4058. [Google Scholar] [CrossRef]
- Ma, Y.H. Hydrogen Separation Membranes. In Advanced Membrane Technology and Applications; Wiley: Hoboken, NJ, USA, 2008; pp. 671–681. ISBN 978-0-471-73167-2. [Google Scholar]
- Mejdell, A.L.; Klette, H.; Ramachandran, A.; Borg, A.; Bredesen, R. Hydrogen Permeation of Thin, Free-Standing Pd/Ag23% Membranes before and after Heat Treatment in Air. J. Membr. Sci. 2008, 307, 96–104. [Google Scholar] [CrossRef]
- Daynes, H.A. The Process of Diffusion through a Rubber Membrane. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1920, 97, 286–307. [Google Scholar] [CrossRef]
- Yuan, M.; Lee, K.; Van Campen, D.G.; Liguori, S.; Toney, M.F.; Wilcox, J. Hydrogen Purification in Palladium-Based Membranes: An Operando X-Ray Diffraction Study. Ind. Eng. Chem. Res. 2019, 58, 926–934. [Google Scholar] [CrossRef]
- Wang, D.; Flanagan, T.B.; Shanahan, K.L. Permeation of Hydrogen through Pre-Oxidized Pd Membranes in the Presence and Absence of CO. J. Alloys Compd. 2004, 372, 158–164. [Google Scholar] [CrossRef]
- Gorbunov, S.V.; Kannykin, S.V.; Penkina, T.N.; Roshan, N.R.; Chustov, E.M.; Burkhanov, G.S. Palladium–Lead Alloys for the Purification of Hydrogen-Containing Gas Mixtures and the Separation of Hydrogen from Them. Russ. Metall. Met. 2017, 2017, 54–59. [Google Scholar] [CrossRef]
- Keurentjes, J.T.F.; Gielens, F.C.; Tong, H.D.; Van Rijn, C.J.M.; Vorstman, M.A.G. High-Flux Palladium Membranes Based on Microsystem Technology. Ind. Eng. Chem. Res. 2004, 43, 4768–4772. [Google Scholar] [CrossRef]
- Lundin, S.-T.B.; Yamaguchi, T.; Wolden, C.A.; Oyama, S.T.; Way, J.D. The Role (or Lack Thereof) of Nitrogen or Ammonia Adsorption-Induced Hydrogen Flux Inhibition on Palladium Membrane Performance. J. Membr. Sci. 2016, 514, 65–72. [Google Scholar] [CrossRef]
- Yan, Y.; Li, F.; Wang, D.; Huang, X.; Zhu, J.; Zhu, H.; Wang, X.; Tang, T. Determining Flux-Limiting Mechanism of Hydrogen Permeation through Palladium Membrane by n Value. Int. J. Hydrogen Energy 2024, 55, 1122–1130. [Google Scholar] [CrossRef]
- Budhi, Y.W.; Irawan, H.K.; Fitri, R.A.; Wibisono, T.A.S.E.; Restiawaty, E.; Miyamoto, M.; Uemiya, S. Effect of Co-Existing Gases on Hydrogen Permeation through a Pd82–Ag18/α-Al2O3 Membrane during Transient Start-Up. Heliyon 2023, 9, e16979. [Google Scholar] [CrossRef]
- Petr, S.; Lukas, K.; Tomas, J. Selectivity and Separation Factor for Components During Multicomponent Membrane Gas Separation. Chem. Eng. Trans. 2022, 92, 109–114. [Google Scholar] [CrossRef]
- Koros, W.J.; Ma, Y.H.; Shimidzu, T. Terminology for Membranes and Membrane Processes (IUPAC Recommendations 1996). Pure Appl. Chem. 1996, 68, 1479–1489. [Google Scholar] [CrossRef]
- Shirasaki, Y.; Tsuneki, T.; Ota, Y.; Yasuda, I.; Tachibana, S.; Nakajima, H.; Kobayashi, K. Development of Membrane Reformer System for Highly Efficient Hydrogen Production from Natural Gas. Int. J. Hydrogen Energy 2009, 34, 4482–4487. [Google Scholar] [CrossRef]
- Maier, W.F.; Stöwe, K.; Sieg, S. Combinatorial and High-Throughput Materials Science. Angew. Chem. Int. Ed. 2007, 46, 6016–6067. [Google Scholar] [CrossRef] [PubMed]
- Potyrailo, R.; Rajan, K.; Stoewe, K.; Takeuchi, I.; Chisholm, B.; Lam, H. Combinatorial and High-Throughput Screening of Materials Libraries: Review of State of the Art. ACS Comb. Sci. 2011, 13, 579–633. [Google Scholar] [CrossRef]
- Fleutot, B.; Miller, J.B.; Gellman, A.J. Apparatus for Deposition of Composition Spread Alloy Films: The Rotatable Shadow Mask. J. Vac. Sci. Technol. Vac. Surf. Films 2012, 30, 061511. [Google Scholar] [CrossRef]
- Yin, C.; Guo, Z.; Gellman, A.J. Surface Segregation Across Ternary Alloy Composition Space: CuxAuyPd1−x−y. J. Phys. Chem. C 2020, 124, 10605–10614. [Google Scholar] [CrossRef]
- Ludwig, A. Discovery of New Materials Using Combinatorial Synthesis and High-Throughput Characterization of Thin-Film Materials Libraries Combined with Computational Methods. Npj Comput. Mater. 2019, 5, 70. [Google Scholar] [CrossRef]
- Lewis, A.; Zhao, H.; Hopkins, S. Designing and Validating Ternary Pd Alloys for Optimum Sulfur/Carbon Resistance in Hydrogen Separation and Carbon Capture Membrane Systems Using High-Throughput Combinatorial Methods; Cornell University: Ithaca, NY, USA; Georgia Institute of Technology: Atlanta, GA, USA; Colorado School of Mines: Golden, CO, USA, 2014; p. 1172598. [Google Scholar]
- Gregoire, J.M.; van Dover, R.B.; Jin, J.; DiSalvo, F.J.; Abruña, H.D. Getter Sputtering System for High-Throughput Fabrication of Composition Spreads. Rev. Sci. Instrum. 2007, 78, 072212. [Google Scholar] [CrossRef] [PubMed]
- Pişkin, F. A Combinatorial Study on Hydrogen Separation Membranes. Çoğulcu yaklaşımla hidrojen ayırıcı membranların geliştirilmesi. Ph.D. Thesis, Middle East Technical University, Çankaya/Ankara, Türkiye, 2018. [Google Scholar]
- Pişkin, F.; Akyıldız, H.; Öztürk, T. Ti Modified Pd–Ag Membranes for Hydrogen Separation. Int. J. Hydrogen Energy 2015, 40, 7553–7558. [Google Scholar] [CrossRef]
- Pişkin, F.; Öztürk, T. Combinatorial Screening of Pd-Ag-Ni Membranes for Hydrogen Separation. J. Membr. Sci. 2017, 524, 631–636. [Google Scholar] [CrossRef]
- Pişkin, F.; Öztürk, T. Nb-Pd-Ti BCC Thin Films for Hydrogen Separation. J. Alloys Compd. 2019, 775, 411–418. [Google Scholar] [CrossRef]
- Köse, M.M.; Pişkin, F.; Öztürk, T. Development of Hydrogen Separation Membrane in Palladium Based Ternary Systems. Master’s Thesis, Middle East Technical University, Ankara, Türkiye, 2022. [Google Scholar]
- Tarditi, A.M.; Imhoff, C.; Braun, F.; Miller, J.B.; Gellman, A.J.; Cornaglia, L. PdCuAu Ternary Alloy Membranes: Hydrogen Permeation Properties in the Presence of H2S. J. Membr. Sci. 2015, 479, 246–255. [Google Scholar] [CrossRef]
- Priyadarshini, D.; Kondratyuk, P.; Picard, Y.N.; Morreale, B.D.; Gellman, A.J.; Miller, J.B. High-Throughput Characterization of Surface Segregation in CuxPd1−x Alloys. J. Phys. Chem. C 2011, 115, 10155–10163. [Google Scholar] [CrossRef]
- Yu, X.; Gellman, A.J. Suppression of B2 Phase in Pd Cu1- Alloy Thin Films. Thin Solid Films 2018, 668, 50–55. [Google Scholar] [CrossRef]
- den Broeder, F.J.A.; van der Molen, S.J.; Kremers, M.; Huiberts, J.N.; Nagengast, D.G.; van Gogh, A.T.M.; Huisman, W.H.; Koeman, N.J.; Dam, B.; Rector, J.H.; et al. Visualization of Hydrogen Migration in Solids Using Switchable Mirrors. Nature 1998, 394, 656–658. [Google Scholar] [CrossRef]
- Huiberts, J.N.; Griessen, R.; Rector, J.H.; Wijngaarden, R.J.; Dekker, J.P.; de Groot, D.G.; Koeman, N.J. Yttrium and Lanthanum Hydride Films with Switchable Optical Properties. Nature 1996, 380, 231–234. [Google Scholar] [CrossRef]
- Iannuzzi, D.; Lisanti, M.; Capasso, F. Effect of Hydrogen-Switchable Mirrors on the Casimir Force. Proc. Natl. Acad. Sci. USA 2004, 101, 4019–4023. [Google Scholar] [CrossRef] [PubMed]
- Rosenbaum, T.F.; Hoekstra, A.F. Ultraviolet Triggered Switchable Mirrors. Adv. Mater. 2002, 14, 247–250. [Google Scholar] [CrossRef]
- Griessen, R.; Giebels, I.A.M.E.; Dam, B. Optical Properties of Metal-Hydrides: Switchable Mirrors; Vrije Universiteit: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Gremaud, R.; Broedersz, C.P.; Borsa, D.M.; Borgschulte, A.; Mauron, P.; Schreuders, H.; Rector, J.H.; Dam, B.; Griessen, R. Hydrogenography: An Optical Combinatorial Method to Find New Light-Weight Hydrogen-Storage Materials. Adv. Mater. 2007, 19, 2813–2817. [Google Scholar] [CrossRef]
- Manhard, A.; von Toussaint, U.; Sand, P.; Stienecker, M. Visualizing Spatially Inhomogeneous Hydrogen Isotope Diffusion by Hydrogenography. Nucl. Mater. Energy 2023, 36, 101498. [Google Scholar] [CrossRef]
- Gremaud, R.; Slaman, M.; Schreuders, H.; Dam, B.; Griessen, R. An Optical Method to Determine the Thermodynamics of Hydrogen Absorption and Desorption in Metals. Appl. Phys. Lett. 2007, 91, 231916. [Google Scholar] [CrossRef]
- Borgschulte, A.; Lohstroh, W.; Westerwaal, R.J.; Schreuders, H.; Rector, J.H.; Dam, B.; Griessen, R. Combinatorial Method for the Development of a Catalyst Promoting Hydrogen Uptake. J. Alloys Compd. 2005, 404–406, 699–705. [Google Scholar] [CrossRef]
- de Man, S.; Gonzalez-Silveira, M.; Visser, D.; Bakker, R.; Schreuders, H.; Baldi, A.; Dam, B.; Griessen, R. Combinatorial Method for Direct Measurements of the Intrinsic Hydrogen Permeability of Separation Membrane Materials. J. Membr. Sci. 2013, 444, 70–76. [Google Scholar] [CrossRef]
- Westerwaal, R.J.; Den Besten, C.; Slaman, M.; Dam, B.; Nanu, D.E.; Böttger, A.J.; Haije, W.G. High Throughput Screening of Pd-Alloys for H2 Separation Membranes Studied by Hydrogenography and CVM. Int. J. Hydrogen Energy 2011, 36, 1074–1082. [Google Scholar] [CrossRef][Green Version]
- Westerwaal, R.J.; Bouman, E.A.; Haije, W.G.; Schreuders, H.; Dutta, S.; Wu, M.Y.; Boelsma, C.; Ngene, P.; Basak, S.; Dam, B. The Hydrogen Permeability of Pd–Cu Based Thin Film Membranes in Relation to Their Structure: A Combinatorial Approach. Int. J. Hydrogen Energy 2015, 40, 3932–3943. [Google Scholar] [CrossRef]
- Czitrom, V. One-Factor-at-a-Time Versus Designed Experiments. Am. Stat. Assoc. 1999, 53, 126–131. [Google Scholar] [CrossRef]
- Potyrailo, R.A.; Mirsky, V.M. Combinatorial and High-Throughput Development of Sensing Materials: The First 10 Years. Chem. Rev. 2008, 108, 770–813. [Google Scholar] [CrossRef] [PubMed]
- Agnolin, S.; Gallucci, F. Unravelling the Effects of Surface Modification Pre-Treatments on Porous Hastelloy X Supports for H2 Selective Pd-Based Membranes Preparation with a Statistical Approach. J. Membr. Sci. 2024, 700, 122690. [Google Scholar] [CrossRef]
- Chen, W.-H.; Carrera Uribe, M.; Kwon, E.E.; Lin, K.-Y.A.; Park, Y.-K.; Ding, L.; Saw, L.H. A Comprehensive Review of Thermoelectric Generation Optimization by Statistical Approach: Taguchi Method, Analysis of Variance (ANOVA), and Response Surface Methodology (RSM). Renew. Sustain. Energy Rev. 2022, 169, 112917. [Google Scholar] [CrossRef]
- Chen, W.-H.; Wu, D.-R.; Chang, M.-H.; Rajendran, S.; Ong, H.C.; Lin, K.-Y.A. Modeling of Hydrogen Separation through Pd Membrane with Vacuum Pressure Using Taguchi and Machine Learning Methods. Int. J. Hydrogen Energy 2024, in press. [Google Scholar] [CrossRef]
- Chen, W.-H.; Chen, K.-H.; Chein, R.-Y.; Ong, H.C.; Arunachalam, K.D. Optimization of Hydrogen Enrichment via Palladium Membrane in Vacuum Environments Using Taguchi Method and Normalized Regression Analysis. Int. J. Hydrogen Energy 2022, 47, 42280–42292. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, J. Robust Optimization of the Efficient Syngas Fractions in Entrained Flow Coal Gasification Using Taguchi Method and Response Surface Methodology. Int. J. Hydrogen Energy 2017, 42, 4908–4921. [Google Scholar] [CrossRef]
- Murdock, R.; Kauwe, S.; Wang, A.; Sparks, T. Is Domain Knowledge Necessary for Machine Learning Materials Properties? Integr. Mater. Manuf. Innov. 2020, 9, 221–227. [Google Scholar] [CrossRef]
- Wang, A.Y.-T.; Murdock, R.J.; Kauwe, S.K.; Oliynyk, A.O.; Gurlo, A.; Brgoch, J.; Persson, K.A.; Sparks, T.D. Machine Learning for Materials Scientists: An Introductory Guide toward Best Practices. Chem. Mater. 2020, 32, 4954–4965. [Google Scholar] [CrossRef]
- Chang, M.-H.; Chen, W.-H.; Wu, D.-R.; Ghorbani, M.; Rajendran, S.; Mohd Ashri Wan Daud, W. Analysis of Vacuum Operation on Hydrogen Separation from H2/H2O Mixture via Pd Membrane Using Taguchi Method, Response Surface Methodology, and Multivariate Adaptive Regression Splines. Energy Convers. Manag. X 2024, 23, 100645. [Google Scholar] [CrossRef]
- Chen, W.-H.; Chen, K.-H.; Kuo, J.-K.; Saravanakumar, A.; Chew, K.W. Optimization Analysis of Hydrogen Separation from an H2/CO2 Gas Mixture via a Palladium Membrane with a Vacuum Using Response Surface Methodology. Int. J. Hydrogen Energy 2022, 47, 42266–42279. [Google Scholar] [CrossRef]
- Kondratyuk, P.; Gumuslu, G.; Shukla, S.; Miller, J.B.; Morreale, B.D.; Gellman, A.J. A Microreactor Array for Spatially Resolved Measurement of Catalytic Activity for High-Throughput Catalysis Science. J. Catal. 2013, 300, 55–62. [Google Scholar] [CrossRef]
- Priyadarshini, D.; Kondratyuk, P.; Miller, J.B.; Gellman, A.J. Compact Tool for Deposition of Composition Spread Alloy Films. J. Vac. Sci. Technol. Vac. Surf. Films 2012, 30, 011503. [Google Scholar] [CrossRef]
- O’Brien, C.P.; Miller, J.B.; Morreale, B.D.; Gellman, A.J. The Kinetics of H2–D2 Exchange over Pd, Cu, and PdCu Surfaces. J. Phys. Chem. C 2011, 115, 24221–24230. [Google Scholar] [CrossRef]
- Kulkarni, S.R.; Lezcano, G.; Velisoju, V.K.; Realpe, N.; Castaño, P. Microkinetic Modeling to Decode Catalytic Reactions and Empower Catalytic Design. ChemCatChem 2024, 16, e202301720. [Google Scholar] [CrossRef]
- Fishtik, I.; Callaghan, C.A.; Datta, R. Reaction Route Graphs. I. Theory and Algorithm. J. Phys. Chem. B 2004, 108, 5671–5682. [Google Scholar] [CrossRef]
- Sholl, D.; Steckel, J.A.; Sholl, D.S.; Steckel, J.A. Density Functional Theory: A Practical Introduction; Wiley: Hoboken, NJ, USA, 2009; ISBN 978-0-470-37317-0. [Google Scholar]
- Ke, X.; Kramer, G.J.; Løvvik, O.M. The Influence of Electronic Structure on Hydrogen Absorption in Palladium Alloys. J. Phys. Condens. Matter 2004, 16, 6267–6277. [Google Scholar] [CrossRef]
- Lee, K.; Yuan, M.; Wilcox, J. Understanding Deviations in Hydrogen Solubility Predictions in Transition Metals through First-Principles Calculations. J. Phys. Chem. C 2015, 119, 19642–19653. [Google Scholar] [CrossRef]
- Kang, S.; Hao, S.; Sholl, D.S. Using First-Principles Models to Advance Development of Metal Membranes for High Temperature Hydrogen Purification. In Membrane Science and Technology; Elsevier: Amsterdam, The Netherlands, 2011; Volume 14, pp. 309–331. ISBN 978-0-444-53728-7. [Google Scholar]
- Ozdogan, E.; Wilcox, J. Investigation of H 2 and H 2 S Adsorption on Niobium- and Copper-Doped Palladium Surfaces. J. Phys. Chem. B 2010, 114, 12851–12858. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, P.; Yang, D.; Yang, P.; Liao, N. First-Principles Evaluation of Pd–Pt–Ag and Pd–Pt–Au Ternary Alloys as High Performance Membranes for Hydrogen Separation. Int. J. Hydrogen Energy 2024, 68, 607–613. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, Z.; Gellman, A.J.; Kitchin, J.R. Simulating Segregation in a Ternary Cu–Pd–Au Alloy with Density Functional Theory, Machine Learning, and Monte Carlo Simulations. J. Phys. Chem. C 2022, 126, 1800–1808. [Google Scholar] [CrossRef]
- Opetubo, O.; Ibitoye, A.I.; Oyinbo, S.T.; Jen, T.-C. Analysis of Hydrogen Embrittlement in Palladium–Copper Alloys Membrane from First Principal Method Using Density Functional Theory. Vacuum 2022, 205, 111439. [Google Scholar] [CrossRef]
- Kamakoti, P.; Sholl, D.S. Towards First Principles-Based Identification of Ternary Alloys for Hydrogen Purification Membranes. J. Membr. Sci. 2006, 279, 94–99. [Google Scholar] [CrossRef]
- Ko, W.-S.; Oh, J.-Y.; Shim, J.-H.; Suh, J.-Y.; Yoon, W.Y.; Lee, B.-J. Design of Sustainable V-Based Hydrogen Separation Membranes Based on Grain Boundary Segregation. Int. J. Hydrogen Energy 2014, 39, 12031–12044. [Google Scholar] [CrossRef]
- Fiolhais, C.; Nogueira, F.; Marques, M.A.L. (Eds.) A Primer in Density Functional Theory; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2003; Volume 620, ISBN 978-3-540-03083-6. [Google Scholar]
- Koch, W.; Holthausen, M.C. A Chemist’s Guide to Density Functional Theory, 2nd ed.; 5. Reprint; Wiley-VCH: Weinheim, Germany, 2008; ISBN 978-3-527-30372-4. [Google Scholar]
- Chen, Y.; Zhang, L.; Wang, H.; E, W. DeePKS: A Comprehensive Data-Driven Approach toward Chemically Accurate Density Functional Theory. J. Chem. Theory Comput. 2020, 17, 170–181. [Google Scholar] [CrossRef] [PubMed]
- Kaxiras, E. Atomic and Electronic Structure of Solids, 1st ed.; Cambridge University Press: Cambridge, UK, 2003; ISBN 978-0-521-81010-4. [Google Scholar]
- Cramer, C.J.; Truhlar, D.G. Density Functional Theory for Transition Metals and Transition Metal Chemistry. Phys. Chem. Chem. Phys. 2009, 11, 10757. [Google Scholar] [CrossRef] [PubMed]
- Rosenblatt, F. The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Jemaa, N.; Grandjean, B.P.A.; Kaliaguine, S. Diffusion Coefficient of Hydrogen in a Pd-Ag Membrane: Effect of Hydrogen Solubility. Can. J. Chem. Eng. 1995, 73, 405–410. [Google Scholar] [CrossRef]
- Takahashi, K.; Takahashi, L. An Introduction to Materials Informatics and Catalysts Informatics. In Materials Informatics and Catalysts Informatics; Springer Nature: Singapore, 2024; pp. 1–24. ISBN 978-981-97-0216-9. [Google Scholar]
- Warde, J.; Knowles, D.M. Application of Neural Networks to Mechanical Property Determination of Ni-Base Superalloys. ISIJ Int. 1999, 39, 1006–1014. [Google Scholar] [CrossRef][Green Version]
- Warde, J.; Knowles, D.M. Use of Neural Networks for Alloy Design. ISIJ Int. 1999, 39, 1015–1019. [Google Scholar] [CrossRef]
- De Pablo, J.J.; Jones, B.; Kovacs, C.L.; Ozolins, V.; Ramirez, A.P. The Materials Genome Initiative, the Interplay of Experiment, Theory and Computation. Curr. Opin. Solid State Mater. Sci. 2014, 18, 99–117. [Google Scholar] [CrossRef]
- Feldman, K.; Agnew, S.R. The Materials Genome Initiative at the National Science Foundation: A Status Report after the First Year of Funded Research. JOM 2014, 66, 336–344. [Google Scholar] [CrossRef]
- Howard, B. Hydrogen Permeance of Palladium–Copper Alloy Membranes over a Wide Range of Temperatures and Pressures. J. Membr. Sci. 2004, 241, 207–218. [Google Scholar] [CrossRef]
- Magnone, E.; Shin, M.C.; Lee, J.I.; Park, J.H. Relationship between Hydrogen Permeability and the Physical-Chemical Characteristics of Metal Alloy Membranes. J. Membr. Sci. 2023, 674, 121513. [Google Scholar] [CrossRef]
- Sayeed, H.M.; Mohanty, T.; Sparks, T.D. Annotating Materials Science Text: A Semi-Automated Approach for Crafting Outputs with Gemini Pro. Integr. Mater. Manuf. Innov. 2024, 13, 445–452. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Chen, F.L.; Furukawa, M.; Mine, K. X-Ray Studies of the Absorption of Hydrogen by Palladium-Rich Pd (Tb, Tm, Lu) Alloys. J. Common Met. 1990, 159, 191–198. [Google Scholar] [CrossRef]
- Ward, L.; Dunn, A.; Faghaninia, A.; Zimmermann, N.E.R.; Bajaj, S.; Wang, Q.; Montoya, J.; Chen, J.; Bystrom, K.; Dylla, M.; et al. Matminer: An Open Source Toolkit for Materials Data Mining. Comput. Mater. Sci. 2018, 152, 60–69. [Google Scholar] [CrossRef]
- Dunn, A.; Wang, Q.; Ganose, A.; Dopp, D.; Jain, A. Benchmarking Materials Property Prediction Methods: The Matbench Test Set and Automatminer Reference Algorithm. Npj Comput. Mater. 2020, 6, 138. [Google Scholar] [CrossRef]
- Song, F.; Guo, Z.; Mei, D. Feature Selection Using Principal Component Analysis. In Proceedings of the 2010 International Conference on System Science, Engineering Design and Manufacturing Informatization, Yichang, China, 12–14 November 2010; IEEE: New York, NY, USA, 2010; pp. 27–30. [Google Scholar]
- Ouyang, R.; Curtarolo, S.; Ahmetcik, E.; Scheffler, M.; Ghiringhelli, L.M. SISSO: A Compressed-Sensing Method for Identifying the Best Low-Dimensional Descriptor in an Immensity of Offered Candidates. Phys. Rev. Mater. 2018, 2, 083802. [Google Scholar] [CrossRef]
- Liu, L.C.; Wang, J.W.; He, Y.H.; Gong, H.R. Solubility, Diffusivity, and Permeability of Hydrogen at PdCu Phases. J. Membr. Sci. 2017, 542, 24–30. [Google Scholar] [CrossRef]
- Liu, L.C.; Gong, H.R.; Zhou, S.F.; Gong, X. Adsorption, Diffusion, and Permeation of Hydrogen at PdCu Surfaces. J. Membr. Sci. 2019, 588, 117206. [Google Scholar] [CrossRef]
- Nayebossadri, S.; Speight, J.D.; Book, D. Pd–Cu–M (M = Y, Ti, Zr, V, Nb, and Ni) Alloys for the Hydrogen Separation Membrane. ACS Appl. Mater. Interfaces 2017, 9, 2650–2661. [Google Scholar] [CrossRef] [PubMed]
- Tosques, J.; Honrado Guerreiro, B.; Martin, M.H.; Roué, L.; Guay, D. Hydrogen Solubility of Bcc PdCu and PdCuAg Alloys Prepared by Mechanical Alloying. J. Alloys Compd. 2017, 698, 725–730. [Google Scholar] [CrossRef]
- Semidey-Flecha, L.; Ling, C.; Sholl, D.S. Detailed First-Principles Models of Hydrogen Permeation through PdCu-Based Ternary Alloys. J. Membr. Sci. 2010, 362, 384–392. [Google Scholar] [CrossRef]
- Fatima; Liao, Y.; Tolba, S.A.; Ruiz Pestana, L.A.; Xia, W. Electronic Structure and Density Functional Theory. In Fundamentals of Multiscale Modeling of Structural Materials; Elsevier: Amsterdam, The Netherlands, 2023; pp. 3–35. ISBN 978-0-12-823021-3. [Google Scholar]
- Løvvik, O.M.; Peters, T.A.; Bredesen, R. First-Principles Calculations on Sulfur Interacting with Ternary Pd–Ag-Transition Metal Alloy Membrane Alloys. J. Membr. Sci. 2014, 453, 525–531. [Google Scholar] [CrossRef]
- Han, Z.; Xu, K.; Liao, N.; Xue, W. Theoretical Investigations of Permeability and Selectivity of Pd–Cu and Pd–Ni Membranes for Hydrogen Separation. Int. J. Hydrogen Energy 2021, 46, 23715–23722. [Google Scholar] [CrossRef]
- Semidey-Flecha, L.; Sholl, D.S. Combining Density Functional Theory and Cluster Expansion Methods to Predict H2 Permeance through Pd-Based Binary Alloy Membranes. J. Chem. Phys. 2008, 128, 144701. [Google Scholar] [CrossRef]
- Ling, C.; Semidey-Flecha, L.; Sholl, D.S. First-Principles Screening of PdCuAg Ternary Alloys as H2 Purification Membranes. J. Membr. Sci. 2011, 371, 189–196. [Google Scholar] [CrossRef]
- Stergiou, K.; Ntakolia, C.; Varytis, P.; Koumoulos, E.; Karlsson, P.; Moustakidis, S. Enhancing Property Prediction and Process Optimization in Building Materials through Machine Learning: A Review. Comput. Mater. Sci. 2023, 220, 112031. [Google Scholar] [CrossRef]
- Al-Mufachi, N.A.; Steinberger-Wilckens, R. X-Ray Diffraction Study on the Effects of Hydrogen on Pd60Cu40 Wt% Foil Membranes. J. Membr. Sci. 2018, 545, 266–274. [Google Scholar] [CrossRef]
- Lundin, S.-T.B.; Patki, N.S.; Fuerst, T.F.; Wolden, C.A.; Way, J.D. Inhibition of Hydrogen Flux in Palladium Membranes by Pressure–Induced Restructuring of the Membrane Surface. J. Membr. Sci. 2017, 535, 70–78. [Google Scholar] [CrossRef]
- Ferrin, P.; Kandoi, S.; Nilekar, A.U.; Mavrikakis, M. Hydrogen Adsorption, Absorption and Diffusion on and in Transition Metal Surfaces: A DFT Study. Surf. Sci. 2012, 606, 679–689. [Google Scholar] [CrossRef]
- Zhu, Q.; Huang, W.; Huang, C.; Gao, L.; Su, Y.; Qiao, L. The d Band Center as an Indicator for the Hydrogen Solution and Diffusion Behaviors in Transition Metals. Int. J. Hydrogen Energy 2022, 47, 38445–38454. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Theoretical Surface Science and Catalysis—Calculations and Concepts. In Advances in Catalysis; Elsevier: Amsterdam, The Netherlands, 2000; Volume 45, pp. 71–129. ISBN 978-0-12-007845-5. [Google Scholar]
- Zhou, Y.J.; Zhang, Y.; Wang, Y.L.; Chen, G.L. Solid Solution Alloys of AlCoCrFeNiTix with Excellent Room-Temperature Mechanical Properties. Appl. Phys. Lett. 2007, 90, 181904. [Google Scholar] [CrossRef]
- MacLeod, B.P.; Parlane, F.G.L.; Rupnow, C.C.; Dettelbach, K.E.; Elliott, M.S.; Morrissey, T.D.; Haley, T.H.; Proskurin, O.; Rooney, M.B.; Taherimakhsousi, N.; et al. A Self-Driving Laboratory Advances the Pareto Front for Material Properties. Nat. Commun. 2022, 13, 995. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Zheng, K. Methods, Progresses, and Opportunities of Materials Informatics. InfoMat 2023, 5, e12425. [Google Scholar] [CrossRef]
- Lookman, T.; Balachandran, P.V.; Xue, D.; Yuan, R. Active Learning in Materials Science with Emphasis on Adaptive Sampling Using Uncertainties for Targeted Design. Npj Comput. Mater. 2019, 5, 21. [Google Scholar] [CrossRef]
- Mohanty, T.; Chandran, K.S.R.; Sparks, T.D. Machine Learning Guided Optimal Composition Selection of Niobium Alloys for High Temperature Applications. APL Mach. Learn. 2023, 1, 036102. [Google Scholar] [CrossRef]
- Halpren, E.; Yao, X.; Chen, Z.W.; Singh, C.V. Machine Learning Assisted Design of BCC High Entropy Alloys for Room Temperature Hydrogen Storage. Acta Mater. 2024, 270, 119841. [Google Scholar] [CrossRef]
- Cao, B.; Su, T.; Yu, S.; Li, T.; Zhang, T.; Zhang, J.; Dong, Z.; Zhang, T.-Y. Active Learning Accelerates the Discovery of High Strength and High Ductility Lead-Free Solder Alloys. Mater. Des. 2024, 241, 112921. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).