Evaluation of Mixing Process in Batch Mixer Using CFD-DEM Simulation and Automatic Post-Processing Method
Abstract
1. Introduction
2. CFD-DEM Coupling Simulation
2.1. Cohesive Force Model
2.2. DEM Control Equations
2.3. CFD Control Equations
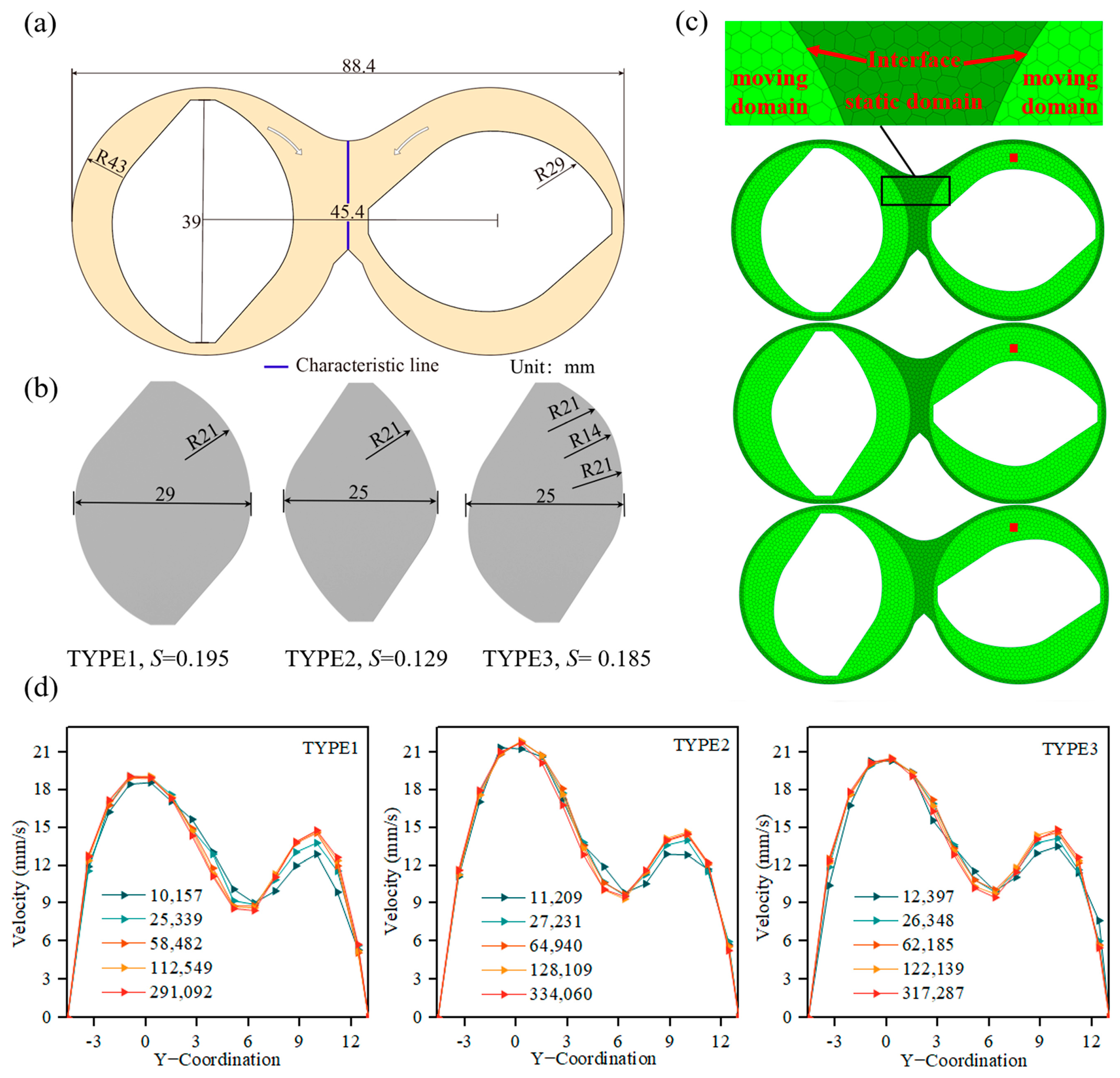
2.4. Mixing Process Simulation
3. Quantitative Evaluation of Mixing Process
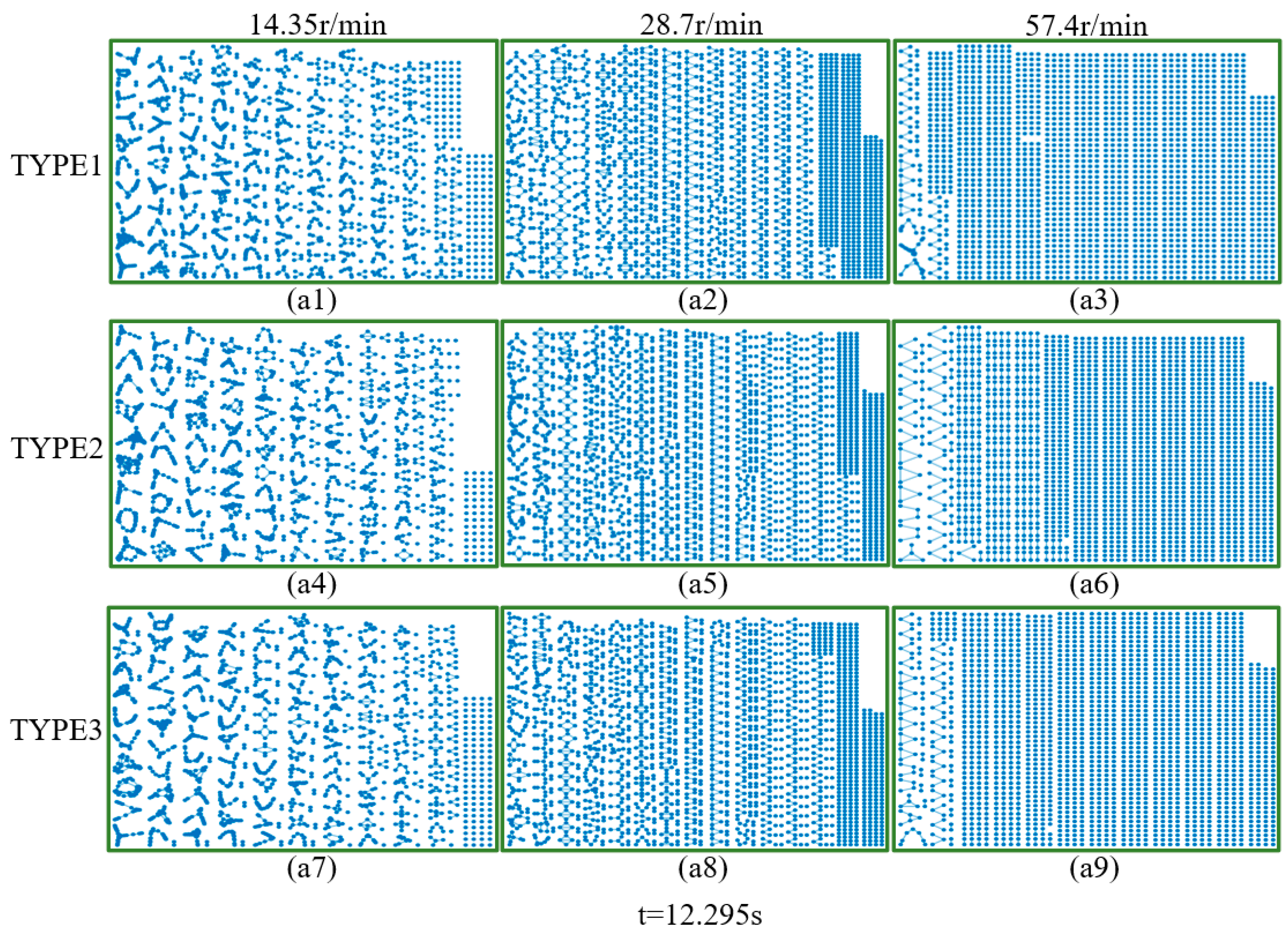
3.1. Breakup Process
3.2. Distributive Process
4. Results and Discussions
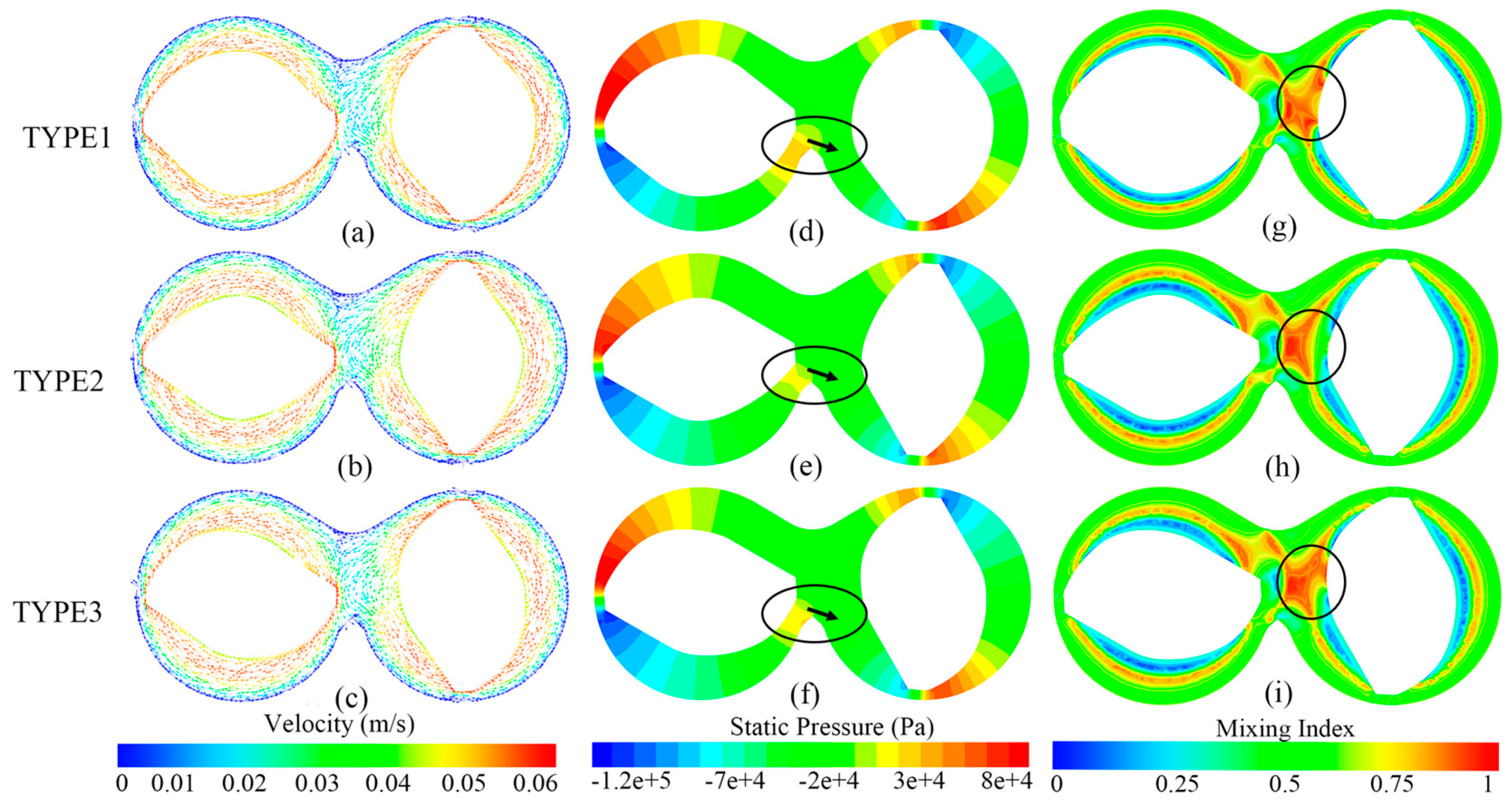
4.1. Flow Field and Mixing Process
4.2. Mixing Process
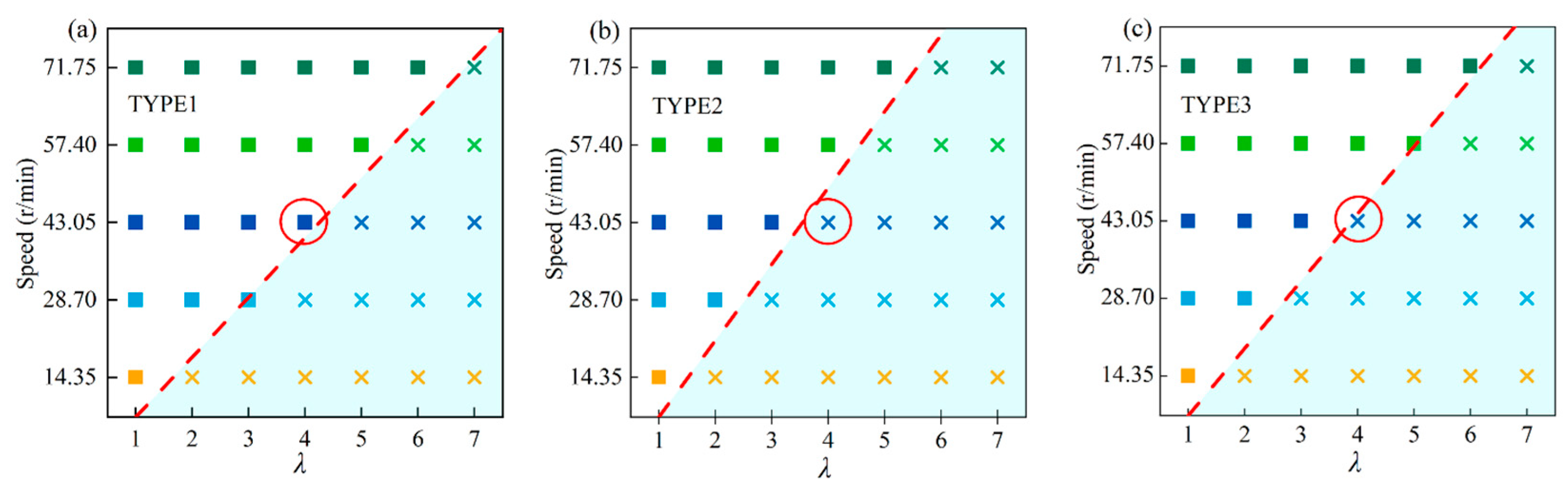
4.3. Evaluation and Kinematics Analyzation
4.4. Breakup-Line
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boudenne, A.; Ibos, L.; Fois, M.; Majesté, J.; Géhin, E. Electrical and thermal behavior of polypropylene filled with copper particles. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1545–1554. [Google Scholar] [CrossRef]
- Hernandez, F.H.; Rangel, R.H. Breakup of drops in simple shear flows with high-confinement geometry. Comput. Fluids 2017, 146, 23–41. [Google Scholar] [CrossRef]
- Avolio, R.; Castaldo, R.; Avella, M.; Cocca, M.; Gentile, G.; Fiori, S.; Errico, M.E. PLA-based plasticized nanocomposites: Effect of polymer/plasticizer/filler interactions on the time evolution of properties. Compos. Part B Eng. 2018, 152, 267–274. [Google Scholar] [CrossRef]
- Azoug, A.; Nevière, R.; Pradeilles-Duval, R.; Constantinescu, A. Influence of crosslinking and plasticizing on the viscoelasticity of highly filled elastomers. J. Appl. Polym. Sci. 2014, 131, 40392. [Google Scholar] [CrossRef]
- Gopalkrishnan, P.; Manas-Zloczower, I.; Feke, D. Investigating dispersion mechanisms in partially infiltrated agglomerates: Interstitial fluid effects. Powder Technol. 2005, 156, 111–119. [Google Scholar] [CrossRef]
- Fanelli, M.; Feke, D.L.; Manas-Zloczower, I. Prediction of the dispersion of particle clusters in the nano-scale—Part II, unsteady shearing responses. Chem. Eng. Sci. 2006, 61, 4944–4956. [Google Scholar] [CrossRef]
- Pomchaitaward, C.; Manas-Zloczower, I.; Feke, D. Investigation of the dispersion of carbon black agglomerates of various sizes in simple-shear flows. Chem. Eng. Sci. 2003, 58, 1859–1865. [Google Scholar] [CrossRef]
- Potente, H.; Kretschmer, K.; Flecke, J. A physical-mathematical model for the dispersion process in continuous mixers. Polym. Eng. Sci. 2004, 42, 19–32. [Google Scholar] [CrossRef]
- Hosseini, M.S.; Nazockdast, H.; Anderson, P.D.; Meijer, H.E.H. Simulation of Agglomerate Dispersion in Cubic Cavity Flow. Macromol. Theory Simul. 2009, 18, 201–208. [Google Scholar] [CrossRef]
- Jiang, G.; Huang, H. Melt-compounding of PP/clay nanocomposite and relationship between its microstructure and shear strain in the flow field based on rheological analysis. Polym. Eng. Sci. 2011, 51, 2345–2352. [Google Scholar] [CrossRef]
- Wéry, F.; Vandewalle, L.A.; Marin, G.B.; Heynderickx, G.J.; Van Geem, K.M. Hydrodynamic CFD-DEM model validation in a gas–solid vortex unit. Chem. Eng. J. 2023, 455, 140529. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, S.; Kuang, S.; Luo, K.; Fan, J.; Yu, A. CFD-DEM modelling of hydraulic conveying of solid particles in a vertical pipe. Powder Technol. 2019, 354, 893–905. [Google Scholar] [CrossRef]
- Esgandari, B.; Golshan, S.; Zarghami, R.; Sotudeh-Gharebagh, R.; Chaouki, J. CFD-DEM analysis of the spouted fluidized bed with non-spherical particles. Can. J. Chem. Eng. 2021, 99, 2303–2319. [Google Scholar] [CrossRef]
- Frungieri, G.; Boccardo, G.; Buffo, A.; Marchisio, D.; Karimi-Varzaneh, H.A.; Vanni, M. A CFD-DEM approach to study the breakup of fractal agglomerates in an internal mixer. Can. J. Chem. Eng. 2020, 98, 1880–1892. [Google Scholar] [CrossRef]
- Manas-Zloczower, I.; Cheng, H.F. Influence of design on mixing efficiency in the kneading disc region of co-rotating twin screw extruders. J. Reinf. Plast Compos. 1998, 17, 1076–1086. [Google Scholar] [CrossRef]
- Connelly, R.K.; Kokini, J.L. Examination of the mixing ability of single and twin screw mixers using 2D finite element method simulation with particle tracking. J. Food Eng. 2007, 79, 956–969. [Google Scholar] [CrossRef]
- Mewes, D. The kinematics of mixing: Stretching, chaos, and transport. AlChE J. 1990, 38, 316–317. [Google Scholar]
- Danckwerts PVJIICE. The definition and measurement of some characteristics of mixtures. Appl. Sci. Res. 1981, 3, 268–287. [Google Scholar]
- Nakayama, Y.; Kajiwara, T.; Masaki, T. Strain mode of general flow: Characterization and implications for flow pattern structures. AIChE J. 2016, 62, 2563–2569. [Google Scholar] [CrossRef]
- Ferrás, L.L.; Fernandes, C.; Semyonov, D.; Nóbrega, J.M.; Covas, J.A. Dispersion of Graphite Nanoplates in Polypropylene by Melt Mixing: The Effects of Hydrodynamic Stresses and Residence Time. Polymers 2021, 13, 102. [Google Scholar] [CrossRef]
- Berzin, F.; Vergnes, B.; Lafleur, P.G.; Grmela, M. A theoretical approach to solid filler dispersion in a twin-screw extruder. Polym. Eng. Sci. 2002, 42, 473–481. [Google Scholar] [CrossRef]
- Labib, M.; Philpott, D.N.; Wang, Z.; Nemr, C.; Chen, J.B.; Sargent, E.H.; Kelley, S.O. Magnetic Ranking Cytometry: Profiling Rare Cells at the Single-Cell Level. Accounts Chem. Res. 2020, 53, 1445–1457. [Google Scholar] [CrossRef] [PubMed]
- Frungieri, G.; Boccardo, G.; Buffo, A.; Karimi–Varzaneh, H.A.; Vanni, M. CFD-DEM characterization and population balance modelling of a dispersive mixing process. Chem. Eng. Sci. 2022, 260, 117859. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Guo, Y.; Wassgren, C.; Curtis, J.S.; Xu, D. A bonded sphero-cylinder model for the discrete element simulation of elasto-plastic fibers. Chem. Eng. Sci. 2018, 175, 118–129. [Google Scholar] [CrossRef]
- Vallejos, J.A.; Salinas, J.M.; Delonca, A.; Ivars, D.M. Calibration and Verification of Two Bonded-Particle Models for Simulation of Intact Rock Behavior. Int. J. Géoméch. 2017, 17, 06016030. [Google Scholar] [CrossRef]
- Hare, C.; Ghadiri, M.; Guillard, N.; Bosworth, T.; Egan, G. Analysis of milling of dry compacted ribbons by distinct element method. Chem. Eng. Sci. 2016, 149, 204–214. [Google Scholar] [CrossRef]
- Ge, R.; Ghadiri, M.; Bonakdar, T.; Zheng, Q.; Zhou, Z.; Larson, I.; Hapgood, K. Deformation of 3D printed agglomerates: Multiscale experimental tests and DEM simulation. Chem. Eng. Sci. 2020, 217, 115526. [Google Scholar] [CrossRef]
- Giménez, C.S.; Finke, B.; Nowak, C.; Schilde, C.; Kwade, A. Structural and mechanical characterization of lithium-ion battery electrodes via DEM simulations. Adv. Powder Technol. 2018, 29, 2312–2321. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 2003, 20, 153–159. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, A.; Yu, X.; Liu, Z.; Tang, X.; Wang, S. Experimental tests and CFD simulations of a horizontal wave flow turbine under the joint waves and currents. Ocean Eng. 2021, 237, 109480. [Google Scholar] [CrossRef]
- Greaves, D. A quadtree adaptive method for simulating fluid flows with moving interfaces. J. Comput. Phys. 2004, 194, 35–56. [Google Scholar] [CrossRef]
- Brown, S.; Ransley, E.; Greaves, D. Developing a coupled turbine thrust methodology for floating tidal stream concepts: Verification under prescribed motion. Renew. Energy 2020, 147, 529–540. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, X.; Feng, Z.; Cao, S.-J. Application of polyhedral meshing strategy in indoor environment simulation: Model accuracy and computing time. Indoor Built Environ. 2022, 31, 719–731. [Google Scholar] [CrossRef]
- Dizaji, F.F.; Marshall, J.S.; Grant, J.R. Collision and breakup of fractal particle agglomerates in a shear flow. J. Fluid Mech. 2019, 862, 592–623. [Google Scholar] [CrossRef]
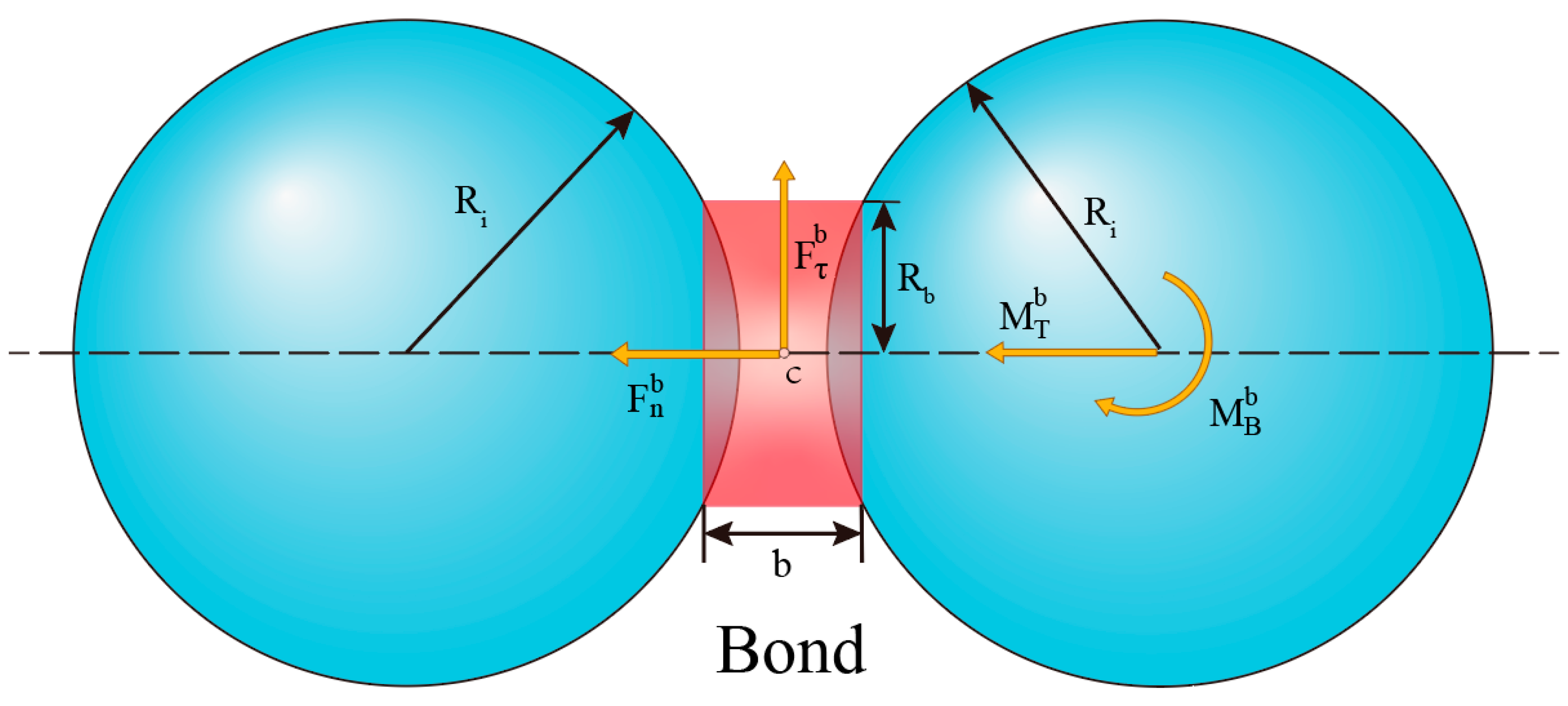




| Normal Stiffness per Area (N/m3) | Normal Stress Limit (Pa) | Tangential Stiffness per Area (N/m3) | Tangential Stress Limit (Pa) |
|---|---|---|---|
| λ × 1010 | λ × 109 | λ × 1010 | λ × 109 |
| Simulation Method | Parameters | Value |
|---|---|---|
| CFD | Melt Viscosity (Pa∙s) | 576 |
| Melt Density (Kg/m3) | 900 | |
| Time Step | 0.001 | |
| DEM | Shape | Sphere |
| Diameter (mm) | 0.2 | |
| Density (Kg/m3) | 2710 | |
| Restitution coefficient | 0.3 | |
| Distance Factor | 0.2 | |
| Damping Ratio | 0.1 | |
| Adhesive Distance | 0.1 | |
| Gap Scale Factor | 1.1 | |
| Time Step | 1 × 10−9 | |
| Particle number | 2120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Zhang, Z.; Xiang, J.; Zhao, H.; Jiao, F.; Chen, T.; Li, G. Evaluation of Mixing Process in Batch Mixer Using CFD-DEM Simulation and Automatic Post-Processing Method. Processes 2024, 12, 2840. https://doi.org/10.3390/pr12122840
Li G, Zhang Z, Xiang J, Zhao H, Jiao F, Chen T, Li G. Evaluation of Mixing Process in Batch Mixer Using CFD-DEM Simulation and Automatic Post-Processing Method. Processes. 2024; 12(12):2840. https://doi.org/10.3390/pr12122840
Chicago/Turabian StyleLi, Guangming, Zhenbang Zhang, Jiahong Xiang, Haili Zhao, Feng Jiao, Tao Chen, and Guo Li. 2024. "Evaluation of Mixing Process in Batch Mixer Using CFD-DEM Simulation and Automatic Post-Processing Method" Processes 12, no. 12: 2840. https://doi.org/10.3390/pr12122840
APA StyleLi, G., Zhang, Z., Xiang, J., Zhao, H., Jiao, F., Chen, T., & Li, G. (2024). Evaluation of Mixing Process in Batch Mixer Using CFD-DEM Simulation and Automatic Post-Processing Method. Processes, 12(12), 2840. https://doi.org/10.3390/pr12122840






