Finite Element Simulation of Aerosol Particle Trajectories in a Cantilever-Enhanced Photoacoustic Spectrometer for Characterization of Inertial Deposition Loss
Abstract
1. Introduction
2. Materials and Methods
2.1. Flow System of a CEPAS
2.2. Fluid Flow Model
2.3. Particle Trajectories Model
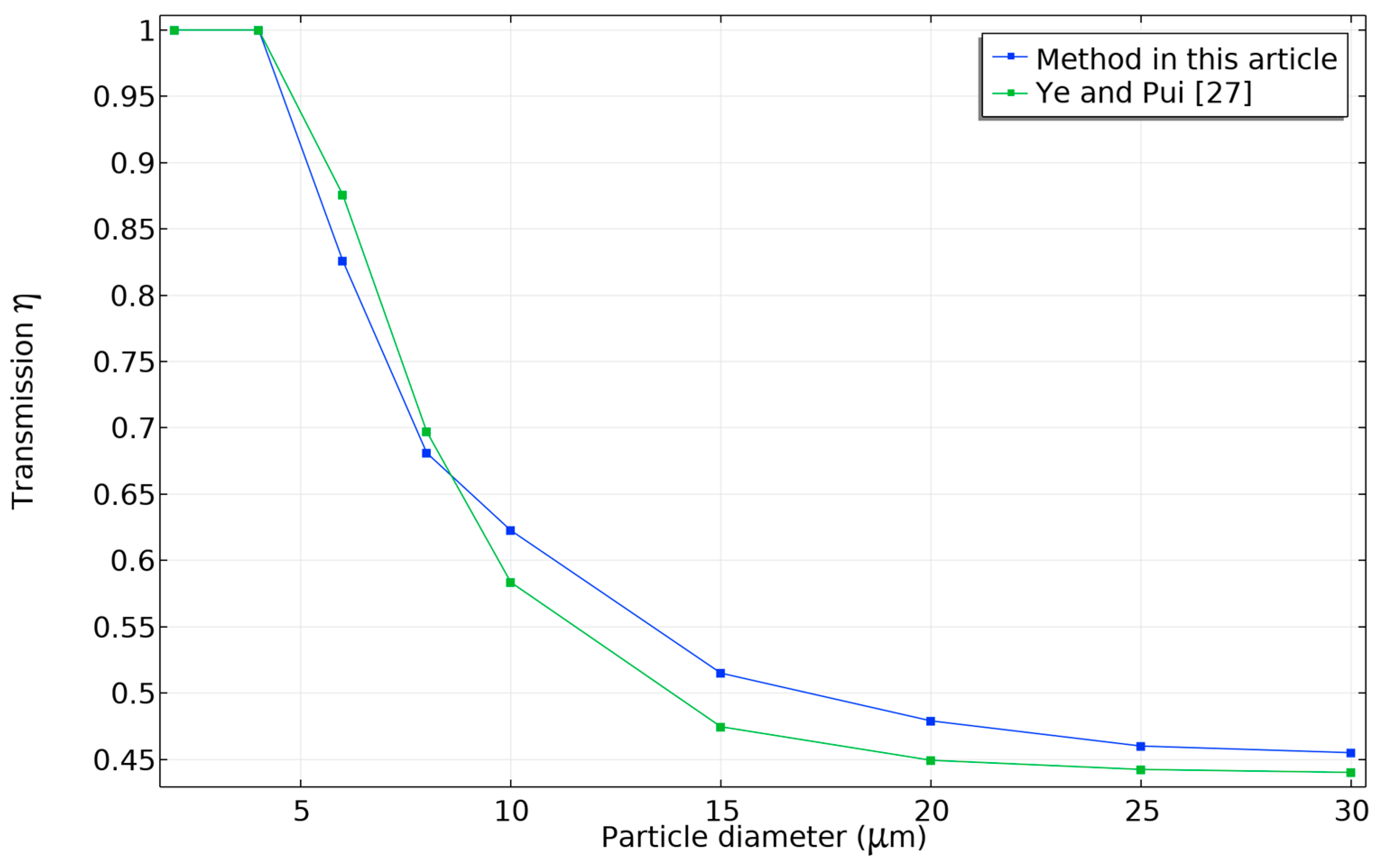
2.4. Validation Examples
3. Results and Discussion
3.1. Results for Validation Examples
3.2. Inertial Deposition in CEPAS
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Belyaev, S.P.; Levin, L.M. Techniques for Collection of Representative Aerosol Samples. J. Aerosol Sci. 1974, 5, 325–338. [Google Scholar] [CrossRef]
- Friedlander, S.K.; Johnstone, H.F. Deposition of Suspended Particles from Turbulent Gas Streams. Ind. Eng. Chem. 1957, 49, 1151–1156. [Google Scholar] [CrossRef]
- Tian, L.; Ahmadi, G. Particle Deposition in Turbulent Duct Flows—Comparisons of Different Model Predictions. J. Aerosol Sci. 2007, 38, 377–397. [Google Scholar] [CrossRef]
- Hangal, S.; Willeke, K. Aspiration Efficiency: Unified Model for All Forward Sampling Angles. Environ. Sci. Technol. 1990, 24, 688–691. [Google Scholar] [CrossRef]
- Kumar, P.; Fennell, P.; Symonds, J.; Britter, R. Treatment of Losses of Ultrafine Aerosol Particles in Long Sampling Tubes during Ambient Measurements. Atmos. Environ. 2008, 42, 8819–8826. [Google Scholar] [CrossRef]
- Okazaki, K.; Wiener, R.W.; Willeke, K. The Combined Effect of Aspiration and Transmission on Aerosol Sampling Accuracy for Horizontal Isoaxial Sampling. Atmos. Environ. (1967) 1987, 21, 1181–1185. [Google Scholar] [CrossRef]
- Linke, C.; Ibrahim, I.; Schleicher, N.; Hitzenberger, R.; Andreae, M.O.; Leisner, T.; Schnaiter, M. A Novel Single-Cavity Three-Wavelength Photoacoustic Spectrometer for Atmospheric Aerosol Research. Atmos. Meas. Tech. 2016, 9, 5331–5346. [Google Scholar] [CrossRef]
- Karhu, J.; Kuula, J.; Virkkula, A.; Timonen, H.; Vainio, M.; Hieta, T. Cantilever-Enhanced Photoacoustic Measurement of Light-Absorbing Aerosols. Aerosol Sci. Technol. 2021, 56, 92–100. [Google Scholar] [CrossRef]
- Murray, C.J.L.; Aravkin, A.Y.; Zheng, P.; Abbafati, C.; Abbas, K.M.; Abbasi-Kangevari, M.; Abd-Allah, F.; Abdelalim, A.; Abdollahi, M.; Abdollahpour, I.; et al. Global Burden of 87 Risk Factors in 204 Countries and Territories, 1990–2019: A Systematic Analysis for the Global Burden of Disease Study 2019. Lancet 2020, 396, 1223–1249. [Google Scholar] [CrossRef]
- Chen, J.; Hoek, G. Long-Term Exposure to PM and All-Cause and Cause-Specific Mortality: A Systematic Review and Meta-Analysis. Environ. Int. 2020, 143, 105974. [Google Scholar] [CrossRef]
- Lelieveld, J.; Pozzer, A.; Pöschl, U.; Fnais, M.; Haines, A.; Münzel, T. Loss of Life Expectancy from Air Pollution Compared to Other Risk Factors: A Worldwide Perspective. Cardiovasc. Res. 2020, 116, 1910–1917. [Google Scholar] [CrossRef] [PubMed]
- Chaurasiya, B.; Zhao, Y.-Y. Dry Powder for Pulmonary Delivery: A Comprehensive Review. Pharmaceutics 2021, 13, 31. [Google Scholar] [CrossRef] [PubMed]
- Drossinos, Y.; Stilianakis, N.I. What Aerosol Physics Tells Us about Airborne Pathogen Transmission. Aerosol Sci. Technol. 2020, 54, 639–643. [Google Scholar] [CrossRef]
- Zuo, Y.Y.; Uspal, W.E.; Wei, T. Airborne Transmission of COVID-19: Aerosol Dispersion, Lung Deposition, and Virus-Receptor Interactions. ACS Nano 2020, 14, 16502–16524. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Fan, X.; Zhao, Y.; Duan, C.; Zhou, C. Particles Movement Behavior and Apparent Density in Gas–Solid Fluidized Bed as Determined by an Electronic Dynamometer and Electrical Capacitance Tomography. Chem. Eng. J. 2022, 429, 132463. [Google Scholar] [CrossRef]
- Yu, B.; Peng, Y.; Luo, X.; Zhu, X.; Gong, H.; Liu, Y. Effects of Particle Wettability and Water Moisture on Separation Efficiency and Drop Size Distribution of Particle-Laden Droplets in Oil. Colloids Surf. A Physicochem. Eng. Asp. 2023, 659, 130790. [Google Scholar] [CrossRef]
- Brockmann, J.E. Aerosol Transport in Sampling Lines and Inlets. In Aerosol Measurement: Principles, Techniques, and Applications; Kulkarni, P., Baron, P.A., Willeke, K., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 68–105. ISBN 978-1-118-00168-4. [Google Scholar]
- Hapidin, D.A.; Saputra, C.; Maulana, D.S.; Munir, M.M.; Khairurrijal, K. Aerosol Chamber Characterization for Commercial Particulate Matter (PM) Sensor Evaluation. Aerosol Air Qual. Res. 2019, 19, 181–194. [Google Scholar] [CrossRef]
- Granek, H.; Gras, J.; Paterson, D. The Aerosol Transmission Efficiency of the Cape Grim Baseline Air Pollution Station 10 m Sampling Inlet. J. Aerosol Sci. 2003, 34, 1523–1537. [Google Scholar] [CrossRef]
- Reineking, A.; Porstendörfer, J. Measurements of Particle Loss Functions in a Differential Mobility Analyzer (TSI, Model 3071) for Different Flow Rates. Aerosol Sci. Technol. 1986, 5, 483–486. [Google Scholar] [CrossRef]
- Ren, J.; Tang, M.; Novoselac, A. Experimental Study to Quantify Airborne Particle Deposition onto and Resuspension from Clothing Using a Fluorescent-Tracking Method. Build. Environ. 2022, 209, 108580. [Google Scholar] [CrossRef]
- Novosselov, I.V.; Gorder, R.A.; Van Amberg, J.A.; Ariessohn, P.C. Design and Performance of a Low-Cost Micro-Channel Aerosol Collector. Aerosol Sci. Technol. 2014, 48, 822–830. [Google Scholar] [CrossRef]
- Allen, M.D.; Raabe, O.G. Slip Correction Measurements of Spherical Solid Aerosol Particles in an Improved Millikan Apparatus. Aerosol Sci. Technol. 1985, 4, 269–286. [Google Scholar] [CrossRef]
- Baron, P.A. Description of an Aerosol Calculator. In Proceedings of the Seventh International Aerosol Conference, Saint Paul, MN, USA, 10–15 September 2006; p. 555. [Google Scholar]
- von der Weiden, S.-L.; Drewnick, F.; Borrmann, S. Particle Loss Calculator—A New Software Tool for the Assessment of the Performance of Aerosol Inlet Systems. Atmos. Meas. Tech. 2009, 2, 479–494. [Google Scholar] [CrossRef]
- Pui, D.Y.H.; Romay-Novas, F.; Liu, B.Y.H. Experimental Study of Particle Deposition in Bends of Circular Cross Section. Aerosol Sci. Technol. 1987, 7, 301–315. [Google Scholar] [CrossRef]
- Ye, Y.; Pui, D.Y.H. Particle Deposition in a Tube with an Abrupt Contraction. J. Aerosol Sci. 1990, 21, 29–40. [Google Scholar] [CrossRef]
- Feng, J.Q. Aerosol Deposition in 90° Circular Tube Bends with Laminar Flows: Effects of Inertial Impaction and Gravitational Settling. Aerosol Sci. Eng. 2023, 7, 107–117. [Google Scholar] [CrossRef]
- Crane, R.I.; Evans, R.L. Inertial Deposition of Particles in a Bent Pipe. J. Aerosol Sci. 1977, 8, 161–170. [Google Scholar] [CrossRef]
- Gormley, P.G.; Kennedy, M. Diffusion from a Stream Flowing through a Cylindrical Tube. Proc. R. Ir. Academy. Sect. A Math. Phys. Sci. 1948, 52, 163–169. [Google Scholar]
- Grahn, P. COMSOL Models for Inertial Deposition of Particles in Laminar Flow, Zenodo: Geneva, Switzerland, 2024. [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grahn, P.; Kuula, J. Finite Element Simulation of Aerosol Particle Trajectories in a Cantilever-Enhanced Photoacoustic Spectrometer for Characterization of Inertial Deposition Loss. Processes 2024, 12, 2827. https://doi.org/10.3390/pr12122827
Grahn P, Kuula J. Finite Element Simulation of Aerosol Particle Trajectories in a Cantilever-Enhanced Photoacoustic Spectrometer for Characterization of Inertial Deposition Loss. Processes. 2024; 12(12):2827. https://doi.org/10.3390/pr12122827
Chicago/Turabian StyleGrahn, Patrick, and Joel Kuula. 2024. "Finite Element Simulation of Aerosol Particle Trajectories in a Cantilever-Enhanced Photoacoustic Spectrometer for Characterization of Inertial Deposition Loss" Processes 12, no. 12: 2827. https://doi.org/10.3390/pr12122827
APA StyleGrahn, P., & Kuula, J. (2024). Finite Element Simulation of Aerosol Particle Trajectories in a Cantilever-Enhanced Photoacoustic Spectrometer for Characterization of Inertial Deposition Loss. Processes, 12(12), 2827. https://doi.org/10.3390/pr12122827






