Optimal Air Flow Modeling in Real Healthcare Facilities for Quick Removal of Contaminated Air
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
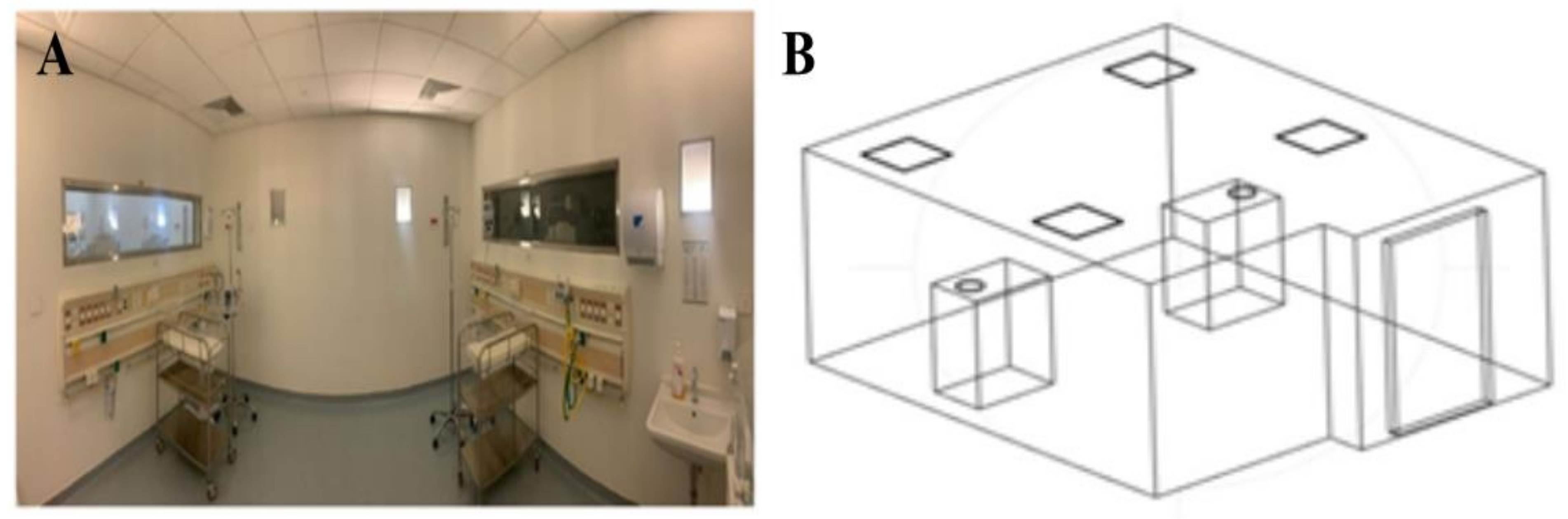
2.2. Three-Dimensional Model Construction
2.3. Simulation Design
3. Results
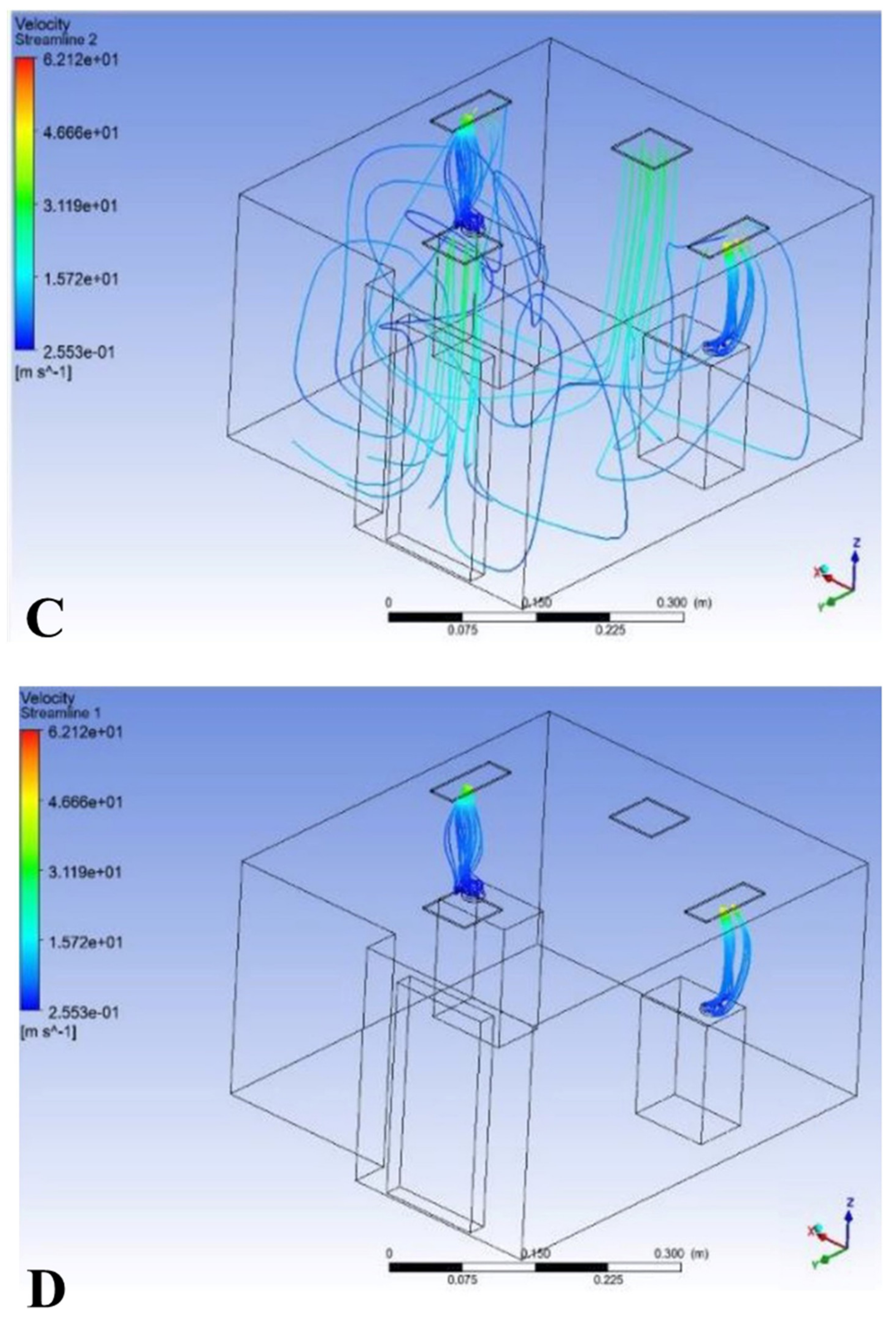
3.1. Result of Model 1
3.2. Results of Model 2
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Monegro, A.; Muppidi, V.; Regunath, H. Hospital Acquired Infections. In Cambridge Handbook of Psychology, Health and Medicine; Cambridge University Press: Cambridge, UK, 2022; pp. 736–738. [Google Scholar]
- Settimo, G.; Gola, M.; Capolongo, S. The relevance of indoor air quality in hospital settings: From an exclusively biological issue to a global approach in the Italian context. Atmosphere 2020, 11, 361. [Google Scholar] [CrossRef]
- Mohamadi, F.; Fazeli, A. A review on applications of CFD modeling in COVID-19 pandemic. Arch. Comput. Methods Eng. 2022, 29, 3567–3586. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.-X.; Cao, X.; Chen, Y.-P. An air distribution optimization of hospital wards for minimizing cross-infection. J. Clean. Prod. 2021, 279, 123431. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, F.; Samsudin, E.Z.; Ishak, A.R.; Sathasivam, J. Hospital indoor air quality and its relationships with building design, building operation, and occupant-related factors: A mini-review. Front. Public Health 2022, 10, 1067764. [Google Scholar] [CrossRef]
- Kanchongkittiphon, W.; Mendell, M.J.; Gaffin, J.M.; Wang, G.; Phipatanakul, W. Indoor environmental exposures and exacerbation of asthma: An update to the 2000 review by the Institute of Medicine. Environ. Health Perspect. 2015, 123, 6–20. [Google Scholar] [CrossRef] [PubMed]
- Baudet, A.; Baurès, E.; Guegan, H.; Blanchard, O.; Guillaso, M.; Le Cann, P.; Gangneux, J.-P.; Florentin, A. Indoor air quality in healthcare and care facilities: Chemical pollutants and microbiological contaminants. Atmosphere 2021, 12, 1337. [Google Scholar] [CrossRef]
- Tellier, R. Aerosol transmission of influenza A virus: A review of new studies. J. R. Soc. Interface 2009, 6 (Suppl. 6), S783–S790. [Google Scholar] [CrossRef] [PubMed]
- Morawska, L.; Cao, J. Airborne transmission of SARS-CoV-2: The world should face the reality. Environ. Int. 2020, 139, 105730. [Google Scholar] [CrossRef]
- Gralton, J.; Tovey, E.; McLaws, M.L.; Rawlinson, W.D. The role of particle size in aerosolised pathogen transmission: A review. J. Infect. 2011, 62, 1–13. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Roadmap to Improve and Ensure Good Indoor Ventilation in the Context of COVID-19; World Health Organization: Geneva, Switzerland, 2021. [Google Scholar]
- Bolashikov, Z.D.; Melikov, A.K. Methods for air cleaning and protection of building occupants from airborne pathogens. Build. Environ. 2009, 44, 1378–1385. [Google Scholar] [CrossRef] [PubMed]
- Aryal, P.; Leephakpreeda, T. CFD analysis on thermal comfort and indoor air quality affected by partitions in air-conditioned building. Appl. Mech. Mater. 2016, 836, 121–126. [Google Scholar] [CrossRef]
- Jia, L.-R.; Han, J.; Chen, X.; Li, Q.-Y.; Lee, C.-C.; Fung, Y.-H. Interaction between thermal comfort, indoor air quality and ventilation energy consumption of educational buildings: A comprehensive review. Buildings 2021, 11, 591. [Google Scholar] [CrossRef]
- Tsang, T.-W.; Mui, K.-W.; Wong, L.-T. Computational Fluid Dynamics (CFD) studies on airborne transmission in hospitals: A review on the research approaches and the challenges. J. Build. Eng. 2023, 63, 105533. [Google Scholar] [CrossRef]
- Mousavi, E.S.; Kananizadeh, N.; Martinello, R.A.; Sherman, J.D. COVID-19 outbreak and hospital air quality: A systematic review of evidence on air filtration and recirculation. Environ. Sci. Technol. 2020, 55, 4134–4147. [Google Scholar] [CrossRef]
- Altwijri, O.; Javed, R.; Albedah, A.; Addokhi, A. 3D Modeling and Simulation of Airflow and Aerosol Deposition of Idealized Human Oral Airways. J. Biomater. Tissue Eng. 2018, 8, 933–940. [Google Scholar] [CrossRef]
- Kim, M.; Jeong, S.G.; Park, J.; Lee, J.H. Assessment of pre-filter systems to control indoor inflow of particulate matter. J. Build. Eng. 2021, 43, 103052. [Google Scholar] [CrossRef]
- Algabri, Y.A.; Altwijri, O.; Chatpun, S. Visualization of Blood Flow in AAA Patient-Specific Geometry: 3-D Reconstruction and Simulation Procedures. BioNanoScience 2019, 9, 966–976. [Google Scholar] [CrossRef]
- Sola Martinez, R.A.; Pastor Hernandez, J.M.; Yanes Torrado, O.; Canovas Diaz, M.; de Diego Puente, T.; Vinaixa Crevillent, M. Exhaled volatile organic compounds analysis in clinical pediatrics: A systematic review. Pediatr. Res. 2021, 89, 1352–1363. [Google Scholar] [CrossRef] [PubMed]
- Maurya, L.; Kaur, P.; Chawla, D.; Mahapatra, P. Non-contact breathing rate monitoring in newborns: A review. Comput. Biol. Med. 2021, 132, 104321. [Google Scholar] [CrossRef] [PubMed]
- Kaewchoothong, N.; Algabri, Y.A.; Assawalertsakul, T.; Nuntadusit, C.; Chatpun, S. Computational Study of Abdominal Aortic Aneurysms with Severely Angulated Neck Based on Transient Hemodynamics Using an Idealized Model. Appl. Sci. 2022, 12, 2113. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altwijri, O.; Javed, R.; Algabri, Y.A.; Fakhouri, A.; Alqarni, K.; Altamimi, R.; Alqahtani, S.; Almijalli, M.; Saad, A. Optimal Air Flow Modeling in Real Healthcare Facilities for Quick Removal of Contaminated Air. Processes 2024, 12, 2799. https://doi.org/10.3390/pr12122799
Altwijri O, Javed R, Algabri YA, Fakhouri A, Alqarni K, Altamimi R, Alqahtani S, Almijalli M, Saad A. Optimal Air Flow Modeling in Real Healthcare Facilities for Quick Removal of Contaminated Air. Processes. 2024; 12(12):2799. https://doi.org/10.3390/pr12122799
Chicago/Turabian StyleAltwijri, Omar, Ravish Javed, Yousif A. Algabri, Abdulaziz Fakhouri, Khaled Alqarni, Reema Altamimi, Sarah Alqahtani, Mohammed Almijalli, and Ali Saad. 2024. "Optimal Air Flow Modeling in Real Healthcare Facilities for Quick Removal of Contaminated Air" Processes 12, no. 12: 2799. https://doi.org/10.3390/pr12122799
APA StyleAltwijri, O., Javed, R., Algabri, Y. A., Fakhouri, A., Alqarni, K., Altamimi, R., Alqahtani, S., Almijalli, M., & Saad, A. (2024). Optimal Air Flow Modeling in Real Healthcare Facilities for Quick Removal of Contaminated Air. Processes, 12(12), 2799. https://doi.org/10.3390/pr12122799







