Improved Algorithms Based on Trust Region Framework for Solving Unconstrained Derivative Free Optimization Problems
Abstract
1. Introduction
- (1)
- To enhance the goodness of fit and ensure the sparsity of the surrogate model, a correction strategy is implemented to guarantee the feasibility of the proposed algorithm when applying LASSO to find the surrogate model.
- (2)
- ADMM is utilized to determine the coefficients of the sparse interpolation model and for LASSO modeling.
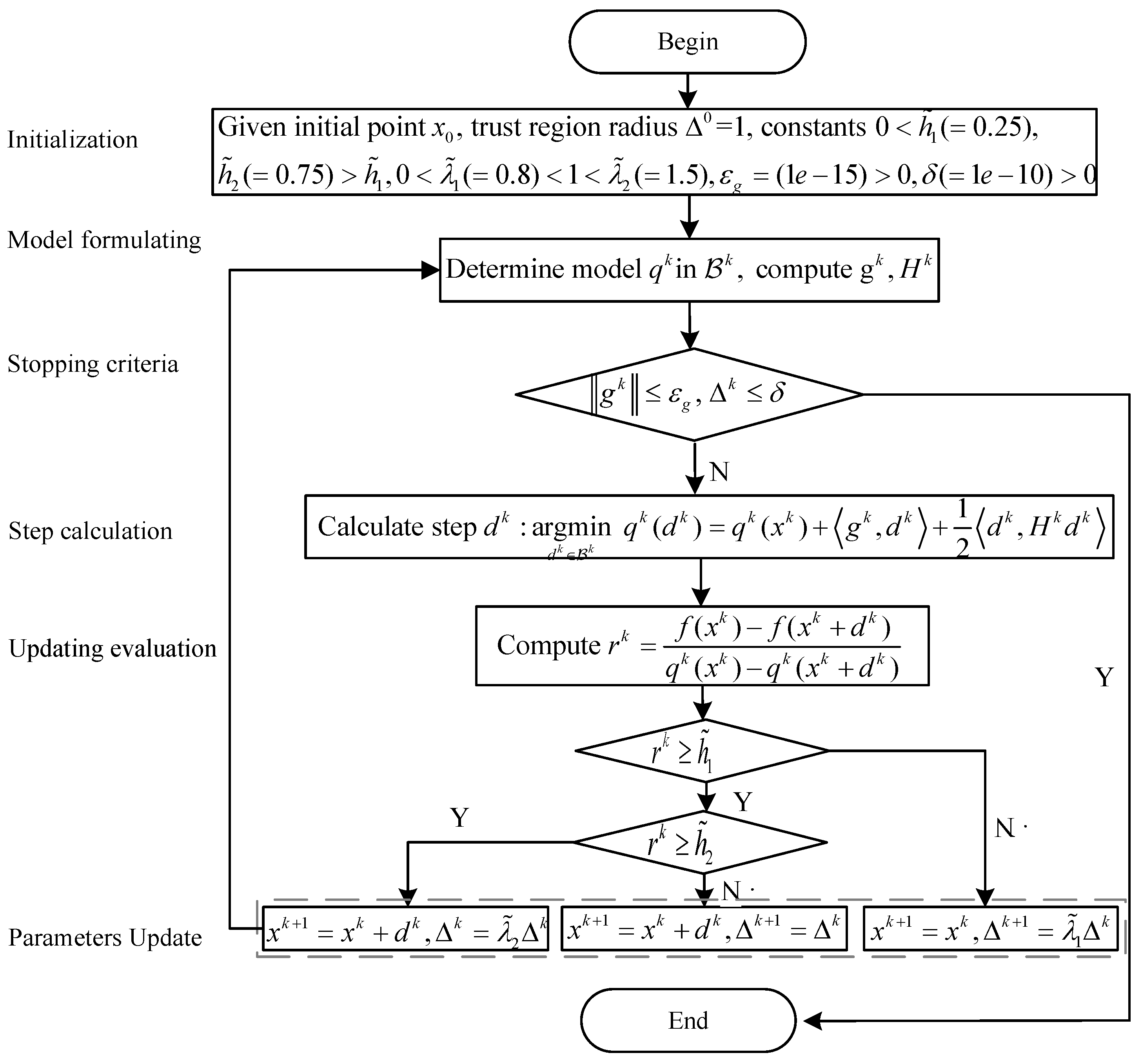
2. The Framework of Algorithms
3. Description of the Proposed Approach
3.1. Interpolation Based Surrogate Model Formulation
3.2. Sparse Surrogate Model Formulation
3.2.1. Formulation of Sparse Model
3.2.2. ADMM Algorithm for Estimating Model Coefficient
| Algorithm 1 ADMM algorithm to solve problem (13) |
Initialization: Determine the initial point , ,
|
- (1)
- Initialization: Given the constant , . And set the initial value and , where defined for a vector with ;
- (2)
- Use Algorithm 1 to find value of ;
- (3)
- R-square statistic [34] is used to test for goodness of fit, and is used to judge the sparsity of the coefficient, where denotes the number of elements in satisfying . Define , where , . is the mean value. And is a vector of all elements with 1.
- (4)
- Determine shrink or expansion of factor :If , and , then .If , then .
3.2.3. Ensure the Geometry of the Interpolation Set
3.3. Derivative Free Algorithms
3.3.1. DFO-ADMM-TR
3.3.2. DFO-LASSOADMM-TR
- (0)
- Initialization. Parameters and sample of interpolation set are both initialized. As for parameter initialization, it can be divided into the following three steps.
- (a)
- Parameter in ADMM
- : the original variables in the optimization problem;
- : the scaled variable;
- : a constant satisfies ;
- : tolerances for the primal and dual feasibility conditions, which used to be define the stopping criteria.
- (b)
- Parameter in correction strategy
- : controls the sparsity of coefficient vector in problem (12);
- : determine shrink or expansion of factor .
- (c)
- General parameter in DFO.
- , , and : denote the initial, maximum, and minimum trust region radius, respectively.
- and : denote the radius shrink and expansion factor respectively;
- : the smallest norm-square of gradient to stop;
- : level to judge whether the current iteration is successful;
- : level to expand trust region radius;
- : the maximum number of iteration of the DFO algorithms;
- , : the minimum change value of function ;
- (1)
- Model building and trust region step calculation. At the first iteration, the initial interpolation set is used to create the quadratic surrogate model either by the quadratic interpolation method or the LASSO method, depending on the number of samples. Without loss of generality, at the k-th () iteration, the surrogate model is formulated based on the updated sample set. Simultaneously, is computed by solving the sub-optimization problem (3). Then, is calculated. The algorithm’s termination is determined based on the values of and k.
- (2)
- Iteration point and trust region radius updating. Computethen updating and according to . If , .
- (3)
- Sample set updating. Calculate the square of the Euclidean distance between all points in the sample set and the next trial point , where for . Denote . Then, update the sample set according to the step (lines 28–43). In Algorithm 2, denotes the number of samples in the set .
| Algorithm 2 DFO-LASSOADMM-TR: a novel derivative free algorithm |
Initialization: Give the initial algorithm parameters, and construct the initial sample sets as well as compute the corresponding objective values.
|
4. Numerical Experiments
4.1. Benchmark Functions and Experimental Design
4.2. Parameter Correction Strategy Tests
4.3. Experimental Results
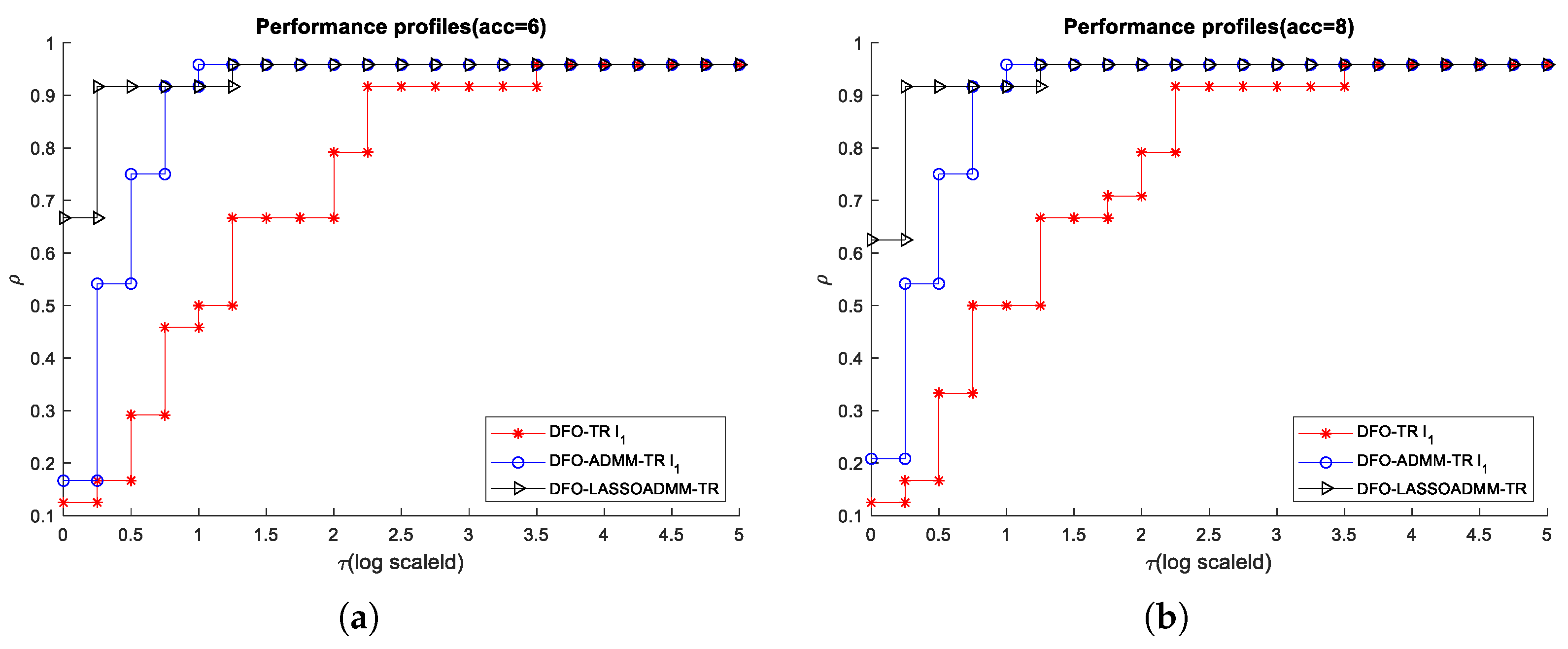
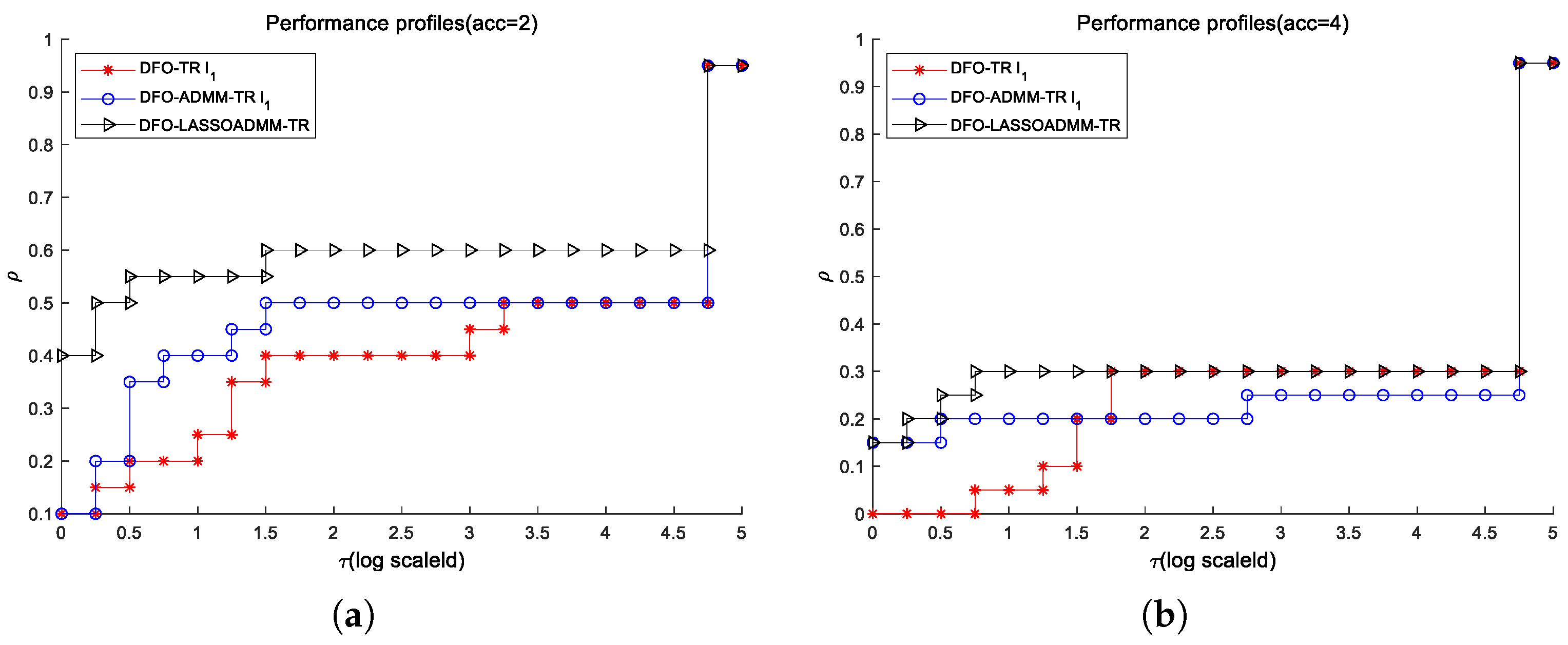
- (1)
- Performance profile. Let be the computing time required to solve problem by solver . Let denotes the performance ratio, it is defined as followswhere , and ‘properly’ means that solver s solves p with the certain accuracy. Definewhere is the cumulative probability of , it is named as the performance profile. And is the number of problems in the test sets .
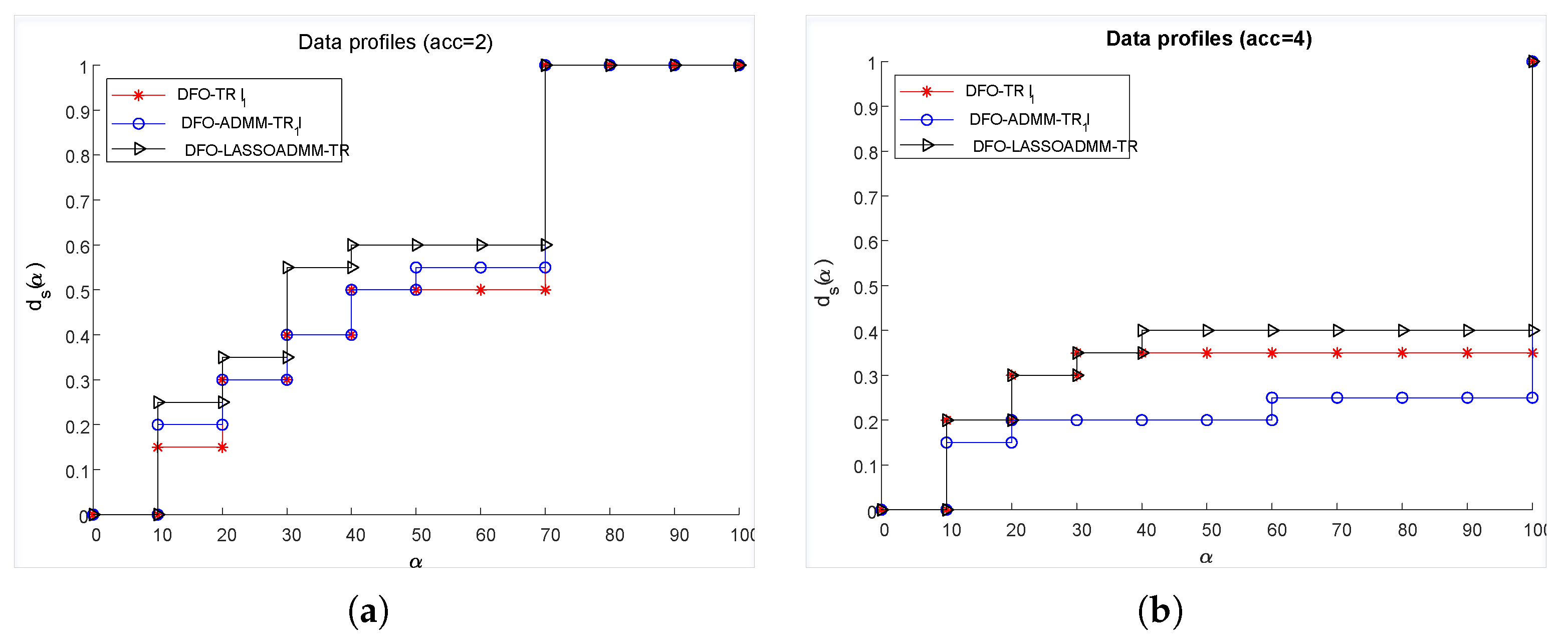
- (2)
- Data profile. For a given tolerance , let be the number of function evaluations satisfy (33) when solver is adopted to solve problem .where is a tolerance, is the initial point for solving problem, here, is an accurate estimate of at a global minimum point. Thus, the data profile of a solver is defined aswhere is the number of variables in problem p.
4.3.1. Numerical Experiments for Smooth Case
4.3.2. Numerical Experiments for Noisy Case
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Tang, L.; Liu, J.; Tang, Z. A dynamic analytics method based on multistage modeling for a BOF steelmaking process. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1097–1109. [Google Scholar] [CrossRef]
- Tang, L.; Meng, Y. Data analytics and optimization for smart industry. Front. Eng. Manag. 2020, 8, 157–171. [Google Scholar] [CrossRef]
- Feyzioglu, O.; Pierreval, H.; Deflandre, D. A simulation-based optimization approach to size manufacturing systems. Int. J. Prod. Res. 2005, 43, 247–266. [Google Scholar] [CrossRef]
- Coelho, G.F.; Pinto, L.R. Kriging-based simulation optimization: An emergency medical system application. J. Oper. Res. Soc. 2018, 69, 2006–2020. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Zhang, J.; Li, Y.; Shi, Y.H. Orthogonal learning particle swarm optimization. IEEE Trans. Evol. Comput. 2011, 15, 832–847. [Google Scholar] [CrossRef]
- Srinivas, M.; Patnaik, L.M. Genetic algorithms: A survey. Computer 1994, 27, 17–26. [Google Scholar] [CrossRef]
- Du, K.L.; Swamy, M.N.S. Estimation of Distribution Algorithms. In Search and Optimization by Metaheuristics: Techniques and Algorithms Inspired by Nature; Springer International Publishing: Cham, Switzerland, 2016; pp. 105–119. [Google Scholar]
- Spendley, W.; Hex, G.R.; Himsworth, F.R. Sequential application for simplex designs in optimisation and evolutionary operation. Technometrics 1962, 4, 441–461. [Google Scholar] [CrossRef]
- Powell, M.J.D. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964, 7, 155–162. [Google Scholar] [CrossRef]
- Conn, A.R.; Scheinberg, K.; Vicente, L. Introduction to Derivative-Free Optimization; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. [Google Scholar]
- Berahas, A.S.; Sohab, O.; Vicente, L.N. Full-low evaluation methods for derivative-free optimization. Optim. Methods Softw. 2023, 38, 386–411. [Google Scholar] [CrossRef]
- Gaudioso, M.; Liuzzi, G.; Lucidi, S. A clustering heuristic to improve a derivative-free algorithm for nonsmooth optimization. Optim. Lett. 2024, 18, 57–71. [Google Scholar] [CrossRef]
- Rios, L.M.; Sahinidis, N.V. Derivative-free optimization: A review of algorithms and comparison of software implementations. J. Glob. Optim. 2013, 56, 1247–1293. [Google Scholar] [CrossRef]
- Audet, C.; Hare, W. Derivative-Free and Blackbox Optimization; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Gao, H.; Waechter, A.; Konstantinov, I.A.; Arturo, S.G.; Broadbelt, L.J. Application and comparison of derivative-free optimization algorithms to control and optimize free radical polymerization simulated using the kinetic Monte Carlo method. Comput. Chem. Eng. 2018, 108, 268–275. [Google Scholar] [CrossRef]
- Lucidi, S.; Maurici, M.; Paulon, L.; Rinaldi, F.; Roma, M. A derivative-free approach for a simulation-based optimization problem in healthcare. Optim. Lett. 2015, 10, 219–235. [Google Scholar] [CrossRef]
- Boukouvala, F.; Floudas, C.A. ARGONAUT: Algorithms for global optimization of constrained grey-box computational problems. Optim. Lett. 2017, 11, 895–913. [Google Scholar] [CrossRef]
- Boukouvala, F.; Hasan, M.M.F.; Floudas, C.A. Global optimization of general constrained grey-box models: New method and its application to constrained PDEs for pressure swing adsorption. J. Glob. Optim. 2017, 67, 3–42. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, L.; Liu, C.; Su, L.; Wu, J. Black box operation optimization of basic oxygen furnace steelmaking process with derivative free optimization algorithm. Comput. Chem. Eng. 2021, 150, 107311. [Google Scholar] [CrossRef]
- Powell, M.J.D. On the global convergence of trust region algorithms for unconstrained minimization. Math. Program. 1984, 29, 297–303. [Google Scholar] [CrossRef]
- Conn, A.R.; Toint, P.L. An algorithm using quadratic interpolation for unconstrained derivative free optimization. In Nonlinear Optimization and Applications; Springer: Boston, MA, USA, 1996; pp. 27–47. [Google Scholar]
- Conn, A.R.; Scheinberg, K.; Toint, P.L. On the convergence of derivative-free methods for unconstrained optimization. In Approximation theory and optimization: Tributes to M. J. D. Powell; Iserles, A., Buhmann, M., Eds.; Cambridge University Press: Cambridge, UK, 1997; pp. 83–108. [Google Scholar]
- Sauer, T.; Xu, Y. On Multivariate Lagrange Interpolation. Math. Comput. 1995, 64, 1147–1170. [Google Scholar] [CrossRef]
- Powell, M.J.D. On trust region methods for unconstrained minimization without derivatives. Math. Program. 2003, 97, 605–623. [Google Scholar] [CrossRef]
- Conn, A.R.; Scheinberg, K.; Vicente, L.N. Geometry of interpolation sets in derivative free optimization. Math. Program. 2008, 111, 141–172. [Google Scholar] [CrossRef]
- Fasano, G.; Morales, J.L.; Nocedal, J. On the geometry phase in model-based algorithms for derivative-free optimization. Optim. Methods Softw. 2009, 24, 145–154. [Google Scholar] [CrossRef][Green Version]
- Powell, M.J.D. The NEWUOA software for unconstrained optimization without derivatives. Large-Scale Nonlinear Optim. 2006, 83, 255–297. [Google Scholar]
- Scheinberg, K.; Toint, P.L. Self-correcting geometry in model-based algorithms for derivative-free unconstrained optimization. SIAM J. Optim. 2010, 20, 3512–3532. [Google Scholar] [CrossRef]
- Bandeira, A.S.; Scheinberg, K.; Vicente, L.N. Computation of sparse low degree interpolating polynomials and their application to derivative-free optimization. Math. Program. 2012, 134, 223–257. [Google Scholar] [CrossRef]
- Conn, A.R.; Scheinberg, K.; Vicente, L.N. Geometry of sample sets in derivative-free optimization: Polynomial regression and underdetermined interpolation. Ima J. Numer. Anal. 2008, 28, 721–748. [Google Scholar] [CrossRef]
- Foucart, S.; Rauhut, H. A Mathematical Introduction to Compressive Sensing; Birkhauser: New York, NY, USA, 2013. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Society. Ser. B (Methodol.) 1994, 58, 267–288. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers; Now Foundations and Trends: Hanover, MA, USA, 2011. [Google Scholar]
- Yan, X.; Su, X. Linear Regression Analysis: Theory and Computing; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2009. [Google Scholar]
- Rauhut, H. Compressive sensing and structured random matrices. Theor. Found. Numer. Methods Sparse Recovery 2010, 9, 1–92. [Google Scholar]
- Gould, N.I.M.; Orban, D.; Toint, P.L. CUTEr and SifDec: A constrained and unconstrained testing environment, revisited. ACM Trans. Math. Softw. 2003, 29, 373–394. [Google Scholar] [CrossRef]
- More, J.; Garbow, B.S.; Hillstrom, K.E. Testing unconstrained optimization software. ACM Trans. Math. Softw. 1981, 7, 17–41. [Google Scholar] [CrossRef]
- Conn, A.R.; Gould, N.I.M.; Lescrenier, M.J.A.; Toint, P.L. Performance of a multifrontal scheme for partially separable optimization. In Advances in Optimization and Numerical Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994; pp. 79–96. [Google Scholar]
- Buckley, A. Test Functions for Unconstrained Minimization; Dalhousie University: Halifax, NS, Canada, 1989. [Google Scholar]
- Toint, P.L. Test Problems for Partially Separable Optimization and Results for the Routine PSPMIN; Technology Report 83/4; Department of Mathematics, University of Namur: Brussels, Belgium, 1983. [Google Scholar]
- Fletcher, R. An optimal positive definite update for sparse hessian matrices. SIAM J. Optim. 1995, 5, 192–218. [Google Scholar] [CrossRef]
- Hansen, N.; Auger, A.; Finck, S.; Ros, R. Real-Parameter Black-Box Optimization Benchmarking 2010: Experimental Setup; Research Report; INRIA: Talence, France, 2010. [Google Scholar]
- Hock, W.; Schittkowski, K. Test Examples for Nonlinear Programming Codes; Springer: Berlin/Heidelberg, Germany, 1980; Volume 187. [Google Scholar]
- Dola, E.D.; More, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
- More, J.J.; Wild, S.M. Benchmarking derivative-free optimization algorithms. SIAM J. Optim. 2009, 20, 172–191. [Google Scholar] [CrossRef]

| Problem | Sourse or Formula Form | n |
|---|---|---|
| ARGLINB | [37], Problem 33 | 10 |
| ARGLINC | [37], Problem 34 | 8 |
| ARWHEAD | [38], Problem 55 | 15 |
| BDQRTIC | [38], Problem 61 | 10 |
| BROYDN3DLS | [37], Problem 30 | 10 |
| DIXMAANC | [39], Page 49 | 12 |
| DIXMAANG | [39], Page 49 | 12 |
| DIXMAANI | [39], Page 49 | 12 |
| DIXMAANK | [39], Page 49 | 12 |
| DIXON3DQ | [39], Page 51 | 12 |
| DQDRTIC | [40], Problem 22 | 10 |
| FLETCHCR | [41], Problem 2 | 10 |
| FREUROTH | [37], Problem 2 | 10 |
| GENHUMPS | 10 | |
| HIMMELBH | [39], Page 60 | 2 |
| MOREBVNE | [39], Page 75 | 10 |
| NONDIA | [39], Page 76 | 10 |
| NONDQUAR | 10 | |
| POWELLSG | [37], Problem 13 | 4 |
| POWER | [39], Page 83 | 18 |
| ROSENBR | [37], Problem 1 | 2 |
| TRIDIA | [40], Problem 8 | 10 |
| VARDIM | [37], Problem 25 | 10 |
| WOODS | [37], Problem 14 | 4 |
| Problem | Noise | n |
|---|---|---|
| Sphere | moderate gaussian noise | 2, 4, 10 |
| moderate uniform noise | ||
| severe gaussian noise | 2, 4 | |
| severe uniform noise | ||
| Rosenbrock | moderate gaussian noise | 2, 4, 10 |
| moderate uniform noise | ||
| severe gaussian noise | 2, 4 | |
| severe uniform noise |
| S | 0.0001 | 0.0005 | 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | 0.5 | 1 | 5 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARGLINB | 0.72 | 0.58 | 0.56 | 0.59 | 0.54 | 0.55 | 0.56 | 0.53 | 0.54 | 0.61 | 0.54 | 0.54 |
| ARGLINC | 0.53 | 0.48 | 0.47 | 0.49 | 0.47 | 0.52 | 0.48 | 0.46 | 0.51 | ∼ | 0.46 | 0.49 |
| BDQRTIC | 1.57 | 1.42 | ∼ | 1.57 | 1.26 | ∼ | 1.46 | 1.20 | 1.32 | 1.31 | 1.64 | 1.33 |
| DIXMAANC | 2.07 | 1.32 | 1.36 | ∼ | 1.19 | 1.36 | 1.46 | ∼ | ∼ | ∼ | ∼ | ∼ |
| DIXMAANI | 2.26 | ∼ | ∼ | ∼ | 0.92 | 0.82 | 0.97 | ∼ | ∼ | ∼ | ∼ | ∼ |
| DIXON3DQ | 0.84 | 0.64 | 0.67 | 0.70 | 0.50 | 0.96 | 0.94 | ∼ | 0.76 | 0.77 | ∼ | ∼ |
| DQDRTIC | 0.42 | ∼ | ∼ | ∼ | ∼ | 0.86 | ∼ | 0.84 | 0.93 | 0.87 | ∼ | ∼ |
| FREUROTH | 1.81 | ∼ | ∼ | 1.80 | 1.57 | 1.44 | ∼ | ∼ | 1.48 | 1.43 | 1.36 | ∼ |
| POWER | 0.83 | 0.80 | 0.84 | 0.82 | 0.83 | 0.75 | 0.79 | 0.75 | 0.80 | ∼ | 0.88 | ∼ |
| TRIDIA | 0.63 | 0.73 | 0.71 | 0.70 | 0.57 | 0.67 | ∼ | ∼ | ∼ | ∼ | 0.75 | ∼ |
| DFO-TR | DFO-TR | DFO-LASSOADMM-TR | |
|---|---|---|---|
| moderate noise | 58.33% | 58.33% | 75.00% |
| severe noise | 50.00% | 50.00% | 62.50% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Xu, T. Improved Algorithms Based on Trust Region Framework for Solving Unconstrained Derivative Free Optimization Problems. Processes 2024, 12, 2753. https://doi.org/10.3390/pr12122753
Liu Y, Xu T. Improved Algorithms Based on Trust Region Framework for Solving Unconstrained Derivative Free Optimization Problems. Processes. 2024; 12(12):2753. https://doi.org/10.3390/pr12122753
Chicago/Turabian StyleLiu, Yongxia, and Te Xu. 2024. "Improved Algorithms Based on Trust Region Framework for Solving Unconstrained Derivative Free Optimization Problems" Processes 12, no. 12: 2753. https://doi.org/10.3390/pr12122753
APA StyleLiu, Y., & Xu, T. (2024). Improved Algorithms Based on Trust Region Framework for Solving Unconstrained Derivative Free Optimization Problems. Processes, 12(12), 2753. https://doi.org/10.3390/pr12122753






