A Comprehensive Review of Mixed Convective Heat Transfer in Tubes and Ducts: Effects of Prandtl Number, Geometry, and Orientation
Abstract
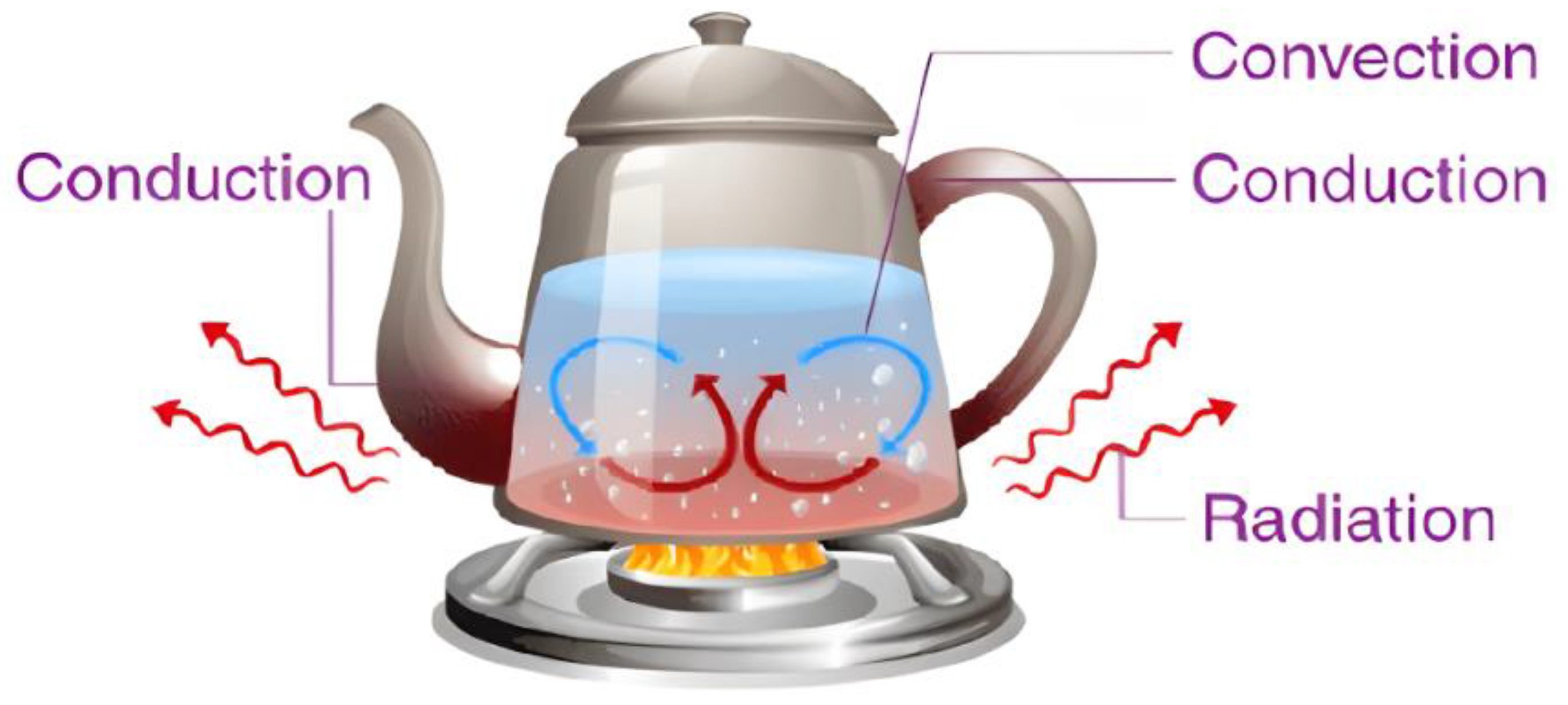
1. Introduction
k
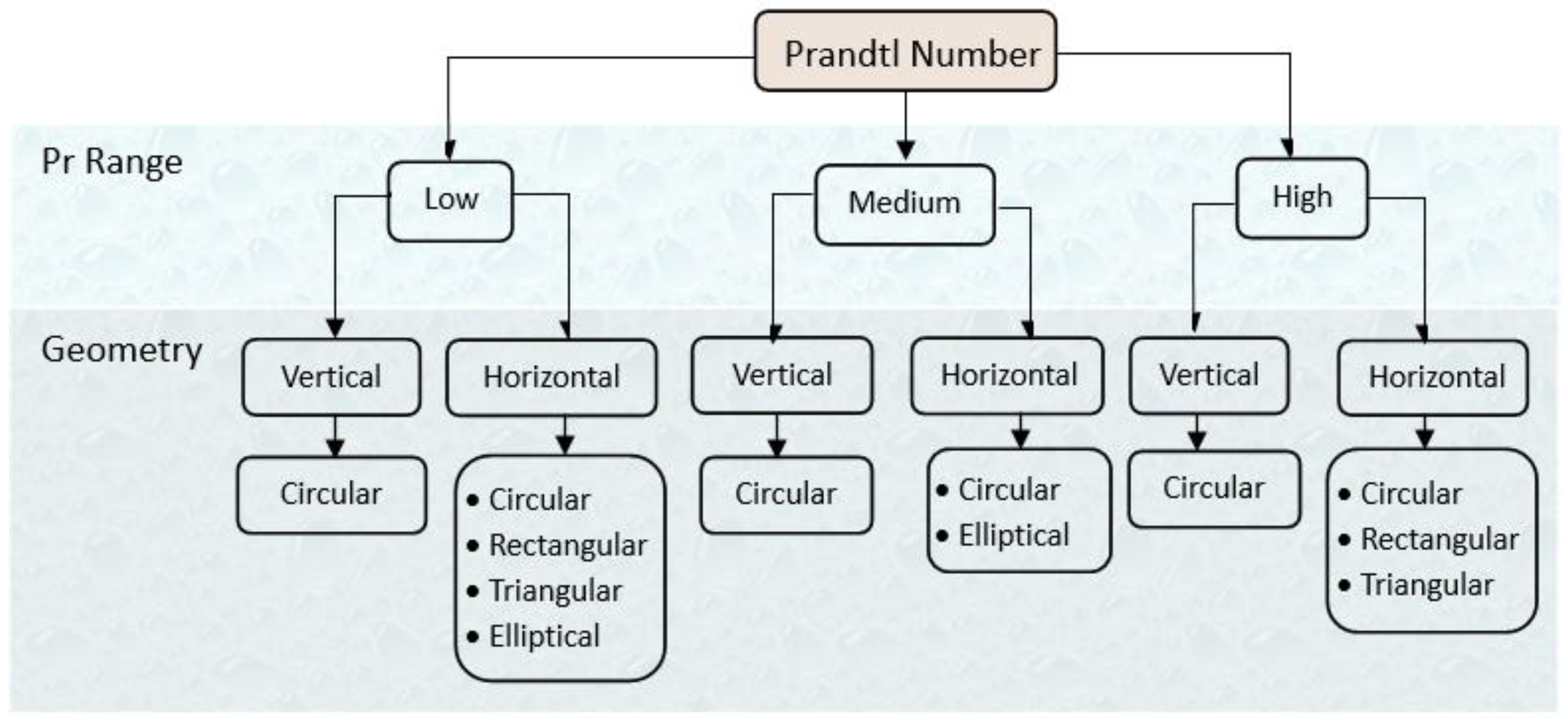
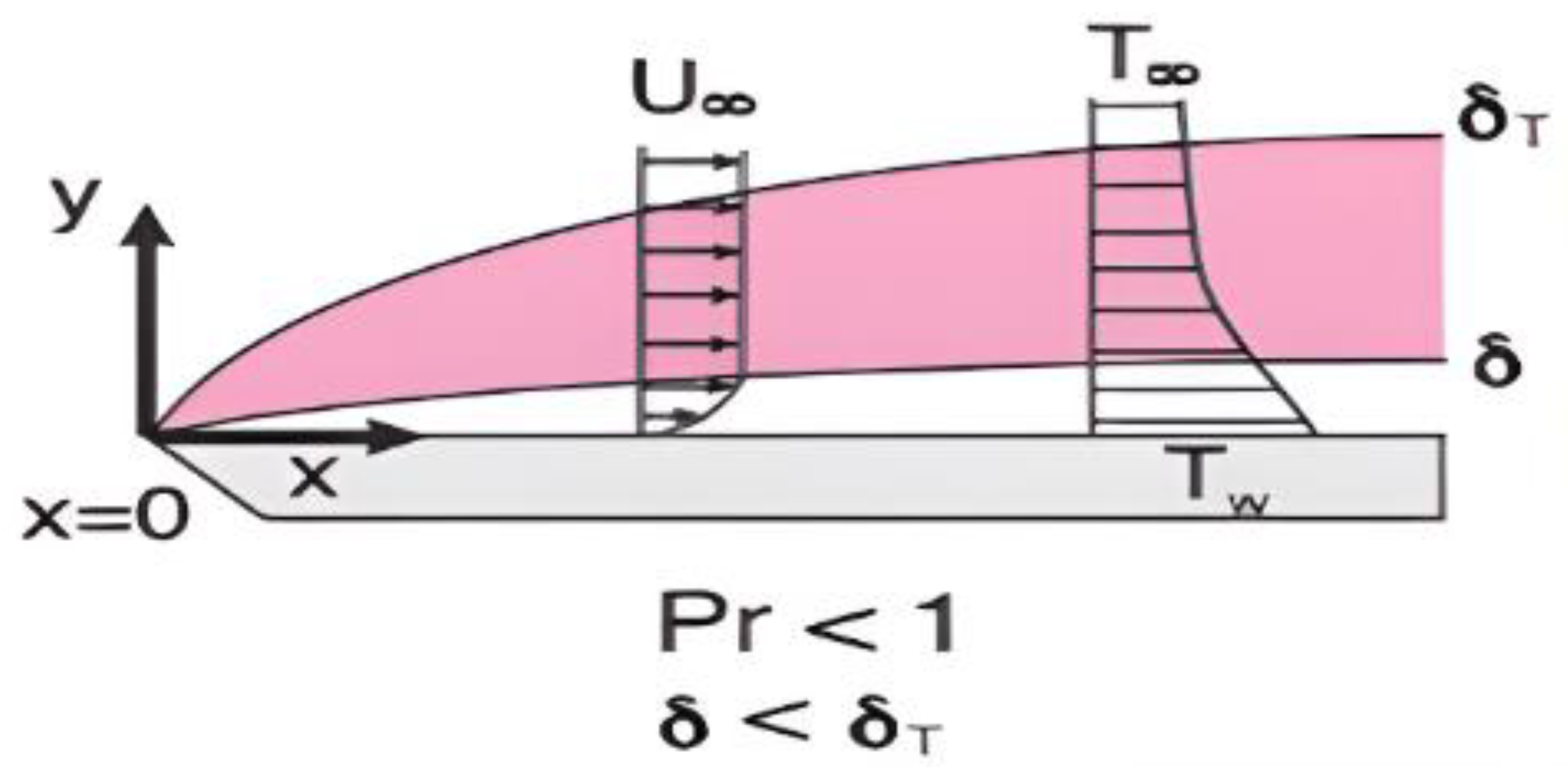
2. Low Prandtl Number
2.1. Low Prandtl Number—Vertical Circular Tube
2.2. Low Prandtl Number—Horizontal Circular Tube
2.3. Low Prandtl Number—Horizontal Rectangular Duct
2.4. Low Prandtl Number—Horizontal Triangular Duct
2.5. Low Prandtl Number—Horizontal Elliptical Tube
3. High Prandtl Number
3.1. High Prandtl Number—Vertical Circular Tube
3.2. High Prandtl Number—Horizontal Circular Tube
- (a)
- the longitudinal vortices produced (from rotating fluid after guiding of spiral coin)
- (b)
- the secondary flow intensity increases greatly.
- (c)
- mixing of fluid with different temperatures.
- (d)
- enhancement of heat transfer performance in the tube.
3.3. High Prandtl Number—Horizontal (Circular/Square/Triangular Ducts)
- i.
- Higher transfer of heat by convection at the pipe entry rather than the exit.
- ii.
- Correlation between Re, Nu, and St regards air flow speed inside the pipe.
- iii.
- Heat flux is directly proportional to Re and Nu (Q increased, both Re and Nu increased).
- iv.
- At high air speed, Nu is higher, but St is lower.
- v.
- At low air speed, St is higher, but Nu is lower.
4. Medium Prandtl Number
4.1. Medium Prandtl Number—Vertical Circular Tube
4.2. Medium Prandtl Number—Horizontal Circular Tube
4.3. Medium Prandtl Number—Horizontal Elliptical Tube
5. Findings
6. Limitations
7. Future Recommendations
- (a)
- According to the reviewed literature, limited research and the potential of having a medium Prandtl number as a working fluid parameter in convective heat transfer provide optimism for future development.
- (b)
- From the observation of previous studies, most of the researchers had chosen circular geometry as a working tube over rectangular, triangular and elliptical. Most of the findings also showed better results in terms of Nusselt number, heat transfer coefficient, and pressure drops.
- (c)
- In terms of flow orientation, horizontal ducting had become the most preferred choice in carrying out mixed convective heat transfer analysis over the vertical due to lower gravitational effects, good flow uniformity, lower pressure drops, less thermal stratification, and better accessibility for maintenance.
- (d)
- As an agreement to statements (2) and (3) above, most of the industrial players also carried out mixed convective heat transfer applications using circular ducts with horizontal orientation; however, to some extent, few also applied extra measures by adding passive methods to these circular horizontal ducting settings, such as helical coils, corrugations, swirl generators, and ribs; therefore, it is recommended to aid this passive method in a combination to the favored circular horizontal ducting in the future research.
- (e)
- In addition, apart from the geometry concern, it is also recommended to give more attention to the effectiveness of secondary flow creation and its impact on increasing the rate of heat transfer. Certain fine tunes related to the design of geometry as an aid to the occurrence of this secondary flow should be taken into consideration. Passive method design, including the introduction of baffles, dimples, and grooves, might assist in creating more turbulence in the flow and, ultimately, the secondary flow.
8. Conclusions
- (a)
- Most researchers conducted experiments in circular tubes with a horizontal axis for mixed heat convective heat transfer.
- (b)
- Lower Prandtl numbers brought different dynamics to the heat transfer process as thermal diffusivity dominates, leading to a thinner thermal boundary layer. This scenario resulted in higher heat transfer coefficients.
- (c)
- Higher Prandtl numbers influenced the mixing (convection) in turbulent flow and improved the heat transfer as the momentum diffusivity dominates.
- (d)
- Research on mixed convective heat transfer in horizontal circular tubes typically focuses on fluids with either very low or very high Prandtl numbers, such as air or oil; however, there is limited research on fluids with medium Prandtl numbers, such as molten salts used in liquid-fuel and solid-fuel Molten Salt Reactors (MSRs).
- (e)
- Nanofluids have been shown to enhance thermal performance across all types of geometries studied. They offer significant potential for improving cooling, thermal storage, solar energy applications, heat exchangers, and related cooling technologies.
- (f)
- Experimental investigations into the convective heat transfer characteristics of tubes with four different cross-sectional shapes under constant heat flux reveal that variations in tube geometry influence heat transfer efficiency.
- (g)
- In convective heat transfer applications, the shape and design of the cavity play a crucial role in achieving optimal results. The effectiveness of the cavities depends on their intended use, making it essential to select the appropriate cavity design for thermal systems.
- (h)
- Various geometries, including circular, square, triangular, and elliptical, are used in heat transfer studies. The literature suggests that circular cavities generally offer the best performance due to their high heat transfer rate, low pumping power requirements, and efficiency at low Reynolds numbers.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Greek letters | ||
| C | coefficient used in correlations | B | thermal expansion coefficient |
| Cp | constant—pressure specific heat | ϵ | surface roughness |
| Di | inner diameter | μ | dynamic viscosity |
| Do | outer diameter | μf | fluid dynamic viscosity |
| EB | energy balance | v | kinematic viscosity |
| f | friction factor | ρ | Density |
| fcr | friction factor at Recr | ɣ | non–dimensional conductance ratio |
| fqt | friction factor at Reqt | Subscripts | |
| g | gravitational acceleration | b | Bulk |
| Gr | Grashof number | c | cross-section |
| Gr* | modified Grashof number | CFD | computational fluid dynamic |
| Gz | Graetz number | cor | Correlation |
| h | heat transfer coefficient | exp | Experimental |
| I | current j Colburn j–factor | i | Inlet |
| k | thermal conductivity | L | Laminar |
| Kf | fluid thermal conductivity | MCD | Mixed Convection Developing region |
| L | length | o | outer/outlet |
| Lt | thermal entrance length | QT | quasi-turbulent |
| M | measurement or calculated value | ref | Reference s surface |
| ṁ | mass flow rate | ||
| Nu | Nusselt number | ||
| P | pressure | ||
| Pe | Peclet number | ||
| Pr | Prandtl number | ||
| Q | heat transfer rate | ||
| Qe | electrical input rate | ||
| Qw | water heat transfer rate | ||
| q | heat flux | ||
| Ra | Rayleigh number | ||
| Ret | start of turbulent flow regime | ||
| ΔRe | width of transitional flow regime | ||
| St | Stanton number | ||
| T | Temperature | ||
| ΔT | temperature difference between surrounding fluid and object surface | ||
| TGf | transition gradient in terms of friction factor results | ||
| TGj | transition gradient in terms of Colburn j-factor results | ||
| V | velocity | ||
| x | |||
References
- Zafar, M.; Sakidin, H.; Sheremet, M.; Dzulkarnain, I.; Nazar, R.M.; Hussain, A.; Said, Z.; Afzal, F.; Al-Yaari, A.; Khan, M.S.; et al. The impact of cavities in different thermal applications of nanofluids: A review. Nanomaterials 2023, 13, 1131. [Google Scholar] [CrossRef] [PubMed]
- EngineeringCheatSheet. Why Is Heat Transfer Important? 2023. Available online: https://engineeringcheatsheet.com/heat-transfer/why-is-heat-transfer-important/ (accessed on 23 April 2024).
- BYJU’S. Heat Transfer—Radiation, Convection and Conduction. 2024. Available online: https://byjus.com/physics/heat-transfer-conduction-convection-and-radiation/ (accessed on 28 October 2024).
- Fahzy, M.C.; Pardede, Y.P.; Yesa, D.R.; Bahi, M.R.; Sahim, K. Experimental study of the convective heat transfers form tubes with various cross—Section. Indones. J. Eng. Sci. 2022, 3, 019–027. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.; Zhang, Y.; Zhang, Z. Heat transfer characteristics of triple—Tube latent heat storage system placed horizontally and vertically. J. Energy Storage 2023, 71, 108163. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, X.; Dominguez-Ontiveros, E.E. Numerical Study on Convective Heat Transfer and Friction Characteristics of Molten Salts in Circular Tubes. Ann. Nucl. Energy 2021, 142, 107375. [Google Scholar] [CrossRef]
- Taler, D.; Taler, J. Simple heat transfer correlations for turbulent tube flow. E3S Web Conf. 2017, 13, 02008. [Google Scholar] [CrossRef]
- Nuclear-Power.com. What Is Prandtl—Number. 2024. Available online: https://www.nuclear-power.com/nuclear-engineering/heat-transfer/introduction-to-heat-transfer/characteristic-numbers/what-is-prandtl-number/ (accessed on 4 July 2024).
- Cengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer-Fundamental & Applications, 5th ed.; Mc Graw Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Malviya, R.; Agrawal, A.; Baredar, P.V. A comprehensive review of different heat transfer working fluids for solar thermal parabolic through concentrator. Mater. Today Proc. 2020, 46, 5490–5500. [Google Scholar] [CrossRef]
- Campo, A.; Papari, M.M.; Abu-Nada, E. Estimation of the minimum Prandtl number for binary gas mixtures formed with light helium and certain heavier gases: Application to thermoacoustic refrigerators. Appl. Therm. Eng. 2011, 31, 3142–3146. [Google Scholar] [CrossRef]
- Pandey, S.; Park, Y.G.; Ha, M.Y. An exhaustive review of studies on natural convection in enclosures with and without internal bodies of various shapes. Int. J. Heat Mass Transf. 2019, 138, 762–795. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Salman, Y.K. Combined natural and forced convection heat transfer for assisting thermally developing flow in a uniformly heated vertical circular cylinder. Int. Commun. Heat Mass Transf. 2007, 34, 474–491. [Google Scholar] [CrossRef]
- Maughan, J.R.; Incropera, E.P. Fully developed mixed convection in a horizontal channel heated uniformly from above and below. Numer. Heat Transf. Part. A Appl. 1990, 17, 417–430. [Google Scholar] [CrossRef]
- Hishida, M.; Nagano, Y.; Montesclaros, M.S. Combined forced and free convection in the entrance region of an isothermally heated horizontal pipe. J. Heat Transf. 1982, 104, 153–159. [Google Scholar] [CrossRef]
- Chou, F.C.; Hwang, G.J. Numerical analysis of the Graetz problem with natural convection in a uniformly heated horizontal tube. Int. J. Heat Mass Transf. 1988, 31, 1299–1308. [Google Scholar] [CrossRef]
- Eiamsa-Ard, S.; Nivesrangsan, P.; Chokphoemphun, S.; Promvonge, P. Influence of combined non-uniform wire coil and twisted tape inserts on thermal performance characteristics. Int. Commun. Heat Mass Transf. 2010, 37, 850–856. [Google Scholar] [CrossRef]
- Wang, M.; Tsuji, T.; Nagano, Y. Mixed convection with flow reversal in the thermal entrance region of horizontal and vertical pipes. Int. J. Heat Mass Transf. 1994, 37, 2305–2319. [Google Scholar] [CrossRef]
- Smith, J.E.-A.; Narin, K.; Pongjet, P. Heat Transfer Behavior in a Square Duct with Tandem Wire Coil Element Insert. Chin. J. Chem. Eng. 2012, 20, 863–869. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Liu, Z.C.; Liu, W. Numerical studies on heat transfer and flow characteristics for laminar flow in a tube with multiple regularly spaced twisted tapes. Int. J. Therm. Sci. 2012, 58, 157–167. [Google Scholar] [CrossRef]
- Saleh, A.; Rasheed, S.; Smasem, R. Convection Heat Transfer in a Channel of Different Cross Section Filled with Porous Media. Kufa J. Eng. 2018, 9, 57–73. [Google Scholar] [CrossRef]
- Rasheed, S.A.; Abood, J.M. Force Convection Heat transfer from a Different Cross Section Cylinder Embedded in Porous Media. J. Eng. Sci. 2017, 20, 727–736. [Google Scholar] [CrossRef]
- Ibrahim, T.A.; Gomaa, A. Thermal Performance Criteria of Elliptic Tube Bundle in Crossflow. Int. J. Therm. Sci. 2009, 48, 2148–2158. [Google Scholar] [CrossRef]
- Yang, M.; Wang, X.; Wang, Z.; Li, Z.; Zhang, Y. Correlation for turbulent convection heat transfer in elliptical tubes by numerical simulations. Front. Heat Mass Transf. (FHMT) 2018, 11, 1–6. [Google Scholar] [CrossRef]
- Kumar, M.; Baig, F.; Asrar, W. Evolution of chaotic natural convection in a rectangular enclosure with mixed boundary conditions. Numer. Heat Transf. Part. A Appl. 1998, 43, 4037–4054. [Google Scholar] [CrossRef]
- Brown, C.K.; Gauvin, W.H. Combined free and forced convection heat transfer in aiding flow. Can. Chem. Eng. J. 1965, 306–318. [Google Scholar] [CrossRef]
- Sieder, E.N.; Tate, C.E. Heat transfer and pressure drop of liquids in tubes. Ind. Eng. Chem. 1936, 2, 1429–1435. [Google Scholar] [CrossRef]
- Petukhov, B.S.; Polyakov, A.F. Experimental investigation of gravitational fluid flow in a horizontal tube. High Temp. 1967, 5, 75–81. [Google Scholar]
- Thomas, S.; Sobhan, C.B.P. A review of experimental investigations on thermal phenomena in nanofluids. Nanoscale Res. Lett. 2011, 6, 377. [Google Scholar] [CrossRef]
- Choi, U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles. ASME FED 1995, 231, 99–103. [Google Scholar]
- Maiga, S.E.B.; Nguyen, C.T.; Galanis, N.; Roy, G. Heat transfer enhancement in forced convection laminar tube flow by using nanofluids. In Proceedings of the CHT-04 ICHMT International Symposium Advances Computational Heat Transfer, Bergen, Norway, 19–24 April 2004. Paper No. CHT-04-101 25p. [Google Scholar]
- Pop, C.; Fohanno, S.; Polidori, G.; Nguyen, C.T. Analysis of laminar-to-turbulent threshold with water γ Al2O3 and ethylene glycol Al2O3 nanofluids in free convection. In Proceedings of the 5th IASME/WSEAS Int. Conference on Heat Transfer, Thermal Engineering and Environment, Athens, Greece, 25–27 August 2007; p. 188. [Google Scholar]
- Farajollahi, B.; Etemad, S.G.; Hojjat, M. Heat transfer of nanofluids in a shell and tube heat exchanger. Int. J. Heat Mass Transf. 2010, 53, 12–17. [Google Scholar] [CrossRef]
- Sow, T.M.O.; Halelfadl, S.; Lebourlout, S.; Nguyen, C.T. Experimental study of the freezing point of Al2O3 water nanofluid. Adv. Mech. Eng. 2012, 162961. [Google Scholar] [CrossRef]
- Beiki, H.; Esfahany, M.N.; Etesami, N. Laminar forced convective mass transfer of γ-Al2O3/electrolyte nanofluid in a circular tube. Int. J. Therm. Sci. 2013, 64, 251–256. [Google Scholar] [CrossRef]
- Esmaeilzadeh, E.; Almohammadi, H.; Nokhosteen, A.; Motezaker, A.; Omrani, A.N. Study on heat transfer and friction factor characteristics of Al2O3/water through circular tube with twisted tape inserts with different thicknesses. Int. J. Therm. Sci. 2014, 82, 72–83. [Google Scholar] [CrossRef]
- Abdul-Aziz, M.; Azza, H.A.; Elkhatib, H.; Othman, S.H. Effect of operating parameters on the transient behaviour of gravity-assisted heat-pipe using radio chemically prepared Al2O3 nano-fluid. Adv. Powder Technol. 2016, 27, 1651–1662. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ganesh, N.V.; Hakeem, A.K.A.; Ganga, B.; Lorenzini, G. Influences of an effective Prandtl number model on nano boundary layer flow of Al2O3–H2O and Al2O3–C2H6O2 over a vertical stretching sheet. Int. J. Heat Mass Transf. 2016, 98, 616–623. [Google Scholar] [CrossRef]
- Ganesh, N.V.; Al-Mdallal, Q.M.; Kameswaran, P.K. Numerical study of MHD effective Prandtl number boundary layer flow of Al2O3 nanofluids past a melting surface. Case Stud. Therm. Eng. 2019, 13, 100413. [Google Scholar] [CrossRef]
- Putra, N.; Roetzel, W.; Das, S.K. Natural convection of nano-fluids. Heat Mass Transf. 2003, 39, 775–784. [Google Scholar] [CrossRef]
- Okada, M.; Suzuki, T. Natural convection of water-fine particle suspension in a rectangular cell. Int. J. Heat Mass Transf. 1997, 40, 3201–3208. [Google Scholar] [CrossRef]
- Kang, C.; Okada, M.; Hattori, A.; Oyama, K. Natural convection of water-fine particle suspension in a rectangular vessel heated and cooled from opposing vertical walls (classification of the natural convection in the case of suspension with narrow-size distribution). Int. J. Heat Mass Transf. 2001, 44, 2973–2982. [Google Scholar] [CrossRef]
- Okada, M.; Oyama, K.; Kang, C. Natural convection of water or aqueous solution-fine particle suspension in a rectangular cell. In Proceedings of the 11th International Heat Transfer Conference, Kyongju, Republic of Korea, 23–28 August 1998; Taylor: Levittown, PA, USA, 1998; Volume 3, pp. 525–530. [Google Scholar]
- Colla, L.; Fedele, L.; Buschmann, M.H. Laminar mixed convection of TiO2-water nanofluid in horizontal uniformly heated pipe flow. Int. J. Therm. Sci. 2015, 97, 26–40. [Google Scholar] [CrossRef]
- Mahmood, Z.; Eldin, S.M.; Soliman, A.F.; Assiri, T.A.; Khan, U.; Mahmoud, S.R. Impact of an effective Prandtl number model on the flow of nanofluids past an obliques stagnation point in convective surface. Heliyon 2023, 9, e13224. [Google Scholar] [CrossRef]
- Maiga, S.E.B.; Palm, S.J.; Nguyen, C.T.; Roy, G.; Galanis, N. Heat transfer enhancement by using nanofluids in forced convection flows. Int. J. Heat Fluid Flow 2005, 26, 530–546. [Google Scholar] [CrossRef]
- Coutier, J.P.; Greif, R. An investigation of laminar mixed convection inside a horizontal tube with isothermal wall conditions. Int. J. Heat Mass Transf. 1985, 28, 1293–1305. [Google Scholar] [CrossRef]
- Li, W.; Feng, Z. Laminar mixed convection of large-Prandtl-number in-tube nanofluid flow, Part I: Experimental Study. Int. J. Heat Mass Transf. 2013, 65, 919–927. [Google Scholar] [CrossRef]
- Li, W.; Feng, Z. Laminar mixed convection of large-Prandtl-number in-tube nanofluid flow Part II: Correlations. Int. J. Heat Mass Transf. 2013, 65, 928–935. [Google Scholar] [CrossRef]
- Park, H.-K.; Chung, B.-J. Optimal tip clearance in the laminar forced convection heat transfer of a finned plate in a square duct. Int. J. Heat Mass Transf. 2015, 63, 73–81. [Google Scholar] [CrossRef]
- Barletta, A.; Magyari, E. Forced convection with viscous dissipation in the thermal entrance region of a circular duct with prescribed wall heat flux. Int. J. Heat Mass Transf. 2007, 50, 26–35. [Google Scholar] [CrossRef]
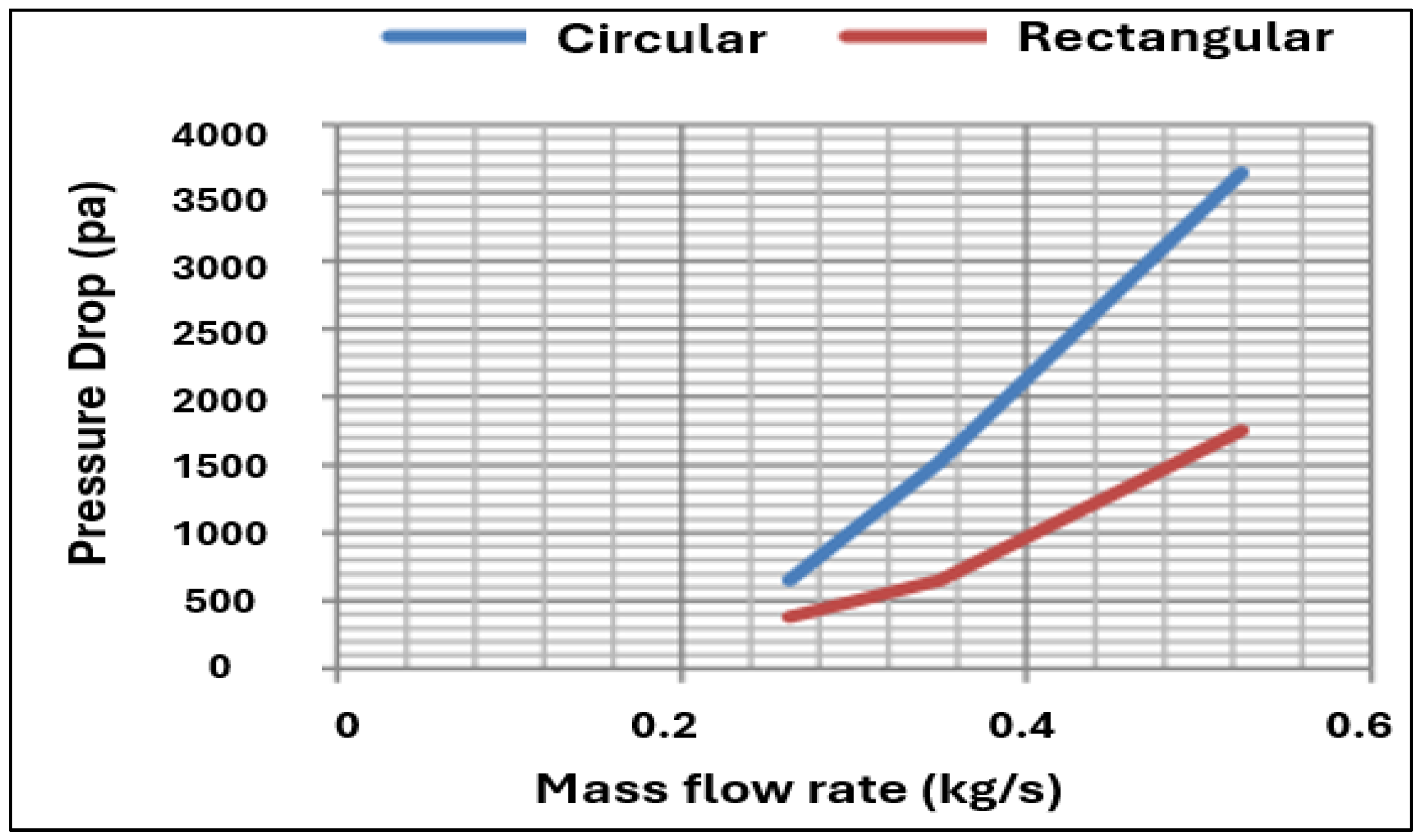
- Bisht, P.; Joshi, M.; Gupta, A. Comparison of Heat Transfer between a Circular and Rectangular Tube Heat Exchanger by using Ansys Fluent. Int. J. Therm. Technol. 2014, 4, 88–92. [Google Scholar]
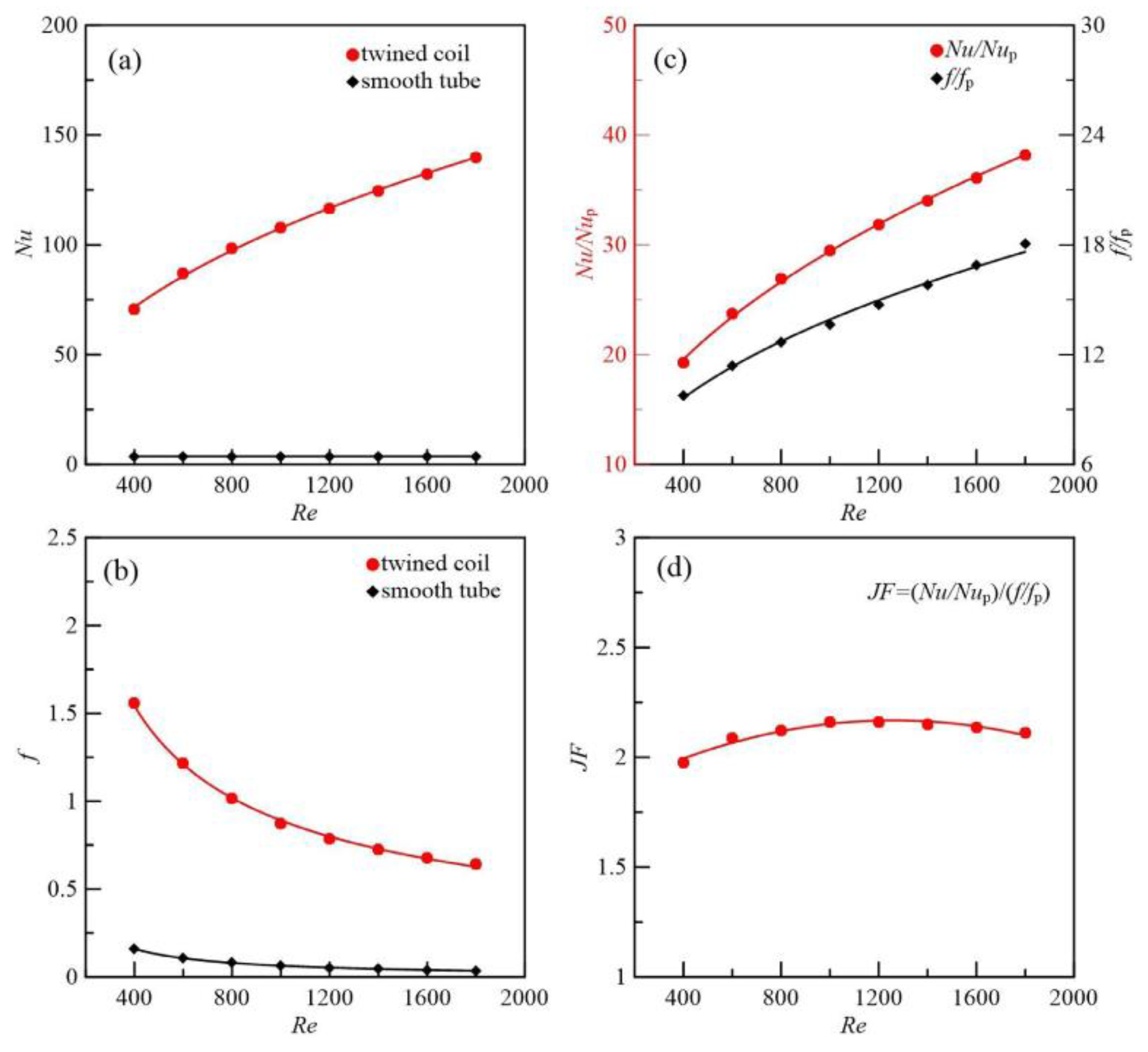
- Dang, W.; Wang, L.B. Convective heat transfer enhancement mechanisms in circular tube inserted with a type of twined coil. Int. J. Heat Mass Transf. 2021, 169, 120960. [Google Scholar] [CrossRef]
- Lin, Z.M.; Wang, L.B.; Lin, M.; Dang, W.; Zhang, Y.H. Numerical study of the laminar flow and heat transfer characteristics in a tube inserting a twisted tape having parallelogram winglet vortex generators. Appl. Therm. Eng. 2017, 115, 644–658. [Google Scholar] [CrossRef]
- Saysroy, A.; Eiamsa-ard, S. Enhancing convective heat transfer in laminar and turbulent flow regions using multi-channel twisted tape inserts. Int. J. Therm. Sci. 2017, 121, 55–74. [Google Scholar] [CrossRef]
- Saysroy, A.; Eiamsa-ard, S. Periodically fully-developed heat and fluid flow behaviours in a turbulent tube flow with square-cut twisted tape inserts. Appl. Therm. Eng. 2017, 112, 895–910. [Google Scholar] [CrossRef]
- Agarwal, S.K.; Rao, M.R. Heat transfer augmentation for the flow of a viscous liquid in circular tubes using twisted tape inserts. Int. J. Heat Mass Transf. 1996, 39, 3547–3557. [Google Scholar] [CrossRef]
- Li, P.X.; Liu, Z.C.; Liu, W.; Chen, G. Numerical study on heat transfer enhancement characteristics of tube inserted with centrally hollow narrow twisted tapes. Int. J. Heat Mass Transf. 2015, 88, 481–491. [Google Scholar] [CrossRef]
- Garcia, A.; Vicente, P.G.; Viedma, A. Experimental study of heat transfer enhancement with wire coil inserts in laminar-transition-turbulent regimes at different Prandtl numbers. Int. J. Heat Mass Transf. 2005, 48, 4640–4651. [Google Scholar] [CrossRef]
- Vahidifar, S.; Kahrom, M. Experimental study of heat transfer enhancement in a heated tube caused by wire-coil and rings. J. Appl. Fluid Mech. 2015, 8, 885–892. [Google Scholar] [CrossRef]
- Hong, Y.X.; Du, J.; Wang, S.F.; Huang, S.M.; Ye, W.B. Heat transfer and fluid flow behaviors in a tube with modified wire coils. Int. J. Heat Mass Transf. 2018, 124, 1347–1360. [Google Scholar] [CrossRef]
- Hong, Y.X.; Du, J.; Wang, S.F.; Ye, W.B.; Huang, S.M. Turbulent thermal-hydraulic and thermodynamic characteristics in a traverse corrugated tube fitted with twin and triple wire coils. Int. J. Heat Mass Transf. 2019, 130, 483–495. [Google Scholar] [CrossRef]
- Du, J.; Hong, Y.X.; Wang, S.F.; Ye, W.B.; Huang, S.M. Experimental thermal and flow characteristics in a traverse corrugated tube fitted with regularly spaced modified wire coils. Int. J. Therm. Sci. 2018, 133, 330–340. [Google Scholar] [CrossRef]
- Promvonge, P. Thermal performance in circular tube fitted with coiled square wires. Energy Convers. Manag. 2008, 49, 980–987. [Google Scholar] [CrossRef]
- Keklikcioglu, O.; Ozceyhan, V. Experimental investigation on heat transfer enhancement in a circular tube with equilateral triangle cross sectioned coiled-wire inserts. Appl. Therm. Eng. 2018, 131, 686–695. [Google Scholar] [CrossRef]
- Chae, M.S.; Chung, B.J. Laminar mixed-convection experiments in horizontal pipes and derivation of a semi-empirical buoyancy coefficient. Int. J. Therm. Sci. 2014, 84, 335–346. [Google Scholar] [CrossRef]
- Sutthivirode, K.; Suparos, T. A study of forced convection heat transfer: Constant heat flux. In Proceedings of the 2018 5th International Conference on Business and Industrial Research: Smart Technology for Next Generation of Information, Engineering, Business and Social Science, ICBIR 2018, Bangkok, Thailand, 17–18 May 2018; pp. 236–241. [Google Scholar] [CrossRef]
- Bernier, M.A.; Baliga, B.R. Conjugate conduction and laminar mixed convection in vertical pipes for upward flow and uniform wall heat flux. Numer. Heat Transf. Part A Appl. 1992, 21, 313–332. [Google Scholar] [CrossRef]
- Khan, A.; Bera, P. Linear instability of concentric annular flow: Effect of Prandtl number and gap between cylinders. Int. J. Heat Mass Transf. 2020, 152, 119530. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.-R.; Wu, C.-M.; Liu, Q.-S. Flow pattern transition and destabilization mechanism of thermocapillary convection for low Prandtl number fluid in a deep annular pool with surface heat dissipation. Int. J. Heat Mass Transf. 2018, 126, 118–127. [Google Scholar] [CrossRef]
- Liu, H.; Zeng, Z.; Yin, L.; Qiu, Z.; Qiao, L. Influence of aspect ratio on the onset of thermocapillary flow instability in annular pool heated from inner wall. Int. J. Heat Mass Transf. 2019, 129, 746–752. [Google Scholar] [CrossRef]
- Liu, H.; Zeng, Z.; Yin, L.; Qiao, L.; Zhang, L. Instability mechanisms for thermocapillary flow in an annular pool heated from inner wall. Int. J. Heat Mass Transf. 2018, 127, 996–1003. [Google Scholar] [CrossRef]
- Liu, H.; Zeng, Z.; Yin, L.; Qiu, Z.; Zhang, L. Effect of the Prandtl number on the instabilities of the thermocapillary flow in an annular pool. Phys. Fluids 2019, 31, 034103. [Google Scholar] [CrossRef]
- Meyer, J.P.; Everts, M. Single—Phase mixed convection of developing and fully developed flow in smooth horizontal circular tubes in the laminar and transitional flow regimes. Int. J. Heat Mass Transf. 2018, 117, 1251–1273. [Google Scholar] [CrossRef]
- Everts, M.; Meyer, J.P. Heat transfer of developing and fully in smooth horizontal tubes in the transitional flow regime. Int. J. Heat Mass Transf. 2018, 117, 1331–1351. [Google Scholar] [CrossRef]
- Meyer, J.P.; Everts, M. Relationship between pressure drop and heat transfer of developing and fully developed flow in smooth horizontal circular tubes in laminar, transitional, quasi-turbulent and turbulent flow regimes. Int. J. Heat Mass Transf. 2018, 117, 1231–1250. [Google Scholar] [CrossRef]
- Zhang, S. Mixed convective heat transfer of medium Prandtl number fluids in horizontal circular tubes. Int. J. Heat Mass Transf. 2022, 190, 122740. [Google Scholar] [CrossRef]
- Feng, Z.; Luo, X.; Guo, F.; Li, H.; Zhang, J. Numerical investigation on laminar flow and heat transfer in rectangular microchannel heat sink with wire coil inserts. Appl. Therm. Eng. 2017, 116, 597–609. [Google Scholar] [CrossRef]
- Saha, S.K. Thermal and friction characteristics of laminar flow through rectangular and square ducts with transverse ribs and wire coil inserts. Exp. Therm. Fluid Sci. 2010, 34, 63–72. [Google Scholar] [CrossRef]
- Saha, S.K. Thermal and friction characteristics of turbulent flow through rectangular and square ducts with transverse ribs and wire-coil inserts. Exp. Therm. Fluid Sci. 2010, 34, 575–589. [Google Scholar] [CrossRef]
- Taher, et.al. Poiseuille-Rayleigh-Benard mixed convection flow in a channel: Heat transfer and fluid flow patterns. Int. J. Heat Mass Transf. 2021, 180, 121745. [Google Scholar] [CrossRef]
- Hermany, L.; Lorenzini, G.; Klein, R.J.; Zinani, F.F.; dos Santos, E.D.; Isolid, L.A.; Rocha, L.A.O. Constructal Design Applied to Elliptic Tubes in Convective Heat Transfer Cross-Flow of Viscoplastic Fluids. Int. J. Heat Mass Transf. 2018, 116, 1054–1063. [Google Scholar] [CrossRef]


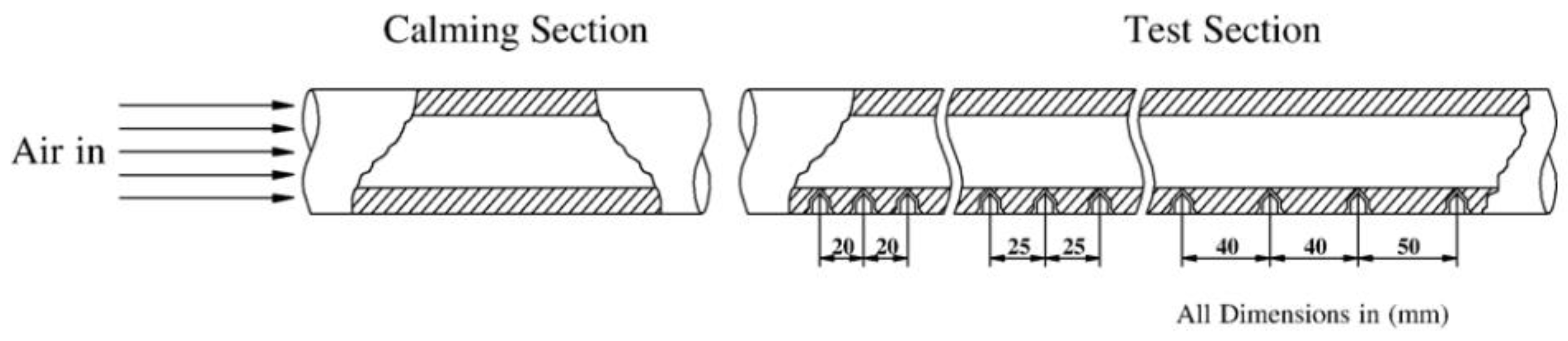
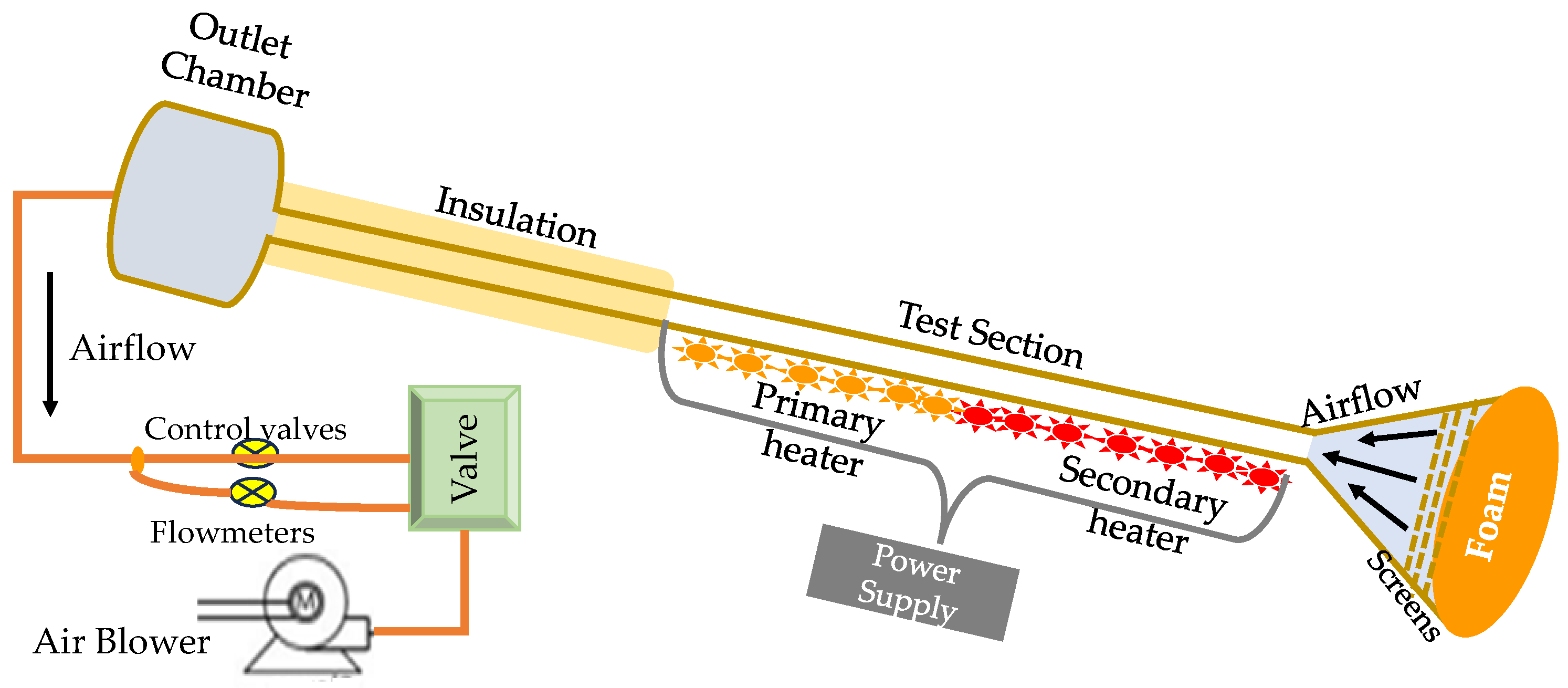
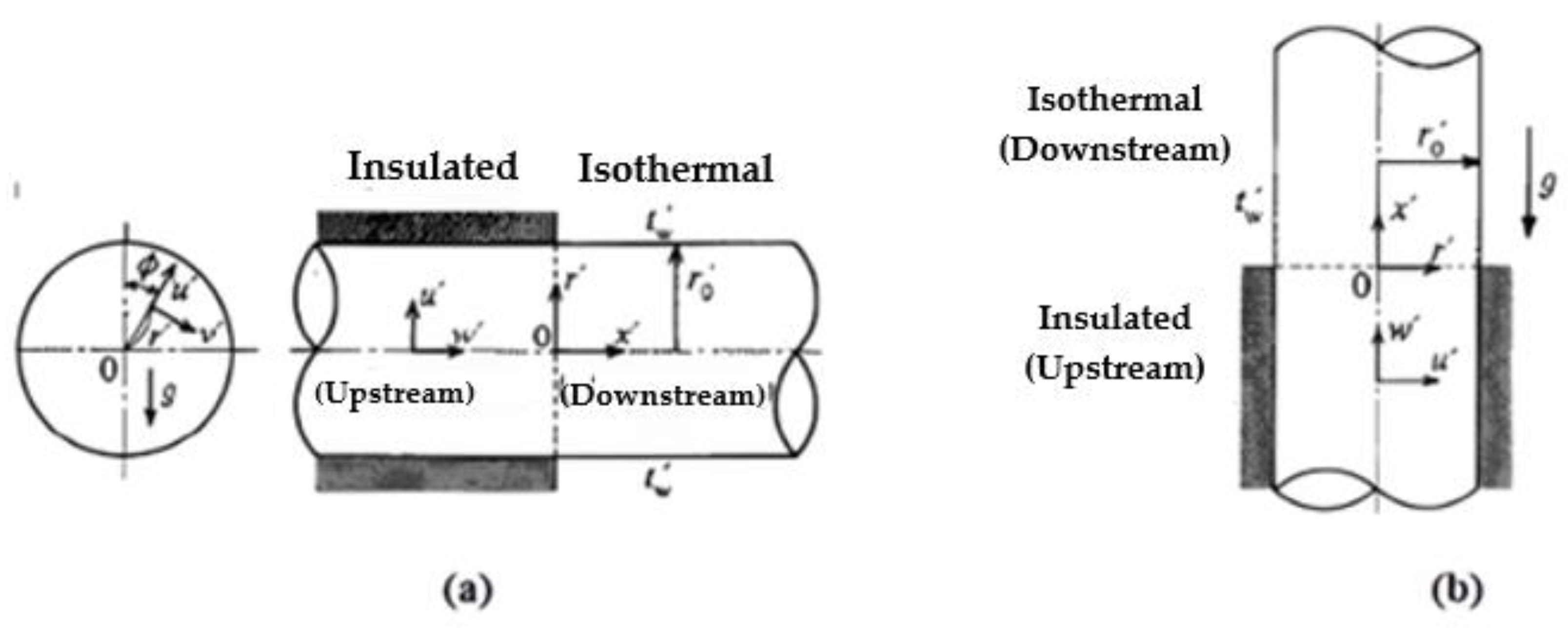
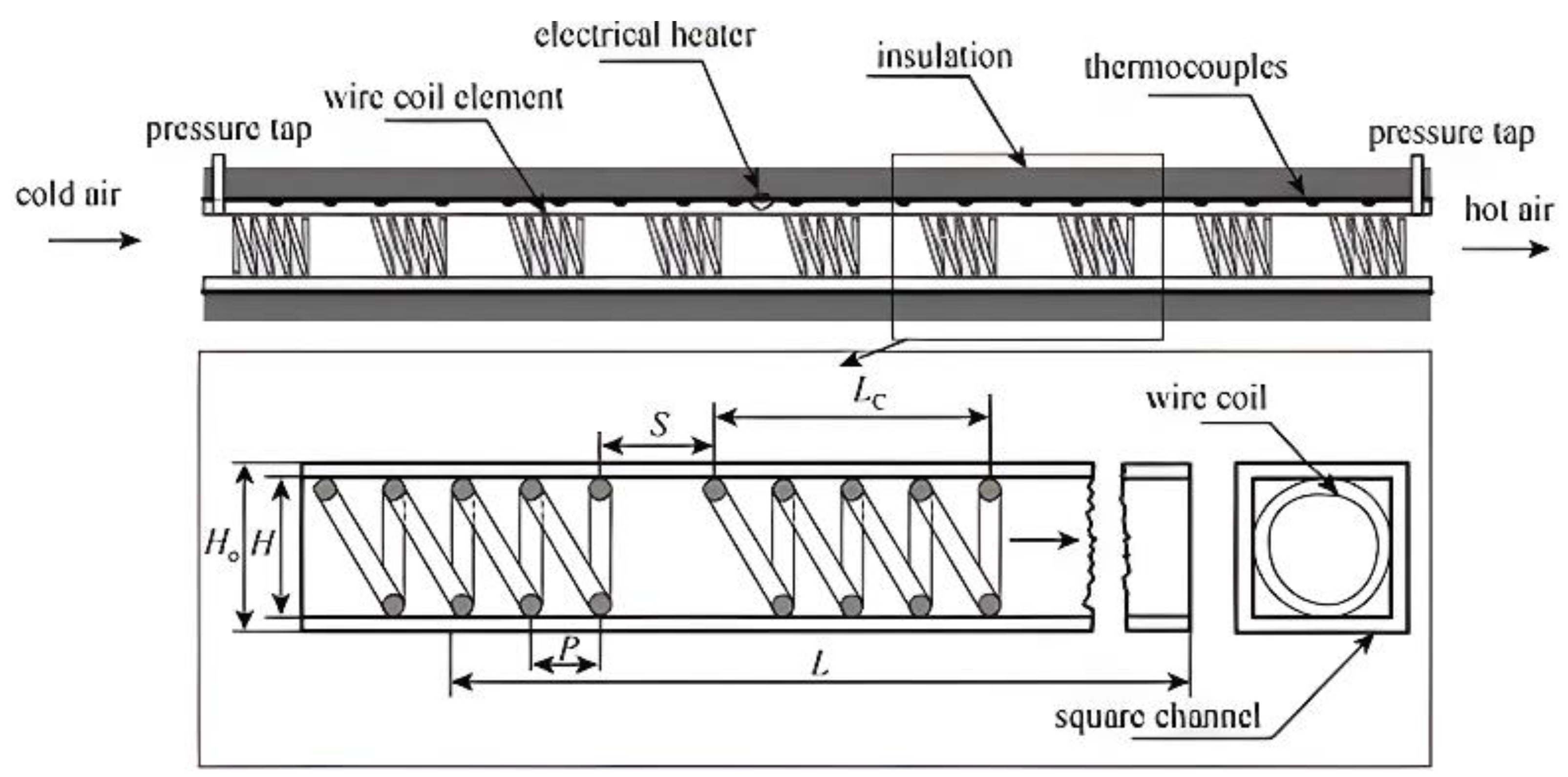
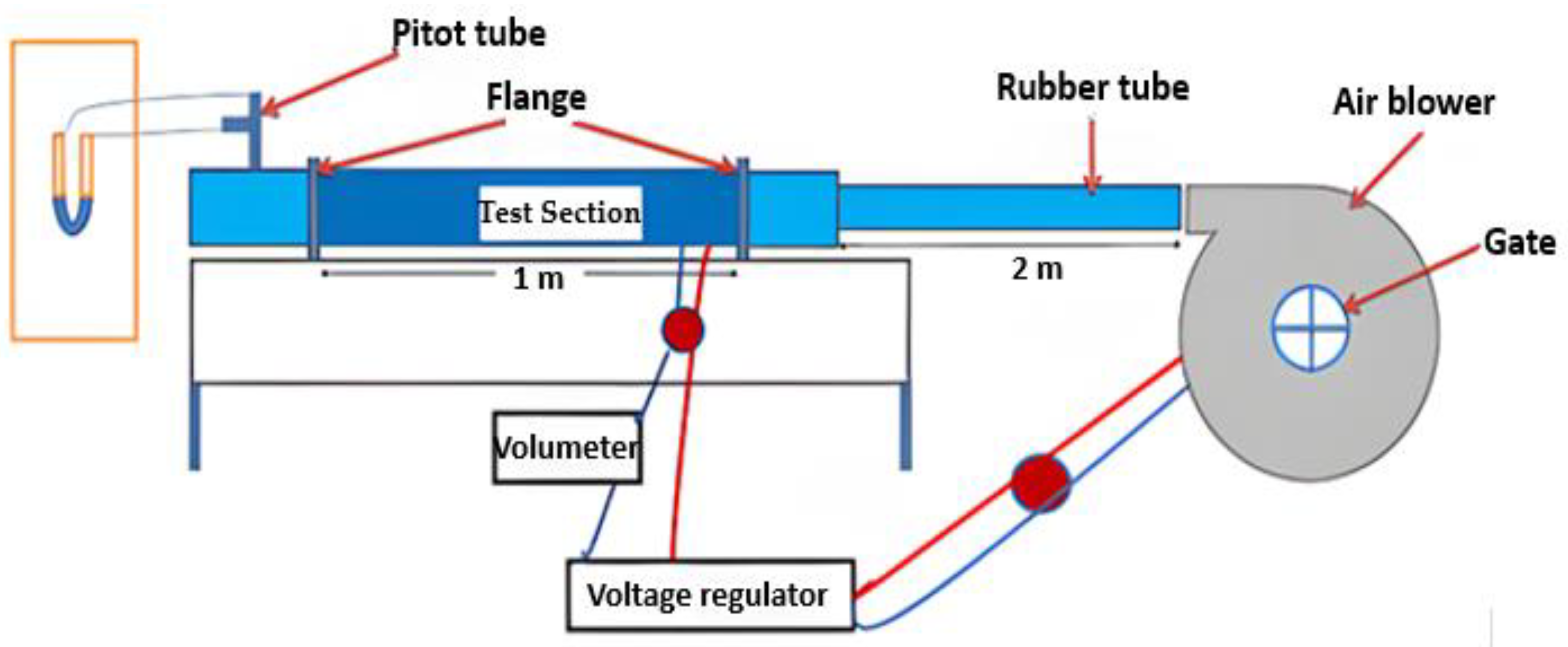


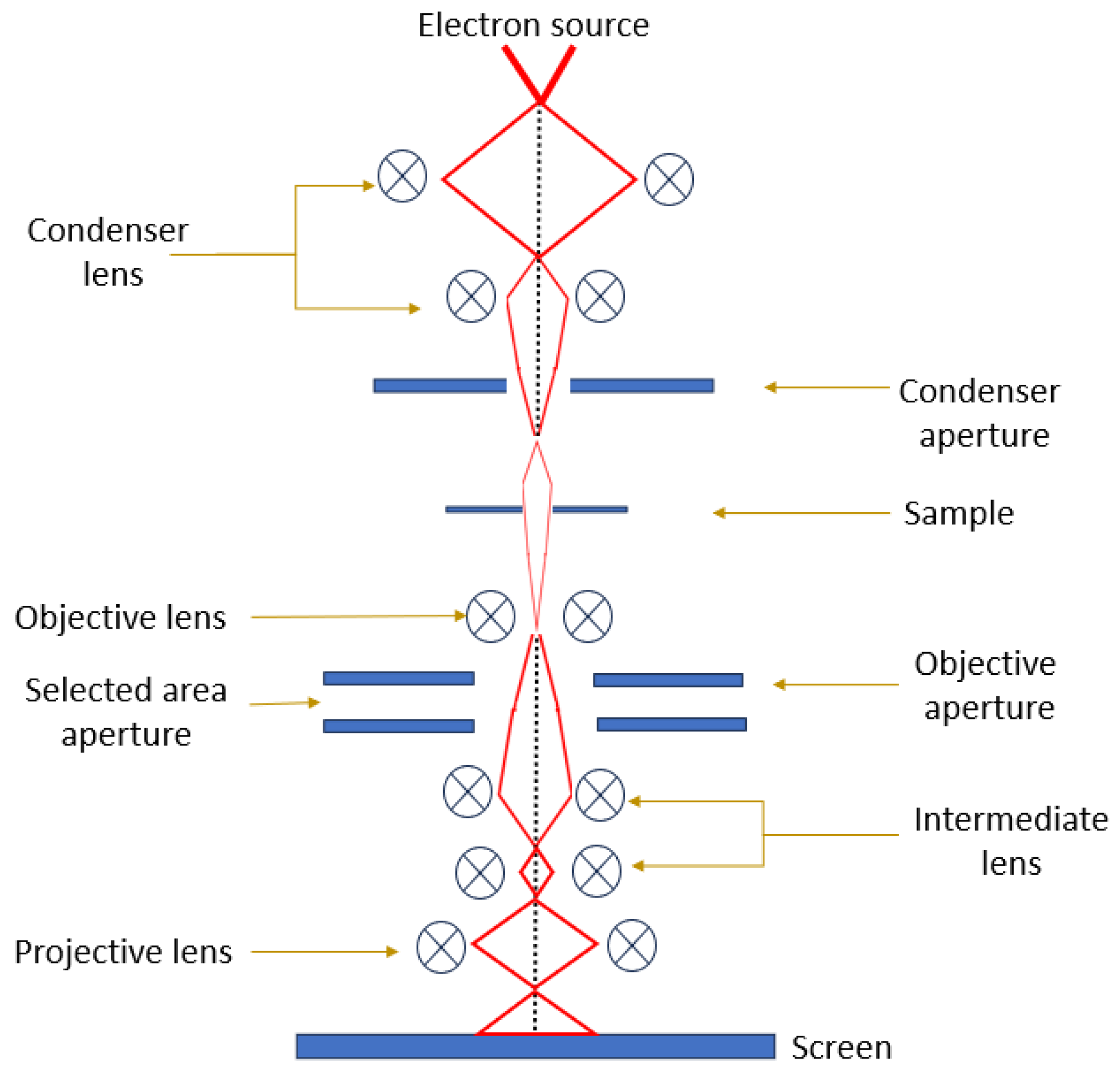

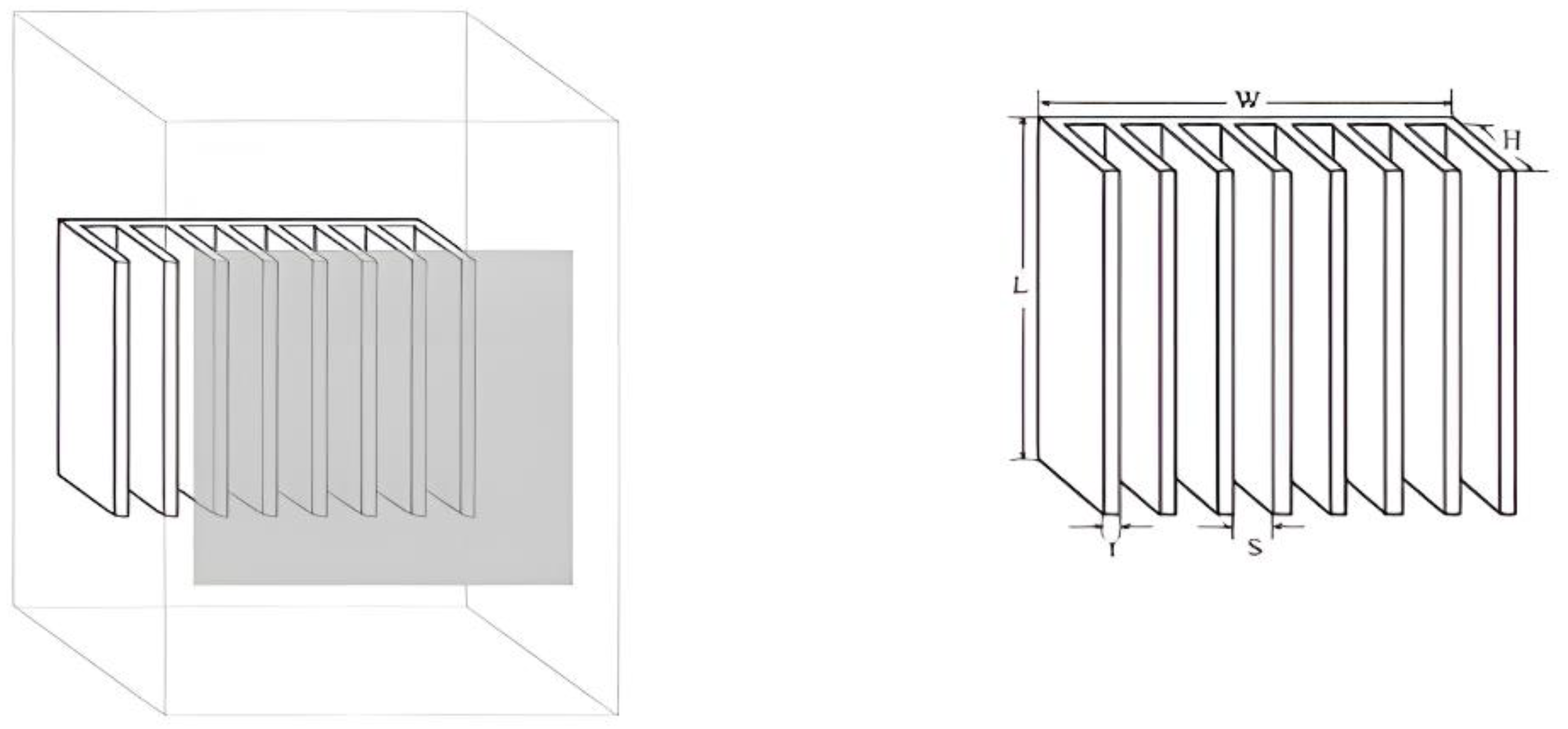
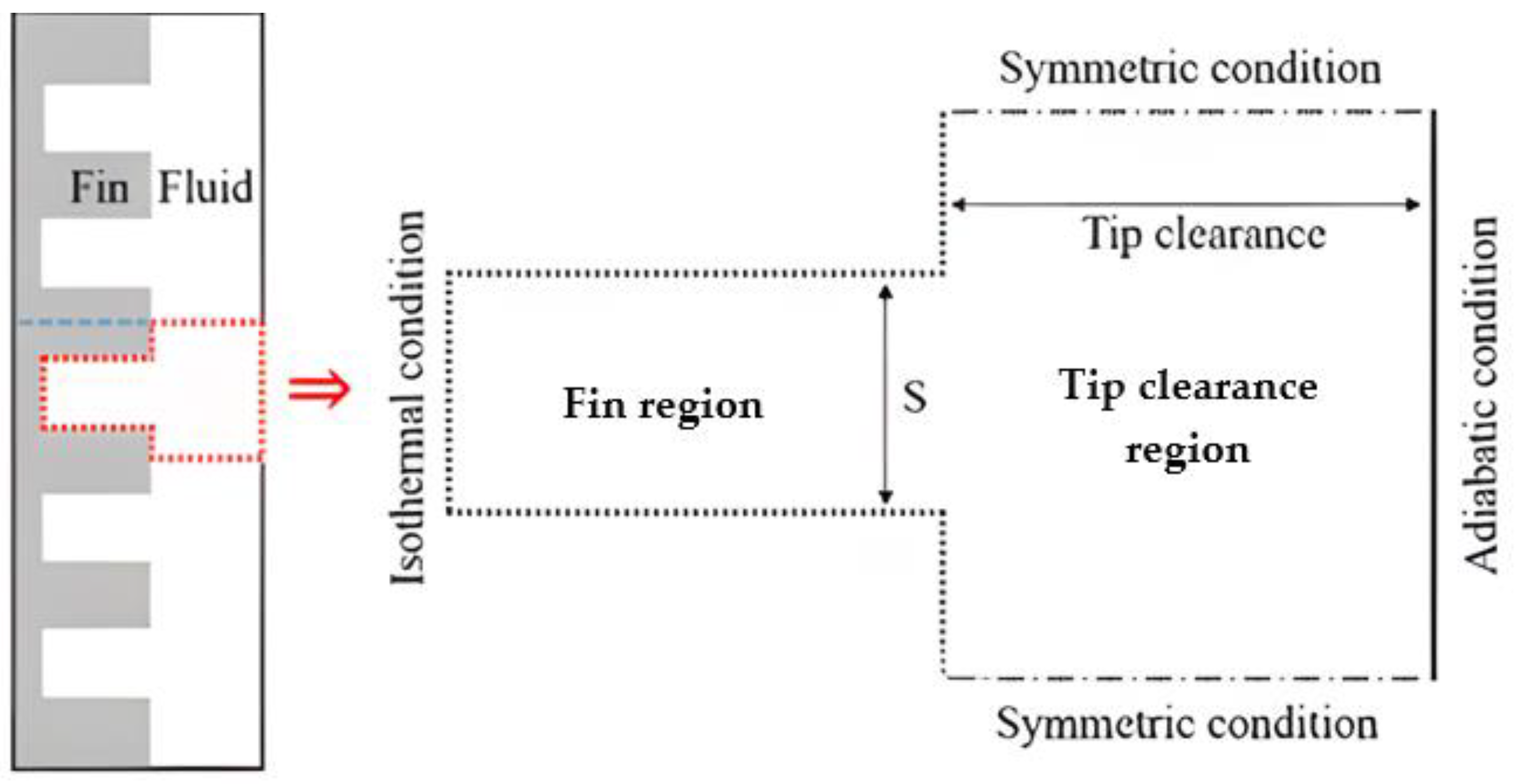
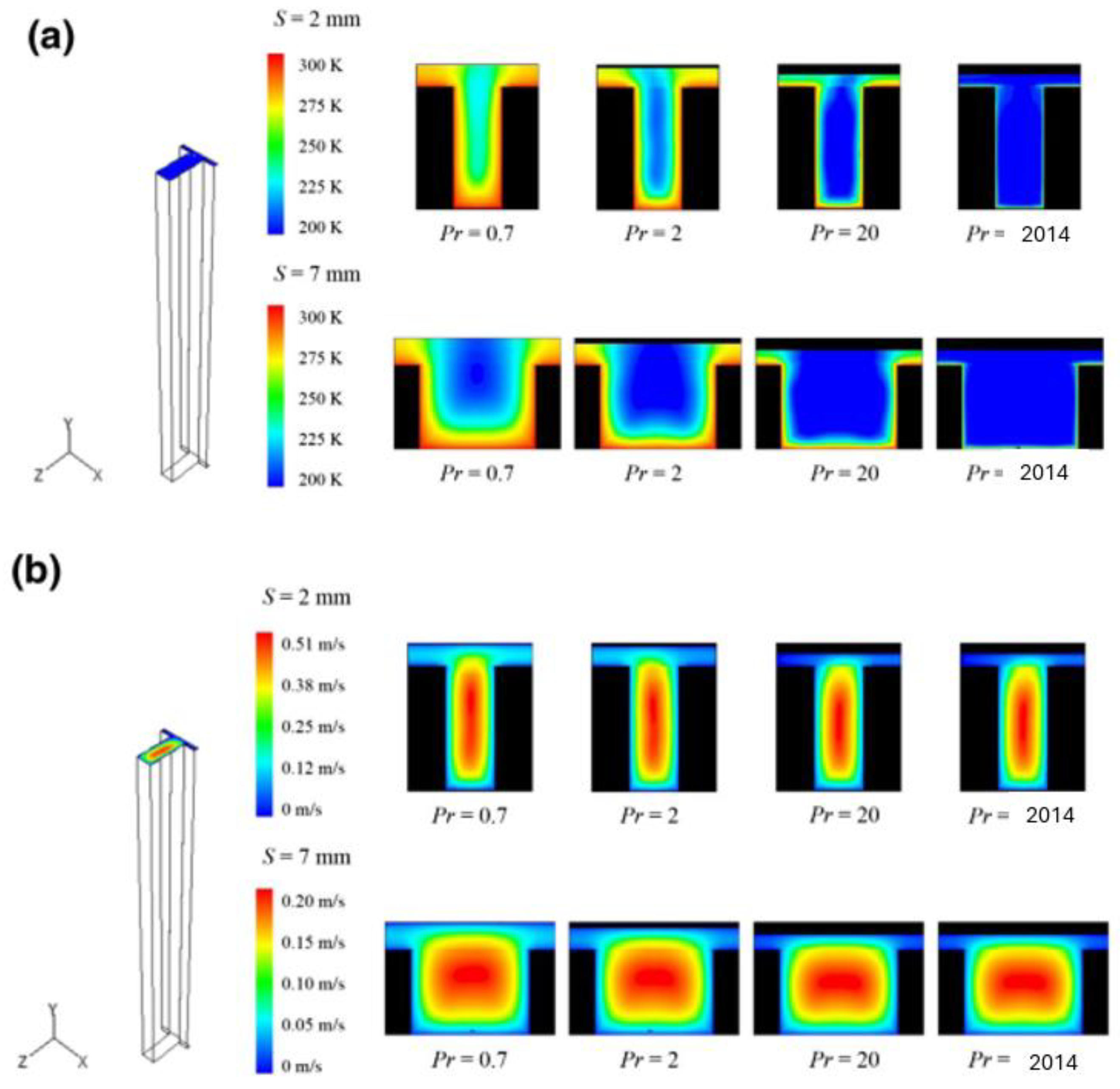
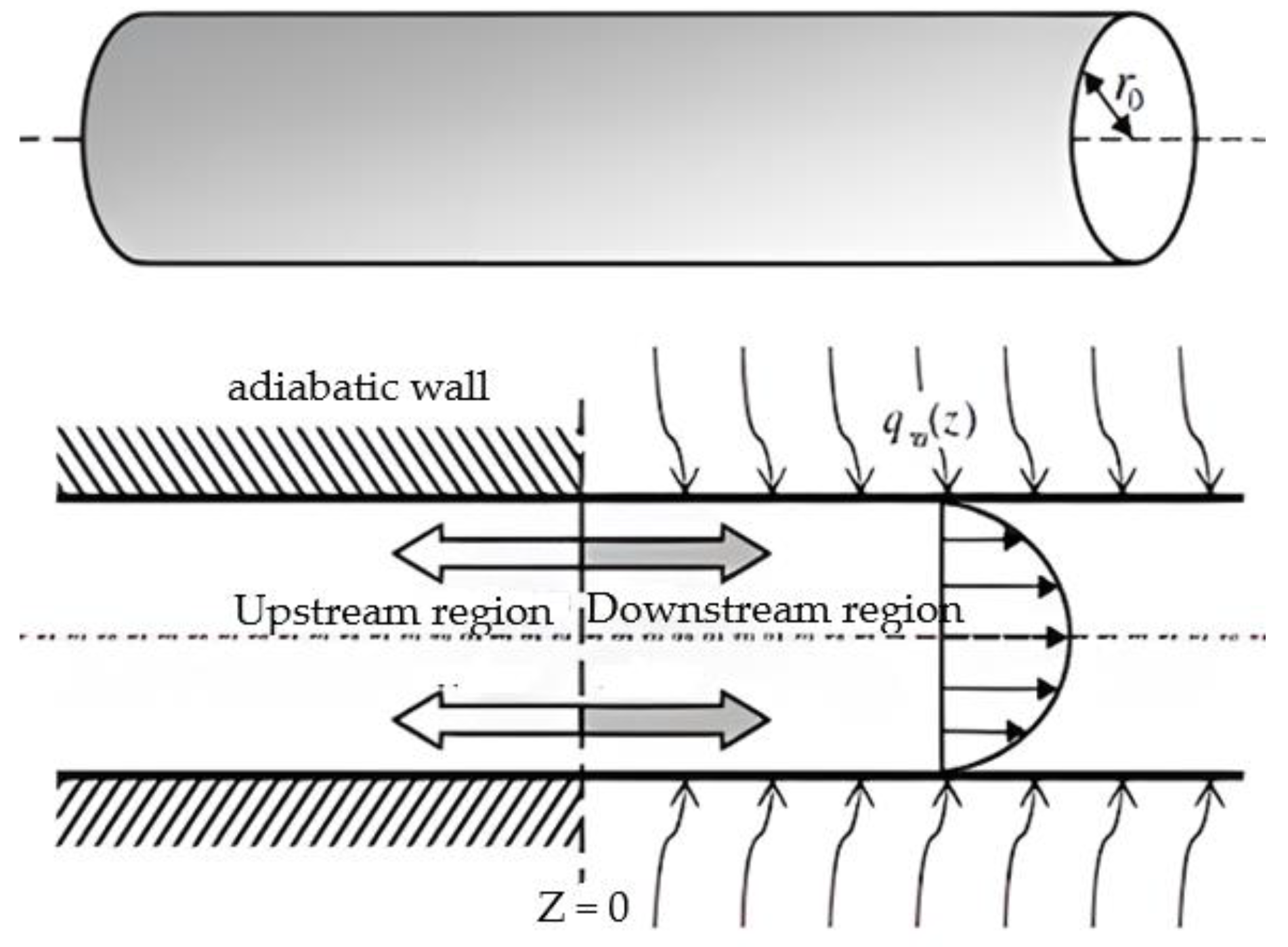
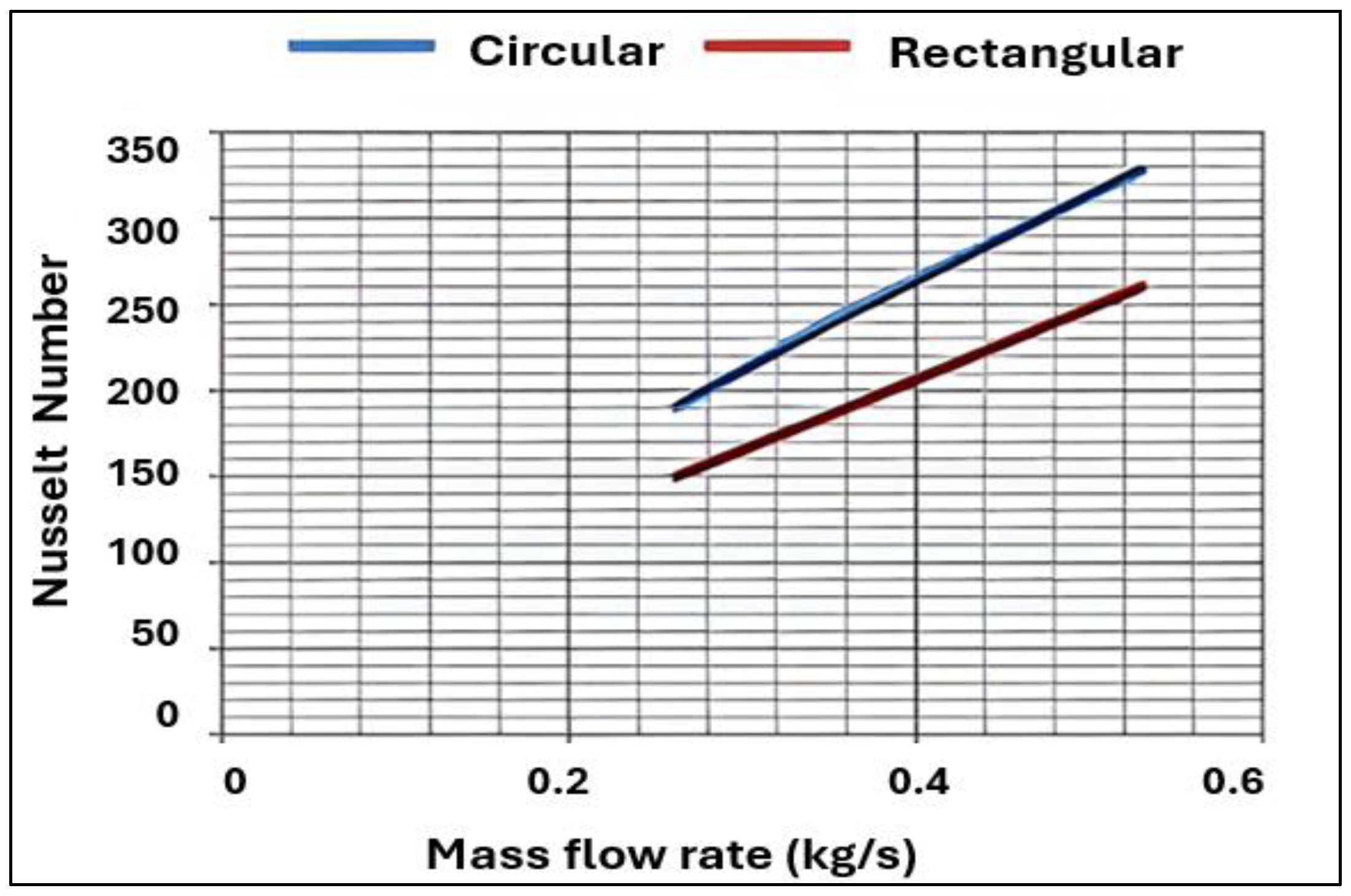
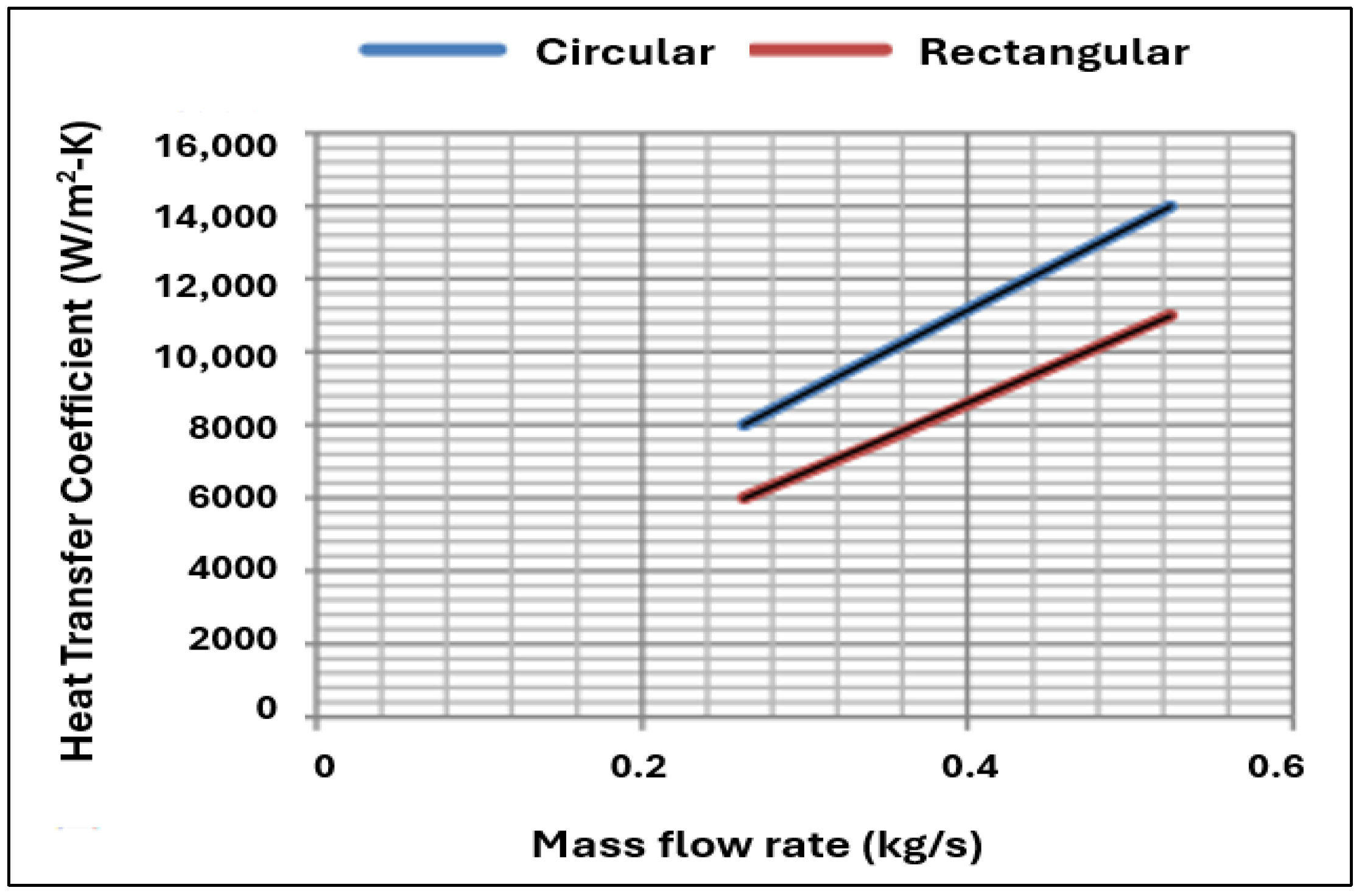


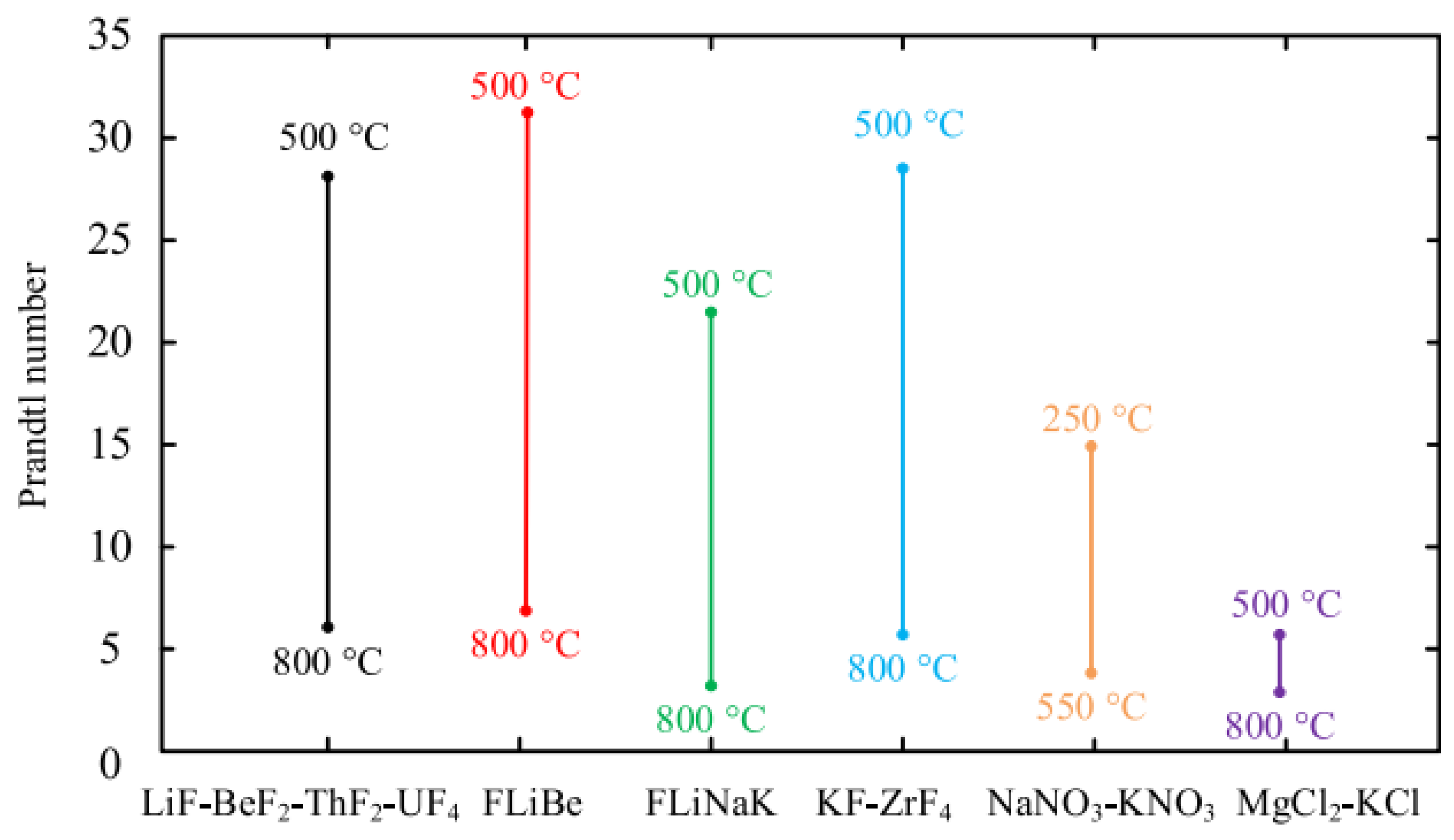
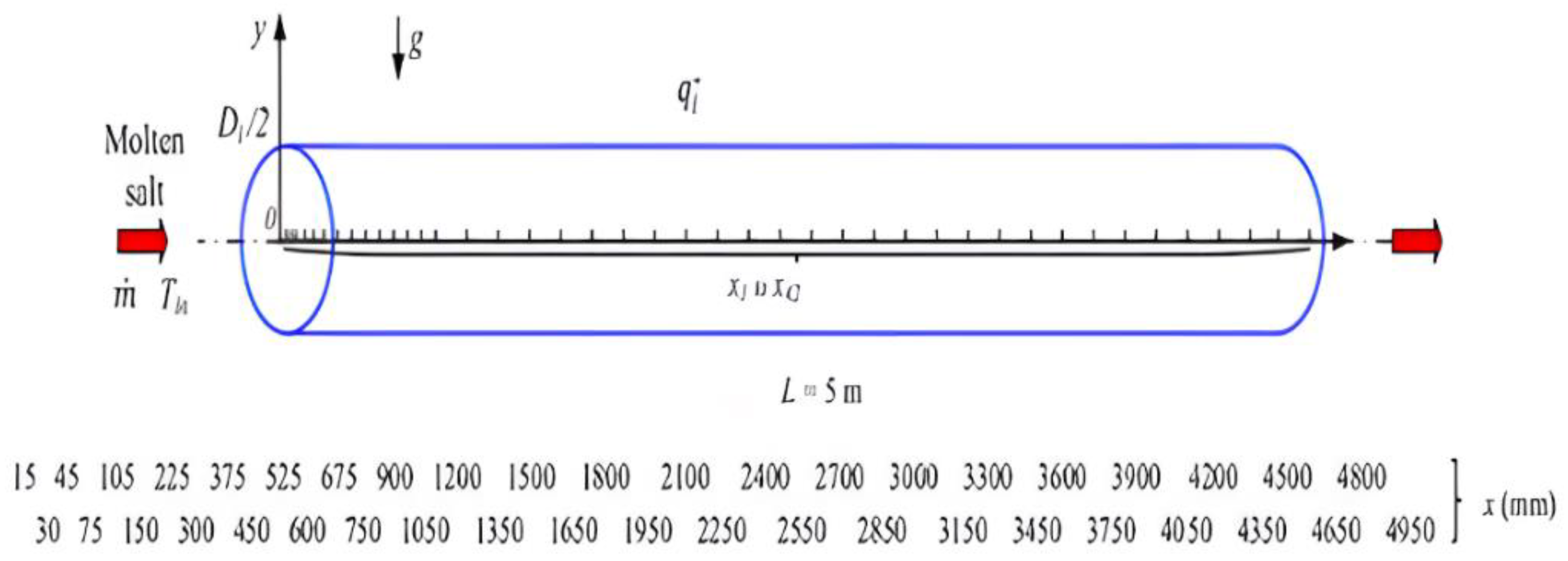

| Working Medium | Pr | Applications | ||
|---|---|---|---|---|
| Prandtl Number classification | Low | Liquid Metals Mercury | 0.0015 |
|
| Binary Helium Mix [11] He + CH4 He + N2 He + O2 He + CO2 He + SF6 He + CF4 He + Xe | 0.60 0.48 0.48 0.43 0.28 0.20 0.12 |
| ||
| Air | 0.699 |
| ||
| Oxygen (O2) | 0.63 |
| ||
| Hydrogen (H) | 0.684 |
| ||
| Carbon dioxide (CO2) | 0.76 |
| ||
| Medium -to- High | Molten salts [10,11]
| 6–28 7–31 3–21 5–27 4–15 3–5 |
| |
| Ammonia | 1.38 |
| ||
| Water (H2O) | 5–10 |
| ||
| Glycerol | 1000 |
| ||
| Glycerin | 2450 |
| ||
| Polymer melts | 10,000 |
| ||
| Inclination angle change | 90° → 0° | 0° → 90° | ||
| Position | Vertical → Horizontal | Horizontal → Vertical | ||
| Heat flux | Constant | Constant | Constant | Constant |
| Convection type | Free convection dominant | Forced convection dominant | Free convection dominant | Forced convection dominant |
| Surface temp. | ↓ | ↑ | - | - |
| Nusselt number | ↑ | - | - | ↑ |
| Reynolds number | ↓ | - | - | ↑ |
| Parameter | Horizontal Pipe | Vertical Pipe | |
|---|---|---|---|
| 1 | Distortion of transverse temperature and velocity profiles. |
|
|
| 2 | Secondary flow |
| - |
| 3 | Reversal flow |
|
|
| 4 | Wall shear stress |
|
|
| 5 | Local Nusselt number |
|
|
| Cross Section | Material | Number of Heaters | Resistance (Ohm) | Diameter of Coil (mm) | Number of Coils |
|---|---|---|---|---|---|
| Circular | Stainless steel | 4 | 27.027 | 8 | 23 |
| Rectangular | Nickel chrome | 2 | 20.8 | 0.25 | 52 |
| Triangular | Nickel chrome | 2 | 18.2 | 0.25 | 54 |
| (a): Vertical Axis | |||||
|---|---|---|---|---|---|
| Authors | Working Fluids | Tube Type | Methodology | Heat Transfers Correlation | Findings |
| Mohammed; Salman (2007) [13] | Air (Pr:0.7) | Vertical Circular Cylinder |
| = 3.7151 (/)0.11868
| When cylinder inclination θ moves:
|
| (b): Horizontal Axis | |||||
| Authors | Working Fluids | Tube Type | Method | Heat Transfer Correlation | Findings |
| Maughan and Incropera (1990) [14] | Air (Pr:0.7) | Horizontal, Parallel Plate Channel | Uniformly heated (top and bottom plates) | For smaller Ra: Nu = Convective Force Limit For larger Ra: Nu = 0.20Ra1/3 |
|
| Chou and Hwang (1988) [16] | Air (Pr:0.7) | Horizontal Tube | Uniformly heated | Re.Ra = ( Gr+ [25] Ra*= [26] |
|
| Wang et al. (1994) [18] | Hg (Pr < < 0.1) Na (Pr < < 0.1) | Horizontal and Vertical Circular Tubes | Uniformly heated | Nu vs. Abscissa Gz for Ra |
|
| ρ (kg/m3) | Cp (J/kgK) | K (W/mK) | Pr | |
|---|---|---|---|---|
| Pure water (H2O) | 998.3 | 4182 | 0.60 | 6.96 |
| ethylene glycol (C2H6O2). | 1116.6 | 2382 | 0.249 | 204 |
| Al2O3 | 3970 | 765 | 40 | - |
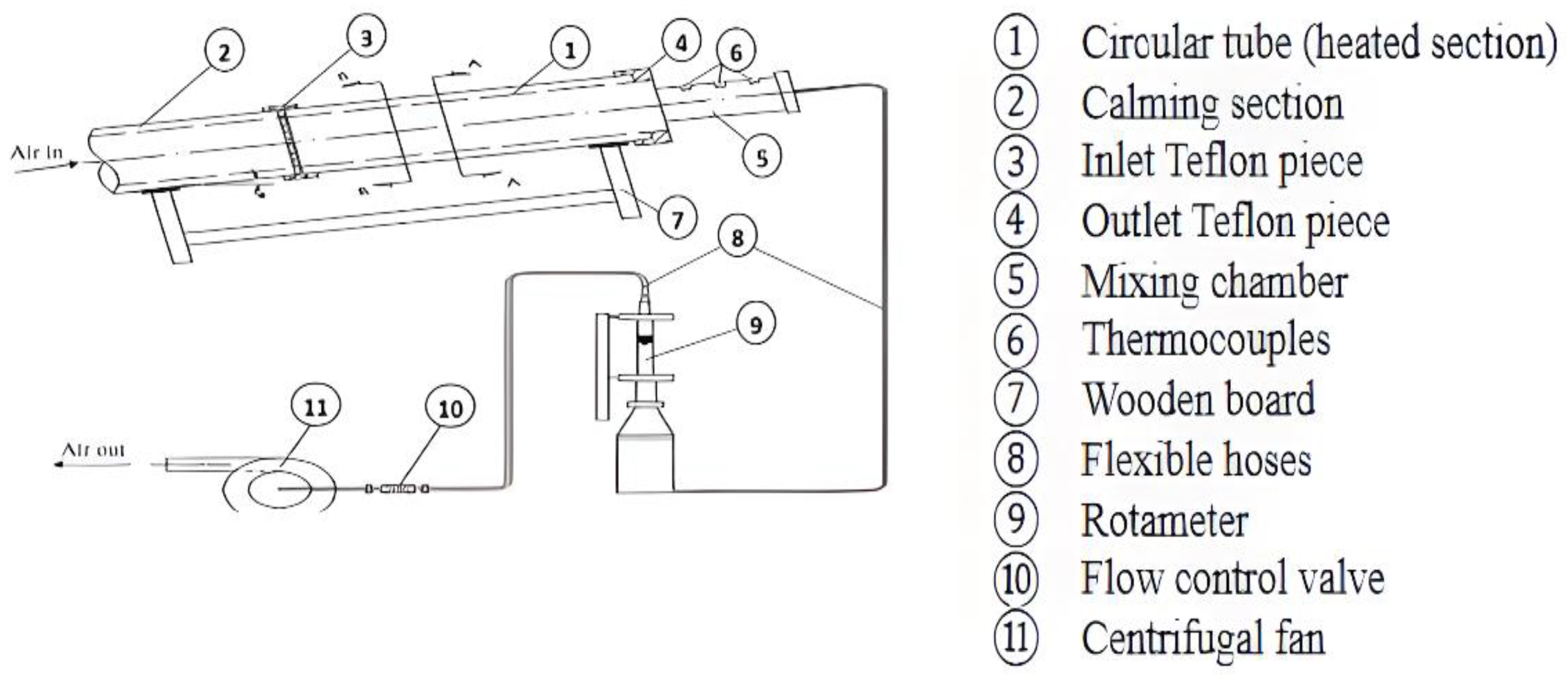
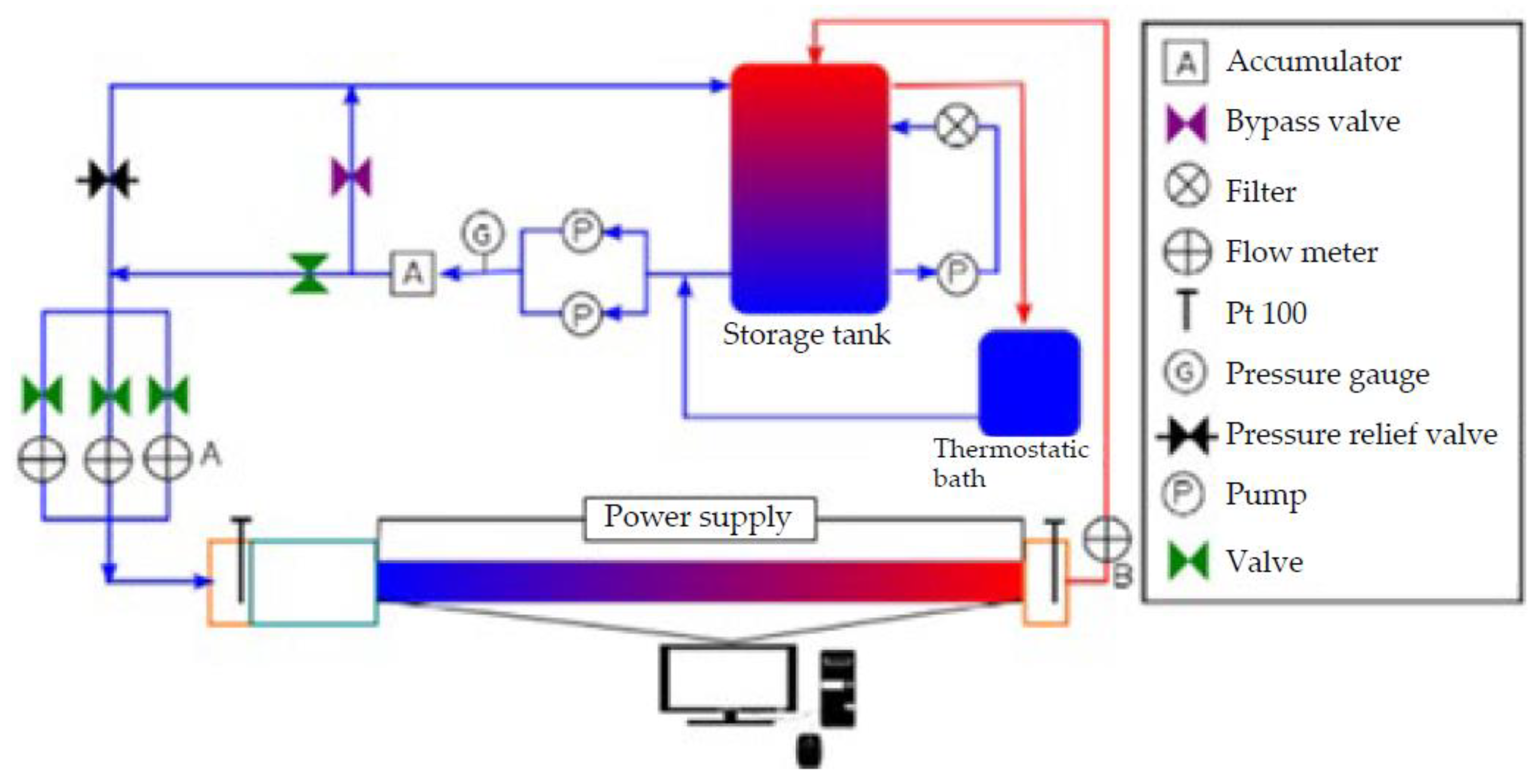
| Apparatus | Description | Process Flow | |
|---|---|---|---|
| I | Reservoir tank | Storage of fluid (Water) |
|
| 2 | High pressure Nitrogen tank | Contain compressed nitrogen gas to push the fluid from the reservoir tank. | |
| 3 | Flowmeter | To measure fluid volume/mass for flow rate determination. | |
| 4 | Needle valve | To regulate the fluid flowing through the circuit effectively and safely. | |
| 5 | Constant temperature valve | To maintain a set-point in the primary circuit of a hot water-based heating system. | |
| 6 | Test Section |
| |
| 7 | Container | The container was placed on a balance, and the average mas flow rate was determined by calculating the mass increment per unit time. | |
| 8 | Pressure indicator | To measure the state of the fluid in the system (indicate pressure) | |
| 9 | Pressure regulator | Control the pressure of a fluid by reducing a high input pressure to a lower output pressure. | |
| 10 | Safety valve | To protect other equipment/parameters by opening automatically at a certain pressure and prevent damage due to excessive pressure in the process and storage system. | |
| 11 | Data acquisition system | To collect and convert analog signals from sensors or instruments into digital values for processing. | |
| 12 | DC power supply | To supply a one-directional flow of electric charge that flows through a conductor (i.e., wire). |
| Geometry Setting | Circular Model | Rectangular Model |
|---|---|---|
| Tube length (m) | 3.0 | 3.0 |
| Diameter (m) | 0.015 | 0.015 |
| Working fluid | Water | Water |
| Inlet water temperature (K) | 323 | 323 |
| Outlet water temperature (K) | 343 | 343 |
| Constant wall temperature (K) | 373 | 373 |
| Properties of Water | Circular Model | Rectangular Model |
| Density (kg/m3) | 990 | 990 |
| Specific heat Cp (J/kg-k) | 4184 | 4184 |
| Thermal conductivity (W/m-K) | 0.65 | 0.65 |
| Kinematic viscosity (m2/s) | 0.516 × 10−6 | 0.516 × 10−6 |
| Prandtl number (Pr) | 3.15 | 3.15 |
| Duct Types | Circular, Square, and Triangle |
|---|---|
| Heat rate (W) | 920 |
| Heat flux (W/m2) | 16 to 250 |
| Air velocity (m/s) | 8 to 24 |
| Correlations | Reynolds (Re), Nusselt (Nu), and Stanton (St) numbers |
| Test Condition | Parameters | Findings |
|---|---|---|
| (i) Same air speed (Q = 10–14 W/s2) | Low air speed (8 m/s) |
|
| High air speed (24 m/s) | From low to high air speed (8 m/s to 24 m/s):
| |
| (ii) Constant Heat Flux | Q = 16 W/m2 Air speed 8–24 m/s |
|
| Range | 0 < Pr < 0.02 | 0.02 < Pr < 0.5 | 0.5 < Pr |
|---|---|---|---|
| Flow Instability | Oscillatory flow | Stationary bifurcation | Hopf bifurcation [73] |
| Authors | Working Fluids | Tube Type | Method | Findings |
|---|---|---|---|---|
| Bernier, Baliga (1992) [68] | Water | Vertical circular tube | Uniform wall heat flux |
|
| Khan, Bera (2020) [69] | Water | Vertical circular tube | Upward flow |
|
| Authors | Working Fluids | Tube Type | Method | Findings |
|---|---|---|---|---|
| Meyer and Everts (2018) [75] | Water | Horizontal circular tubes | Constant heat flux | -The flow transitioned faster with increasing free convection effects and Reynolds number. |
| Taher et al. (2021) [81] | Water | Horizontal Rect. channel | Uniformly heated | -Numerical simulations of heat transfer characteristics for Rayleigh number and Reynolds number in the range of 104 ≤ Ra ≤ 106 and 25 ≤ Re ≤ 100, respectively, have shown that the mixed convection flow offers higher heat transfer enhancement compared with pure forced convection flow. |
| Colla et al. (2015) [44] | TiO2 water nanofluid | Horizontal circular tubes | Uniformly heated | -Nanofluid thermophysical properties closely equivalent to base fluid (i.e., thermal conductivity, dynamic viscosity, heat capacity) |
| Wang et al. (1994) [18] | Super critical CO2 | Horizontal circular tubes | Uniformly heated. | -Avg Nu decreased with increasing Ra at low Pr (occurrence of reverse flow) |
| Modes | No. | Challenges | Explanation |
|---|---|---|---|
| Experimental | 1. | Material limitations |
|
| 2. | Measurement accuracy |
| |
| 3. | Flow instabilities |
| |
| 4. | Scaling effects |
| |
| Numerical | 1. | Computational complexity |
|
| 2. | Turbulence modeling |
| |
| 3. | Convergence Issues |
| |
| 4. | Validation against experimental data |
|
| Prandtl No | Low | Medium | High | Σ | ||||
|---|---|---|---|---|---|---|---|---|
| Orientation | Ver | Hor | Ver | Hor | Ver | Hor | ||
| Geometry | Circular | Ref.13,2007 Σ = 1 | Ref.14,1990 Ref.15,1982 Ref.16,1988 Ref.17,2010 Ref.18,1994 Σ = 5 | Ref.69,1992 Ref.70,2020 Ref.71,2018 Ref.72,2019 Ref.73,2018 Ref.74,2019 Σ = 6 | Ref.75,2018 Ref.76,2018 Ref.77,2018 Ref.78,2022 Ref.79,2017 Ref.80,2010 Ref.81,2010 Σ = 7 | Ref.29,2011 Σ = 1 | Ref.30,1995 Ref 31,2005 Ref.32,2004 Ref.33,2007 Ref.34,2010 Ref.35,2012 Ref.36,2013 Ref.37,2014 Ref.38,2016 Ref.39,2016 Ref.40,1997 Ref.41,1997 Ref.42,2001 Ref.43,1998 Ref.44,2015 Ref.45,2023 Ref.46,2019 Ref.47,2010 Ref.48,1985 Ref.49,2013 Ref.50,2013 Ref.51,2015 Ref.52,2007 Ref.53,2015 Ref.54,2021 Ref.55,2017 Ref.56,2017 Ref.57,2017 Ref.58,1996 Ref.59,2015 Ref.60,2005 Ref.61,2015 Ref.62,2018 Ref.63,2019 Ref.64,2018 Ref.65,2008 Ref.66,2018 Ref.67,2014 Ref.68,2018 [Σ = 39] | 59 |
| Rectangular | - | Ref.19,2012 Ref.20,2012 [Σ = 2] | - | Ref.68,2018 [Σ = 1] | - | Ref.68,2018 [Σ = 1] | 4 | |
| Triangular | - | Ref.21,2018 Ref.22,2017 [Σ = 2] | - | Ref.68,2018 [Σ = 1] | - | Ref.68,2018 [Σ = 1] | 4 | |
| Elliptical | - | Ref.23,2009 Ref.24,2018 [Σ = 2] | - | Ref.82,2018 [Σ = 1] | - | - | 3 | |
| Σ | 1 | 11 | 6 | 10 | 1 | 41 | ||
| Remark (Σ) | Low Pr = 12 | Med Pr = 16 | Hi Pr = 42 | |||||
| Vertical = 8; | Σ Horizontal = 62 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amran, M.F.; Sultan, S.M.; Tso, C.P. A Comprehensive Review of Mixed Convective Heat Transfer in Tubes and Ducts: Effects of Prandtl Number, Geometry, and Orientation. Processes 2024, 12, 2749. https://doi.org/10.3390/pr12122749
Amran MF, Sultan SM, Tso CP. A Comprehensive Review of Mixed Convective Heat Transfer in Tubes and Ducts: Effects of Prandtl Number, Geometry, and Orientation. Processes. 2024; 12(12):2749. https://doi.org/10.3390/pr12122749
Chicago/Turabian StyleAmran, Mohd Farid, Sakhr M. Sultan, and C. P. Tso. 2024. "A Comprehensive Review of Mixed Convective Heat Transfer in Tubes and Ducts: Effects of Prandtl Number, Geometry, and Orientation" Processes 12, no. 12: 2749. https://doi.org/10.3390/pr12122749
APA StyleAmran, M. F., Sultan, S. M., & Tso, C. P. (2024). A Comprehensive Review of Mixed Convective Heat Transfer in Tubes and Ducts: Effects of Prandtl Number, Geometry, and Orientation. Processes, 12(12), 2749. https://doi.org/10.3390/pr12122749







