Hierarchical Power System Scheduling and Energy Storage Planning Method Considering Heavy Load Rate
Abstract
1. Introduction
- (1)
- Dimensionless indicators are proposed to evaluate the impact of renewable energy on transmission line load and illustrate high-risk lines’ TLHL. By simulating scheduling operations, the increasingly serious problem of TLHL in a power system with an increasing proportion of renewable energy but an unchanged transmission network is pointed out.
- (2)
- Compared to conventional scheduling and ESP methods, the ESP–scheduling integrated model considering both maximum transmission capacity and TLHL are proposed to enhance operational security and economic benefits.
- (3)
- Finally, a penalty term for heavy loads was incorporated into the objective function and methods of rescheduling and planning energy storage considering the heavy load penalty function are proposed. The dispatching layer outputs the system operation data, and the planning layer conducts energy storage planning based on the operational data.
2. Problem Formulation and Model Construction
2.1. Scenario Construction and Renewable Energy Output Models
- (1)
- Initialization: selection of k initial clustering centers.
- (2)
- Assignment: assign each data point to the nearest clustering center.
- (3)
- Update: recalculate the center of each cluster.
- (4)
- Iterate: repeat the allocation and update steps until the termination condition is met.
2.2. Scheduling Optimization Model
2.2.1. Scheduling Objective Function
2.2.2. Constraints for Scheduling
2.3. Energy Storage Planning Model
2.3.1. Planning Objective Function
2.3.2. Constraints for Planning
2.4. Evaluation Index of Transmission Line Load
2.5. Adaptability to Other Systems
3. Simulation Results and Discussion
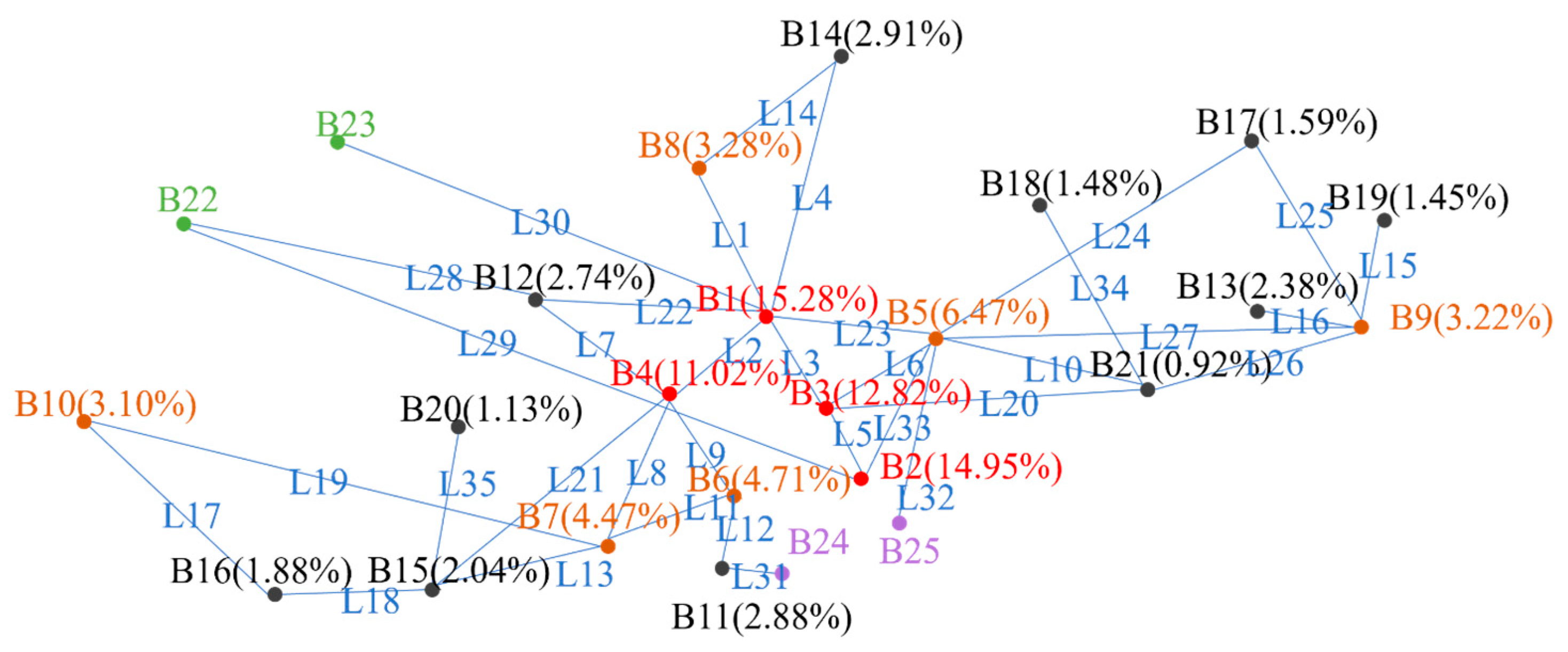
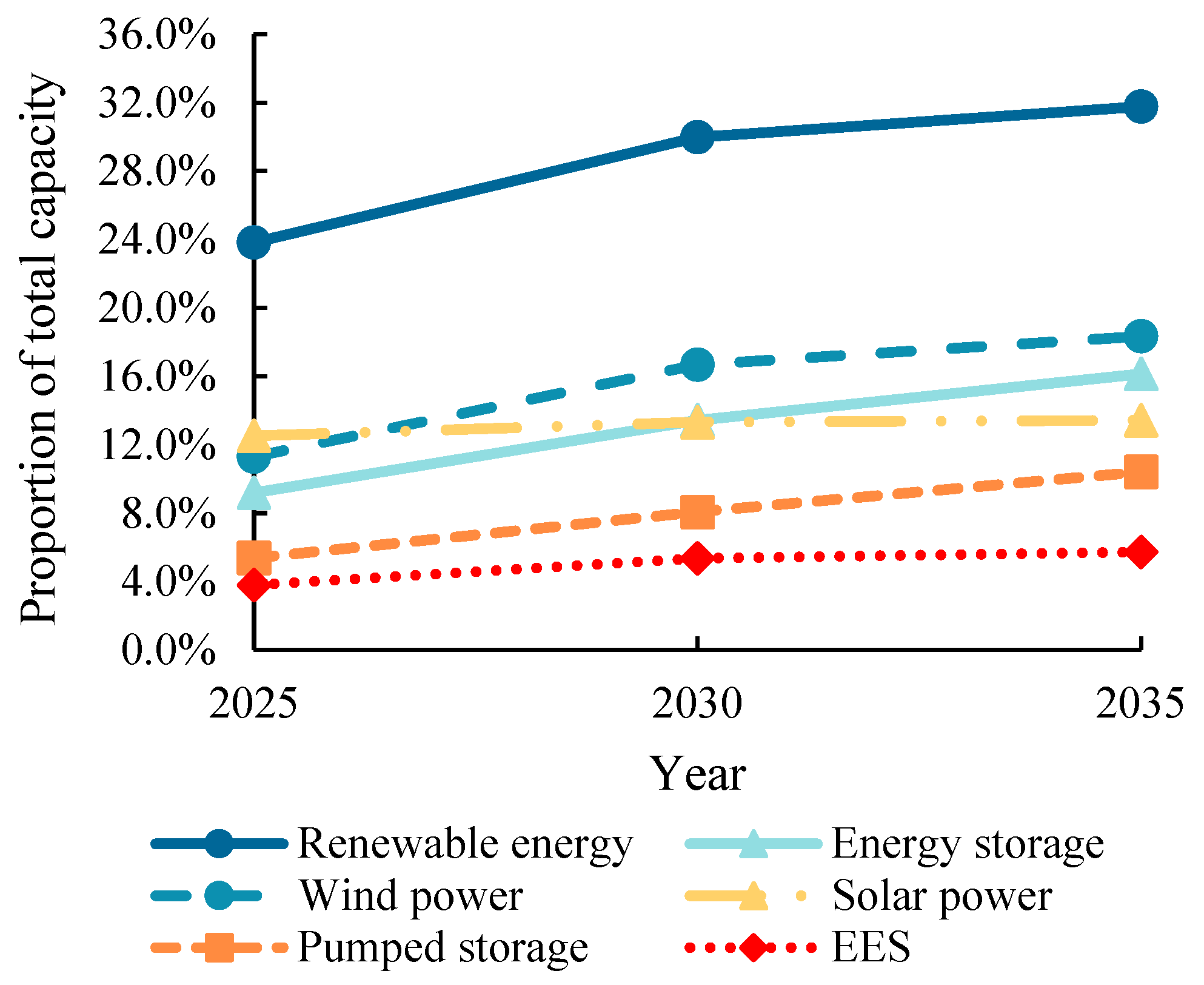
3.1. Power System Description and Scenario Classification Results
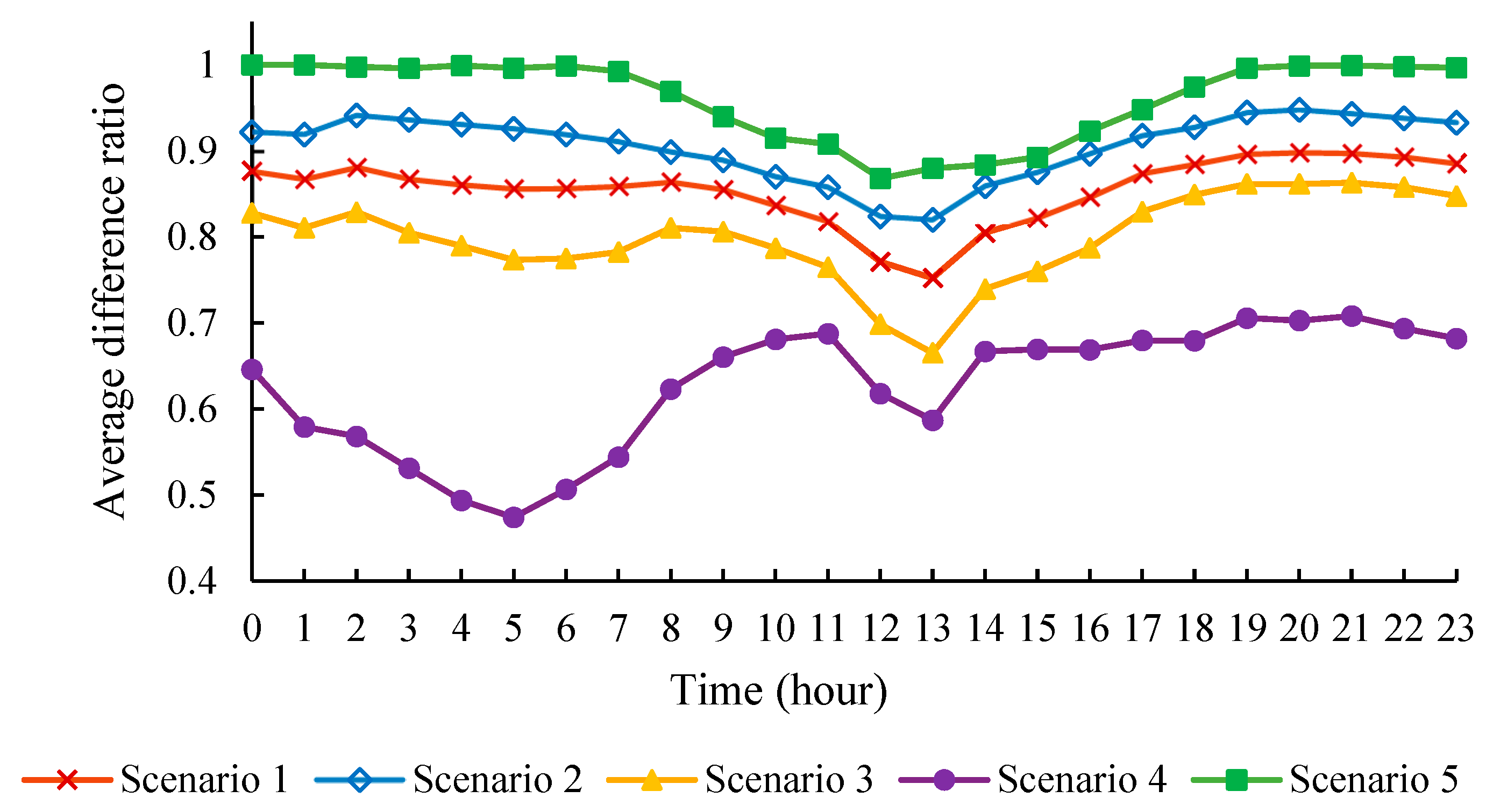
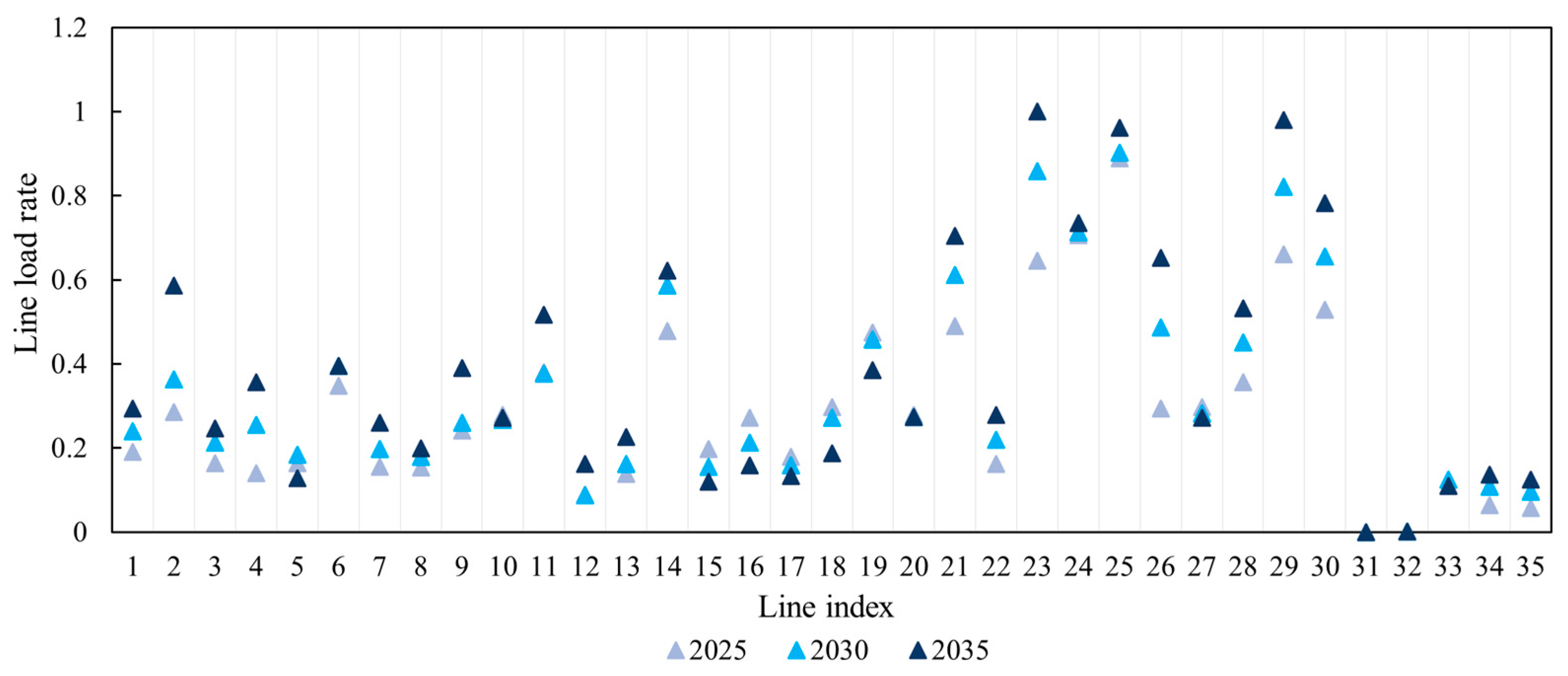
3.2. Result Analysis
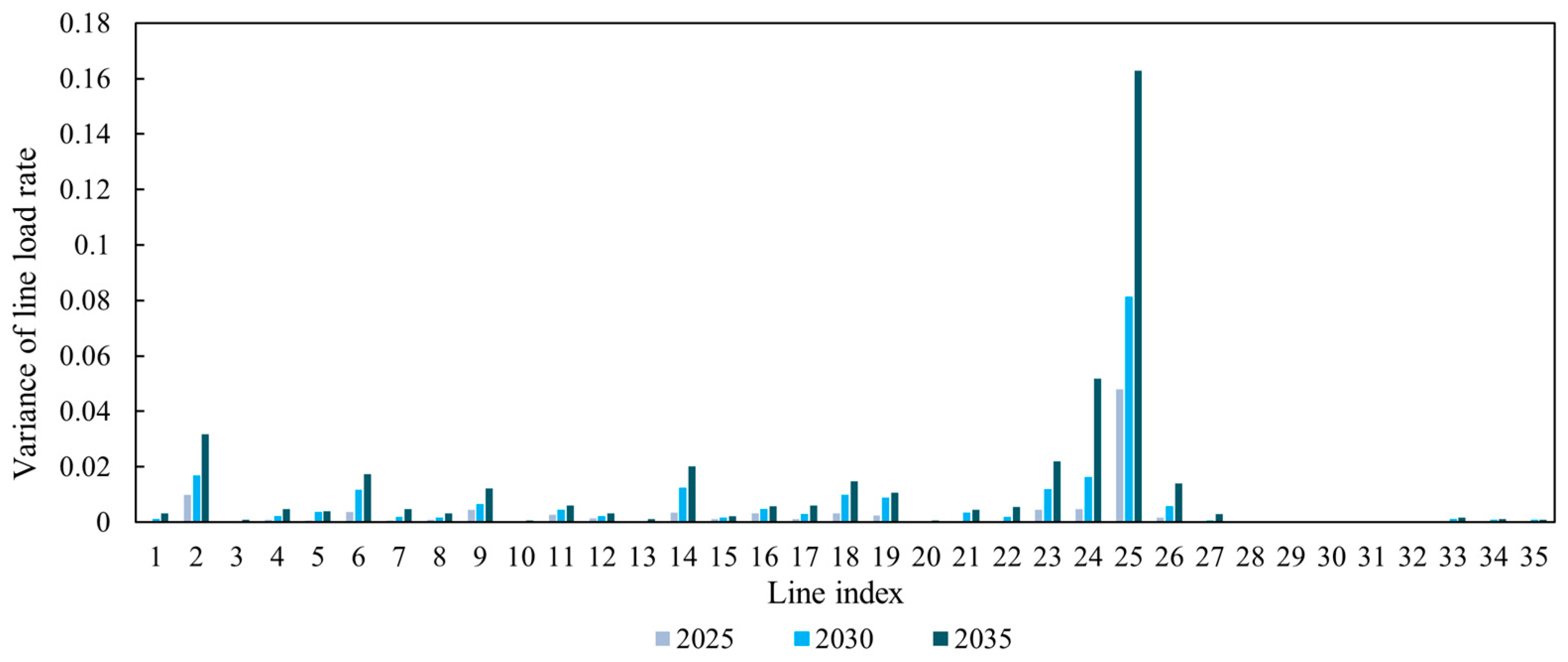
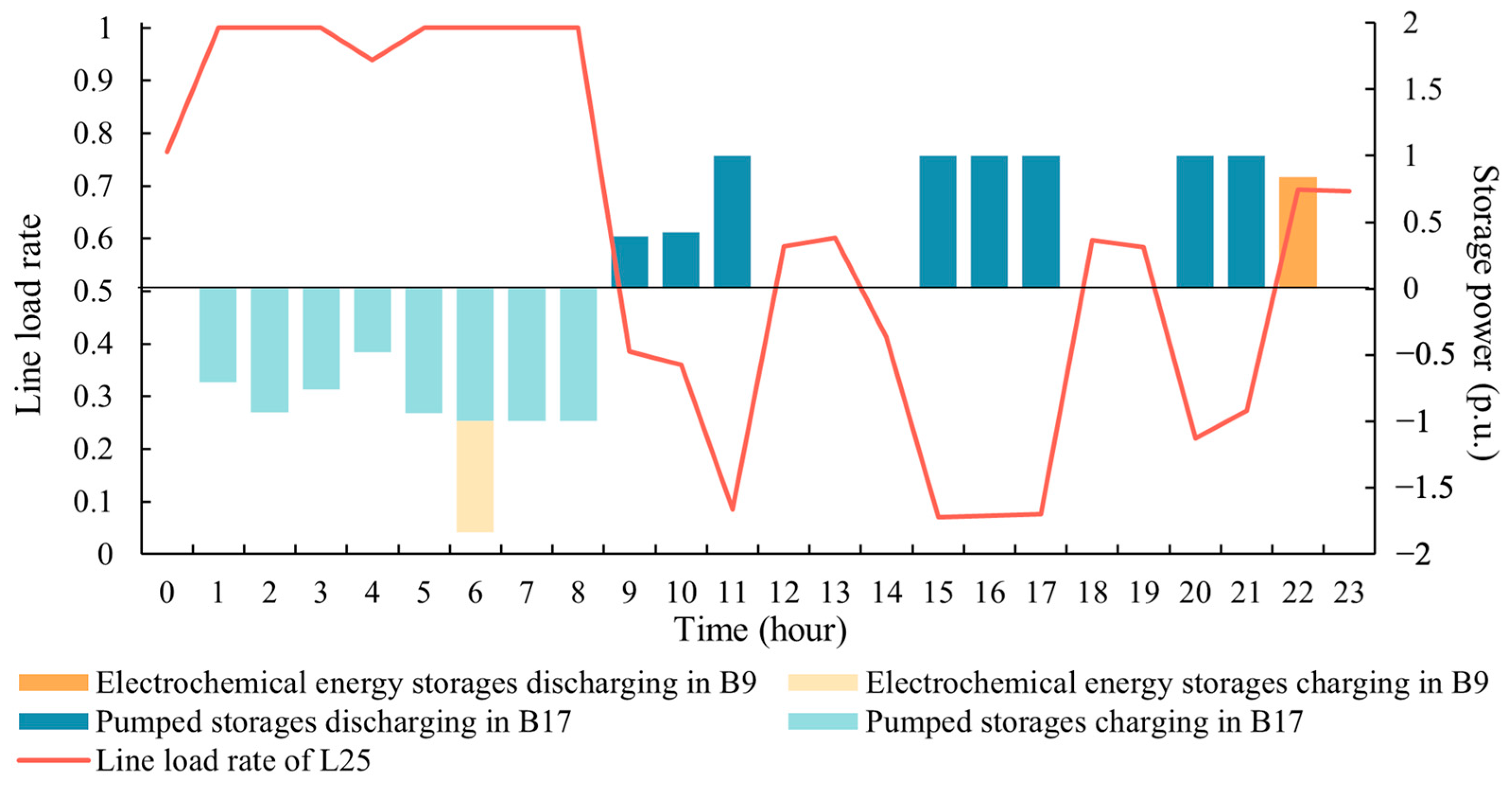
3.3. Results of Line Heavy Load-Alleviated Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | Meaning |
| RE | Renewable Energy |
| TLHL | Transmission Line Heavy Load |
| GEP | Generation Expansion Planning |
| TEP | Transmission Expansion Planning |
| ESP | Energy Storage Planning |
| PTDF | Power Transfer Distribution Factor |
| LLR | Line Load Rate |
| ALR | Average Load Rate |
| LRV | Load Rate Variance |
| ToHL | Time Of Heavy Load |
| ECMWF | European Center for Medium-Range Weather Forecasts |
References
- Alomoush, M.I. Performance indices to measure and compare system utilization and congestion severity of different dispatch scenarios. Electr. Power Syst. Res. 2005, 74, 223–230. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, J.; Li, X.; Liu, H. A Bi-level transmission expansion planning model considering planning-operation coordination of line load rate indices. Power Syst. Technol. 2024, 48, 1846–1854. [Google Scholar]
- Sun, W.; Wang, C.; Zeng, P.; Han, J. Review on evaluation method and index of power system homogeneity. Power Syst. Technol. 2015, 39, 1205–1212. [Google Scholar]
- Yu, Q.; Cao, N.; Guo, J. Analysis on influence of load rate on power system self-organized criticality. Autom. Electr. Power Syst. 2012, 36, 24–27. [Google Scholar]
- Dong, J.; Kong, L.; Li, C. Reduce the heavy overload rate of 10 kV distribution lines. Rur. Electr. 2021, 6, 50–53. [Google Scholar]
- Koltsaklis, N.E.; Dagoumas, A.S. State-of-the-art generation expansion planning: A review. Appl. Energy 2018, 230, 563–589. [Google Scholar] [CrossRef]
- Huang, H.; Li, Z.; Sampath, L.P.M.I.; Yang, J.; Nguyen, H.D.; Gooi, H.B.; Liang, R.; Gong, D. Blockchain-enabled carbon and energy trading for network-constrained coal mines with uncertainties. IEEE Trans. Sustain. Energy 2023, 14, 1634–1647. [Google Scholar] [CrossRef]
- Yang, N.; Xiong, Z.; Ding, L.; Liu, Y.; Wu, L.; Liu, Z.; Shen, X.; Zhu, B.; Li, Z.; Huang, Y. A Game-Based Power System Planning Approach Considering Real Options and Coordination of All Types of Participants. Energy 2024, 312, 133400. [Google Scholar] [CrossRef]
- Singh, V.; Fozdar, M.; Malik, H.; Márquez, F.P.G. Transmission congestion management through sensitivity-based rescheduling of generators using improved monarch butterfly optimization. Int. J. Electr. Power Energy Syst. 2023, 145, 108729. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Wang, P.; Xiao, G. Restoration of a Multi-Energy Distribution System with Joint District Network Reconfiguration via Distributed Stochastic Programming. IEEE Trans. Smart Grid 2024, 15, 2667–2680. [Google Scholar] [CrossRef]
- Oree, V.; Hassen, S.Z.S.; Fleming, P.J. Generation expansion planning optimisation with renewable energy integration: A review. Renew. Sustain. Energy Rev. 2017, 69, 790–803. [Google Scholar] [CrossRef]
- Mahdavi, M.; Antunez, C.S.; Ajalli, M.; Romero, R. Transmission Expansion Planning: Literature Review and Classification. IEEE Syst. J. 2019, 13, 3129–3140. [Google Scholar] [CrossRef]
- Saboori, H.; Hemmati, R.; Ghiasi, S.M.S.; Dehghan, S. Energy storage planning in electric power distribution networks—A state-of-the-art review. Renew. Sustain. Energy Rev. 2017, 79, 1108–1121. [Google Scholar] [CrossRef]
- Feng, C.; Shao, L.; Wang, J.; Zhang, Y.; Wen, F. Short-term Load Forecasting of Distribution Transformer Supply Zones Based on Federated Model-Agnostic Meta Learning. IEEE Trans. Power Syst. 2024, 1–13. [Google Scholar] [CrossRef]
- Li, Z.; Wu, L.; Xu, Y.; Moazeni, S.; Tang, Z. Multi-stage real-time operation of a multi-energy microgrid with electrical and thermal energy storage assets: A data-driven MPC-ADP approach. IEEE Trans. Smart Grid 2021, 13, 213–226. [Google Scholar] [CrossRef]
- Development and Reform Commission, Energy Bureau. Notice on Further Promoting the Participation of New Energy Storage in the Electricity Market and Dispatching Application (Operation of the Development and Reform Office [2022] No. 475). Beijing. Available online: https://zfxxgk.nea.gov.cn/2022-06/07/c_1310615910.htm (accessed on 1 October 2024).
- Mansuwan, K.; Jirapong, P.; Thararak, P. Optimal battery energy storage planning and control strategy for grid modernization using improved genetic algorithm. Energy Rep. 2022, 9, 236–241. [Google Scholar] [CrossRef]
- Yu, H.; Ye, C.; Ding, Y.; Song, Y. Power System Optimal Dispatch Integrating the Responsive High-Speed Train Fleet. IEEE Trans. Smart Grid 2024. [Google Scholar] [CrossRef]
- Chen, J.; Hu, H.; Wang, M.; Ge, Y.; Wang, K.; Huang, Y.; Yang, K.; He, Z.; Xu, Z.; Li, Y.R. Power Flow Control-Based Regenerative Braking Energy Utilization in AC Electrified Railways: Review and Future Trends. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6345–6365. [Google Scholar] [CrossRef]
- Yao, L.; Zhang, Q.; Wu, J.; Saniye, M. Study on MES optimal probability power flow considering source and load uncertainties. Pow. Capacit. React. Pow. Compens. 2022, 47, 57–66. [Google Scholar]




| Study | Focus Area | Advantages | Limitations | Improvements |
|---|---|---|---|---|
| [1,2,3] | Distribution network scheduling and energy storage planning | Enhances flexibility, reduces RE curtailment | Limited focus on sustained heavy loads | Integrates energy storage planning with LLR |
| [4,5,6] | Multi-objective load management | Balances cost and load, effective for short-term overloads | Limited adaptation to prolonged heavy load conditions | Adds a heavy load penalty to improve resilience under sustained high loads |
| [7,8,9] | Hybrid energy storage and RE integration | Reduces RE waste, improves economic efficiency | Lacks line-specific heavy load management | Uses scenario clustering and load penalties for stability in high-RE scenarios |
| [10,11,12] | RE variability and dynamic dispatch | Supports stability with RE variability and market | Limited to short-term scenarios, lacks sustained load solutions | Adapts to RE variability using scenario clustering and heavy load penalties |
| [13,14,15] | Transmission load balancing and grid stability | Manages peak loads, prevents overloads | Focused on immediate congestion, lacks long-term load management | Mitigates cumulative heavy loads with continuous heavy load penalty |
| [16,17] | RE integration with demand response and grid resilience | Increases flexibility under RE conditions | Lacks tools for managing sustained heavy loads | Introduces multi-layered penalty to enhance resilience under high RE |
| Coal-Fired Power | Gas-Fired Power | Nuclear Power | Hydro-Power | Wind Power | Solar Power | EES | Pumped Storage | External Power |
|---|---|---|---|---|---|---|---|---|
| 302 | 601 | 100 | 0 | 0 | 0 | 120 | 6 | 240 |
| Model | Cut-In Speed (m/s) | Cut-Out Speed (m/s) | Rate Speed (m/s) | Rate Power (MW) | Application Scenario |
|---|---|---|---|---|---|
| MySE3.6-135 | 3 | 25 | 10.9 | 3.6 | onshore |
| MySE6.45-18 | 3 | 30 | 10.5 | 6.45 | offshore |
| Scenario | 2025 | 2030 | 2035 | Same |
|---|---|---|---|---|
| Scenario 1 | 108 | 96 | 115 | 82 |
| Scenario 2 | 150 | 153 | 134 | 134 |
| Scenario 3 | 107 | 116 | 116 | 99 |
| Total | - | - | - | 315 |
| Scenario | Year | ALR | LRV | MLR | ToHL | |
|---|---|---|---|---|---|---|
| General scenarios | Scenario 1 | 2025 | 0.233 | 0.002 | 0.932 | 9 |
| 2030 | 0.260 | 0.006 | 1 | 11 | ||
| 2035 | 0.272 | 0.009 | 1 | 47 | ||
| Scenario 2 | 2025 | 0.242 | 0.003 | 0.952 | 7 | |
| 2030 | 0.267 | 0.007 | 1 | 16 | ||
| 2035 | 0.284 | 0.012 | 1 | 53 | ||
| Scenario 3 | 2025 | 0.207 | 0.003 | 0.941 | 3 | |
| 2030 | 0.228 | 0.008 | 0.899 | 12 | ||
| 2035 | 0.254 | 0.010 | 1 | 51 | ||
| Extreme scenarios | Scenario 4 | 2025 | 0.178 | 0.003 | 0.756 | 0 |
| 2030 | 0.216 | 0.009 | 1 | 40 | ||
| 2035 | 0.245 | 0.015 | 1 | 73 | ||
| Scenario 5 | 2025 | 0.230 | 0.003 | 0.889 | 7 | |
| 2030 | 0.236 | 0.006 | 0.902 | 13 | ||
| 2035 | 0.260 | 0.012 | 1 | 46 |
| Bus Number | Capacity Proportion | Relational Lines | |
|---|---|---|---|
| Pumped storage | 1 | 4.4% | L1, L2, L3, L4, L22, L23, L30 |
| 2 | 4.4% | L5, L29, L33 | |
| 3 | 4.4% | L3, L5, L6, L20 | |
| 6 | 8.8% | L9, L11, L12 | |
| 7 | 30.8% | L8, L11, L13, L19 | |
| 15 | 13.2% | L13, L18, L21, L35 | |
| 21 | 26.4% | L10, L20, L26, L34 | |
| EES | 15 | 2.2% | L13, L18, L21, L35 |
| 20 | 5.5% | L35 |
| Scenario | Method | ALR | LRV | MLR | ToHL |
|---|---|---|---|---|---|
| Scenario 1 | Original | 0.272 | 0.009 | 1 | 47 |
| Rescheduling | 0.268 | 0.007 | 0.986 | 28 | |
| Conventional plan | 0.271 | 0.010 | 1 | 56 | |
| Plan with heavy load | 0.221 | 0.014 | 0.8 | 0 | |
| Scenario 2 | Original | 0.284 | 0.012 | 1 | 53 |
| Rescheduling | 0.284 | 0.009 | 1 | 36 | |
| Conventional plan | 0.285 | 0.012 | 1 | 54 | |
| Plan with heavy load | 0.235 | 0.012 | 0.8 | 0 | |
| Scenario 3 | Original | 0.254 | 0.010 | 1 | 51 |
| Rescheduling | 0.249 | 0.007 | 0.95 | 40 | |
| Conventional plan | 0.262 | 0.012 | 1 | 57 | |
| Plan with heavy load | 0.208 | 0.012 | 1 | 27 | |
| Scenario 4 | Original | 0.245 | 0.015 | 1 | 73 |
| Rescheduling | 0.236 | 0.017 | 1 | 66 | |
| Conventional plan | 0.246 | 0.015 | 1 | 74 | |
| Plan with heavy load | 0.237 | 0.017 | 1 | 54 | |
| Scenario 5 | Original | 0.260 | 0.012 | 1 | 46 |
| Rescheduling | 0.260 | 0.009 | 0.969 | 44 | |
| Conventional plan | 0.261 | 0.012 | 1 | 43 | |
| Plan with heavy load | 0.249 | 0.012 | 0.8 | 0 |
| Scenario | Method | L2 | L21 | L23 | L25 | L26 | L29 |
|---|---|---|---|---|---|---|---|
| Scenario 1 | Original | 0 | 0 | 11 | 6 | 6 | 24 |
| Rescheduling | 0 | 0 | 2 | 2 | 0 | 24 | |
| Plan | 0 | 1 | 12 | 7 | 12 | 24 | |
| Plan with heavy load | 0 | 0 | 0 | 0 | 0 | 0 | |
| Scenario 2 | Original | 0 | 4 | 14 | 8 | 3 | 24 |
| Rescheduling | 0 | 2 | 4 | 4 | 2 | 24 | |
| Plan | 0 | 6 | 13 | 9 | 2 | 24 | |
| Plan with heavy load | 0 | 0 | 0 | 0 | 0 | 0 | |
| Scenario 3 | Original | 0 | 0 | 16 | 0 | 11 | 24 |
| Rescheduling | 0 | 0 | 13 | 0 | 3 | 24 | |
| Plan | 0 | 0 | 19 | 0 | 14 | 24 | |
| Plan with heavy load | 2 | 24 | 0 | 1 | 0 | 0 | |
| Scenario 4 | Original | 1 | 24 | 11 | 0 | 20 | 17 |
| Rescheduling | 0 | 24 | 11 | 0 | 20 | 11 | |
| Plan | 1 | 24 | 12 | 0 | 20 | 17 | |
| Plan with heavy load | 0 | 24 | 9 | 0 | 14 | 7 | |
| Scenario 5 | Original | 0 | 0 | 15 | 7 | 0 | 24 |
| Rescheduling | 0 | 0 | 17 | 3 | 0 | 24 | |
| Plan | 0 | 0 | 13 | 6 | 0 | 24 | |
| Plan with heavy load | 0 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Xie, P.; Lin, Y.; Liu, Y.; Yang, Y.; Lin, X. Hierarchical Power System Scheduling and Energy Storage Planning Method Considering Heavy Load Rate. Processes 2024, 12, 2725. https://doi.org/10.3390/pr12122725
Lu Q, Xie P, Lin Y, Liu Y, Yang Y, Lin X. Hierarchical Power System Scheduling and Energy Storage Planning Method Considering Heavy Load Rate. Processes. 2024; 12(12):2725. https://doi.org/10.3390/pr12122725
Chicago/Turabian StyleLu, Qiuyu, Pingping Xie, Yingming Lin, Yang Liu, Yinguo Yang, and Xu Lin. 2024. "Hierarchical Power System Scheduling and Energy Storage Planning Method Considering Heavy Load Rate" Processes 12, no. 12: 2725. https://doi.org/10.3390/pr12122725
APA StyleLu, Q., Xie, P., Lin, Y., Liu, Y., Yang, Y., & Lin, X. (2024). Hierarchical Power System Scheduling and Energy Storage Planning Method Considering Heavy Load Rate. Processes, 12(12), 2725. https://doi.org/10.3390/pr12122725





