Simulation of Shale Gas Reservoir Production Considering the Effects of the Adsorbed Water Layer and Flow Differences
Abstract
1. Introduction
2. Theory and Methods
2.1. Conceptual Model
2.2. Mathematical Models
2.2.1. Permeability Correction Model
2.2.2. Single-Phase Flow in Organic Matrix System
2.2.3. Two-Phase Flow in Inorganic Matrix System
2.2.4. Two-Phase Flow in Fracture System
2.3. Solution-Determining Conditions
2.3.1. Initial Conditions
2.3.2. Boundary Conditions
2.4. Mathematical Transformation and Production Method for the Well
2.4.1. Mathematical Transformation for the Well
2.4.2. Constant Bottomhole Flowing Pressure
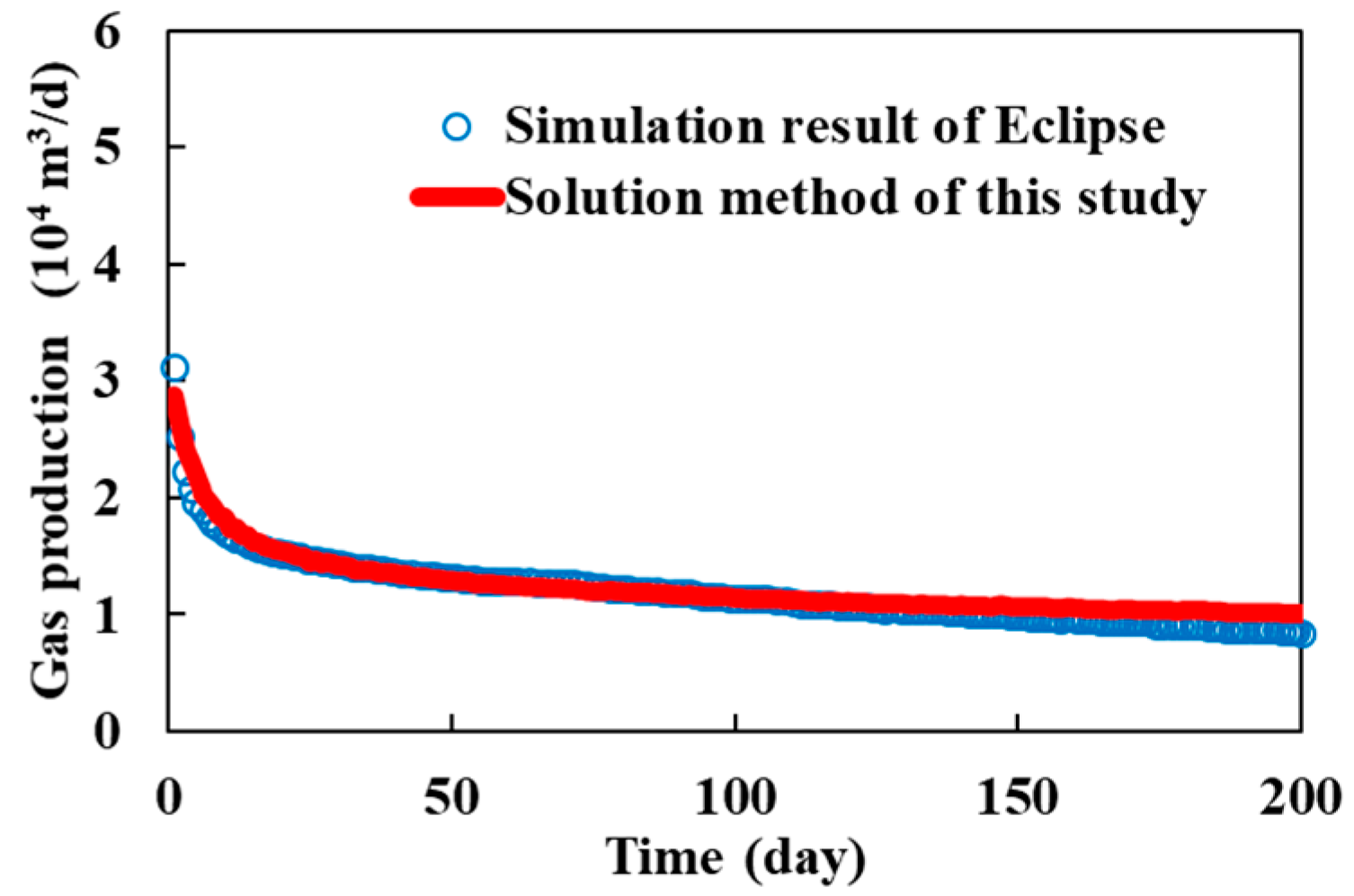
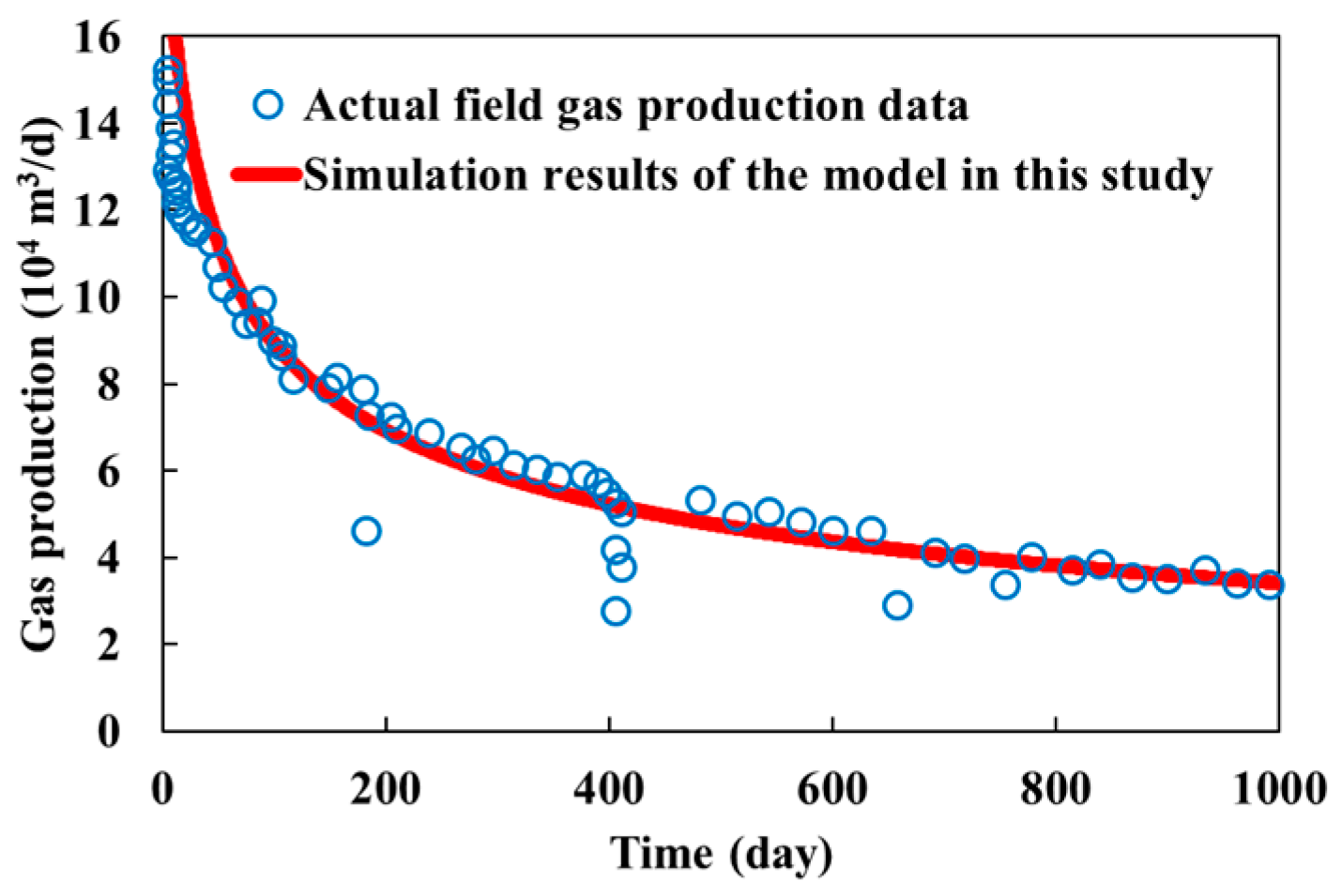
3. Model Validation
4. Results and Discussion
4.1. Analysis of Dynamic Pressure
4.2. Analysis of Langmuir Adsorption Constants
4.3. Analysis of Hydraulic Fracturing Parameters
4.4. Analysis of Adsorbed Water Layer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | rarefaction coefficient, dimensionless |
| b | slip factor, dimensionless |
| gas volume factor, dimensionless | |
| water volume factor, dimensionless | |
| stress sensitivity coefficient (compressibility coefficient), MPa−1 | |
| vertical depth of the fluid, m | |
| initial pore diameter, m | |
| effective pore diameter, m | |
| g | gravitational acceleration, 9.8 m/s2 |
| thickness of the grid block, m | |
| are coordinates of the grid block, dimensionless | |
| absolute permeability, m2 | |
| Boltzmann constant, J·K−1 | |
| absolute permeability of inorganic matrix, m2 | |
| relative permeability of gas in inorganic matrix, dimensionless | |
| relative permeability of water in inorganic matrix, dimensionless | |
| relative permeability of gas in hydraulic fractures, dimensionless | |
| relative permeability of water in hydraulic fractures, dimensionless | |
| relative permeability of l phase (either gas or water) in the fracture system | |
| relative permeability of gas in microfractures, dimensionless | |
| relative permeability of water in microfractures, dimensionless | |
| initial permeability of microfractures, m2 | |
| Knudsen number, dimensionless | |
| absolute permeability of organic matrix, m2 | |
| permeability of microfractures considering stress sensitivity, m2 | |
| permeability of hydraulic fractures considering stress sensitivity, m2 | |
| length of a single inorganic nanochannel, m | |
| n | normal vector, dimensionless |
| capillary pressure, MPa | |
| capillary pressure in inorganic matrix, MPa | |
| pressure of gas in inorganic matrix, MPa | |
| pressure of water in inorganic matrix, MPa | |
| initial gas pressure in inorganic matrix, MPa | |
| displacement pressure, MPa | |
| capillary pressure in hydraulic fractures, MPa | |
| pressure of gas in hydraulic fractures, MPa | |
| pressure of water in hydraulic fractures, MPa | |
| initial gas pressure in hydraulic fractures, MPa | |
| Langmuir pressure of organic matrix, MPa | |
| Langmuir pressure of inorganic matrix, MPa | |
| capillary pressure in microfractures, MPa | |
| pressure of gas in microfractures, MPa | |
| pressure of water in microfractures, MPa | |
| initial gas pressure in microfractures, MPa | |
| initial pressure in microfractures, MPa | |
| gas pressure in organic matrix, MPa | |
| initial gas pressure in organic matrix, MPa | |
| bottomhole flowing pressure, MPa | |
| gas exchange term from inorganic matrix to microfractures, sm3/m3/s | |
| water exchange term from inorganic matrix to microfractures, sm3/m3/s | |
| volume of gas produced per unit volume of shale, sm3/m3/s | |
| gas exchange term from microfractures to hydraulic fractures, sm3/m3/s | |
| water exchange term from microfractures to hydraulic fractures, sm3/m3/s | |
| gas exchange term from organic matrix to inorganic matrix, sm3/m3/s | |
| volume of water produced per unit volume of shale, sm3/m3/s | |
| equivalent radius of the grid block at the well location, m | |
| throat radius of the nanopores, m | |
| radius of the wellbore, m | |
| skin factor, dimensionless | |
| saturation of gas in inorganic matrix, dimensionless | |
| saturation of water in inorganic matrix, dimensionless | |
| initial saturation of water in inorganic matrix, dimensionless | |
| normalized water saturation, dimensionless | |
| saturation of gas in hydraulic fractures, dimensionless | |
| saturation of water in hydraulic fractures, dimensionless | |
| initial saturation of water in hydraulic fractures, dimensionless | |
| saturation of gas in microfractures, dimensionless | |
| saturation of water in microfractures, dimensionless | |
| initial saturation of water in microfractures, dimensionless | |
| gas saturation in organic matrix, dimensionless | |
| irreducible water saturation, dimensionless | |
| Langmuir volume of organic matrix, m3/kg | |
| Langmuir volume of inorganic matrix, m3/kg | |
| Hamilton operator, dimensionless | |
| shape factor, 1/m2 | |
| porosity of inorganic matrix, dimensionless | |
| initial porosity of microfractures, dimensionless | |
| porosity of organic matrix, dimensionless | |
| porosity of hydraulic fractures considering stress sensitivity, dimensionless | |
| porosity of microfractures considering stress sensitivity, dimensionless | |
| distribution index of pore size, dimensionless | |
| half-transmissibility of gas, m2/Pa/s | |
| half-transmissibility of water, m2/Pa/s | |
| viscosity of gas, MPa·s | |
| viscosity of water, MPa·s | |
| density of shale rock, kg/m3 | |
| density of gas in inorganic matrix, kg/m3 | |
| density of water in inorganic matrix, kg/m3 | |
| density of gas in hydraulic fractures, kg/m3 | |
| density of water in hydraulic fractures, kg/m3 | |
| density of gas in microfractures, kg/m3 | |
| density of water in microfractures, kg/m3 | |
| density of gas in organic matrix, kg/m3 | |
| effective collision diameter of gas molecules, m | |
| Dirac function, dimensionless | |
| permeability correction factor, dimensionless | |
| permeability correction factor of inorganic matrix, dimensionless | |
| permeability correction factor of organic matrix, dimensionless |
References
- Zou, C.; Yang, Z.; He, D.; Wei, Y.S.; Li, J.; Jia, A.; Chen, J.J.; Zhao, Q.; Li, Y.L.; Li, J.; et al. Theory, technology and prospects of conventional and unconventional natural gas. Petrol. Explor. Dev. 2018, 45, 604–618. [Google Scholar] [CrossRef]
- Garum, M.; Glover, P.W.; Lorinczi, P.; Micklethwaite, S.; Hassanpour, A. Integration of multiscale imaging of nanoscale pore microstructures in gas shales. Energy Fuels 2021, 35, 10721–10732. [Google Scholar] [CrossRef]
- Wang, H.; Chen, L.; Qu, Z.; Yin, Y.; Kang, Q.; Yu, B.; Tao, W.Q. Modeling of multiscale transport phenomena in shale gas production—A critical review. Appl. Energy 2020, 262, 114575. [Google Scholar] [CrossRef]
- Ma, Y.; Zhong, N.; Li, D.; Pan, Z.; Cheng, L.; Liu, K. Organic matrix/clay mineral intergranular pores in the Lower Cambrian Lujia Shale in the north–eastern part of the upper Yangtze area, China: A possible microscopic mechanism for gas preservation. Int. J. Coal Geol. 2015, 137, 38–54. [Google Scholar] [CrossRef]
- Sang, G.; Elsworth, D.; Miao, X.; Mao, X.; Wang, J. Numerical study of a stress dependent triple porosity model for shale gas reservoirs accommodating gas diffusion in kerogen. J. Nat. Gas Sci. Eng. 2016, 32, 423–438. [Google Scholar] [CrossRef]
- Hu, B.; Wang, J.G.; Zhang, K.; Ye, Z. A new triple–porosity multiscale fractal model for gas transport in fractured shale gas reservoirs. J. Nat. Gas Sci. Eng. 2020, 78, 103335. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, J.; Li, W.; Leong, Y.K.; Elsworth, D.; Guo, J. Shale gas reservoir modeling and production evaluation considering complex gas transport mechanisms and dispersed distribution of kerogen. Petrol. Sci. 2021, 18, 195–218. [Google Scholar] [CrossRef]
- Javadpour, F. Nanopores and apparent permeability of gas flow in mudrocks (shales and siltstone). J. Can. Petrol. Technol. 2009, 48, 16–21. [Google Scholar] [CrossRef]
- Chalmers, G.R.L.; Bustin, R.M. Geological evaluation of Halfway-Doig-Montney hybrid gas shale-tight gas reservoir, northeastern British Columbia. Mar. Petrol. Geol. 2012, 38, 53–72. [Google Scholar] [CrossRef]
- Xiong, J.; Tang, J.; Zhou, X.; Liu, X.; Liang, L.; Hou, L. Molecular dynamics simulation and experimental studies of the wettability behaviors of shales. Energy Fuels 2022, 36, 3526–3538. [Google Scholar] [CrossRef]
- Yang, Y.; Song, H.; Imani, G.; Zhang, Q.; Liu, F.; Zhang, L.; Sun, H.; Zhong, J.; Zhang, K.; Yao, J. Adsorption behavior of shale oil and water in the kerogen–kaolinite pore by molecular simulations. J. Mol. Liq. 2024, 393, 123549. [Google Scholar] [CrossRef]
- Passey, Q.R.; Bohacs, K.M.; Esch, W.L.; Klimentidis, R.; Sinha, S. From oil–prone source rock to gas–producing shale reservoir–geologic and petrophysical characterization of unconventional shale–gas reservoirs. In Proceedings of the SPE International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010; p. SPE-131350. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, L.; Li, Y.; Yu, W.; He, X.; Liu, N.; Li, X.; Wang, T. Diffusion and flow mechanisms of shale gas through matrix pores and gas production forecasting. In Proceedings of the SPE Canada Unconventional Resources Conference, Calgary, AB, Canada, 5–7 November 2013; p. SPE-167226. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Wang, X.; Li, Y.; Wu, K.; Shi, J.; Liu, Y.; Dong, F.; Tao, Z.; Yu, P. Water distribution characteristic and effect on methane adsorption capacity in shale clay. Int. J. Coal Geol. 2016, 159, 135–154. [Google Scholar] [CrossRef]
- Jin, Z.; Firoozabadi, A. Effect of water on methane and carbon dioxide sorption in clay minerals by Monte Carlo simulations. Fluid Phase Equilibr. 2014, 382, 10–20. [Google Scholar] [CrossRef]
- Liu, J.; Wen, Y.; Jiang, L.; Yuan, H.; Liu, Z.; Shui, Z.; Wang, B.; Yan, X. Molecular dynamics simulation of micro mechanisms of gas and water migration and diffusion in shale reservoirs. Colloid Surf. A 2024, 682, 132865. [Google Scholar] [CrossRef]
- Jia, P.; Cheng, L.; Clarkson, C.R.; Williams-Kovacs, J.D. Flow behavior analysis of two–phase (gas/water) flowback and early–time production from hydraulically–fractured shale gas wells using a hybrid numerical/analytical model. Int. J. Coal Geol. 2017, 182, 14–31. [Google Scholar] [CrossRef]
- Olorode, O.M.; Freeman, C.M.; Moridis, G.J.; Blasingame, T.A. High–resolution numerical modeling of complex and irregular fracture patterns in shale gas reservoirs and tight gas reservoirs. SPE Reserv. Eval. Eng. 2013, 16, 443–455. [Google Scholar] [CrossRef]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of an efficient embedded discrete fracture model for 3D compositional reservoir simulation in fractured reservoirs. SPE J. 2014, 19, 289–303. [Google Scholar] [CrossRef]
- Yang, R.; Huang, Z.; Li, G.; Yu, W.; Sepehrnoori, K.; Lashgari, H.R.; Tian, S.; Song, X.; Sheng, M. A semianalytical approach to model two–phase flowback of shale–gas wells with complex–fracture–network geometries. SPE J. 2017, 22, 1808–1833. [Google Scholar] [CrossRef]
- Xu, Y.; Cavalcante Filho, J.S.; Yu, W.; Sepehrnoori, K. Discrete–fracture modeling of complex hydraulic–fracture geometries in reservoir simulators. SPE Reserv. Eval. Eng. 2017, 20, 403–422. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Nobakht, M.; Kaviani, D.; Ertekin, T. Production analysis of tight–gas and shale–gas reservoirs using the dynamic–slippage concept. SPE J. 2012, 17, 230–242. [Google Scholar] [CrossRef]
- Huang, T.; Li, E.P.; Tao, Z.W.; Guo, X. A nonlinear seepage model of gas and water transport in multiscale shale gas reservoirs based on dynamic permeability. J. Geophys. Eng. 2018, 15, 1255–1268. [Google Scholar] [CrossRef]
- Li, L.; Sheng, G.L.; Su, Y.L. Water-gas two-phase flow behavior of multi-fractured horizontal wells in shale gas reservoirs. Processes 2019, 7, 664. [Google Scholar] [CrossRef]
- Cui, G.; Tan, Y.; Chen, T.; Feng, X.T.; Elsworth, D.; Pan, Z.; Wang, C. Multidomain two–phase flow model to study the impacts of hydraulic fracturing on shale gas production. Energy Fuels 2020, 34, 4273–4288. [Google Scholar] [CrossRef]
- Cheng, S.; Huang, P.; Wang, K.; Wu, K.; Chen, Z. Comprehensive modeling of multiple transport mechanisms in shale gas reservoir production. Fuel 2020, 277, 118159. [Google Scholar] [CrossRef]
- Xu, E.; Yu, L.; Fan, M.; Chen, T.; Pan, Z.; Tan, Y.; Cui, G. Two–phase flow model for numerical investigation of impact of water retention on shale gas production. Geofluids 2021, 2021, 2637217. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, G.; Zhu, J.; Yang, Y.; Yu, L.; Gao, F. Multiscale and multiphase fractal model considering water reflux in shale gas extraction. J. Nat. Gas Sci. Eng. 2022, 101, 104501. [Google Scholar] [CrossRef]
- Wang, W.; Xie, Q.; Li, J.; Sheng, G.; Lun, Z. Fracturing fluid imbibition impact on gas-water two phase flow in shale fracture–matrix system. Nat. Gas Ind. 2023, 10, 323–332. [Google Scholar] [CrossRef]
- Wang, D.; Liu, H.; Yao, J.; Wang, W.; Hu, X.; Wang, Y. Macroscale gas-water two–phase transport simulation in shales considering nanomicroscale effects. Int. J. Energy Res. 2024, 2024, 7198722. [Google Scholar] [CrossRef]
- Mathia, E.J.; Bowen, L.; Thomas, K.M.; Aplin, A.C. Evolution of porosity and pore types in organic–rich, calcareous, Lower Toarcian Posidonia Shale. Mar. Petrol. Geol. 2016, 75, 117–139. [Google Scholar] [CrossRef]
- Gao, Z.; Liang, Z.; Hu, Q.; Jiang, Z.; Xuan, Q. A new and integrated imaging and compositional method to investigate the contributions of organic matrix and inorganic minerals to the pore spaces of lacustrine shale in China. Mar. Petrol. Geol. 2021, 127, 104962. [Google Scholar] [CrossRef]
- Lyu, F.; Ning, Z.; Wu, X.; Wang, Q.; Gu, K.; Cheng, Z.; Mu, Z. A comparative study of gas transport in dry and moisturized shale matrix considering organic matrix volume fraction and water distribution characteristics. J. Petrol. Sci. Eng. 2022, 208, 109483. [Google Scholar] [CrossRef]
- De Swaan, O.A. Analytic solutions for determining naturally fractured reservoir properties by well testing. SPE J. 1976, 16, 117–122. [Google Scholar] [CrossRef]
- Beskok, A.; Karniadakis, G.E.; Trimmer, W. Rarefaction and compressibility effects in gas microflows. J. Fluids Eng. 1996, 118, 448–456. [Google Scholar] [CrossRef]
- Civan, F. Effective correlation of apparent gas permeability in tight porous media. Transp. Porous Med. 2010, 82, 375–384. [Google Scholar] [CrossRef]
- Ziarani, A.S.; Aguilera, R. Knudsen’s permeability correction for tight porous media. Transp. Porous Med. 2012, 91, 239–260. [Google Scholar] [CrossRef]
- Beskok, A.; Karniadakis, G.E. Report: A model for flows in channels, pipes, and ducts at micro and nano scales. Nanosc. Microsc. Therm. 1999, 3, 43–77. [Google Scholar] [CrossRef]
- Cao, P.; Liu, J.; Leong, Y.K. General gas permeability model for porous media: Bridging the gaps between conventional and unconventional natural gas reservoirs. Energy Fuels 2016, 30, 5492–5505. [Google Scholar] [CrossRef]
- Pan, Z.; Connell, L.D. Modelling permeability for coal reservoirs: A review of analytical models and testing data. Int. J. Coal Geol. 2012, 92, 1–44. [Google Scholar] [CrossRef]
- Peaceman, D.W. Interpretation of well–block pressures in numerical reservoir simulation with nonsquare grid blocks and anisotropic permeability. SPE J. 1983, 23, 531–543. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous media and their relation to drainage design. T. ASABE 1964, 4, 26–28. [Google Scholar]
- Li, Y.; Li, X.; Teng, S.; Xu, D. Improved models to predict gas-water relative permeability in fractures and porous media. J. Nat. Gas Sci. Eng. 2014, 19, 190–201. [Google Scholar] [CrossRef]
- Fanchi, J.R. Principles of Applied Reservoir Simulation, 4th ed.; Gulf Professional: Houston, TX, USA, 2018; pp. 241–256. [Google Scholar]
- Grieser, B.; Shelley, B.; Soliman, M. Predicting production outcome from multi–stage, horizontal Barnett completions. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium/Production and Operations Symposium, Oklahoma City, OK, USA, 4–8 April 2009; p. SPE-120271. [Google Scholar] [CrossRef]
- Al–Ahmadi, H.A.; Wattenbarger, R.A. Triple–porosity models: One further step towards capturing fractured reservoirs heterogeneity. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 15–18 May 2011; p. SPE-149054. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Simulation of gas desorption and geomechanics effects for unconventional gas reservoirs. In Proceedings of the SPE Western Regional Meeting, Monterey, CA, USA, 19–25 April 2013; p. SPE-165377. [Google Scholar] [CrossRef]
- Cao, P.; Liu, J.; Leong, Y.K. A multiscale–multiphase simulation model for the evaluation of shale gas recovery coupled the effect of water flowback. Fuel 2017, 199, 191–205. [Google Scholar] [CrossRef]











| Researcher | Three Media | Characteristics of Model |
|---|---|---|
| Clarkson et al. [22] (2012) | Hydraulic fracture, inorganic matrix, organic matrix. | The desorption, diffusion, and slippage effect are considered. The matrix system is roughly regarded as single-phase gas flow. |
| Huang et al. [23] (2018) | Hydraulic fracture, natural fracture, matrix. | Both the matrix system and the natural fracture system are treated as a single porous medium. It failed to capture the distinct physical properties of the organic versus inorganic matrix. |
| Li et al. [24] (2019) | Hydraulic fracture, inorganic matrix, organic matrix. | The reservoir is divided into the unstimulated reservoir volume (USRV) region and the effectively stimulated reservoir volume (ESRV) region, without considering the slippage effect. It focuses on analyzing the gas-water flow behavior in different regions. |
| Cui et al. [25] (2020) | Natural fracture, inorganic matrix, organic matrix. | The model describes two-phase flow in fractures and single-phase gas flow in the matrix. It does not consider the influence of the water phase on gas production in the inorganic matrix. |
| Cheng et al. [26] (2020) | Fracture system (natural fracture and hydraulic fracture), inorganic matrix, organic matrix. | This model takes into account desorption, diffusion, and the slippage effect. It does not differentiate between the gas-water flow characteristics in the organic and inorganic matrices. |
| Xu et al. [27] (2021) | Hydraulic fracture, inorganic matrix, organic matrix. | The inorganic matrix solely considers the slippage effect, while both desorption and diffusion processes are overlooked. |
| Hu et al. [28] (2022) | Fracture system (natural fracture and hydraulic fracture), inorganic matrix, organic matrix. | The fracture system involves gas-water two-phase flow, while only single-phase gas flow is considered in the inorganic matrix. Both organic and inorganic matrices have ignored the slippage effect. |
| Wang et al. [29] (2023) | Hydraulic fracture, natural fracture, matrix. | The matrix system did not differentiate both the physical properties and gas-water flow differences of organic and inorganic matrices. |
| Wang et al. [30] (2024) | Hydraulic fracture, microfracture, matrix. |
| Coordinates | Horizontal Well | Vertical Well | |
|---|---|---|---|
| Horizontal Section is Parallel to the X-Axis | Horizontal Section is Parallel to the y-Axis | ||
| L | Y | X | X |
| M | Z | Z | Y |
| N | X | Y | Z |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| x-direction dimension (dimensionless) | 10 | Initial pressure (MPa) | 28 |
| y-direction dimension (dimensionless) | 10 | Formation temperature (K) | 373.15 |
| z-direction dimension (dimensionless) | 3 | Porosity (dimensionless) | 0.1 |
| x-direction grid step (m) | 40 | Gas compressibility factor (MPa−1) | 1.29 × 10−2 |
| y-direction grid step (m) | 40 | Water compressibility factor (MPa−1) | 4.35 × 10−4 |
| z-direction grid step (m) | 10 | Rock compressibility factor (MPa−1) | 1.0 × 10−4 |
| x-direction permeability (m2) | 1 × 10−15 | Water density (kg/m3) | 1000 |
| y-direction permeability (m2) | 1 × 10−15 | Gas specific gravity (dimensionless) | 0.648 |
| z-direction permeability (m2) | 1 × 10−16 | Water viscosity (MPa·s) | 1 × 10−9 |
| Gas saturation (dimensionless) | 0.5 | Wellbore radius (m) | 0.08 |
| Reservoir depth (m) | 2180 | Bottomhole flowing pressure (MPa) | 16 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Reservoir grid size (dimensionless) | 60 × 22 × 3 | Water compressibility factor (MPa−1) | 4.5 × 10−4 |
| Grid side length (m) | 10 | Inorganic matrix Langmuir volume (m3/kg) | 2 × 10−3 |
| Organic matrix porosity (%) | 5 | Inorganic matrix Langmuir pressure (MPa) | 5 |
| Organic matrix permeability (m2) | 1 × 10−20 | Initial water saturation in inorganic matrix | 0.3 |
| Inorganic matrix porosity (%) | 4 | Organic matrix Langmuir pressure (MPa) | 10 |
| Inorganic matrix permeability (m2) | 1 × 10−19 | Organic matrix Langmuir volume (m3/kg) | 4 × 10−3 |
| Microfracture porosity (%) | 2 | Organic matrix nanopore throat radius (m) | 2 × 10−9 |
| Microfracture permeability (m2) | 7.5 × 10−17 | Inorganic matrix nanopore throat radius (m) | 1 × 10−9 |
| Gas-phase critical pressure (MPa) | 4.6 | Initial water saturation in fractures (dimensionless) | 0.5 |
| Gas-phase critical temperature (K) | 181 | Fracture compressibility factor (MPa−1) | 2 × 10−3 |
| Slip factor (dimensionless) | −1 | Hydraulic fracture porosity (%) | 1.6 |
| Initial formation pressure (MPa) | 30 | Number of hydraulic fractures (dimensionless) | 4 |
| Reservoir temperature (K) | 362.15 | Hydraulic fracture spacing (m) | 100 |
| Shale rock density (kg/m3) | 2500 | Hydraulic fracture length (m) | 140 |
| Rock compressibility factor (MPa−1) | 1.5 × 10−3 | Hydraulic fracture width (m) | 3 × 10−3 |
| Fick diffusion coefficient (m2/s) | 5.86 × 10−8 | Hydraulic fracture permeability (m2) | 1.5 × 10−14 |
| Wellbore radius (m) | 0.06 | Formation water density (kg/m3) | 1100 |
| Reservoir depth (m) | 2500 | Formation water viscosity (MPa·s) | 1 × 10−9 |
| Total days of simulation (day) | 1000 | Bottomhole flowing pressure (MPa) | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Liu, J.; Ding, Q.; Jiang, L.; Liu, Z.; He, W.; Wen, Y. Simulation of Shale Gas Reservoir Production Considering the Effects of the Adsorbed Water Layer and Flow Differences. Processes 2024, 12, 2693. https://doi.org/10.3390/pr12122693
Yuan H, Liu J, Ding Q, Jiang L, Liu Z, He W, Wen Y. Simulation of Shale Gas Reservoir Production Considering the Effects of the Adsorbed Water Layer and Flow Differences. Processes. 2024; 12(12):2693. https://doi.org/10.3390/pr12122693
Chicago/Turabian StyleYuan, Hua, Jianyi Liu, Qunchao Ding, Lu Jiang, Zhibin Liu, Wenting He, and Yimin Wen. 2024. "Simulation of Shale Gas Reservoir Production Considering the Effects of the Adsorbed Water Layer and Flow Differences" Processes 12, no. 12: 2693. https://doi.org/10.3390/pr12122693
APA StyleYuan, H., Liu, J., Ding, Q., Jiang, L., Liu, Z., He, W., & Wen, Y. (2024). Simulation of Shale Gas Reservoir Production Considering the Effects of the Adsorbed Water Layer and Flow Differences. Processes, 12(12), 2693. https://doi.org/10.3390/pr12122693






