Towards National Energy Internet: Novel Optimization Method for Preliminary Design of China’s Multi-Scale Power Network Layout
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Objective and Contribution of This Study
2. Determination of Geographical Location of Energy Supply and Use Hub Nodes
2.1. Basic Method
2.2. Geographical Distribution of Energy Supply Hub Nodes
2.2.1. Coal Resources
2.2.2. Solar Energy
2.2.3. Water Energy
2.2.4. Wind Energy
2.3. Geographical Distribution of Energy Use Hub Nodes
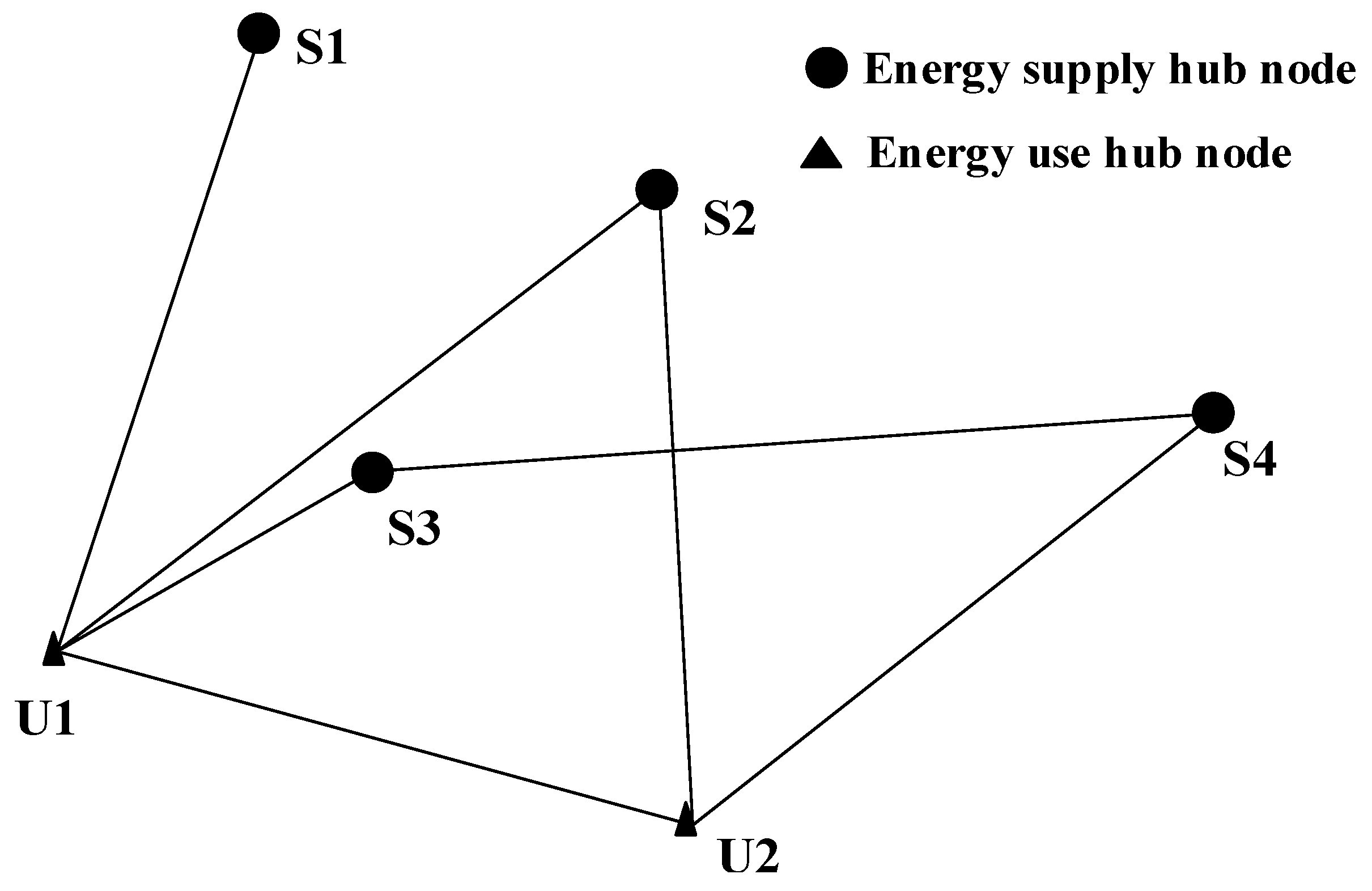
3. Synchronous Optimization Model
3.1. Model Description
- The maximum electric supply amount of each energy supply hub node and the maximum electric consumption of each energy use hub node are fixed values, which are calculated in Section 2 of this paper.
- The transmission voltages at both supply and use nodes are constant. Moreover, the technical requirements as well as the economics of different voltage levels are not considered.
- Only steady-state power transmission processes are considered.
- All physical properties of the transmission line connecting the two hub nodes are constant.
- The price of electricity is the average price of electricity in each region. The effect of peak-valley electricity price is not taken into account.
- The increase of load/use and the penetration of renewable energies or distributed resources are not considered.
3.2. Objective Function
3.3. Constraint Conditions
3.3.1. Energy Flow Constraints
3.3.2. Feasibility Constraints
3.3.3. Penalty Constraints
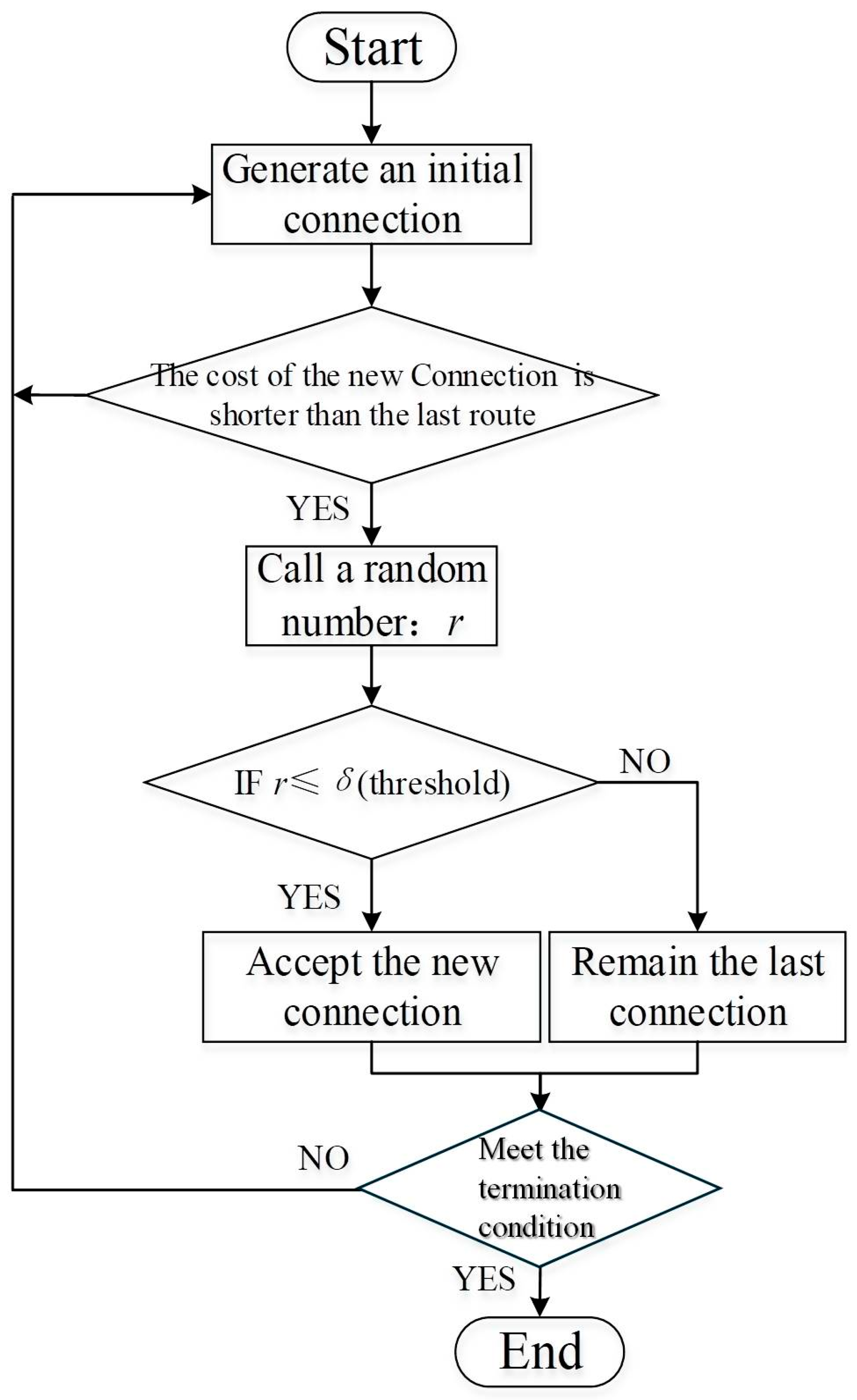
3.4. Model-Solving Strategy
3.4.1. Initialization
3.4.2. Evolution
3.4.3. Selection and Variation
3.4.4. Terminate the Iteration
4. Results and Discussions
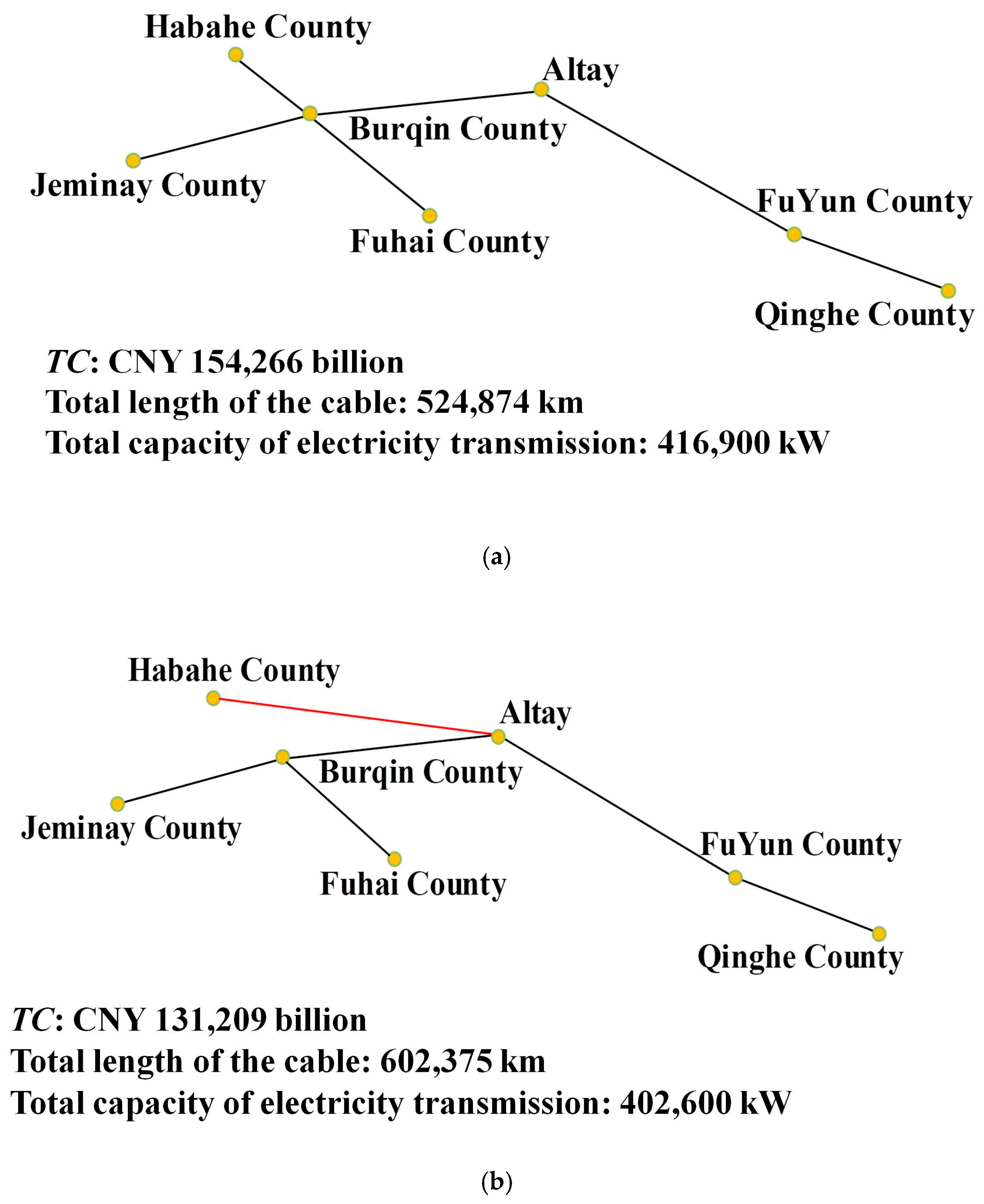
4.1. Optimal Layout of Municipal Power Network
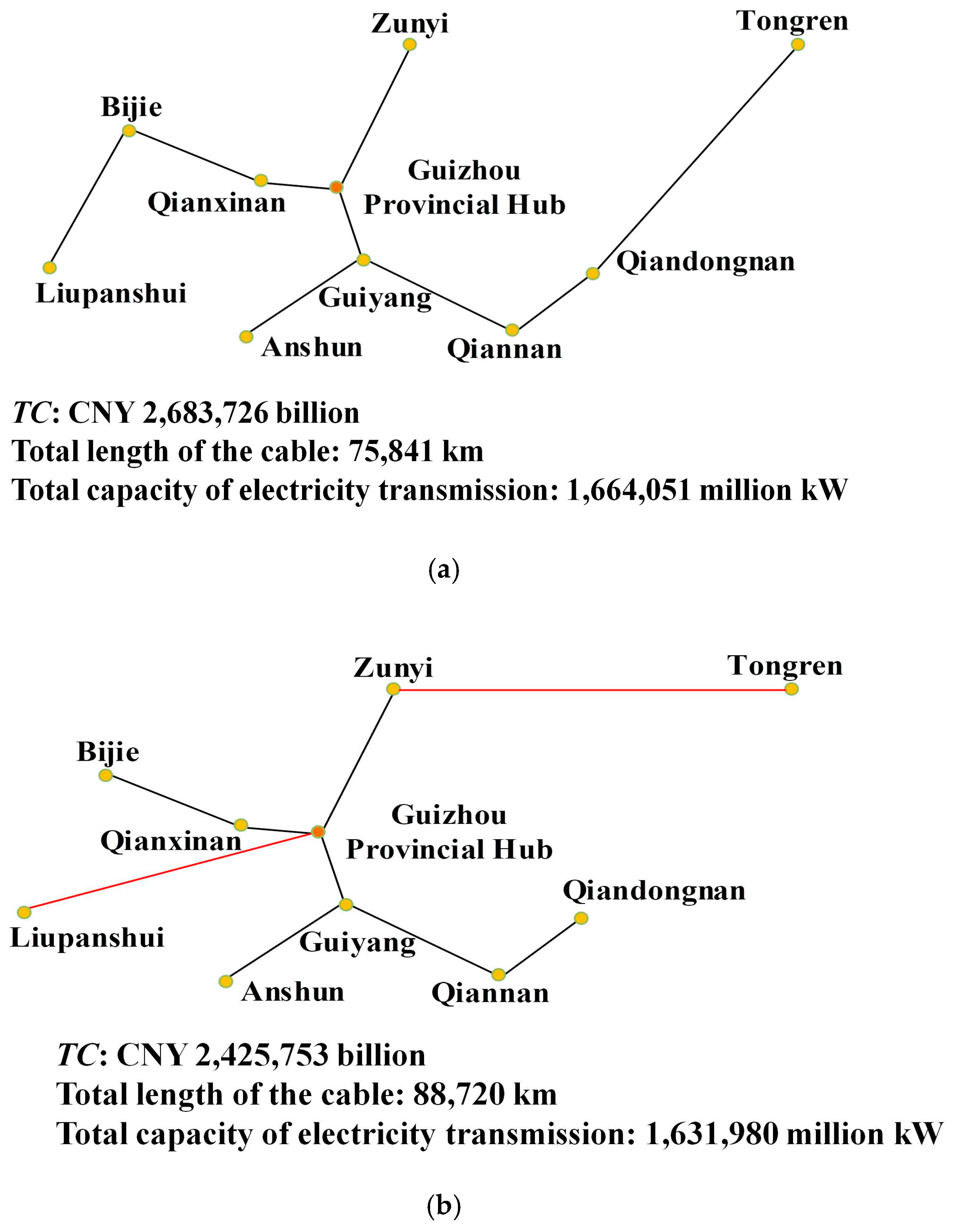
4.2. Optimal Layout of Provincial Power Network
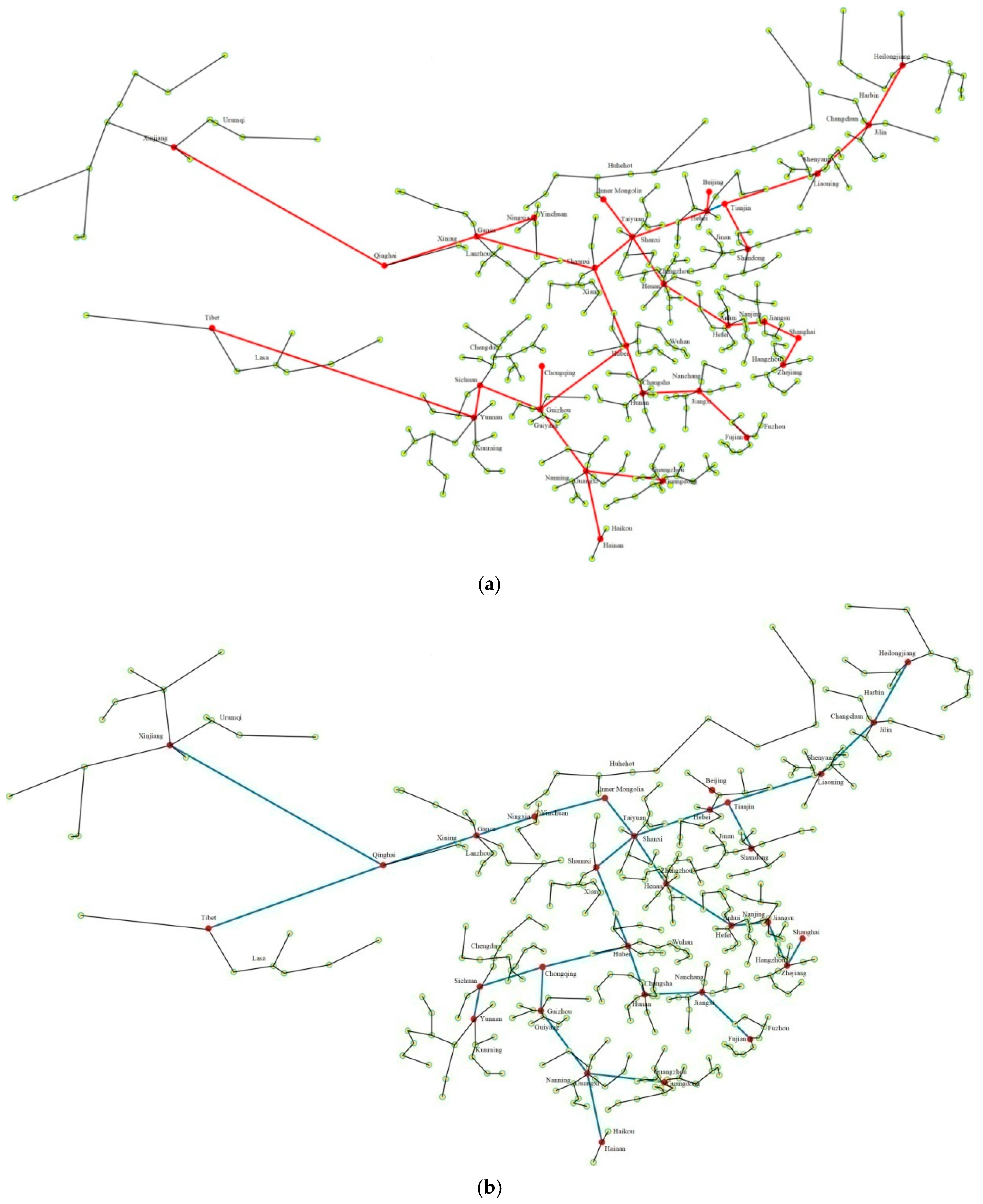
4.3. Optimal Layout of National Power Network
4.4. Discussions
5. Conclusions
- The geographical coordinates and potential energy amounts of the coal, solar, water, and wind energy supply hub nodes in China are calculated in detail, and used as the basic data for subsequent optimization.
- A synchronous optimization model of the multi-scale power network in China is proposed, which takes the length of transmission lines and the power transmission between different nodes as the optimization variables, and the total cost of the network as the optimization objective. The RWCE was used to solve the established model to better approximate the global optimal solution of the problem.
- Results of optimization by the synchronous method show that, compared with the optimization method that only optimizes the transmission line length, although the proposed method will cause a slight increase in investment cost, it can obviously reduce the operating cost of the network, so as to bring a significant improvement in network economy on the basis of ensuring the balance between power supply and use.
- Taking Altay City and Guizhou Province as examples for municipal and provincial power networks, the saving of total annual cost of power network optimized by the proposed method is CNY 230.60 million and CNY 2.58 billion, respectively. Moreover, for the nationwide power network, the total cost savings over 30 years of operation amount to CNY 179 billion.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Calculation Results of China’s Four Major Energy Resources
| Province/City | Reserves (108 tons) | Longitude (°) | Latitude (°) |
|---|---|---|---|
| Beijing | 2.66 | 115.5520 | 39.6650 |
| Hebei | 43.27 | 113.7625 | 39.2490 |
| Shangxi | 916.19 | 111.8173 | 37.1350 |
| Neimeng | 510.27 | 110.1176 | 38.2114 |
| Liaoning | 26.73 | 112.8835 | 42.0870 |
| Jilin | 9.71 | 126.0475 | 43.4540 |
| Heiliongjiang | 62.28 | 128.0715 | 47.6155 |
| Anhui | 82.37 | 116.8580 | 32.9425 |
| Shandong | 75.67 | 117.3716 | 35.0898 |
| Henan | 85.58 | 113.7733 | 35.3830 |
| Hainan | 1.19 | 109.7747 | 19.1877 |
| Chongqing | 18.03 | 106.4540 | 29.9010 |
| Sichuan | 53.21 | 105.5810 | 32.5490 |
| Guizhou | 110.93 | 105.3275 | 27.2105 |
| Yunnan | 59.58 | 102.4336 | 25.0382 |
| Shaanxi | 162.93 | 109.5455 | 35.3570 |
| Gansu | 27.32 | 104.0905 | 36.4370 |
| Qinghai | 12.39 | 97.1730 | 36.8218 |
| Ningxia | 37.45 | 107.0003 | 36.6217 |
| Xinjiang | 162.31 | 84.4719 | 41.1917 |
| Province/City | Theoretical Generating Capacity (1014 kWh) | Longitude (°) | Latitude (°) |
|---|---|---|---|
| Beijing/Tianjing/Hebei | 3.224646 | 116.0782 | 39.9118 |
| Shangxi | 2.243232 | 112.4405 | 38.2721 |
| Neimeng | 17.28671 | 113.0702 | 42.3019 |
| Liaoning | 2.008588 | 122.3996 | 41.1839 |
| Jilin | 2.421405 | 125.1836 | 43.9146 |
| Heiliongjiang | 5.813514 | 127.7743 | 46.9314 |
| Shanghai/Jiangsu | 1.685354 | 119.4043 | 33.1718 |
| Zhejiang | 1.254029 | 120.1877 | 29.3330 |
| Anhui | 1.650294 | 116.9937 | 32.2194 |
| Fujian | 1.519828 | 117.8737 | 25.7658 |
| Jiangxi | 1.988142 | 115.9776 | 28.1739 |
| Shandong | 2.134186 | 117.7973 | 36.3849 |
| Henan | 2.128344 | 113.7414 | 34.0587 |
| Hubei | 2.177025 | 113.1811 | 31.0684 |
| Hunan | 2.408748 | 112.1432 | 27.5411 |
| Guangdong | 2.343515 | 113.5553 | 22.9223 |
| Guangxi | 2.766068 | 108.2855 | 23.3804 |
| Hainan | 0.463445 | 109.6606 | 19.165 |
| Chongqing/Sichuan | 7.165879 | 101.8854 | 30.4218 |
| Guizhou | 1.844045 | 106.5153 | 26.5120 |
| Yunnan | 5.621710 | 101.1811 | 24.7487 |
| Tibet | 22.98339 | 90.09129 | 30.1256 |
| Shaanxi | 2.532398 | 109.2059 | 35.7986 |
| Gansu | 6.523287 | 102.2071 | 37.3745 |
| Qinghai | 13.29972 | 99.41850 | 35.4423 |
| Ningxia | 1.062225 | 106.0558 | 37.3519 |
| Xinjiang | 25.34629 | 83.0180 | 41.4895 |
| Province/City | Reserves (108 m3) | Longitude (°) | Latitude (°) |
|---|---|---|---|
| Beijing | 12.00 | 117.5588 | 40.0513 |
| Tianjing | 8.80 | 117.1171 | 38.9123 |
| Hebei | 60.00 | 114.4203 | 38.0915 |
| Shangxi | 87.80 | 110.6886 | 36.5396 |
| Neimeng | 194.10 | 108.0026 | 40.6843 |
| Liaoning | 161.00 | 123.1850 | 41.5388 |
| Jilin | 339.80 | 127.5406 | 43.0842 |
| Heiliongjiang | 626.50 | 130.2082 | 46.8707 |
| Shanghai/Jiangsu | 323.20 | 119.0226 | 33.0688 |
| Zhejiang | 881.90 | 120.1771 | 31.2082 |
| Anhui | 717.80 | 117.5140 | 31.5181 |
| Fujian | 1054.20 | 118.8065 | 25.3104 |
| Jiangxi | 1637.20 | 116.3918 | 29.0029 |
| Shandong | 139.10 | 117.0219 | 34.7939 |
| Henan | 311.20 | 111.7925 | 34.8207 |
| Hubei | 1219.30 | 111.2846 | 30.7292 |
| Hunan | 1905.70 | 112.8319 | 29.0996 |
| Guangdong | 1777.00 | 113.1769 | 22.8857 |
| Guangxi | 2386.00 | 108.6833 | 23.9132 |
| Hainan | 380.50 | 110.2425 | 20.1054 |
| Chongqing | 656.10 | 106.1997 | 29.2453 |
| Sichuan | 2466.00 | 102.6462 | 27.4700 |
| Guizhou | 1051.50 | 108.1130 | 26.7552 |
| Yunnan | 2202.60 | 102.8034 | 27.0470 |
| Tibet | 4749.90 | 95.5998 | 29.3096 |
| Shaanxi | 422.60 | 110.9940 | 34.1321 |
| Gansu | 231.80 | 103.7621 | 36.1671 |
| Qinghai | 764.30 | 99.5951 | 36.0251 |
| Ningxia | 8.70 | 106.1384 | 38.2543 |
| Xinjiang | 969.50 | 85.1164 | 43.4107 |
| Province/City | Theoretical Power (108 kW) | Longitude (°) | Latitude (°) |
|---|---|---|---|
| Beijing/Tianjing/Hebei | 321.438197 | 115.7220 | 37.9880 |
| Shangxi | 193.6615 | 112.6320 | 37.1680 |
| Neimeng | 4086.0580 | 109.4982 | 42.8271 |
| Liaoning | 390.8169 | 119.8430 | 41.3150 |
| Jilin | 631.2966 | 127.6805 | 43.2225 |
| Heiliongjiang | 1429.701 | 126.7491 | 46.7967 |
| Shanghai/Jiangsu | 183.679 | 119.9900 | 32.3740 |
| Zhejiang | 67.38223 | 120.5867 | 30.3367 |
| Anhui | 159.7708 | 116.0650 | 34.1350 |
| Fujian | 50.66145 | 119.6480 | 26.8360 |
| Jiangxi | 98.82727 | 115.2900 | 25.3900 |
| Shandong | 302.6211 | 118.1510 | 35.8620 |
| Henan | 156.5264 | 113.8100 | 33.2050 |
| Hubei | 89.44367 | 116.2863 | 30.6830 |
| Hunan | 77.96374 | 112.2640 | 27.7670 |
| Guangdong | 154.8294 | 115.8675 | 23.5050 |
| Guangxi | 163.2147 | 106.2250 | 23.9225 |
| Hainan | 34.33998 | 109.4967 | 18.8767 |
| Chongqing/Sichuan | 179.0371 | 99.7425 | 29.9175 |
| Guizhou | 52.4084 | 105.2850 | 25.4450 |
| Yunnan | 193.5417 | 101.7770 | 26.6065 |
| Tibet | 2158.727 | 85.0147 | 33.1050 |
| Shaanxi | 129.4038 | 108.6650 | 37.9300 |
| Gansu | 656.4527 | 99.9950 | 39.2550 |
| Qinghai | 1264.5400 | 94.7903 | 34.6343 |
| Ningxia | 80.79878 | 104.8236 | 38.4762 |
| Xinjiang | 3528.9320 | 87.3124 | 44.3123 |
Appendix B. Annual Electricity Consumption by Provinces/Cities in China
| Province/City | Electricity Consumption (108 kWh) | Longitude (°) | Latitude (°) |
|---|---|---|---|
| Beijing | 1067 | 116.4000 | 39.9000 |
| Tianjin | 806 | 117.2000 | 39.1200 |
| Hebei | 3442 | 116.1948 | 38.7079 |
| Shangxi | 1991 | 112.4037 | 37.3669 |
| Neimeng | 2892 | 113.3114 | 41.7971 |
| Liaoning | 2135 | 122.5665 | 40.7352 |
| Jilin | 703 | 125.5946 | 43.6953 |
| Heiliongjiang | 929 | 126.7323 | 46.3745 |
| Shanghai | 1527 | 121.4700 | 31.2300 |
| Jiangsu | 5808 | 119.4758 | 32.1554 |
| Zhejiang | 4193 | 120.6236 | 29.6742 |
| Anhui | 1921 | 117.3997 | 31.9565 |
| Fujian | 2113 | 118.4834 | 25.3841 |
| Jiangxi | 1294 | 115.7359 | 28.0929 |
| Shandong | 5430 | 118.5676 | 36.4514 |
| Henan | 3166 | 113.6574 | 34.3753 |
| Hubei | 1869 | 113.2574 | 30.8349 |
| Hunan | 1582 | 112.4219 | 27.9361 |
| Guangdong | 5959 | 113.5609 | 22.8685 |
| Guangxi | 1442 | 109.1553 | 23.3798 |
| Hainan | 305 | 109.9758 | 19.4097 |
| Chongqing | 993 | 106.5500 | 29.5700 |
| Sichuan | 2205 | 104.3886 | 30.1842 |
| Guizhou | 1385 | 106.5823 | 26.9690 |
| Yunnan | 1538 | 102.2383 | 24.8396 |
| Tibet | 58 | 91.6423 | 30.0076 |
| Shaanxi | 1495 | 108.8434 | 34.9058 |
| Gansu | 1164 | 103.6010 | 36.5189 |
| Qinghai | 687 | 100.7710 | 36.5750 |
| Ningxia | 978 | 106.1654 | 38.2048 |
| Xinjiang | 2001 | 84.8932 | 43.2275 |
Appendix C. Model-Solving Strategy Only Taking the Transmission Line Length as the Optimization Variable
Appendix C.1. Initialization
Appendix C.2. Evolution
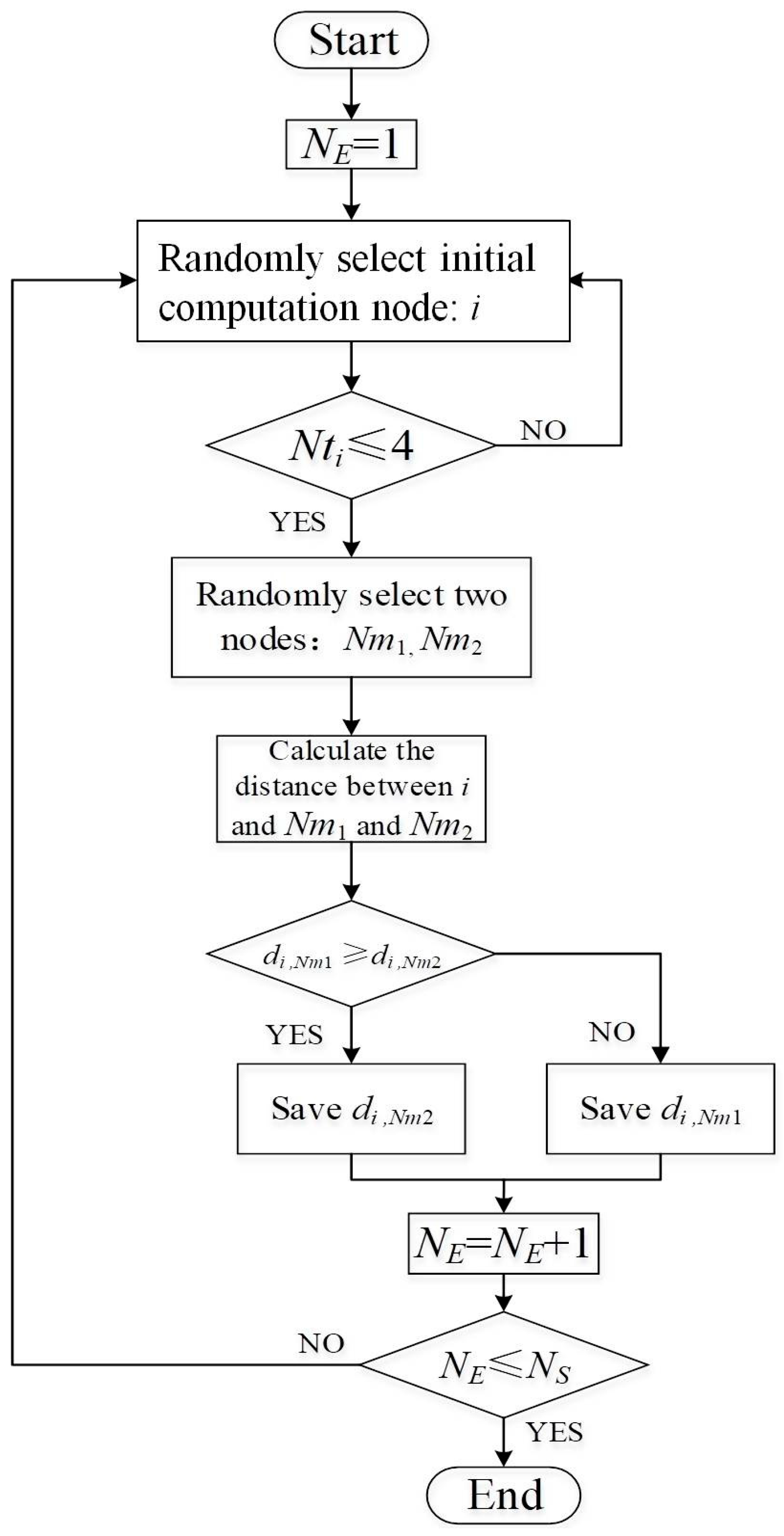
Appendix C.3. Variation
Appendix C.4. Terminate the Iteration
References
- Wang, Z.; Zheng, H.; Pei, L.; Jin, T. Decomposition of the factors influencing export fluctuation in China’s new energy. Energy Policy 2017, 109, 22–35. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Z.; Jiang, Y.; Zhang, T.; Yang, L.; Tan, W.; Lu, F. Modelling and discussion on emission reduction transformation path of China’s electric power industry under “double carbon” goal. Heliyon 2022, 8, 10497. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Tan, R. How to reduce CO2 emissions in pharmaceutical industry of China: Evidence from total-factor carbon emissions performance. J. Clean. Prod. 2022, 337, 130505. [Google Scholar] [CrossRef]
- Yao, X.; Fan, Y.; Zhao, F.; Ma, S. Economic and climate benefits of vehicle-to-grid for low-carbon transitions of power systems: A case study of China’s 2030 renewable energy target. J. Clean. Prod. 2022, 330, 129833. [Google Scholar] [CrossRef]
- Zeng, S.; Su, B.; Zhang, M.; Gao, Y.; Liu, J.; Luo, S.; Tao, Q. Analysis and forecast of China’s energy use structure. Energy Policy 2021, 159, 112630. [Google Scholar] [CrossRef]
- Solarin, S.; Bello, M.; Tiwari, A. The impact of technological innovation on renewable energy production: Accounting for the roles of economic and environmental factors using a method of moments quantile regression. Heliyon 2022, 8, 09913. [Google Scholar] [CrossRef]
- Mao, Y. China’s Transmission Trunk Line Layout Optimization: Considering Renewable Energy Development and Transmission Technology Selection; China University of Geoscience: Wuhan, China, 2019. (In Chinese) [Google Scholar]
- Quitzow, R.; Huenteler, J.; Asmussen, H. Development trajectories in China’s wind and solar energy industries: How technology-related differences shape the dynamics of industry localization and catching up. J. Clean. Prod. 2017, 158, 122–133. [Google Scholar] [CrossRef]
- Kurukuru, V.S.; Haque, A.; Khan, A.; Blaabjerg, F. Resource management with kernel-based approaches for grid-connected solar photovoltaic systems. Heliyon 2021, 7, 08609. [Google Scholar] [CrossRef]
- Kha, M.; Zahedi, R.; Eskandarpanah, R.; Mirzaei, A.; Farahani, O.; Malek, I.; Rezaei, N. Optimal sizing of residential photovoltaic and battery system connected to the power grid based on the cost of energy and peak load. Heliyon 2023, 9, 14414. [Google Scholar]
- Quelhas, A.; Gil, E.; McCalley, J.D.; Ryan, S.M. A multiperiod generalized network flow model of the U.S. integrated energy system: Part I—Model description. IEEE Trans. Power Syst. 2007, 22, 829–836. [Google Scholar] [CrossRef]
- Quelhas, A.; McCalley, J.D. A multiperiod generalized network flow model of the U.S. integrated energy system: Part II—Simulation results. IEEE Trans. Power Syst. 2007, 22, 837–844. [Google Scholar] [CrossRef]
- Unsihuay, L.; Marangon-Lima, J.W.; de Souza, A.C.Z. Integrated power generation and natural gas expansion planning. In Proceedings of the IEEE Power Tech Conference, Lausanne, Switzerland, 1–5 July 2007; pp. 1404–1409. [Google Scholar]
- Adetokun, B.; Muriithi, C. Application and control of flexible alternating current transmission system devices for voltage stability enhancement of renewable-integrated power grid: A comprehensive review. Heliyon 2021, 7, 06461. [Google Scholar] [CrossRef] [PubMed]
- Sharan, I.; Balasubramanian, R. Integrated generation and transmission expansion planning including power and fuel transportation constraints. Energy Policy 2012, 43, 275–284. [Google Scholar] [CrossRef]
- Wang, C.; Ye, M.; Cai, W.; Chen, J. The value of a clear, long-term climate policy agenda: A case study of China’s power sector using a multi-region optimization model. Appl. Energy 2014, 25, 276–288. [Google Scholar] [CrossRef]
- Guo, Z.; Ma, L.; Liu, P.; Jones, I.; Li, Z. A multi-regional modelling and optimization approach to China’s power generation and transmission planning. Energy 2016, 116, 1348–1359. [Google Scholar] [CrossRef]
- Yi, B.; Xu, J.; Fan, Y. Inter-regional power grid planning up to 2030 in China considering renewable energy development and regional pollutant control: A multi-region bottom-up optimization model. Appl. Energy 2016, 184, 641–658. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, T.; Guo, F. A multi-regional energy transport and structure model for China’s electricity system. Energy 2018, 161, 907–919. [Google Scholar] [CrossRef]
- Wang, H.; Su, B.; Mu, H.; Li, N.; Gui, S.; Duan, Y.; Kong, X. Optimal way to achieve renewable portfolio standard policy goals from the electricity generation, transmission, and trading perspectives in southern China. Energy Policy 2020, 139, 111319. [Google Scholar] [CrossRef]
- Zheng, Y.; Hu, Z.; Wang, J.; Wen, Q. IRSP (integrated resource strategic planning) with interconnected smart grids in integrating renewable energy and implementing DSM (use side management) in China. Energy 2014, 76, 863–874. [Google Scholar] [CrossRef]
- Yu, S.; Zheng, Y.; Li, L. A comprehensive evaluation of the development and utilization of China’s regional renewable energy. Energy Policy 2019, 127, 73–86. [Google Scholar] [CrossRef]
- Yu, S.; Hu, X.; Li, L.; Chen, H. Does the development of renewable energy promote carbon reduction? Evidence from Chinese provinces. J. Environ. Manag. 2020, 268, 110634. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Yao, J. In the “post-parity” era, the new energy industry is looking for new breakthroughs. China Energy News, 10 November 2020. (In Chinese) [Google Scholar]
- Hui, J.; Cai, W.; Wang, C.; Ye, M. Analyzing the penetration barriers of clean generation technologies in China’s power sector using a multi-region optimization model. Appl. Energy 2017, 185, 1809–1820. [Google Scholar] [CrossRef]
- Sun, M.; Cremer, J.; Strbac, G. A novel data-driven scenario generation framework for transmission expansion planning with high renewable energy penetration. Appl. Energy 2018, 228, 546–555. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, Y.; Zhou, Y.; Clarke, L.E.; Edmonds, J.A. Roles of wind and solar energy in China’s power sector: Implications of intermittency constraints. Appl. Energy 2018, 213, 22–30. [Google Scholar] [CrossRef]
- Ramirez, J.M.; Hernandez-Tolentino, A.; Marmolejo-Saucedo, J.A. A stochastic robust approach to deal with the generation and transmission expansion planning problem embedding renewable sources. In Uncertainties in Modern Power Systems; Academic Press: Cambridge, MA, USA, 2021; Volume 1, pp. 57–91. [Google Scholar]
- Aghaei, J.; Akbari, M.A.; Roosta, A.; Baharvandi, A. Multiobjective generation expansion planning considering power system adequacy. Electr. Power Syst. Res. 2013, 102, 8–19. [Google Scholar] [CrossRef]
- Guerra, O.J.; Tejada, D.A.; Reklaitis, G.V. An optimization framework for the integrated planning of generation and transmission expansion in interconnected power systems. Appl. Energy 2016, 170, 1–21. [Google Scholar] [CrossRef]
- Pereira, S.; Ferreira, P.; Vaz, A.I.F. Generation expansion planning with high share of renewables of variable output. Appl. Energy 2017, 190, 1275–1288. [Google Scholar] [CrossRef]
- Luz, T.; Mour, P.; de Almeida, A. Multi-objective power generation expansion planning with high penetration of renewables. Renew. Sustain. Energy Rev. 2018, 81, 2637–2643. [Google Scholar] [CrossRef]
- Moura, P.S.; de Almeida, A.T. Multi-objective optimization of a mixed renewable system with use-side management. Renew. Sustain. Energy Rev. 2020, 14, 1461–1468. [Google Scholar] [CrossRef]
- Tafarte, P.; Das, S.; Eichhorn, M.; Thran, D. Small adaptations, big impacts: Options for an optimized mix of variable renewable energy sources. Energy. 2014, 72, 80–92. [Google Scholar] [CrossRef]
- Rodriguez, R.A.; Becker, S.; Greiner, M. Cost-optimal design of a simplified, highly renewable pan-European electricity system. Energy 2015, 83, 658–668. [Google Scholar] [CrossRef]
- Koltsaklis, N.E.; Dagoumas, A.S. State-of-the-art generation expansion planning: A review. Appl. Energy 2018, 230, 563–589. [Google Scholar] [CrossRef]
- Yu, S.; Zhou, S.; Qin, J. Layout optimization of China’s power transmission lines for renewable power integration considering flexible resources and grid stability. Int. J. Electr. Power Energy Syst. 2022, 135, 107507. [Google Scholar] [CrossRef]
- Murtagh, B.A.; Saunders, M.A. Large-scale linearly constrained optimization. Math. Program. 1978, 14, 41–72. [Google Scholar] [CrossRef]
- Viswanathan, J.; Grossmann, I.E. A combined penalty function and outer-approximation method for MINLP optimization. Comput. Chem. Eng. 1990, 14, 769–782. [Google Scholar] [CrossRef]
- Rosenthal, R.E. GAMS—A User’s Guide; GAMS Development Corporatio: Washington, DC, USA, 2010. [Google Scholar]
- Xiao, Y.; Cui, G. A novel Random Walk algorithm with Compulsive Evolution for heat exchanger network synthesis. Appl. Therm. Eng. 2017, 115, 1118–1127. [Google Scholar] [CrossRef]
- Xiao, Y.; Cui, G.; Zhang, G.; Ai, L. Parallel optimization route promoted by accepting imperfect solutions for the global optimization of heat exchanger networks. J. Clean. Prod. 2022, 336, 130354. [Google Scholar] [CrossRef]
- Xu, Y.; Cui, G.; Han, X.; Xiao, Y.; Zhang, G. Optimization route arrangement: A new concept to achieve high efficiency and quality in heat exchanger network synthesis. Int. J. Heat Mass Tran. 2021, 178, 121622. [Google Scholar] [CrossRef]
- Liu, L.; Cui, G.; Chen, J.; Huang, X.; Li, D. Two-stage superstructure model for optimization of distributed energy systems (DES) part I: Mode development and verification. Energy 2022, 245, 123227. [Google Scholar] [CrossRef]
- NBSC (National Bureau of Statistics of China). China Statistical Yearbook, 2019–2020; China Statistics Press: Beijing, China, 2020; (In Chinese).
- Pierri, E.; Binder, O.; Hemdan, N.G.; Kurrat, M. Challenges and opportunities for a European HVDC grid. Renew. Sustain. Energy Rev. 2017, 70, 427–456. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, L.; Jovcic, D. DC transmission grid with low speed protection using mechanical DC circuit breakers. IEEE Trans. Power Deliv. 2015, 30, 1383–1391. [Google Scholar]
- Chaudhuri, N.; Chaudhuri, B.; Majumder, R.; Yazdani, A. Multi-Terminal Direct-Current Grids Modeling, Analysis, and Control; Wiley-IEEE Press: Hoboken, NJ, USA, 2014. [Google Scholar]
- Zhang, X. Multiterminal voltage-sourced converter-based HVDC models for power flow analysis. IEEE Trans. Power Syst. 2014, 19, 1877–1884. [Google Scholar] [CrossRef]
- Deng, X.; Lv, T. Power system planning with increasing variable renewable energy: A review of optimization models. J. Clean. Prod. 2020, 246, 118962. [Google Scholar] [CrossRef]
- Zhang, N.; Hu, Z.; Shen, B.; He, G.; Zheng, Y. An integrated source-grid-load planning model at the macro level: Case study for China’s power sector. Energy 2017, 126, 231–246. [Google Scholar] [CrossRef]
- Vozikis, D.; Psaras, V.; Alsokhiry, F.; Adam, G.; Al-Turki, Y. Customized converter for cost-effective and DC-fault resilient HVDC Grids. Int. J. Electr. Power Energy Syst. 2021, 131, 107038. [Google Scholar] [CrossRef]
- Gonzalez-Torres, J.C.; Damm, G.; Costan, V.; Benchaib, A.; Lamnabhi-Lagarrigue, F. A novel distributed supplementary control of multi-terminal VSC-HVDC grids for rotor angle stability enhancement of AC/DC systems. IEEE Trans. Power Syst. 2021, 36, 623–634. [Google Scholar] [CrossRef]
- Ye, Y.; Qiao, Y.; Xie, L.; Lu, Z. A comprehensive power flow approach for multiterminal VSC-HVDC system considering cross-regional primary frequency responses. J. Mod. Power Syst. Clean Energy. 2020, 8, 238–248. [Google Scholar] [CrossRef]
- Renedo, J.; Garcia-Cerrada, A.; Rouco, L.; Sigrist, L. Coordinated Design of Supplementary Controllers in VSC-HVDC Multi-Terminal Systems to Damp Electromechanical Oscillations. IEEE Trans. Power Syst. 2021, 36, 712–721. [Google Scholar] [CrossRef]
- Beerten, J.; Cole, S.; Belmans, R. Modeling of multi-terminal VSC HVDC systems with distributed DC voltage control. IEEE Trans. Power Syst. 2014, 29, 34–42. [Google Scholar] [CrossRef]
- Li, G.; Du, Z.; Shen, C.; Yuan, Z.; Wu, G. Coordinated design of droop control in MTDC grid based on model predictive control. IEEE Trans. Power Syst. 2017, 99, 1. [Google Scholar] [CrossRef]
- Sau-Bassols, J.; Prieto-Araujo, E.; Gomis-Bellmunt, O.; Hassan, F. Selective Operation of Distributed Current Flow Controller Devices for Meshed HVDC Grids. IEEE Trans. Power Deliv. 2019, 34, 107–118. [Google Scholar] [CrossRef]
- Wang, P.; Feng, S.; Liu, P.; Jiang, N.; Zhang, X. Nyquist stability analysis and capacitance selection for DC current flow controllers in meshed multi-terminal HVDC grids. CSEE J. Power Energy Syst. 2021, 1, 114–127. [Google Scholar]
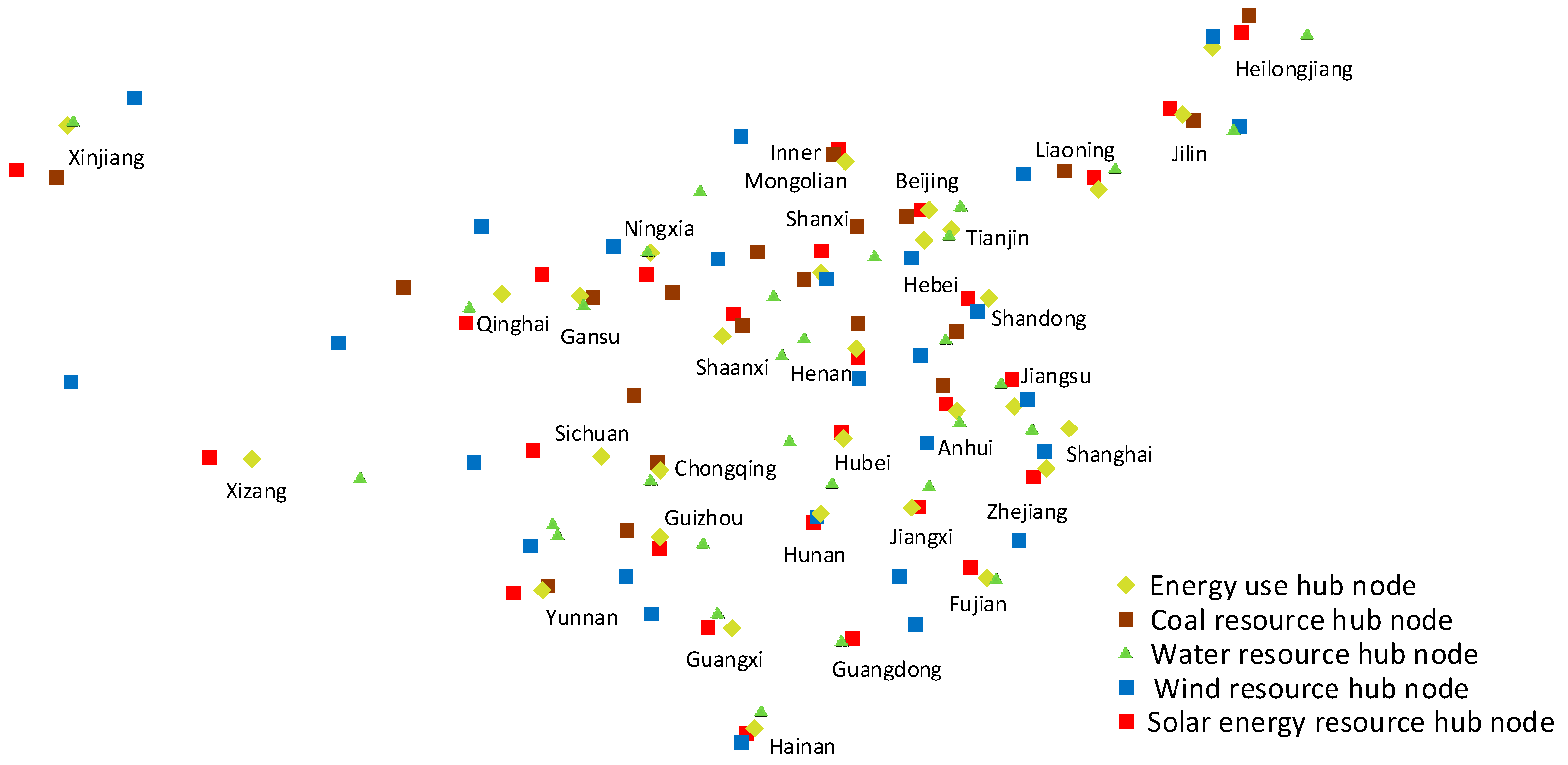
| Province/City | Coal | Solar | Water | Wind |
|---|---|---|---|---|
| Beijing | 40.2834 | 113.8918 | 11.4763 | 6.0829 |
| Tianjin | - | 0.1669 | 10.0915 | |
| Hebei | 655.2860 | 16.0928 | 164.3516 | |
| Shangxi | 13,874.8862 | 79.2291 | 32.6802 | 108.7642 |
| Neimeng | 7727.5894 | 610.5521 | 67.0221 | 2294.8120 |
| Liaoning | 404.8023 | 70.9417 | 32.7416 | 219.4906 |
| Jilin | 147.0494 | 85.5220 | 52.0232 | 354.5488 |
| Heiliongjiang | 943.1757 | 205.3285 | 18.4838 | 802.9487 |
| Shanghai | - | 59.5250 | 20.8019 | 7.7368 |
| Jiangsu | - | 95.4209 | ||
| Zhejiang | - | 44.2913 | 366.9260 | 37.8432 |
| Anhui | 1247.4213 | 58.2870 | 90.5679 | 89.7304 |
| Fujian | - | 53.6791 | 701.4053 | 28.4525 |
| Jiangxi | - | 70.2195 | 322.5589 | 55.5034 |
| Shandong | 1145.9552 | 75.3777 | 15.9629 | 169.9580 |
| Henan | 1296.0334 | 75.1713 | 152.1022 | 87.9084 |
| Hubei | - | 76.8907 | 1809.8562 | 50.2333 |
| Hunan | - | 85.0750 | 846.7218 | 43.7860 |
| Guangdong | - | 82.7710 | 702.2210 | 86.9553 |
| Guangxi | - | 97.6952 | 1259.4223 | 91.6646 |
| Hainan | 18.0215 | 16.3685 | 9.3256 | 19.2860 |
| Chongqing | 273.0485 | 253.0928 | 348.2183 | 4.5412 |
| Sichuan | 805.8186 | 4700.9097 | 96.0096 | |
| Guizhou | 1679.9374 | 65.1301 | 1387.2926 | 29.4336 |
| Yunnan | 902.2865 | 198.5541 | 3943.0686 | 108.6969 |
| Tibet | - | 811.7540 | 75.3651 | 1212.3841 |
| Shaanxi | 2467.4313 | 89.3971 | 220.7372 | 72.6758 |
| Gansu | 413.7373 | 230.3971 | 493.8871 | 368.6769 |
| Qinghai | 187.6357 | 469.7349 | 459.2729 | 710.1908 |
| Ningxia | 567.1472 | 37.5169 | 17.6687 | 45.3782 |
| Xinjiang | 2458.0414 | 930.5289 | 365.1824 | 1981.9191 |
| Province | Optimizing the Length Only | Synchronous Optimization | Cost Saving | ||
|---|---|---|---|---|---|
| FI (108 CNY) | FO (108 CNY/a) | FI (108 CNY) | FO (108 CNY/a) | ΔTC Over a 30-Year Operating Period (108 CNY) | |
| Hebei | 935.16 | 42.597 | 949.579 | 39.128 | 89.651 |
| Shanxi | 461.173 | 29.212 | 463.874 | 27.932 | 35.699 |
| Neimeng | 1643.459 | 57.967 | 1798.906 | 43.046 | 292.183 |
| Jilin | 143.186 | 11.396 | 161.696 | 4.339 | 193.2 |
| Heilongjiang | 373.235 | 17.279 | 386.849 | 6.728 | 302.916 |
| Jiangsu | 984.131 | 91.06 | 985.027 | 88.867 | 64.894 |
| Zhejiang | 652.097 | 82.2 | 653.259 | 73.649 | 255.368 |
| Anhui | 407.546 | 37.963 | 412.632 | 28.756 | 271.124 |
| Fujian | 343.38 | 41.726 | 344.251 | 35.997 | 170.999 |
| Jiangxi | 285.255 | 24.571 | 300.514 | 19.695 | 131.021 |
| Shandong | 1251.312 | 64.086 | 1255.622 | 62.672 | 38.11 |
| Hubei | 559.133 | 23.549 | 597.83 | 17.361 | 146.943 |
| Guangdong | 674.446 | 43.449 | 710.088 | 37.435 | 144.778 |
| Ningxia | 86.156 | 19.185 | 93.08 | 16.396 | 76.746 |
| Sichuan | 887.824 | 41.417 | 923.337 | 39.431 | 24.067 |
| Yunnan | 633.238 | 30.338 | 701.377 | 25.98 | 62.601 |
| Shaanxi | 460.92 | 29.243 | 511.983 | 26.756 | 23.547 |
| Hunan | 327.89 | 29.327 | 332.084 | 21.085 | 243.066 |
| Liaoning | 408.671 | 28.922 | 436.321 | 27.333 | 20.02 |
| Tibet | 92.473 | 1.088 | 92.473 | 1.088 | 0 |
| Guizhou | 223.138 | 21.714 | 268.373 | 16.788 | 102.545 |
| Gansu | 401.086 | 20.688 | 401.593 | 19.386 | 38.553 |
| Guangxi | 355.592 | 28.522 | 376.532 | 23.752 | 122.16 |
| Henan | 596.156 | 62.21 | 600.56 | 42.515 | 586.446 |
| Xinjiang | 1026.656 | 39.8 | 1162.424 | 31.779 | 104.862 |
| Connections | Transmission Line Length (km) | Transmission Capacity (104 kW) | Voltage (kV) | Transmission Line Type (number × mm2) | Conversion Coefficient φ |
|---|---|---|---|---|---|
| Xinjiang–Qinghai | 1307.338 | 4142.580 | 1000 | 6 × 630 | 66.4097 |
| Tibet–Sichuan | 1551.299 | 2327.183 | 1000 | 6 × 630 | 66.4097 |
| Qinghai–Gansu | 512.964 | 5122.507 | 1000 | 6 × 630 | 66.4097 |
| Gansu–Shaanxi | 648.010 | 4880.241 | 1000 | 6 × 630 | 66.4097 |
| Shaanxi–Shanxi | 281.223 | 7214.146 | 1000 | 6 × 630 | 66.4097 |
| Neimeng–Shanxi | 285.185 | 8737.356 | 1000 | 6 × 630 | 66.4097 |
| Hubei–Shanxi | 540.611 | 1063.445 | 1000 | 6 × 630 | 66.4097 |
| Guizhou–Hubei | 640.620 | 4685.388 | 1000 | 6 × 630 | 66.4097 |
| Sichuan–Guizhou | 376.310 | 10,203.601 | 1000 | 6 × 630 | 66.4097 |
| Yunnan–Sichuan | 209.373 | 4034.224 | 1000 | 6 × 630 | 66.4097 |
| Heilongjiang–Jilin | 421.663 | 1135.864 | 1000 | 6 × 630 | 66.4097 |
| Gansu–Ningxia | 322.887 | 426.751 | 500 | 6 × 630 | 37.7957 |
| Guizhou–Chongqing | 286.314 | 431.861 | 500 | 6 × 630 | 37.7957 |
| Shanxi–Hebei | 412.146 | 11,101.509 | 1000 | 6 × 630 | 66.4097 |
| Hebei–Beijing | 133.726 | 1172.642 | 500 | 4 × 630 | 45.0535 |
| Hebei–Tianjin | 98.302 | 6660.212 | 1000 | 6 × 630 | 66.4097 |
| Tianjin–Shandong | 320.137 | 4873.526 | 1000 | 6 × 630 | 66.4097 |
| Tianjin–Liaoning | 491.480 | 746.398 | 500 | 4 × 630 | 44.4825 |
| Jilin–Liaoning | 412.883 | 1008.031 | 1000 | 6 × 630 | 45.0535 |
| Shanxi–Henan | 349.069 | 18,286.997 | 1000 | 6 × 630 | 66.4097 |
| Henan–Anhui | 440.24 | 15,973.815 | 1000 | 6 × 630 | 66.4097 |
| Anhui–Jiangsu | 196.897 | 14,979.990 | 1000 | 6 × 630 | 66.4097 |
| Jiangsu–Shanghai | 214.907 | 8062.977 | 1000 | 6 × 630 | 66.4097 |
| Shanghai–Zhejiang | 191.075 | 6279.415 | 1000 | 6 × 630 | 66.4097 |
| Hubei–Hunan | 324.772 | 3660.007 | 1000 | 6 × 630 | 66.4097 |
| Hunan–Jiangxi | 325.779 | 2805.578 | 1000 | 6 × 630 | 66.4097 |
| Jiangxi–Fujian | 406.373 | 1703.876 | 1000 | 6 × 630 | 66.4097 |
| Guangxi–Hainan | 449.549 | 300.801 | 500 | 4 × 630 | 45.0535 |
| Guizhou–Guangxi | 483.333 | 6822.137 | 1000 | 6 × 630 | 66.4097 |
| Guangxi–Guangdong | 454.979 | 6251.526 | 1000 | 6 × 630 | 66.4097 |
| Total investment cost FI (1012 CNY) | 2.134 | ||||
| Annual operating cost Fo/a (1012 CNY/a) | 0.115 | ||||
| Total cost over a 30-year operating period TC(30) (1012 CNY) | 5.584 | ||||
| Method | Transmission Line Length (km) | Transmission Capacity (104 kW) | FI (1012 CNY) | FO/a (1012 CNY/a) | TC(30) (1012 CNY) |
|---|---|---|---|---|---|
| I | 12,204.681 | 163,395.003 | 2.073 | 0.123 | 5.763 |
| II | 13,089.440 | 165,094.583 | 2.134 | 0.115 | 5.584 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Cui, G.; Xu, Y. Towards National Energy Internet: Novel Optimization Method for Preliminary Design of China’s Multi-Scale Power Network Layout. Processes 2024, 12, 2678. https://doi.org/10.3390/pr12122678
Liu L, Cui G, Xu Y. Towards National Energy Internet: Novel Optimization Method for Preliminary Design of China’s Multi-Scale Power Network Layout. Processes. 2024; 12(12):2678. https://doi.org/10.3390/pr12122678
Chicago/Turabian StyleLiu, Liuchen, Guomin Cui, and Yue Xu. 2024. "Towards National Energy Internet: Novel Optimization Method for Preliminary Design of China’s Multi-Scale Power Network Layout" Processes 12, no. 12: 2678. https://doi.org/10.3390/pr12122678
APA StyleLiu, L., Cui, G., & Xu, Y. (2024). Towards National Energy Internet: Novel Optimization Method for Preliminary Design of China’s Multi-Scale Power Network Layout. Processes, 12(12), 2678. https://doi.org/10.3390/pr12122678





