Application of SPEA2-MMBB for Distributed Fault Diagnosis in Nuclear Power System
Abstract
:1. Introduction
- (1)
- Optimized Sensor Selection. The SPEA2 algorithm selects the optimal sensor combination from multivariate time-series data, improving diagnostic accuracy.
- (2)
- Efficient Fault Diagnosis. The MMBB model performs feature extraction and classification, achieving high accuracy, low error rates, and robustness across subsystems and the overall system.
- (3)
- Dynamic Feedback Mechanism. SPEA2 dynamically adjusts sensor combinations based on feedback from the MMBB model, optimizing accuracy and resource efficiency.
- (4)
- Real-Time Diagnosis. Once sensor selection and model weights are finalized, the time cost for real-time fault diagnosis is significantly reduced.
2. Theoretical Foundation
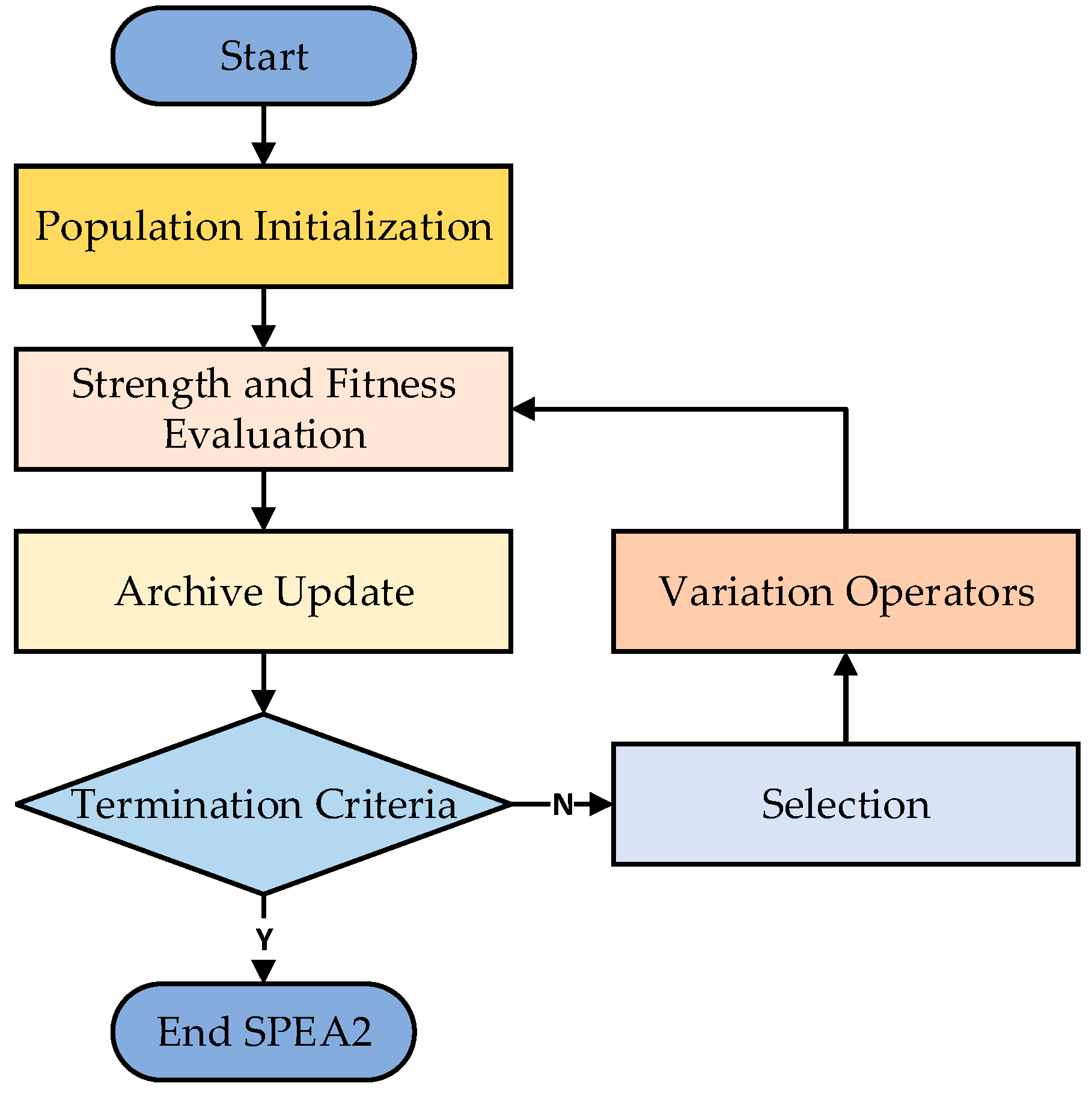
2.1. SPEA2 Algorithm
- Step 1: Population Initialization. An initial population P is randomly generated. The population size N is fixed, ensuring computational efficiency in fitness evaluation. An elite archive R is also initialized to store high-quality non-dominated solutions.
- Step 2: Strength and Fitness Evaluation. For each solution in P and R, the dominance strength and fitness are computed as described above. The fitness values guide the selection process, balancing convergence to the Pareto front and diversity within the solution set.
- Step 3: Archive Update. After fitness evaluation, the elite archive R is updated. Non-dominated solutions are added to R, while dominated solutions are removed. If R exceeds its maximum size, solutions are pruned using a truncation procedure based on proximity to other solutions.
- Step 4: Selection. A mating pool is formed by selecting individuals based on their fitness values. Solutions with lower fitness values (better solutions) have a higher probability of being selected.
- Step 5: Variation Operators. Genetic operators, such as crossover and mutation, are applied to the mating pool to generate a new population. These operators introduce variation, enabling exploration of the solution space.
- Step 6: Termination. The process is repeated for a predefined number of generations or until a termination criterion (e.g., convergence of the population to the Pareto front) is met. The final elite archive R represents the set of non-dominated solutions that approximate the Pareto-optimal front.
2.2. MMBB Model
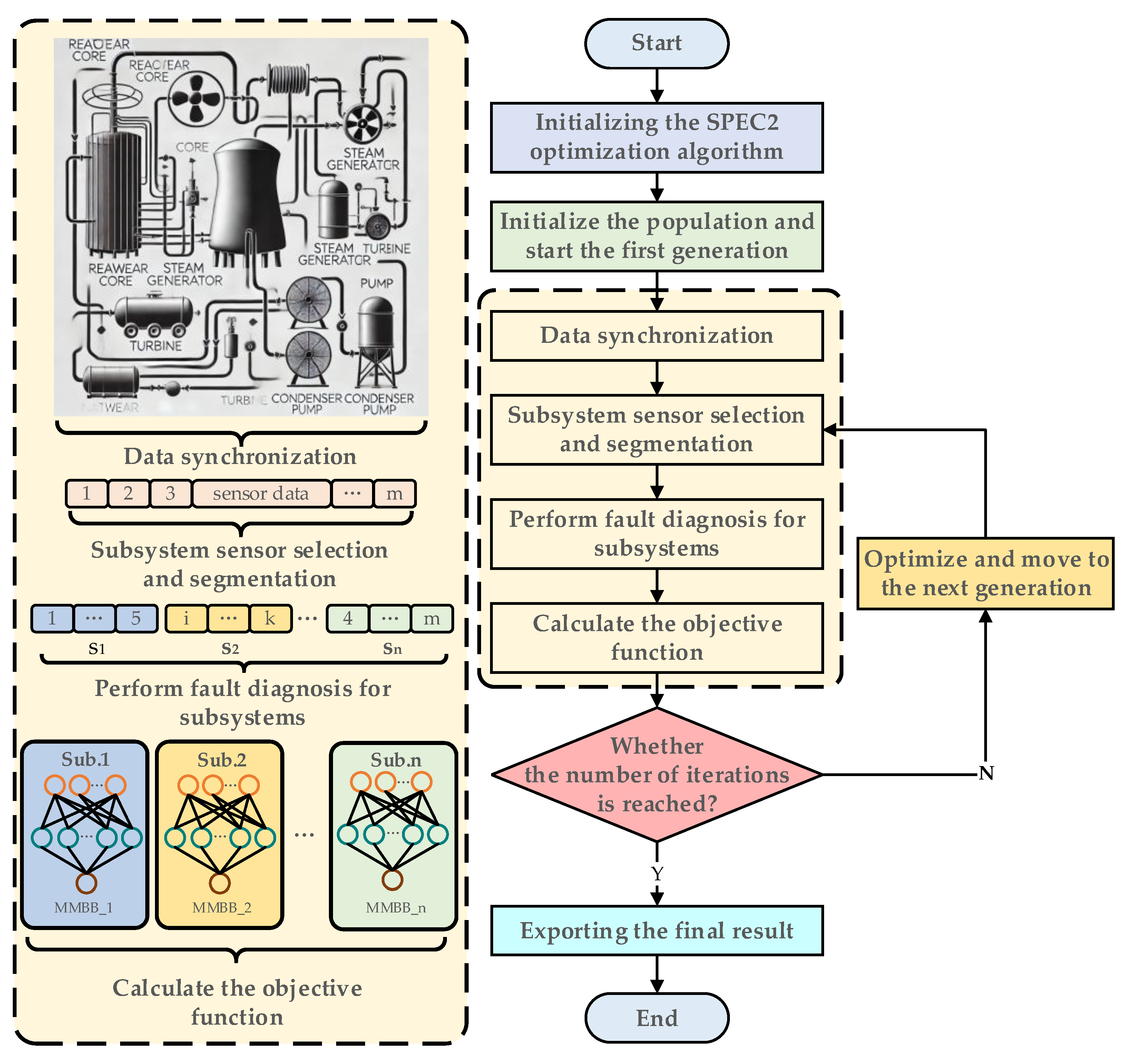
3. Overall Process
3.1. Problem Formulation
3.2. Definition of the Objective Function
3.3. Optimization Process
- Step 1. The SPEA2 algorithm is first executed for initialization, transforming the sensor optimization problem into a matrix-solving task.
- Step 2. Prepare the elite solution and initialize the population to minimize the number of iteration rounds. Then, initiate the fault diagnosis using the first generation of sensor selections.
- Step 3. Fault diagnosis is conducted using the selected sensors. The data are first synchronized to enable the calculation of combined accuracy. Then, the relevant sensor data are extracted and sent to different subsystems for fault diagnosis. Finally, the average accuracy of the subsystems and the combined accuracy of the system (the objective function) are computed.
- Step 4. Check whether the maximum number of iterations has been reached. If not, optimize the sensor selection based on the diagnostic results from the previous round using the SPEA2 algorithm and proceed with a new round of fault diagnosis.
- Step 5. Once the maximum number of iterations is reached, retrieve the elite individuals from the elite pool, which includes the selected sensors, the accuracy of each subsystem, and the combined accuracy of the system.
4. Case Study of the Reactor Coolant System
4.1. Experimental Dataset
4.2. Data Preprocessing
4.2.1. Removal of Low-Variance Data Using Variance Thresholding
4.2.2. Exclusion of Anomalies and Data Standardization
4.2.3. Time Window Data Generation
4.3. Experimental Validation
5. Conclusions
- (1)
- Summary of Contributions
- (2)
- Key Advantages
- The SPEA2 algorithm optimizes sensor feature selection dynamically, ensuring efficient resource utilization and enhanced fault detection capability.
- The MMBB neural network demonstrates robust performance with superior classification accuracy across distributed subsystems.
- The dynamic feedback mechanism between optimization and neural network training ensures adaptability and reliability in complex fault scenarios.
- (3)
- Limitations and Future Directions
- Handling Missing Data and Sensor Failures. Future work will incorporate methods, like GANs, to address incomplete sensor data and enhance robustness against sensor faults in real-world applications.
- Improving Model Interpretability. Future research will explore explainability techniques to make the model’s decision-making process more transparent for safety-critical applications.
- Broader Comparisons. Expanding comparisons to include Bayesian networks and reinforcement learning techniques will provide a more comprehensive evaluation of the proposed approach.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qian, G.; Liu, J. Fault Diagnosis Based on Conditional Generative Adversarial Networks in Nuclear Power Plants. J. Electr. Eng. Technol. 2023, 176, 109267. [Google Scholar] [CrossRef]
- Zio, E. Advancing Nuclear Safety. Front. Nucl. Eng. 2023, 4, 75–90. [Google Scholar] [CrossRef]
- Chen, H.Y.; Wang, Y.C.; Huang, X.Y.; Tian, X.L. Accident Source Term and Radiological Consequences of a Small Modular Reactor. Nucl. Sci. Tech. 2023, 33, 101. [Google Scholar] [CrossRef]
- Peng, M.; Wang, H.; Yang, X.; Liu, Y.; Guo, L.; Li, W.; Jiang, N. Real-Time Simulations to Enhance Distributed on-Line Monitoring and Fault Detection in Pressurized Water Reactors. Ann. Nucl. Energy 2017, 109, 557–573. [Google Scholar] [CrossRef]
- Wu, G.; Duan, Z.; Yuan, D.; Yin, J.; Liu, C.; Ji, D. Distributed Fault Diagnosis Framework for Nuclear Power Plants. Front. Energy Res. 2021, 9, 665502. [Google Scholar] [CrossRef]
- Yang, G.; Su, J.; Du, S.; Duan, Q. Federated Transfer Learning-Based Distributed Fault Diagnosis Method for Rolling Bearings. Meas. Sci. Technol. 2024, 35, 126111. [Google Scholar] [CrossRef]
- Mousavi, A.; Mousavi, R.; Mousavi, Y.; Tavasoli, M.; Arab, A.; Fekih, A. Artificial Neural Networks-Based Fault Localization in Distributed Generation Integrated Networks Considering Fault Impedance. IEEE Access 2024, 12, 82880–82896. [Google Scholar] [CrossRef]
- Castelletti, F.; Niro, F.; Denti, M.; Tessera, D.; Pozzi, A. Bayesian Learning of Causal Networks for Unsupervised Fault Diagnosis in Distributed Energy Systems. IEEE Access 2024, 12, 61185–61197. [Google Scholar] [CrossRef]
- Rajabioun, R.; Afshar, M.; Atan, O.; Mete, M.; Akin, B. Classification of Distributed Bearing Faults Using a Novel Sensory Board and Deep Learning Networks With Hybrid Inputs. IEEE Trans. Energy Convers. 2024, 39, 963–973. [Google Scholar] [CrossRef]
- Feng, B.; Zhou, Q.; Xing, J.; Yang, Q. Distributed Chaotic Bat Algorithm for Sensor Fault Diagnosis in AHUs Based on a Decentralized Structure. J. Build. Eng. 2024, 95, 110031. [Google Scholar] [CrossRef]
- Peng, H.; Mao, Z.; Jiang, B.; Cheng, Y. Multiscale Spatial-Temporal Bayesian Graph Conv-Transformer-Based Distributed Fault Diagnosis for UAVs Swarm System. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 6894–6909. [Google Scholar] [CrossRef]
- Ding, X.; Liao, X.; Cui, W.; Meng, X.; Liu, R.; Ye, Q.; Li, D. A Deep Reinforcement Learning Optimization Method Considering Network Node Failures. Energies 2024, 17, 4471. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Dong, J.; Zhang, C.; Peng, K. Multi-Node Knowledge Graph Assisted Distributed Fault Detection for Large-Scale Industrial Processes Based on Graph Attention Network and Bidirectional LSTMs. Neural Netw. 2024, 173, 106210. [Google Scholar] [CrossRef]
- Ren, C.; Li, H.; Lei, J.; Liu, J.; Li, W.; Gao, K.; Huang, G.; Yang, X.; Yu, T. A CNN-LSTM-Based Model to Fault Diagnosis for CPR1000. Nucl. Technol. 2023, 209, 1365–1372. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, P.; Jiang, F.; Xie, J.; Yu, T. Fault Diagnosis of Nuclear Power Plant Based on Sparrow Search Algorithm Optimized CNN-LSTM Neural Network. Energies 2023, 16, 2934. [Google Scholar] [CrossRef]
- Xu, Y.; Cai, Y.; Song, L. Latent Fault Detection and Diagnosis for Control Rods Drive Mechanisms in Nuclear Power Reactor Based on GRU-AE. IEEE Sens. J. 2023, 23, 6018–6026. [Google Scholar] [CrossRef]
- Jin, I.J.; Lim, D.Y.; Bang, I.C. Deep-Learning-Based System-Scale Diagnosis of a Nuclear Power Plant with Multiple Infrared Cameras. Nucl. Eng. Technol. 2023, 55, 493–505. [Google Scholar] [CrossRef]
- Lin, W.; Miao, X.; Chen, J.; Ye, M.; Xu, Y.; Liu, X.; Jiang, H.; Lu, Y. Fault Detection and Isolation for Multi-Type Sensors in Nuclear Power Plants via a Knowledge-Guided Spatial-Temporal Model. Knowl.-Based Syst. 2024, 300, 112182. [Google Scholar] [CrossRef]
- Huang, X.; Xia, H.; Liu, Y.; Miyombo, M.E. Improved Fault Diagnosis Method of Electric Gate Valve in Nuclear Power Plant. Ann. Nucl. Energy 2023, 194, 109996. [Google Scholar] [CrossRef]
- Dai, H.; Liu, X.; Zhao, J.; Wang, Z.; Liu, Y.; Zhu, G.; Li, B.; Abbasi, H.N.; Wang, X. Modeling and Diagnosis of Water Quality Parameters in Wastewater Treatment Process Based on Improved Particle Swarm Optimization and Self-Organizing Neural Network. J. Environ. Chem. Eng. 2024, 12, 113142. [Google Scholar] [CrossRef]
- Chang, X.; Yang, S.; Li, S.; Gu, X. Rolling Element Bearing Fault Diagnosis Based on Multi-Objective Optimized Deep Auto-Encoder. Meas. Sci. Technol. 2024, 35, 096007. [Google Scholar] [CrossRef]
- Wang, Z.-C.; Wang, S.-C.; Li, D.; Cao, Z.-W.; He, Y.-L. An Intelligent Fault Detection and Diagnosis Model for Refrigeration Systems with a Comprehensive Feature Selection Method. Int. J. Refrig. 2024, 160, 28–39. [Google Scholar] [CrossRef]
- Aghababaeyan, Z.; Abdellatif, M.; Dadkhah, M.; Briand, L. DeepGD: A Multi-Objective Black-Box Test Selection Approach for Deep Neural Networks. ACM Trans. Softw. Eng. Methodol. 2024, 33, 158. [Google Scholar] [CrossRef]
- Ji, C.; Zhang, C.; Suo, L.; Liu, Q.; Peng, T. Swarm Intelligence Based Deep Learning Model via Improved Whale Optimization Algorithm and Bi-Directional Long Short-Term Memory for Fault Diagnosis of Chemical Processes. ISA Trans. 2024, 147, 227–238. [Google Scholar] [CrossRef]
- Yang, P.; Wang, T.; Yang, H.; Meng, C.; Zhang, H.; Cheng, L. The Performance of Electronic Current Transformer Fault Diagnosis Model: Using an Improved Whale Optimization Algorithm and RBF Neural Network. Electronics 2023, 12, 1066. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, M.; Sun, Y.; Chen, Z.; Duan, G.; Cao, X. Automated Design of Fault Diagnosis CNN Network for Satellite Attitude Control Systems. IEEE T. Cybern. 2024, 54, 4028–4038. [Google Scholar] [CrossRef]
- Wang, M.-H.; Chan, F.-C.; Lu, S.-D. Using a One-Dimensional Convolutional Neural Network with Taguchi Parametric Optimization for a Permanent-Magnet Synchronous Motor Fault-Diagnosis System. Processes 2024, 12, 860. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; ETH Zurich: Zürich, Switzerland, 2001; p. 21. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach. IEEE Trans. Evol. Computat. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.-C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for MobileNetV3. arXiv 2019, arXiv:1905.02244. [Google Scholar] [CrossRef]
- Park, J.; Woo, S.; Lee, J.-Y.; Kweon, I.S. BAM: Bottleneck Attention Module. arXiv 2018, arXiv:1807.06514. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. arXiv 2019, arXiv:1801.04381. [Google Scholar] [CrossRef]








| Fault Diagnosis Situation | |
|---|---|
| No missed detections and no misdiagnoses | 1 |
| No missed detections, and only one non-faulty subsystem is misdiagnosed as faulty | 0.5 |
| No missed detections, and only two non-faulty subsystems are misdiagnosed as faulty | 0.2 |
| There is at least one missed diagnosis, or three or more non-faulty subsystems are misdiagnosed as faulty | 0 |
| Type of Faults | Description | Time Points |
|---|---|---|
| Normal | Full power | 3000 |
| Single fault | A hot leg break in Loop 1 (RCS01) | 3000 |
| A cold leg break in Loop 1 (RCS03) | 3000 | |
| A steam generator tube rupture (RCS09) | 3000 | |
| A pressurizer spray line leakage into the containment (RCS13) | 3000 | |
| A pressurizer safety valve stuck open (RCS07) | 3000 | |
| A reactor pressure vessel vent line leakage (RCS11) | 3000 | |
| Combinations of two faults | RCS01 + RCS03 | 3000 |
| RCS03 + RCS07 | 3000 | |
| RCS03 + RCS09 | 3000 | |
| RCS03 + RCS13 | 3000 | |
| RCS07 + RCS11 | 3000 | |
| RCS09 + RCS11 | 3000 | |
| Combinations of three faults | RCS01 + RCS03 + RCS07 | 3000 |
| RCS01 + RCS03 + RCS11 | 3000 | |
| RCS01 + RCS07 + RCS11 | 3000 | |
| RCS03 + RCS09 + RCS13 | 3000 | |
| RCS03 + RCS13 + RCS07 | 3000 | |
| RCS09 + RCS07 + RCS11 | 3000 | |
| Combinations of four faults | RCS01 + RCS03 + RCS09 + RCS11 | 3000 |
| RCS01 + RCS03 + RCS09 + RCS13 | 3000 | |
| RCS01 + RCS09 + RCS07 + RCS11 | 3000 | |
| RCS01 + RCS09 + RCS13 + RCS07 | 3000 | |
| RCS03 + RCS13 + RCS07 + RCS11 | 3000 | |
| RCS09 + RCS13 + RCS07 + RCS11 | 3000 | |
| Combinations of five faults | RCS01 + RCS03 + RCS09 + RCS13 + RCS07 | 3000 |
| RCS01 + RCS03 + RCS13 + RCS07 + RCS11 | 3000 | |
| RCS01 + RCS09 + RCS13 + RCS07 + RCS11 | 3000 | |
| RCS03 + RCS09 + RCS13 + RCS07 + RCS11 | 3000 | |
| Combinations of six faults | RCS01 + RCS03 + RCS09 + RCS13 + RCS07 + RCS11 | 3000 |
| Type of Layer | Input Size and Output Size | Parameter Description |
|---|---|---|
| Conv2d + BatchNorm2d + ReLU | (batch_size, 1, 8, 30) (batch_size, 16, 4, 15) | Conv2d: 16 filters, 3 × 3 kernel, stride = 2, padding = 1 |
| Inverted Residual Block 1 | (batch_size, 16, 4, 15) (batch_size, 24, 2, 8) | Expansion ratio: 4 Stride: 2 |
| BAM Block 1 | (batch_size, 24, 2, 8) (batch_size, 24, 2, 8) | Reduction ratio: 16 Dilation value: 4 |
| Inverted Residual Block 2 | (batch_size, 24, 2, 8) (batch_size, 32, 1, 4) | Expansion ratio: 4 Stride: 2 |
| BAM Block 2 | (batch_size, 32, 1, 4) (batch_size, 32, 1, 4) | Reduction ratio: 16 Dilation value: 4 |
| Inverted Residual Block 3 | (batch_size, 64, 1, 2) (batch_size, 64, 1, 2) | Expansion ratio: 4 Stride: 2 |
| BAM Block 3 | (batch_size, 64, 1, 2) (batch_size, 64, 1, 2) | Reduction ratio: 16 Dilation value: 4 |
| Inverted Residual Block 4 | (batch_size, 96, 1, 2) (batch_size, 96, 1, 2) | Expansion ratio: 4 Stride: 2 |
| BAM Block 4 | (batch_size, 96, 1, 2) (batch_size, 96, 1, 2) | Reduction ratio: 16 Dilation value: 4 |
| AdaptiveAvgPool2d | (batch_size, 96, 1, 2) (batch_size, 96, 1, 1) | -- |
| Flatten | (batch_size, 96, 1, 1) (batch_size, 96) | -- |
| Linear (Classifier) | (batch_size, 96) (batch_size, num_classes) | Fully connected layer Output size: 2 |
| Experimental Group | Learning Rate | Batch Size | Epoch | Optimizer for Weight Updates | Average Accuracy |
|---|---|---|---|---|---|
| Comparison 1 | 0.001 | 64 | 100 | SGD | 85.97% |
| Comparison 2 | 0.001 | 128 | 100 | SGD | 87.26% |
| Comparison 3 | 0.001 | 256 | 100 | SGD | 85.92% |
| Comparison 4 | 0.0001 | 64 | 100 | SGD | 87.94% |
| Comparison 5 | 0.0001 | 128 | 100 | SGD | 90.31% |
| Comparison 6 | 0.0001 | 256 | 100 | SGD | 88.11% |
| Comparison 7 | 0.00001 | 64 | 100 | SGD | 93.62% |
| Comparison 8 | 0.00001 | 128 | 100 | SGD | 94.33% |
| Comparison 9 | 0.00001 | 256 | 100 | SGD | 93.82% |
| Comparison 10 | 0.001 | 64 | 100 | Adam | 86.63% |
| Comparison 11 | 0.001 | 128 | 100 | Adam | 88.51% |
| Comparison 12 | 0.001 | 256 | 100 | Adam | 87.33% |
| Comparison 13 | 0.0001 | 64 | 100 | Adam | 91.22% |
| Comparison 14 | 0.0001 | 128 | 100 | Adam | 92.34% |
| Comparison 15 | 0.0001 | 256 | 100 | Adam | 91.35% |
| Comparison 16 | 0.00001 | 64 | 100 | Adam | 94.22% |
| Comparison 17 | 0.00001 | 128 | 100 | Adam | 95.78% |
| Comparison 18 | 0.00001 | 256 | 100 | Adam | 93.46% |
| Experimental Group | Optimization Algorithm | Neural Network | Subsystem Accuracy | Overall Accuracy | Inference Time | Computational Load |
|---|---|---|---|---|---|---|
| Basic Group | SPEA2 | MMBB | 99.39% 98.89% 99.26% 98.93% 98.85% 97.13% | 95.22% | 25 ms | 26% |
| Comparison 1 | LSTM | 97.56% 98.21% 98.81% 96.91% 97.48% 92.65% | 89.04% | 36 ms | 33% | |
| Comparison 2 | CNN | 98.31% 98.45% 97.76% 98.93% 96.21% 95.32% | 91.13% | 18 ms | 18% | |
| Comparison 3 | DMOPSO | MMBB | 95.34% 94.76% 98.25% 98.62% 94.43% 92.13% | 90.22% | 25 ms | 25% |
| Comparison 4 | LSTM | 97.56% 98.38% 98.81% 95.91% 97.73% 87.65% | 83.04% | 34 ms | 33% | |
| Comparison 5 | CNN | 93.46% 95.53% 93.76% 92.26% 93.35% 87.34% | 79.13% | 18 ms | 18% | |
| Comparison 6 | PSO | MMBB | 99.46% 98.83% 99.57% 98.70% 98.94% 97.41% | 93.74% | 26 ms | 26% |
| Comparison 7 | LSTM | 97.86% 98.33% 98.06% 97.12% 97.26% 92.42% | 84.43% | 33 ms | 32% | |
| Comparison 8 | CNN | 98.36% 98.24% 97.92% 98.89% 96.35% 95.49% | 86.39% | 19 ms | 18% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Ma, J.; Yuan, J. Application of SPEA2-MMBB for Distributed Fault Diagnosis in Nuclear Power System. Processes 2024, 12, 2620. https://doi.org/10.3390/pr12122620
Xu Y, Ma J, Yuan J. Application of SPEA2-MMBB for Distributed Fault Diagnosis in Nuclear Power System. Processes. 2024; 12(12):2620. https://doi.org/10.3390/pr12122620
Chicago/Turabian StyleXu, Ying, Jie Ma, and Jinxiao Yuan. 2024. "Application of SPEA2-MMBB for Distributed Fault Diagnosis in Nuclear Power System" Processes 12, no. 12: 2620. https://doi.org/10.3390/pr12122620
APA StyleXu, Y., Ma, J., & Yuan, J. (2024). Application of SPEA2-MMBB for Distributed Fault Diagnosis in Nuclear Power System. Processes, 12(12), 2620. https://doi.org/10.3390/pr12122620






