Numerical Study of Hydrogen-Rich Fuel Coherent Jet in Blast Furnace Tuyere
Abstract
1. Introduction
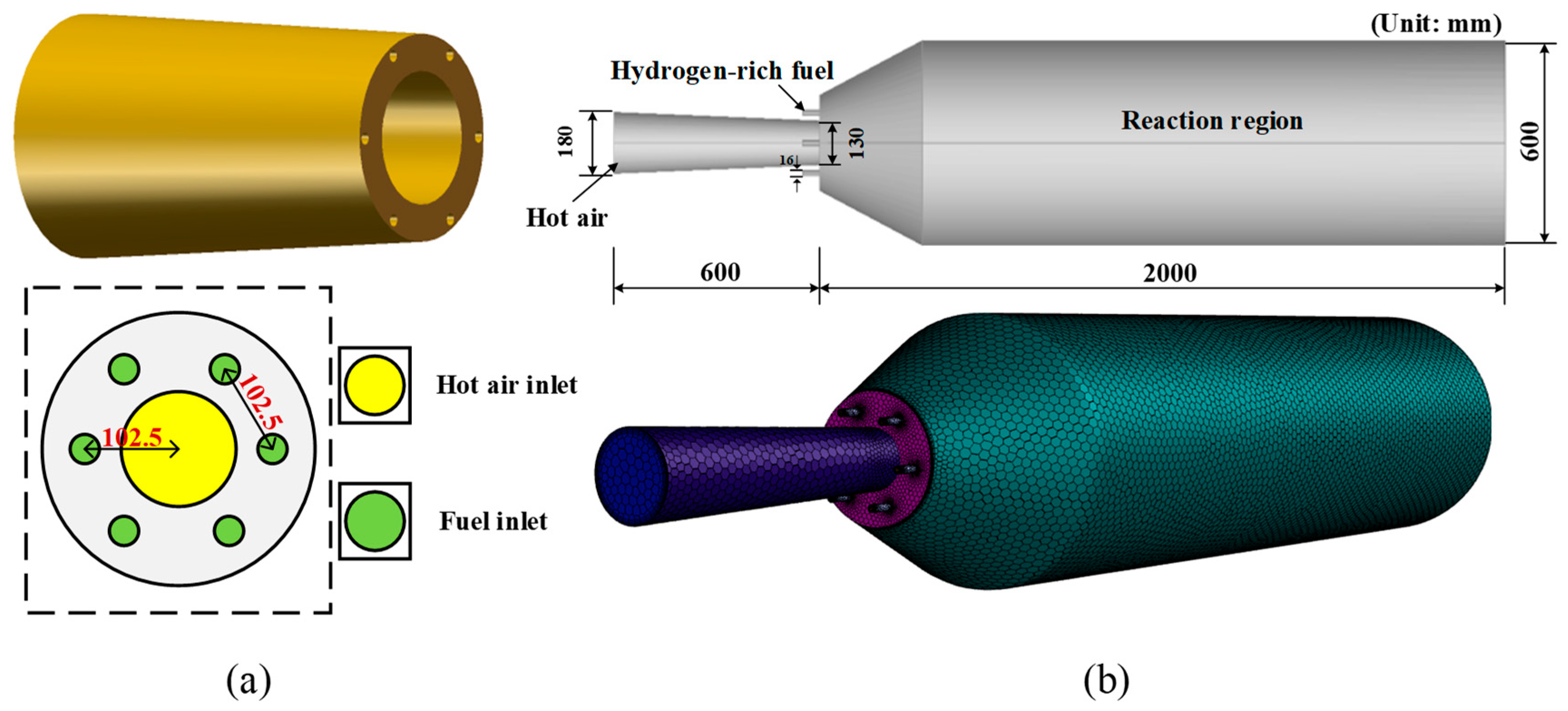
2. Methodology
2.1. Gas Flow Model
2.2. Chemical Reaction Models
2.3. Simulation Conditions
3. Results and Discussion
3.1. Model Validation
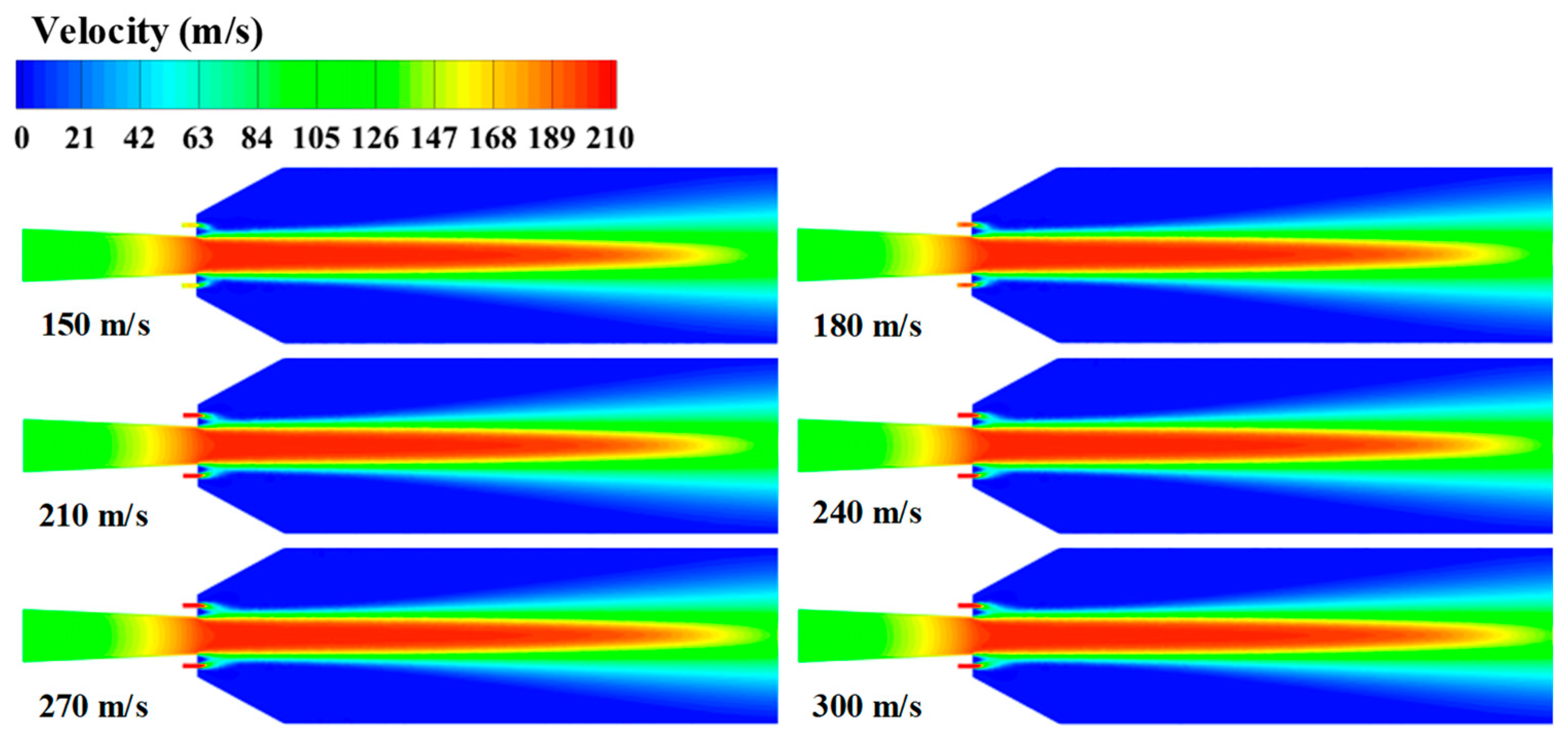
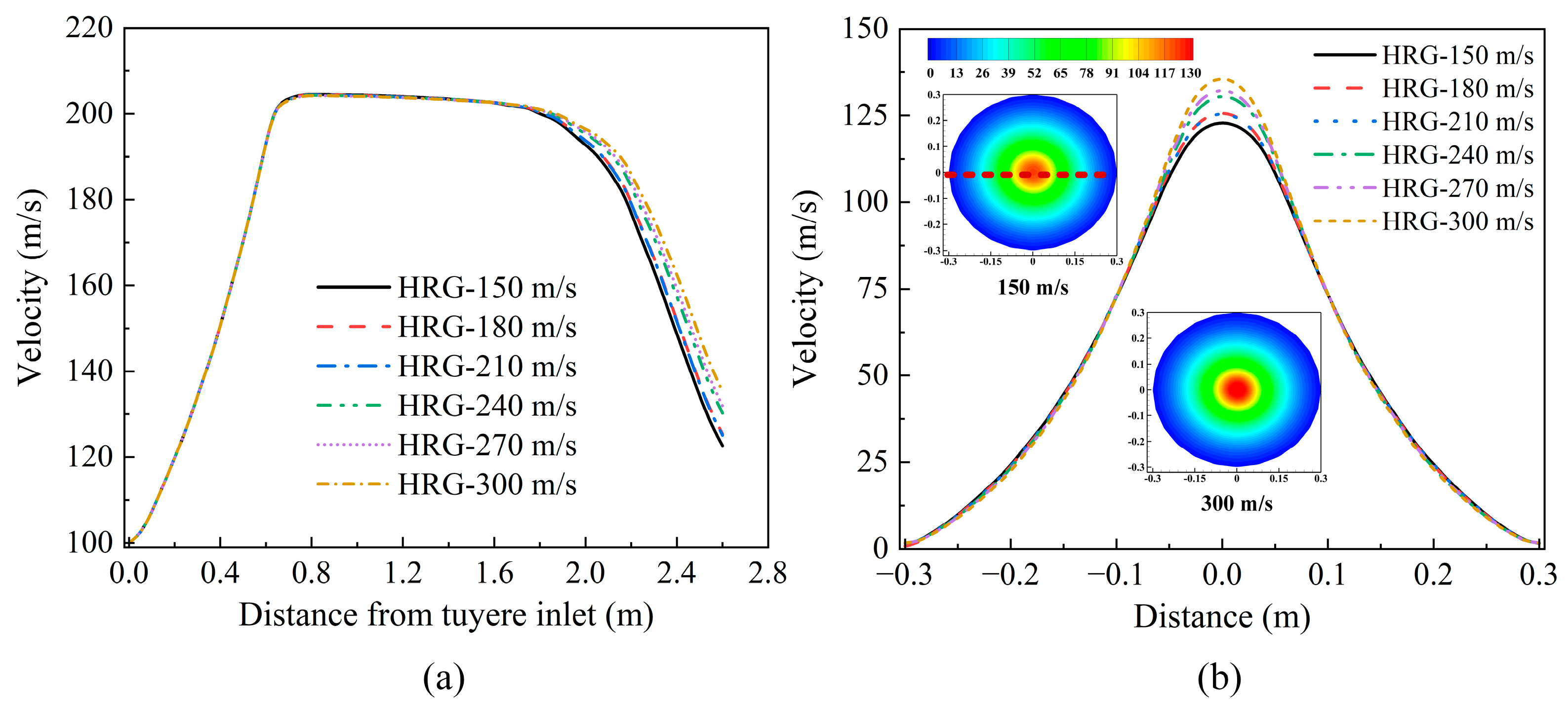
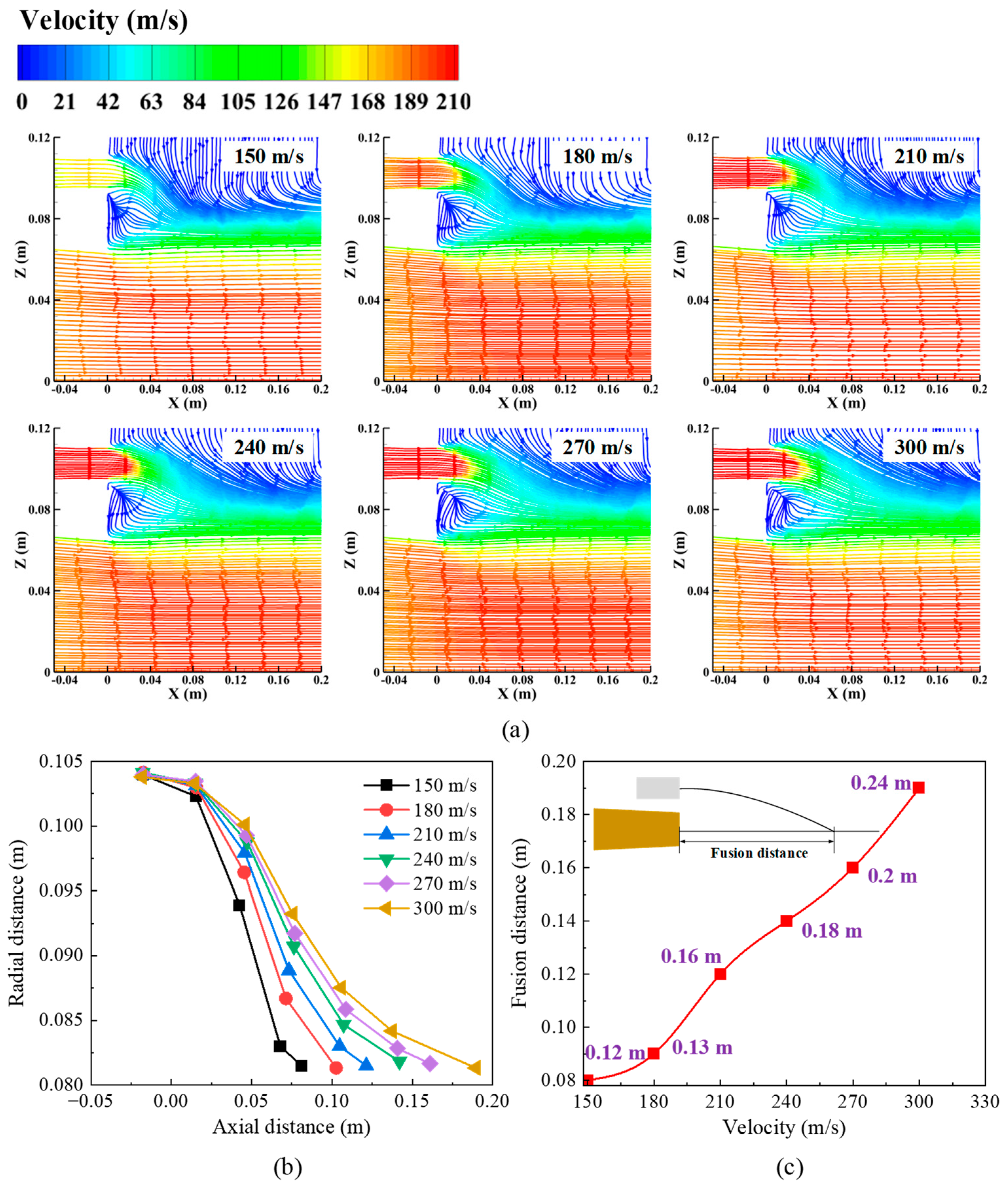
3.2. Gas Velocity
3.3. Gas Temperature
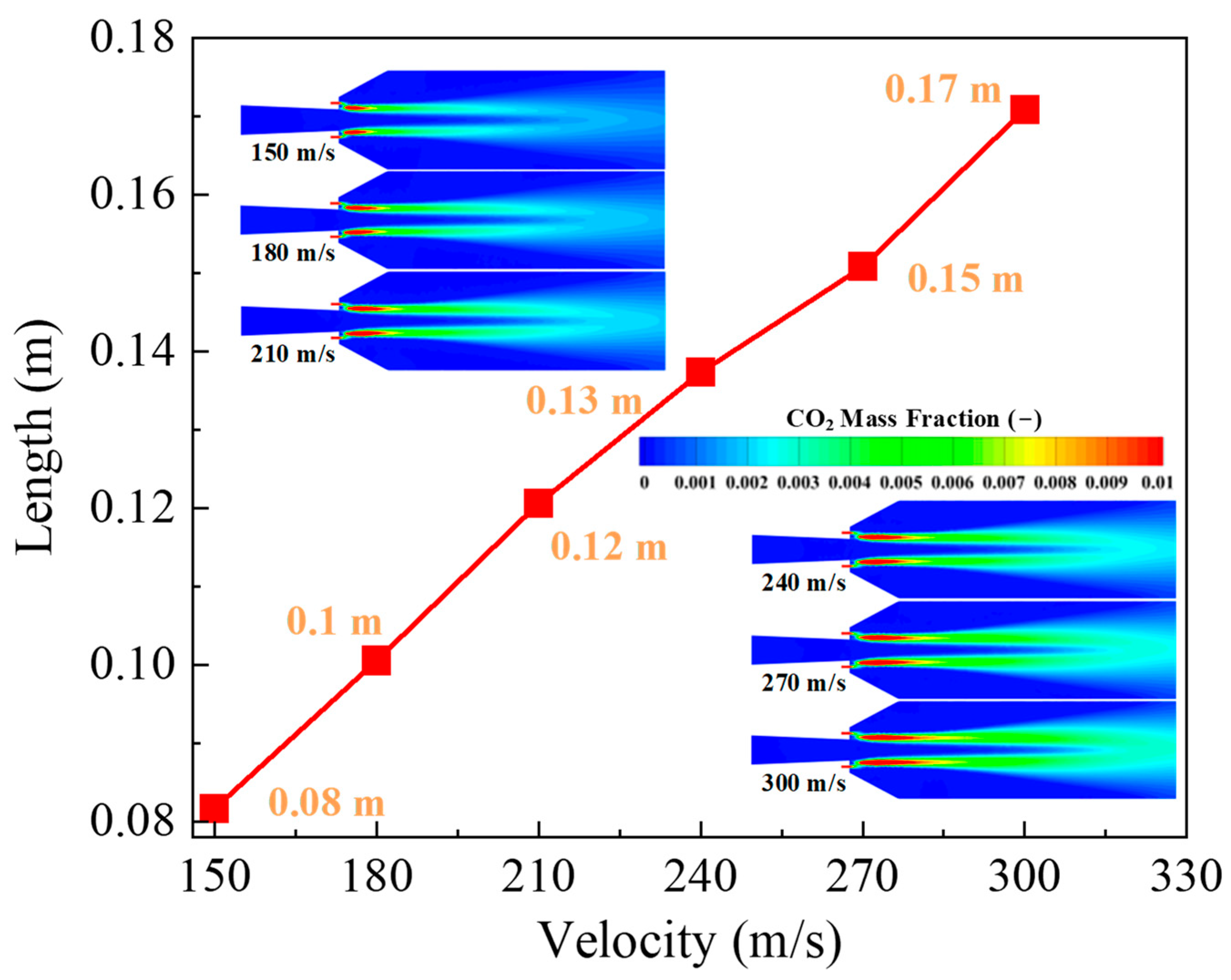
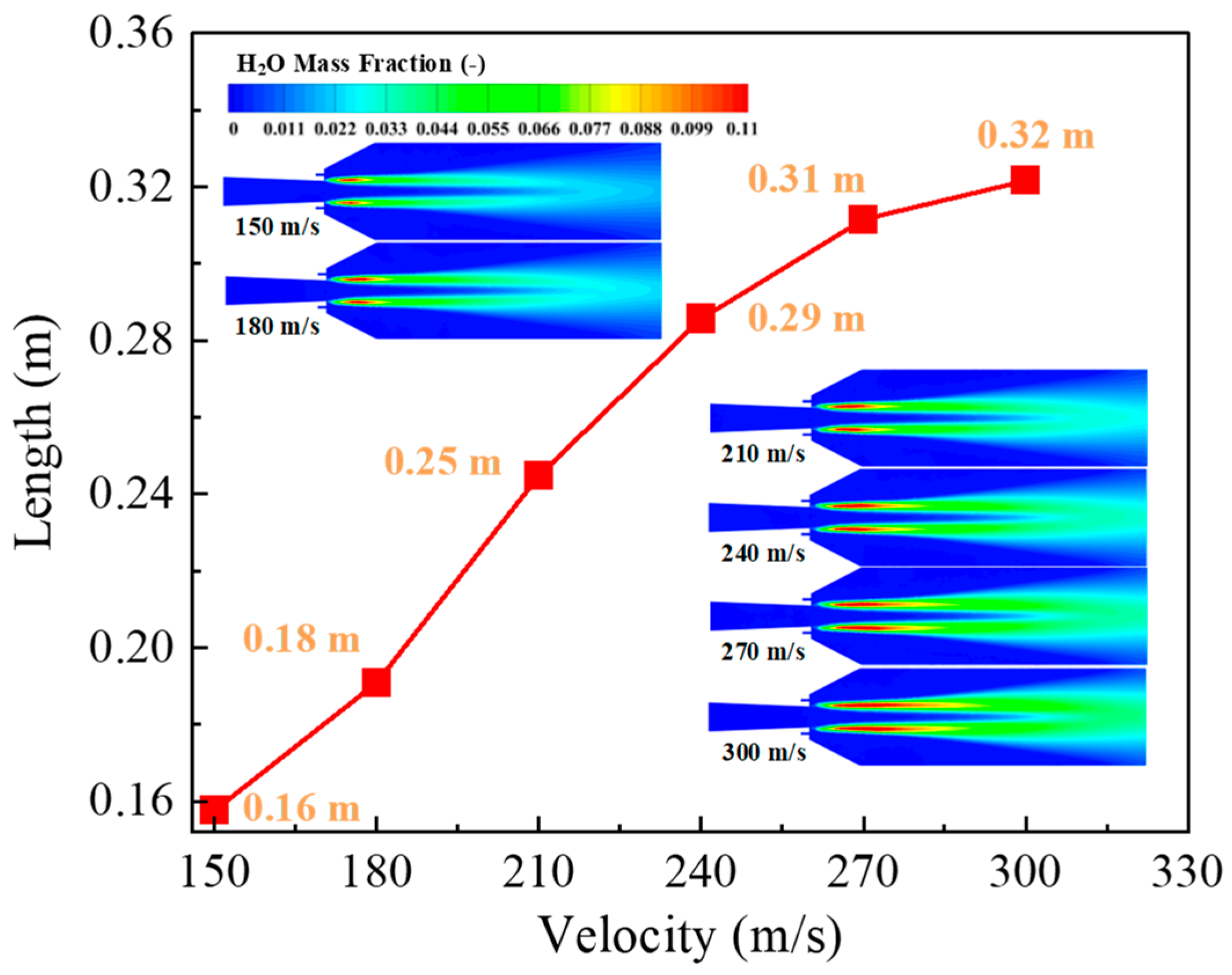
3.4. Gas Species
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Gravitational acceleration, m/s2 | |
| Gb | Turbulence kinetic energy due to buoyancy, m2/s2 |
| Gk | Turbulence kinetic energy generated by the mean velocity gradient, m2/s2 |
| H | Gas total enthalpy, J/kg |
| k | Turbulence kinetic energy, m2/s2 |
| Net rate of production of species i, kg/s | |
| Mw,i | Molecular weight of species i, kg/mol |
| P | Gas pressure, Pa |
| Heat flux of the gas phase, W/m2 | |
| Qrad | Radiation heat exchange between gas and particles, W |
| Molar rate of creation/destruction of species i in reaction r, mol/s | |
| S | Modulus of the mean rate of strain tensor, N/m3 |
| Gas velocity, m/s | |
| Yi | Mass fraction of the ith species |
| YR | Mass fraction of a particular reactant |
| YP | Mass fraction of any product species |
| Greek letters | |
| ε | Turbulence kinetic energy dissipation rate, W/m3 |
| μ | Turbulent viscosity, Pa·s |
| ρ | Gas density, kg/m3 |
| Gas stress tensor, N/m3 |
References
- Zhang, C.L.; Zhang, J.L.; Xu, R.S.; Zheng, A.Y.; Zhu, J.F.; Li, T. Numerical investigation of hydrogen-rich gas and pulverized coal injection in the raceway of a blast furnace with lower carbon emissions. Fuel 2024, 356, 129462. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, J.L.; Zhou, H.; Ni, J.; Hu, Y.F.; Huang, J.; Li, S.; Ma, X.D.; Wu, S.L.; Kou, M.Y. Numerical study of natural gas and pulverized coal co-injection into an ironmaking blast furnace. Appl. Therm. Eng. 2023, 230, 120817. [Google Scholar] [CrossRef]
- Ye, S.X.; Xie, Z.Y.; Wang, Y.; Wu, W.H.; Wang, R.D.; Zhang, Y.W.; Lu, X.G. New insights into the influence of hydrogen on important parameters of blast furnace. J. Clean. Prod. 2023, 425, 139042. [Google Scholar] [CrossRef]
- Nishioka, K.; Ujisawa, Y.; Tonomura, S.; Ishiwata, N.; Sikstrom, P. Sustainable aspects of CO2 ultimate reduction in the steelmaking process (COURSE50 Project), Part1: Hydrogen reduction in the blast furnace. J. Sustain. Metall. 2016, 2, 200–208. [Google Scholar] [CrossRef]
- Quader, M.A.; Ahmed, S.; Dawal, S.Z. Present needs, progress and future trends of energy-efficient Ultra-Low Carbon Dioxide (CO2) Steelmaking (ULCOS) program. Renew. Sust. Energ. Rev. 2016, 55, 537–549. [Google Scholar] [CrossRef]
- Jozwiak, W.K.; Kaczmarek, E.; Maniecki, T.P.; Ignaczak, W.; Maniukiewicz, W. Reduction behavior of iron oxides in hydrogen and carbon monoxide atmospheres. Appl. Catal. A Gen. 2007, 326, 17–27. [Google Scholar] [CrossRef]
- Qie, Y.N.; Lyu, Q.; Liu, X.J.; Li, J.; Lan, C.; Zhang, S.; Yan, C. Effect of hydrogen addition on softening and melting reduction behaviors of ferrous burden in gas-injection blast furnace. Metall. Mater. Trans. B 2018, 49, 2622–2632. [Google Scholar] [CrossRef]
- Park, T.J.; Lee, J.H.; Kim, D.G.; Kim, H. Estimation of the H2 gas utilization ratio using a BF shaft inner reaction simulator. Metall. Mater. Trans. B 2020, 51, 417–421. [Google Scholar] [CrossRef]
- Zhang, C.L.; Zhang, J.L.; Zheng, A.Y.; Xu, R.S.; Jia, G.L.; Zhu, J.F. Effects of hydrogen-rich fuel injection on the states of the raceway in blast furnace. Energy 2023, 274, 127237. [Google Scholar] [CrossRef]
- Zhang, C.L.; Vladislav, L.; Xu, R.S.; Sergey, G.; Jiao, K.X.; Zhang, J.L.; Li, T.; Aleksei, T.; Wang, C.; Wang, G.W. Blast furnace hydrogen-rich metallurgy-research on efficiency injection of natural gas and pulverized coal. Fuel 2022, 311, 122412. [Google Scholar] [CrossRef]
- Liu, Y.R.; Hu, Z.J.; Shen, Y.S. CFD study of hydrogen injection in blast furnaces: Tuyere co-injection of hydrogen and coal. Metall. Mater. Trans. B 2021, 52, 2021–2971. [Google Scholar] [CrossRef]
- Yu, X.B.; Hu, Z.J.; Shen, Y.S. Modeling of hydrogen shaft injection in ironmaking blast furnaces. Fuel 2021, 302, 121092. [Google Scholar] [CrossRef]
- Feng, C.; Liu, F.; Zhu, R.; Dong, K.; Wei, G.; Tao, X. Computational investigation of coherent jet behavior generated by H2 shrouding flow. Metall. Mater. Trans. B 2023, 55, 600–611. [Google Scholar] [CrossRef]
- Hnaien, N.; Mondal, T.; Ajmi, M.; Aich, W.; Ayadi, B.; Kolsi, L. A CFD modelling on effects of ejection angle of a co-flow on the thermal characteristics for a combined wall and offset jet flow. Alex. Eng. J. 2023, 68, 83–91. [Google Scholar] [CrossRef]
- Chen, Y.C.; Luo, Q.X.; Ryan, S.; Busa, N.; Silaen, A.K.; Zhou, C.Q. Effect of coherent jet burner on scrap melting in electric arc furnace. Appl. Therm. Eng. 2022, 212, 118596. [Google Scholar] [CrossRef]
- Hnaien, N.; Mondal, T.; Ajmi, M.; Marzouk, S.; Aich, W.; Kolsi, L. Numerical study on mean flow characteristics for a combined turbulent wall and offset jets with a parallel co-flow. J. Taibah Univ. Sci. 2022, 16, 732–748. [Google Scholar] [CrossRef]
- Tang, G.W.; Chen, Y.C.; Silaen, A.K.; Krotov, Y.; Riley, M.F.; Zhou, C.Q. Effects of fuel input on coherent jet length at various ambient temperatures. Appl. Therm. Eng. 2019, 153, 513–523. [Google Scholar] [CrossRef]
- Ali, N.B.; Basem, A.; Ghodratallah, P.; Singh, P.K.; Jasim, D.J.; Falih, T.K.; Ahmed, M.; Eladeb, A.; Kolsi, L.; El-Shafay, A.S. Computational study of the coaxial air and fuel jet through a 3-lobe strut injector for efficient fuel mixing in a supersonic combustion chamber. Energy 2024, 311, 133276. [Google Scholar]
- Anderson, T.B.; Jackson, R. A fluid mechanical description of fluidized beds, Equations of Motion. Ind. Eng. Chem. Fund. 1967, 6, 527–539. [Google Scholar] [CrossRef]
- Gunn, D.J. Transfer of heat or mass to particles in fixed and fluidized beds. Int. J. Heat Mass Transf. 1978, 21, 467–476. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| Working volume (m3) | 3200 |
| Tuyere number | 32 |
| Productivity (tHM/m3·day) | 2.5 |
| Blast (m3/min) | 5100 |
| Blast temperature (K) | 1473 |
| Oxygen enrichment rate (%) | 9 |
| Hydrogen-rich fuel (m3/tHM) | 70, 80, 90, 100, 110, 120 |
| Hydrogen-rich gas temperature (K) | 1473 |
| H2 (%) | CO (%) | N2 (%) | CO2 (%) |
|---|---|---|---|
| 70 | 28.53 | 0.47 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Xu, P.; Han, P.; He, Z.; Wang, J. Numerical Study of Hydrogen-Rich Fuel Coherent Jet in Blast Furnace Tuyere. Processes 2024, 12, 2441. https://doi.org/10.3390/pr12112441
Shi J, Xu P, Han P, He Z, Wang J. Numerical Study of Hydrogen-Rich Fuel Coherent Jet in Blast Furnace Tuyere. Processes. 2024; 12(11):2441. https://doi.org/10.3390/pr12112441
Chicago/Turabian StyleShi, Jianchun, Peng Xu, Peng Han, Zhijun He, and Jiaying Wang. 2024. "Numerical Study of Hydrogen-Rich Fuel Coherent Jet in Blast Furnace Tuyere" Processes 12, no. 11: 2441. https://doi.org/10.3390/pr12112441
APA StyleShi, J., Xu, P., Han, P., He, Z., & Wang, J. (2024). Numerical Study of Hydrogen-Rich Fuel Coherent Jet in Blast Furnace Tuyere. Processes, 12(11), 2441. https://doi.org/10.3390/pr12112441





