Refracturing Time Optimization Considering the Effect of Induced Stress by Pressure Depletion in the Shale Reservoir
Abstract
1. Introduction
2. Coupled Fluid Flow/Geomechanics Models
2.1. Coupled Fluid Flow/Geomechanics Model Based on Pore-Elasticity Theory
2.2. Storage and Transport Mechanism
2.3. Fully Coupled Fluid Flow/Geomechanics with EDFM
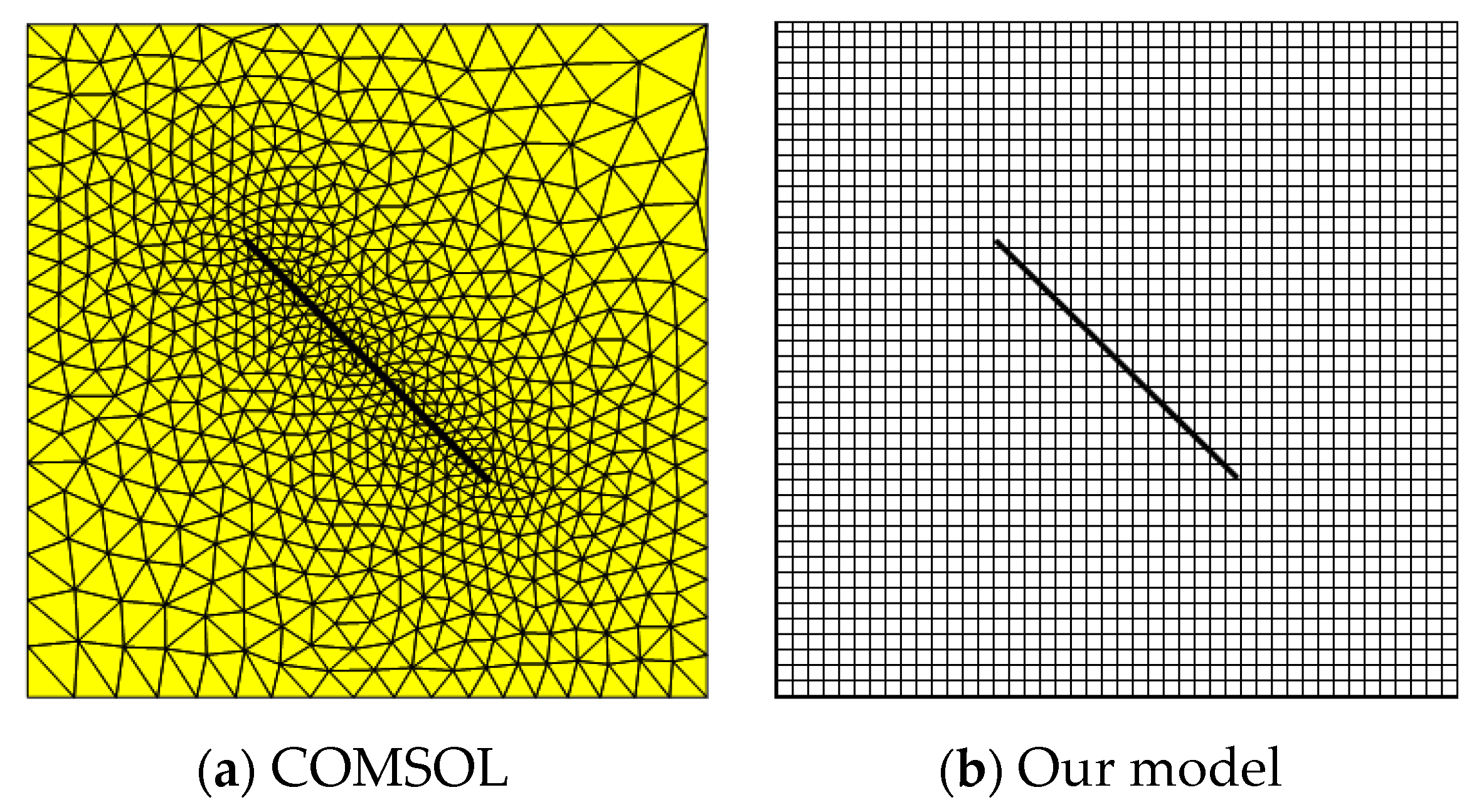
3. Numerical Discretization
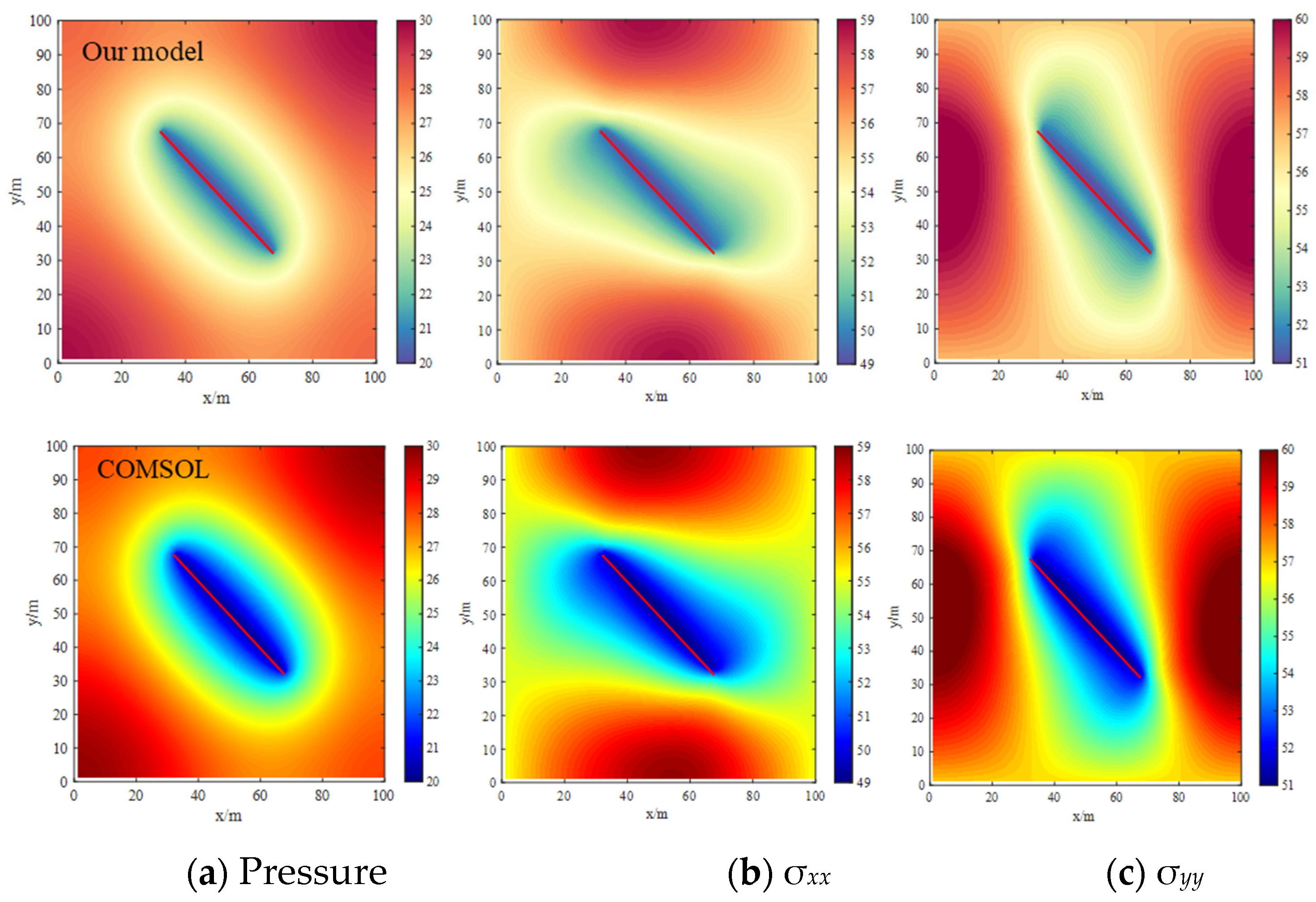
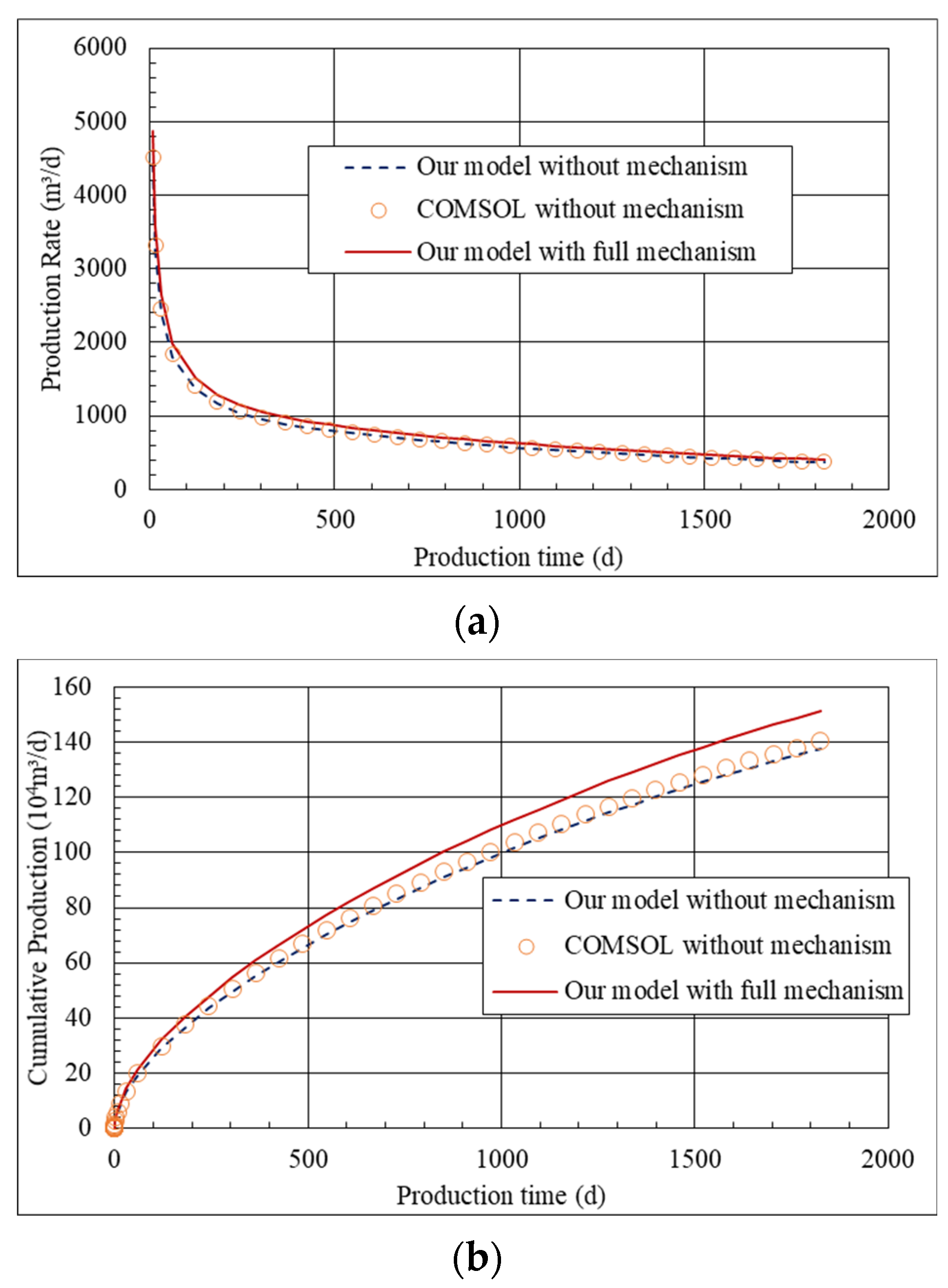
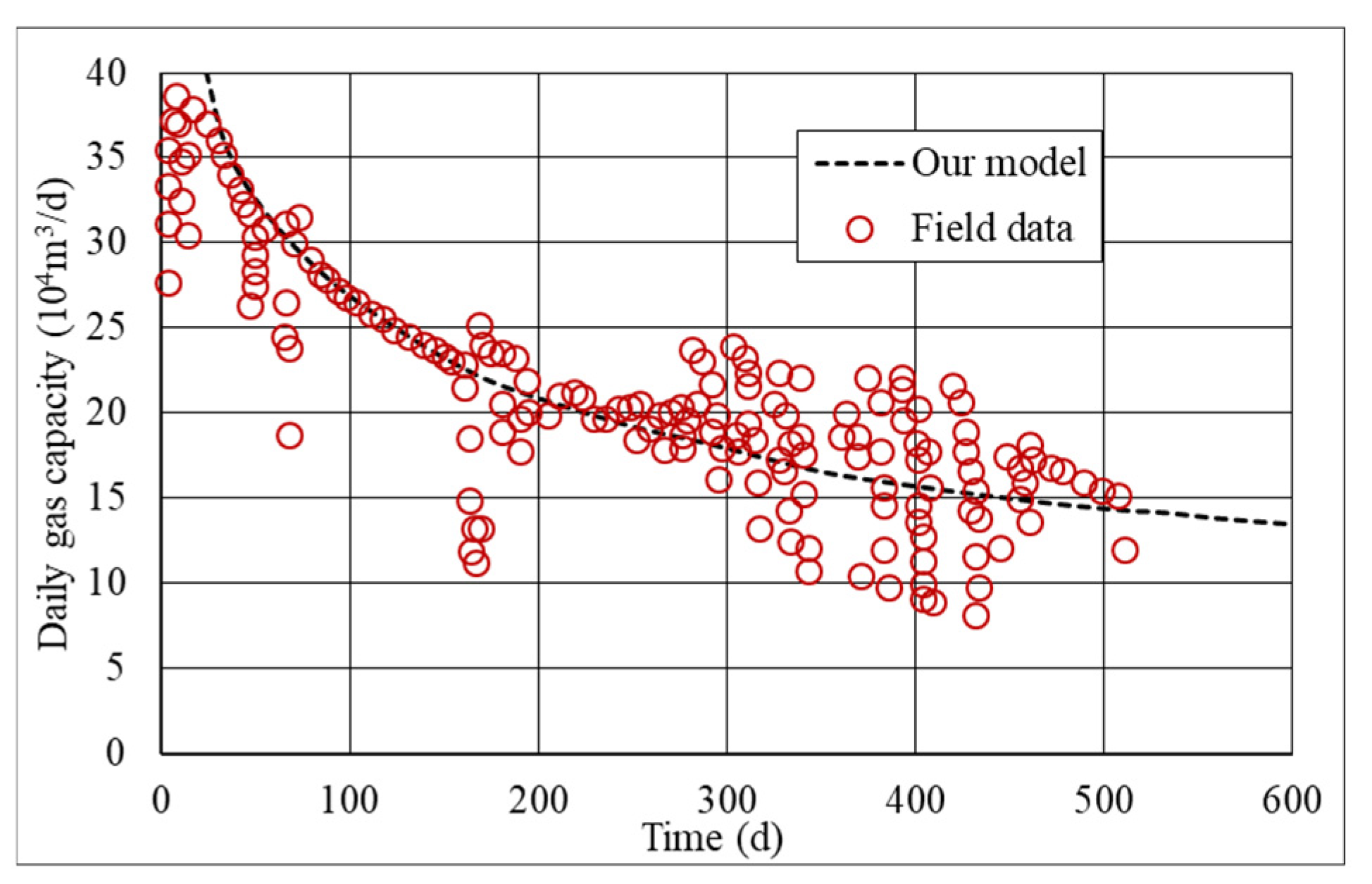
4. Model Verification
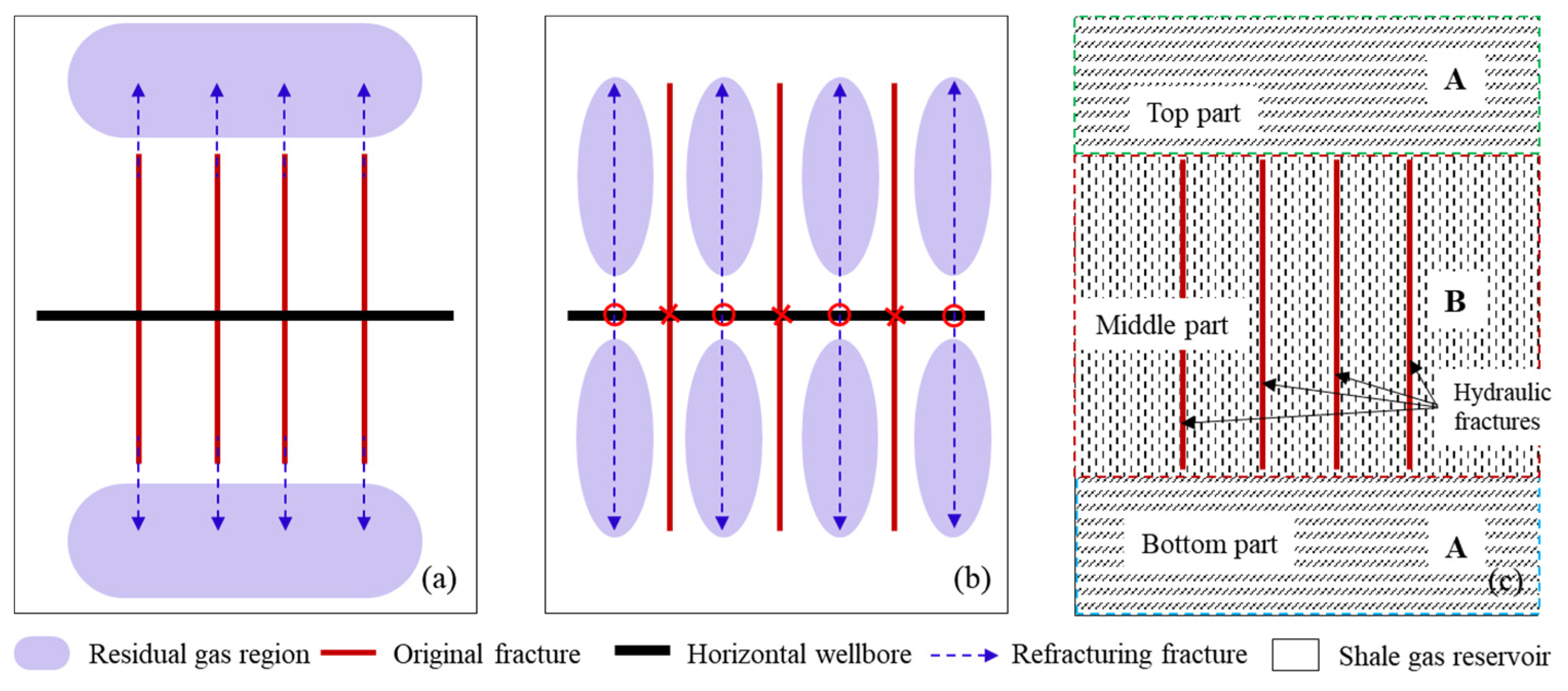
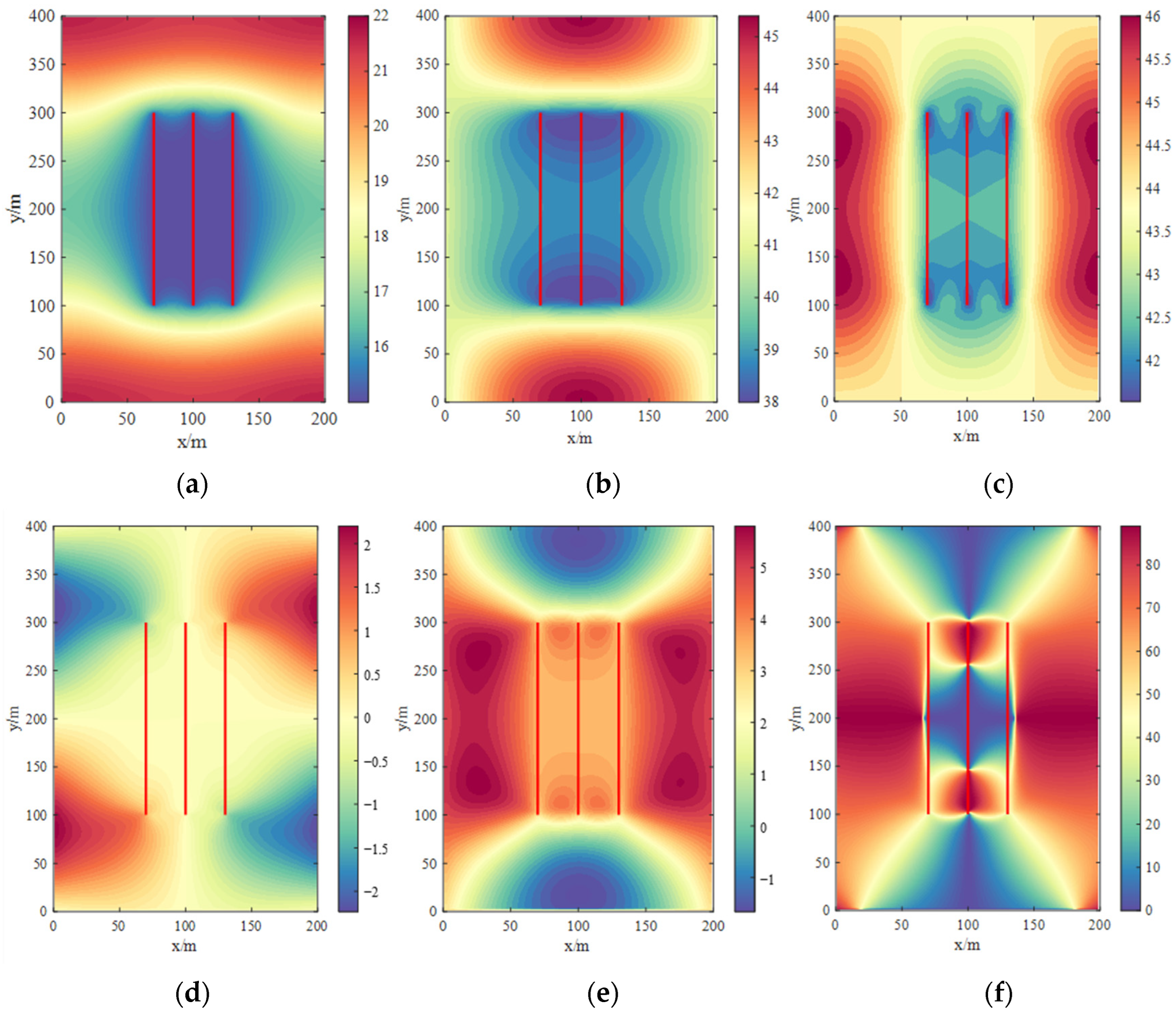
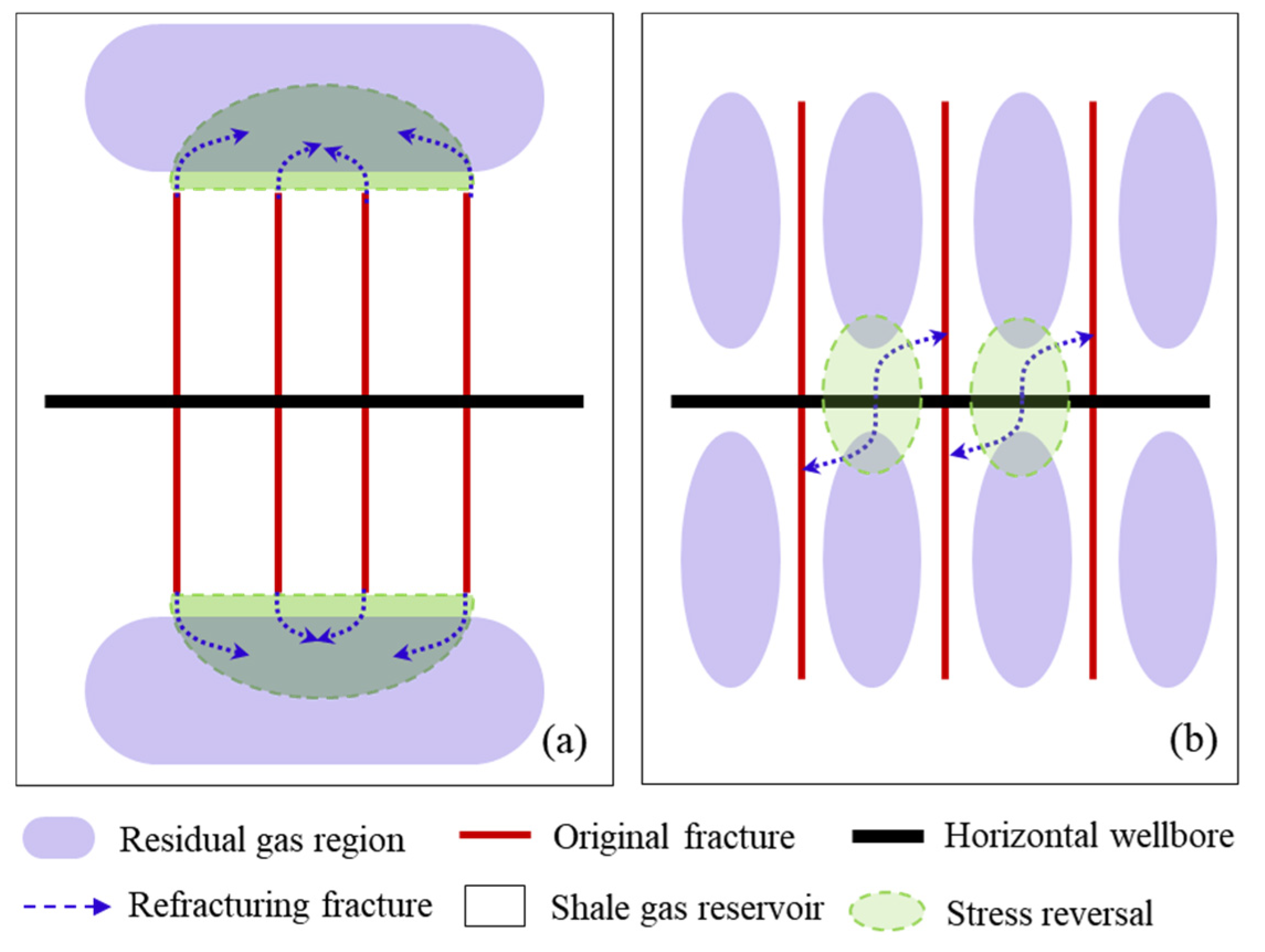
5. Evolution Law of Stress Field and Timing Analysis of Refracturing
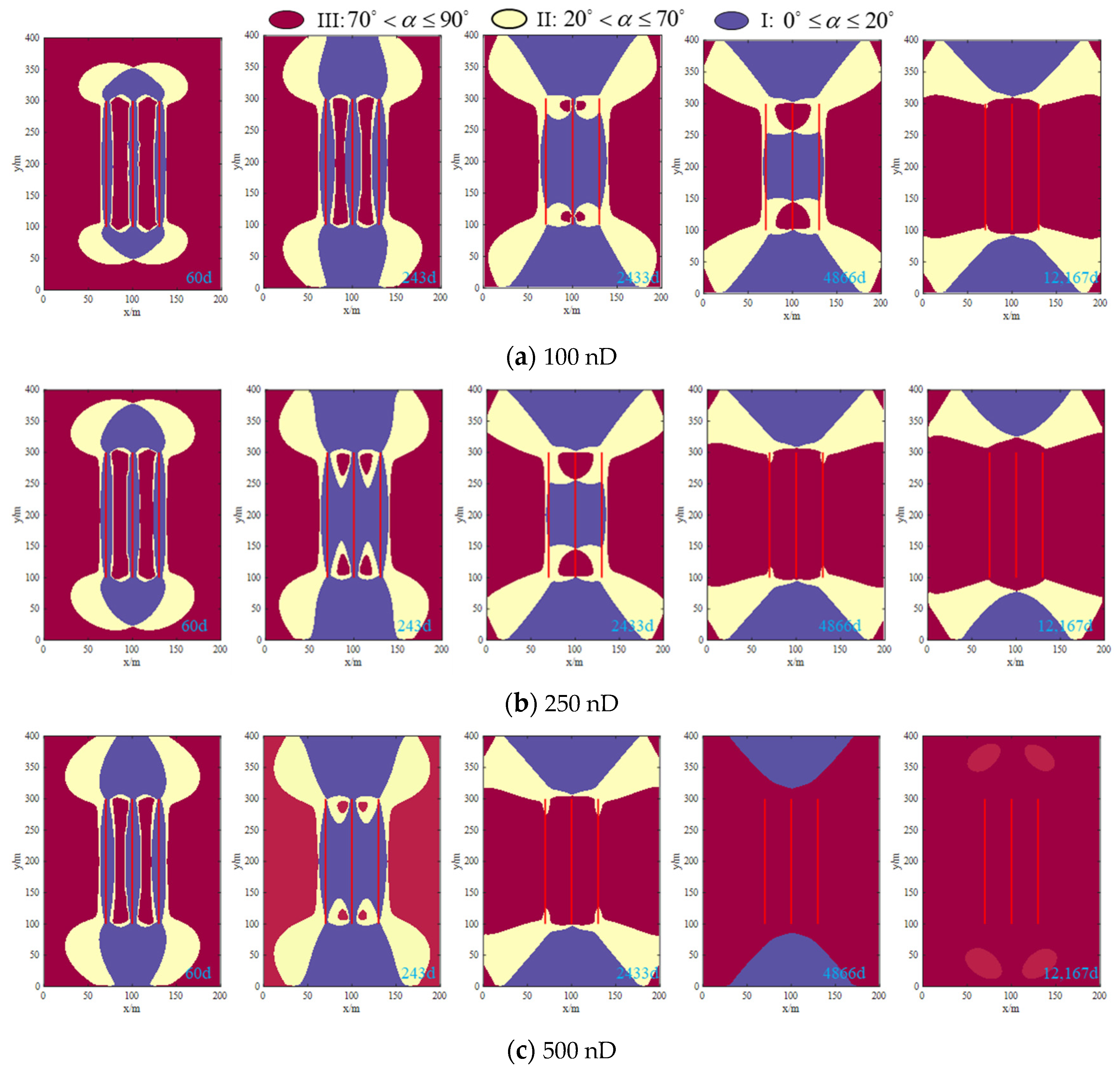
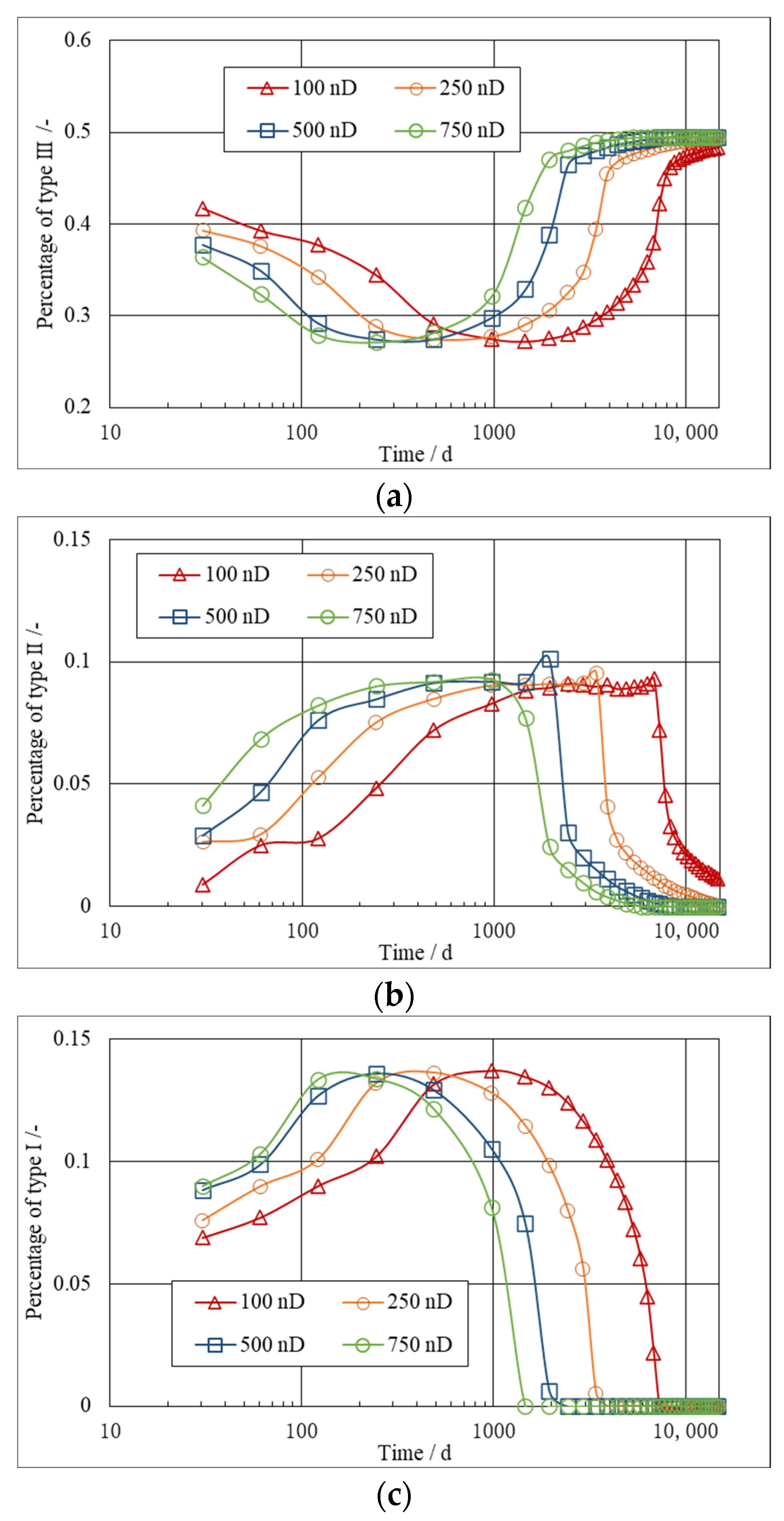
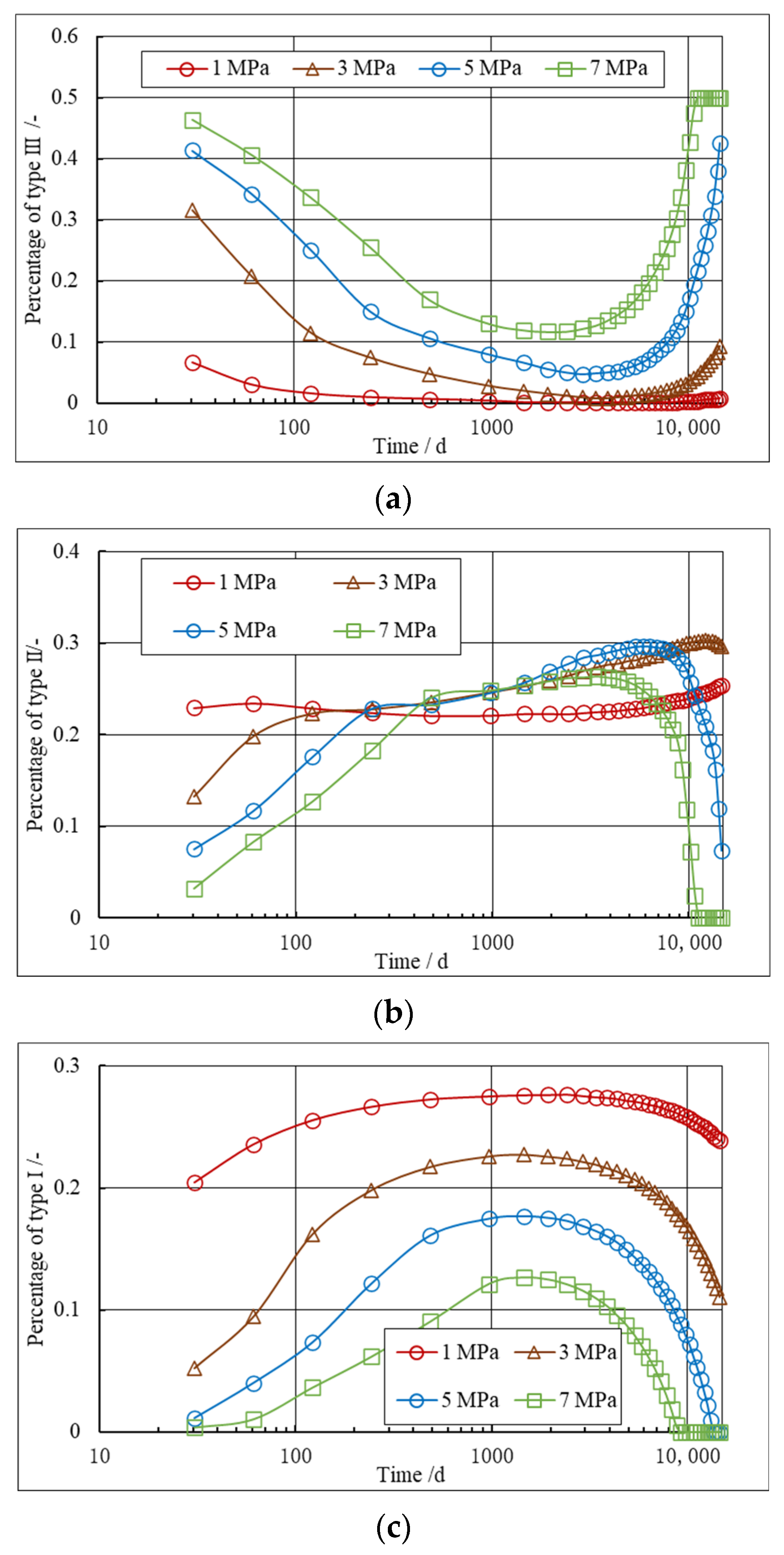
5.1. Effect of Permeability on Stress Orientation and Refracturing Timing
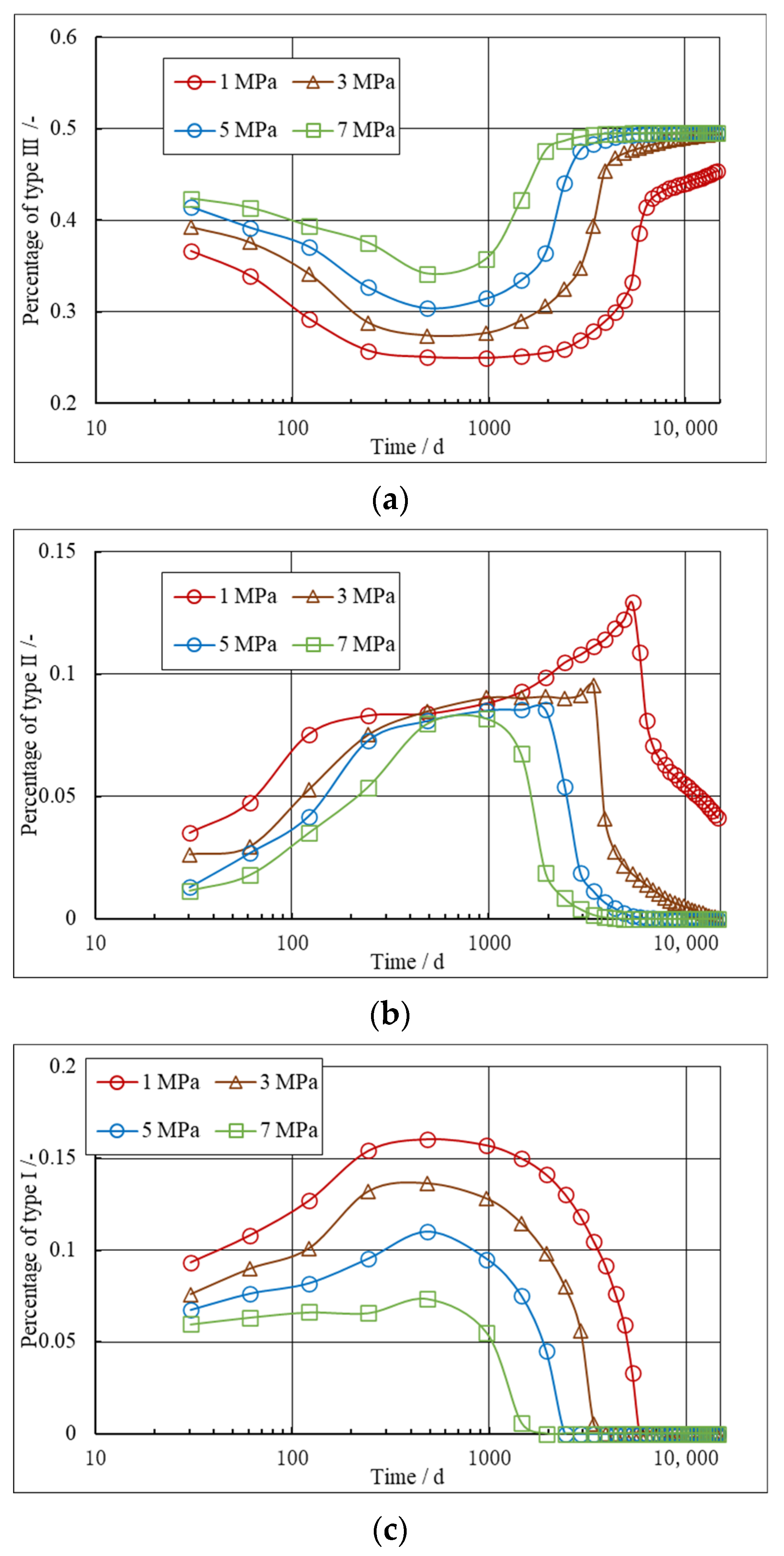
5.2. Effect of Initial Stress Difference on Stress Orientation and Refracturing Timing
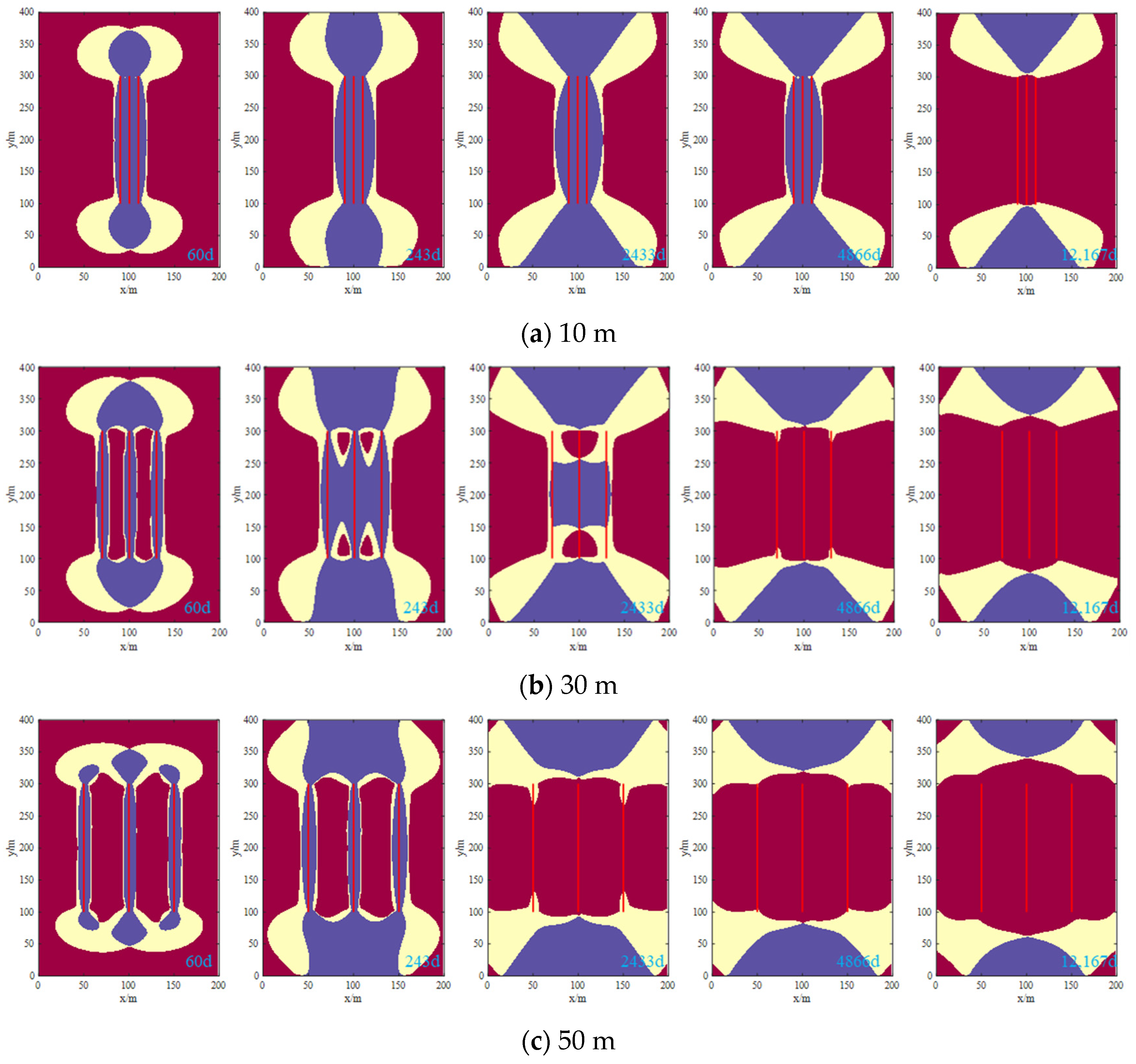
5.3. Influence of Cluster Spacing on Stress Orientation and Refracturing Timing
5.4. Influence of Fracture Half-Length on Stress Orientation and Refracturing Timing
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Ji, B.; Wei, B.; Meng, Z.; Li, Y.; Lu, J.; Tang, J. Experimental simulation of enhanced oil recovery on shale rocks using gas injection from material to characterization: Challenges and solutions. Fuel 2024, 356, 129588. [Google Scholar] [CrossRef]
- Chen, H.; Li, H.; Li, Z.; Li, S.; Wang, Y.; Wang, J.; Li, B. Effects of matrix permeability and fracture on production characteristics and residual oil distribution during flue gas flooding in low permeability/tight reservoirs. J. Pet. Sci. Eng. 2020, 195, 107813. [Google Scholar] [CrossRef]
- Guo, X.; Wu, K.; An, C.; Tang, J.; Killough, J. Numerical Investigation of Effects of Subsequent Parent-Well Injection on Interwell Fracturing Interference Using Reservoir-Geomechanics-Fracturing Modeling. SPE J. 2019, 24, 1884–1902. [Google Scholar] [CrossRef]
- Heidari, S.; Li, B.; Jacquey, A.B. Finite element modeling of wellbore stability in a fractured formation for the geothermal development in northern Quebec, Canada. Geoenergy Sci. Eng. 2023, 231, 212350. [Google Scholar] [CrossRef]
- Liu, L.J.; Liu, Y.; Yao, J.; Huang, C. Efficient coupled multiphase-flow and geomechanics modeling of well performance and stress evolution in shale-gas reservoirs considering dynamic fracture properties. SPE J. 2019, 25, 1523–1542. [Google Scholar] [CrossRef]
- Safari, R.; Lewis, R.; Ma, X.; Mutlu, U.; Ghassemi, A. Fracture curving between tightly spaced horizontal wells. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 20–22 July 2015. [Google Scholar]
- Safari, R.; Lewis, R.; Ma, X.; Mutlu, U.; Ghassemi, A. Infill-well fracturing optimization in tightly spaced horizontal wells. SPE J. 2017, 22, 582–595, SPE-178513-PA. [Google Scholar] [CrossRef]
- Pei, Y.; Sepehrnoori, K. Investigation of Parent—Well Production Induced Stress Interference in Multilayer Unconventional Reservoirs. Rock Mech. Rock Eng. 2022, 55, 2965–2986. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, Y.; Zhao, J.; Chen, S.; Fu, C.; Zhao, C. Numerical simulation of fracture initiation, propagation and fracture complexity in the presence of multiple perforations. J. Nat. Gas Sci. Eng. 2020, 83, 103486. [Google Scholar] [CrossRef]
- Kumar, D.; Ghassemi, A. 3D geomechanical analysis of refracturing of horizontal wells. In Proceedings of the Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017. [Google Scholar] [CrossRef]
- Wang, J.; Olson, J.E. Auto-optimization of hydraulic fracturing design with three-dimensional fracture propagation in naturally fractured multi-layer formations. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Virtual, 20–22 July 2020. [Google Scholar]
- Shah, M.; Shah, S.; Sircar, A. A comprehensive overview on recent developments in refracturing technique for shale gas reservoirs. J. Nat. Gas Sci. Eng. 2017, 46, 350–364. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, C.; Zhao, J.; Yan, Z.; Kang, S.; Hu, Y.; Ren, L. Numerical simulation of planar hydraulic fracture propagation with consideration to transition from turbulence to laminar flow regime. Eng. Fract. Mech. 2022, 262, 108258. [Google Scholar]
- Wang, Q.; Zhao, J.; Wang, B.; Li, D.; Ran, L.; Hu, Y.; Zhao, C. Secondary growth and closure behavior of planar hydraulic fractures during shut-in. J. Pet. Sci. Eng. 2022, 213, 110420. [Google Scholar] [CrossRef]
- Zhang, D.X.; Zhang, L.H.; Tang, H.Y.; Zhao, Y.L. Fully coupled fluid-solid productivity numerical simulation of multistage fractured horizontal well in tight oil reservoirs. Pet. Explor. Dev. 2022, 49, 382–393. [Google Scholar] [CrossRef]
- Elbel, J.L.; Mack, M.G. Refracturing: Observations and theories. In SPE Oklahoma City Oil and Gas Symposium/Production and Operations Symposium; Society of Petroleum Engineers: Houston, TX, USA, 1992. [Google Scholar]
- Wright, C.A.; Conant, R.A.; Golich, G.M.; Bondor, P.L.; Murer, A.S.; Dobie, C.A. Hydraulic fracture orientation and production/injection induced reservoir stress changes in diatomite waterfloods. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 8–10 March 1995. [Google Scholar]
- Gupta, J.K.; Zielonka, M.G.; Albert, R.A.; El-Rabaa, W.; Burnham, H.A.; Choi, N.H. Integrated methodology for optimizing development of unconventional gas resources. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 6–8 February 2012. [Google Scholar]
- Roussel, N.P.; Sharma, M.M. Quantifying transient effects in altered-stress refracturing of vertical wells. SPE J. 2010, 15, 770–782. [Google Scholar] [CrossRef]
- Roussel, N.P.; Florez, H.A.; Rodriguez, A.A. Hydraulic Fracture Propagation from Infill Horizontal Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–2 October 2013. [Google Scholar]
- Hagemann, B. Investigation of hydraulic fracture reorientation effects in tight gas reservoirs. In Proceedings of the 2012 COMSOL Conference, Milan, Italy, 10 October 2012. [Google Scholar]
- Li, X.; Wang, J.; Elsworth, D. Stress redistribution and fracture propagation during restimulation of gas shale reservoirs. J. Pet. Sci. Eng. 2017, 154, 150–160. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, F.; Duan, Y.; Yan, X.; Liang, H. Effect of depletion-induced stress reorientation on infill well fracture propagation. In Proceedings of the 53rd U.S. Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 18–25 June 2019. [Google Scholar]
- Sangnimnuan, A.; Li, J.; Wu, K.; Holditch, S.A. Application of efficiently coupled fluid flow and geomechanics model for refracturing in highly fractured reservoirs. In Proceedings of the SPE Hydraulic Fracturing Technology Conference & Exhibition, The Woodlands, TX, USA, 23–25 January 2018. [Google Scholar]
- Sangnimnuan, A.; Li, J.; Wu, K. Development of efficiently coupled fluid-flow/geomechanics model to predict stress evolution in unconventional reservoirs with complex-fracture geometry. SPE J. 2018, 23, 640–660. [Google Scholar] [CrossRef]
- Xu, T.; Lindsay, G.; Zheng, W.; Baihly, J.; Ejofodomi, E.; Malpani, R.; Shan, D. Proposed refracturing-modeling methodology in the haynesville shale, a US Unconventional Basin. SPE Prod. Oper. 2019, 34, 725–734. [Google Scholar] [CrossRef]
- Ibáñez, E.; Bezerra de Melo, R.C.; Wang, Y.; Dong, Y.; Alvarellos, J.; Lakshmikantha, M.R.; Webb, C. Improved refracturing evaluation workflow: An integrated methodology incorporating advanced geomechanical modeling. In Proceedings of the SPE Canada Unconventional Resources Conference, Calgary, AB, Canada, 18–19 March 2020. [Google Scholar]
- Wang, X.H.; Zhang, F.S.; Yin, Z.R.; Weng, D.W.; Liang, H.B.; Zhou, J.P.; Xu, B. Numerical investigation of refracturing with/without temporarily plugging diverters in tight reservoirs. Pet. Sci. 2022, 19, 2210–2226. [Google Scholar] [CrossRef]
- Liao, S.; Hu, J.; Zhang, Y. Numerical evaluation of refracturing fracture deflection behavior under non-uniform pore pressure using XFEM. J. Pet. Sci. Eng. 2022, 219, 111074. [Google Scholar] [CrossRef]
- Wang, A.; Chen, Y.; Wei, J.; Li, J.; Zhou, X. Experimental study on the mechanism of five point pattern refracturing for vertical & horizontal wells in low permeability and tight oil reservoirs. Energy 2023, 272, 127027. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of elasticity and consolidation for a porous anisotropic solid. J. Appl. Phys. 1955, 26, 182–185. [Google Scholar] [CrossRef]
- Kim, J.; Tchelepi, H.A.; Juanes, R. Stability and convergence of sequential methods for coupled flow and geomechanics: Drained and undrained splits. Comput. Meth. Appl. Mech. Eng. 2011, 200, 2094–2116. [Google Scholar] [CrossRef]
- Kim, J.; Tchelepi, H.A.; Juanes, R. Stability and convergence of sequential methods for coupled flow and geomechanics: Fixed-stress and fixed-strain splits. Comput. Meth. Appl. Mech. Eng. 2011, 200, 1591–1606. [Google Scholar] [CrossRef]
- Zeng, Z.; Grigg, R. A criterion for non-Darcy flow in porous media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Simulation of gas desorption and geomechanics effects for unconventional gas reservoirs. Fuel 2014, 116, 455–464. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K.; Patzek, T.W. Modeling gas adsorption in Marcellus shale with Langmuir and bet isotherms. SPE J. 2016, 21, 589–600. [Google Scholar] [CrossRef]
- Yu, W.; Wu, K.; Sepehrnoori, K.; Xu, W. A comprehensive model for simulation of gas transport in shale formation with complex hydraulic-fracture geometry. SPE Reserv. Eval. Eng. 2017, 20, 547–561. [Google Scholar] [CrossRef]
- Florence, F.A.; Rushing, J.; Newsham, K.E.; Blasingame, T.A. Improved Permeability Prediction Relations for Low Permeability Sands; Rocky Mountain Oil & Gas Technology Symposium: Denver, CO, USA, 2007. [Google Scholar] [CrossRef]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of an efficient embedded discrete fracture model for 3D compositional reservoir simulation in fractured reservoirs. SPE J. 2014, 19, 289–303. [Google Scholar] [CrossRef]
- Li, L.; Lee, S.H. Efficient field-scale simulation of black oil in a naturally fractured reservoir through discrete fracture networks and homogenized media. SPE Res. Eval. Eng. 2008, 11, 750–758. [Google Scholar] [CrossRef]
- Gao, Q.; Ghassemi, A. Pore pressure and stress distributions around a hydraulic fracture in heterogeneous rock. Rock Mech. Rock Eng. 2017, 50, 3157–3173. [Google Scholar] [CrossRef]
- Xu, Y. Implementation and Application of the Embedded Discrete Fracture Model (EDFM) for Reservoir Simulation in Fractured Reservoirs. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2015. [Google Scholar]
- Yu, W.; Xu, Y.; Weijermars, R.; Wu, K.; Sepehrnoori, K. A numerical model for simulating pressure response of well interference and well performance in tight oil reservoirs with complex-fracture geometries using the fast embedded-discrete-fracture-model method. SPE Res. Eval. Eng. 2018, 21, 489–502. [Google Scholar] [CrossRef]
- Tang, T.; Hededal, O.; Cardiff, P. On finite volume method implementation of poro-elasto-plasticity soil model. Int. J. Numer. Anal. Meth. Geomech. 2015, 39, 1410–1430. [Google Scholar] [CrossRef]


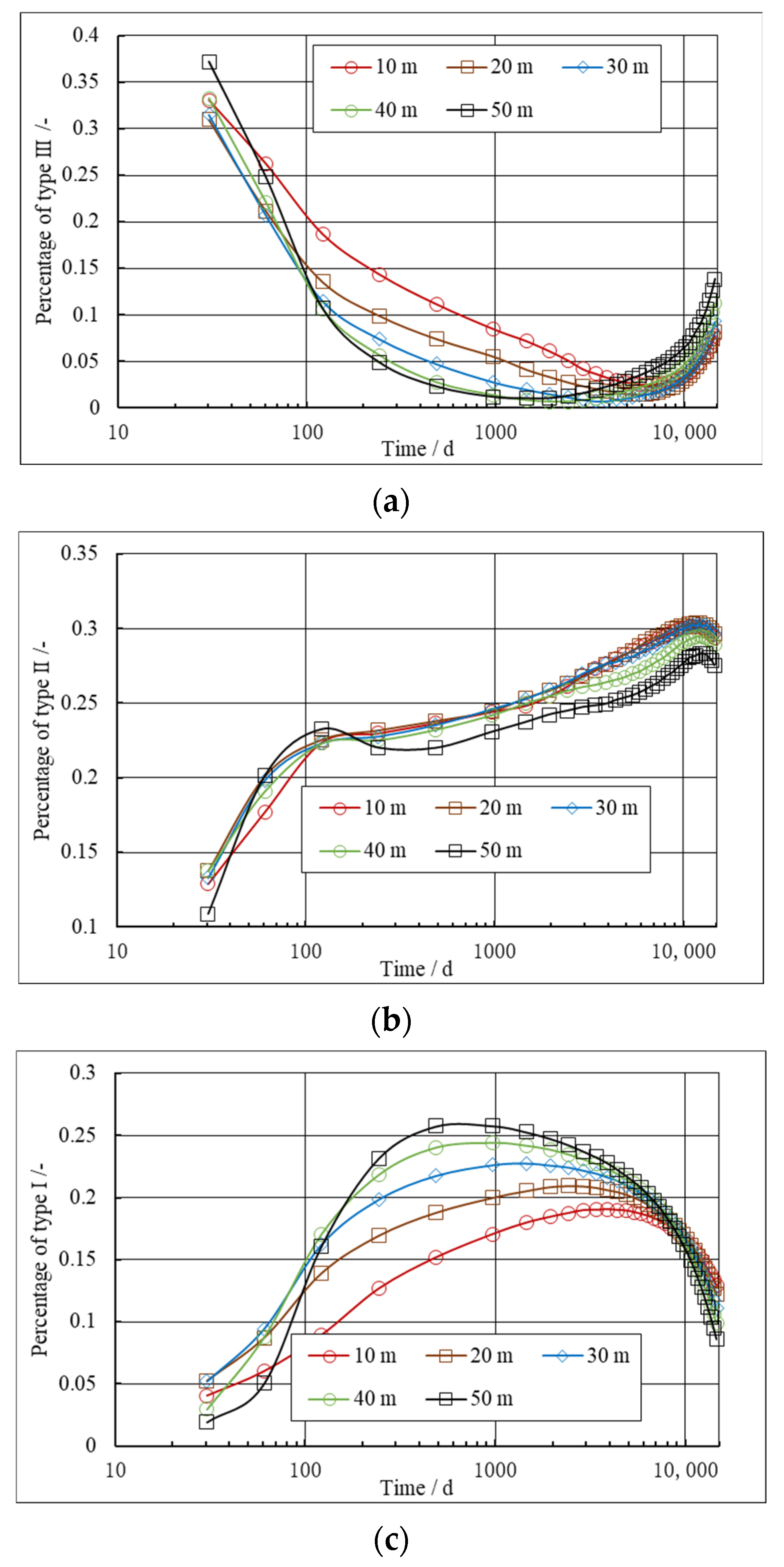
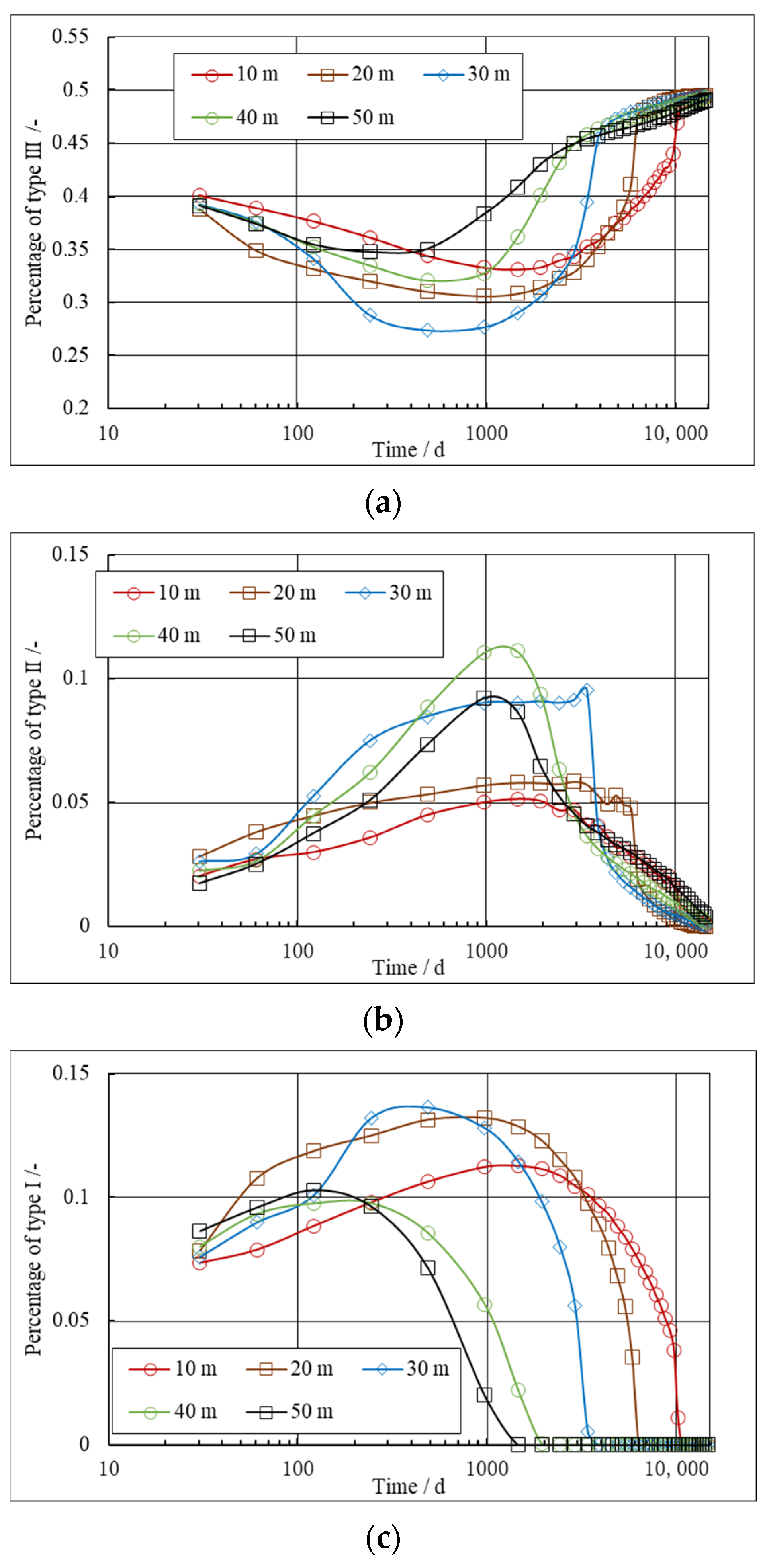
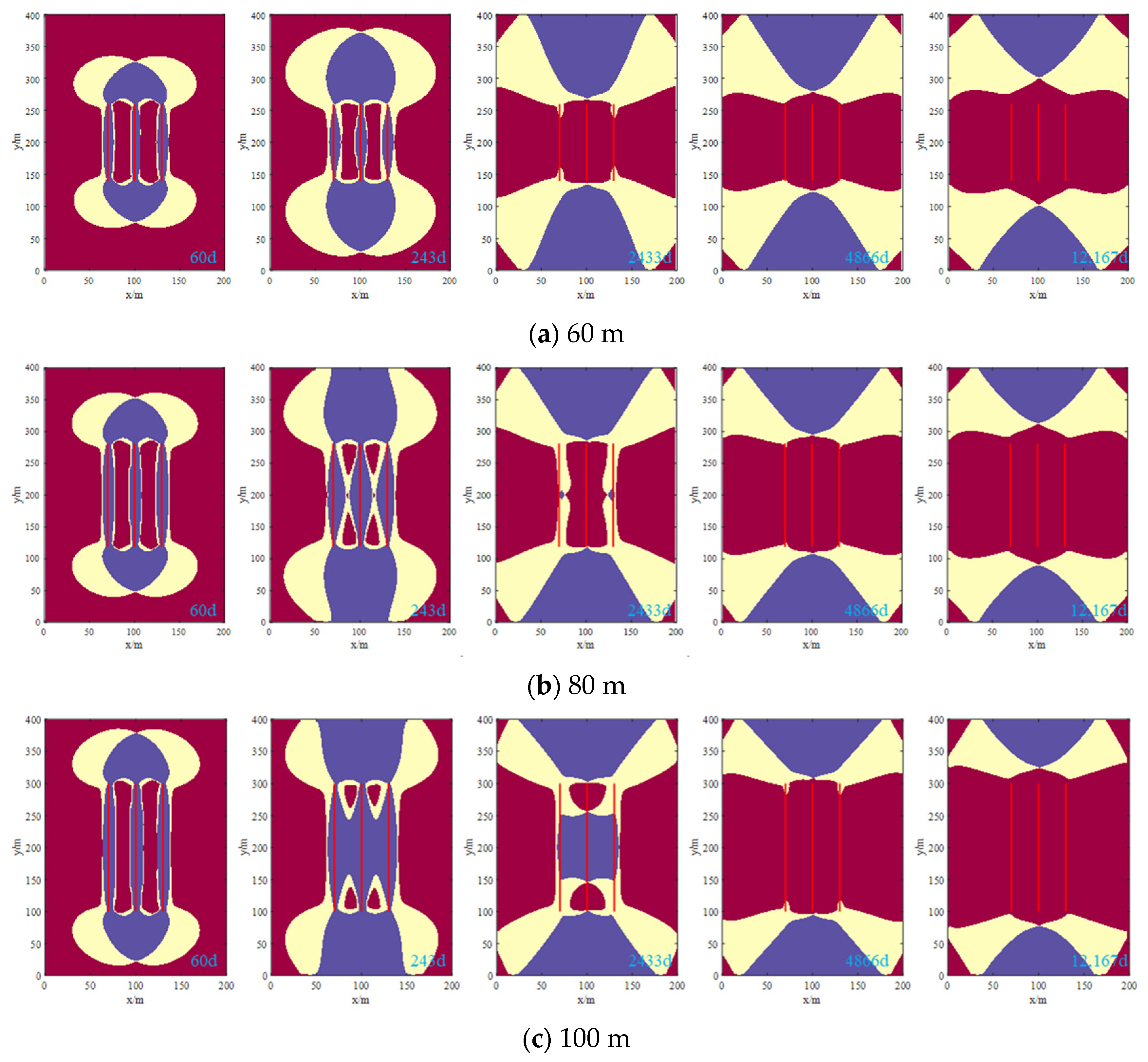

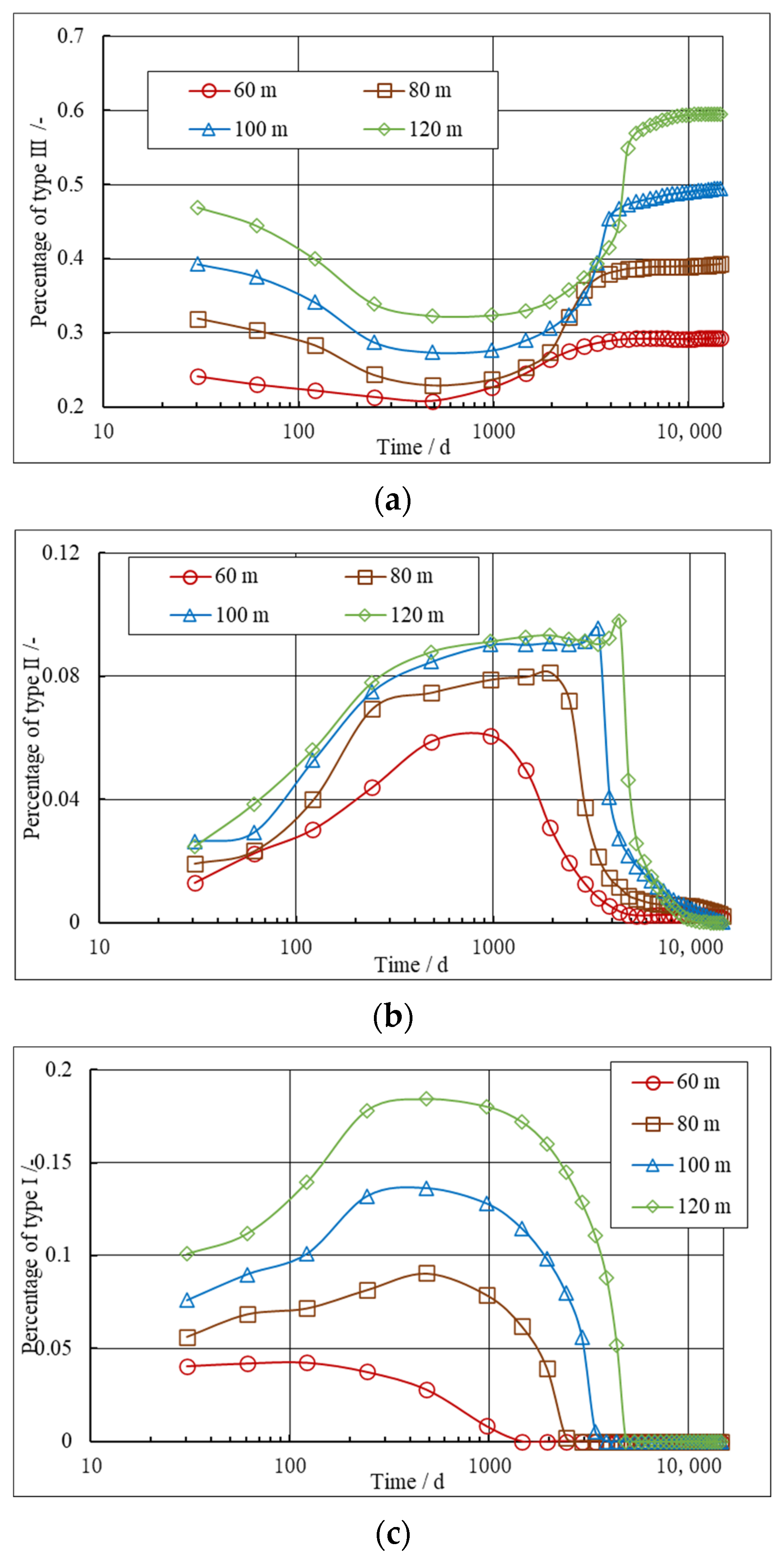
| Parameters | Unit | Value | Parameters | Unit | Value |
|---|---|---|---|---|---|
| Initial pressure | MPa | 40 | Fracture half-length | m | 100 |
| Langmuir pressure | MPa | 4 | Reservoir permeability | nD | 300 |
| formation temperature | K | 343.15 | Fracture permeability | D | 2 |
| Langmuir volume | m3/kg | 0.018 | Fracture width | m | 1 × 10−3 |
| Matrix porosity | - | 0.06 | Bottom hole pressure | MPa | 20 |
| Matrix compressibility coefficient | 1/MPa | 1.0 × 10−3 | Time | years | 5 |
| Fracture porosity | - | 1.0 | The dimensions of the domain (x, y, z) | m | (100, 100, 20) |
| Young’s modulus | GPa | 26 | Stress along the x-axis | MPa | 55 |
| Poisson’s ratio | - | 0.15 | Stress along the y-axis | MPa | 57 |
| Biot coefficient | - | 0.8 | Stress along the z-axis | MPa | 58 |
| Parameters | Unit | Value | Parameters | Unit | Value |
|---|---|---|---|---|---|
| Matrix compression coefficient | 1/MPa | 4.4 × 10−4 | Initial stress along y-axis | MPa | 44 |
| Matrix permeability | nD | 100–750 | Initial stress along z-axis | MPa | 45 |
| Elastic modulus | GPa | 24 | Time | years | 40 |
| Poisson ratio | - | 0.15 | The dimensions of the domain (x, y, z) | m | (200, 400, 20) |
| Initial stress along x-axis | MPa | 41 | Biot coefficient | - | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, B.; Song, Y.; Hu, Y.; Wang, Q.; Du, Y.; Tang, D.; Chen, K.; Dong, Y. Refracturing Time Optimization Considering the Effect of Induced Stress by Pressure Depletion in the Shale Reservoir. Processes 2024, 12, 2365. https://doi.org/10.3390/pr12112365
Zeng B, Song Y, Hu Y, Wang Q, Du Y, Tang D, Chen K, Dong Y. Refracturing Time Optimization Considering the Effect of Induced Stress by Pressure Depletion in the Shale Reservoir. Processes. 2024; 12(11):2365. https://doi.org/10.3390/pr12112365
Chicago/Turabian StyleZeng, Bo, Yi Song, Yongquan Hu, Qiang Wang, Yurou Du, Dengji Tang, Ke Chen, and Yan Dong. 2024. "Refracturing Time Optimization Considering the Effect of Induced Stress by Pressure Depletion in the Shale Reservoir" Processes 12, no. 11: 2365. https://doi.org/10.3390/pr12112365
APA StyleZeng, B., Song, Y., Hu, Y., Wang, Q., Du, Y., Tang, D., Chen, K., & Dong, Y. (2024). Refracturing Time Optimization Considering the Effect of Induced Stress by Pressure Depletion in the Shale Reservoir. Processes, 12(11), 2365. https://doi.org/10.3390/pr12112365






