Abstract
Stirling engines (SEs) have long attracted the attention of renewable energy researchers due to their external combustion design and flexibility in operating with various heat sources. The mathematical analysis of these devices is conducted by using a broad range of models ranging from basic zero-order to highly detailed fourth-order models, which are implemented through Computational Fluid Dynamics (CFD) simulations. The unique features of this last approach, combined with the increase in computing power, have promoted the use of CFD as a tool for analyzing SEs in recent years, significantly reducing the costs associated with prototype construction. However, Stirling CFD simulations are sophisticated due to the variety of physical phenomena involved, such as volume change, conjugated heat transfer, turbulent compressible fluid dynamics, and flow through porous media in the regenerator. Furthermore, there is currently no comprehensive review of CFD simulations of SEs in the literature; therefore, this contribution aims to fill that gap. Emphasis has been placed on identifying the type of engine, the physical phenomena modeled, the simplifying assumptions, and specific numerical aspects, such as mesh type, spatial and temporal discretization, and the order of the numerical schemes used. As a result, it has been found that in many cases, CFD numerical reports lack sufficient detail to ensure the reproducibility of the simulations. This work proposes guidelines for reporting CFD studies on Stirling engines to address this issue. Additionally, the need for a sufficiently detailed experimental benchmark database to validate future CFD studies is stressed. Finally, the use of Large Eddy Simulations on coupled key engine components—such as compression and expansion spaces, pistons, displacer, and regenerator—is suggested to provide further insights into the specific flow and heat transfer characteristics in Stirling engines.
1. Introduction
A Stirling engine, SE, is a thermal system that converts thermal energy into mechanical work by cyclically compressing and expanding a gas at varying temperatures. It requires two zones for its operation, the cold zone and the hot zone, normally separated by the regenerator so that the heat of the working fluid can be rejected or absorbed. Because of its nature as an external combustion system, its heat source can be very diverse: concentrated solar energy, biomass combustion, or waste heat [1]. An SE operates on the Stirling cycle, a highly efficient thermodynamic cycle with a theoretical efficiency equivalent to the Carnot cycle. The SE elements include volumes at different temperatures that must constantly change to meet the engine’s thermodynamic, gas dynamics, and heat transfer requirements.
Throughout history, the advancement of Stirling engines has been overshadowed by the emergence of new technologies. Internal combustion engines, electric motors, and, more recently, photovoltaic systems have relegated the Stirling system to the background [2]. However, this engine is currently reappearing as one of the tools for clean energy generation [3]. For this purpose, currently, the Stirling engine has emerged as a promising technology due to its flexibility in energy sources, low vibrations, ability to operate across a wide range of temperatures, broad application potential, high efficiency, ease of maintenance, and compact design [2].
On the other hand, the external combustion in this engine results in a slow response to power demand. This characteristic is why Stirling engines are primarily used in stationary applications, with their commercial models mainly focused on micro-cogeneration or solar energy utilization; the power output of these systems ranges between 1 and 9 kW at relatively high temperatures (650–800 °C) [4]. The complexity of this technology, which requires precise balances between thermal efficiency, power output, dead volumes, working fluid dynamics, the power transfer mechanism, and tolerances, necessitates highly elaborate designs; however, part of the efficiency problems presented by Stirling engines using mechanical power transfer systems are solved by the free piston configuration [5]. Its performance can be further increased using membranes instead of pistons [6], as this approach eliminates all frictional losses while ensuring efficient sealing [7].
The ideal Stirling cycle consists of two isothermal processes and two isochoric processes; heat supply and rejection are performed in the isothermal processes at temperatures T3-4 and T1-2, respectively, where T1-2 is the temperature of the cold zone (Tmin) and T3-4, the temperature of the hot zone (Tmax) as shown in Figure 1. The regenerator gains heat in the isochoric process of 4-1, where the working gas pressure is reduced to P1, and the temperature is reduced to T1-2. Then, the system is compressed until it reaches P2. Finally, the heat from the regenerator returns to the working fluid in an isochoric process, and the temperature and pressure reach T3-4 and P3, respectively (Figure 1) [8]. The actual processes of regenerator efficiency must be considered; points 3′ and 4′ represent the level of regenerator efficiency. A higher value of regenerator efficiency decreases the total heat input and increases the thermal efficiency [8]. However, this generates more head losses in the working fluid.
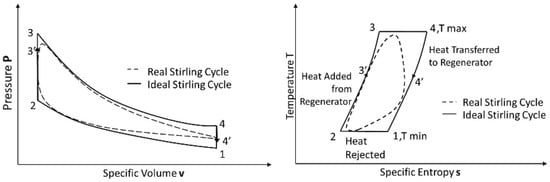
Figure 1.
Schematics of Pv and Ts diagrams (ideal versus real) of the closed cycle of a regenerative Stirling engine.
The Stirling engine is complex in its manufacturing process. The motion between the piston and the displacer is not ideal, and the heat transfer processes do not become isothermal; the actual behavior of the cycle in a P-v diagram is “rounded” (dashed lines in Figure 1) [8].
It should be noted that Stirling engines can be classified according to the power delivery system, mechanically to a flywheel or free piston [9], or also according to the arrangement of its cylinders, the way of operation, and the piston coupling [7]. Wang et al. [10] classified SEs according to the arrangement of pistons as α, β, or γ type (see Figure 2) and according to the drive system as kinetic, thermoacoustic, free-piston, or liquid piston Stirling engines.
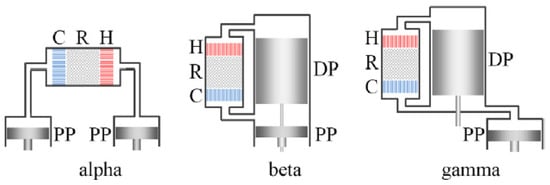
Figure 2.
Schematics of α, β, and γ Stirling engines after [10] (C: cooler; R: regenerator; H: heater; DP: displacer; PP: power piston). Reproduced with permission.
An α-type SE consists of two pistons articulated by the transmission mechanism, housed in independent chambers linked by a series of heat exchangers. The advantage of this engine lies in the relative ease of manufacture. Often, researchers use internal combustion engine mechanisms and compressors [11] to reduce manufacturing costs and frictional losses in this mechanism. This type of engine has technical problems due to the durability of its seals, dead volume, and friction due to the lateral forces of the rings on the expansion and compression cylinders [12]. The β-type engine has a power piston and a displacer in the same chamber. By superimposing both movements, a higher compression ratio is obtained in the engine, and a higher power output can be obtained than in an α-type engine. However, this configuration demands more effort in its design [10,12]. Finally, γ-type engines, like β-type engines, feature a displacer and a power piston. However, in γ-type engines, these components are housed in separate cylinders. This design allows for a clear separation between the heat exchangers associated with the displacer cylinder and the compression and expansion workspace linked to the piston. As a result, γ-type engines typically have slightly larger dead (or unswept) volumes than both α and β engines [13].
Kinetic Stirling engines are named as such because the mechanical pistons are actuated by a kinetic drive system (crank-slider, rhombic drives, among others). The system is configured so that the piston at the hot end consistently moves ahead of the piston at the cold end. In thermoacoustic SEs, the motion of the working fluid is driven by an acoustic wave; in this way, mechanical pistons are avoided by connecting tubes to both ends of the regenerator. The pistons in free-piston SEs are not mechanically connected, and their motion is adjusted to the operating conditions by resonant mechanisms of a piston–spring type. Finally, liquid piston Stirling engines employ liquid columns instead of mechanical pistons; the motion of the working gas is caused by the oscillation of liquid columns between cold and hot areas [10].
The increasing interest in Stirling engines is evident from the numerous reviews published over the past decade, addressing various aspects of their design, modeling, and operation. The most relevant of these are described in the following paragraphs.
Wang et al. [10] performed a revision of different technologies, based on the Stirling cycle, employed for recovering low and moderate heat. Among them, their kinetic configurations, including low-temperature differential LTD devices, thermoacoustic, free-piston, diaphragm, and liquid piston (two-phase and solid–liquid) Stirling engines, are described and discussed. For each of them, the technological details, features, working characteristics, and performances are summarized. After analyzing accessible experimental databases, costs, and potential, it was concluded that kinetic and thermoacoustic engines offered the most promising prospects for the intended application. The review performed in [14] dealt with the analysis of thermal models applied to determine the performance of Stirling engines. Several methods, including those of finite-time thermodynamic analysis, finite-speed thermodynamic analysis, isothermal, non-ideal adiabatic, combined adiabatic–finite speed (CAFS), and polytropic analysis with various loss mechanisms (PSVL), were presented and examined. As a case study, such methods were applied to the well-known GPU-3 Stirling engine [15], with the PSVL model providing the best comparison. Singh and Kumar [16] reviewed the development and performance of solar Stirling engines, stressing the fact that this is “the most efficient way to generate electricity using solar energy”. It was identified that the power and efficiency of solar Stirling can be enhanced by increasing the receiver gas temperature and concentration ratio combined with the use of Helium as fluid; moreover, these authors pointed out the use of such systems in micro-cogeneration in order to maximize energy savings and minimize CO2 emissions and the LCOE (levelized cost of energy).
Regarding specific applications such as the cogeneration of heat and power (CHP), [17] reviewed the combination of Stirling engines with thermochemical biomass conversion. This is an attractive solution for future energy decentralization. The authors discuss the main difficulties and challenges new developments must face to produce commercially viable devices. The main problem is the fouling of the heat exchangers due to low ash melting temperatures, which reflects on short maintenance intervals; the alternatives employed to mitigate such phenomena usually lead to an efficiency reduction. One promising option to solve such difficulties, pointed out in [17], was employing fluidized bed combustion at a small scale combined with Stirling engines, which was being tested at the laboratory level. Getie et al. [18] revised the key studies on applying reverse regenerative Stirling cycles to refrigeration from low to moderate temperature applications. Apart from explaining the working principles of the device, the contribution discusses and analyzes various strategies to enhance the performance of such refrigerators.
A review of the application of “soft computing methods” to design and optimize Stirling engines was conducted in [19]. Such methods aim to provide approximated solutions to complex problems without the need for exact algorithms and precise answers. The authors explored the main literature contributions focused on genetic algorithms, particle swarm optimization, fuzzy logic, and artificial neural networks. They concluded that to achieve more reliable and cost-effective solutions, the best approach was to combine several previous methods rather than relying on just one. Solar dish Stirling systems (SDSSs) were considered in [20], where aspects such as design, geometrical and optical configurations, thermal performance, and economic analyses, as well as their applications, were comprehensively reviewed. The authors pointed out some directions of future work in these kinds of systems: (1) Integrating different elements in the receiver as complex tube metals and heat pipe and phase change materials (PCMs) to optimize heat transfer. (2) Including the pressure, friction, and throttling regenerator losses in optimization studies. (3) Performing more studies in SDSS-powered hybrid desalination plants for fresh water and electricity cogeneration. (4) Encouraging experimental work on hybrid innovative multi-generation systems to produce electricity and heat. Malik et al. [21] presented another review of parabolic solar dish Stirling (PSDS) systems, similar to [20], but with a greater focus on the dish concentrator. In the same context, [22] discussed and revised the use of an α Stirling hydrogen engines in concentrated solar power, which could reach efficiencies as high as 42% based on some CAE (Computer-Aided Engineering) estimations.
The applications of Stirling devices for CHP were reviewed in [23]. Different aspects were taken into account, such as the use of different heat sources, commercial and techno-economic challenges, tri-generation arrangements, and future prospects. In particular, the free-piston Stirling engine was identified as a good candidate to be implemented in residential applications because of its low maintenance, vibrations, noise, and emissions, fuel source flexibility, and high efficiency (thermal to electric). Zhang et al. [24] carried out a bibliometric study to find out the research trends of Stirling engines and their energy supply applications. The authors identified that a recurrent investigation hotspot was the “multi-objective optimization on the thermodynamic analysis and CHP technology”; consequently, they reviewed the main related techniques, highlighting them as prominent tools for predicting and optimizing Stirling engine performance.
As can be realized, none of the previous reviews has dealt with the topic of CFD simulations in Stirling engines; therefore, the present contribution aims to close this gap in the literature.
2. Computational Analysis Methods of Stirling Engines
The classification of the mathematical models for Stirling engines has been adjusted over time in response to the development of new techniques and advancements in computational capacity; however, the classifications of these mathematical models, in most cases, are based on the old works presented by [25,26]. In general, the types of mathematical modeling of SEs are named zero-, first-, second-, third-, and fourth-order.
Zero-order models rely on experimental data rather than being models per se, such as those performed by Beale or West, which estimate a specific power at the motor shaft from a few input parameters. For instance, West [27] provided Equation (1), which allows the direct calculation of the indicated work (γ configuration) as a function of the average engine pressure (Pm), the angle between displacer and power piston (α), the volume displaced by the displacer (VD), the volume displaced by the power piston (VP), the dead volume (Vs), and the temperatures Th and Tk of the gas in the hot and cold heat exchangers, respectively.
First-order models integrate a set of equations in sinusoidal variations of the expansion and compression volumes. They give an approximate idea of heat flows and power as a function of their dimensions. However, they do not take into account losses and nonlinear phenomena. These models are a starting point for more complex models during design. One of the most common of this type is the isothermal model proposed by Schmidt. This model’s drawback is that it assumes isothermal behavior in the engine chambers, generating a “paradox” because the heat exchangers are presented as adiabatic [28].
Second-order models are based on solving a set of equations derived from mass and energy balances in the various engine components. These equations are coupled with the sinusoidal variations of the expansion and compression chambers, leading to closed-form solutions. The convergence of these models is generally achieved with numerical methods. For example, Urieli’s adiabatic model [29] belongs to this category; in addition to engine power, these models allow the calculation of heat fluxes in heat exchangers. Thermal and load losses are calculated independently; hence, this model type is also called decoupled. Second-order models are more accurate than the previous ones but are still inappropriate for evaluating nonlinear phenomena. Some losses considered in second-order models are the following: (1) Energy dissipation by pressure drop in heat exchangers. (2) Internal conduction energy loss between the hot and cold components of the engine through the various heat exchangers. (3) Conduction energy loss in the regenerator. (4) Shuttle loss: this effect comes from the reciprocating action of the displacer (piston) from the hot end to the cold end. (5) Hysteresis loss due to gas hysteresis in the pressure/volume relationship.
Third-order models, also known as nodal analyses, consist of three basic procedures: (1) perform a spatial discretization of the engine in a series of nodes; (2) establish the conservation laws for mass, momentum, and energy as a set of differential equations, with the addition of the equation of state for the working gas; and (3) solve the system using proper numerical methods. In this way, the temperatures and pressures at each node and instant of time are known; since it is a coupled model, the losses are also evaluated. The Finkelstein or Lewis models are of this type [30].
Finally, fourth-order models consider multidimensional analysis, usually under a Computational Fluid Dynamics (CFD) approach [31], which can provide accurate results for engine performance predictions. However, this approach is quite challenging, and it is computationally expensive to model the entire engine [32]. Nevertheless, due to current increases in computational capability, CFD analyses of Stirling engines have increased, incorporating instabilities and pumping loss effects in their main components and auxiliary systems; the use of dynamic meshes in the expansion and compression chambers allows for obtaining more accurate results compared to isothermal or adiabatic models. In addition, it is possible to analyze the regime changes of the working fluid as it passes through the different components. Of course, the success of these models depends largely on several factors, such as the adequate establishment of boundary and initial conditions, mesh quality, convergence, and time steps, among others.
Regarding the performance of the low-order models compared to CFD computations, [33] mentions, “The assumption of uniform chamber temperatures and the use of constant heat transfer coefficients to account for heat transfer adopted by some zero- or one-dimensional models are too crude to reflect the reality.” Also, [34] pointed out, “One of the biggest advantages of using CFD in such kind of problems, is that it allows to reduce models uncertainty resulting from inaccurate assumptions inherent in the low-order models (analytical formulas for heat transfer coefficient or pressure losses etc.). Such empirical formulas are based on the literature data; therefore, they are valid only for some range of engines’ operational conditions.” Finally, regarding the accuracy of the results, Makhamov [35] provides quantitative data: “The comparison of theoretical and experimental data has demonstrated that the second-order analysis predicts the value of the indicated power with ~30% accuracy when the 3D CFD model calculates pressure and temperature variations in different locations of the engine and the area of the pressure-volume diagrams with a 12–18% accuracy.”
2.1. Main Features of Computational Fluid Dynamics
Computational Fluid Dynamics (CFD) is a branch of fluid mechanics that employs numerical methods and algorithms to solve and analyze problems related to fluid flow, heat transfer, and associated phenomena across various engineering applications, including those related to energy [36]. It makes it possible to study complex systems, optimize designs, and predict performance without costly physical prototypes. It can also be used to conduct parametric studies during the early design stages or even for troubleshooting, offering insights that may be difficult to obtain through experimental methods. Furthermore, an additional advantage of CFD is that it enables testing under extreme or dangerous conditions, such as high temperatures or velocities, in a safe and controlled virtual environment.
However, despite its advantages, CFD also has limitations. One of the main drawbacks is the high computational cost and time required for accurate simulations, especially for complex geometries or turbulent flows. CFD requires powerful computing resources, and the results are highly dependent on the mesh quality, boundary conditions, and turbulence models chosen, which can introduce uncertainties [37]. Additionally, CFD simulations are based on numerical approximations, meaning that the results are not always as accurate as desired and need validation through experiments.
Regarding the methodology, CFD comprises three main stages: pre-processing, solving, and post-processing. In the pre-processing phase, the physical phenomena to model and the geometry of the system are defined, and the fluid domain is discretized into a mesh of smaller elements. Boundary conditions, initial conditions, and fluid properties are also set during this phase. The solving stage involves selecting the appropriate numerical methods and algorithms to solve the governing fluid flow equations, such as the Navier–Stokes equations, possibly combined with other models (turbulence, reactions, …), over the discretized domain. Finally, the results are visualized and analyzed in the post-processing step, including flow patterns, pressure distributions, and temperature variations, to gain insights and draw conclusions about the system’s behavior [38].
The use of CFD has become a standard tool in energy engineering, covering different applications such as the following: wind turbine design, optimizing blade shapes and turbine efficiency by analyzing airflow patterns around the blades and predicting aerodynamic performance under various wind conditions [39,40,41]; combustion in power plants, helping to simulate combustion processes in gas turbines, coal-fired power plants, and internal combustion engines, allowing engineers to optimize fuel efficiency, reduce emissions, and control temperature distributions [42,43,44]; solar power systems, applied to model heat transfer in solar receivers and predict fluid behavior in heat exchangers, improving the overall efficiency of solar thermal energy capture [45,46]; in hydropower it is used to analyze water flow through turbines in hydropower plants, helping to optimize turbine design, reduce cavitation, and improve energy generation efficiency [38,47,48,49,50]; fuel cell technology, in modeling the behavior of gases and liquids in fuel cells, such as in the proton exchange membrane (PEM) and solid oxide fuel cells (SOFCs), to enhance cell efficiency and ensure a uniform fuel distribution [51,52]; HVAC (Heating, Ventilation, and Air Conditioning) and transport systems, applied in the design of such systems in energy-efficient buildings, optimizing airflow and particle transport, ensuring effective temperature control with minimal energy consumption [53,54,55,56,57].
In this context, during the last two decades, several studies dealing with the CFD of different Stirling engine configurations have been published. However, as the introduction points out, no systematic review of them has yet been published; therefore, this contribution addresses such an endeavor in the following sections.
2.2. Specific Aspects of CFD Applied to Stirling Engines
The large number of physical phenomena interacting in the operation of a Stirling engine makes its CFD simulation very sophisticated. In order to describe the real operating conditions of this device, CFD computations must combine, among others, the following features:
- Three-dimensionality;
- Transience;
- Compressibility;
- Working fluid described as a real gas;
- Turbulent flow dynamics;
- Conjugate heat transfer, likely including radiation if operating at a high temperature;
- Porous media flow in the regenerator;
- Dynamic hybrid meshes need to be used;
- High-order numerical discretization schemes, spatial and temporal, are needed.
However, not all of these requirements are included in SE CFD studies, and simplifications are frequently made. Therefore, it is common to find one or more of the following simplified numerical setups: two-dimensional, laminar, periodic boundary conditions, coarse meshes, ideal gas treatment, or neglecting of radiation.
As commented, several physical phenomena are simultaneously present in the real operation of Stirling engines; therefore, the number of such phenomena to be considered, as well as their level of numerical description, often dictates the simulation software choice. In this context, the software used is almost always commercial, with ANSYS-Fluent being the preferred choice. Actually, in the present review, only two groups have been identified employing in-house codes; the first one, named USTREAM, was designed to perform laminar simulations with fairly coarse meshes [33,58,59,60], while the second code (no name is provided) [61] deals with a two-dimensional steady turbulent simulation (standard k-ε model) of a low-temperature differential Stirling engine (LTDSE). On the other hand, the open source code OpenFoam was employed in the 2D study of [62]. Other commercial software has been utilized, such as ANSYS-CFX [63], SolidWorks [64], StarCCM [33,65], and COMSOL [32,66,67,68]. Therefore, it can be concluded that due to the complex interactions of physical phenomena in the operation of Stirling engines, CFD simulations require a high level of sophistication. This often necessitates the robustness only well-developed and extensively tested commercial software can offer. Among all of them, this review has found that ANSYS-Fluent is by far the most employed, especially when unsteady three-dimensional turbulent CFD simulations are pursued.
3. CFD Simulations of Stirling Engines
This section reviews the most relevant CFD simulations of Stirling engines (SEs) that have been identified. Due to the number of studies, kinetic SEs (α, β, and γ) are considered first. Following the classification in [10], LTDSEs are included as γ-type because they are usually implemented in such a configuration.
Simulations of other SE types, such as thermoacoustic and free piston, are described later in this section. Finally, no CFD simulations have been found for liquid piston SEs.
It is necessary to mention that in the following, we examine numerical studies dealing with the interacting main components of SEs. Works devoted to studying specific aspects of one element (e.g., regenerators or heat exchangers) are not included here but considered in a later section.
Table 1, Table 2 and Table 3 collect the significant contributions dealing with SEs of the α, β, and γ type, respectively. They are organized as follows: the first column identifies the study; the second gives information about the dimensionality (two or three-dimensional) and flow regime (laminar of turbulent) of the simulation; the third lists the simulated main components, which are usually coupled; and the fourth column comments on some particular aspects, including the kind of comparison with experiments.

Table 1.
CFD simulations of α-type Stirling engines.

Table 2.
CFD simulations of β-type Stirling engines.

Table 3.
CFD simulations of γ-type Stirling engines.
After examining such studies, it has been found that all contributions employ one or more of the simplifications enumerated in Section 2.2. For instance, the turbulent dynamics of the flow in a 3D configuration are considered only in around 30% of the reviewed articles. Moreover, when performing a three-dimensional simulation, a reduced computational domain is typically used in combination with periodic boundary conditions, exploiting the engine’s geometrical symmetry.
The validation of numerical simulations is usually performed by comparison with global performance indices of the engine such as power output, heat transfer, or pressure–volume cycles. In order to improve reliability, it would be necessary to extend such comparisons to local and instantaneous values of some variables, such as pressure and temperature, at definite locations. In this regard, experimental studies are encouraged to provide data for as many variables as possible in key SE zones, aiming to create a comprehensive database that can be used for validating numerical computations.
On the other hand, reports of the CFD numerical setup are very often incomplete, preventing the proper reproducibility of the computational studies; for instance, verification study reports on the influence of the time step are rare, and the total number of simulated expansion–compression cycles is frequently omitted. As mentioned earlier, this fact can be attributed to the sophistication of SE numerical simulations, which implies many details of the problem setup; however, a proper numerical report is essential to judge the quality and reliability of the CFD results. In this context, Section 4 below offers several guidelines for adequately reporting numerical setups, sensitivity studies, and results obtained in SEs. Nevertheless, a few notable exceptions have been identified, which are detailed in the following.
Among the reviewed literature, the study of Kuban et al. [34] deserves special mention due to the completeness of their CFD report. These authors deal with a γ Stirling engine, named ST05G (see geometry in Figure 3), considering all the major components: cylinders volume, heater tubes, the tube connecting both cylinders and the regenerator, modeled as a porous medium. In order to reduce the computational effort, only half of the domain is simulated, assuming symmetry conditions in the corresponding plane (Figure 4a). In this work, the motions of the piston and the displacer are defined by prescribed expressions; fluid properties and initial operating conditions are carefully reported, as well as boundary conditions. After that, the three-dimensional compressible governing equations (Unsteady Reynolds Averaged Navier–Stokes, URANS) to compute the fluid velocity, pressure, and temperature fields are provided in combination with appropriate turbulence models. In this case, the working fluid (air) is described as an ideal gas. Numerical details such as the mesh size, the order of the discretization schemes, spatial and temporal details, and time step are clearly identified. Moreover, the relevant parameters of the porous medium in the regenerator are adequately reported.

Figure 3.
Geometrical CAD model of the ST05G γ Stirling engine employed in [34] identifying its main parts. Reproduced with permission.
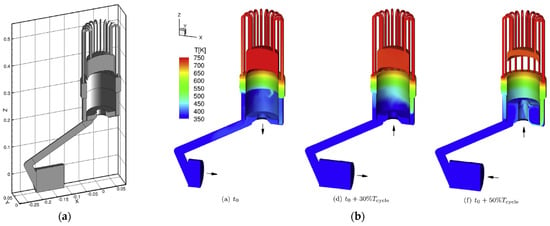
Figure 4.
(a) Computational domain of the SE considered in [34]. (b) Instantaneous temperature field at the middle plane and walls at three different instants of the expansion–compression cycle ( is the cycle period). Reproduced with permission.
Kuban et al. showed an exhaustive Grid Independence Study (GIS), showing the mesh details in the most critical areas. The piston and displacer motion implies a dynamic volume change in the expansion and compression cylinders, which is handled numerically using dynamic meshes. In this case, the authors employ a layering scheme, which adds or removes cell layers as the volume grows or reduces, respectively. One remarkable fact is that [34] provides a sensitivity of the results regarding the turbulence modeling, realizable k-ε and k-ω Shear Stress Transport models, comparing curves for temperature and heat flux. As a result, a difference of around 3% in the total engine power output is found. This verification is not commonly found in the relevant literature.
In the results section, the analysis is comprehensive, illustrating contour fields of all the relevant variables, including the turbulent ones, which is also not common in the related literature. Figure 4b shows, as an example, the evolution of the temperature field at the walls and symmetry plane at three instants of the compression–expansion cycle. Figure 5 presents, additionally, in the same plane sample fields of the vorticity magnitude and turbulent variables such as turbulent kinetic energy (TKE) and its dissipation rate , at various instants of the cycle. Based on these results, the authors conclude that “taking into account that the flow in the Stirling engine is strongly irregular and asymmetric, as shown above, the CFD should be performed for full 3D configurations without simplifying assumption”. Finally, the validation compares the numerical power obtained versus the heater temperature, filling pressure, and engine rotational speed with different experimental sources.
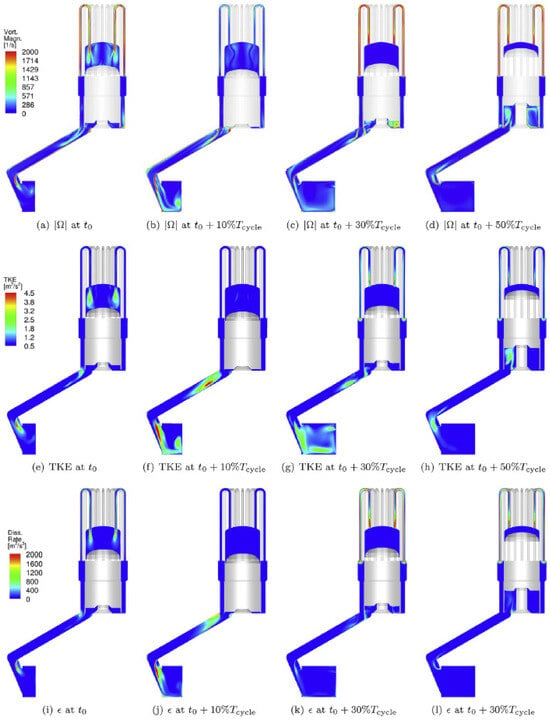
Figure 5.
Instantaneous fields of turbulent variables at the symmetry plane at the different moments of the expansion cycle [34]: vorticity magnitude (top), turbulent kinetic TKE (middle), dissipation rate (bottom) ( is the cycle period). Reproduced with permission.
El Gahfour et al. [76] also provided a comprehensive description of their performed simulation on the β-type GPU-3 Stirling engine (see geometry in Figure 6). The included elements comprised the heater, cooler, cooler-end connection, regenerator (modeled as a porous medium), and expansion and compression chambers, as well as the displacer. Owing to the geometrical symmetry, only one-eighth of it is considered as the computational domain, using periodic boundary conditions where appropriate. The description of the meshing methodology, deforming mesh strategy, initial and boundary conditions, simulation setup, employed numerical schemes, and solution scheme is very detailed and can be taken as an example for further CFD studies. Additionally, apart from the GIS, a time-step independence study is also reported. An important contribution of [76] is the conducted sensitivity analysis on turbulence modeling involving six different models. Different versions of k-ε (standard, realizable, RNG), Shear Stress Transport (low Re and transition) and Spalart–Allmaras turbulence models were considered and the results compared with the experiments of [85]; the realizable k-ε was the model that provided the closest results to the experimental values, which is demonstrated in Figure 7. However, the results section only presented contour plots for the temperature, in the center plane of the domain and the regenerator, and the flow field in the compression and expansion spaces aimed at illustrating the heat transfer coefficient on the walls. No figures or discussions about the behavior of the turbulent variables were reported, which would have contributed to improving the significance of [76] in the Stirling CFD community. Finally, this work found that the large temperature oscillation in the regenerator matrix is caused by flow jetting and ejecting processes occurring during the expansion strokes.
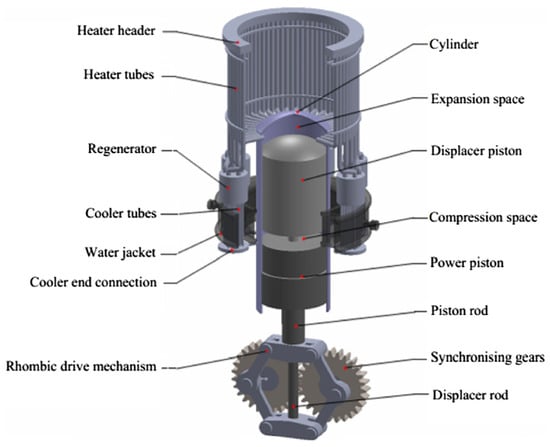
Figure 6.
Geometrical CAD model of the GPU-3 β Stirling engine considered by [76] showing its components. Reproduced with permission.
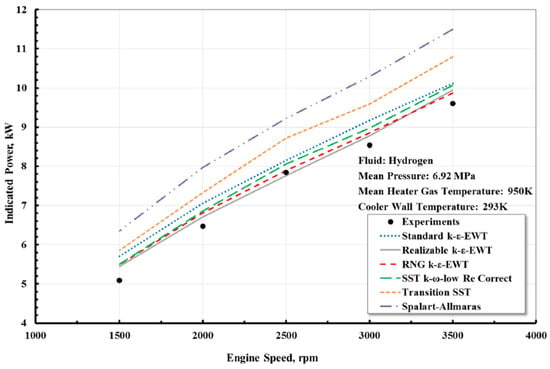
Figure 7.
Sensitivity study of the GPU-3 β Stirling engine performance (power vs. rotational speed), regarding the turbulence model employed [76] (EWT stands for Enhanced Wall Treatment). Experimental points from [85]. Reproduced with permission.
The following subsections are devoted to reviewing CFD studies of thermoacoustic and free-piston SEs (which considered the coupled main components), as well as CFD simulations focused on specific aspects of the modeling and operation of Stirling engines.
3.1. Simulation of Non-Kinetic Stirling Engines
Another kind of Stirling engines, apart from the kinetic, have been simulated by CFD. In [86], a thermoacoustic Stirling engine is considered. Different nonlinear phenomena are considered, such as self-excited thermoacoustic oscillation, acoustical and thermal performance, and vortex formation in the traveling-wave loop, comparing favorably with own experimental data. The authors of [87] examine the resonant frequency of the moving magnet linear compressor within a Stirling-type cryocooler. Chen et al. [88] performed high-fidelity LES simulations of the oscillatory turbulent flow in a thermoacoustic engine. Only the hot buffer, stack, and resonator were simulated, assuming a linear temperature variation along the stack length; therefore, no moving surfaces were considered. Additionally, only one-quarter of the complete geometry was considered in the computational domain to reduce the simulation time. The authors compared the performance of LES and URANS, concluding that the first outperformed the second when compared with theoretical estimations of the frequency and growth rate of the oscillating flow in the engine. In this context, Chen et al. suggested the LES approach as a suitable tool for studying thermally induced oscillatory flow in more complex configurations.
In an early study, Makhamov [89] handled the 2D axisymmetric CFD simulation of a solar V-type Stirling engine, including the heater, cooler, and expansion and compression spaces, as well as the regenerator. Its main contribution was the computation of velocity, pressure, and temperature fields in the different regions of the engine, which was a novelty at that time. The author concluded that the CFD results differed significantly from those of second-order models. The authors of [66] computed by CFD the temperature distribution in the heat exchanger tube of a solar concentrator system coupled with an α Stirling engine; however, the objective of the simulation was not the engine itself.
A free-piston Stirling engine (FPSE) for combined heat and power (CHP) applications was considered in [90]. The idea was to develop a new design by combining thermodynamic models, CFD, and structural simulations; however, the authors do not provide any detail about the performed CFD simulation beyond showing some contour plots (velocity and temperature) in specific components of the FPSE. In a later study [91], the same authors report CFD simulations of the same device but focused on conjugate heat transfer with the walls. Owing to the geometrical symmetry, only one-fifteenth of the engine was included in the computational domain, imposing periodic boundary conditions. The considered components were the heater (head and tubes), cylinder, regenerator, heat rejecter, water jacket, and flexure bearing; however, the volume variation of the expansion and compression spaces was not explicitly simulated by a dynamic mesh but was handled by an oscillating boundary condition. The latter simplifications render the simulation as idealized. On the other hand, this simulation used more refined grids than previous studies, necessary to describe correctly the energy coupling between the fluid and solid walls; moreover, the authors performed a sensitivity analysis of the employed turbulence model, concluding that the standard k-ε model with enhanced wall functions yielded reasonable results. Zhao et al. [91] concluded that ejecting and injecting fluid streams generated a highly non-uniform temperature, density, and pressure in the regenerator, but still, a linear temperature distribution was obtained in the solid matrix.
The study reported in [92] dealt with the computation of displacer pumping losses in an FPSE. The considered 2D domain comprised the cold and hot heat exchangers, bounce space, regenerator (modeled as a porous medium), and clearance seals. As a result, the authors determine the “optimum displacer and piston seal clearance at different charge pressure and operating frequencies”. An FPSE cooler was numerically studied in [93]; the focus was on “the effect of the heat transfer area of the regenerator on the cooling performance and pressure loss of the FPSC”. It was found that a larger heat transfer area of the regenerator implied a lower temperature of the cool end but also a higher pressure loss, which translated into a reduced system efficiency. Dai et al. [65] numerically studied the heater of an FPSE intended for space applications. Fins were added to the heater to improve the heat transfer; a linear growth relationship was identified between the fins’ height and pressure drop and Nusselt number ratio. Moreover, an optimal fin height was determined based on the geometric constraints. An improved piston Stirling cryocooler design was considered in [63]; a 3D CFD simulation was employed to reveal the details of the flow dynamics and heat transfer in the cryocooler, whose results were eventually validated versus experiments. Finally, it is necessary to indicate that in most of the studies of such Stirling engine variations, the CFD simulations were two-dimensional.
3.2. CFD Simulations of the Regenerator Considering Its Microstructure
In a series of papers [94,95,96,97], Costa et al. performed steady 3D CFD simulations of the flow through the regenerator of a Stirling engine, while [98] considered the heat exchangers. In those computations, the regenerator microstructure was taken into account, leading to quite complex geometries. The study in [94] is devoted to developing correlations (up to a Reynolds number of 400) for the friction pressure drop through a Stirling engine regenerator made of both stacked and wound woven wire matrices (aligned and misaligned). Laminar and turbulent (RNG k-ε) flow simulations were performed depending on the Reynolds number. The derived friction pressure drop correlation equation compared favorably with experiments, showing deviations within 5%. The obtained expressions could be combined with CFD simulations to characterize the flow through the regenerator in Stirling engines.
In [95], the same authors studied the heat transfer characteristics in the previous regenerator matrices. A similar simulation setup was employed as in [94], but this time the energy equation was also solved in a transient state. A correlation of Nusselt versus Reynolds numbers was developed for the case of a wound woven-wire matrix model. As an example, Figure 8a presents the grid employed in [95] in the case of stacked woven-wire matrices, whereas corresponding vector velocity fields are displayed in Figure 8b,c for a time of 0.02s. In Figure 8b, vectors are colored by velocity magnitude, and by temperature in Figure 8c. The obtained numerical results [94,95] in the previous matrix were tested experimentally in [96]. After a preliminary appraisal, the authors stated that “the model validity is required to be further assessed over a very large parametric range and woven wire mesh configurations for future Stirling regenerator applications”. In a further paper [97], the same group considered thermal non-equilibrium porous media modeling in the wound woven-wire matrix of the Stirling regenerator. CFD was employed to obtain the porous media coefficients instead of using experiments. The obtained results were applied to successfully model oscillating flow through a full-scale regenerator porous medium. In this way, Costa et al. demonstrated that low-cost CFD models can complement and even substitute for the most costly experimental studies. A more elaborate CFD simulation of the flow through a regenerator was performed in [99]; here, the turbulent characteristics of the flow were described by the Large Eddy Simulation technique, which is said to be more precise than usual turbulence models at the cost of a considerable increment in computing time. The solid matrix consisted of bent and twisted cylindrical wires, which were staggered to study the influence of their misalignment and spacing on pressure drop through the regenerator.

Figure 8.
Grid employed in [95] in the case of a stacked woven-wire matrix (a) and instantaneous vector field through the same regenerator matrix colored by velocity magnitude (b) and by gas temperature (c). Reproduced with permission.
In [100], a novel manufacturing method, Selective Laser Melting (SLM), for Stirling regenerator matrices is presented and demonstrated. CFD simulations are employed to visualize the matrix’s pressure, velocity, and temperature fields. However, no details about such computations are provided, not even the employed software. Paper [101] studied by CFD the thermal efficiency and pressure drop of two stacked regenerators in staggered and in-line configurations under oscillating flow conditions and considering the microstructure of the matrix. The simulations of the regenerator were three-dimensional, unsteady, and turbulent (RNG k-ε), with coarse meshes. Moreover, radiation is included using the Discrete Ordinates (DO) method. This work demonstrated that changes in the geometry of the regenerator matrix substantially affect thermal efficiency and pressure drop, in spite of keeping the same mass and geometrical arrangement.
3.3. Stirling CFD Studies Including Radiation Model
A few contributions include radiation in the computations. In [69], a comparison of α, β, and γ Stirling engines is performed, including also radiation as a heat transfer mechanism “to make the model more realistic”. Two radiation models are compared: the surface to surface (S2S) and Discrete Ordinates models. Following these authors, the S2S model becomes prohibitively expensive in terms of computing time, and therefore, the DO model is used instead in all the reported simulations. Unfortunately, the authors do not provide comparisons of engine power output or thermal efficiency with and without the radiation model.
The same authors in [82] (one year earlier than [69]) evaluated numerically the influence of radiative heat transfer on the performance of a β-type Stirling engine with no regenerator. Surface to surface (S2S) and discrete ordinates (DO) models were considered. The CFD model was validated against the experimental data of [75], showing excellent agreement, with a maximum deviation of 7%. These findings also indicated that neglecting radiative heat transfer leads to an underestimation of power output by approximately 13% compared to the experimental data used for validation (see Figure 9). Additionally, the DO model was more accurate than the S2S model and also less demanding in computer time. This finding explains why DO is the radiation model usually employed in numerical simulations of Stirling engines.
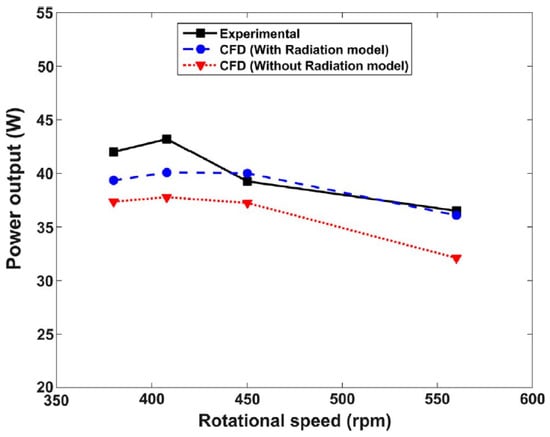
Figure 9.
Comparison of CFD results from [82] for SE performance, with and without radiation model, against the experimental data from [75]. Reproduced with permission.
The authors of [71] performed 2D turbulent simulations of a Stirling engine considering all the heat transfer mechanisms, including radiation, using the DO method. The objective was to evaluate the performance of the investigated α-type engine using various metrics, including the coefficient of performance (COP), irreversibility factor, and exergy efficiency. These metrics were applied to assess different strategies for heating and cooling the engine, revealing that the processes in the regenerative channel are crucial, those in the expansion and compression chambers being less relevant. However, no results were presented without including the radiation model.
In [72], the same authors studied the influence of the regenerator on its performance under different operating conditions using the same engine. Also, radiation was included as a heat transfer mechanism. The authors developed a sensitivity analysis of the results with the turbulence model employed (several two equation and Reynolds stress RSM models). The cycle work varied within 10% when the turbulence model was changed, except for the standard k-ε model with standard wall functions, which over-predicted them; therefore, the authors recommend employing either the RSM or k-ω models. It was found that with a regenerator, the engine efficiency increases by 10% under typical conditions; moreover, the computational setup was employed to determine the optimal regenerator packing porosity for the analyzed engine.
The authors of [79] developed a strategy to reduce the error in predicting the power output of Stirling engines by transient CFD simulations (3D turbulent). The approach consisted of estimating the engine’s pressure by a first-order model; then, the temperature on the displacer faces was computed by a steady-state simulation. Both data were employed as initial boundary conditions for the unsteady CFD computation. A key element was the consideration of radiation, using the DO method, which resulted in an enhanced engine power prediction versus the experimental values. The error was reduced from around 14% to 2.56% when the simulation included radiation. The study reported in [101] included radiation in the evaluation of the performance of two regenerator microstructures, as has been discussed previously. However, no results were presented in the absence of a radiation model.
3.4. CFD Simulations of Stirling Cryocooler
In a series of papers [102,103,104], Zhao and co-workers performed simulations of different elements of a Stirling cryocooler. In particular, they studied numerically and experimentally the flow and heat transfer characteristics of a miniature coaxial Stirling-type pulse tube cryocooler (PTC). The focus of [102] was put on the two-dimensional CFD simulation of the device operating at 128 Hz. The elements considered in the numerical domain were the warm and cold heat exchangers, aftercooler, and regenerator, this last component being modeled as a porous medium. Although the case was simulated as transient, no details were given about the tube motion and dynamic grid handling. Several cases were simulated assuming thermal equilibrium and non-equilibrium between the fluid and solid matrix for different temperatures and operating conditions. Discussions on the pressure loss in the solid matrix and interfacial heat transfer using both models were performed, concluding that the non-equilibrium model must be employed for more accurate simulations. In [103], a comparison with experimental measurements in the same PTC was performed at temperatures between 30 and 35 K. The numerical results were in qualitative agreement with measurements of the cold tip temperature and the cooling capacity; however, there were quantitative discrepancies that the authors attribute to the “assumed ideal heat transfer condition between heat exchangers and the environment in the model”. Later, [104] extends the frequency operating range of the PTC studied in [102] to 90–170 Hz, using the same numerical setup and including comparisons with experiments. The authors conclude that “there exists an optimum frequency for given dimensions”; if the frequency is too low, substantial mixing between the warm and cold fluids results, greatly reducing the cooling efficiency. Conversely, if the frequency is too high, it will cause a downward flow from the warm end towards the axis. This would create larger temperature gradients in radial directions, thus compromising the cooling performance. Finally, the numerical results reproduced the trend of the experimental data but showed some quantitative deviations attributed to the same factors as in [103].
Clearman et al. [105] studied the pressure drop in Stirling cryocooler regenerators, assuming a steady-state laminar two-dimensional flow through a porous medium. Using the CFD simulations to match the experimentally measured pressure drop, the authors determined the axial and radial Forchheimer inertial coefficients; they concluded that the regenerator behaves as an anisotropic medium. On the other hand, the research in [87] examines the resonant frequency of the moving magnet linear compressor within a Stirling-type cryocooler. A combination of Fluent and ANSYS Mechanical was employed for the numerical study, whereas a specific experiment was carried out to test such a frequency. CFD simulation was performed in a two-dimensional, laminar flow setting, but the authors do not provide more details about the rest of the numerical parameters. Additionally, no clear comparisons of the numerical and experimental results were reported.
Caughley et al. [63] analyzed a novel design of Stirling cryocooler, which was piston-free; the device used a metallic diaphragm pressure wave generator to allow the motion of the displacer. A domain consisting of a sector of the full device was simulated under 3D laminar flow conditions, allowing an understanding of the heat transfer and fluid dynamics in the cryocooler. The numerical domain included the compression space, membranes, regenerator, and cold expansion space. As a result, the CFD model corroborated the experimental findings about the location of the area of largest cooling in the center of the expansion space; moreover, the simulations gave clues as to improvement directions. Therefore, the authors concluded that CFD was an appropriate tool “to predict the heat flow and transfer inside the diaphragm Stirling cryocooler”. In [68], the numerical study of a small-scale α-type Stirling cryocooler was considered under 2D and laminar flow conditions. Pistons, expansion and compression spaces, and the regenerator composed the numerical domain. The numerical results were validated with previous experimental results [106]. Subsequently, the effect of a variation in several parameters on the device’s cooling capacities was addressed to enhance its performance. As a conclusion, the authors highlight the potential of CFD as a tool to improve the design of Stirling cryocoolers.
The very recent work of Sun et al. [107] focused on the CFD simulation of the 3D turbulent flow inside a coiled resonance tube of a Stirling cryocooler. The objective was to investigate the origin of the acoustic power losses found experimentally in the coiled tube. Simulations allowed the identification of two secondary flow vortices during the reverse flow that were responsible for the primary losses. A further parametric study demonstrated that reducing the tube diameter results in a higher acoustic loss, while the acoustic and flow fields were virtually independent of the spiral pitch.
Finally, further CFD studies mention Stirling engines but without performing a real simulation of them. For instance, the authors of [108] examined computationally the characteristics of Thermal-Lag engines (TLEs) as an alternative to traditional SEs. The study reported in [109] focused on the CFD numerical modeling of a heat receiver of a solar-concentrated SE. Li et al. [110,111] developed a model of a porous-sheet heat exchanger and regenerator to be coupled with an α-type SE; although some CFD vector plots were reported in [111], no details were provided about the simulation. The research of [112] was centered on designing a non-tubular heat exchanger to be used in a “Stirling solar engine micro-CHP unit” using CFD, which allowed the estimation of the supplied heat power to the working gas during a cycle.
4. Guidelines for Reporting CFD Simulation Studies of Stirling Engines
This paragraph suggests some guidelines for reporting a CFD simulation in Stirling engines in order to make the work reproducible by further studies. Of course, some of them adhere to general CFD best practices [113,114]. Such guidelines are thought to be useful for researchers dealing with future numerical simulation of SEs.
- The computational domain must be properly defined, specifying clearly its geometry and dimensions. The deformable subdomains must be clearly identified from those that keep a fixed shape and volume. At this point, the porous zones (i.e., regenerators) must also be distinguished;
- Meshing. The type of mesh employed (structured, unstructured, hybrid) and the algorithm employed for describing the grid deformation in dynamic meshes must be stated. Moreover, the characteristics of the near-wall mesh need to be given, especially in turbulent flows, where the number of layers employed to resolve the boundary layer behavior must be specified;
- Physical models. The governing laws in each subdomain must be stated, illustrating the variables to be solved. Also, the simplifications of such laws, if any, must be highlighted. For instance, the fluid governing equations expressing mass, momentum, and energy conservation, generally valid, can be simplified in cases of incompressible, Newtonian, constant-property fluids and solved in two- or three-dimensional configurations in a steady or transient state. In Stirling engines, the regenerator is typically considered as a porous zone and the corresponding ruling expressions should also be reported, as well as the relevant parameters (e.g., porosity, friction factors…) In the case of turbulent flows, the model of turbulence has to be clearly identified;
- Boundary conditions must be clearly highlighted in a figure and fully specified. If geometrical symmetry is employed to reduce the computational domain (and computational effort) it should be emphasized, and the corresponding symmetry or periodic boundary conditions must be properly identified;
- If certain internal or external surfaces or volumes are subject to some motion and/or deformation, either prescribed or as a result of the interaction with the working fluid, they must be pinpointed. Also, such a motion must be unambiguously documented;
- Initial conditions have to be provided for all variables in every subdomain;
- Physical properties of the employed materials (solid walls, working fluids, regenerator solid matrix) must be reported (e.g., density, viscosity, ideal or real gas considered);
- Numerical schemes. The type and order of the discretization schemes for both space and time have to be stated for each considered variable, possibly in a table. In the case of transient simulation, the time step should be clearly identified;
- Verification: Spatial and temporal discretization independence studies must be reported using at least three levels, to ensure that the results have become independent of the mesh density and time step employed;
- Sensitivity study of results versus employed turbulence model. Report of the maximum and average values of the variable and Courant number;
- Comprehensive report of results attending not only to integral parameters, such as power output or heat transfer efficiency, but also to local and instantaneous fields. Contour plots are suggested to illustrate the behavior of the main variables such as velocity, pressure, and temperature. In the case of turbulent flow corresponding variables such as turbulent kinetic energy, the turbulent viscosity ratio, and dissipation also have to be illustrated;
- Finally, a validation of the computational results must be provided versus reference experiments or a comparison with previous simulations, if experiments are not available. Ideally, such a validation should be carried out not only with integral parameters but also with some local or instantaneous variables. However, this requirement is acknowledged to be quite difficult in Stirling engines, given the nature of the experiments.
5. Conclusions and Perspectives
As has been identified, the validation of the numerical simulations of Stirling engines are usually carried out by comparison with experimental global variables such as output power and heat transfer or P-V cycles. A more detailed set of experimental flow and heat transfer measurements inside Stirling engines, aimed at creating a benchmark database (velocity, pressure, temperature, turbulent kinetic energy fields), would be extremely valuable to validate future CFD-based numerical computations.
Regarding the numerical approaches, using the Large Eddy Simulation (LES) technique for describing the turbulent flow developing in SEs may reveal additional details about the flow and heat transfer. However, its use has been very restricted in SEs, dealing only with fixed domains [88,99]. However, LES is a technique that has been successfully employed in the simulation of internal combustion engines since more than a decade ago [115]; therefore, it is surprising that it has not been applied more to SEs. The reason may be found in the comments of Zhao et al. [91] about their study: “The geometry of the current engine is very complicated with a lot of small flow channels in the regenerator and cooler, dead zones, and large separation regions. Therefore, although the DNS and LES simulations can present more accurate results in the CFD simulations, it is still quite difficult to conduct the DNS and LES simulations in the current complex engineering application.” In our opinion, LES provides unique opportunities for SE design optimization, and now it is an open way.
Moreover, future research should focus on considering the coupled three-dimensional simulation of the major components of the Stirling engine with a refined enough grids, avoiding the use of periodic and symmetry boundary conditions. The few studies that have approached this task (e.g., [35,78]) have employed very coarse grids due to computing facility restrictions (Figure 10).
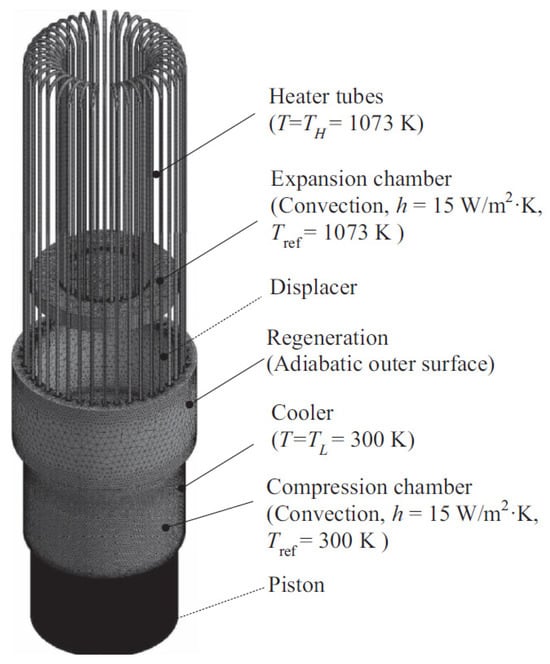
Figure 10.
Illustration of surface mesh and thermal boundary conditions in the β Stirling engine of [78]. Reproduced with permission.
Finally, it is recommended that future numerical studies on Stirling engines adhere to the provided guidelines for reporting both the setup and results. In particular, the fields of turbulent variables in the compression and expansion spaces at various points of the piston stroke should be clearly illustrated. Following these proposed guidelines will facilitate reproducing and accurately comparing different simulation studies on the same Stirling configuration.
Author Contributions
Conceptualization, S.L. and J.R.V.; methodology, S.L.; formal analysis, S.L., V.V. and J.R.V.; investigation, S.L. and V.V.; data curation, V.V.; writing—original draft preparation, S.L. and V.V.; writing—review and editing, S.L. and J.R.V.; supervision, S.L.; project administration, S.L.; funding acquisition, S.L. and J.R.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research and APC were funded by Universidad Autónoma de Occidente Cali (Colombia), project number 21INTER-379.
Data Availability Statement
Data sharing is not applicable.
Acknowledgments
The support of the Vicerrectoría de Investigación, Innovación y Emprendimiento of Universidad Autónoma de Occidente is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Moonka, G.; Surana, H.; Singh, H.R. Study on some aspects of Stirling engine: A path to solar Stirling engines. Mater. Today Proc. 2022, 63, 737–744. [Google Scholar] [CrossRef]
- Yang, C. Promising Stirling Engine: Advancement and Applications. Highlights Sci. Eng. Technol. 2024, 88, 827–834. [Google Scholar] [CrossRef]
- Kubule, A.; Kramens, J.; Bimbere, M.; Pedišius, N.; Blumberga, D. Trends for Stirling Engines in Households: A Systematic Literature Review. Energies 2024, 17, 383. [Google Scholar] [CrossRef]
- Bianchi, M.; De Pascale, A. Bottoming cycles for electric energy generation: Parametric investigation of available and innovative solutions for the exploitation of low and medium temperature heat sources. Appl. Energy 2011, 88, 1500–1509. [Google Scholar] [CrossRef]
- Perozziello, C.; Grosu, L.; Vaglieco, B.M. Free-Piston Stirling Engine Technologies and Models: A Review. Energies 2021, 14, 7009. [Google Scholar] [CrossRef]
- Der Minassians, A. Stirling Engines for Low-Temperature Solar-Thermal-Electric Power Generation. Ph.D. Thesis, University of Berkeley, Berkeley, CA, USA, 2007. [Google Scholar]
- Féniès, G.; Formosa, F.; Ramousse, J.; Badel, A. Double acting Stirling engine: Modelling, experiments and optimization. Appl. Energy 2015, 159, 350–361. [Google Scholar] [CrossRef]
- Thombare, D.G.; Verma, S.K. Technological development in the Stirling cycle engines. Renew. Sustain. Energy Rev. 2008, 12, 1–38. [Google Scholar] [CrossRef]
- Vineeth, C.S. Stirling Engines: A Beginners Guide, 2nd ed.; 2011; Available online: https://www.google.com.co/books/edition/Stirling_Engines/zTdzKxQaqNcC?hl=es-419&gbpv=0 (accessed on 26 May 2024).
- Wang, K.; Sanders, S.R.; Dubey, S.; Choo, F.H.; Duan, F. Stirling cycle engines for recovering low and moderate temperature heat: A review. Renew. Sustain. Energy Rev. 2016, 62, 89–108. [Google Scholar] [CrossRef]
- Zeiler, M.; Padinger, R.; Spitzer, J.; Podesser, E. Operating experiences with biomass driven Stirling engines; 3 kW and 30 kW. In Proceedings of the 13th International Stirling Conference, Tokyo, Japan, 23–26 September 2007. [Google Scholar]
- Bataineh, K. Mathematical formulation of alpha-type Stirling engine with Ross Yoke mechanism. Energy 2018, 164, 1178–1199. [Google Scholar] [CrossRef]
- Vinoth Kumar, D. Modification of an alpha stirling engine with an venturi based working fluid control system to promote its automotive applications. Int. J. Mech. Eng. Robot. Res. 2014, 3, 101–113. [Google Scholar]
- Ahmadi, M.H.; Ahmadi, M.A.; Pourfayaz, F. Thermal models for analysis of performance of Stirling engine: A review. Renew. Sustain. Energy Rev. 2017, 68, 168–184. [Google Scholar] [CrossRef]
- Timoumi, Y.; Tlili, I.; Ben Nasrallah, S. Design and performance optimization of GPU-3 Stirling engines. Energy 2008, 33, 1100–1114. [Google Scholar] [CrossRef]
- Singh, U.R.; Kumar, A. Review on solar Stirling engine: Development and performance. Therm. Sci. Eng. Prog. 2018, 8, 244–256. [Google Scholar] [CrossRef]
- Schneider, T.; Müller, D.; Karl, J. A review of thermochemical biomass conversion combined with Stirling engines for the small-scale cogeneration of heat and power. Renew. Sustain. Energy Rev. 2020, 134, 110288. [Google Scholar] [CrossRef]
- Getie, M.Z.; Lanzetta, F.; Bégot, S.; Admassu, B.T.; Hassen, A.A. Reversed regenerative Stirling cycle machine for refrigeration application: A review. Int. J. Refrig. 2020, 118, 173–187. [Google Scholar] [CrossRef]
- Zare, S.; Tavakolpour-saleh, A.R.; Aghahosseini, A.; Sangdani, M.H.; Mirshekari, R. Design and optimization of Stirling engines using soft computing methods: A review. Appl. Energy 2021, 283, 116258. [Google Scholar] [CrossRef]
- Zayed, M.E.; Zhao, J.; Elsheikh, A.H.; Li, W.; Sadek, S.; Aboelmaaref, M.M. A comprehensive review on Dish/Stirling concentrated solar power systems: Design, optical and geometrical analyses, thermal performance assessment, and applications. J. Clean. Prod. 2021, 283, 124664. [Google Scholar] [CrossRef]
- Malik, M.Z.; Shaikh, P.H.; Zhang, S.; Lashari, A.A.; Leghari, Z.H.; Baloch, M.H.; Memon, Z.A.; Caiming, C. A review on design parameters and specifications of parabolic solar dish Stirling systems and their applications. Energy Rep. 2022, 8, 4128–4154. [Google Scholar] [CrossRef]
- Boretti, A. α–Stirling hydrogen engines for concentrated solar power. Int. J. Hydrogen Energy 2021, 46, 16241–16247. [Google Scholar] [CrossRef]
- Zhu, S.; Yu, G.; Liang, K.; Dai, W.; Luo, E. A review of Stirling-engine-based combined heat and power technology. Appl. Energy 2021, 294, 116965. [Google Scholar] [CrossRef]
- Zhang, L.; Han, K.; Wang, Y.; Zhu, Y.; Zhong, S.; Zhong, G. A bibliometric analysis of Stirling engine and in-depth review of its application for energy supply systems. Energy Rev. 2023, 2, 100048. [Google Scholar] [CrossRef]
- Martini, R. Stirling Engine Design Manual, 2nd ed.; NASA Report CR-168088; NASA: Washington, DC, USA, 1983.
- Chen, N.C.J.; Griffin, F.P. A Review of Stirling Engine Mathematical Models; Oak Ridge National Laboratory ORNL/CON-135; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 1983. [Google Scholar]
- West, C.D. Principles and Applications of Stirling Engines, 1st ed.; Van Nostrand Reinhold: New York, NY, USA, 1986. [Google Scholar]
- Urieli, I.; Berchowitz, D.M. Stirling Cycle Engine Analysis, 1st ed.; Taylor and Francis: London, UK, 1984. [Google Scholar]
- Urieli, I. A Computer Simulation of Stirling Cycle Machines. Ph.D. Thesis, University of Johannesburg, Johannesburg, South Africa, 1977. [Google Scholar]
- Finkelstein, T. Generalized Thermodynamic Analysis of Stirling Engines; SAE Technical Paper 600222; SAE: Warrendale, PA, USA, 1960. [Google Scholar] [CrossRef]
- Dyson, R.W.; Wilson, S.D.; Tew, R.C. Review of Computational Stirling Analysis Methods; NASA/TM—2004-213300 Report; NASA: Washington, DC, USA, 2004.
- Alfarawi, S.; Al-Dadah, R.; Mahmoud, S. Influence of phase angle and dead volume on gamma-type Stirling engine power using CFD simulation. Energy Convers. Manag. 2016, 124, 130–140. [Google Scholar] [CrossRef]
- Chen, W.L.; Wong, K.L.; Chang, Y.F. A computational fluid dynamics study on the heat transfer characteristics of the working cycle of a low-temperature-differential γ-type Stirling engine. Int. J. Heat Mass Transf. 2014, 75, 145–155. [Google Scholar] [CrossRef]
- Kuban, L.; Stempka, J.; Tyliszczak, A. A 3D-CFD study of a γ-type Stirling engine. Energy 2019, 169, 142–159. [Google Scholar] [CrossRef]
- Mahkamov, K. Design Improvements to a Biomass Stirling Engine Using Mathematical Analysis and 3D CFD Modeling. J. Energy Resour. Technol. 2006, 128, 203–215. [Google Scholar] [CrossRef]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson: Essex, UK, 2007. [Google Scholar]
- López, O.D.; Quiñones, J.J.; Lain, S. RANS and Hybrid RANS-LES simulations of an H-type Darrieus vertical axis water turbine. Energies 2018, 11, 2348. [Google Scholar] [CrossRef]
- Lain, S.; García, M.; Quintero, B.; Orrego, S. CFD numerical simulations of Francis turbines. Rev. Fac. Ing. Univ. Antioq. 2010, 51, 24–33. [Google Scholar] [CrossRef]
- O’Brien, J.M.; Young, T.M.; Early, J.M.; Griffin, P.C. An assessment of commercial CFD turbulence models for near wake HAWT modelling. J. Wind. Eng. Ind. Aerodyn. 2018, 176, 32–53. [Google Scholar] [CrossRef]
- Sanaye, S.; Farvizi, A. Optimizing a vertical axis wind turbine with helical blades: Application of 3D CFD and Taguchi method. Energy Rep. 2024, 12, 2527–2547. [Google Scholar] [CrossRef]
- Lain, S.; Taborda, M.A.; López, O.D. Numerical study of the effect of winglets on the performance of a straight blade Darrieus water turbine. Energies 2018, 11, 297. [Google Scholar] [CrossRef]
- Nassini, P.C.; Pampaloni, D.; Meloni, R.; Andreini, A. Lean blow-out prediction in an industrial gas turbine combustor through a LES-based CFD analysis. Combust. Flame 2021, 229, 111391. [Google Scholar] [CrossRef]
- Baratta, M.; Chiriches, S.; Goel, P.; Misul, D. CFD modelling of natural gas combustion in IC engines under different EGR dilution and H2-doping conditions. Transp. Eng. 2020, 2, 100018. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Santhosh, R.; Mashruk, S.; Yadav, R.; Valera-Medina, A. Prediction of NOx emissions and pathways in premixed ammonia-hydrogen-air combustion using CFD-CRN methodology. J. Energy Inst. 2023, 111, 101406. [Google Scholar] [CrossRef]
- Li, Z.; Tang, D.; Du, J.; Li, T. Study of the radiation flux and temperature distributions of the concentrator-receiver system in a solar dish/Stirling power facility. Appl. Therm. Eng. 2011, 31, 1780–1789. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Ghodrati, P.; Mahian, O.; Kang, Y.T. CFD study of rib-enhanced printed circuit heat exchangers for precoolers in solar power plants’ supercritical CO2 cycle. Energy 2024, 292, 130418. [Google Scholar] [CrossRef]
- Tarodiya, R.; Khullar, S.; Levy, A. Particulate flow and erosion modeling of a Pelton turbine injector using CFD-DEM simulations. Powder Technol. 2022, 399, 117168. [Google Scholar] [CrossRef]
- Ahmed, S.; Hassan, A.; Zubair, R.; Rashid, S.; Ullah, A. Design modification in an industrial multistage orifice to avoid cavitation using CFD simulation. J. Taiwan Inst. Chem. Eng. 2023, 148, 104833. [Google Scholar] [CrossRef]
- López, O.D.; Mejía, O.E.; Escorcia, K.M.; Suárez, F.; Lain, S. Comparison of sliding and overset mesh techniques in the simulation of a vertical axis turbine for hydrokinetic applications. Processes 2021, 9, 1933. [Google Scholar] [CrossRef]
- Krzemianowski, Z.; Kaniecki, M. Low-head high specific speed Kaplan turbine for small hydropower—Design, CFD loss analysis and basic, cavitation and runaway investigations: A case study. Energy Convers. Manag. 2023, 276, 116558. [Google Scholar] [CrossRef]
- Tushar Choudahry, S. Computational analysis of IR-SOFC: Thermodynamic, electrochemical process and flow configuration dependency. Int. J. Hydrogen Energy 2016, 41, 1259–1271. [Google Scholar] [CrossRef]
- Gadhewal, R.; Ananthula, V.V.; Patnaikuni, V.S. CFD simulation of hot spot in PEM fuel cell with diverging and converging flow channels. Mater. Today Proc. 2023, 72, 410–416. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, X.; Lv, Q.; Cao, F.; Wang, X. Study of transient indoor temperature for a HVAC room using a modified CFD method. Energy Procedia 2019, 160, 420–427. [Google Scholar] [CrossRef]
- Lain, S.; Sommerfeld, M.; Quintero, B. Numerical simulation of secondary flow in pneumatic conveying of solid particles in a horizontal circular pipe. Braz. J. Chem. Eng. 2009, 26, 583–594. [Google Scholar] [CrossRef]
- Zhang, J.; Poon, K.H.; Kwok, H.H.L.; Hou, F.; Cheng, J.C.P. Predictive control of HVAC by multiple output GRU—CFD integration approach to manage multiple IAQ for commercial heritage building preservation. Build. Environ. 2023, 245, 110802. [Google Scholar] [CrossRef]
- Lain, S.; Sommerfeld, M. A study of the pneumatic conveying of non-spherical particles in a turbulent horizontal channel flow. Braz. J. Chem. Eng. 2007, 24, 535–546. [Google Scholar] [CrossRef]
- Islam, M.T.; Chen, Y.; Seong, D.; Verhougstraete, M.; Son, Y.J. Effects of recirculation and air change per hour on COVID-19 transmission in indoor settings: A CFD study with varying HVAC parameters. Heliyon 2024, 10, e35092. [Google Scholar] [CrossRef]
- Salazar, J.L.; Chen, W.L. A computational fluid dynamics study on the heat transfer characteristics of the working cycle of a β -type Stirling engine. Energy Convers. Manag. 2014, 88, 177–188. [Google Scholar] [CrossRef]
- Chen, W.L. A study on the effects of geometric parameters in a low-temperature differential gamma-type Stirling engine using CFD. Int. J. Heat Mass Transf. 2017, 107, 1002–1013. [Google Scholar] [CrossRef]
- Chen, W.L.; Yang, Y.C.; Salazar, J.L. CFD parametric study on the performance of a low-temperature-differential γ -type Stirling engine. Energy Convers. Manag. 2015, 106, 635–643. [Google Scholar] [CrossRef]
- Kato, Y.; Saitoh, S.; Ishimatsu, K.; Iwamoto, M. Effect of geometry and speed on the temperatures estimated by CFD for an isothermal model of a gamma configuration low temperature differential Stirling engine with Flat-shaped heat exchangers. Appl. Therm. Eng. 2017, 115, 111–122. [Google Scholar] [CrossRef]
- Mohammadi, M.A.; Jafarian, A. CFD simulation to investigate hydrodynamics of oscillating flow in a beta-type Stirling engine. Energy 2018, 153, 287–300. [Google Scholar] [CrossRef]
- Caughley, A.; Sellier, M.; Gschwendtner, M.; Tucker, A. CFD analysis of a diaphragm free-piston Stirling cryocooler. Cryogenics 2016, 79, 7–16. [Google Scholar] [CrossRef]
- Regalado-Rodríguez, N.; Militello, C. Comparative study of the effects of increasing heat transfer area within compression and expansion chambers in combination with modified pistons in Stirling engines. A simulation approach based on CFD and a numerical thermodynamic model. Energy Convers. Manag. 2022, 263, 115930. [Google Scholar] [CrossRef]
- Dai, Z.; Wang, C.; Zhang, D.; Tian, W.; Qiu, S.; Su, G.H. Design and heat transfer optimization of a 1 kW free-piston Stirling engine for space reactor power system. Nucl. Eng. Technol. 2021, 53, 2184–2194. [Google Scholar] [CrossRef]
- Papurello, D.; Bertino, D.; Santarelli, M. CFD Performance Analysis of a Dish-Stirling System for Microgeneration. Processes 2021, 9, 1142. [Google Scholar] [CrossRef]
- Almajri, A.K.; Mahmoud, S.; Al-Dadah, R. Modelling and parametric study of an efficient Alpha type Stirling engine performance based on 3D CFD analysis. Energy Convers. Manag. 2017, 145, 93–106. [Google Scholar] [CrossRef]
- Ahmed, H.; Almajri, A.K.; Mahmoud, S.; Al-Dadah, R.; Ahmad, A. CFD modelling and parametric study of small-scale Alpha type Stirling Cryocooler. Energy Procedia 2017, 142, 1668–1673. [Google Scholar] [CrossRef]
- Abuelyamen, A.; Ben-Mansour, R. Energy efficiency comparison of Stirling engine types (α, β, and γ) using detailed CFD modeling. Int. J. Therm. Sci. 2018, 132, 411–423. [Google Scholar] [CrossRef]
- Bulińsky, Z.; Szczygieł, I.; Krysinski, T.; Stanek, W.; Czarnowska, L.; Gładysz, P.; Kabaj, A. Finite time thermodynamic analysis of small alpha-type Stirling engine in non-ideal polytropic conditions for recovery of LNG cryogenic exergy. Energy 2017, 141, 2559–2571. [Google Scholar] [CrossRef]
- Bulińsky, Z.; Szczygieł, I.; Kabaj, A.; Krysinski, T.; Gładysz, P.; Czarnowska, L.; Stanek, W. Performance analysis of the small-scale α-type stirling engine using computational fluid dynamics tools. J. Energy Resour. Technol. 2018, 140, 032001. [Google Scholar] [CrossRef]
- Bulińsky, Z.; Kabaj, A.; Krysiński, T.; Szczygieł, I.; Stanek, W.; Rutczyk, B.; Czarnowska, L.; Gładysz, P. A Computational Fluid Dynamics analysis of the influence of the regenerator on the performance of the cold Stirling engine at different working conditions. Energy Convers. Manag. 2019, 195, 125–138. [Google Scholar] [CrossRef]
- Xiao, G.; Sultan, U.; Ni, M.; Peng, H.; Zhou, X.; Wang, S.; Luo, Z. Design optimization with computational fluid dynamic analysis of β-type Stirling engine. Appl. Therm. Eng. 2018, 113, 87–102. [Google Scholar] [CrossRef]
- Kumaravelu, T.; Saadon, S.; Abu Talib, A.R. Heat transfer enhancement of a Stirling engine by using fins attachment in an energy recovery system. Energy 2022, 239, 121881. [Google Scholar] [CrossRef]
- Aksoy, F.; Cinar, C. Thermodynamic analysis of a beta-type Stirling engine with rhombic drive mechanism. Energy Convers. Manag. 2013, 75, 319–324. [Google Scholar] [CrossRef]
- El-Ghafour, S.A.; El-Ghandour, M.; Mikhael, N.N. Three-dimensional computational fluid dynamics simulation of Stirling engine. Energy Convers. Manag. 2019, 180, 533–549. [Google Scholar] [CrossRef]
- Chi, C.; Mou, J.; Lin, M.; Hong, G. CFD simulation and investigation on the operating mechanism of a beta-type free piston Stirling engine. Appl. Therm. Eng. 2020, 166, 114751. [Google Scholar] [CrossRef]
- Cheng, C.H.; Chen, Y.F. Numerical simulation of thermal and flow fields inside a 1-kW beta-type Stirling engine. Appl. Therm. Eng. 2017, 121, 554–561. [Google Scholar] [CrossRef]
- Castro Caetano, B.; Figueiredo Lara, I.; Ungaretti Borges, M.; Sandoval, O.R.; Molina Valle, R. A novel methodology on beta-type Stirling engine simulation using CFD. Energy Convers. Manag. 2019, 184, 510–520. [Google Scholar] [CrossRef]
- Rogdakis, E.; Bitsikas, P.; Dogkas, G.; Antonakos, G. Three-dimensional CFD study of a β-type Stirling Engine. Therm. Sci. Eng. Prog. 2019, 11, 302–316. [Google Scholar] [CrossRef]
- Bitsikas, P.; Rogdakis, E.; Dogkas, G. CFD study of heat transfer in Stirling engine regenerator. Therm. Sci. Eng. Prog. 2020, 17, 100492. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Abuelyamen, A.; Mokheimer, E.M.A. CFD analysis of radiation impact on Stirling engine performance. Energy Convers. Manag. 2017, 152, 354–356. [Google Scholar] [CrossRef]
- Arslan, T.A.; Solmaz, H.; Ipci, D.; Aksoy, F. Investigation of the effect of compression ratio on performance of a beta type Stirling engine with rhombic mechanism by CFD analysis. Environ. Prog. Sustain. Energy 2023, 42, e14076. [Google Scholar] [CrossRef]
- Abuelyamen, A.; Ben-Mansour, R.; Abualhamayel, H.; Mokheimer, E.M.A. Parametric study on beta-type Stirling engine. Energy Convers. Manag. 2017, 145, 53–63. [Google Scholar] [CrossRef]
- Thieme, L. High-Power Baseline and Motoring Test Results for the GPU-3 Stirling Engine; DOE/NASA/51040-31, NASA TM-82646; NASA: Washington, DC, USA, 1981.
- Yu, G.Y.; Luo, E.C.; Dai, W.; Hu, J.Y. Study of nonlinear processes of a large experimental thermoacoustic-Stirling heat engine by using computational fluid dynamics. J. Appl. Phys. 2007, 102, 074901. [Google Scholar] [CrossRef]
- Xia, M.; Chen, X. Analysis of resonant frequency of moving magnet linear compressor of stirling cryocooler. Int. J. Refrig. 2010, 33, 739–744. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Y.; Tang, L.; Wang, K.; Yu, Z. Large Eddy Simulation of thermally induced oscillatory flow in a thermoacustic engine. Appl. Energy 2020, 276, 115458. [Google Scholar] [CrossRef]
- Mahkamov, K. An Axisymmetric Computational Fluid Dynamics Approach to the Analysis of the Working Process of a Solar Stirling Engine. J. Sol. Energy Eng. 2006, 128, 45–53. [Google Scholar] [CrossRef]
- Qiu, S.; Gao, Y.; Rinker, G.; Yanaga, K. Development of an advanced free-piston Stirling engine for micro combined heating and power application. Appl. Energy 2019, 235, 987–1000. [Google Scholar] [CrossRef]
- Zhao, W.; Li, R.; Li, H.; Zhang, Y.; Qiu, S. Numerical analysis of fluid dynamics and thermodynamics in Stirling engine. Appl. Therm. Eng. 2021, 189, 116727. [Google Scholar] [CrossRef]
- Umair, M.; Shah, A.N.; Kamran, M.S.; Farhan, M.; Anwar, Z. The CFD methodology for simulating pumping loss from displacer and piston seals of free piston Stirling engine. Therm. Sci. 2022, 26, 13–23. [Google Scholar] [CrossRef]
- Kim, H.S.; Gwak, I.C.; Lee, S.H. Numerical analysis of heat transfer area effect on cooling performance in regenerator of free-piston Stirling cooler. Case Stud. Therm. Eng. 2022, 32, 101875. [Google Scholar] [CrossRef]
- Costa, S.C.; Barrutia, H.; Esnaola, J.A.; Tutar, M. Numerical study of the pressure drop phenomena in wound woven wire matrix of a Stirling regenerator. Energy Convers. Manag. 2013, 67, 57–65. [Google Scholar] [CrossRef]
- Costa, S.C.; Barrutia, H.; Esnaola, J.A.; Tutar, M. Numerical study of the heat transfer in wound woven wire matrix of a Stirling regenerator. Energy Convers. Manag. 2014, 79, 255–264. [Google Scholar] [CrossRef]
- Costa, S.C.; Tutar, M.; Barreno, I.; Esnaola, J.A.; Barrutia, H.; García, D.; Gonzalez, M.A.; Prieto, J.I. Experimental and numerical flow investigation of Stirling engine regenerator. Energy 2014, 72, 800–812. [Google Scholar] [CrossRef]
- Costa, S.C.; Barreno, I.; Tutar, M.; Esnaola, J.A.; Barrutia, H. The thermal non-equilibrium porous media modelling for CFD study of woven wire matrix of a Stirling regenerator. Energy Convers. Manag. 2015, 89, 473–483. [Google Scholar] [CrossRef]
- Barreno, I.; Costa, S.C.; Cordon, M.; Tutar, M.; Urrutibeascoa, I.; Gomez, X.; Castillo, G. Numerical correlation for the pressure drops in Stirling engine heat exchangers. Int. J. Therm. Sci. 2015, 97, 68–81. [Google Scholar] [CrossRef]
- York, B.T.; MacDonald, B.D. Influence of misalignment and spacing on the pressure drop through wire mesh Stirling engine regenerators. Energy Convers. Manag. 2021, 245, 114588. [Google Scholar] [CrossRef]
- Mancisidor, A.M.; Gil, E.; Garciandia, F.; San Sebastian, M.; Lizaso, O.; Escubi, M. Stirling engine regenerator based on lattice structures manufactured by selective laser melting. Procedia CIRP 2018, 74, 72–75. [Google Scholar] [CrossRef]
- Beni, H.M.; Mortazavi, H. Mathematical modeling of the solar regenerative heat exchanger under turbulent oscillating flow: Applications of renewable and sustainable energy and artificial heart. Results Eng. 2022, 13, 100321. [Google Scholar] [CrossRef]
- Zhao, Y.; Dang, H. CFD simulation of a miniature coaxial Stirling-type pulse tube cryocooler operating at 128 Hz. Cryogenics 2016, 73, 53–59. [Google Scholar] [CrossRef]
- Dang, H.; Zhao, Y. CFD modeling and experimental verification of a single-stage coaxial Stirling-type pulse tube cryocooler without either double-inlet or multi-bypass operating at 30–35 K using mixed stainless steel mesh regenerator matrices. Cryogenics 2016, 78, 40–50. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, G.; Tan, J.; Mao, X.; Li, J.; Zha, R.; Li, N.; Dang, H. CFD modeling and experimental verification of oscillating flow and heat transfer processes in the micro coaxial Stirling-type pulse tube cryocooler operating at 90–170 Hz. Cryogenics 2018, 90, 30–40. [Google Scholar] [CrossRef]
- Clearman, W.M.; Cha, J.S.; Ghiaasiaan, S.M.; Kirkconnell, C.S. Anisotropic steady-flow hydrodynamic parameters of microporous media applied to pulse tube and Stirling cryocooler regenerators. Cryogenics 2008, 48, 112–121. [Google Scholar] [CrossRef]
- Karabulut, H.; Yücesu, H.S.; Koca, A. Manufacturing and testing of a V-type Stirling engine. Turk. J. Eng. Environ. Sci. 2000, 24, 71–80. [Google Scholar]
- Sun, H.; Yu, G.; Zhao, D.; Dai, W.; Luo, E. Numerical and experimental investigations on coiled resonance tube of a duplex Stirling cryocooler. Appl. Therm. Eng. 2024, 238, 121930. [Google Scholar] [CrossRef]
- Phung, D.T.; Cheng, C.H. Investigating dynamic characteristics and thermal-lag phenomenon in a thermal-lag engine using a CFD-mechanism dynamics model. Appl. Therm. Eng. 2024, 236, 121926. [Google Scholar] [CrossRef]
- Papis-Fraczek, K.; Zoładek, M.; Filipowicz, M. The possibilities of upgrading an existing concentrating solar thermal system—Case study. Energy Rep. 2021, 7, 28–32. [Google Scholar] [CrossRef]
- Li, Z.; Haramura, Y.; Tang, D.; Guo, C. Analysis on the heat transfer characteristics of a micro-channel type porous-sheets Stirling regenerator. Int. J. Therm. Sci. 2015, 94, 37–49. [Google Scholar] [CrossRef]
- Li, Z.; Haramura, Y.; Kato, Y.; Tang, D. Analysis of a high-performance model Stirling engine with compact porous-sheets heat exchangers. Energy 2014, 64, 31–43. [Google Scholar] [CrossRef]
- García, D.; Suárez, M.J.; Blanco, E.; Prieto, J.I. Experimental correlations and CFD model of a non-tubular heater for a Stirling solar engine micro-cogeneration unit. Appl. Therm. Eng. 2019, 153, 715–725. [Google Scholar] [CrossRef]
- Andersson, B.; Andersson, R.; Håkanson, L.; Mortensen, M.; Sudiyo, R.; van Wachem, B. Best practice guidelines. In Computational Fluid Dynamics for Engineers, 1st ed.; Cambridge University Press: Cambridge, UK, 2012; pp. 174–180. [Google Scholar] [CrossRef]
- Roache, P.J. Verification and Validation in Computational Science and Engineering, 1st ed.; Hermosa Publishers: Albuquerque, NM, USA, 1998. [Google Scholar]
- Impagnatiello, M.; Bolla, M.; Keskinen, K.; Giannakopoulos, G.; Frouzakis, C.E.; Wright, Y.M.; Bolouchos, K. Systematic assessment of data-driven approaches for wall heat transfer modelling for LES in IC engines using DNS data. Int. J. Heat Mass Transf. 2022, 183, 122109. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).