Deep Learning-Based Fatigue Strength Prediction for Ferrous Alloy
Abstract
1. Introduction
2. Models and Methodology
2.1. Data Processing
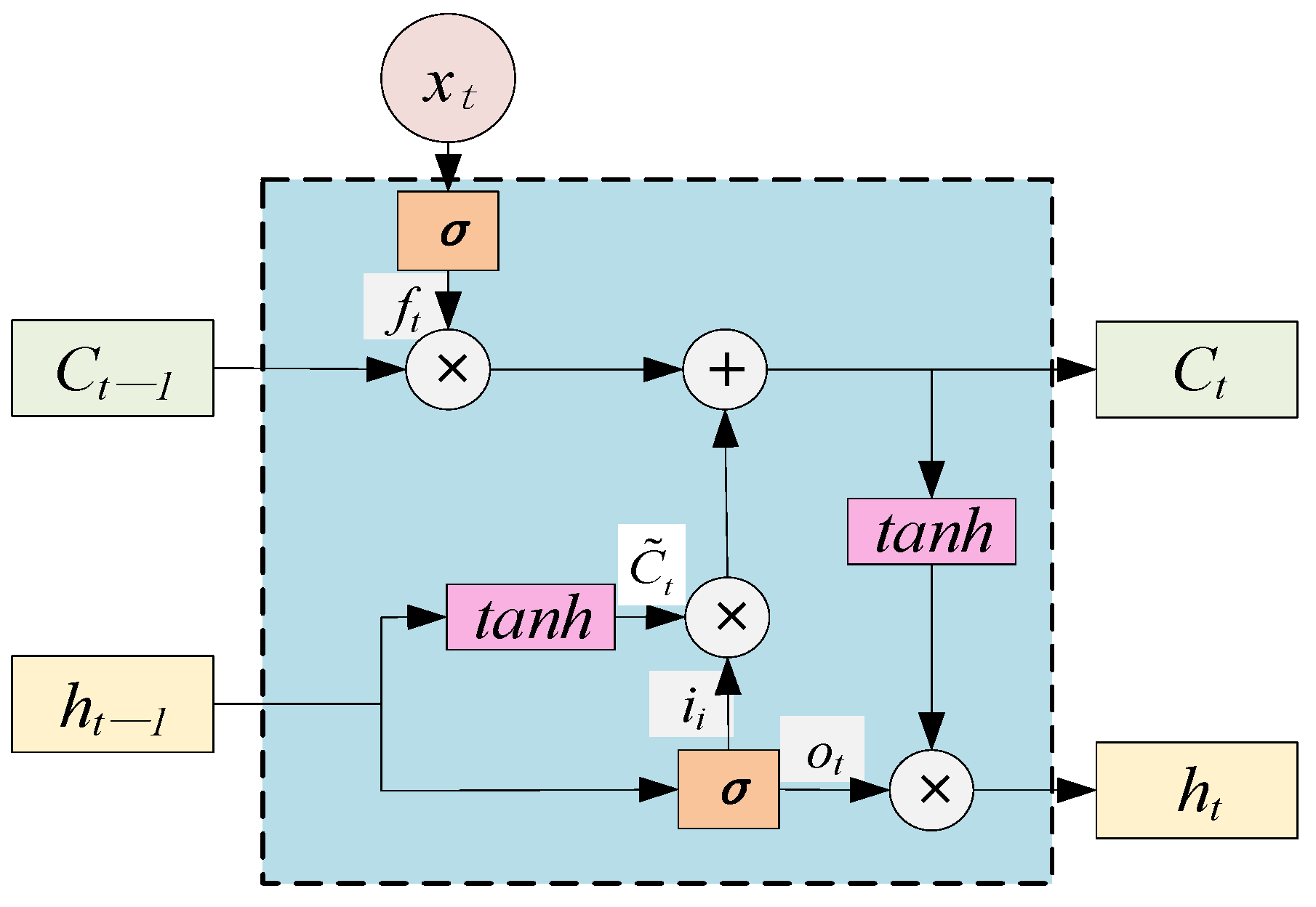
2.2. Deep Learning Regression Predictive Models
2.3. Model Evaluation
2.4. Fatigue Strength Prediction Method
- Data Collection: Gathering data on key features that influence the fatigue strength of ferrous alloys to construct a comprehensive dataset.
- Data Preprocessing: Addressing missing and anomalous data within the dataset and conducting an inter-feature importance analysis to ensure data quality.
- Dataset Splitting: Randomly dividing the complete dataset into a training set and a testing set, typically following an 80:20 ratio.
- Model Training and Prediction: Applying deep learning regression models to train on the dataset and predict fatigue strength values.
- Model Evaluation and Comparative Analysis: Evaluating the performance of various prediction models, including CNN, RNN, GRU, LSTM, and CNN-LSTM, and conducting a comparative analysis to assess their predictive accuracy.
3. Results Analysis
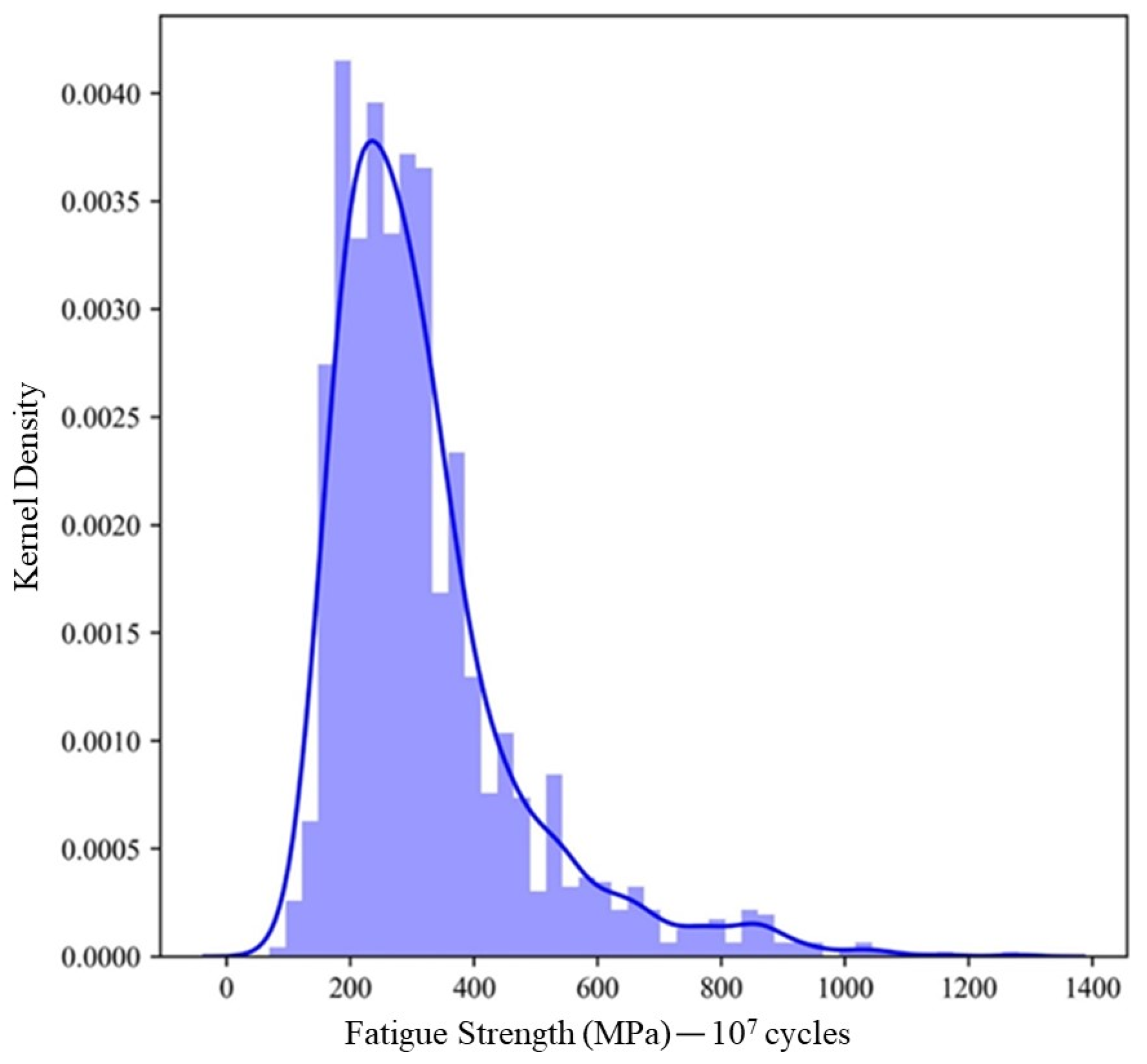
3.1. Fatigue Strength Distribution
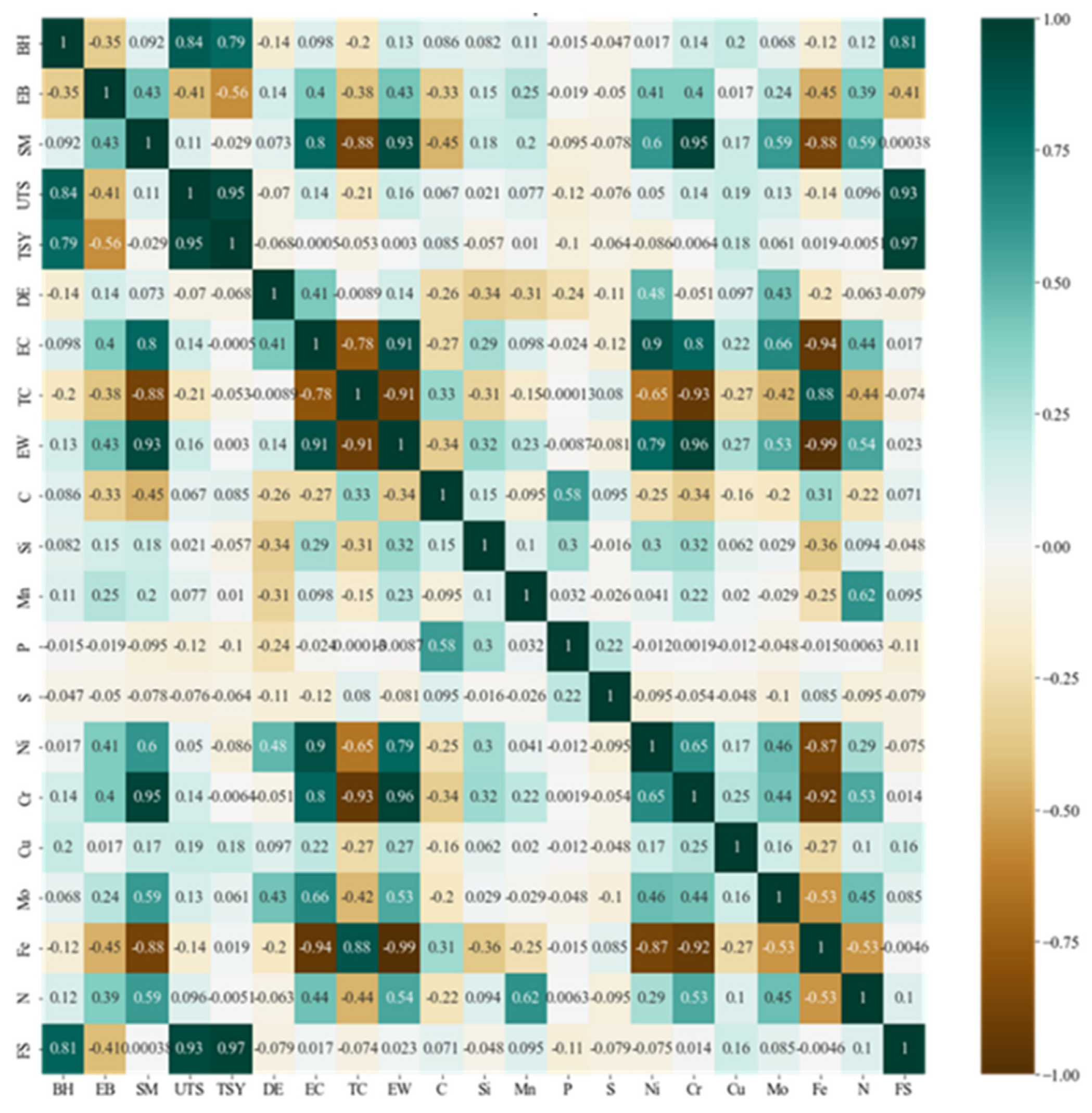
3.2. Feature Analysis
3.3. Network Hyperparameter Settings
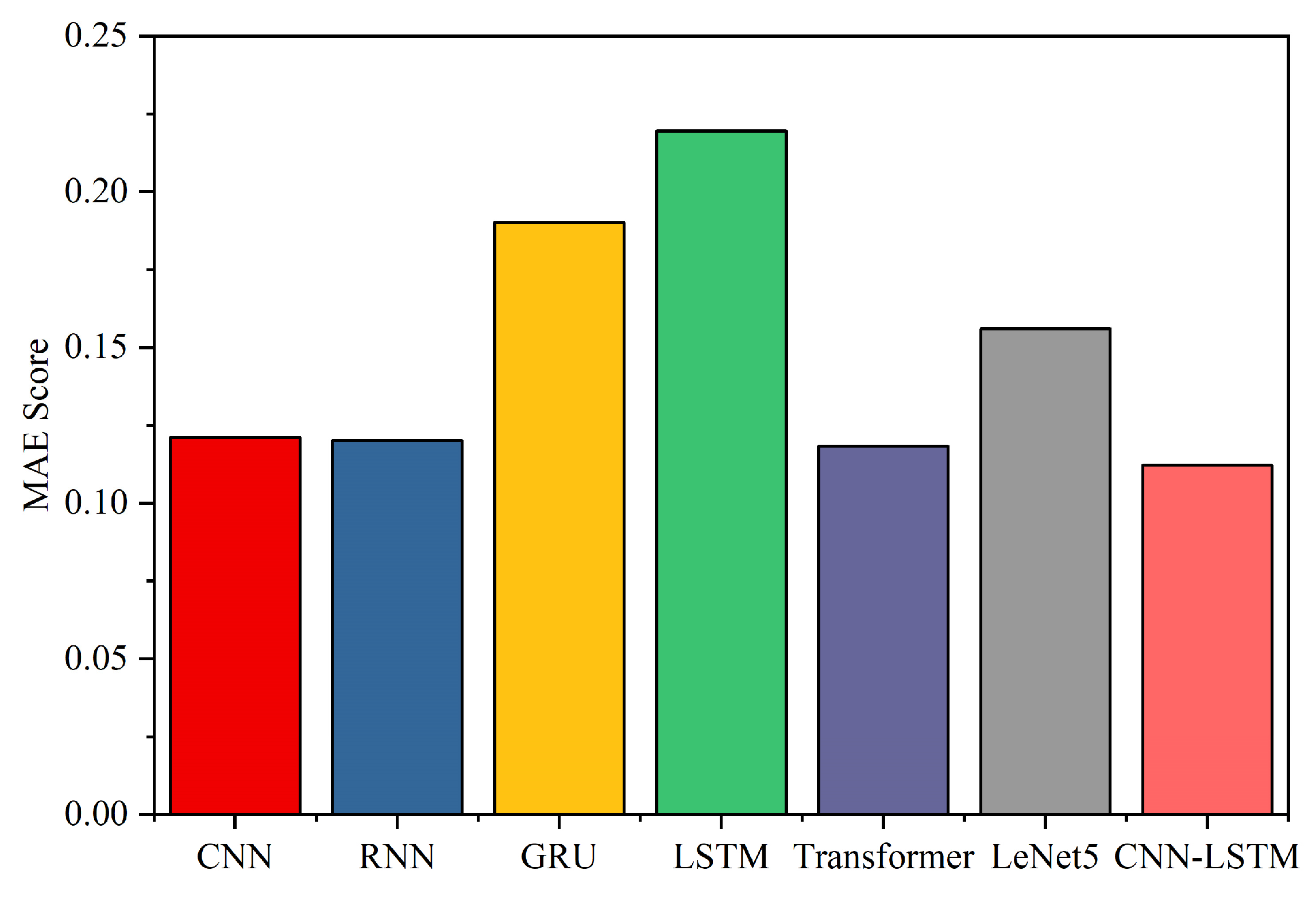
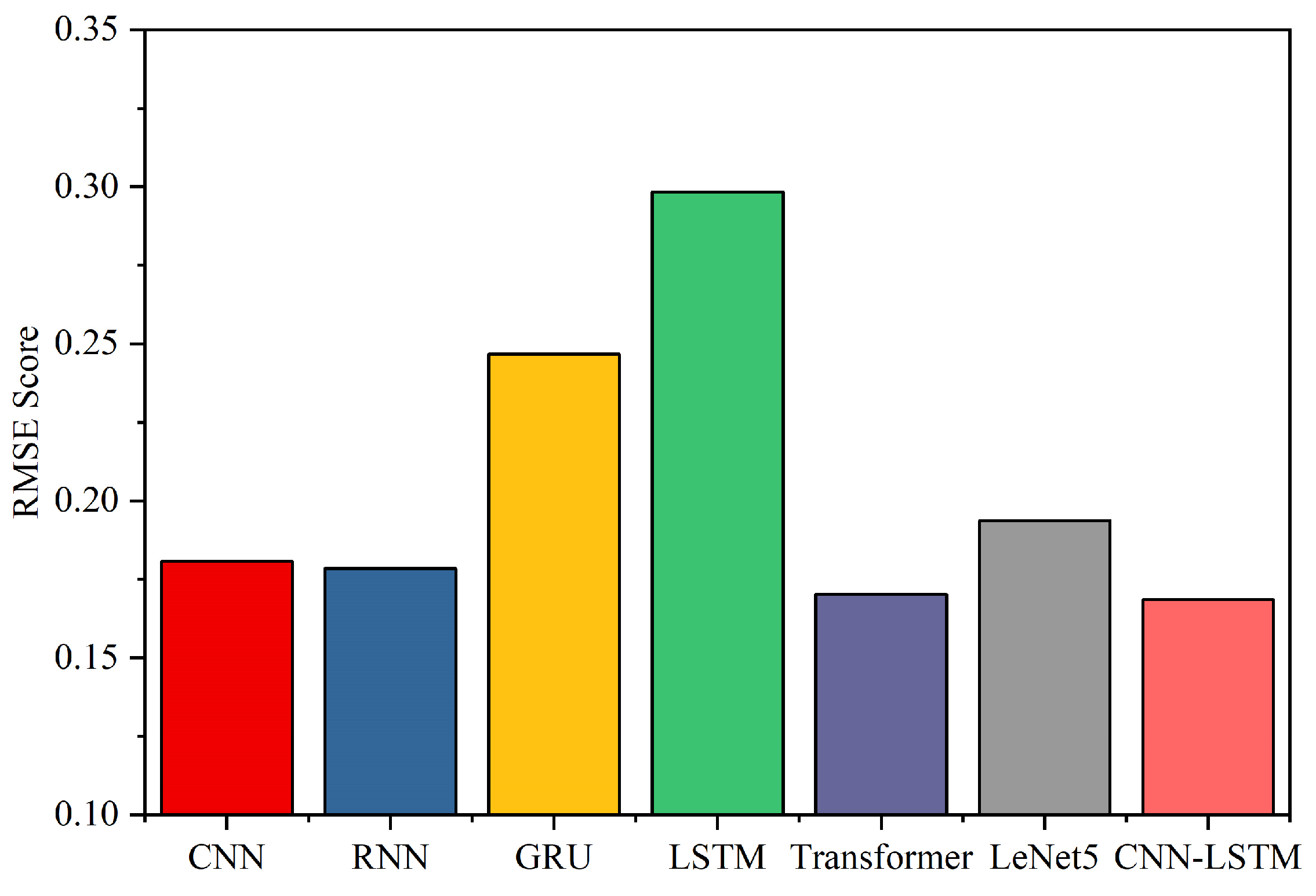
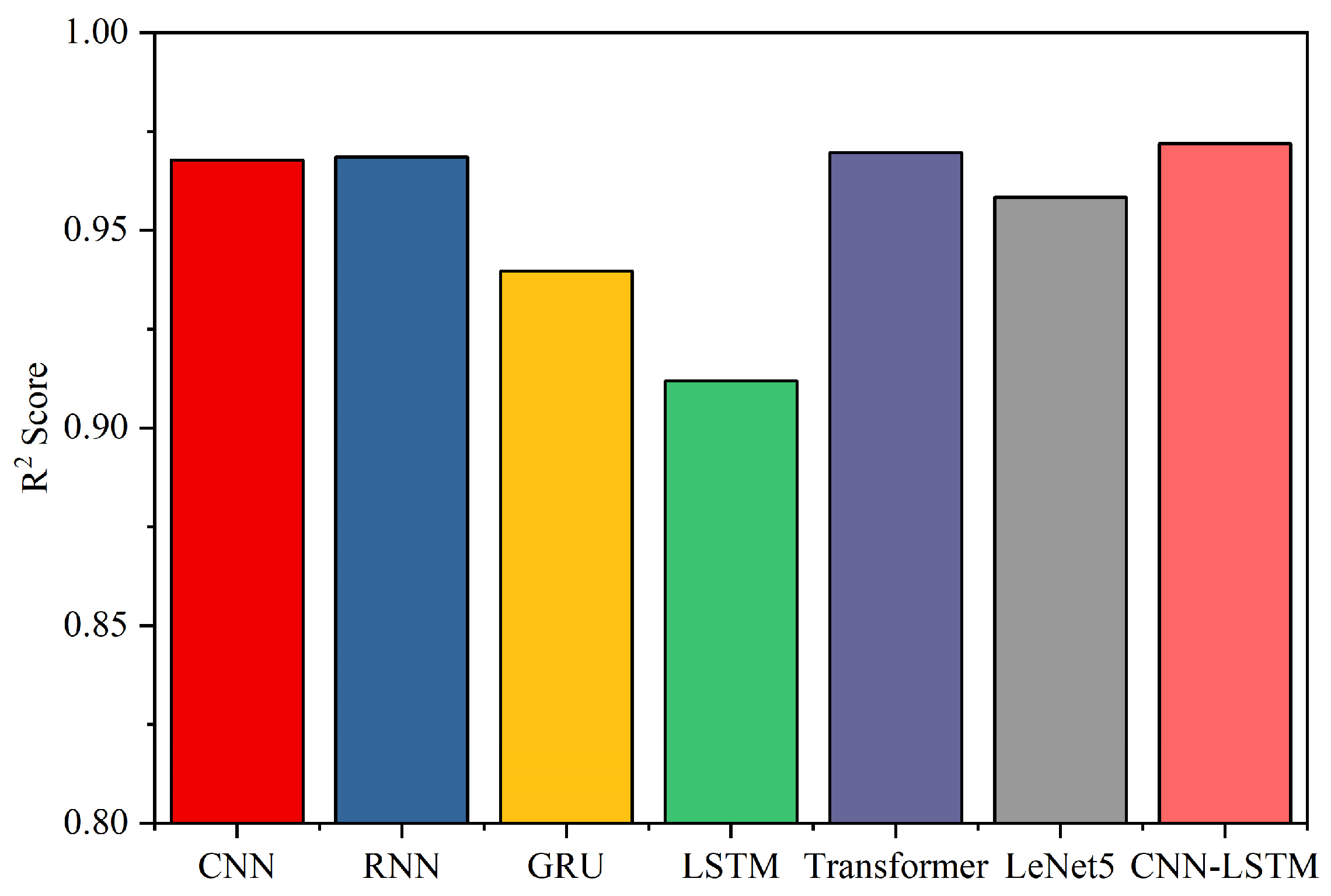
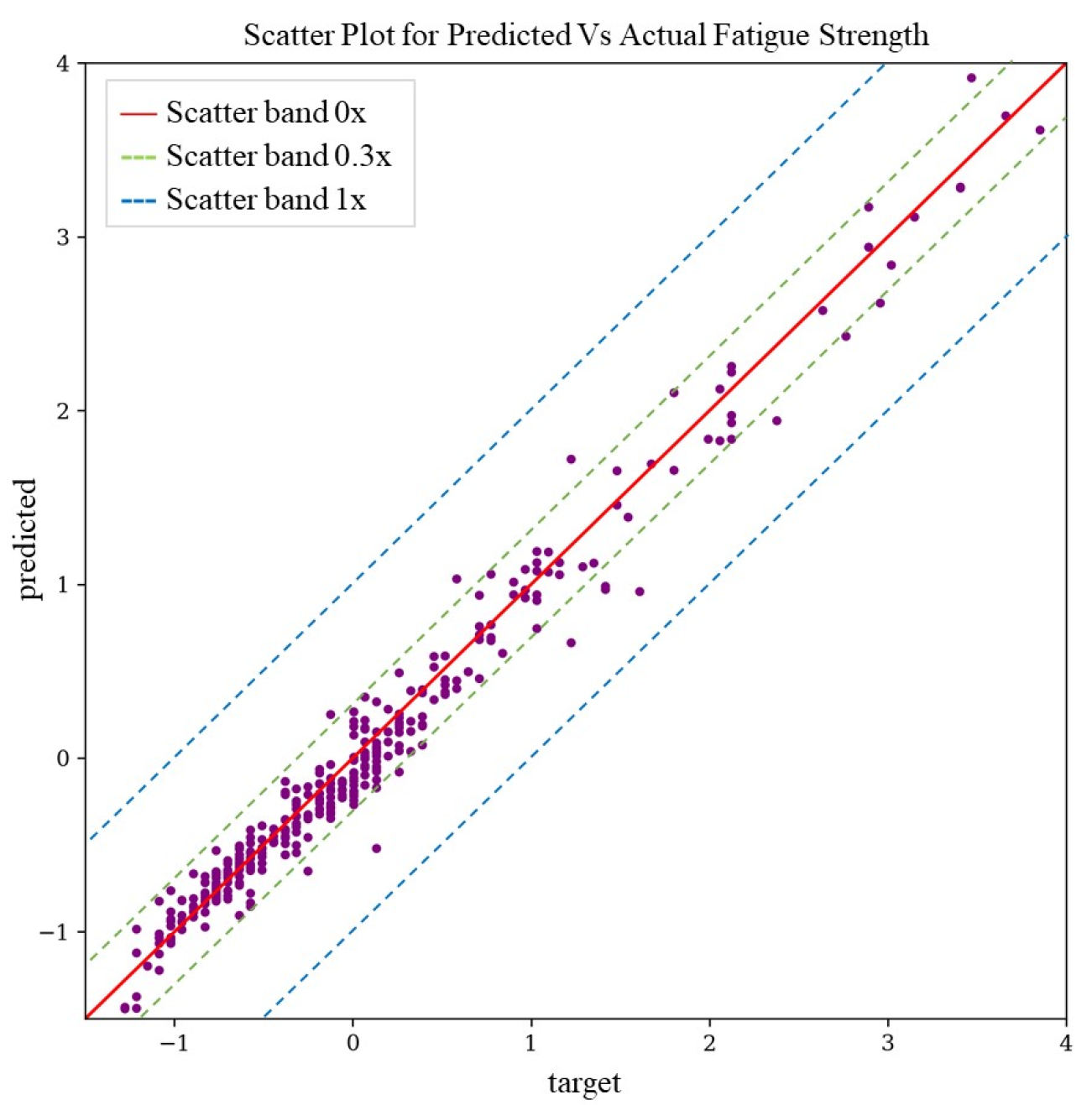
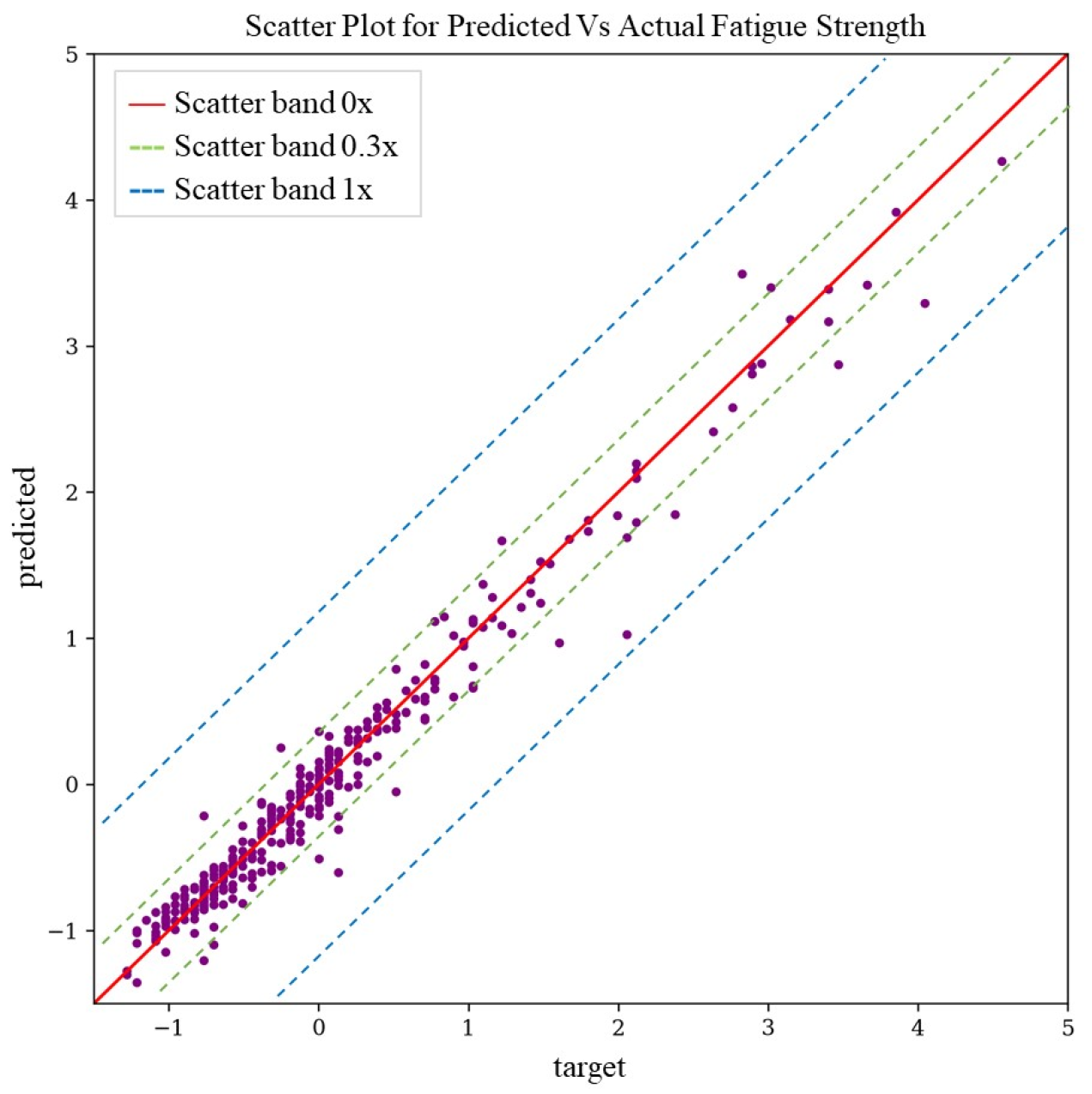
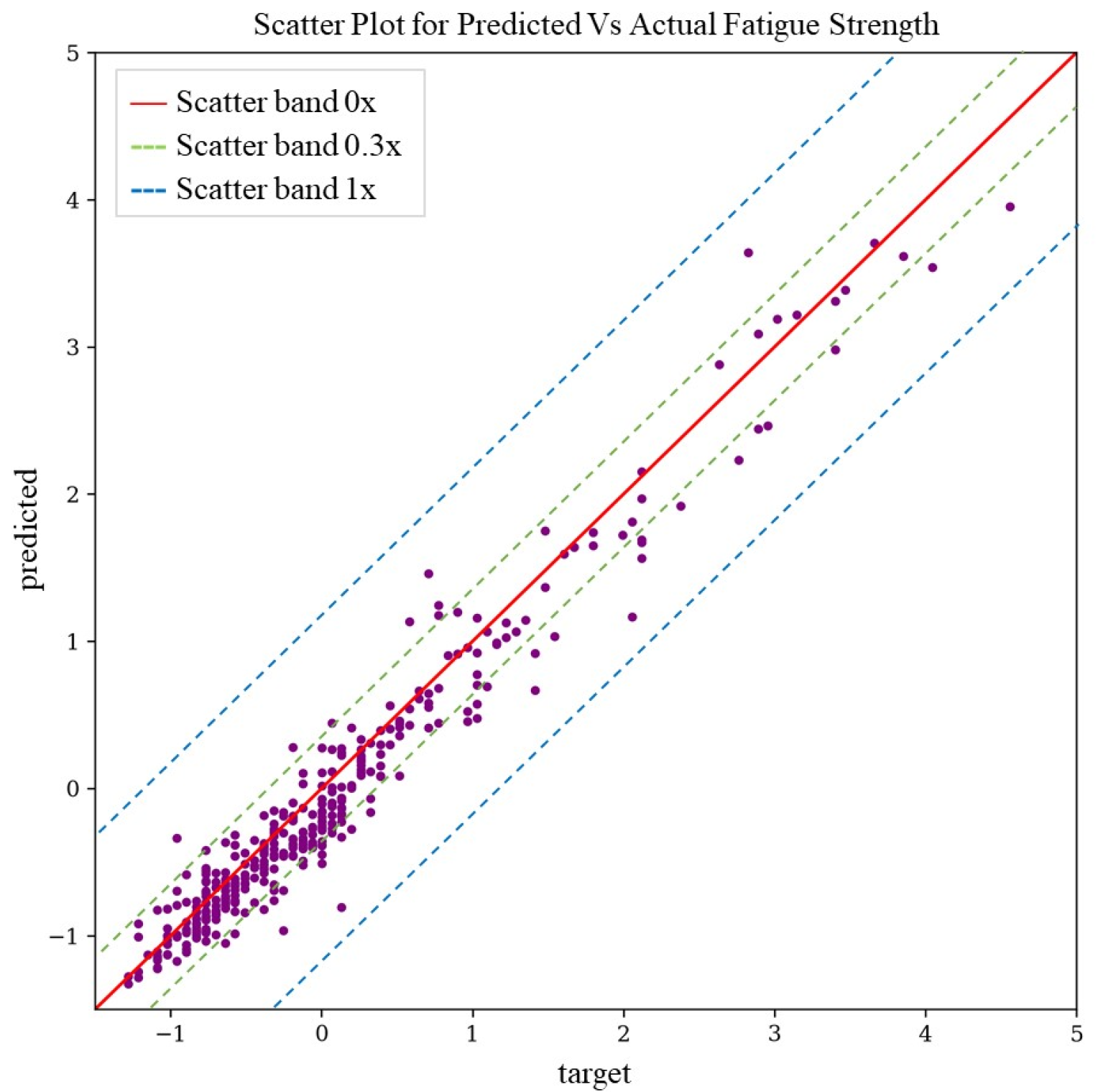
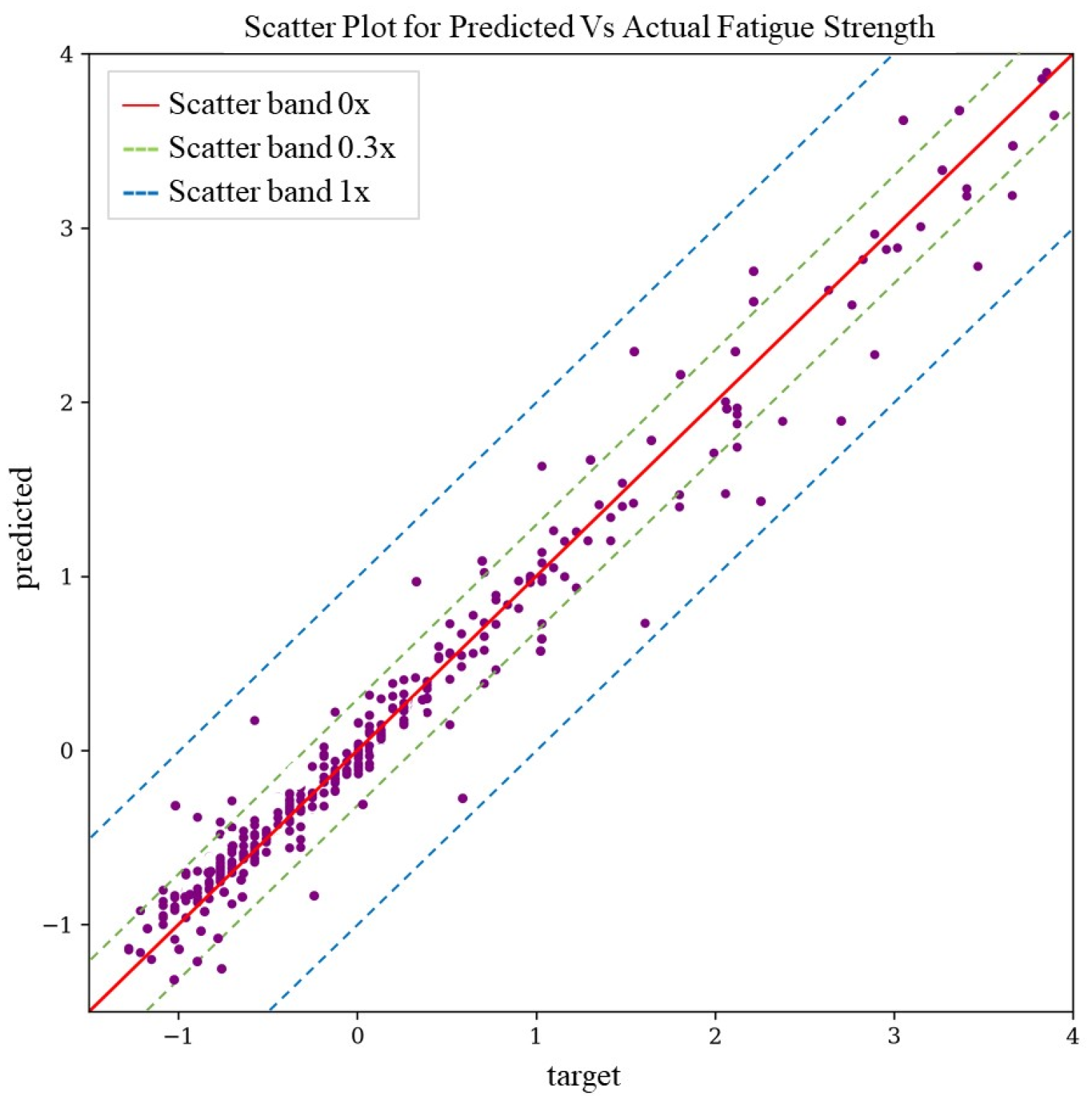
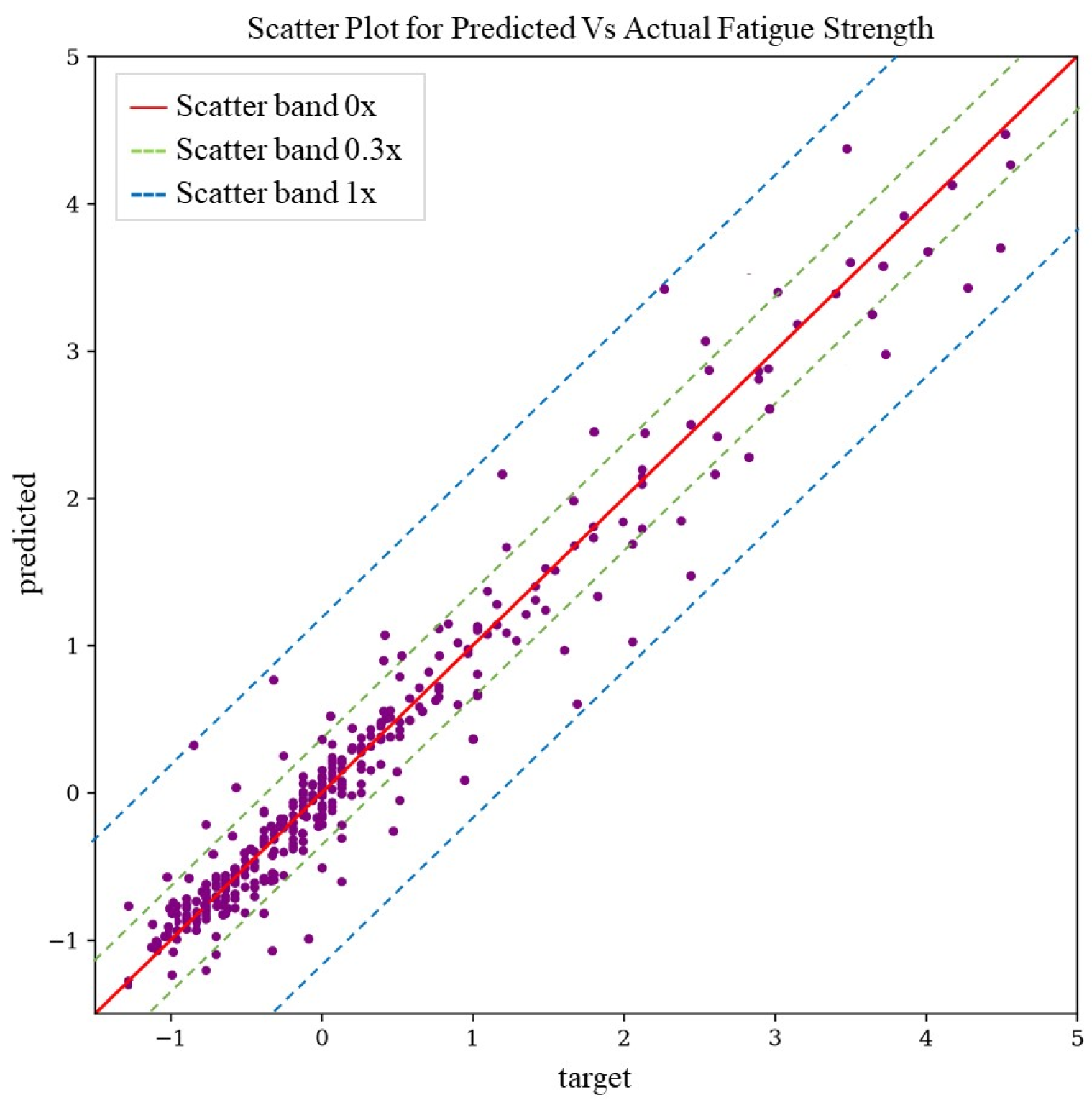
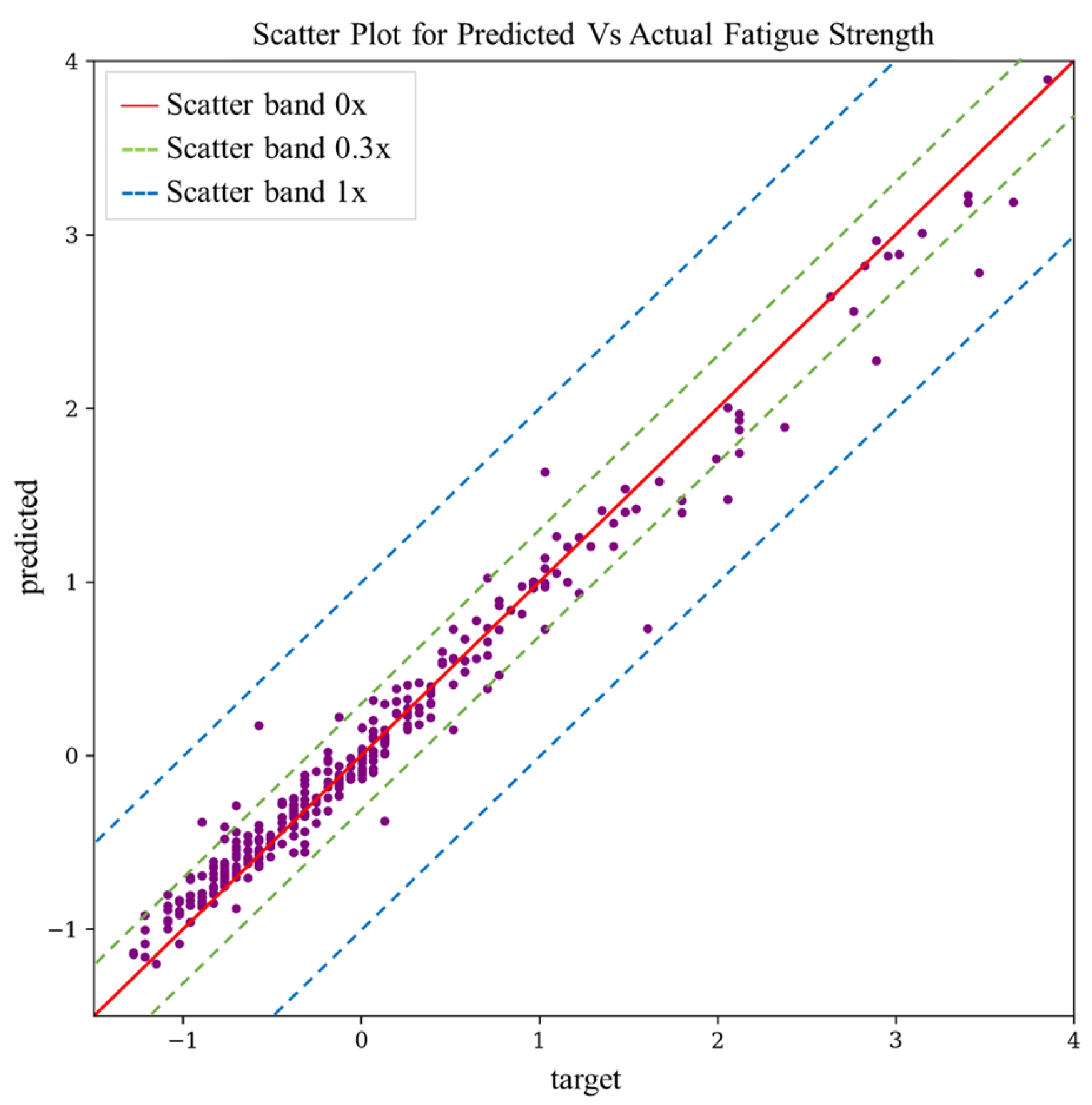
3.4. Predictive Model Evaluation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Xu, Q.; Chen, Y.; Yu, T.; Fu, G.; Huang, S. A fast nonlinear equivalent magnetic network model for magnetic jack type control rod drive mechanism in reactor. Prog. Nucl. Energy 2024, 169, 105058. [Google Scholar] [CrossRef]
- Li, Y.; Sun, L.; Geng, J.; Zhao, X. Semi-analytical investigation on hydrodynamic efficiency and loading of perforated breakwater-integrated OWCs. Ocean Eng. 2024, 309, 118460. [Google Scholar] [CrossRef]
- Guo, J.; Yang, Y.; Li, H.; Wang, J.; Tang, A.; Shan, D.; Huang, B. A hybrid deep learning model towards fault diagnosis of drilling pump. Appl. Energy 2024, 372, 123773. [Google Scholar] [CrossRef]
- Wang, L.; Hu, C.; Ma, T.; Yang, Z.; Guo, W.; Mao, Z.; Guo, J.; Li, H. GTFE-Net-BiLSTM-AM: An intelligent feature recognition method for natural gas pipelines. J. Nat. Gas Sci. Eng. 2024, 125, 205311. [Google Scholar] [CrossRef]
- Shao, Z.; Yin, Y.; Lyu, H.; Soares, C.G.; Cheng, T.; Jing, Q.; Yang, Z. An efficient model for small object detection in the maritime environment. Appl. Ocean Res. 2024, 152, 104194. [Google Scholar] [CrossRef]
- Wang, L.; Xie, Q.; Chen, J.; Ma, T.; Guo, J.; Li, H. Numerical analysis of the effect of hydrogen doping ratio on gas transmission in low-pressure pipeline network. Int. J. Hydrogen Energy 2024, 73, 868–884. [Google Scholar] [CrossRef]
- Wu, H.; Wei, J.; Wu, P.; Zhang, F.; Liu, Y. Dynamic response analysis of high-speed train gearboxes excited by wheel out-of-round: Experiment and simulation. Veh. Syst. Dyn. 2024, 1–27. [Google Scholar] [CrossRef]
- Guo, J.; Wang, Z.; Li, H.; Yang, Y.; Huang, C.G.; Yazdi, M.; Kang, H.S. A hybrid prognosis scheme for rolling bearings based on a novel health indicator and nonlinear Wiener process. Reliab. Eng. Syst. Saf. 2024, 245, 110014. [Google Scholar] [CrossRef]
- Dai, L.; Guo, J.; Wan, J.L.; Wang, J.; Zan, X. A reliability evaluation model of rolling bearings based on WKN-BiGRU and Wiener process. Reliab. Eng. Syst. Saf. 2022, 225, 108646. [Google Scholar] [CrossRef]
- Shao, Z.; Yin, Y.; Lyu, H.; Soares, C.G. A robust method for multi object tracking in autonomous ship navigation systems. Ocean Eng. 2024, 311, 118560. [Google Scholar] [CrossRef]
- Zou, C.L.; Pang, J.; Qiu, Y.; Liu, R.; Li, S.; Jing, G.; Xu, C.; Zhang, Z. The high-cycle fatigue fracture mechanism and fatigue strength prediction of compacted graphite iron. Int. J. Fatigue 2022, 161, 106881. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, P.; Zhang, Z.J.; Wang, B.; Zhang, Z.F. A Practical Model for Efficient Anti-Fatigue Design and Selection of Metallic Materials: I. Model Building and Fatigue Strength Prediction. Mater. Sci. Technol. 2021, 70, 233–249. [Google Scholar] [CrossRef]
- Yuan, X.; Li, C. An Engineering High Cycle Fatigue Strength Prediction Model for Low Plasticity Burnished Samples. Int. J. Fatigue 2017, 103, 318–326. [Google Scholar] [CrossRef]
- Liviu, M.; Francesco, I.; Liviu, D.P.; Vittorio, D.C.; Lucian, R. Engineering prediction of fatigue strength for AM50 magnesium alloys. Int. J. Fatigue 2019, 127, 10–15. [Google Scholar]
- Guo, J.; Yang, Y.; Li, H.; Dai, L.; Huang, B. A parallel deep neural network for intelligent fault diagnosis of drilling pumps. Eng. Appl. Artif. Intell. 2024, 133, 108071. [Google Scholar] [CrossRef]
- Li, F.; Wu, H.; Liu, L.; Ye, Y.; Wang, Y.; Wu, P. Nonlinear optimal frequency control for dynamic vibration absorber and its application. Mech. Syst. Sig. Process. 2025, 223, 111932. [Google Scholar] [CrossRef]
- Guo, J.; Wang, Z.; Yang, Y.; Song, Y.; Wan, J.L.; Huang, C.G. A dual-channel transferable RUL prediction method integrated with Bayesian deep learning and domain adaptation for rolling bearings. Qual. Reliab. Eng. Int. 2024, 40, 2348–2366. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Yang, H.; Wang, Z.; Wen, X.; He, X.; Qing, L.; Chen, H. Degradation Modeling for Restoration-enhanced Object Detection in Adverse Weather Scenes. IEEE Trans. Intell. Veh. 2024, 1–17. [Google Scholar] [CrossRef]
- Yan, F.; Song, K.; Liu, Y.; Chen, S.; Chen, J. Predictions and mechanism analyses of the fatigue strength of steel based on machine learning. J. Mater. Sci. 2020, 55, 15334–15349. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, L.; Zhang, J.; Liu, L.; Chen, W. Prediction of high-cycle fatigue strength in a Ti-17 alloy blade after foreign object damage. Eng. Fract. Mech. 2021, 241, 107385. [Google Scholar] [CrossRef]
- Wang, H.; Li, B.; Gong, J.; Xuan, F.Z. Machine learning-based fatigue life prediction of metal materials: Perspectives of physics-informed and data-driven hybrid methods. Eng. Fract. Mech. 2023, 284, 109242. [Google Scholar] [CrossRef]
- Liu, C.; Wang, X.; Cai, W.; Yang, J.; Su, H. Prediction of the fatigue strength of steel based on interpretable machine learning. Materials 2023, 16, 7354. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Zan, X.; Wang, L.; Lei, L.; Ou, C.; Bai, S. A random forest regression with Bayesian optimization-based method for fatigue strength prediction of ferrous alloys. Eng. Fract. Mech. 2023, 293, 109714. [Google Scholar] [CrossRef]
- Utpat, V.S.; Kulkarni, S.G. Analysis of Various Machine Learning Algorithms for Cast Aluminium Alloy to Estimate Fatigue Strength. J. Inst. Eng. (India) Ser. D 2023, 104, 61–70. [Google Scholar] [CrossRef]
- Kashyzadeh, K.R.; Ghorbani, S. New neural network-based algorithm for predicting fatigue life of aluminum alloys in terms of machining parameters. Eng. Fail. Anal. 2023, 146, 107128. [Google Scholar] [CrossRef]
- Yin, C.; Yang, Y. The Prediction of Fatigue Life Basing Random Forest Algorithm//ASME International Mechanical Engineering Congress and Exposition. Am. Soc. Mech. Eng. 2021, 85680, V012T12A008. [Google Scholar]
- Zhou, K.; Sun, X.; Shi, S.; Kai, S.; Xu, C. Machine learning-based genetic feature identification and fatigue life prediction. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2524–2537. [Google Scholar] [CrossRef]
- Gan, L.; Wu, H.; Zhong, Z. Fatigue life prediction considering mean stress effect based on random forests and kernel extreme learning machine. Int. J. Fatigue 2022, 158, 106761. [Google Scholar] [CrossRef]
- Shiraiwa, T.; Miyazawa, Y.; Enoki, M. Prediction of fatigue strength in steels by linear regression and neural network. Mater. Trans. 2018, 60, 189–198. [Google Scholar] [CrossRef]
- Agrawal, A.; Deshpande, P.D.; Cecen, A.; Basavarsu, G.P.; Choudhary, A.N.; Kalidindi, S.R. Exploration of data science techniques to predict fatigue strength of steel from composition and processing parameters. Integr. Mater. Manuf. Innov. 2014, 3, 90–108. [Google Scholar] [CrossRef]
- Gebhardt, C.; Trimborn, T.; Weber, F.; Bezold, A.; Broeckmann, C.; Herty, M. Simplified ResNet approach for data driven prediction of microstructure-fatigue relationship. Mech. Mater. 2020, 151, 103625. [Google Scholar] [CrossRef]
- Malinov, S.; Sha, W.; McKeown, J.J. Modelling the correlation between processing parameters and properties in titanium alloys using artificial neural network. Comput. Mater. Sci. 2001, 21, 375–394. [Google Scholar] [CrossRef]
- Duan, H.; Pei, L.; Sheng, J.; Tang, G.; Liu, L.; Zhang, Z. A novel model for fatigue strength prediction based on the true stress-strain curves. Ferroelectrics 2022, 596, 137–151. [Google Scholar] [CrossRef]
- Wang, X.; Chen, H.; Gou, H.; He, J.; Wang, Z.; He, X.; Qing, L.; Sheriff, R.E. RestorNet: An efficient network for multiple degradation image restoration. Knowl. Based Syst. 2023, 282, 111116. [Google Scholar] [CrossRef]
- Zhao, Y.; Teng, Q.; Chen, H.; Zhang, S.; He, X.; He, X.; Li, Y.; Sheriff, R.E. Activating more information in arbitrary-scale image super-resolution. IEEE Trans. Multimed. 2024, 26, 7946–7961. [Google Scholar] [CrossRef]
- Guo, J.; Wan, J.L.; Yang, Y.; Dai, L.; Tang, A.; Huang, B.; Zhang, F.; Li, H. A deep feature learning method for remaining useful life prediction of drilling pumps. Energy 2023, 282, 128442. [Google Scholar] [CrossRef]
- Fu, G.Z.; Zhang, X.; Li, W.; Guo, J. Bayesian Fusion of Degradation and Failure Time Data for Reliability Assessment of In-dustrial Equipment Considering Individual Differences. Processes 2024, 12, 268. [Google Scholar] [CrossRef]
- Iron-Alloy Datasets. Available online: https://www.makeitfrom.com/material-group/Iron-Alloy/ (accessed on 4 July 2023).
- Sun, X.; Zhou, T.; Song, K.; Chen, X. An image recognition based multiaxial low-cycle fatigue life prediction method with CNN model. Int. J. Fatigue 2023, 167, 107324. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D 2020, 404, 132306. [Google Scholar] [CrossRef]
- Lu, H.; Yang, G.; Chen, Z.; Zhang, Y.; Fu, C.; Huang, H.; Yuan, X.; Li, Z. Research on Fatigue Crack Propagation and Life Prediction Based on GRU Neural Network. ICMD: International Conference on Mechanical Design. In Advances in Mechanical Design; Springer: Singapore, 2023; pp. 1537–1557. [Google Scholar]
- Yang, J.; Kang, G.; Liu, Y.; Kan, Q. A novel method of multiaxial fatigue life prediction based on deep learning. Int. J. Fatigue 2021, 151, 106356. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, X.; Lei, X.; Wu, C. A novel deep LeNet-5 convolutional neural network model for image recognition. Comput. Sci. Inf. Syst. 2022, 19, 1463–1480. [Google Scholar] [CrossRef]
- Merlini, D.; Sprugnoli, R.; Verri, M.C. The method of coefficients. Am. Math. Mon. 2007, 114, 40–57. [Google Scholar] [CrossRef]



| Abbreviation | Details |
|---|---|
| BH | Brinell Hardness |
| EB | Elongation at Break (%) |
| SM | Shear Modulus (Gpa) |
| UTS | Ultimate tensile strength (MPa) |
| TSY | Tensile Yield Strength (MPa) |
| TC | Thermal Conductivity(W/m-K) |
| DE | Density (g/cm3) |
| EC | Embodied Carbon (kg CO2/kg material) |
| EW | Embodied Water (L/kg) |
| Fe | Iron (%) |
| Mn | Manganese (%) |
| Cr | Chromium (%) |
| Ni | Nickel (%) |
| Si | Silicon (%) |
| C | Carbon (%) |
| Mo | Molybdenum (%) |
| S | Sulfur (%) |
| P | Phosphorus (%) |
| N | Nitrogen (%) |
| Cu | Cuprum (%) |
| FS | Fatigue Strength (MPa)—107 cycles |
| Parameter Name | Optimization Range | Optimized Value |
|---|---|---|
| Number of Convolution Filters | (8, 128) | 64 |
| Convolution Kernel Size | (2, 7) | 3 |
| Dropout Rate | (0.1, 0.5) | 0.2 |
| Number of LSTM Units | (32, 160) | 64 |
| Number of Fully Connected Layer | (4, 16) | 2 |
| Learning Rate | (0.0001, 0.001, 0.01) | 0.001 |
| Model | MAE | RMSE | R2 | MAPE |
|---|---|---|---|---|
| CNN | 0.1211 | 0.1807 | 0.9677 | 2.4876 |
| RNN | 0.1202 | 0.1785 | 0.9685 | 2.1607 |
| GRU | 0.1902 | 0.2468 | 0.9397 | 4.1212 |
| LSTM | 0.2196 | 0.2984 | 0.9119 | 4.6546 |
| Transformer | 0.1183 | 0.1702 | 0.9697 | 1.5630 |
| LeNet5 | 0.1561 | 0.1937 | 0.9583 | 1.8964 |
| CNN-LSTM | 0.1122 | 0.1686 | 0.9719 | 1.1734 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Yan, J.; Zhang, J.; Han, C.; Peng, J.; Cheng, J.; Wang, Z.; Luo, M.; Yin, P. Deep Learning-Based Fatigue Strength Prediction for Ferrous Alloy. Processes 2024, 12, 2214. https://doi.org/10.3390/pr12102214
Huang Z, Yan J, Zhang J, Han C, Peng J, Cheng J, Wang Z, Luo M, Yin P. Deep Learning-Based Fatigue Strength Prediction for Ferrous Alloy. Processes. 2024; 12(10):2214. https://doi.org/10.3390/pr12102214
Chicago/Turabian StyleHuang, Zhikun, Jingchao Yan, Jianlong Zhang, Chong Han, Jingfei Peng, Ju Cheng, Zhenggang Wang, Min Luo, and Pengbo Yin. 2024. "Deep Learning-Based Fatigue Strength Prediction for Ferrous Alloy" Processes 12, no. 10: 2214. https://doi.org/10.3390/pr12102214
APA StyleHuang, Z., Yan, J., Zhang, J., Han, C., Peng, J., Cheng, J., Wang, Z., Luo, M., & Yin, P. (2024). Deep Learning-Based Fatigue Strength Prediction for Ferrous Alloy. Processes, 12(10), 2214. https://doi.org/10.3390/pr12102214





