An Eight-Coil Wireless Power Transfer Method for Improving the Coupling Tolerance Based on Uniform Magnetic Field
Abstract
1. Introduction
2. The Proposed Method
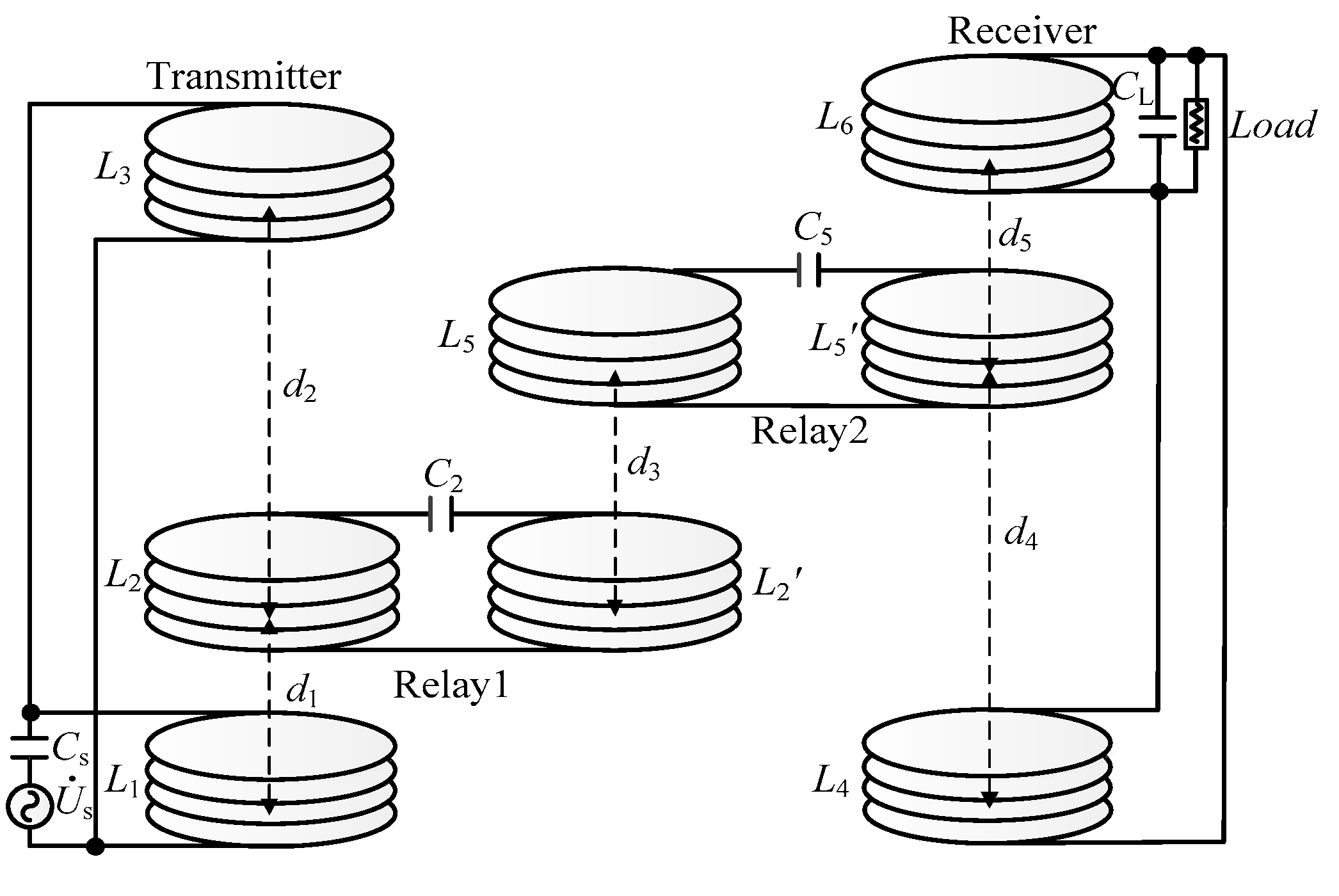
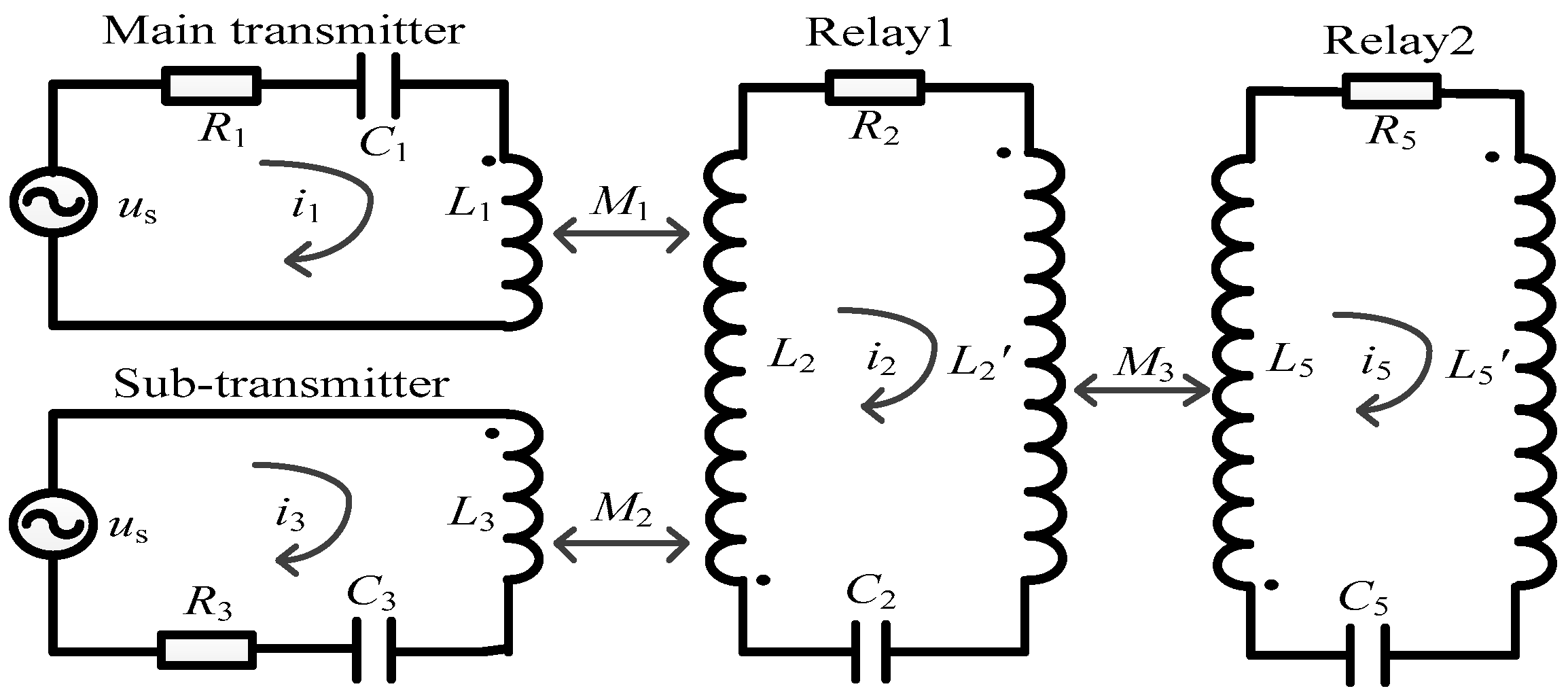
2.1. Model of the Eight-Coil WPT System and Equations of the Transmission Characteristics
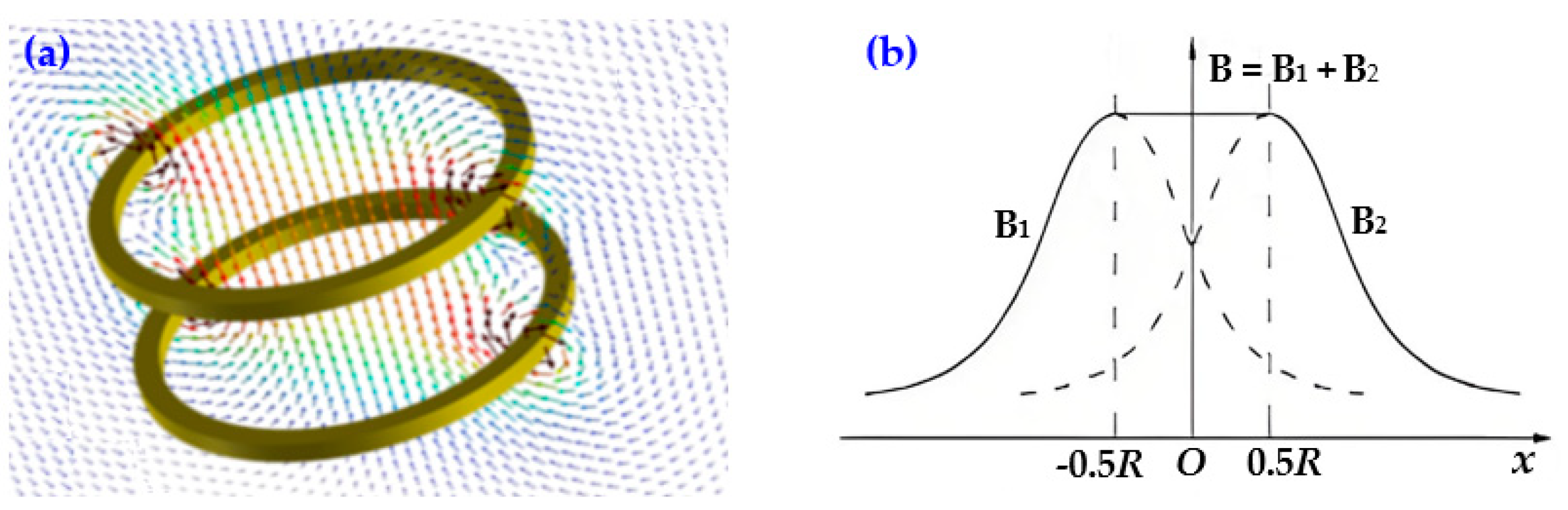
2.2. Model of the Mutual Inductance and Equation of the Impedance Coupled Factor
2.3. Law of the Transmission Characteristics of the Eight-Coil WPT System
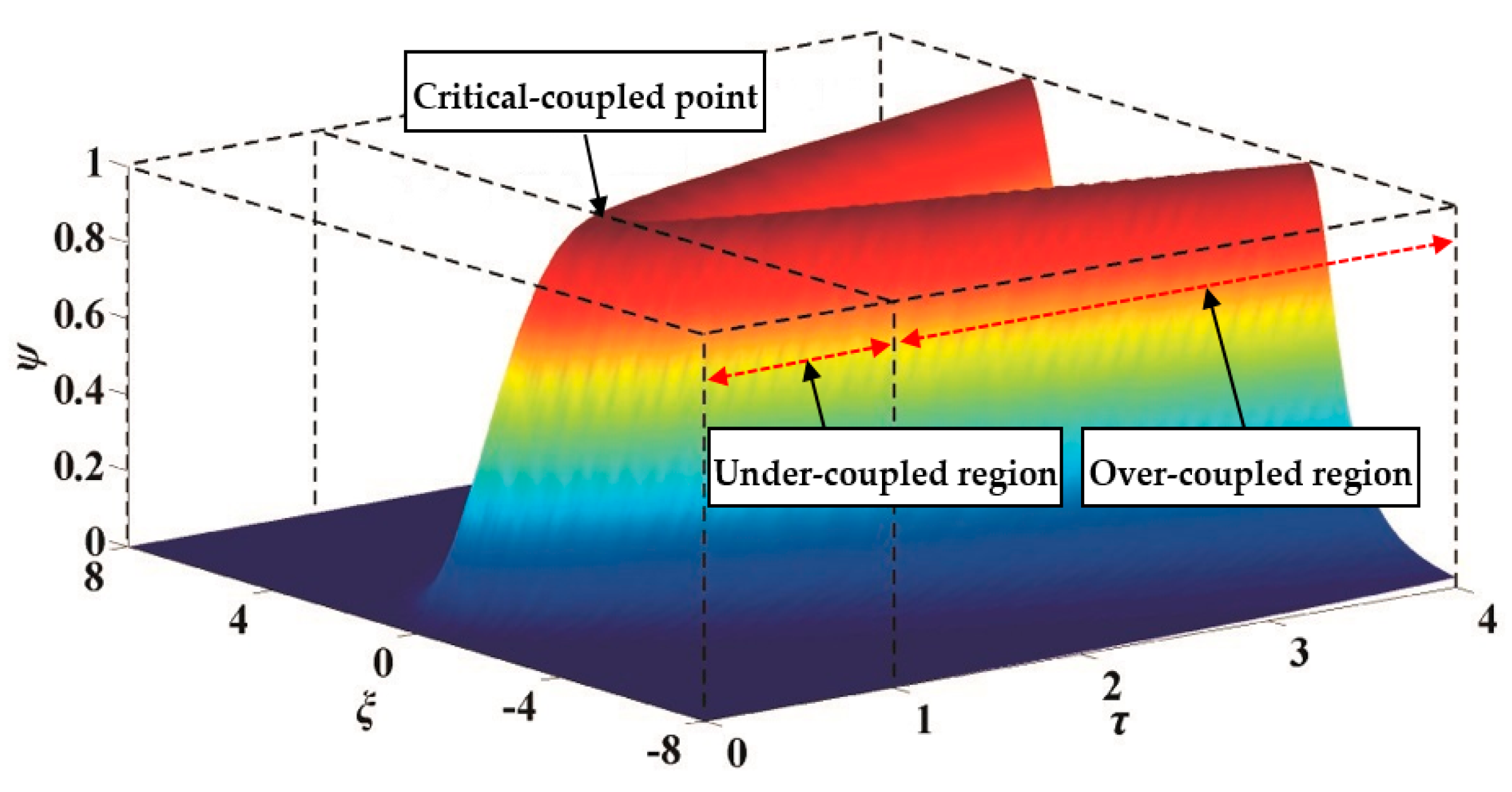
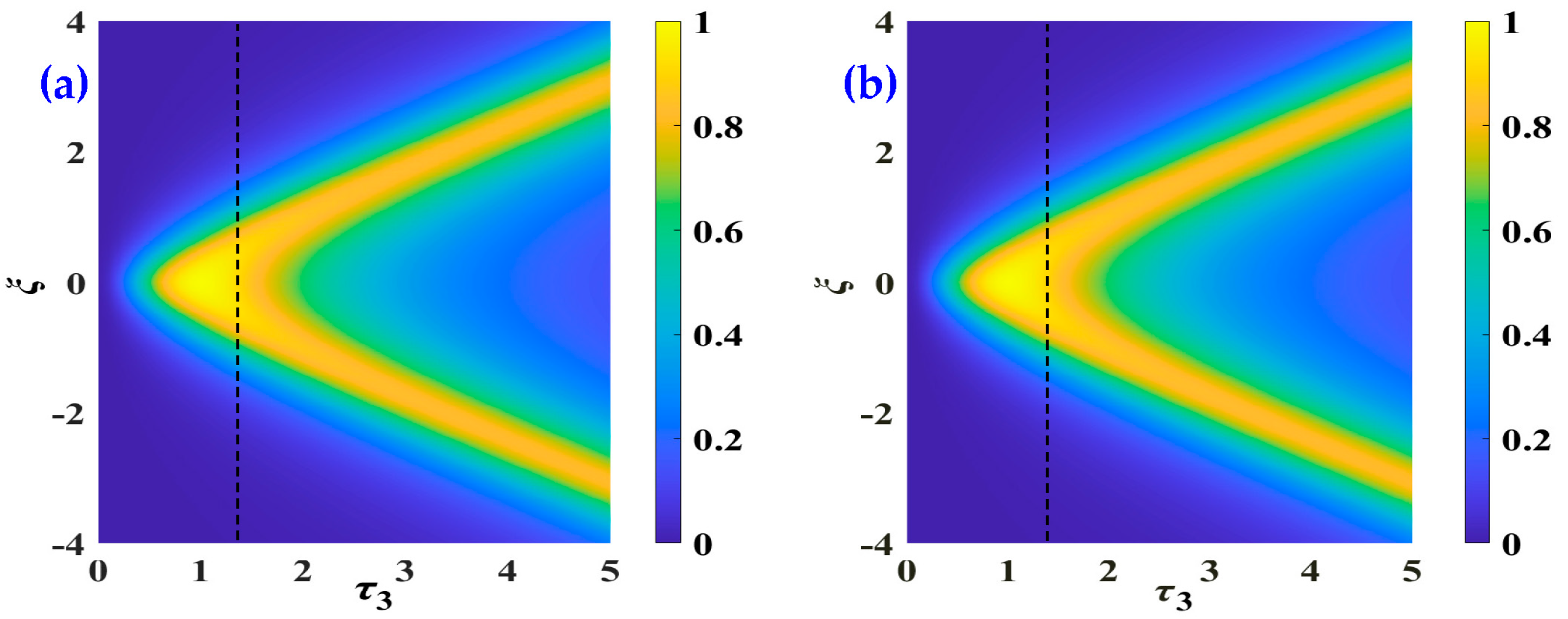
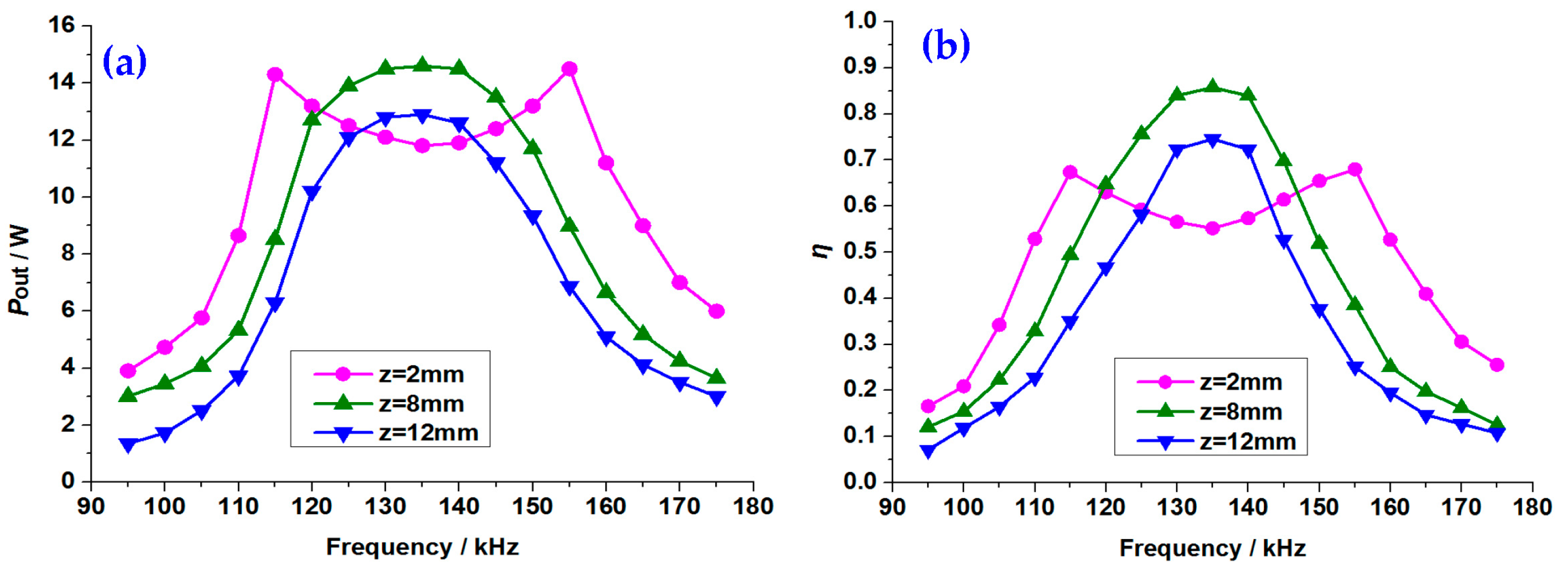
2.3.1. Law of the Transmission Characteristics of the Frequency with Coupling Distance
2.3.2. Law of the Transmission Characteristics of the Two-Tx-Coil System
2.3.3. Law of the Transmission Characteristics of the Two-Rx-Coil System
2.3.4. Law of the Transmission Characteristics of the Relay-Coil System
3. Experimental Results
3.1. Law of the Transmission Characteristics with Frequency for the Eight-Coil WPT System
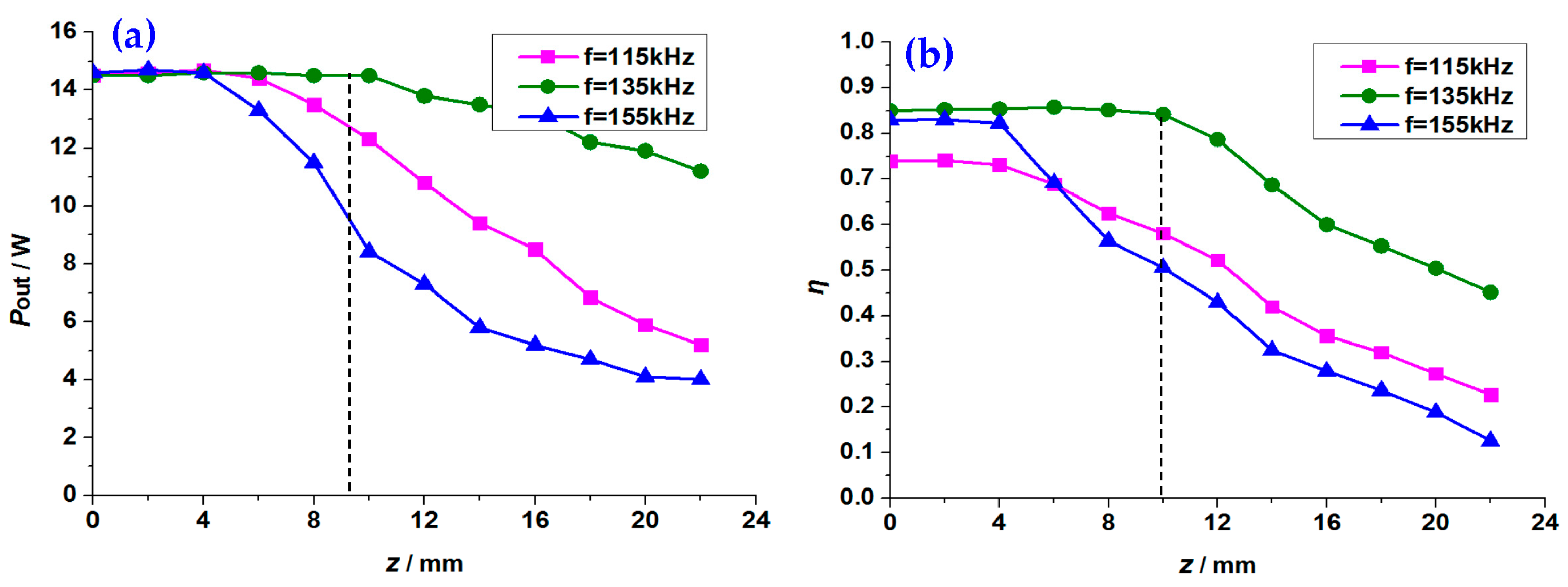
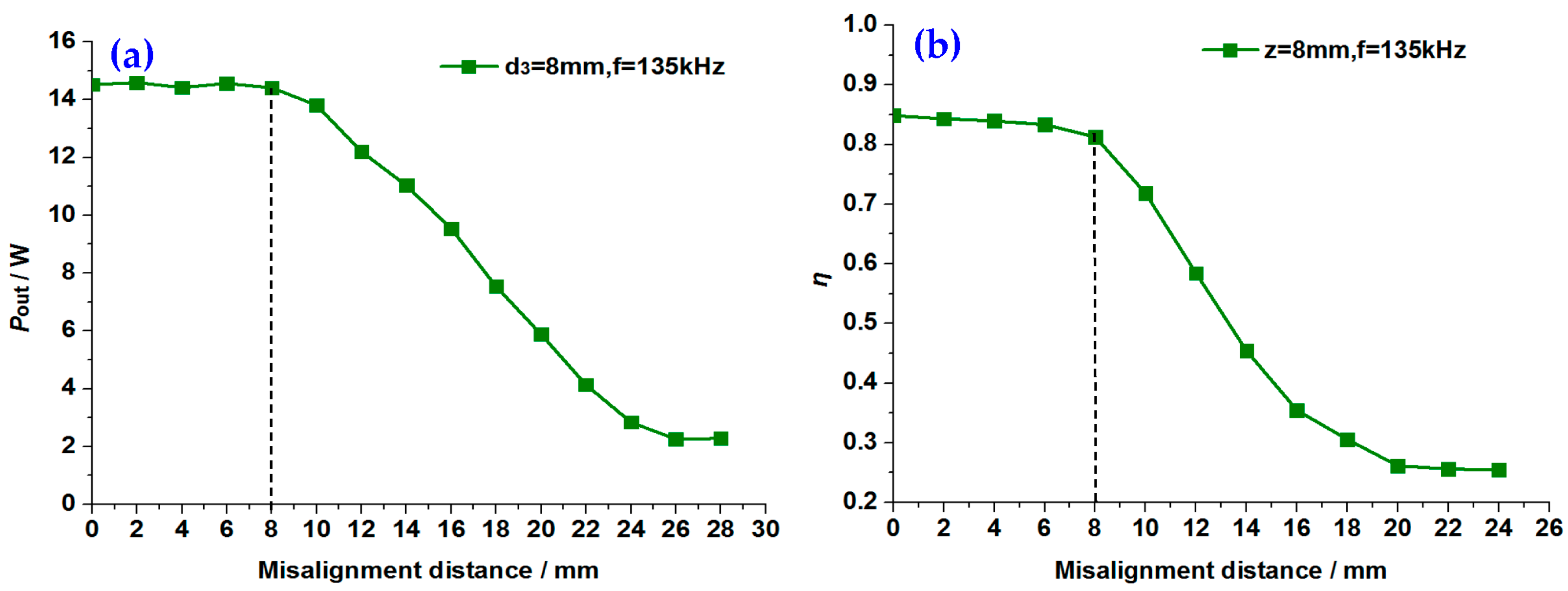
3.2. COP and CTE with Long-Range Coupling and Misalignment Distances
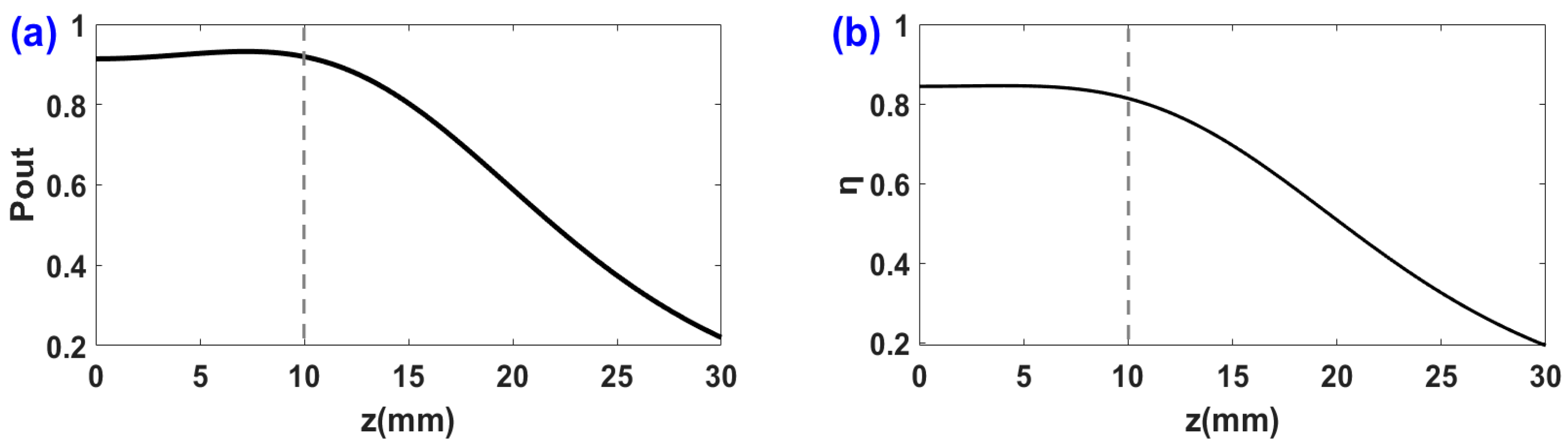
3.2.1. COP and CTE with Long-Range Coupling Distance
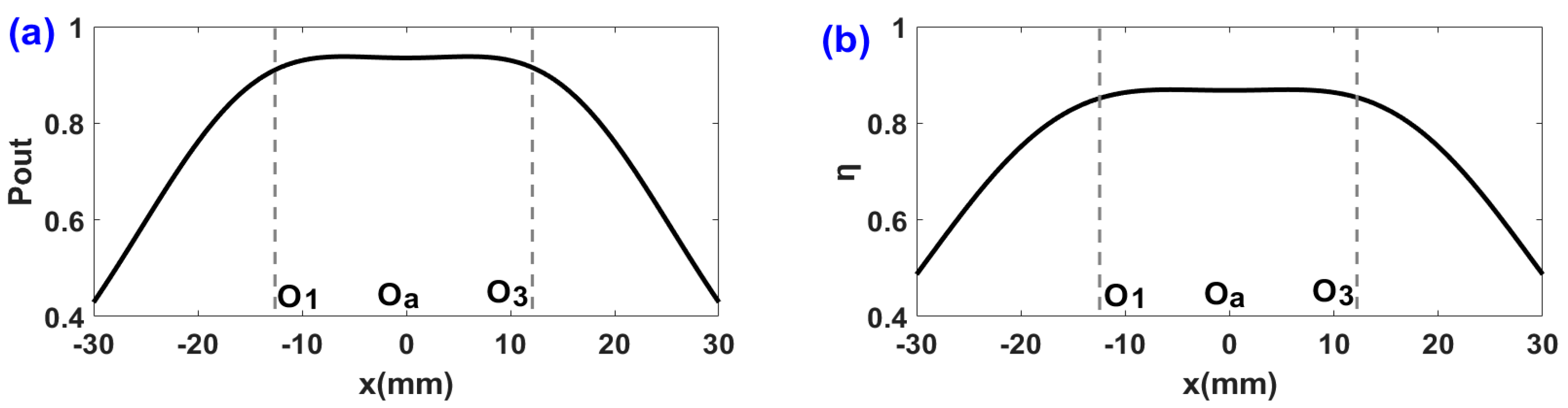
3.2.2. COP and CTE with Long-Range Misalignment Distance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tesla, N. Electrical Energy. U.S. Patent 1,119,732, 1 December 1914. Available online: https://encyclopedia.thefreedictionary.com/Nikola+Tesla (accessed on 9 June 2024).
- Moisello, E.; Liotta, A.; Malcovati, P.; Bonizzoni, E. Recent Trends and Challenges in Near-Field Wireless Power Transfer Systems. IEEE Open J. Solid-State Circuits Soc. 2023, 3, 197–213. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless Power Transfer via Strongly Coupled Magnetic Resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Sagar, A.; Kashyap, A.; Nasab, M.A.; Padmanaban, S.; Bertoluzzo, M.; Kumar, A.; Blaabjerg, F. A Comprehensive Review of the Recent Development of Wireless Power Transfer Technologies for Electric Vehicle Charging Systems. IEEE Access 2023, 11, 83703–83751. [Google Scholar] [CrossRef]
- Sample, A.P.; Meyer, D.T.; Smith, J.R. Analysis, Experimental Results, and Range Adaptation of Magnetically Coupled Resonators for Wireless Power Transfer. IEEE Trans. Ind. Electron. 2011, 58, 544–554. [Google Scholar] [CrossRef]
- Liu, S.; Tan, J.; Wen, X. Modeling of coupling mechanism of wireless power transfer system and vibration phenomenon of receiver-coil in three-coil system. AIP Adv. 2017, 7, 115107. [Google Scholar] [CrossRef]
- Liu, S.; Tan, J. Study on the Vibration Mechanism of the Relay Coil in a Three-Coil WPT System. Prog. Electromagn. Res. M 2018, 70, 117–126. [Google Scholar] [CrossRef]
- Shu, X.; Zhang, B.; Wei, Z.; Rong, C.; Sun, S. Extended-Distance Wireless Power Transfer System with Constant Output Power and Transfer Efficiency Based on Parity-Time-Symmetric Principle. IEEE Trans. Power Electron. 2021, 36, 8861–8871. [Google Scholar] [CrossRef]
- Xiong, W.; Yu, Q.; Liu, Z.; Zhu, Q.; Su, M.; Zhao, L.; Hu, A.P. A Dual-Frequency-Detuning Method for Improving the Coupling Tolerance of Wireless Power Transfer. IEEE Trans. Power Electron. 2023, 38, 6923–6928. [Google Scholar] [CrossRef]
- Seo, D.-W.; Lee, J.-H. Frequency-Tuning Method Using the Reflection Coefficient in a Wireless Power Transfer System. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 959–961. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Y.; Wu, T. Wireless Power Transfer Efficiency Optimization Tracking Method Based on Full Current Mode Impedance Matching. Sensors 2024, 24, 2917. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Sun, J.; Wang, Y.; Xu, D. An Efficiency Optimization Method Based on Double Side Impedance Angle Design for Wireless Power Transfer System. IEEE Trans. Power Electron. 2023, 38, 5000–5012. [Google Scholar] [CrossRef]
- Xu, X.; Liu, Y. The active magnetic compensation coil. Rev. Sci. Instrum. 2024, 95, 081501. [Google Scholar] [CrossRef] [PubMed]
- Ruark, A.E.; Peters, M.F. Helmholtz coils for producing uniform magnetic fields. J. Opt. Soc. Am. 1926, 13, 205–212. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 1998; ISBN 0-13-805326-X. Available online: https://en.wikipedia.org/wiki/Biot-Savart (accessed on 10 June 2024).

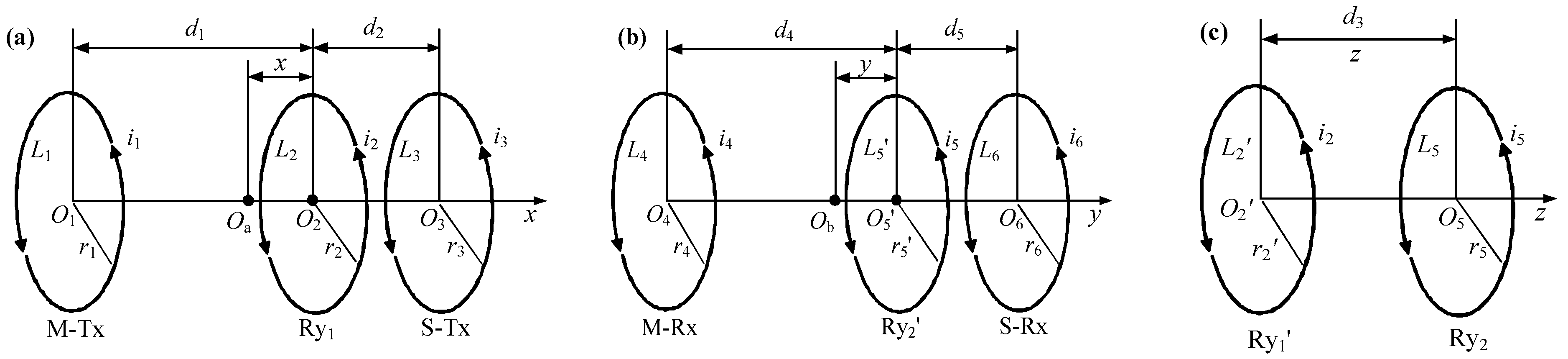


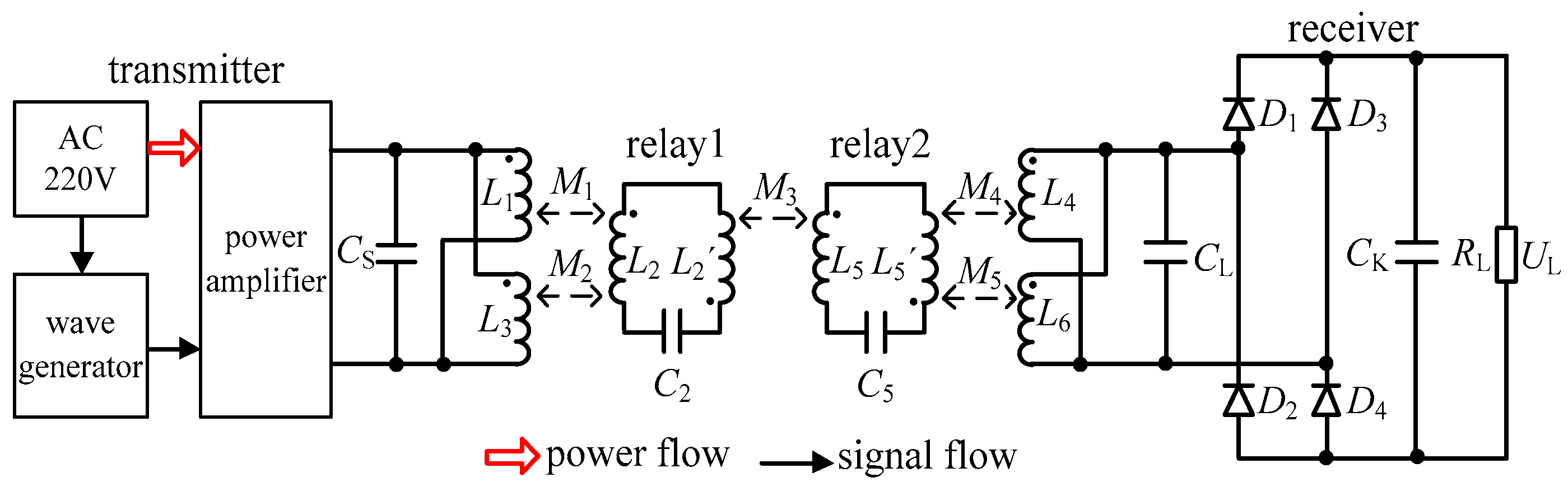

| Parameter | Value |
|---|---|
| Input power | |
| Load voltage | , |
| Winding ohmic resistance of the coil | R1, R2, R3, R4, R5, R6 |
| Load resistance | RL1, RL2 |
| Inductance of the coil | L1, L2, L2′, L3, L4, L5, L5′, L6 |
| Capacitance | CS, C2, C5, CL |
| Coupled distance | d1, d2, d3, d4, d5, ds = d1 + d2, dL = d4 + d5 |
| Mutual inductance | M1, M2, M3, M4, M5 |
| Parameter | Value |
|---|---|
| Capacitances | CS = C2 = C5 = CL = C |
| Inductances | L1 = 2L2 = 2L2′ = L3 =L4 = 2L5 = 2L5′ = L6 = L |
| Resistance | R4 + RL1 = R6 + RL2 = R |
| Ratio | RL1 = RL2 = βR, R1 = R2 = R3 = R5 = σR (σ = 1) |
| Operating angular frequency | ω |
| Resonance frequency | f0 = ω0/2π |
| Frequency detuning factor | ξ = Q0(ω/ω0–ω0/ω) |
| Resonant angular frequency | ω0 = 1/(LC)0.5, ω1 = ω2 = ω3 = ω4 = ω5 = ω6 = ω0 |
| Quality factor | Q0 = ω0L/R = 1/(ω0CR), Q1 = Q2 Q3 = Q5 = ω0L/R1 = 1/(ω0CR1) = Q0/σ, Q4 = Q6 = ω0L/(R4 + RL1) = 1/(ω0C(R6 + RL2)) = Q0 |
| Parameter | Value |
|---|---|
| Permeability of vacuum (H/m) | μ0 = 4π × 10−7 |
| Magnetic induction intensity of L1 at the position of L2 | B1 = μ0(n1n2)0.5r12i1/(2(r12 + d12)3/2) |
| Magnetic induction intensity of L3 at the position of L2 | B2 = μ0(n2n3)0.5r32i3/(2(r32 + d22)3/2) |
| Magnetic induction intensity of L2′ at the position of L5 | B3 = μ0(n2′n5)0.5r2′2i2/(2(r2′2 + d32)3/2) |
| Magnetic induction intensity of L5′ at the position of L4 | B4 = μ0(n4n5′)0.5r5′2i5/(2(r5′2 + d42)3/2) |
| Magnetic induction intensity of L5′ at the position of L6 | B5 = μ0(n5′n6)0.5r5′2i5′/(2(r5′2 + d52)3/2) |
| Radius of the M-Tx, Ry1, S-Tx, Ry1′, Ry2, M-Rx, Ry2′, and S-Rx | r1, r2, r3, r2′, r5, r4, r5′, r6 |
| Turn number of the M-Tx, Ry1, S-Tx, Ry1′, Ry2, M-Rx, Ry2′, and S-Rx | n1, n2, n3, n2′, n5, n4, n5′, n6 |
| Geometric center of the M-Tx, Ry1, S-Tx, Ry1′, Ry2, M-Rx, Ry2′, and S-Rx | O1, O2, O3, O2′, O5, O4, O5′, O6 |
| Mutual inductance between L1 and L2 | M1 = πμ0(n1n2)0.5(r1r2)2/(2(r12 + d12)3/2) |
| Mutual inductance between L3 and L2 | M2 = πμ0(n2n3)0.5(r2r3)2/(2(r32 + d22)3/2) |
| Mutual inductance between L2′ and L5 | M3 = πμ0(n2′n5)0.5(r2′r5)2/(2(r2′2 + d32)3/2) |
| Mutual inductance between L5′ and L4 | M4 = πμ0(n4n5′)0.5(r4r5′)2/(2(r5′2 + d42)3/2) |
| Mutual inductance between L5′ and L6 | M5 = πμ0(n5′n6)0.5(r5′r6)2/(2(r5′2 + d52)3/2) |
| Parameter | M-Tx, S-Tx, M-Rx, S-Rx | Ry1, Ry1′, Ry2, Ry2′ |
|---|---|---|
| Inside diameter of the coil φ/mm | 30 | 32 |
| Outside diameter of the coil Φ/mm | 50 | 40 |
| Layers of the coil | 2 | 3 |
| Number of turns | 30 | 20 |
| Frequency f0/kHz | 135 | 135 |
| Inductance L/μH | 50.0 | 29.0 |
| Capacitance C/nF | 27.83 | 47.98 |
| Distance d1 + d2 or d4 + d5 mm | 24 | |
| Distance d3 mm | 2, 8, or 12 | |
| Impedance scaling factor σ | 1 | |
| Frequency detuning factor ξ | 0 | |
| Load RL Ω | 0.5 | |
| Input Voltage US/V | 16 | |
| Input power W | 40 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Yan, X.; Xu, G.; Wang, G.; Liu, Y. An Eight-Coil Wireless Power Transfer Method for Improving the Coupling Tolerance Based on Uniform Magnetic Field. Processes 2024, 12, 2109. https://doi.org/10.3390/pr12102109
Liu S, Yan X, Xu G, Wang G, Liu Y. An Eight-Coil Wireless Power Transfer Method for Improving the Coupling Tolerance Based on Uniform Magnetic Field. Processes. 2024; 12(10):2109. https://doi.org/10.3390/pr12102109
Chicago/Turabian StyleLiu, Suqi, Xueying Yan, Guiqiang Xu, Gang Wang, and Yuping Liu. 2024. "An Eight-Coil Wireless Power Transfer Method for Improving the Coupling Tolerance Based on Uniform Magnetic Field" Processes 12, no. 10: 2109. https://doi.org/10.3390/pr12102109
APA StyleLiu, S., Yan, X., Xu, G., Wang, G., & Liu, Y. (2024). An Eight-Coil Wireless Power Transfer Method for Improving the Coupling Tolerance Based on Uniform Magnetic Field. Processes, 12(10), 2109. https://doi.org/10.3390/pr12102109






