Effects of the Characterization Methods of Heptane Plus Components (C7+) on the Phase Behavior of Volatile Fluids
Abstract
1. Introduction
- (1)
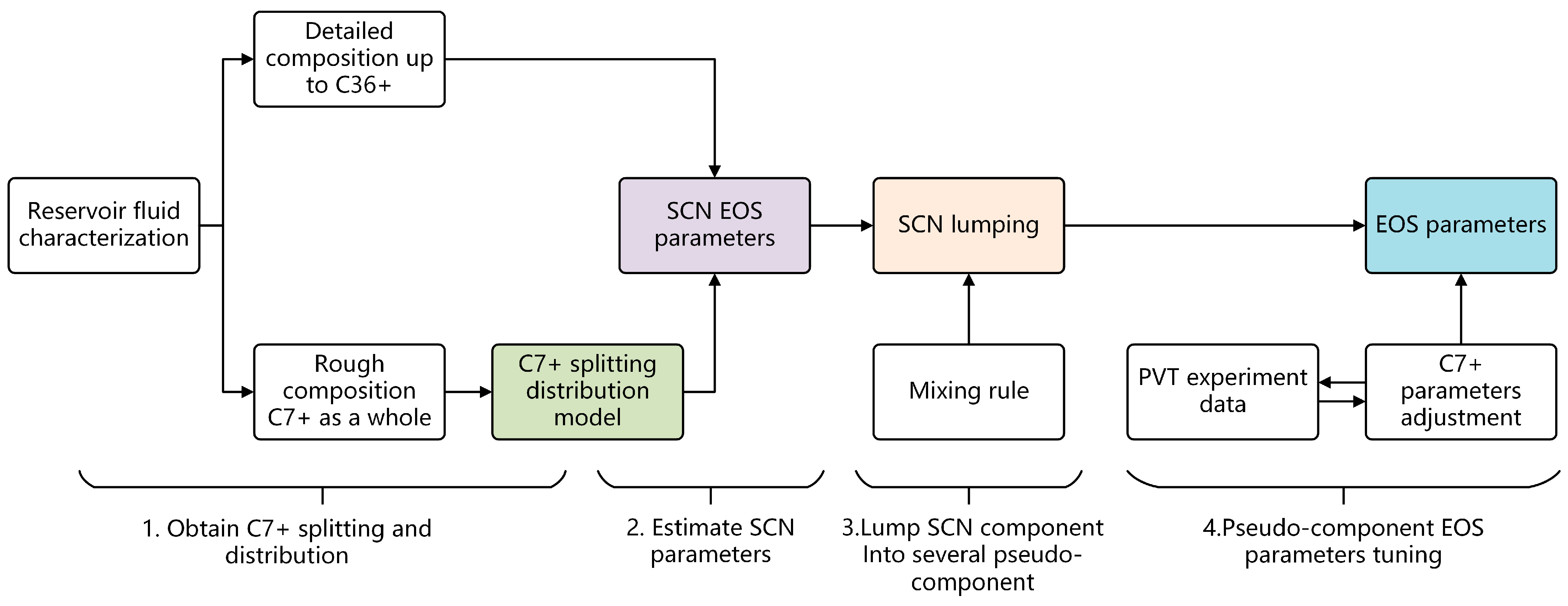
- When detailed gas chromatography experimental data are available, the component distribution of single carbon number (SCN) mixtures ranging from C7 to C36+ can typically be obtained. However, the number of chromatographic components is often excessive, and the direct application of experimental composition data in engineering calculations can significantly increase simulation time. Therefore, lumping the SCN components derived from gas chromatography into several pseudo-components will greatly improve computational efficiency. This raises the question: which lumping method best represents the phase behavior and PVT properties of the original fluid?
- (2)
- In the absence of gas chromatography experimental data, heavy components in reservoir fluids are usually represented as a single component (C7+ or C11+). The mole fraction of this single heavy component can account for over 50% of the entire reservoir fluid. This single lumped component does not accurately represent the heavy component distribution within the reservoir fluid. Consequently, it is necessary to split the single C7+ component to gain a more detailed understanding of the heavy component distribution. Splitting involves using a specific probability distribution method to divide the single C7+ component into multiple single carbon groups (SCNs). Representing the entire C7+ component using the SCN group distribution enables a more accurate characterization of the phase behavior and PVT properties of the reservoir fluids. The components obtained after splitting can be further lumped into several pseudo-components to minimize the total number of components. The critical question is: which method of splitting and lumping can best represent the phase behavior and PVT properties of the original fluid?
- (3)
- After splitting and lumping SCN components, it is necessary to determine the EOS characteristic parameters (such as molecular weight, critical point, and acentric factor) of the resulting pseudo-components. Which methods can reliably obtain the characteristic parameters of these pseudo-components?
- (4)
- How significantly do different methods of splitting and lumping, as well as the calculation methods for the EOS characteristic parameters of the pseudo-components, impact the PVT properties and phase behavior calculation results of reservoir fluids?
2. C7+ Characterization Methods
2.1. Heptane Plus (C7+) Splitting and SCN Distribution Models
2.1.1. Pedersen’s Model
2.1.2. Whitson’s Model
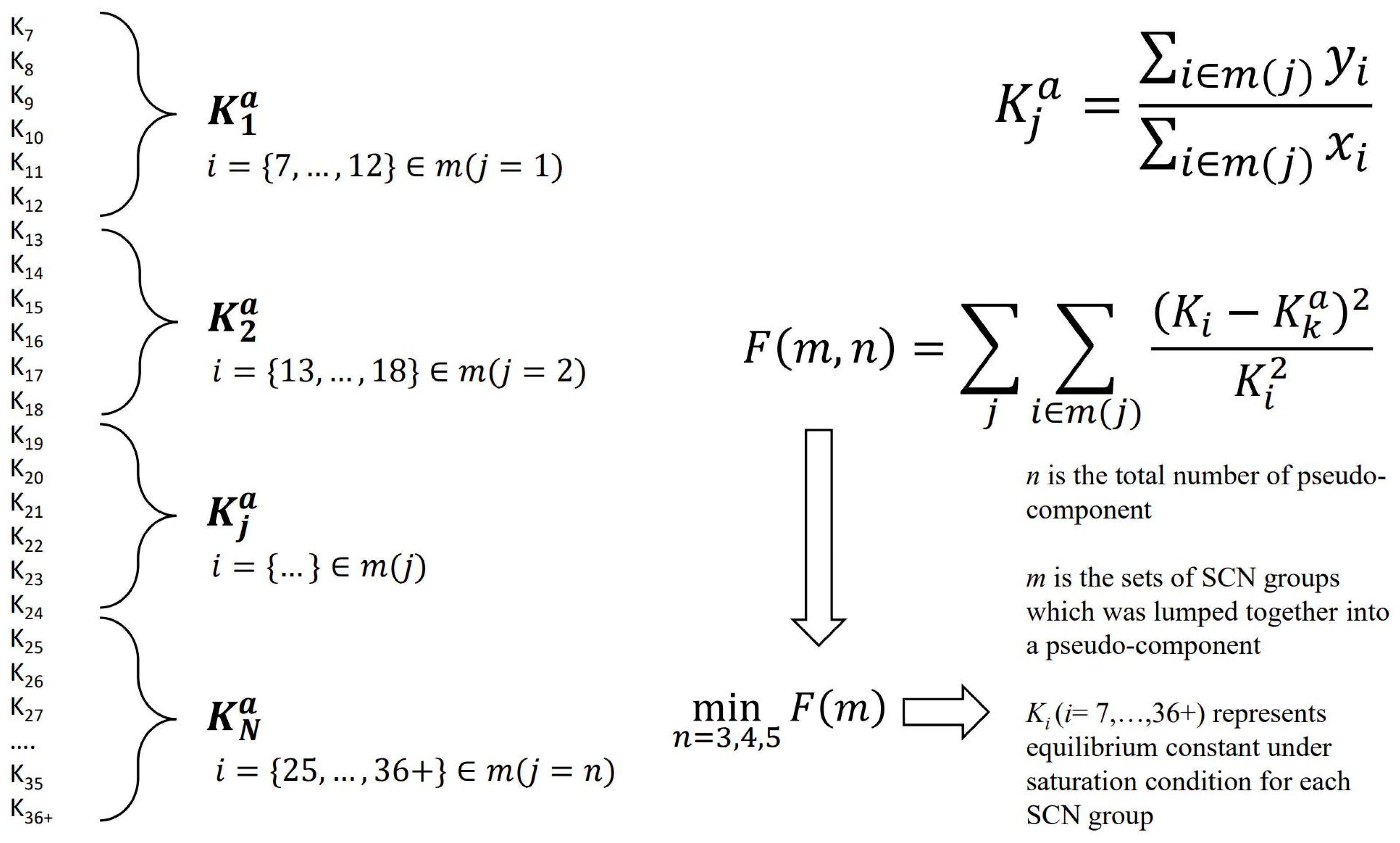
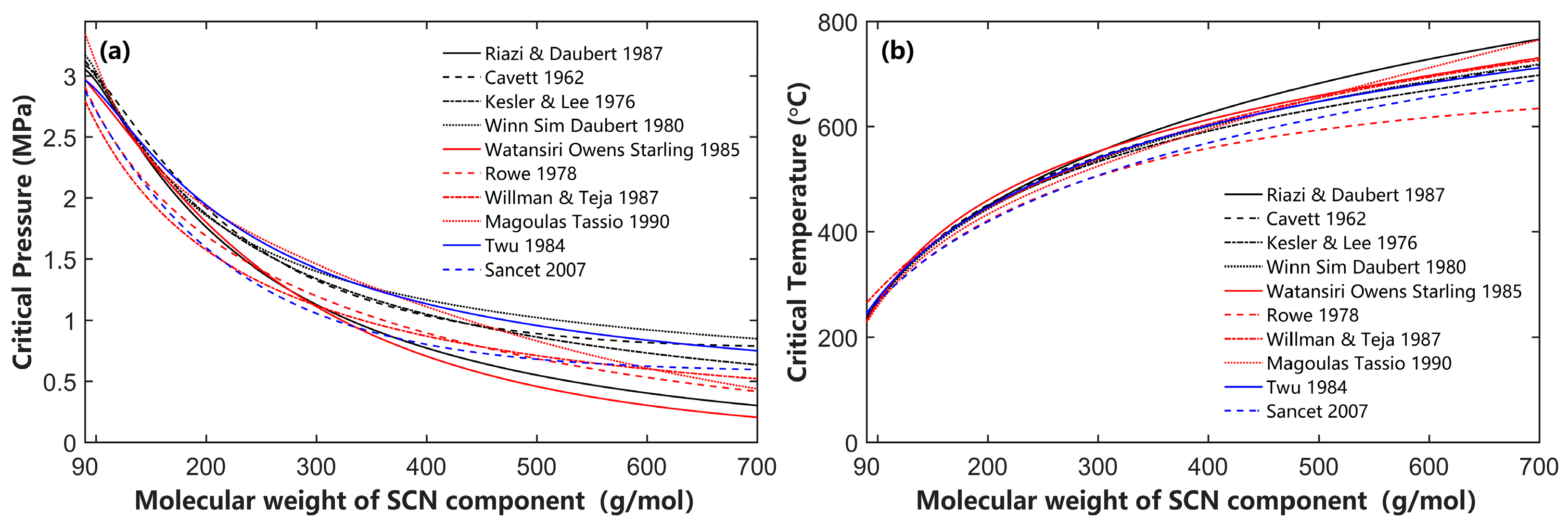
2.2. SCN Group EOS Parameters Estimation
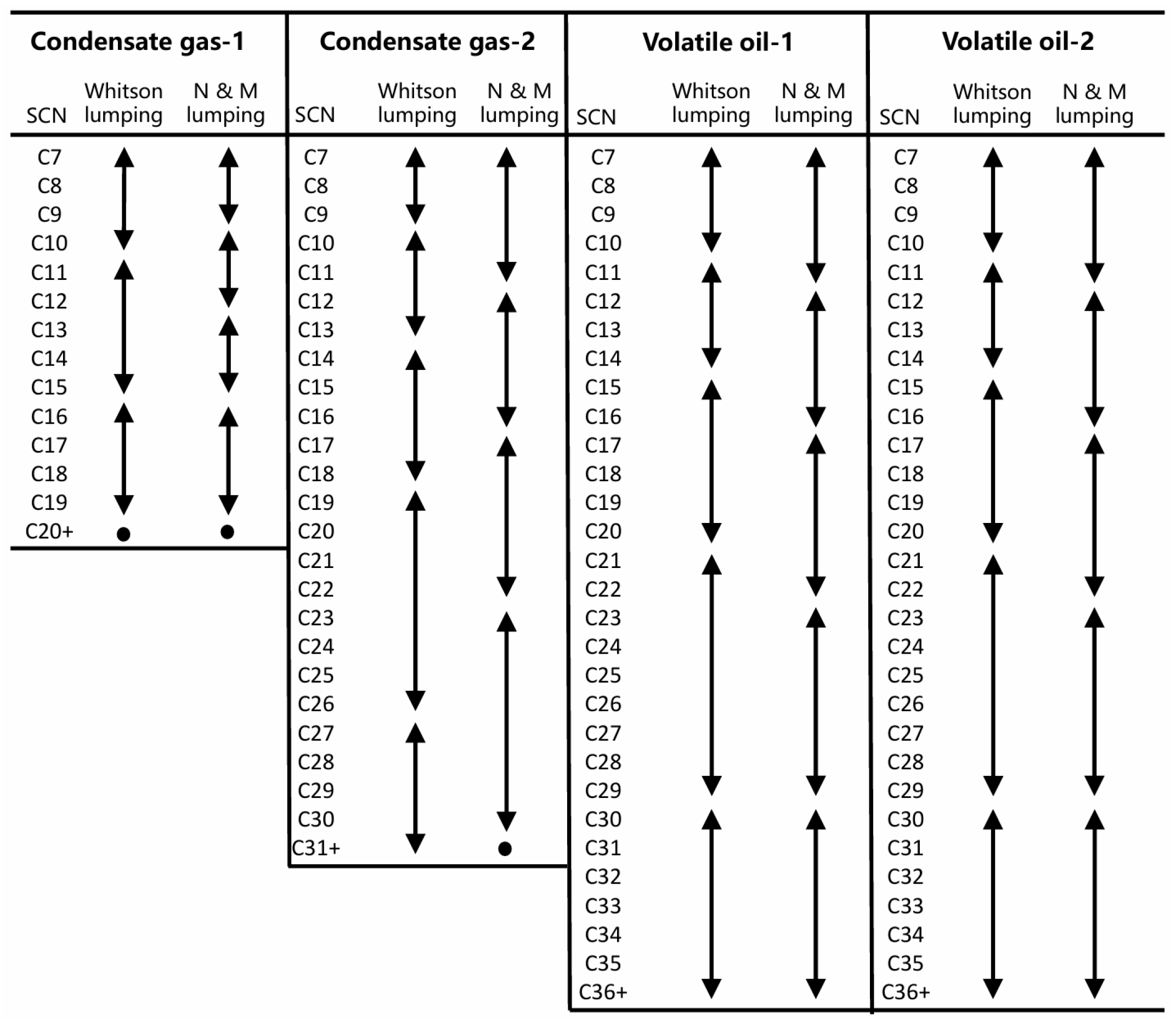
2.3. SCN Group Lumping and Corresponding Mixing Rule
2.3.1. Whitson Lumping Methods
2.3.2. Newley–Merrill Lumping Methods
2.3.3. Hong’s Mixing Rule
3. Fluids Description
4. Results and Discussion
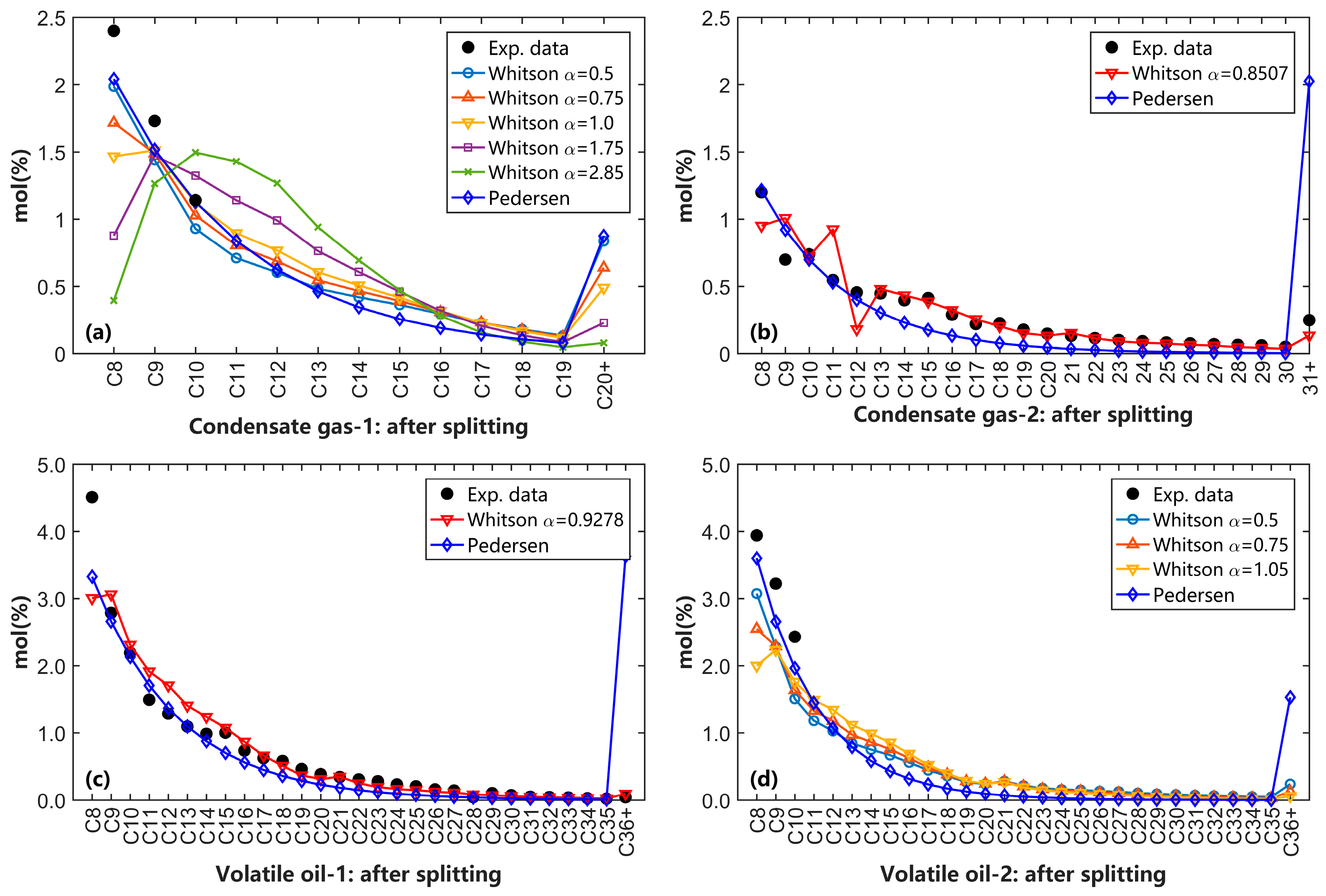
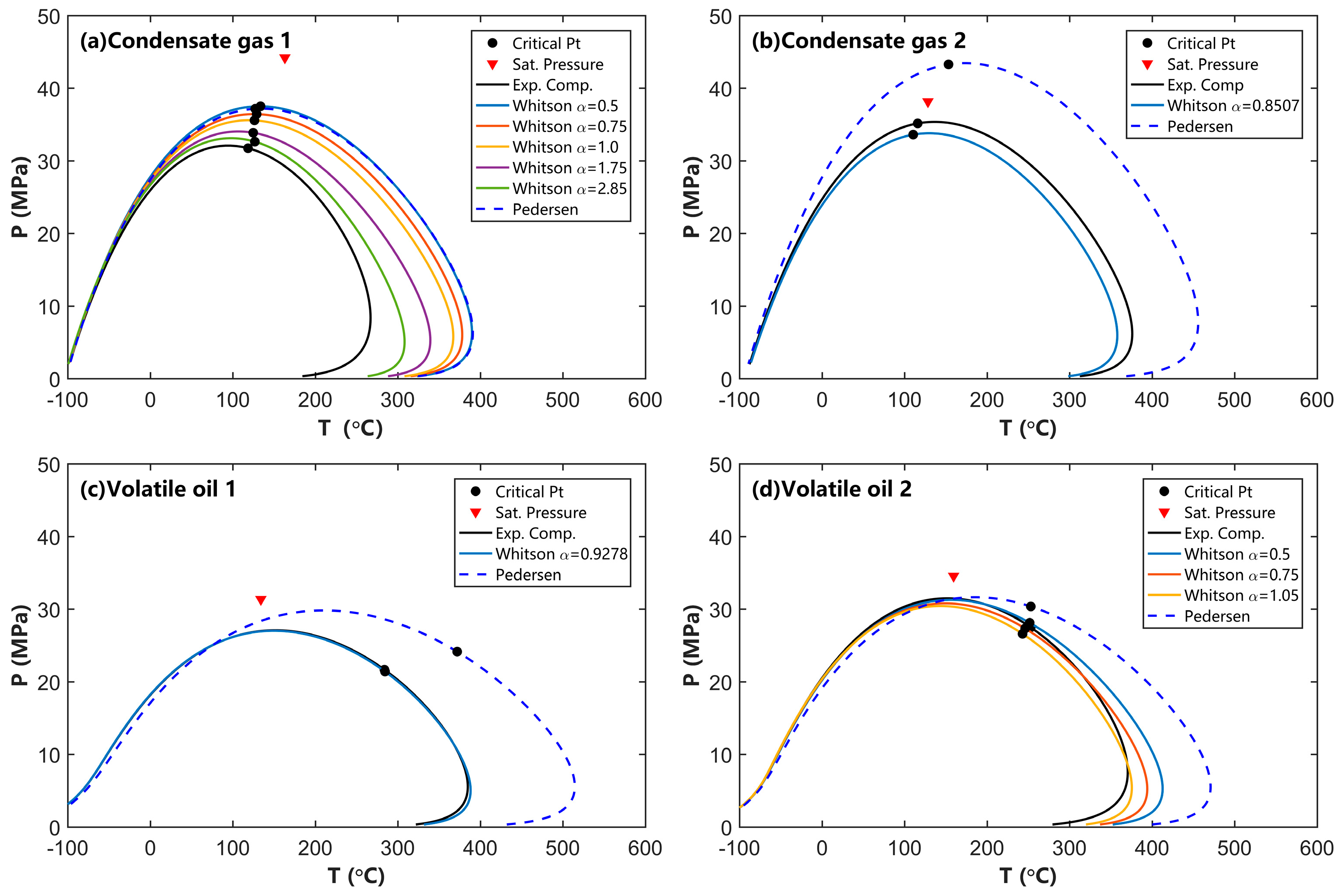
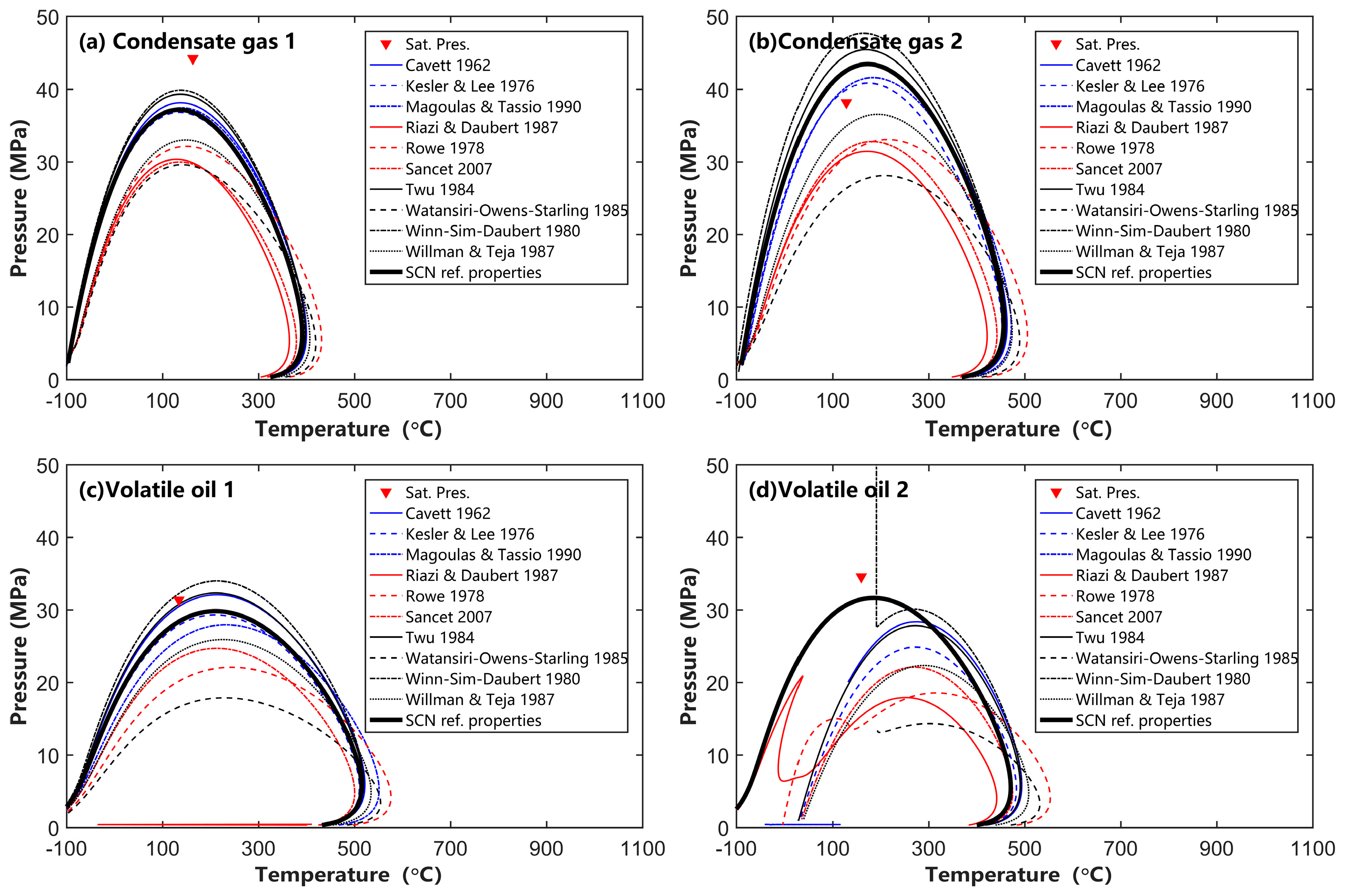
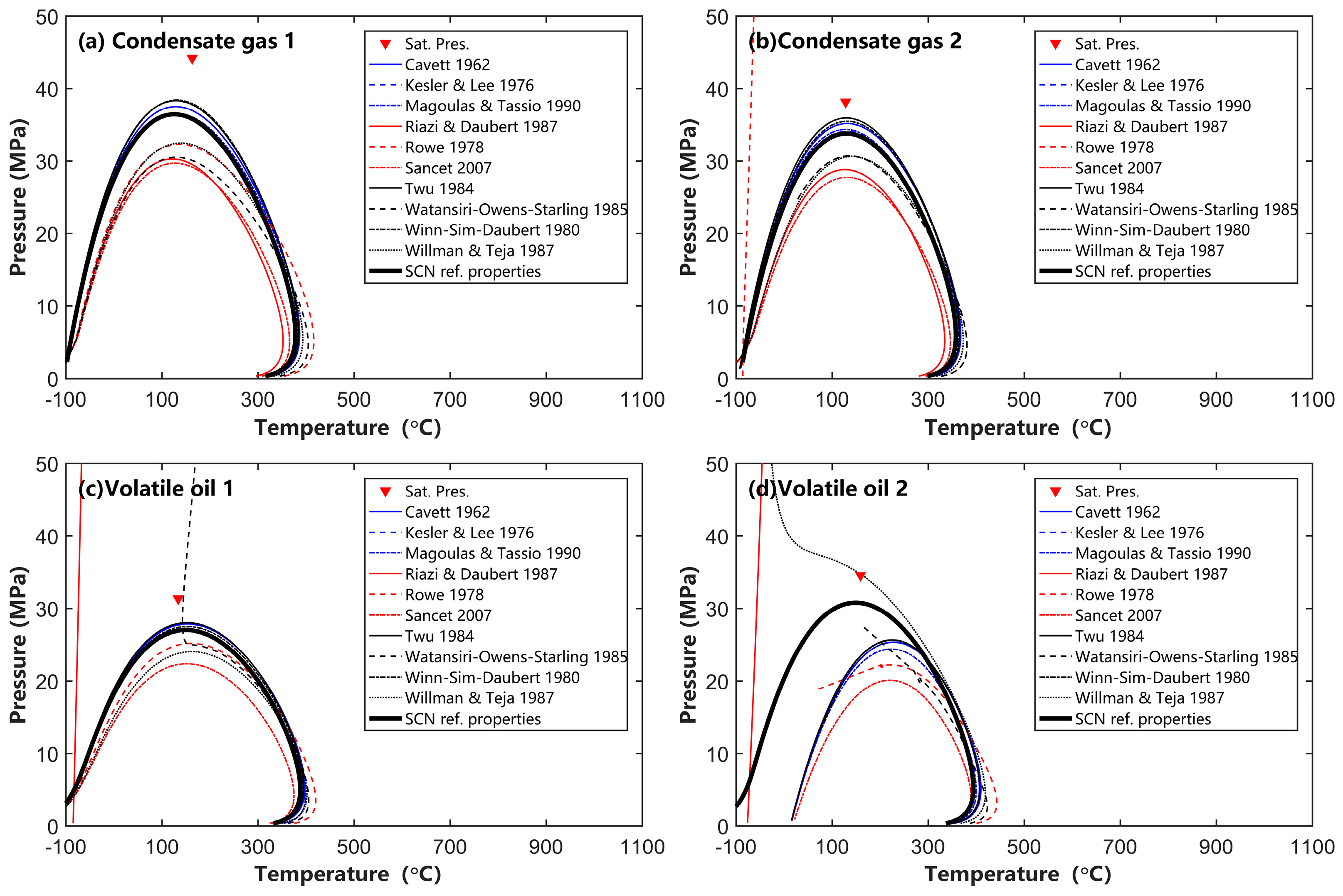
4.1. Effects of C7+ Splitting and SCN Group Distribution on the Phase Behavior Calculation
4.2. Effects of SCN Group Characterization on Phase Behavior Calculation
4.3. Effects of the SCN Group Lumping Scheme on the Phase Behavior Calculation
5. Conclusions
- (1)
- A workflow including three main steps (1. determine distribution pattern; 2. determine EOS parameters for SCN group; and 3. lump individual SCN group) for the characterization of EOS parameters for reservoir fluids was proposed (Figure 1);
- (2)
- The choice of component splitting and SCN group EOS parameter calculation methods significantly impact the phase behavior calculations, whereas the SCN group lumping methods have a minimal impact on the phase behavior calculation results;
- (3)
- The SCN group distribution obtained using the Whitson splitting method is closer to the experimental data compared to Pedersen’s splitting method. Additionally, for condensate gas and volatile oil, we recommended that the parameter α in the Whitson component distribution model ranges between 0.5 and 1.0 for the most accurate representation of component distribution for these reservoir fluids;
- (4)
- The EOS parameter calculation methods proposed by Cavett, Kesler and Lee, Twu, and Magoulas and Tassios, when combined with the Whitson component distribution, can reliably calculate phase behavior for condensate gas and volatile oil. However, other EOS parameter calculation methods are not recommended for engineering calculations of condensate gas and volatile oil reservoirs;
- (5)
- In terms of component lumping methods, the Whitson method and the Newley and Merrill method exhibit similar performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Condensate Gas-1 | Condensate Gas-2 | Volatile Oil-1 | Volatile Oil-2 | ||||
|---|---|---|---|---|---|---|---|
| Reservoir Temp.: 163.1 °C Sat. Pressure: 44.2 MPa C11+ Density: 0.8296 g/cm3 C11+ Mw: 204 g/mol | Reservoir Temp.: 128.3 °C Sat. Pressure: 38.16MPa C31+ Density: 0.9228 g/cm3 C31+ Mw: 503.96 g/mol | Reservoir Temp.: 134.0 °C Sat. Pressure: 31.36MPa C36+ Density: 0.9364 g/cm3 C36+ Mw: 600.55 g/mol | Reservoir Temp.: 159.4 °C Sat. Pressure: 34.56MPa C11+ Density: 0.8659 g/cm3 C11+ Mw: 286 g/mol | ||||
| Component | mol% | Component | mol% | Component | mol% | Component | mol% |
| N2 | 2.21 | N2 | 0.393 | N2 | 3.082 | N2 | 2.87 |
| CO2 | 2.06 | CO2 | 1.776 | CO2 | 0.593 | CO2 | 1.95 |
| C1 | 71.92 | C1 | 68.251 | C1 | 51.095 | C1 | 59.54 |
| C2 | 4.76 | C2 | 7.024 | C2 | 8.654 | C2 | 6.08 |
| C3 | 2.12 | C3 | 6.625 | C3 | 3.104 | C3 | 3.86 |
| iC4 | 0.66 | iC4 | 1.418 | iC4 | 1.732 | iC4 | 1.02 |
| nC4 | 1.21 | nC4 | 2.319 | nC4 | 2.305 | nC4 | 2.09 |
| iC5 | 0.65 | iC5 | 0.873 | iC5 | 1.212 | iC5 | 0.41 |
| nC5 | 0.85 | nC5 | 0.842 | nC5 | 1.345 | nC5 | 1.19 |
| C6 | 2.93 | C6 | 1.723 | C6 | 3.587 | C6 | 2.76 |
| C7 | 2.03 | C7 | 1.724 | C7 | 3.010 | C7 | 2.96 |
| C8 | 2.40 | C8 | 1.199 | C8 | 4.506 | C8 | 3.94 |
| C9 | 1.73 | C9 | 0.698 | C9 | 2.787 | C9 | 3.22 |
| C10 | 1.14 | C10 | 0.738 | C10 | 2.193 | C10 | 2.43 |
| C11+ | 3.33 | C11 | 0.546 | C11 | 1.495 | C11+ | 5.69 |
| C12 | 0.455 | C12 | 1.287 | ||||
| C13 | 0.447 | C13 | 1.095 | ||||
| C14 | 0.396 | C14 | 0.985 | ||||
| C15 | 0.413 | C15 | 1.002 | ||||
| C16 | 0.289 | C16 | 0.737 | ||||
| C17 | 0.219 | C17 | 0.626 | ||||
| C18 | 0.225 | C18 | 0.583 | ||||
| C19 | 0.177 | C19 | 0.464 | ||||
| C20 | 0.147 | C20 | 0.387 | ||||
| C21 | 0.131 | C21 | 0.345 | ||||
| C22 | 0.114 | C22 | 0.310 | ||||
| C23 | 0.1 | C23 | 0.283 | ||||
| C24 | 0.091 | C24 | 0.235 | ||||
| C25 | 0.082 | C25 | 0.207 | ||||
| C26 | 0.075 | C26 | 0.160 | ||||
| C27 | 0.069 | C27 | 0.144 | ||||
| C28 | 0.064 | C28 | 0.043 | ||||
| C29 | 0.06 | C29 | 0.104 | ||||
| C30 | 0.049 | C30 | 0.074 | ||||
| C31+ | 0.248 | C31 | 0.051 | ||||
| C32 | 0.046 | ||||||
| C33 | 0.039 | ||||||
| C34 | 0.028 | ||||||
| C35 | 0.022 | ||||||
| C36+ | 0.042 | ||||||
References
- Zhang, N.; Ya, Q. Evaluation of the phase behavior of CO2 injection in condensate gas wells considering formation water. Xinjiang Oil Gas 2013, 9, 76–80. [Google Scholar]
- Sun, Y.; Meng, Y.; Lian, Z.; Tang, Y.; Chen, K.Z. Influence of the splitting schemes on the heavy fractions characterization procedure. Complex Hydrocarb. Reserv. 2009, 2, 39–43. [Google Scholar]
- Zachopoulos, F.N.; Kokkinos, N.C. Detection methodologies on oil and gas kick: A systematic review. Int. J. Oil Gas Coal Technol. 2023, 33, 1–19. [Google Scholar] [CrossRef]
- Zachopoulos, F.N.; Kokkinos, N.C. Mathematical modeling of oil and gas kick during drilling operations. In Proceedings of the 11th International Conference on Mathematical Modeling in Physical Sciences, Belgrade, Serbia, 5–8 September 2022. [Google Scholar]
- Kokkinos, N.C. Modeling and simulation of biphasic catalytic hydrogenation of a hydroformylated fuel. Int. J. Hydrogen Energy 2021, 46, 19731–19736. [Google Scholar] [CrossRef]
- Peng, D.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, M.; Mei, H.; Liu, Y. Phase behavior of condensate gas reservoir fluids and influencing factors. Xinjiang Oil Gas 2007, 3, 62–66. [Google Scholar]
- Pedersen, K.S.; Thomassen, P.; Fredenslund, A. SRK-EOS calculation for crude oils. Fluid Phase Equilibria 1983, 14, 209–218. [Google Scholar] [CrossRef]
- Pedersen, K.S.; Thomassen, P.; Fredenslund, A. Thermodynamics of petroleum mixtures containing heavy hydrocarbons. 1. Phase envelope calculations by use of the Soave-Redlich-Kwong equation of state. Ind. Eng. Chem. Process Des. Dev. 1984, 23, 163–170. [Google Scholar] [CrossRef]
- Pedersen, K.S.; Christensen, P.L. Phase Behavior of Petroleum Reservoir Fluids; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Whitson, C.H. Characterizing hydrocarbon plus fractions. SPE J. 1983, 23, 683–694. [Google Scholar] [CrossRef]
- Whitson, C.H. Effect of C7+ properties on equation-of-state predictions. SPE J. 1984, 24, 685–696. [Google Scholar] [CrossRef]
- Duan, J.; Wang, W.; Liu, H.; Gong, J. Modeling the characterization of the plus fractions by using continuous distribution function. Fluid Phase Equilibria 2013, 35, 1–10. [Google Scholar] [CrossRef]
- Foroughi, S.; Khoozan, D.; Jamshidi, S. Optimal distribution function determination for plus fraction splitting. Can. J. Chem. Eng. 2019, 97, 2752–2764. [Google Scholar] [CrossRef]
- Ahmed, T. Equations of State and PVT Analysis Applications for Improved Reservoir Modeling; Gulf Professional Publishing: Houston, TX, USA, 2016. [Google Scholar]
- Riazi, M.R.; Daubert, T.E. Characterization parameters for petroleum fractions. Ind. Eng. Chem. Res. 1987, 26, 755–759. [Google Scholar] [CrossRef]
- Sim, W.J.; Daubert, T.E. Prediction of vapor-liquid equilibria of undefined mixtures. Ind. Eng. Chem. Process Des. Dev. 1980, 19, 386–393. [Google Scholar] [CrossRef]
- Watansiri, S.; Owens, V.H.; Starling, K.E. Correlations for estimating critical constants, acentric factor, and dipole moment for undefined coal-fluid fractions. Ind. Eng. Chem. Process Des. Dev. 1985, 24, 294–296. [Google Scholar] [CrossRef]
- Rowe, A.M. Internally consistent correlations for predicting phase compositions for use in reservoir composition simulations. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 1–3 October 1978. [Google Scholar]
- Willman, B.; Teja, A.S. Prediction of dew points of semicontinuous natural gas and petroleum mixtures. 1. Characterization by use of an effective carbon number and ideal solution predictions. Ind. Eng. Chem. Res. 1987, 26, 948–952. [Google Scholar] [CrossRef]
- Magoulas, K.; Tassios, D. Thermophysical properties of n-Alkanes from C1 to C20 and their prediction for higher ones. Fluid Phase Equilibria 1990, 56, 119–140. [Google Scholar] [CrossRef]
- Twu, C.H. An internally consistent correlation for predicting the critical properties and molecular weights of petroleum and coal-tar liquids. Fluid Phase Equilibria 1984, 16, 137–150. [Google Scholar] [CrossRef]
- Sancet, G.F. Heavy fraction C7+ characterization for PR-EOS. In Proceedings of the SPE Annual Technical Conference and Exhibition, Anaheim, CA, USA, 11–14 November 2007. [Google Scholar]
- Newley, T.M.J.; Merrill, R.C., Jr. Pseudocomponent selection for compositional simulation. SPE Reserv. Eng. 1991, 6, 490–496, SPE-19638-PA. [Google Scholar] [CrossRef]
- Hong, K.C. Lumped-component characterization of crude oils for compositional simulation. In Proceedings of the SPE Enhanced Oil Recovery Symposium, Tulsa, OK, USA, 4–7 April 1982. SPE-10691-MS. [Google Scholar]
- Zhao, H.; Song, C.; Zhang, H.; Di, C.; Tian, Z. Improved fluid characterization and phase behavior approaches for gas flooding and application on Tahe light crude oil system. J. Pet. Sci. Eng. 2022, 208 Pt D, 109653. [Google Scholar] [CrossRef]
- Whitson, C.H.; Brulé, M.R. Phase Behavior, SPE Monograph Volume 20; Society of Petroleum Engineers: Houston, TX, USA, 2000. [Google Scholar]
- Michelsen, M.L. Calculation of phase envelopes and critical points for multicomponent mixtures. Fluid Phase Equilibria 1980, 4, 1–10. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| −0.577191652 | |
| 0.988205891 | |
| −0.897056937 | |
| 0.918206857 | |
| −0.756704078 | |
| 0.482199394 | |
| −0.193527818 | |
| 0.035868343 |
| Methods | Input | Output |
|---|---|---|
| 1. Silva and Rodriguez [16] | ||
| 2. Riazi and Daubert [17] | ||
| 3. Cavett [16] | ||
| 4. Kesler and Lee [16] | ||
| 5. Winn–Sim–Daubert [18] | ||
| 6. Watansiri–Owens–Starling [19] | ||
| 7. Edmister [16] | ||
| 8. Rowe [20] | ||
| 9. Willman and Teja [21] | SCN | |
| 10. Magoulas and Tassios [22] | ||
| 11. Twu [23] | ||
| 12. Sancet [24] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, H.; Zhao, H.; Wang, B.; Wu, H.; Nan, R.; An, C. Effects of the Characterization Methods of Heptane Plus Components (C7+) on the Phase Behavior of Volatile Fluids. Processes 2024, 12, 2066. https://doi.org/10.3390/pr12102066
Wang J, Liu H, Zhao H, Wang B, Wu H, Nan R, An C. Effects of the Characterization Methods of Heptane Plus Components (C7+) on the Phase Behavior of Volatile Fluids. Processes. 2024; 12(10):2066. https://doi.org/10.3390/pr12102066
Chicago/Turabian StyleWang, Jia, Hailong Liu, Haining Zhao, Bo Wang, Haonan Wu, Rongli Nan, and Chen An. 2024. "Effects of the Characterization Methods of Heptane Plus Components (C7+) on the Phase Behavior of Volatile Fluids" Processes 12, no. 10: 2066. https://doi.org/10.3390/pr12102066
APA StyleWang, J., Liu, H., Zhao, H., Wang, B., Wu, H., Nan, R., & An, C. (2024). Effects of the Characterization Methods of Heptane Plus Components (C7+) on the Phase Behavior of Volatile Fluids. Processes, 12(10), 2066. https://doi.org/10.3390/pr12102066






