Flow Field Characteristics of Fugitive Dust from Grab Unloading in an Open Space
Abstract
:1. Introduction
2. Research Method
2.1. Experimental Method
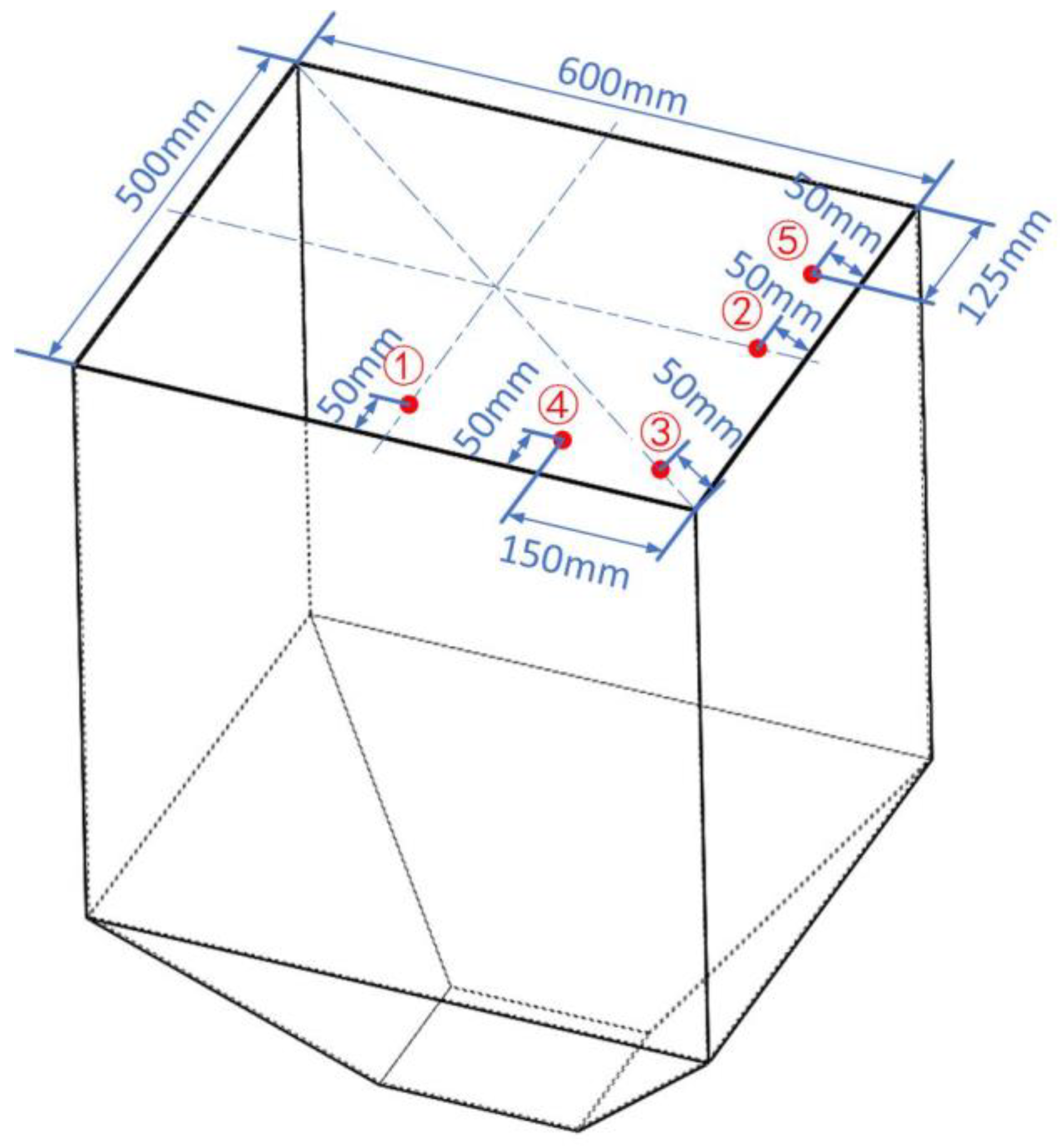
2.1.1. Construction of Grab Unloading Experimental Model
2.1.2. Construction of Experimental Measurement System
2.2. Numerical Simulation Method
2.2.1. CFD-DEM Governing Equations
2.2.2. Fluid–Particle Interaction Forces
2.2.3. Turbulence Model
2.2.4. Motion Equation of Dust
3. Experimental Study on Fugitive Dust from Grab Unloading
3.1. Parameter Calibration of the Bulk Material
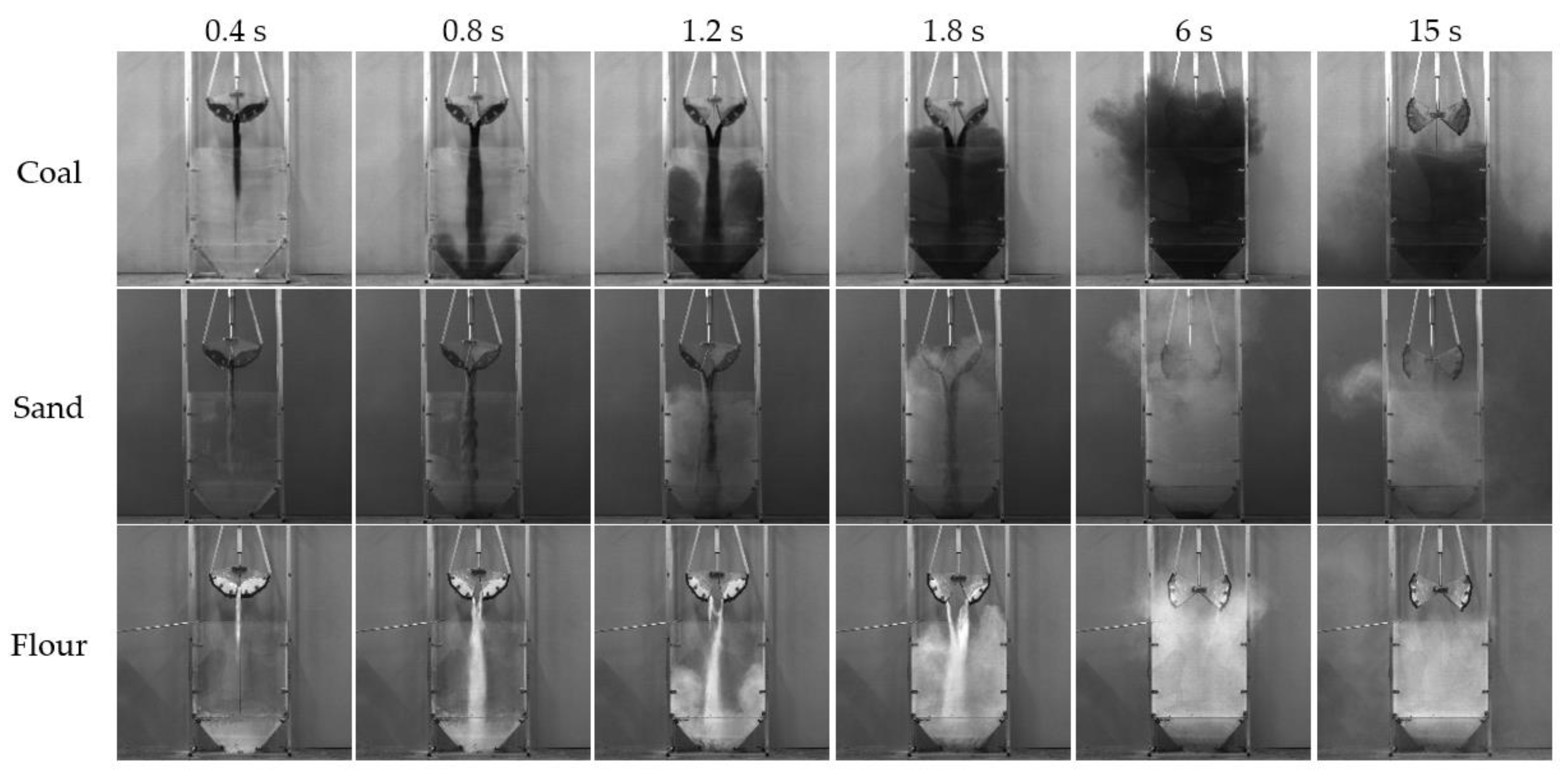
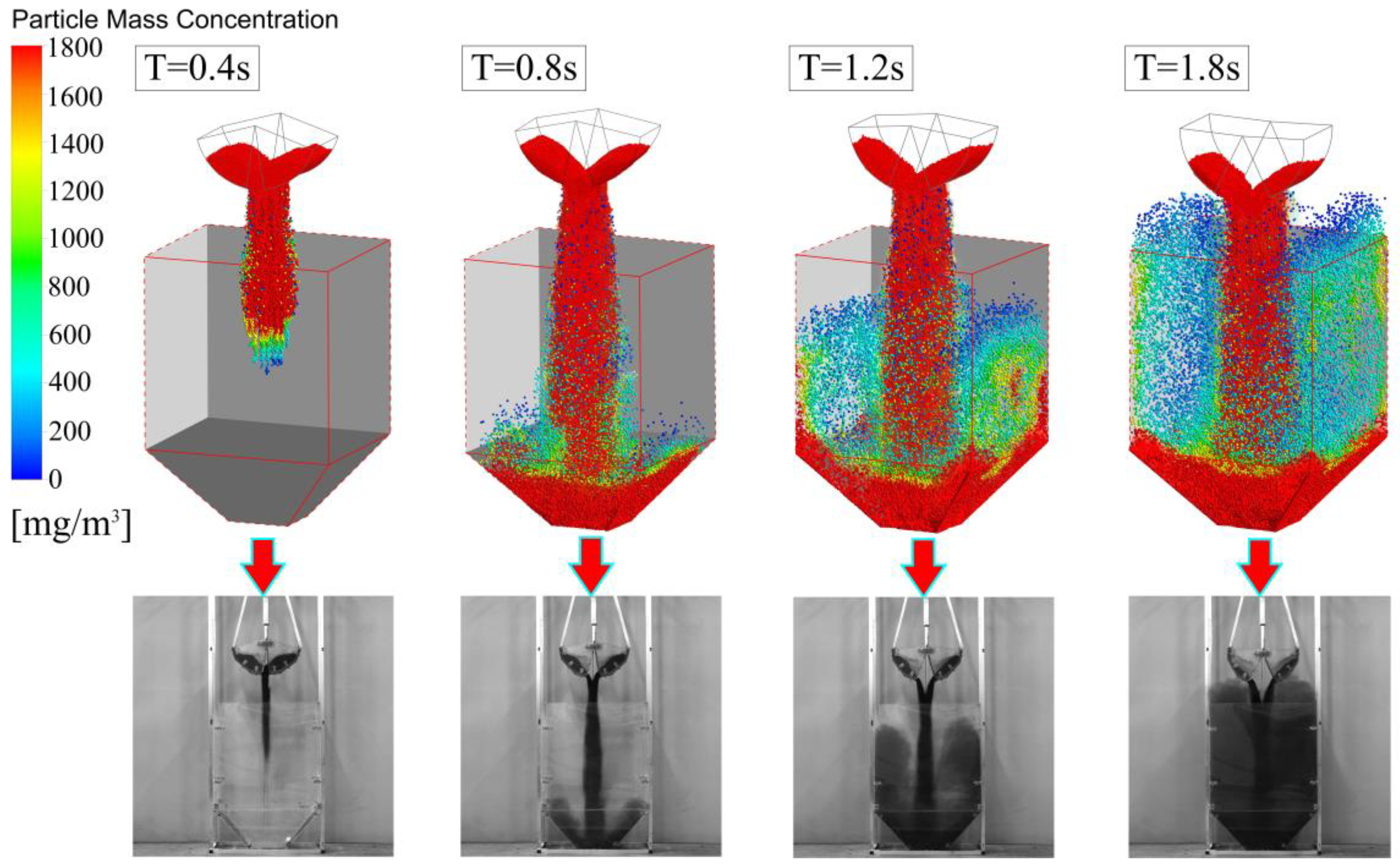
3.2. The Law of Fugitive Dust during Unloading Process
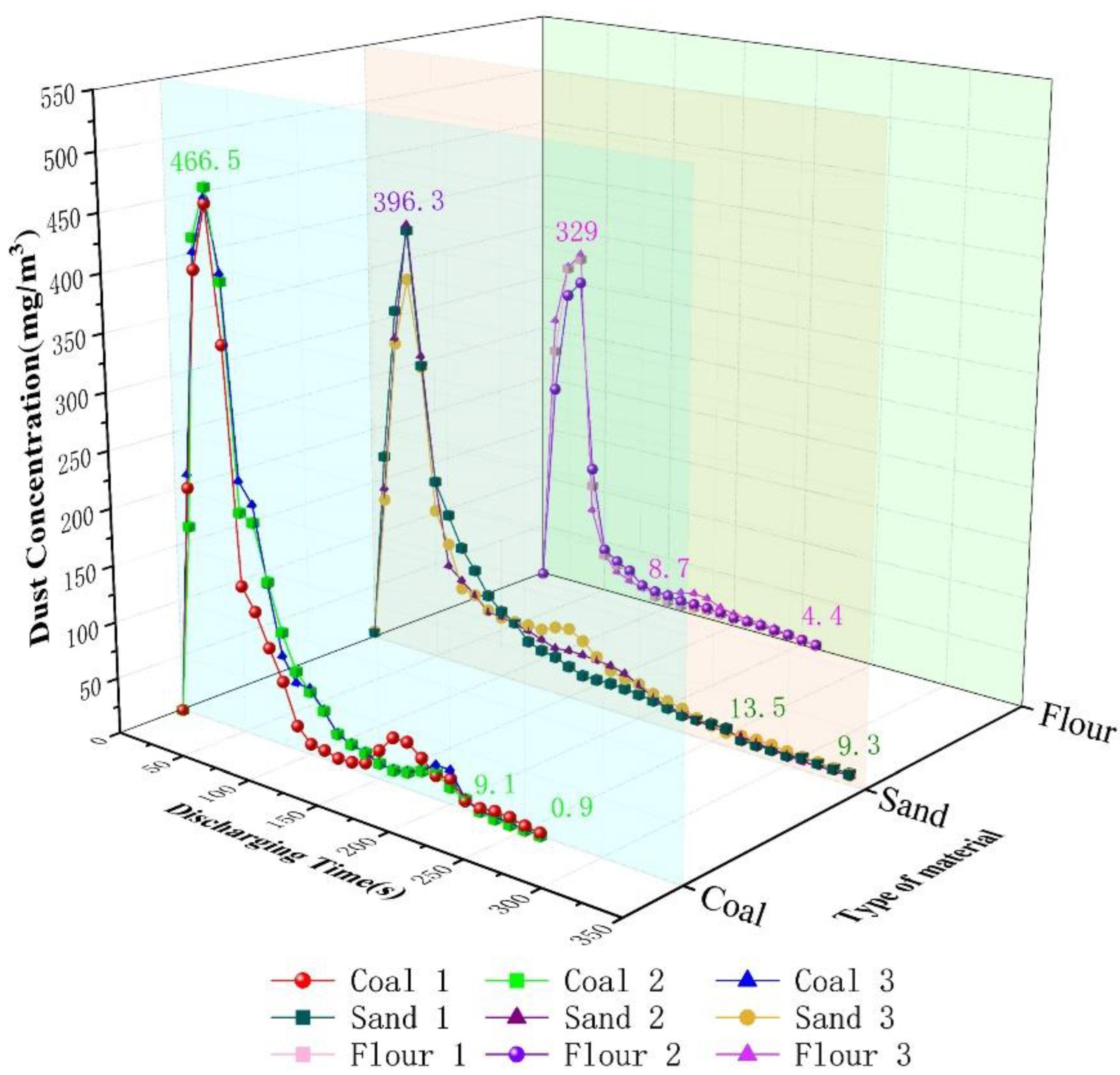
3.3. Variation Law of Dust Concentration during Unloading Process
- (1)
- Variation law of dust concentration at measurement point 1.
- (2)
- Variation law of dust concentration at measurement point 2.
- (3)
- Variation law of dust concentration at measurement point 3.
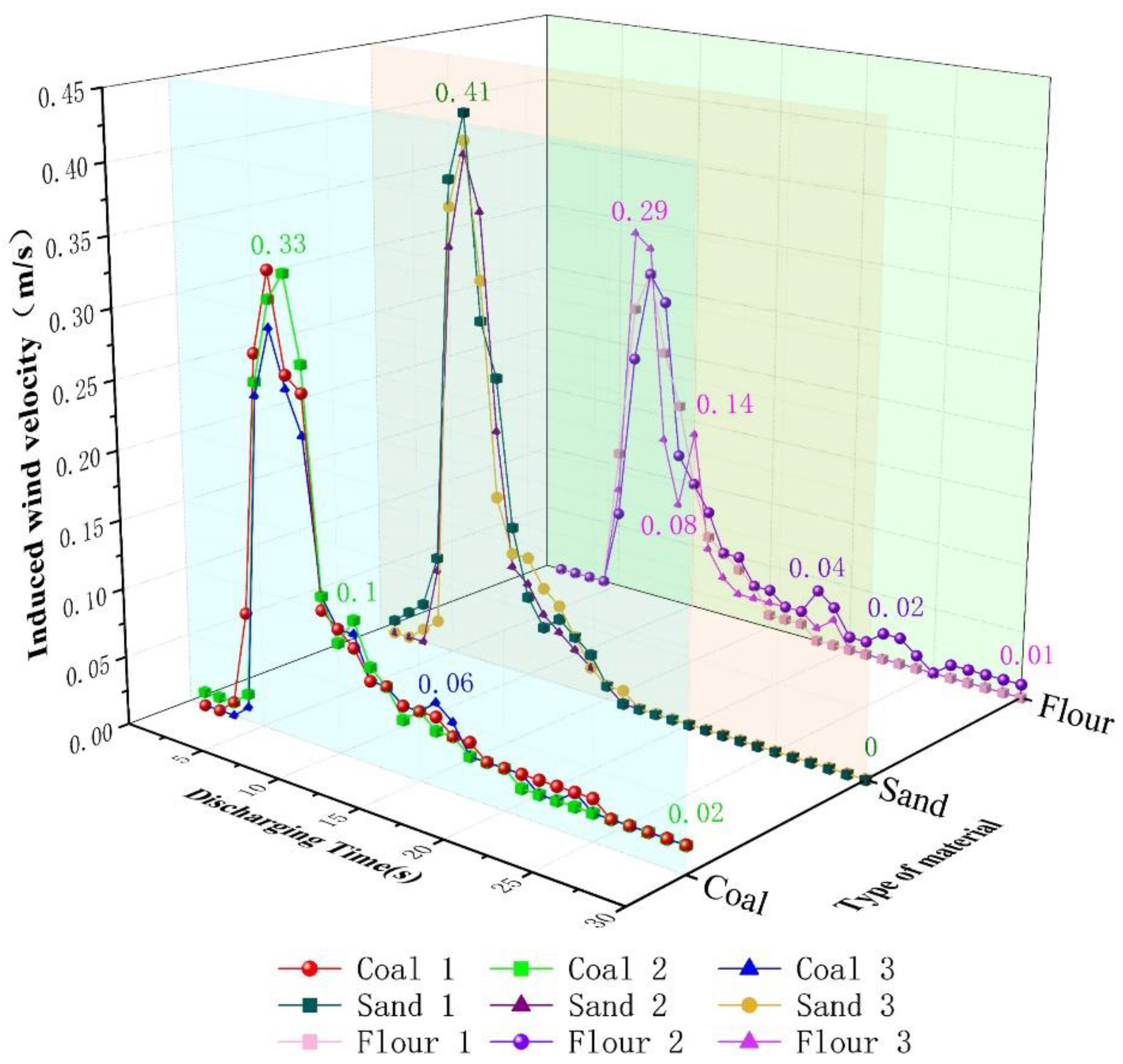
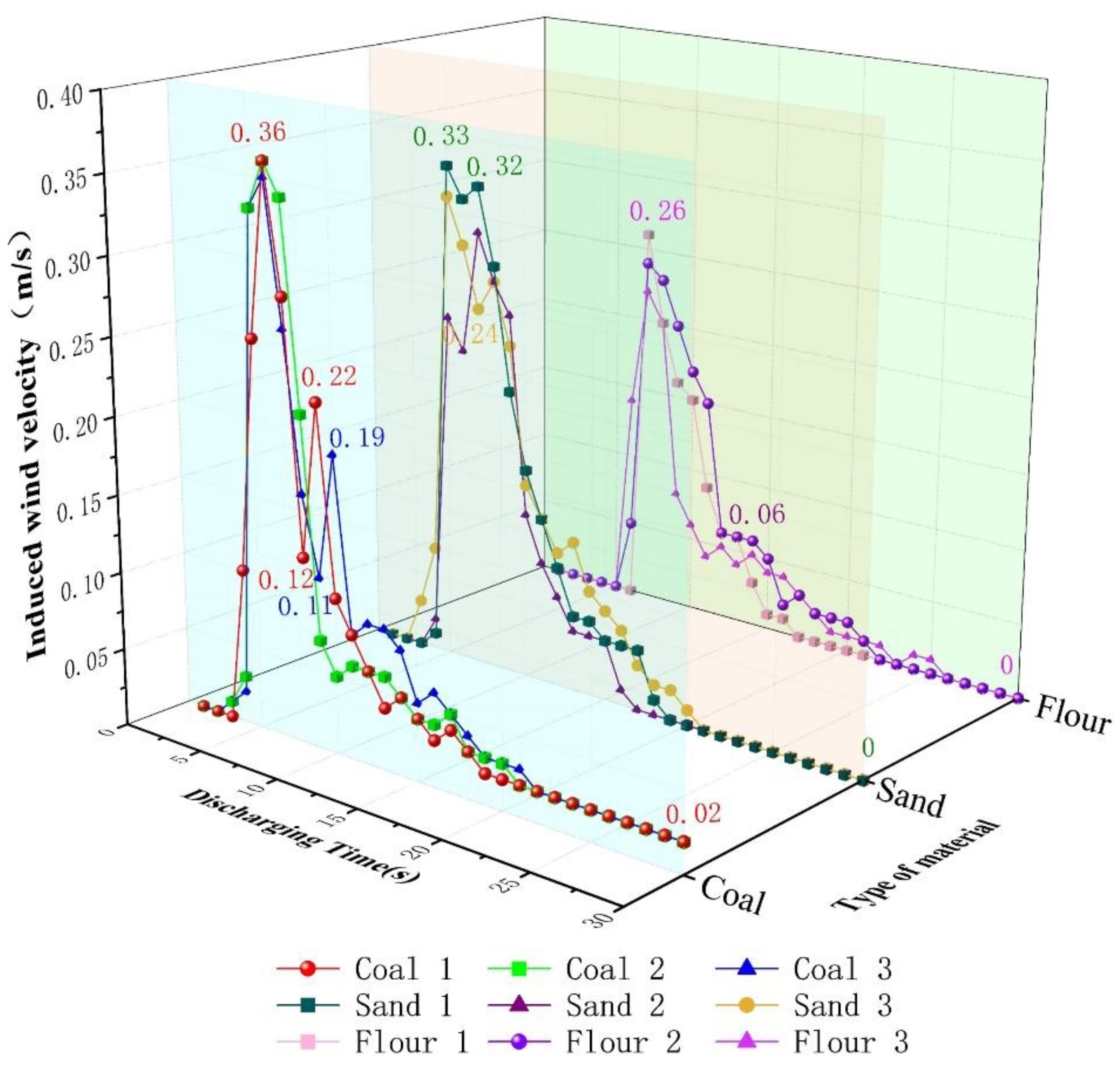
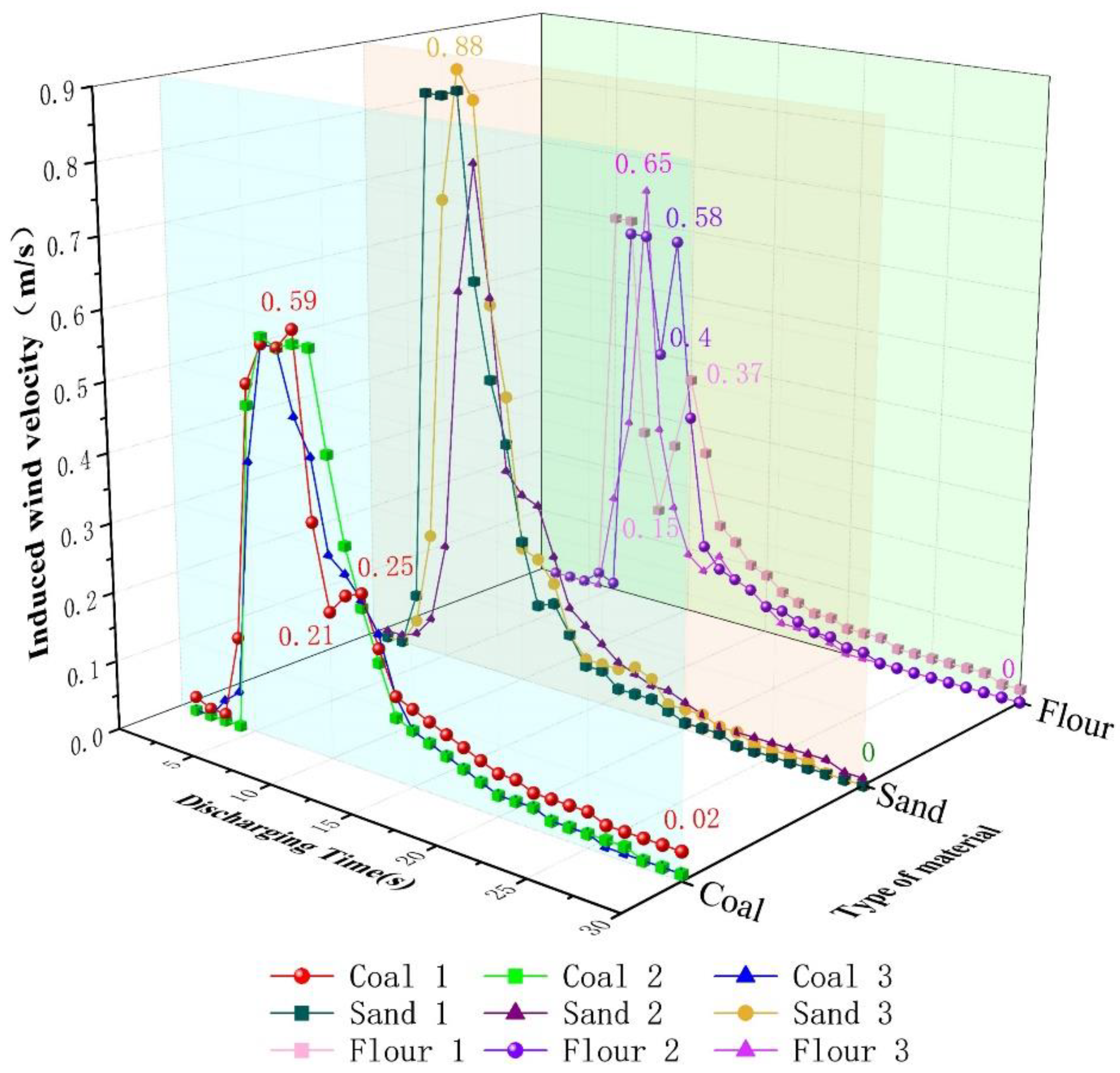
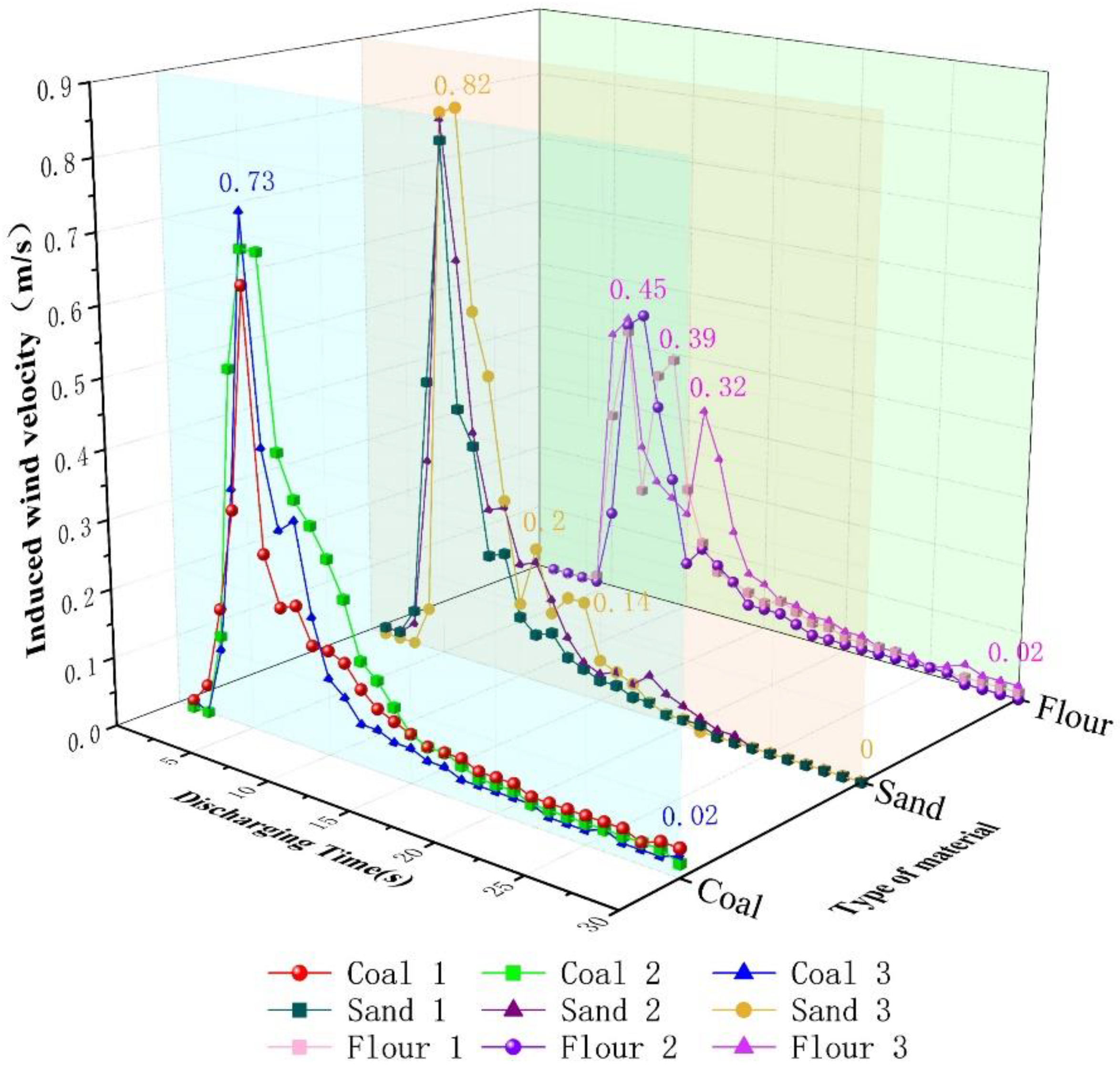
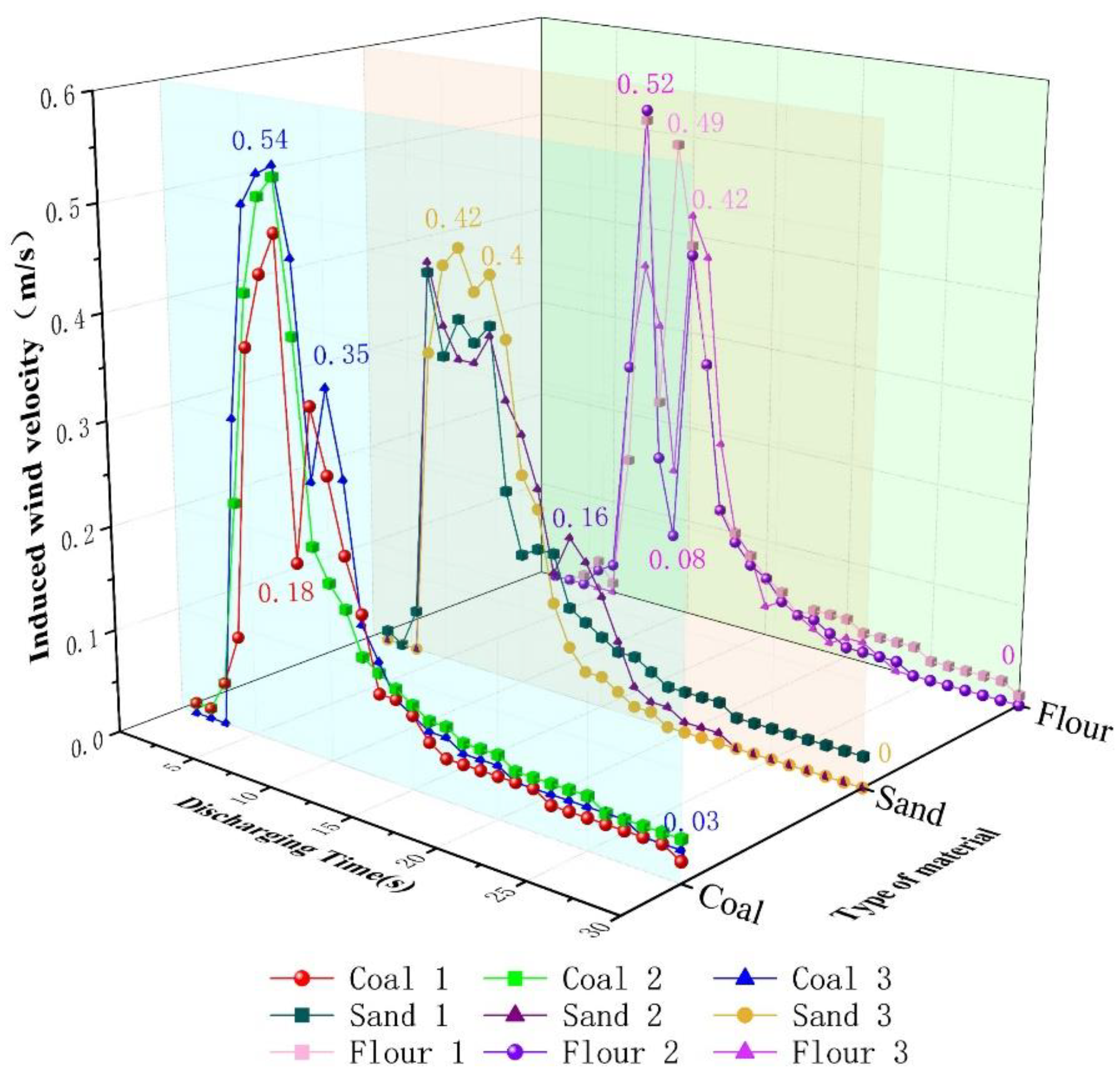
3.4. Variation Law of Induced Wind Velocity during Unloading Process
- (1)
- Variation law of induced wind velocity at measurement point 1.
- (2)
- Variation law of the induced wind velocity at measurement point 2
- (3)
- Variation law of induced wind velocity at measurement point 3
- (4)
- Variation law of induced wind velocity at measurement point 4
- (5)
- Variation law of induced wind velocity at measurement point 5
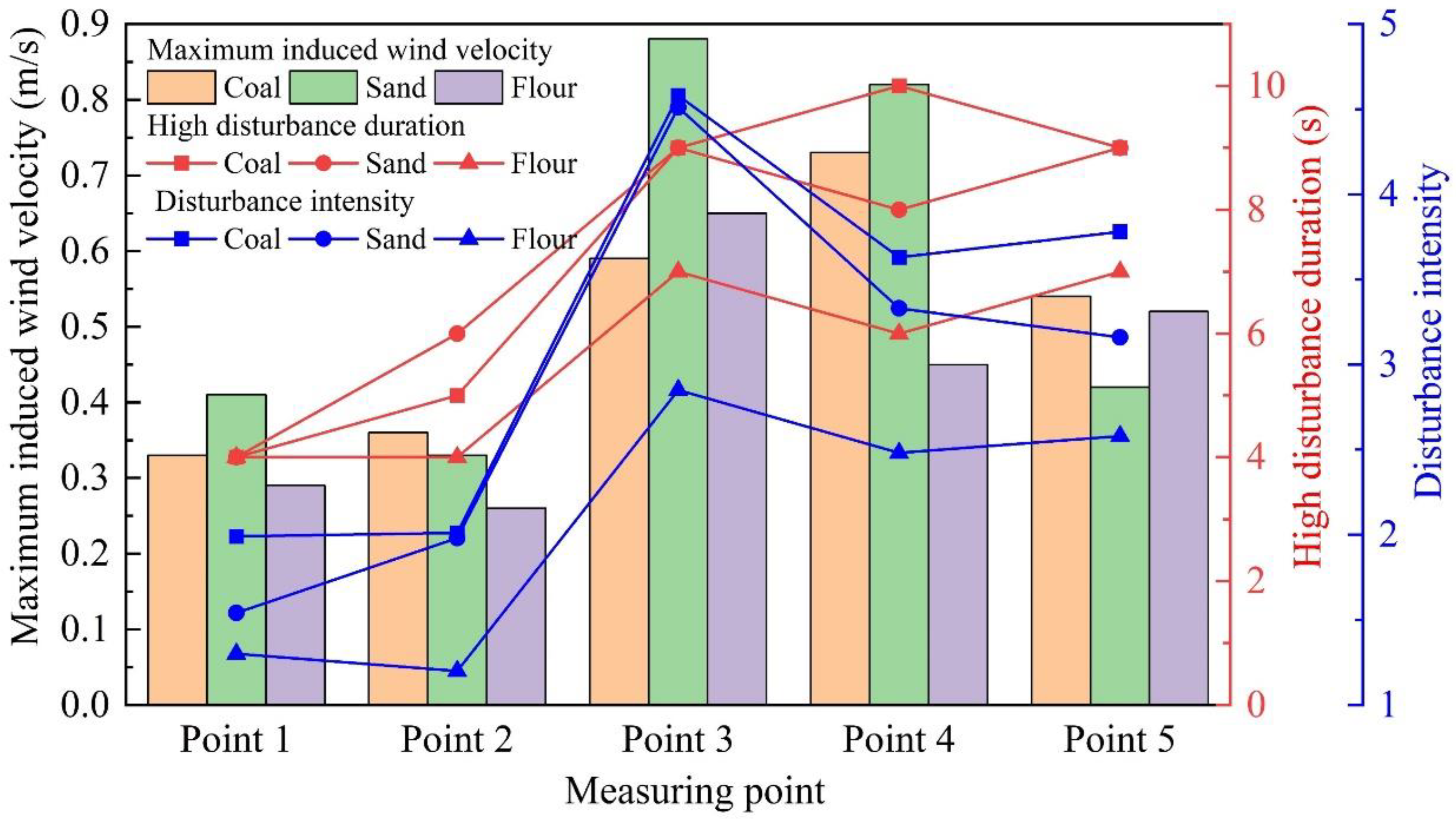
- (1)
- The maximum induced wind velocity, duration of the larger disturbance, and disturbance intensity of the three materials at measurement points 3, 4, and 5 were generally higher, whereas the maximum induced wind velocity, duration of the larger disturbance, and disturbance intensity of the three materials at measurement points 1 and 2 were generally lower.
- (2)
- Comparing the three types of materials at the same measurement point, in terms of the maximum induced wind velocity and the disturbance intensity, the values of coal and sand are close and greater than that of flour; in terms of the duration of the large disturbance, coal and sand are close, whereas the duration of the large disturbance of flour lags behind and is short.
4. Numerical Simulation and Study of Law of Gas–Solid Two-Phase Flow Field during Grab Unloading
4.1. Grid Division and Independence Verification
4.2. Setting of Numerical Simulation Parameters
4.3. Correctness Verification of Numerical Simulation
4.4. Analysis of Simulation Results
4.4.1. Motion Trajectory and Velocity Distribution of Particle Flow Field and Airflow Field
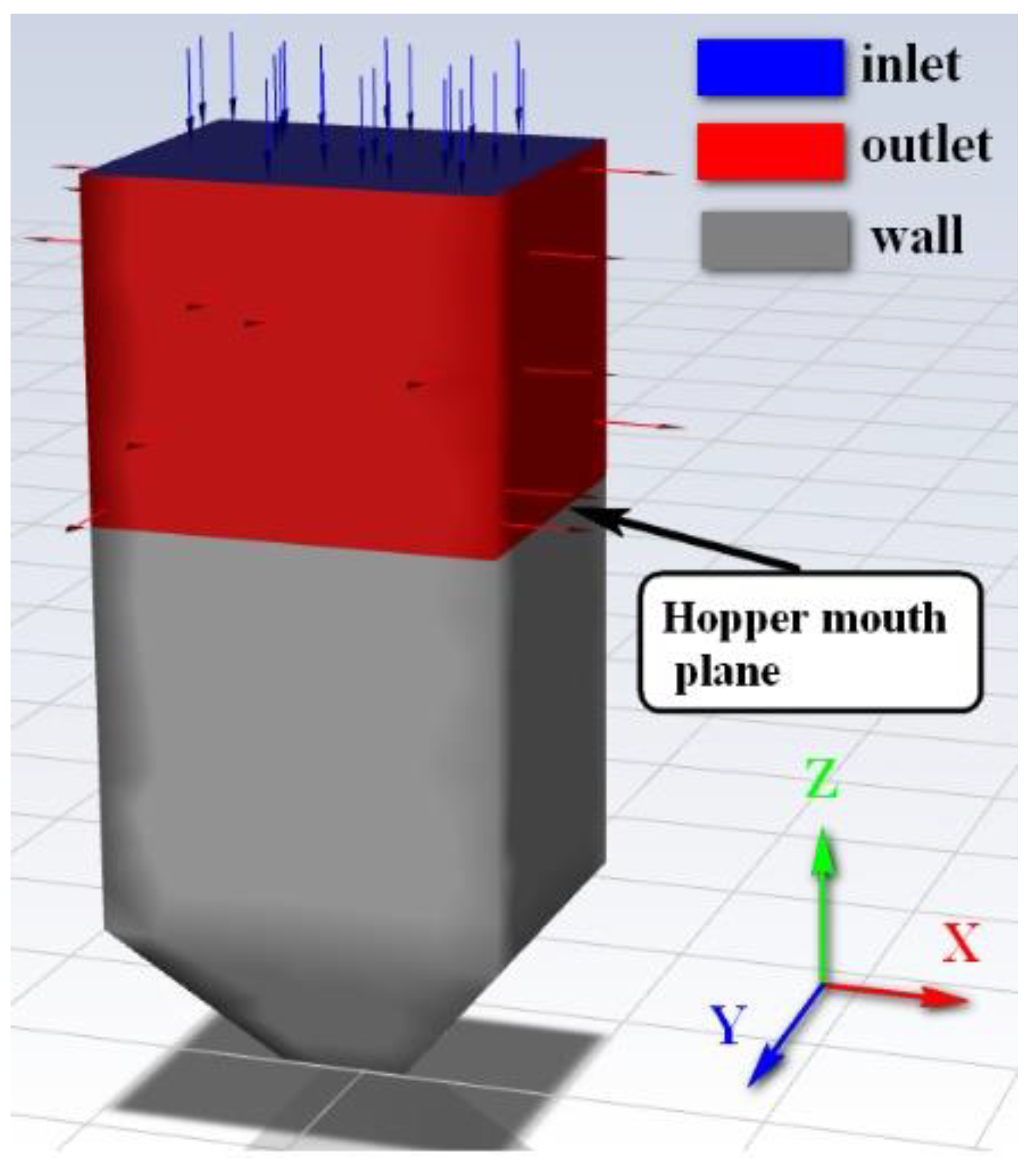
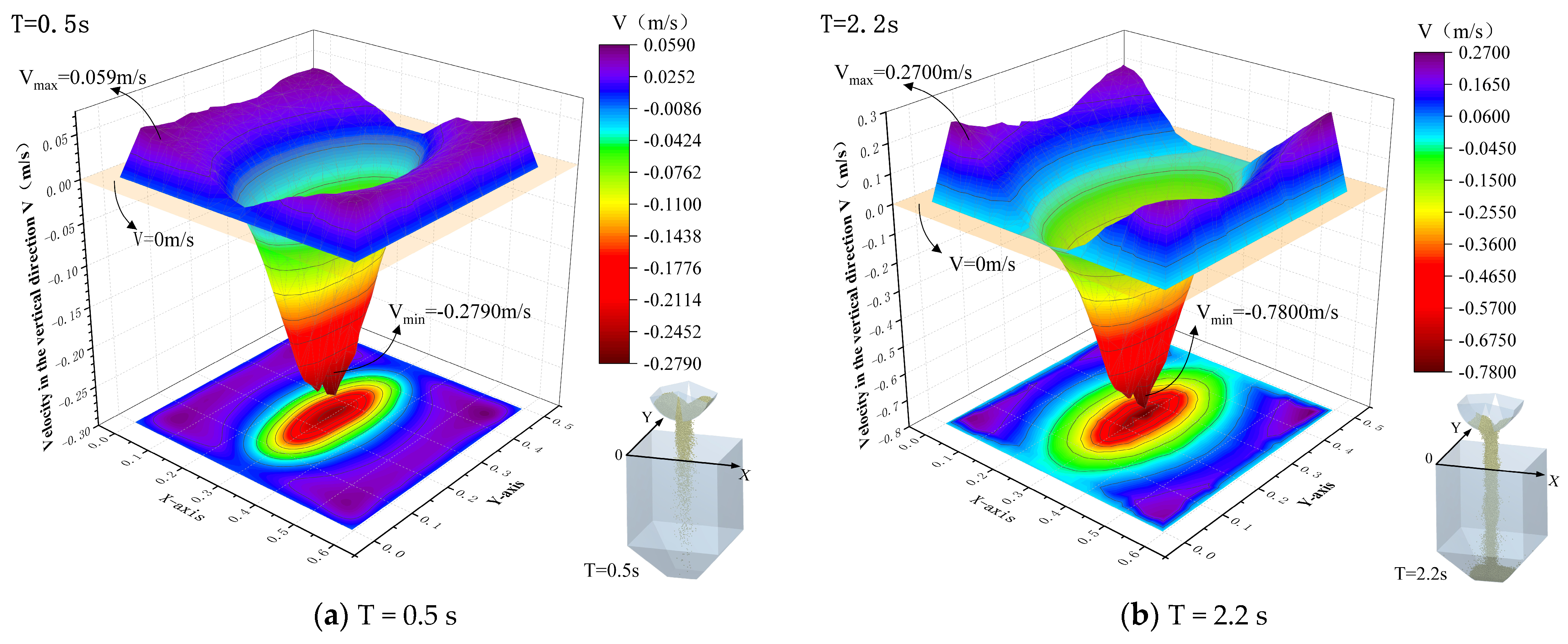
4.4.2. Research on the Airflow Distribution Law of the Hopper Opening Plane
5. Conclusions
- (1)
- According to the parameter calibration of the bulk material and the grab-unloading experiment, for coal and sand, owing to the poor viscosity and high fluidity, the material flow on both sides of the grab was continuous, uniform, and symmetrical. The dust diffusion was relatively symmetrical at the beginning and showed evident disorderly diffusion with the progression of the unloading process. For flour, owing to its high viscosity and poor fluidity, the material flow on both sides of the grab was clearly different, and the material flow was unstable, forming multiple intermittent material flows, and the dust spread in disorder during the entire unloading process. For coal, sand, and flour, the duration of dust rising diffusion was 5.2, 6.5, and 5.3 s, respectively; the emptying times of materials in the grab were 5, 5.7, and 6.3 s, respectively; and the maximum diffusion ranges of dust were 956 mm × 1389 mm, 893 mm × 1540 mm, and 769 mm × 1450 mm, respectively.
- (2)
- The related characteristics of dust concentration were analysed, and the following conclusions were drawn: For measurement points with the same horizontal coordinates and higher positions, the maximum concentration of dust was low, the settling time was short, and the duration of the high-concentration state was short. The maximum concentrations of the three materials at two measurement points in descending order are as follows: sand, flour, and coal.
- (3)
- Analysis of the induced wind velocity-related characteristics of the three types of materials at five measurement points: The maximum induced wind velocity, the duration of the larger disturbance, and the disturbance intensity of the three materials at measurement points 3, 4, and 5 were generally larger, whereas the maximum induced wind velocity, the duration of the larger disturbance, and the disturbance intensity of the three materials at measurement points 1 and 2 were generally smaller. Comparing the three types of materials at the same measurement point, in terms of the maximum induced wind velocity and the disturbance intensity, the values of coal and sand were close and greater than that of flour. In terms of the duration of the large disturbance, coal and sand were close, whereas the duration of the large disturbance of flour was lagging behind and short.
- (4)
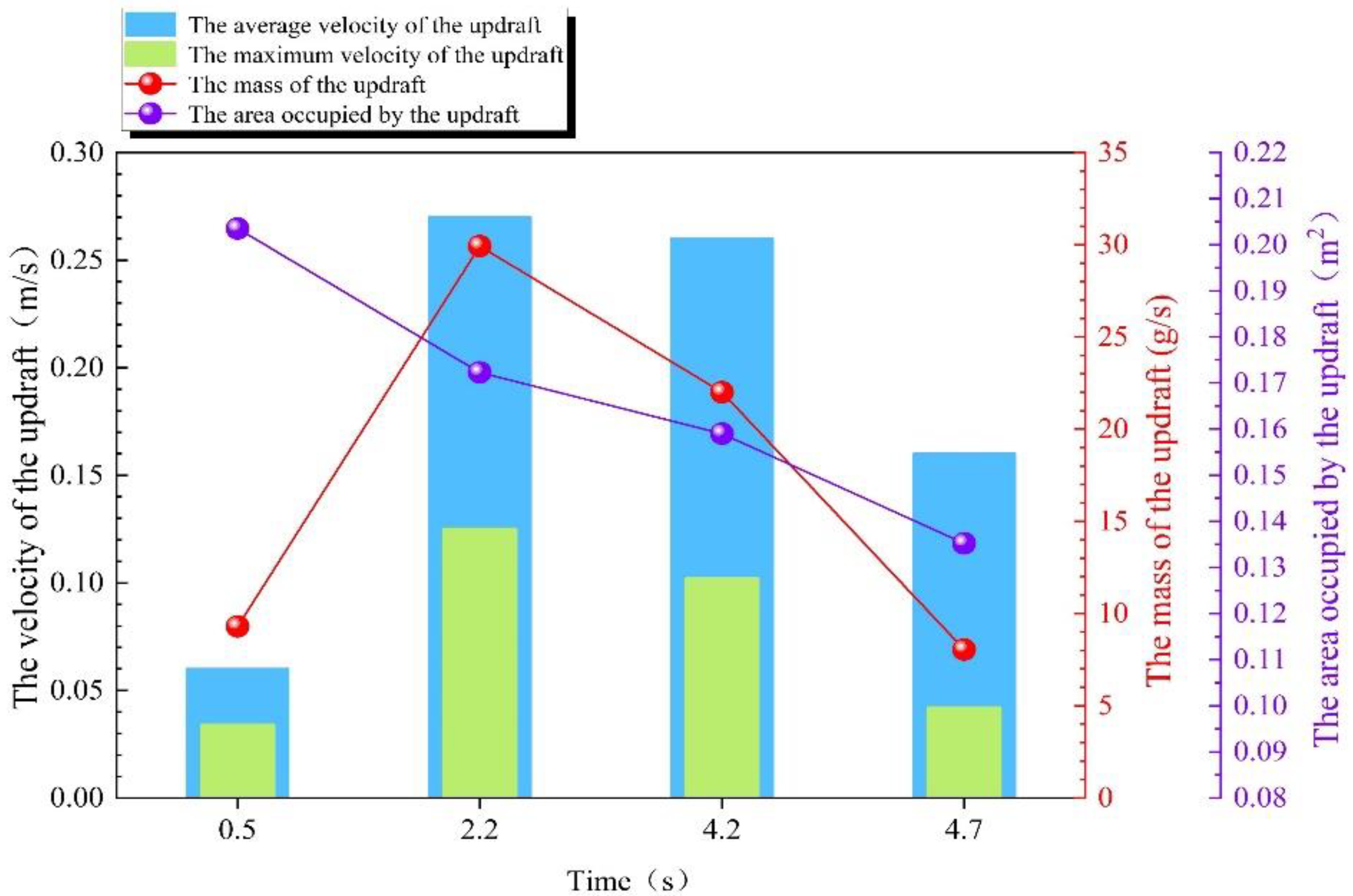
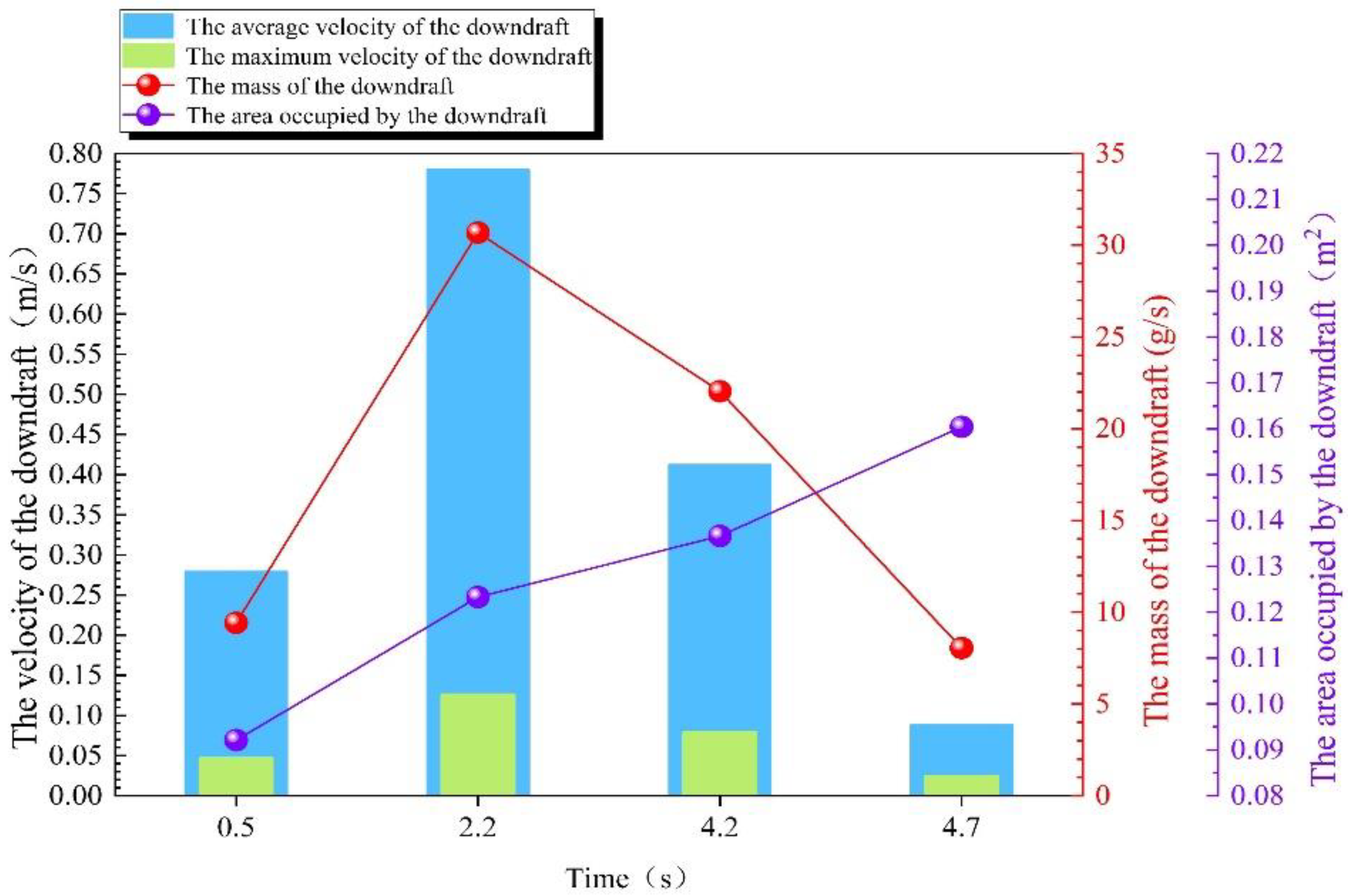
- A gas–solid two-phase flow field based on the CFD-DEM coupling method was adopted, a DPM model of dust was established, and the interaction of the coal particle, coal dust, and airflow fields during the unloading process of the grab was further studied. The study found that the velocity of the airflow field in the particle flow field and nearby areas is relatively large, and the maximum airflow field velocity is located inside the particle flow field, in which the highest velocities of the particle flow field and the airflow field were 4.76 and 1.33 m/s, respectively. The velocity variation in the airflow field at the edge of the particle flow and in nearby areas was clear, which indicated that the airflow shear effect in this area was evident and dust was more easily generated. In other areas, the airflow velocity and gradient of the velocity were smaller but occupied a larger area. In addition, the distribution law of airflow velocity in the vertical direction of the hopper opening plane is as follows: the airflow velocity is symmetrically distributed on the two vertical symmetry planes of the hopper; the airflow at the centre and nearby positions of the hopper moves downwards, whereas the airflow outside moves upwards. In addition, the variation trend of airflow velocity along the two vertical symmetry planes exhibited the same trend, and the velocity gradually decayed to 0 m/s from the centre to the periphery, then gradually increased and rapidly decreased to 0 m/s when it reached the wall of the hopper. Summarising the relevant characteristics of the upward airflow and downward airflow at the hopper mouth plane, it can be observed that as the unloading time increased, the average and maximum velocity and mass flow of the upward and downward airflows first increased and then decreased, reaching the maximum value at T = 2.2 s. The area occupied by the upward airflow gradually decreased, whereas the area occupied by the downward airflow gradually increased, indicating that the interface between the upward- and downward-moving airflows continued to expand outwards with time, and the mass of the upward flow was basically the same as the mass of the downward flow at four moments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, W.; Chen, S. Application of High efficiency Inhibitors in Nonferrous Metal Mines. China Mine Eng. 2017, 46, 19–25. [Google Scholar]
- Zhang, D.; Liu, B. Statistics and Prospect Analysis of Mine Occupational Diseases in China. Energy Environ. Prot. 2017, 39, 173–178. [Google Scholar]
- Chen, H. Dust Generation Mechanism of Bulk Cargo Unloading Process Based on CFD-DEM and Dust Suppression Method of Spiral Hopper; Wuhan University of Technology: Wuhan, China, 2019. [Google Scholar]
- Lu, X.; Lin, j. Can we develop a comprehensive theory of turbulence dynamics and the kinematics of granular materials. Sci. Bull. 2017, 62, 1115–1118. [Google Scholar]
- Levine, A.G. 125 Questions: Exploration and Discovery; The American Association for the Advancement of Science: Washington, DC, USA, 2021. [Google Scholar]
- Sun, X.; Zhao, Y.; Meng, W.; Zhai, Y. Research on average vertical velocity of rubber particles in vertical screw conveyor based on bp neural network. J. Mech. Sci. Technol. 2021, 35, 5107–5116. [Google Scholar]
- Li, X. Design of New Belt Conveyor Transfer Station; Taiyuan University of Science and Technology: Taiyuan, China, 2014. [Google Scholar]
- Jiang, Q. Non-Power Dust Suppression Design of Belt Conveyor Transfer Station; Taiyuan University of Science and Technology: Taiyuan, China, 2015. [Google Scholar]
- Meng, W.; Yin, X.; Jiang, Q. Discrete element analysis of material flow in unpowered dust suppression transfer station. China Powder Technol. 2016, 22, 82–88. [Google Scholar]
- Esmaili, A.; Donohue, T.; Wheeler, C.; McBride, W.; Roberts, A. On the analysis of a coarse particle free falling material stream. Int. J. Miner. Process. 2015, 142, 82–90. [Google Scholar] [CrossRef]
- Zeren, Z.; Neau, H.; Ansart, R.; Simonin, O.; Belut, E. 3D unstationary simulations of a free-falling particle jet using a granular-kinetic hybrid model. Ventilation 2012, 23, 1–6. [Google Scholar]
- Yuan, J.; Jin, C.; Ye, F.; Hu, Z.; Chen, H. Dust Suppression Analysis of a New Spiral Hopper Using CFD-DEM Simulations and Experiments. Processes 2020, 8, 783. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Wu, Z.J.; Feng, Z.P. Experimental investigation of dust amount from free falling particle stream affected by deflector curvature of dust suppression. Adv. Mater. Res. 2014, 864–867, 1789–1792. [Google Scholar]
- Ansart, R.; Letourneau, J.-J.; de Ryck, A.; Dodds, J.A. Dust emission by powder handling: Influence of the hopper outlet on the dust plume. Powder Technol. 2011, 212, 418–424. [Google Scholar] [CrossRef]
- Chen, X.; Wheeler, C.; Donohue, T.; McLean, R.; Roberts, A. Evaluation of dust emissions from conveyor transfer chutes using experimental and CFD simulation. Int. J. Miner. Process. 2012, 110–111, 101–108. [Google Scholar] [CrossRef]
- Jaklič, M.; Kočevar, K.; Srčič, S.; Dreu, R. Particle size-based segregation of pharmaceutical powders in a vertical chute with a closed bottom: An experimental evaluation. Powder Technol. 2015, 278, 171–180. [Google Scholar] [CrossRef]
- Hamzeloo, E.; Massinaei, M.; Mehrshad, N. Estimation of particle size distribution on an industrial conveyor belt using image analysis and neural networks. Powder Technol. 2014, 261, 185–190. [Google Scholar] [CrossRef]
- Li, X.; Li, Q.; Zhang, D.; Jia, B.; Luo, H.; Hu, Y. Model for induced airflow velocity of falling materials in semi-closed transfer station based on similitude theory. Adv. Powder Technol. 2015, 26, 236–243. [Google Scholar] [CrossRef]
- Wang, Y.; Ren, X.; Zhao, J.; Chu, Z.; Cao, Y.; Yang, Y.; Duan, M.; Fan, H.; Qu, X. Experimental study of flow regimes and dust emission in a freefalling particle stream. Powder Technol. 2016, 292, 14–22. [Google Scholar] [CrossRef]
- Ren, X. Study on Diffusion and Dust Production Characteristics of Free Falling Particles; Xi’an University of Architectural Science and Technology: Xi’an, China, 2017. [Google Scholar]
- Li, X.; Li, Q.; Zhang, D. Factors affecting nonlinear variation of air flow induced by blanking at transfer point. Powder Metall. Mater. Sci. Eng. 2014, 19, 508–513. [Google Scholar]
- Wang, D.; Li, X. Study of airflow induced by regular particles in freefall through tubes. Adv. Powder Technol. 2020, 1, 169–180. [Google Scholar] [CrossRef]
- Wang, S.; Ge, S.; Chen, X. Experimental study on influencing factors of air flow induced by transfer point in coal preparation plant. China Sci. Technol. Prod. Saf. 2017, 13, 53–57. [Google Scholar]
- Li, Q. Study on the Law of Belt Falling Coal and Dust Based on the Dynamic Analysis of Induced Air Flow; China University of Mining and Technology: Beijing, China, 2014. [Google Scholar]
- Zhang, X.; Wang, H.; Chen, X.; Fan, C.; Tian, K.; Zhang, X. Experimental study on dust suppression at transhipment point based on the theory of induced airflow dust production. Build. Environ. 2019, 160, 106200. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Wen, C.Y.; Yu, Y.H. Mechanics of fluidization. Chem. Eng. Prog. Symp. Ser. 1966, 62, 100–111. [Google Scholar]
- Sakai, M.; Takahashi, H.; Pain, C.C.; Latham, J.-P.; Xiang, J. Study on a large-scale discrete element model for fine particles in a fluidized bed. Adv. Powder Technol. 2012, 23, 673–681. [Google Scholar] [CrossRef]
- Ran, J.; Zhang, L.; Xin, M. Numerical simulation of gas-solid flow motion characteristics and deposition efficiency of particles in water-film cyclone separator. J. Chem. Ind. Eng. 2003, 54, 1391–1396. [Google Scholar]
- Wang, Z.; Ren, T. Investigation of airflow and respirable dust flow behaviour above an underground bin. Powder Technol. 2013, 250, 103–114. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Cheng, Z.; Sun, R.; Zhang, A. Simulation of construction ventilation in deep diversion tunnels using Euler–Lagrange method. Comput. Fluids 2014, 105, 28–38. [Google Scholar] [CrossRef]
- Gui, C.; Geng, F.; Tang, J.; Niu, H.; Zhou, F.; Liu, C.; Hu, S.; Teng, H. Gas–solid two-phase flow in an underground mine with an optimized air-curtain system: A numerical study. Process Saf. Environ. Prot. 2020, 140, 137–150. [Google Scholar] [CrossRef]
- Benni, S.; Tassinari, P.; Bonora, F.; Barbaresi, A.; Torreggiani, D. Efficacy of greenhouse natural ventilation: Environmental monitoring and CFD simulations of a study case. Energy Build. 2016, 125, 276–286. [Google Scholar] [CrossRef]
- Colella, F.; Rein, G.; Verda, V.; Borchiellini, R. Multiscale modeling of transient flows from fire and ventilation in long tunnels. Comput. Fluids 2011, 51, 16–29. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Sasmito, A.P.; Hassani, F.P.; Mujumdar, A.S. Introduction and evaluation of a novel hybrid brattice for improved dust control in underground mining faces: A computational study. Int. J. Min. Sci. Technol. 2015, 25, 537–543. [Google Scholar] [CrossRef]
- Guo, L.; Nie, W.; Yin, S.; Liu, Q.; Hua, Y.; Cheng, L.; Cai, X.; Xiu, Z.; Du, T. The dust diffusion modeling and determination of optimal airflow rate for removing the dust generated during mine tunneling. Build. Environ. 2020, 178, 106846. [Google Scholar] [CrossRef]
- Xiu, Z.; Nie, W.; Yan, J.; Chen, D.; Cai, P.; Liu, Q.; Du, T.; Yang, B. Numerical simulation study on dust pollution characteristics and optimal dust control air flow rates during coal mine production. J. Clean. Prod. 2020, 248, 119197. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, W.; Liu, L.; Hua, Y.; Guo, L.; Nie, W. Research on the control law of dust in the main ventilation system in excavated tunnels for cleaner production. Build. Environ. 2021, 205, 108282. [Google Scholar] [CrossRef]
- Liu, Q.; Nie, W.; Hua, Y.; Peng, H.; Liu, C.; Wei, C. Research on tunnel ventilation systems: Dust Diffusion and Pollution Behaviour by air curtains based on CFD technology and field measurement. Build. Environ. 2018, 147, 444–460. [Google Scholar] [CrossRef]
- Chen, Y.-S.; Hsiau, S.-S.; Lai, S.-C.; Chyou, Y.-P.; Li, H.-Y.; Hsu, C.-J. Filtration of dust particulates with a moving granular bed filter. J. Hazard. Mater. 2009, 171, 987–994. [Google Scholar] [CrossRef] [PubMed]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhou, L. A two-scale second-order moment particle turbulence model and simulation of dense gas–particle flows in a riser. Powder Technol. 2006, 162, 27–32. [Google Scholar] [CrossRef]














| Bulk Material | Bulk Material Density (kg/m3) | Particle Size Distribution (mm), Percentage of Weight | Moisture Content | Stacking Angle (°) | Type |
|---|---|---|---|---|---|
| Coal | 914 | Particle size 2, accounting for 43.7%, Particle size 5.8, accounting for 56.3%. | 0% | 30.36 | General material, granular and block combinations |
| Sand | 1567 | Particle size 2, accounting for 80.1%, Particle size 5.8, accounting for 19.9%. | 0% | 36.07 | Heavy material, granular |
| Flour | 643 | Particle size 0.106, accounting for 100%. | 12% | 42.71 | General material, dust |
| Bulk Material | Duration of Dust Rising Diffusion (s) | Emptying Time of Materials in the Grab (s) | Maximum Diffusion Range of Dust (mm) | |
|---|---|---|---|---|
| Transverse Dimension | Longitudinal Dimension | |||
| Coal | 0–5.2 | 5 | 953 | 1389 |
| Sand | 0–6.5 | 5.7 | 893 | 1540 |
| Flour | 0–5.3 | 6.3 | 769 | 1450 |
| Name | Type | Parameters | |
|---|---|---|---|
| Bulk Material | Particle diameter distribution | Diameter (mm) | 5.8 and 1 |
| Mass ratio | 56% and 44% | ||
| Distribution | Normal distribution | ||
| Total mass of particles (kg) | 3.5 | ||
| Particle Poisson ratio | 0.4 | ||
| Particle density (kg/m3) | 1200 | ||
| Particle Shear modulus (Pa) | 1.1 × 107 | ||
| Equipment Material | Geometric Poisson ratio | 0.3 | |
| Geometric density (kg/m3) | 7850 | ||
| Geometric Shear modulus (Pa) | 7.9 × 1010 | ||
| Interaction | Particle–particle restitution coefficient | 0.5 | |
| Particle–particle static friction coefficient | 0.6 | ||
| Particle–particle rolling friction coefficient | 0.04 | ||
| Particle–geometry restitution coefficient | 0.5 | ||
| Particle–geometry static friction coefficient | 0.4 | ||
| Particle–geometry rolling friction coefficient | 0.05 | ||
| Calculation | Fixed Time Step (s) | 2 × 10−5 | |
| Total Time (s) | 100 | ||
| Name | Type | Parameters |
|---|---|---|
| General | Type | Pressure-based |
| Time | Transient | |
| Gravity (m/s2) | 9.81 | |
| Models | Model | k-epsilon (2 eqn) |
| k-epsilon Model | Realizable | |
| Near-Wall Treatment | Standard Wall Functions | |
| Boundary Conditions | Pressure inlet | Gauge Pressure = 0 |
| Pressure outlet | Gauge Pressure = 0 | |
| Wall | Wall Motion | Stationary Wall |
| DPM | Reflect | |
| Solution Methods | Scheme | Coupled |
| Discrete Phase | Injections | Coal |
| Diameter Distribution | Rosin-Rammler | |
| Dust Particles | Total Flow Rate (kg/s) | 0.0001 |
| Min.Diameter (mm) | 8.5 × 10−4 | |
| Max.Diameter (mm) | 7.68 × 10−2 | |
| Mean.Diameter (mm) | 2.02 × 10−2 | |
| Spread Parameter | 3.5 | |
| Number of Diameters | 15 | |
| Stop Time (s) | 4.5 | |
| Turbulent Dispersion | Discrete Random Walk Model | on |
| Calculation | Time Step Size(s) | 4 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Meng, W.; Zhang, B.; Yuan, Y.; Yin, X.; Zhao, X.; Liang, W. Flow Field Characteristics of Fugitive Dust from Grab Unloading in an Open Space. Processes 2024, 12, 49. https://doi.org/10.3390/pr12010049
Zhang H, Meng W, Zhang B, Yuan Y, Yin X, Zhao X, Liang W. Flow Field Characteristics of Fugitive Dust from Grab Unloading in an Open Space. Processes. 2024; 12(1):49. https://doi.org/10.3390/pr12010049
Chicago/Turabian StyleZhang, Hanzhong, Wenjun Meng, Biao Zhang, Yuan Yuan, Xuan Yin, Xiaoxia Zhao, and Weiqiang Liang. 2024. "Flow Field Characteristics of Fugitive Dust from Grab Unloading in an Open Space" Processes 12, no. 1: 49. https://doi.org/10.3390/pr12010049
APA StyleZhang, H., Meng, W., Zhang, B., Yuan, Y., Yin, X., Zhao, X., & Liang, W. (2024). Flow Field Characteristics of Fugitive Dust from Grab Unloading in an Open Space. Processes, 12(1), 49. https://doi.org/10.3390/pr12010049






