A Review of Nano and Microscale Heat Transfer: An Experimental and Molecular Dynamics Perspective
Abstract
1. Introduction
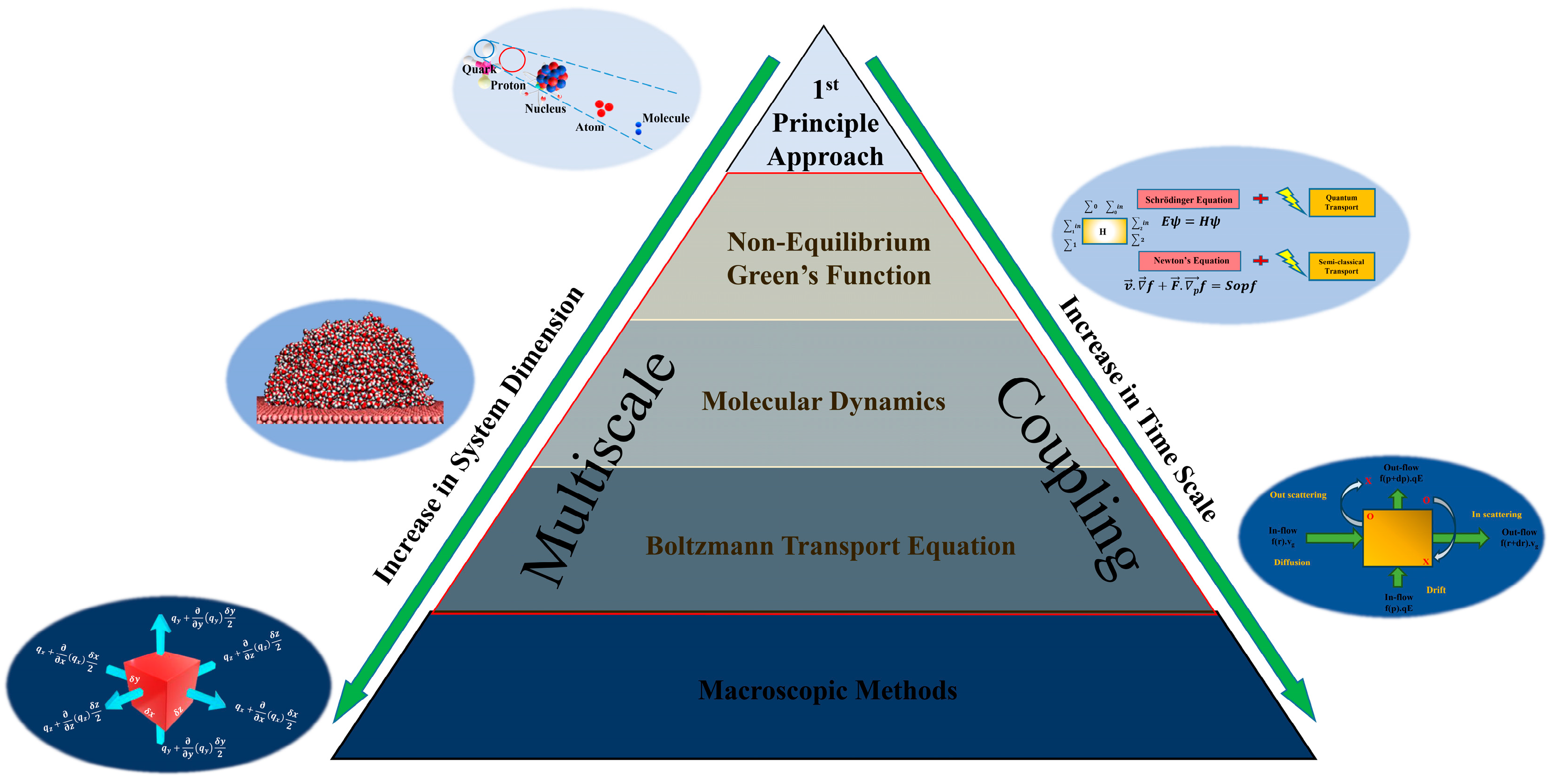
2. Molecular Dynamic Simulations
2.1. Basic Principles of MD
2.2. Example of Some Potential Forms in MD Simulations
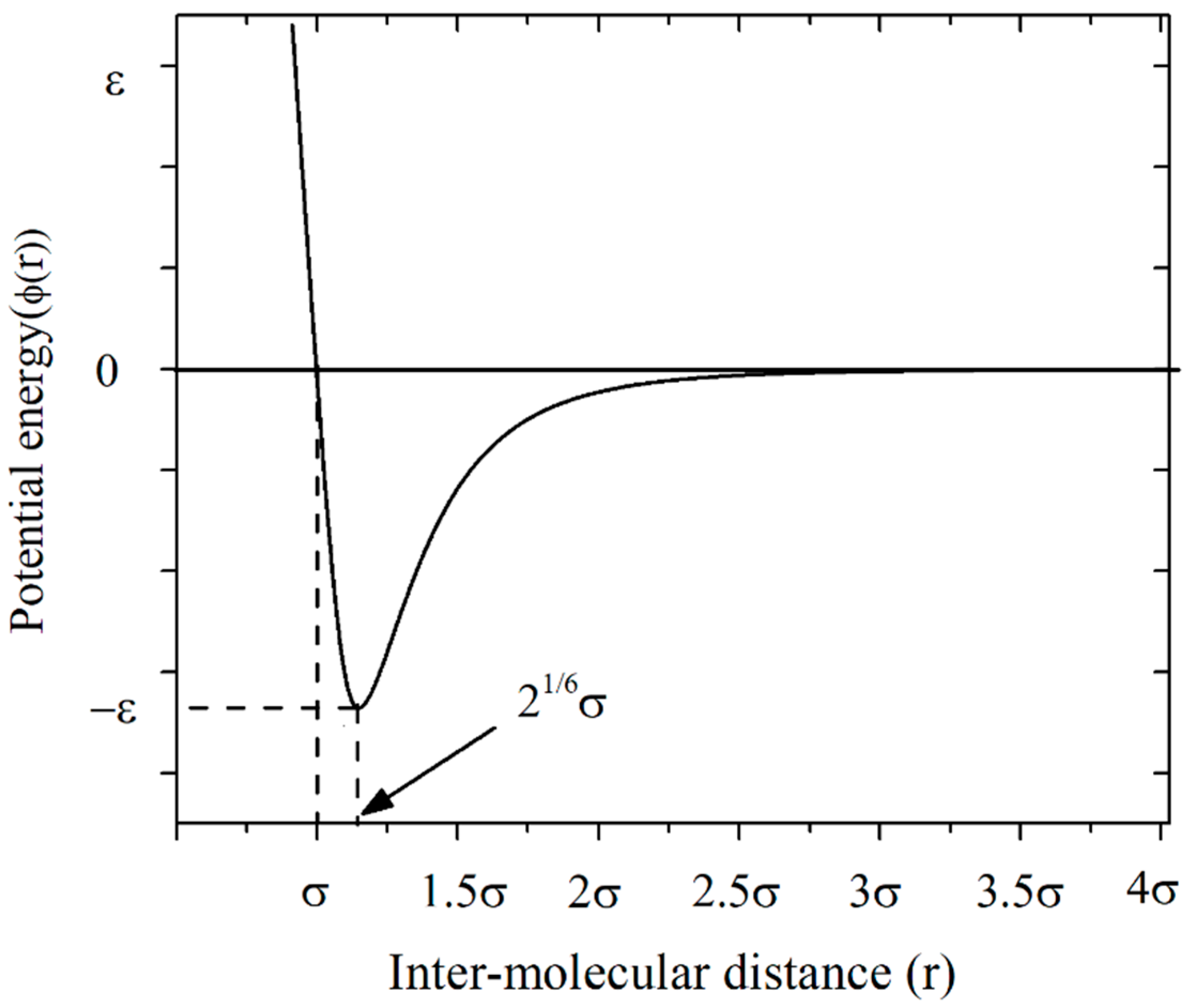
2.2.1. Lennard–Jones Potentials
2.2.2. Water Models and Potentials
- (a)
- TIP4P
- (b) SPC/E
2.2.3. Other Commonly Used Many-Body Potentials
3. Application of Molecular Dynamic Simulations in Micro and Nanoscale Heat Transfer
3.1. Liquid–Vapor Interface
3.1.1. Liquid Droplet at the Vapor Interface and Surface Tension
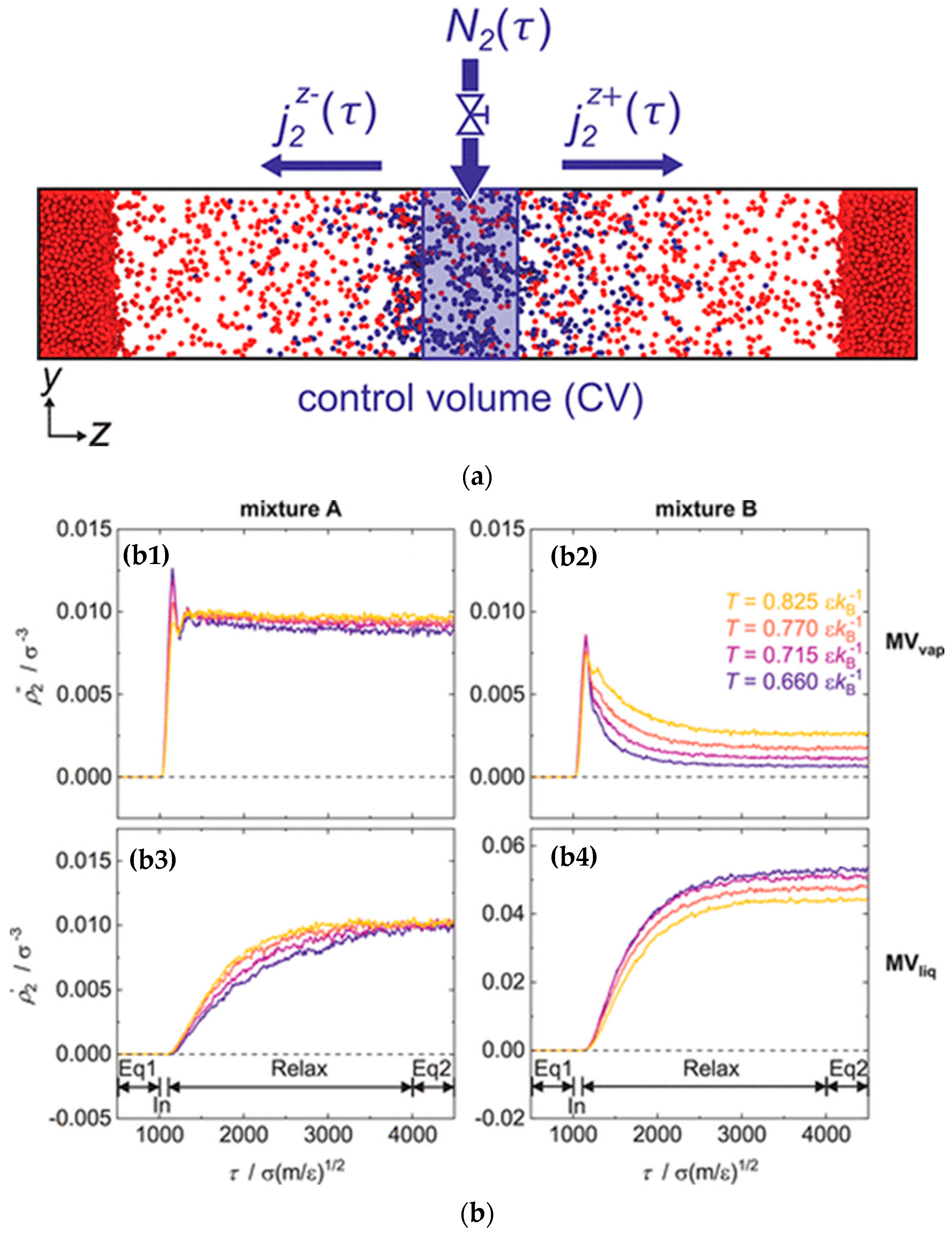
3.1.2. Mass Transfer at the Liquid–Vapor Interface
3.1.3. Evaporation at the Liquid–Vapor Interface
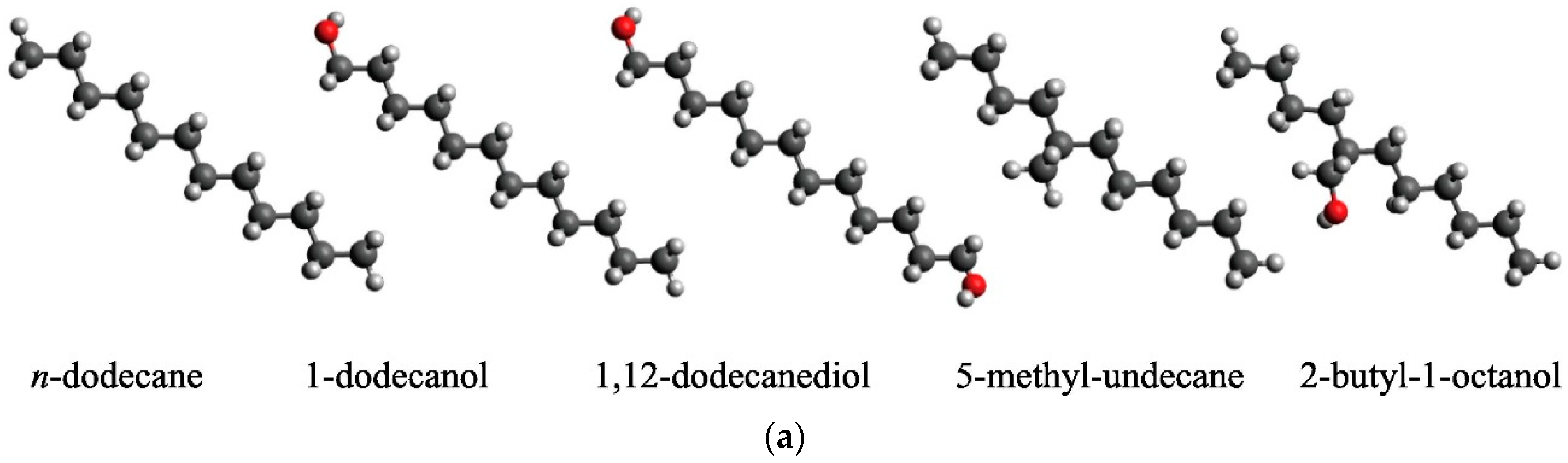
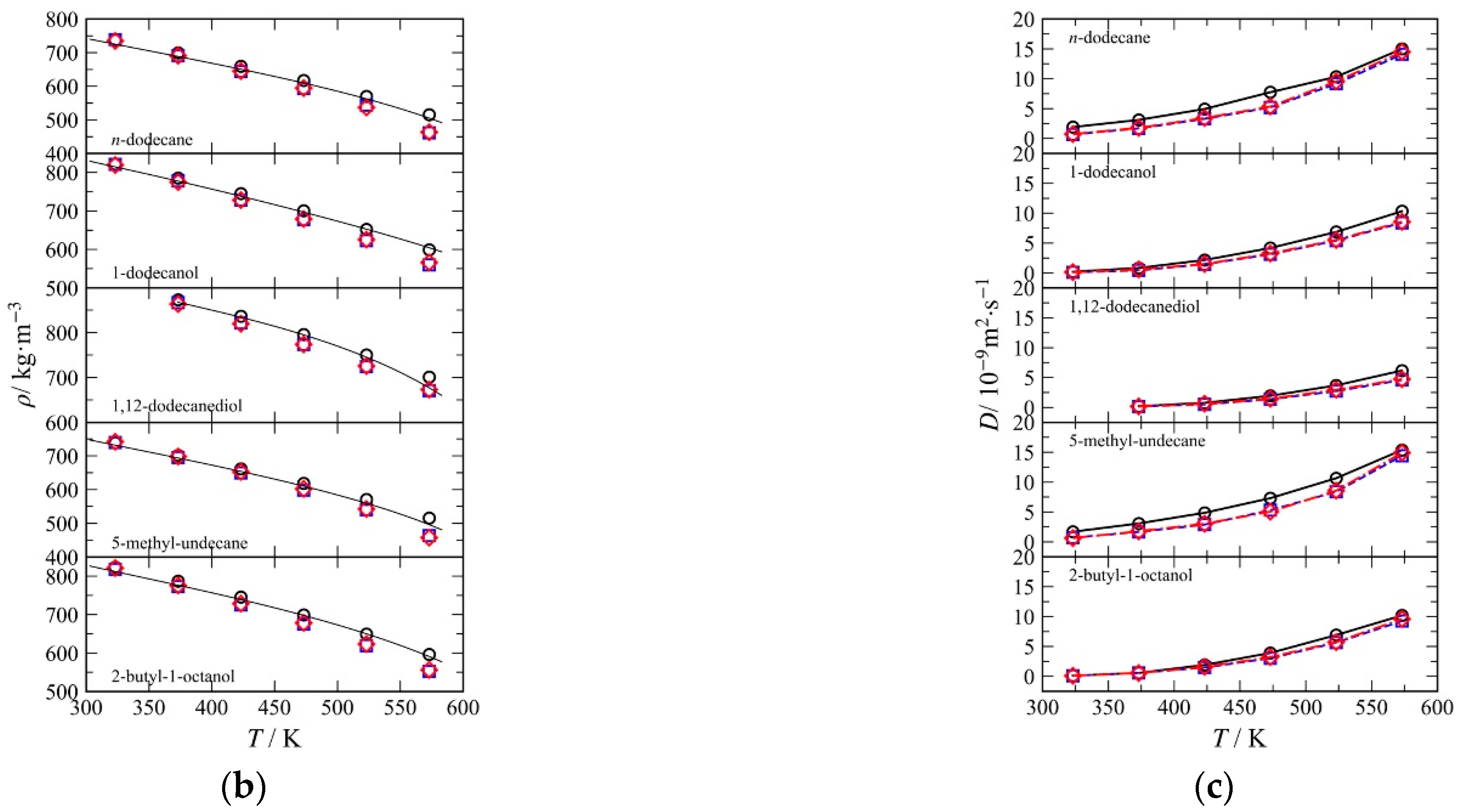
3.1.4. Behavior of Long-Chain Organic Molecules at the Liquid–Vapor Interface
3.1.5. Effects of a Pressure-Varying Field on Vaporization
3.2. Solid–Liquid–Vapor Interface
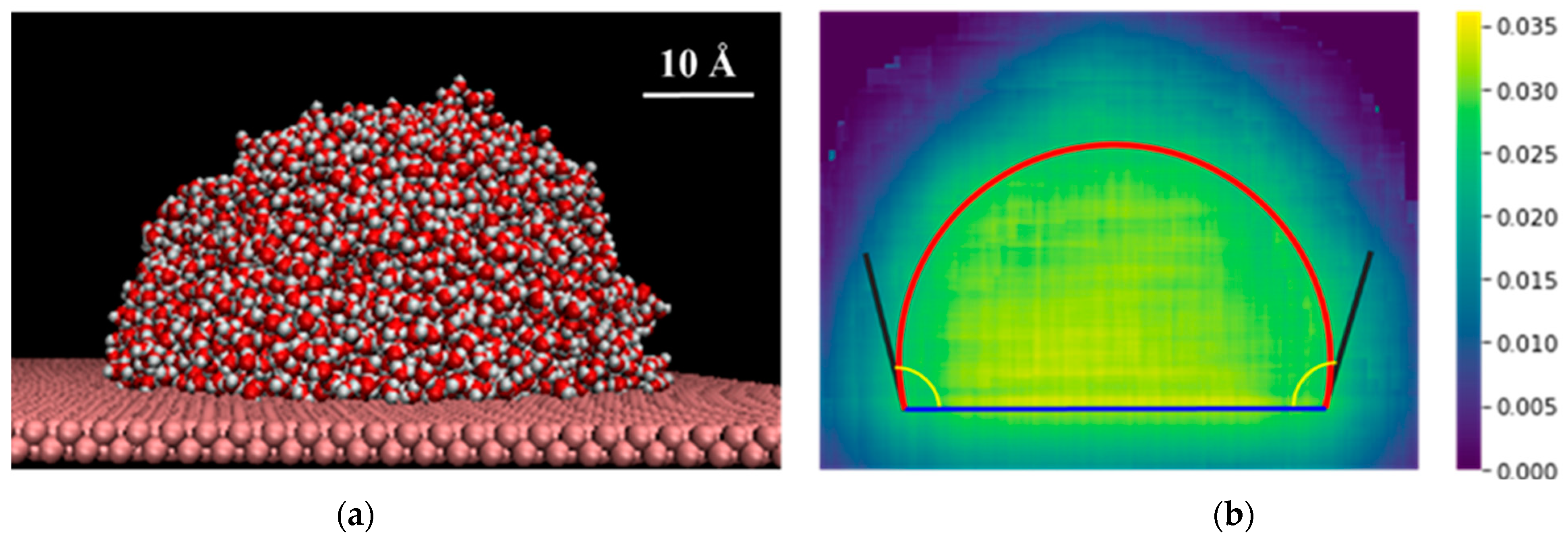
3.2.1. Liquid Droplets on Solid Surfaces
3.2.2. Impact of Interaction Parameter and Molecular Kinetic Theory at the Three-Phase Contact Line
3.2.3. Liquid Droplet–Carbon Nanotube Interface
3.2.4. Bubble Dynamics at the Solid–Liquid–Vapor Interface
3.2.5. Droplet Coalescence
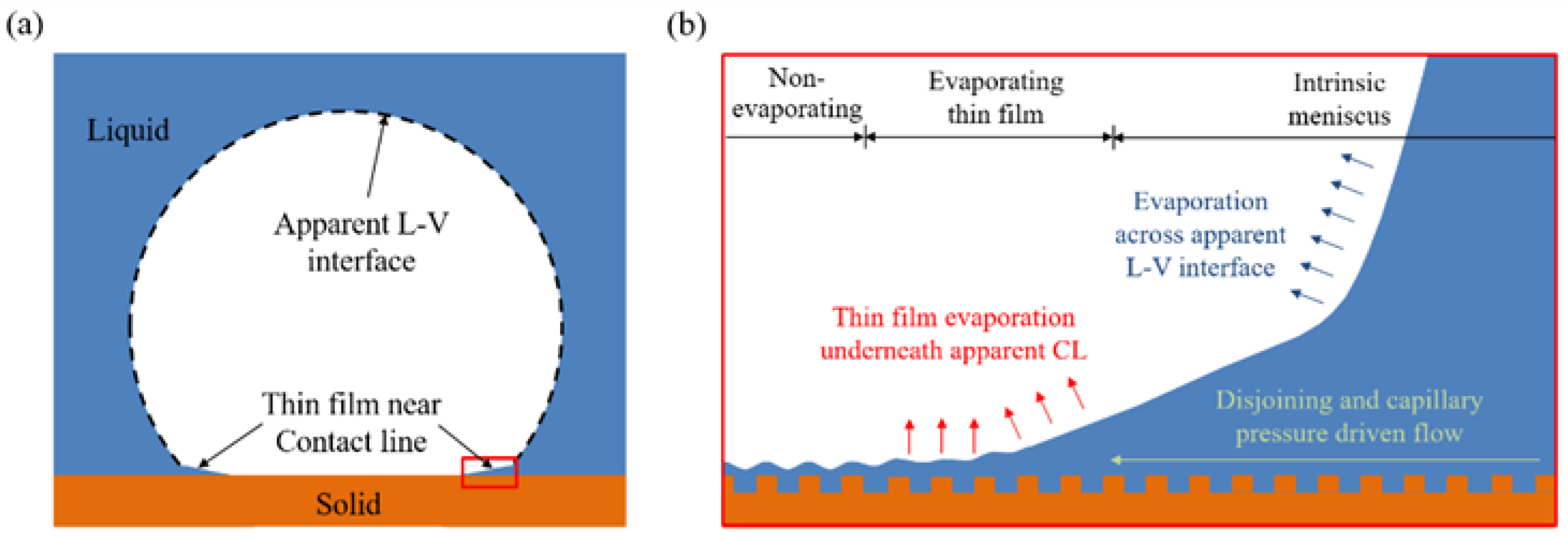
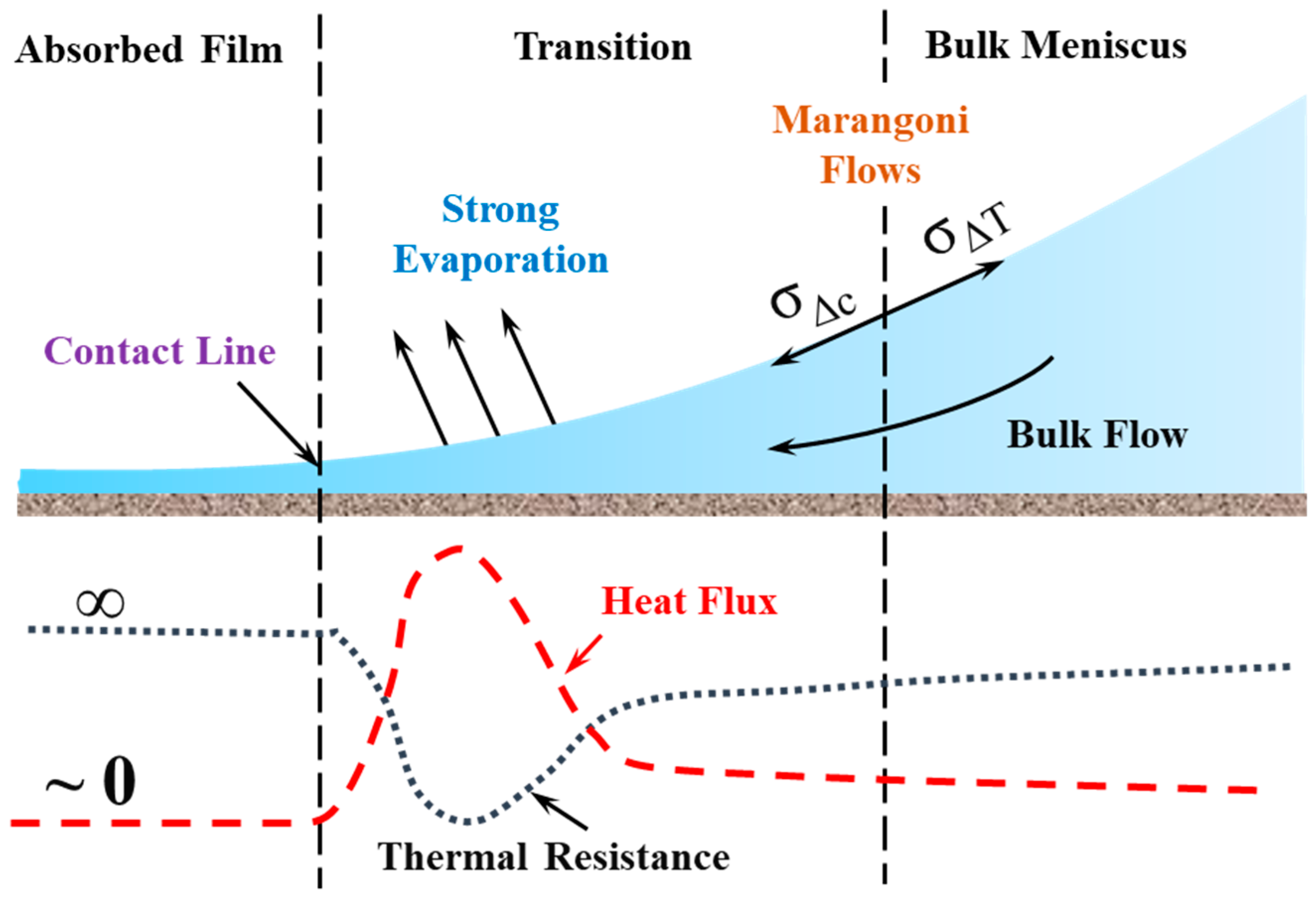
3.2.6. Thin Film Evaporation at the Solid–Liquid–Vapor Interface
3.3. Miscellaneous Works
4. Nanoscale Thermal Transport Theories and Experiments
4.1. Statistical Behavior of Nanoscale Transport Processes
4.1.1. Phonon Transport
4.1.2. Size Effects
4.1.3. Boundary and Interface Effects
4.2. Applications of Micro/Nanoscale Heat Transfer
4.2.1. Microfluidic Devices
4.2.2. Introducing Nanoparticles
4.2.3. Micro/Nano Heat Exchanger
4.2.4. Bubble Entrainment
4.2.5. Energy Conversion at the Nanoscale
4.2.6. Thermoelectric Energy Conversion
4.2.7. Some Industrial Applications
- (a)
- Microprocessors and integrated circuits
- (b) Nanoelectromechanical systems (NEMSs)
- (c) Microscale heat pipes and sinks
4.2.8. Effect of Surface Modification
4.2.9. Thin Film Boiling in Nano/Micro Materials
4.2.10. Evaporation on the Nano/Micro Scale
5. Conclusions and Future Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Idumah, C.I. Recently emerging trends in flame retardancy of phosphorene polymeric nanocomposites and applications. J. Anal. Appl. Pyrolysis 2023, 169, 105855. [Google Scholar] [CrossRef]
- Wang, D.; Lin, S.S.; Huang, S.Q.; Yin, Z.F.; Yang, H.Z.; Bian, P.Y.; Zhang, Y.L.; Dai, M.J.; Zhou, K.S. Research on high temperature wear resistance mechanism of CrN/CrAlN multilayer coatings. Tribol. Int. 2023, 180, 108184. [Google Scholar] [CrossRef]
- Hamed, H.; Eldiasty, M.; Seyedi-Sahebari, S.M.; Abou-Ziki, J.D. Applications, materials, and fabrication of micro glass parts and devices: An overview. Mater. Today 2023, 66, 194–220. [Google Scholar] [CrossRef]
- Yu, Y.; Ma, T.; Huang, H. Semiconducting Quantum Dots for Energy Conversion and Storage. Adv. Funct. Mater. 2023, 33, 2213770. [Google Scholar] [CrossRef]
- Masuduzzaman, M.; Kim, B. Scale Effects in Nanoscale Heat Transfer for Fourier’s Law in a Dissimilar Molecular Interface. ACS Omega 2020, 5, 26527–26536. [Google Scholar] [CrossRef]
- Luo, T.; Chen, G. Nanoscale heat transfer—From computation to experiment. Phys. Chem. Chem. Phys. 2013, 15, 3389. [Google Scholar] [CrossRef]
- Knepp, Z.J.; Masso, G.B.; Fredin, L.A. Efficiently predicting directional carrier mobilities in organic materials with the Boltzmann transport equation. J. Chem. Phys. 2023, 158, 064704. [Google Scholar] [CrossRef]
- Fiorentino, A.; Baroni, S. From Green-Kubo to the full Boltzmann kinetic approach to heat transport in crystals and glasses. Phys. Rev. B 2023, 107, 054311. [Google Scholar] [CrossRef]
- Pan, H.; Ding, Z.K.; Zeng, B.W.; Luo, N.N.; Zeng, J.; Tang, L.M.; Chen, K.Q. Ab initio Boltzmann approach to coupled magnon-phonon thermal transport in ferromagnetic crystals. Phys. Rev. B 2023, 107, 104303. [Google Scholar] [CrossRef]
- Chang, C.W.; Okawa, D.; Garcia, H.; Majumdar, A.; Zettl, A. Breakdown of Fourier’s Law in Nanotube Thermal Conductors. Phys. Rev. Lett. 2008, 101, 075903. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Shen, K.; Qiu, Y.; Xie, J. Further decrease of the thermal conductivity of superlattice through embedding nanoparticle. Int. J. Heat Mass Transf. 2023, 203, 123789. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Fan, R.; Yang, P.; Majumdar, A. Thermal conductivity of Si/SiGe superlattice nanowires. Appl. Phys. Lett. 2003, 83, 3186–3188. [Google Scholar] [CrossRef]
- Cahill, D.G.; Ford, W.K.; Goodson, K.E.; Majumdar, A.; Maris, H.J.; Merlin, R.; Phillpot, S.R. Nanoscale thermal transport. J. Appl. Phys. 2003, 93, 793–818. [Google Scholar] [CrossRef]
- Biehs, S.A.; Rousseau, E.; Greffet, J.J. Mesoscopic Description of Radiative Heat Transfer at the Nanoscale. Phys. Rev. Lett. 2010, 105, 234301. [Google Scholar] [CrossRef] [PubMed]
- Kloppstech, K.; Könne, N.; Biehs, S.A.; Rodriguez, A.W.; Worbes, L.; Hellmann, D.; Kittel, A. Giant heat transfer in the crossover regime between conduction and radiation. Nat. Commun. 2017, 8, 14475. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Yi, W.; Zhang, D.L. 3ω method for specific heat and thermal conductivity measurements. Rev. Sci. Instrum. 2001, 72, 2996–3003. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, W.; Hui, F.; Lanza, M.; Borca-Tasciuc, T.; Muñoz Rojo, M. A Review on Principles and Applications of Scanning Thermal Microscopy (SThM). Adv. Funct. Mater. 2020, 30, 1900892. [Google Scholar] [CrossRef]
- Gomès, S.; Assy, A.; Chapuis, P.O. Scanning thermal microscopy: A review. Phys. Status Solidi 2015, 212, 477–494. [Google Scholar] [CrossRef]
- Andrew NSmith, J.L.H. Thermal boundary resistance measurements using a transient thermoreflectance technique. Microscale Thermophys Eng. 2000, 4, 51–60. [Google Scholar] [CrossRef]
- Stevens, R.J.; Smith, A.N.; Norris, P.M. Measurement of Thermal Boundary Conductance of a Series of Metal-Dielectric Interfaces by the Transient Thermoreflectance Technique. J. Heat Transfer. 2005, 127, 315–322. [Google Scholar] [CrossRef]
- Fischer, M.C.; Wilson, J.W.; Robles, F.E.; Warren, W.S. Invited Review Article: Pump-probe microscopy. Rev. Sci. Instrum. 2016, 87, 031101. [Google Scholar] [CrossRef]
- Antonio, K.A.; Schultz, Z.D. Advances in Biomedical Raman Microscopy. Anal. Chem. 2014, 86, 30–46. [Google Scholar] [CrossRef]
- Bebb, H.B.; Williams, E.W. Chapter 4 Photoluminescence I: Theory; Elsevier: Amsterdam, The Netherlands, 1972; pp. 181–320. [Google Scholar] [CrossRef]
- Xiong, Y.; Shepherd, S.; Tibbs, J.; Bacon, A.; Liu, W.; Akin, L.D.; Ayupova, T.; Bhaskar, S.; Cunningham, B.T. Photonic Crystal Enhanced Fluorescence: A Review on Design Strategies and Applications. Micromachines 2023, 14, 668. [Google Scholar] [CrossRef]
- Maqbool, Z.; Hanief, M.; Parveez, M. Review on performance enhancement of phase change material based heat sinks in conjugation with thermal conductivity enhancers for electronic cooling. J. Energy Storage 2023, 60, 106591. [Google Scholar] [CrossRef]
- Li, R.; Wang, J.X.; Lee, E.; Luo, T. Physics-informed deep learning for solving phonon Boltzmann transport equation with large temperature non-equilibrium. NPJ Comput. Mater. 2022, 8, 29. [Google Scholar] [CrossRef]
- Reddy, P.; Castelino, K.; Majumdar, A. Diffuse mismatch model of thermal boundary conductance using exact phonon dispersion. Appl. Phys. Lett. 2005, 87, 211908. [Google Scholar] [CrossRef]
- Noothong, W.; Suwannapan, S.; Thianpong, C.; Promvonge, P. Enhanced heat transfer in a heat exchanger square-duct with discrete V-finned tape inserts. Chin. J. Chem. Eng. 2015, 23, 490–498. [Google Scholar] [CrossRef]
- Eid, M.R.; Al-Hossainy, A.F. Synthesis, DFT calculations, and heat transfer performance large-surface TiO2, ethylene glycol nanofluid and coolant applications. Eur. Phys. J. Plus 2020, 135, 596. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Studies in Molecular Dynamics. I. General Method. J. Chem. Phys. 1959, 31, 459–466. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Rahman, A. Improved simulation of liquid water by molecular dynamics. J. Chem. Phys. 1974, 60, 1545–1557. [Google Scholar] [CrossRef]
- Nielsch, K.; Bachmann, J.; Kimling, J.; Böttner, H. Thermoelectric Nanostructures: From Physical Model Systems towards Nanograined Composites. Adv. Energy Mater. 2011, 1, 713–731. [Google Scholar] [CrossRef]
- Mingo, N.; Yang, L. Phonon transport in nanowires coated with an amorphous material: An atomistic Green’s function approach. Phys. Rev. B 2003, 68, 245406. [Google Scholar] [CrossRef]
- Sadasivam, S.; Waghmare, U.V.; Fisher, T.S. Phonon-eigenspectrum-based formulation of the atomistic Green’s function method. Phys. Rev. B 2017, 96, 174302. [Google Scholar] [CrossRef]
- Peraud, J.P.M.; Landon, C.D.; Hadjiconstantinou, N.G. MONTE CARLO METHODS FOR SOLVING THE BOLTZMANN TRANSPORT EQUATION. Annu. Rev. Heat Transf. 2014, 17, 205–265. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D.G.B. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A.C.; Wegner, J.L. Nonlocal Continuum Field Theories. Appl. Mech. Rev. 2003, 56, B20–B22. [Google Scholar] [CrossRef]
- Wu, J.W.; He, J.T.; Lin, J. Nonlocal symmetries and new interaction waves of the variable-coefficient modified Korteweg–de Vries equation in fluid-filled elastic tubes. Eur. Phys. J. Plus 2022, 137, 814. [Google Scholar] [CrossRef]
- Kiani, K. Vibration behavior of simply supported inclined single-walled carbon nanotubes conveying viscous fluids flow using nonlocal Rayleigh beam model. Appl. Math. Model. 2013, 37, 1836–1850. [Google Scholar] [CrossRef]
- Kiani, K. Nanofluidic flow-induced longitudinal and transverse vibrations of inclined stocky single-walled carbon nanotubes. Comput. Methods Appl. Mech. Eng. 2014, 276, 691–723. [Google Scholar] [CrossRef]
- Feng, Y.; Sato, Y.; Inoue, T.; Liu, M.; Chiashi, S.; Xiang, R.; Suenaga, K.; Maruyama, S. Drastically reduced thermal conductivity of self-bundled single-walled carbon nanotube. Carbon 2023, 201, 433–438. [Google Scholar] [CrossRef]
- Keblinski, P.; Prasher, R.; Eapen, J. Thermal conductance of nanofluids: Is the controversy over? J. Nanoparticle Res. 2008, 10, 1089–1097. [Google Scholar] [CrossRef]
- Iqbal, M.; Kouloulias, K.; Sergis, A.; Hardalupas, Y. Critical analysis of thermal conductivity enhancement of alumina–water nanofluids. J. Therm. Anal. Calorim. 2023, 148, 9361–9389. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Souza, P.C.T.; Alessandri, R.; Barnoud, J.; Thallmair, S.; Faustino, I.; Grünewald, F.; Patmanidis, I.; Abdizadeh, H.; Bruininks, B.M.H.; Wassenaar, T.A.; et al. Martini 3, a general purpose force field for coarse-grained molecular dynamics. Nat. Methods 2021, 18, 382–388. [Google Scholar] [CrossRef] [PubMed]
- Mahadevi, A.S.; Sastry, G.N. Cation–π Interaction: Its Role and Relevance in Chemistry, Biology, and Material Science. Chem. Rev. 2013, 113, 2100–2138. [Google Scholar] [CrossRef] [PubMed]
- Fischer, J.; Wendland, M. On the history of key empirical intermolecular potentials. Fluid Phase Equilib 2023, 573, 113876. [Google Scholar] [CrossRef]
- Mark, P.; Nilsson, L. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J. Phys. Chem. A 2001, 105, 9954–9960. [Google Scholar] [CrossRef]
- van der Spoel, D.; van Maaren, P.J.; Berendsen, H.J.C. A systematic study of water models for molecular simulation: Derivation of water models optimized for use with a reaction field. J. Chem. Phys. 1998, 108, 10220–10230. [Google Scholar] [CrossRef]
- Jian, Z.; Kaiming, Z.; Xide, X. Modification of Stillinger-Weber potentials for Si and Ge. Phys. Rev. B 1990, 41, 12915–12918. [Google Scholar] [CrossRef]
- Dodson, B.W. Development of a many-body Tersoff-type potential for silicon. Phys. Rev. B 1987, 35, 2795–2798. [Google Scholar] [CrossRef]
- Becquart, C.S.; Decker, K.M.; Domain, C.; Ruste, J.; Souffez, Y.; Turbatte, J.C.; Duysen, J.C.V. Massively parallel molecular dynamics simulations with EAM potentials. Radiat. Eff. Defects Solids 1997, 142, 9–21. [Google Scholar] [CrossRef]
- Xu, W.; Kim, W.K. Molecular dynamics simulation of the uniaxial tensile test of silicon nanowires using the MEAM potential. Mech. Mater. 2019, 137, 103140. [Google Scholar] [CrossRef]
- Lee, E.; Lee, K.R.; Baskes, M.I.; Lee, B.J. A modified embedded-atom method interatomic potential for ionic systems. Phys. Rev. B 2016, 93, 144110. [Google Scholar] [CrossRef]
- Toghraie Semironi, D.; Azimian, A.R. Molecular dynamics simulation of liquid–vapor phase equilibrium by using the modified Lennard-Jones potential function. Heat Mass Transf. 2010, 46, 287–294. [Google Scholar] [CrossRef]
- Alejandre, J.; Tildesley, D.J.; Chapela, G.A. Molecular dynamics simulation of the orthobaric densities and surface tension of water. J. Chem. Phys. 1995, 102, 4574–4583. [Google Scholar] [CrossRef]
- Panagiotopoulos, A.Z. Direct Determination of Fluid Phase Equilibria by Simulation in the Gibbs Ensemble: A Review. Mol. Simul. 1992, 9, 1–23. [Google Scholar] [CrossRef]
- Chen, F.; Smith, P.E. Simulated surface tensions of common water models. J. Chem. Phys. 2007, 126, 221101. [Google Scholar] [CrossRef]
- Zakharov, V.V.; Brodskaya, E.N.; Laaksonen, A. Surface tension of water droplets: A molecular dynamics study of model and size dependencies. J. Chem. Phys. 1997, 107, 10675–10683. [Google Scholar] [CrossRef]
- Schaefer, D.; Stephan, S.; Langenbach, K.; Horsch, M.T.; Hasse, H. Mass Transfer through Vapor–Liquid Interfaces Studied by Non-Stationary Molecular Dynamics Simulations. J. Phys. Chem. B 2023, 127, 2521–2533. [Google Scholar] [CrossRef]
- Bernagozzi, M.; Georgoulas, A.; Miché, N.; Marengo, M. Heat pipes in battery thermal management systems for electric vehicles: A critical review. Appl. Therm. Eng. 2023, 219, 119495. [Google Scholar] [CrossRef]
- Long, L.N.; Micci, M.M.; Wong, B.C. Molecular dynamics simulations of droplet evaporation. Comput. Phys. Commun. 1996, 96, 167–172. [Google Scholar] [CrossRef]
- Walther, J.H.; Koumoutsakos, P. Molecular Dynamics Simulation of Nanodroplet Evaporation. J. Heat Transf. 2001, 123, 741–748. [Google Scholar] [CrossRef]
- Yang, T.H.; Pan, C. Molecular dynamics simulation of a thin water layer evaporation and evaporation coefficient. Int. J. Heat Mass Transf. 2005, 48, 3516–3526. [Google Scholar] [CrossRef]
- Persad, A.H.; Ward, C.A. Expressions for the Evaporation and Condensation Coefficients in the Hertz-Knudsen Relation. Chem. Rev. 2016, 116, 7727–7767. [Google Scholar] [CrossRef] [PubMed]
- Heinen, M.; Vrabec, J. Evaporation sampled by stationary molecular dynamics simulation. J. Chem. Phys. 2019, 151, 044704. [Google Scholar] [CrossRef] [PubMed]
- He, R.; Fu, Y.; He, J.; Yi, P.; Li, T. Analysis of subcritical to supercritical transition of n-heptane/ethanol blends by molecular dynamics simulation. At. Sprays 2022, 32, 87–106. [Google Scholar] [CrossRef]
- Yang, T.; Shen, J.; Zhu, C.; Wu, J. Molecular dynamics investigation on the vapor–liquid interface behavior of long-chain alkanes, alcohols, and their mixtures. J. Mol. Liq. 2023, 375, 121283. [Google Scholar] [CrossRef]
- Daiguji, H. Molecular dynamics study of n-alcohols adsorbed on an aqueous electrolyte solution. J. Chem. Phys. 2001, 115, 1538–1549. [Google Scholar] [CrossRef]
- Arcidiacono, S.; Poulikakos, D.; Ventikos, Y. Oscillatory behavior of nanodroplets. Phys. Rev. E 2004, 70, 011505. [Google Scholar] [CrossRef] [PubMed]
- Sheu, W.J.; Liou, N.C. Effect of temporal variation of pressure on vaporization of liquid droplets. Int. J. Heat Mass Transf. 1999, 42, 4043–4054. [Google Scholar] [CrossRef]
- Liu, L.H.; Han, Y.F.; Wang, Q.; Fu, Q.F. Molecular dynamics simulation of droplet evaporation in a one-dimensional standing wave acoustic field. Int. J. Therm. Sci. 2023, 184, 107939. [Google Scholar] [CrossRef]
- Chatterjee, S.; Singh, A.; Chakraborty, M. Molecular Insights into the Effect of Crystal Planes on Droplet Wetting. Langmuir 2023, 39, 4789–4798. [Google Scholar] [CrossRef] [PubMed]
- Dussan, E.B. On the Spreading of Liquids on Solid Surfaces: Static and Dynamic Contact Lines. Annu. Rev. Fluid Mech. 1979, 11, 371–400. [Google Scholar] [CrossRef]
- Koplik, J.; Banavar, J.R. Continuum Deductions from Molecular Hydrodynamics. Annu. Rev. Fluid Mech. 1995, 27, 257–292. [Google Scholar] [CrossRef]
- Chakraborty, M.; Ghosh, U.U.; Chakraborty, S.; DasGupta, S. Thermally enhanced self-propelled droplet motion on gradient surfaces. RSC Adv. 2015, 5, 45266–45275. [Google Scholar] [CrossRef]
- Bertrand, E.; Blake, T.D.; Coninck, J.D. Influence of solid–liquid interactions on dynamic wetting: A molecular dynamics study. J. Phys. Condens Matter. 2009, 21, 464124. [Google Scholar] [CrossRef]
- Blake, T.; De Coninck, J. The influence of solid–liquid interactions on dynamic wetting. Adv. Colloid Interface Sci. 2002, 96, 21–36. [Google Scholar] [CrossRef] [PubMed]
- Blake, T.D. The physics of moving wetting lines. J. Colloid Interface Sci. 2006, 299, 1–13. [Google Scholar] [CrossRef]
- Chakraborty, M.; Chowdhury, A.; Bhusan, R.; DasGupta, S. Molecular Dynamics Study of Thermally Augmented Nanodroplet Motion on Chemical Energy Induced Wettability Gradient Surfaces. Langmuir 2015, 31, 11260–11268. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.; Pathak, S.; Chakraborty, M. Molecular Investigation of Contact Line Movement in Electrowetted Nanodroplets. Langmuir 2020, 36, 12580–12589. [Google Scholar] [CrossRef]
- Pathak, S.; Chakraborty, M.; DasGupta, S. Molecular Investigation of the Actuation of Electrowetted Nanodroplets. Langmuir 2022, 38, 3656–3665. [Google Scholar] [CrossRef] [PubMed]
- Walther, J.H.; Jaffe, R.L.; Kotsalis, E.M.; Werder, T.; Halicioglu, T.; Koumoutsakos, P. Hydrophobic hydration of C60 and carbon nanotubes in water. Carbon 2004, 42, 1185–1194. [Google Scholar] [CrossRef]
- Werder, T.; Walther, J.H.; Jaffe, R.L.; Halicioglu, T.; Koumoutsakos, P. On the Water–Carbon Interaction for Use in Molecular Dynamics Simulations of Graphite and Carbon Nanotubes. J. Phys. Chem. B 2008, 112, 14090. [Google Scholar] [CrossRef]
- Walther, J.H.; Jaffe, R.; Halicioglu, T.; Koumoutsakos, P. Carbon Nanotubes in Water: Structural Characteristics and Energetics. J. Phys. Chem. B 2001, 105, 9980–9987. [Google Scholar] [CrossRef]
- Casto, A.; Bellussi, F.M.; Diego, M.; Fatti, N.D.; Banfi, F.; Maioli, P.; Fasano, M. Water filling in carbon nanotubes with different wettability and implications on nanotube/water heat transfer via atomistic simulations. Int. J. Heat Mass Transf. 2023, 205, 123868. [Google Scholar] [CrossRef]
- Jabbari, F.; Rajabpour, A.; Saedodin, S.; Wongwises, S. Effect of water/carbon interaction strength on interfacial thermal resistance and the surrounding molecular nanolayer of CNT and graphene flake. J. Mol. Liq. 2019, 282, 197–204. [Google Scholar] [CrossRef]
- Du, Y.; Zhou, T.; Zhao, C.; Ding, Y. Molecular dynamics simulation on thermal enhancement for carbon nano tubes (CNTs) based phase change materials (PCMs). Int. J. Heat Mass Transf. 2022, 182, 122017. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Ian Murdoch, A. Surface stress in solids. Int. J. Solids Struct. 1978, 14, 431–440. [Google Scholar] [CrossRef]
- Murdoch, A.I. The propagation of surface waves in bodies with material boundaries. J. Mech. Phys. Solids 1976, 24, 137–146. [Google Scholar] [CrossRef]
- Kiani, K. Nonlocal free dynamic analysis of periodic arrays of single-walled carbon nanotubes in the presence of longitudinal thermal and magnetic fields. Comput. Math. Appl. 2018, 75, 3849–3872. [Google Scholar] [CrossRef]
- Kiani, K. Thermo-mechanical analysis of functionally graded plate-like nanorotors: A surface elasticity model. Int. J. Mech. Sci. 2016, 106, 39–49. [Google Scholar] [CrossRef]
- Kiani, K. Stress analysis of thermally affected rotating nanoshafts with varying material properties. Acta Mech. Sin. 2016, 32, 813–827. [Google Scholar] [CrossRef]
- Zenkour, A.M. Nonlocal transient thermal analysis of a single-layered graphene sheet embedded in viscoelastic medium. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 79, 87–97. [Google Scholar] [CrossRef]
- Semmah, A.; Beg, O.A.; Mahmoud, S.R.; Heireche, H.; Tounsi, A. Thermal buckling properties of zigzag single-walled carbon nanotubes using a refined nonlocal model. Adv. Mater. Res. 2014, 3, 77–89. [Google Scholar] [CrossRef]
- Zare Pakzad, S.; Nasr Esfahani, M.; Tasdemir, Z.; Wollschläger, N.; Li, T.; Li, X.; Yilmaz, M.; Leblebici, Y.; Alaca, B.E. Nanomechanical Modeling of the Bending Response of Silicon Nanowires. ACS Appl. Nano Mater. 2023, 6, 15465–15478. [Google Scholar] [CrossRef]
- Chen, T.; Chiu, M.S.; Weng, C.N. Derivation of the generalized Young-Laplace equation of curved interfaces in nanoscaled solids. J. Appl. Phys. 2006, 100, 074308. [Google Scholar] [CrossRef]
- Zare Pakzad, S.; Nasr Esfahani, M.; Tasdemir, Z.; Wollschlaeger, N.; Li, X.; Li, T.; Yilmaz, M.; Leblebici, Y.; Alaca, B.E. A new characterization approach to study the mechanical behavior of silicon nanowires. MRS Adv. 2021, 6, 500–505. [Google Scholar] [CrossRef]
- Tasdemir, Z.; Peric, O.; Sacchetto, D.; Fantner, G.E.; Leblebici, Y.; Alaca, B.E. Monolithic Fabrication of Silicon Nanowires Bridging Thick Silicon Structures. IEEE Trans. Nanotechnol. 2018, 17, 1299–1302. [Google Scholar] [CrossRef]
- He, J.; Lilley, C.M. Surface Effect on the Elastic Behavior of Static Bending Nanowires. Nano Lett. 2008, 8, 1798–1802. [Google Scholar] [CrossRef]
- Nasr Esfahani, M.; Zare Pakzad, S.; Li, T.; Li, X.; Tasdemir, Z.; Wollschläger, N.; Leblebici, Y.; Alaca, B.E. Effect of Native Oxide on Stress in Silicon Nanowires: Implications for Nanoelectromechanical Systems. ACS Appl. Nano Mater. 2022, 5, 13276–13285. [Google Scholar] [CrossRef]
- Sun, K.; Shi, J.; Ma, L. Atomistic Insights into the Effects of Residual Stress during Nanoindentation. Crystals 2017, 7, 240. [Google Scholar] [CrossRef]
- Kinjo, T.; Matsumoto, M. Cavitation processes and negative pressure. Fluid Phase Equilib 1998, 144, 343–350. [Google Scholar] [CrossRef]
- Kimura, T.; Maruyama, S. Molecular dynamics simulation of heterogeneous nucleation of a liquid droplet on a solid surface. Microscale Thermophys Eng. 2002, 6, 3–13. [Google Scholar] [CrossRef]
- Nagayama, G.; Tsuruta, T.; Cheng, P. Molecular dynamics simulation on bubble formation in a nanochannel. Int. J. Heat Mass Transf. 2006, 49, 4437–4443. [Google Scholar] [CrossRef]
- She, X.; Shedd, T.A.; Lindeman, B.; Yin, Y.; Zhang, X. Bubble formation on solid surface with a cavity based on molecular dynamics simulation. Int. J. Heat Mass Transf. 2016, 95, 278–287. [Google Scholar] [CrossRef]
- Moseler, M.; Landman, U. Formation, Stability, and Breakup of Nanojets. Science 2000, 289, 1165–1169. [Google Scholar] [CrossRef] [PubMed]
- Roy, S. Coalescence preference and droplet size inequality during fluid phase segregation. EPL Europhys. Lett. 2018, 121, 34001. [Google Scholar] [CrossRef]
- Yi, N.; Huang, B.; Dong, L.; Quan, X.; Hong, F.; Tao, P.; Song, C.; Shang, W.; Deng, T. Temperature-Induced Coalescence of Colliding Binary Droplets on Superhydrophobic Surface. Sci. Rep. 2014, 4, 4303. [Google Scholar] [CrossRef]
- Li, T.; Li, M.; Zhang, L.; Yan, M.; Li, H. Molecular Dynamics Study of the Temperature-Dependent Coalescence of Liquid Nanodrops: Implications for Microfluidics. ACS Appl. Nano Mater. 2019, 2, 7978–7988. [Google Scholar] [CrossRef]
- Song, F.; Niu, H.; Fan, J.; Chen, Q.; Wang, G.; Liu, L. Molecular dynamics study on the coalescence and break-up behaviors of ionic droplets under DC electric field. J. Mol. Liq. 2020, 312, 113195. [Google Scholar] [CrossRef]
- Han, H. Multiscale Modeling of Nanostructure-Enhanced Two-Phase Heat Transfer; Drexel University: Philadelphia, PA, USA, 2016. [Google Scholar]
- Hu, H.; Sun, Y. Molecular dynamics simulations of disjoining pressure effect in ultra-thin water film on a metal surface. Appl. Phys. Lett. 2013, 103, 263110. [Google Scholar] [CrossRef]
- Hu, H.; Sun, Y. Effect of nanopatterns on Kapitza resistance at a water-gold interface during boiling: A molecular dynamics study. J. Appl. Phys. 2012, 112, 053508. [Google Scholar] [CrossRef]
- Dai, D.; Li, Y.; Wang, Y.; Bao, H.; Wang, G. Rethinking the image feature biases exhibited by deep convolutional neural network models in image recognition. CAAI Trans. Intell. Technol. 2022, 7, 721–731. [Google Scholar] [CrossRef]
- Tunyasuvunakool, K.; Adler, J.; Wu, Z.; Green, T.; Zielinski, M.; Žídek, A.; Bridgland, A.; Cowie, A.; Meyer, C.; Laydon, A. Highly accurate protein structure prediction for the human proteome. Nature 2021, 596, 590–596. [Google Scholar] [CrossRef] [PubMed]
- Meskhidze, H. Can Machine Learning Provide Understanding? How Cosmologists Use Machine Learning to Understand Observations of the Universe. Erkenntnis 2023, 88, 1895–1909. [Google Scholar] [CrossRef] [PubMed]
- Mallikarjuna, S.B.; Shivakumara, P.; Khare, V.; Basavanna, M.; Pal, U.; Poornima, B. Multi-gradient-direction based deep learning model for arecanut disease identification. CAAI Trans. Intell. Technol. 2022, 7, 156–166. [Google Scholar] [CrossRef]
- Chugo, D.; Muramatsu, S.; Yokota, S.; She, J.H.; Hashimoto, H. Stand-Up Assistive Devices Allowing Patients to Perform Voluntary Movements Within the Safety Movement Tolerance. J. Artif. Intell. Technol. 2022, 2, 164–173. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM Methods for Biomolecular Systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef]
- Kulik, H.J.; Zhang, J.; Klinman, J.P.; Martínez, T.J. How Large Should the QM Region Be in QM/MM Calculations? The Case of Catechol O -Methyltransferase. J. Phys. Chem. B 2016, 120, 11381–11394. [Google Scholar] [CrossRef] [PubMed]
- Wan, X.; Feng, W.; Wang, Y.; Wang, H.; Zhang, X.; Deng, C.; Yang, N. Materials Discovery and Properties Prediction in Thermal Transport via Materials Informatics: A Mini Review. Nano Lett. 2019, 19, 3387–3395. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Bao, H.; Ruan, X. Perspective: Predicting and optimizing thermal transport properties with machine learning methods. Energy AI 2022, 8, 100153. [Google Scholar] [CrossRef]
- Khodakarami, S.; Fazle Rabbi, K.; Suh, Y.; Won, Y.; Miljkovic, N. Machine learning enabled condensation heat transfer measurement. Int. J. Heat Mass Transf. 2022, 194, 123016. [Google Scholar] [CrossRef]
- Rustam, S.; Schram, M.; Lu, Z.; Chaka, A.M.; Rosenthal, W.S.; Pfaendtner, J. Optimization of Thermal Conductance at Interfaces Using Machine Learning Algorithms. ACS Appl. Mater. Interfaces 2022, 14, 32590–32597. [Google Scholar] [CrossRef]
- Ma, A.; Dinner, A.R. Automatic Method for Identifying Reaction Coordinates in Complex Systems. J. Phys. Chem. B 2005, 109, 6769–6779. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, T.D.; Ren, P.; Ponder, J.W.; Jensen, F. Force field modeling of conformational energies: Importance of multipole moments and intramolecular polarization. Int. J. Quantum. Chem. 2007, 107, 1390–1395. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Quantum mechanics of many-electron systems. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1929, 123, 714–733. [Google Scholar] [CrossRef]
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef]
- Vitalini, F.; Mey, A.S.J.S.; Noé, F.; Keller, B.G. Dynamic properties of force fields. J. Chem. Phys. 2015, 142, 084101. [Google Scholar] [CrossRef] [PubMed]
- Hansen, K.; Montavon, G.; Biegler, F.; Fazli, S.; Rupp, M.; Scheffler, M.; von Lilienfeld, O.A.; Tkatchenko, A.; Müller, K.R. Assessment and Validation of Machine Learning Methods for Predicting Molecular Atomization Energies. J. Chem. Theory Comput. 2013, 9, 3404–3419. [Google Scholar] [CrossRef] [PubMed]
- Unke, O.T.; Chmiela, S.; Sauceda, H.E.; Gastegger, M.; Poltavsky, I.; Schütt, K.T.; Tkatchenko, A.; Müller, K.M. Machine Learning Force Fields. Chem. Rev. 2021, 121, 10142–10186. [Google Scholar] [CrossRef]
- Hansen, K.; Biegler, F.; Ramakrishnan, R.; Pronobis, W.; von Lilienfeld, O.A.; Müller, K.R.; Tkatchenko, A. Machine Learning Predictions of Molecular Properties: Accurate Many-Body Potentials and Nonlocality in Chemical Space. J. Phys. Chem. Lett. 2015, 6, 2326–2331. [Google Scholar] [CrossRef] [PubMed]
- Kadupitiya, J.C.; Sun, F.; Fox, G.; Jadhao, V. Machine learning surrogates for molecular dynamics simulations of soft materials. J. Comput. Sci. 2020, 42, 101107. [Google Scholar] [CrossRef]
- Wang, Y.; Lamim Ribeiro, J.M.; Tiwary, P. Machine learning approaches for analyzing and enhancing molecular dynamics simulations. Curr. Opin. Struct. Biol. 2020, 61, 139–145. [Google Scholar] [CrossRef]
- Behler, J.; Parrinello, M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98, 146401. [Google Scholar] [CrossRef] [PubMed]
- Bartók, A.P.; Payne, M.C.; Kondor, R.; Csányi, G. Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett. 2010, 104, 136403. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.S.; Isayev, O.; Roitberg, A.E. ANI-1, an extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci. 2017, 8, 3192–3203. [Google Scholar] [CrossRef]
- Bao, H.; Chen, J.; Gu, X.; Cao, B. A Review of Simulation Methods in Micro/Nanoscale Heat Conduction. ES Energy Environ. 2018, 1, 16–55. [Google Scholar] [CrossRef]
- Wang, Y.; Vallabhaneni, A.K.; Qiu, B.; Ruan, X. Two-Dimensional Thermal Transport in Graphene: A Review of Numerical Modeling Studies. Nanoscale Microscale Thermophys Eng. 2014, 18, 155–182. [Google Scholar] [CrossRef]
- Saito, R.; Mizuno, M.; Dresselhaus, M.S. Ballistic and Diffusive Thermal Conductivity of Graphene. Phys. Rev. Appl. 2018, 9, 024017. [Google Scholar] [CrossRef]
- Li, H.-P.; Zhang, R.-Q. Anomalous effect of hydrogenation on phonon thermal conductivity in thin silicon nanowires. EPL Europhys. Lett. 2014, 105, 56003. [Google Scholar] [CrossRef]
- Tian, Z.; Hu, H.; Sun, Y. A molecular dynamics study of effective thermal conductivity in nanocomposites. Int. J. Heat Mass Transf. 2013, 61, 577–582. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, M. Phonon hydrodynamics and its applications in nanoscale heat transport. Phys. Rep. 2015, 595, 1–44. [Google Scholar] [CrossRef]
- Chen, G.; Yang, R.; Chen, X. Nanoscale heat transfer and thermal-electric energy conversion. J. Phys. IV 2005, 125, 499–504. [Google Scholar] [CrossRef]
- Silva, A.C.A.; Neto, E.S.F.; da Silva, S.W.; Morais, P.C.; Dantas, N.O. Modified Phonon Confinement Model and Its Application to CdSe/CdS Core–Shell Magic-Sized Quantum Dots Synthesized in Aqueous Solution by a New Route. J. Phys. Chem. C 2013, 117, 1904–1914. [Google Scholar] [CrossRef]
- Song, Q.; Chen, G. Evaluation of the diffuse mismatch model for phonon scattering at disordered interfaces. Phys. Rev. B 2021, 104, 085310. [Google Scholar] [CrossRef]
- Lindsay, L.; Broido, D.A.; Mingo, N. Lattice thermal conductivity of single-walled carbon nanotubes: Beyond the relaxation time approximation and phonon-phonon scattering selection rules. Phys. Rev. B-Condens. Matter. Mater. Phys. 2009, 80, 125407. [Google Scholar] [CrossRef]
- Mingo, N.; Broido, D.A. Length dependence of carbon nanotube thermal conductivity and the “problem of long waves”. Nano Lett. 2005, 5, 1221–1225. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ouyang, Y.; Cheng, Y.; Chen, J.; Li, N. Size-dependent phononic thermal transport in low-dimensional nanomaterials. Phys. Rep. 2020, 860, 1–26. [Google Scholar] [CrossRef]
- Polanco, J.; Fitzgerald, R.M.; Maradudin, A.A. Scattering of surface plasmon polaritons by one-dimensional surface defects. Phys. Rev. B-Condens. Matter. Mater. Phys. 2013, 87, 155417. [Google Scholar] [CrossRef]
- Xiong, S.; Kosevich, Y.A.; Sääskilahti, K.; Ni, Y.; Volz, S. Tunable thermal conductivity in silicon twinning superlattice nanowires. Phys. Rev. B-Condens. Matter. Mater. Phys. 2014, 90, 195439. [Google Scholar] [CrossRef]
- Xiong, S.; Sääskilahti, K.; Kosevich, Y.A.; Han, H.; Donadio, D.; Volz, S. Blocking Phonon Transport by Structural Resonances in Alloy-Based Nanophononic Metamaterials Leads to Ultralow Thermal Conductivity. Phys. Rev. Lett. 2016, 117, 025503. [Google Scholar] [CrossRef] [PubMed]
- Maire, J.; Anufriev, R.; Nomura, M. Ballistic thermal transport in silicon nanowires. Sci. Rep. 2017, 7, 41794. [Google Scholar] [CrossRef] [PubMed]
- Raja, S.N.; Rhyner, R.; Vuttivorakulchai, K.; Luisier, M.; Poulikakos, D. Length scale of diffusive phonon transport in suspended thin silicon nanowires. Nano Lett. 2017, 17, 276–283. [Google Scholar] [CrossRef]
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys. Rev. B-Condens. Matter. Mater. Phys. 2002, 65, 144306. [Google Scholar] [CrossRef]
- Sellan, D.P.; Landry, E.S.; Turney, J.E.; McGaughey, A.J.H.; Amon, C.H. Size effects in molecular dynamics thermal conductivity predictions. Phys. Rev. B-Condens. Matter. Mater. Phys. 2010, 81, 214305. [Google Scholar] [CrossRef]
- Ye, Z.Q.; Cao, B.Y. Spectral phonon thermal properties in graphene nanoribbons. Carbon 2015, 93, 915–923. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977–1026. [Google Scholar] [CrossRef]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef]
- Bhagat, A.A.S.; Bow, H.; Hou, H.W.; Tan, S.J.; Han, J.; Lim, C.T. Microfluidics for cell separation. Med. Biol. Eng. Comput. 2010, 48, 999–1014. [Google Scholar] [CrossRef]
- Chaudhury, M.K.; Whitesides, G.M. How to make water run uphill. Science 1992, 256, 1539–1541. [Google Scholar] [CrossRef]
- Im, Y.; Dietz, C.; Lee, S.S.; Joshi, Y. Flower-like CuO nanostructures for enhanced boiling. Nanoscale Microscale Thermophys Eng. 2012, 16, 145–153. [Google Scholar] [CrossRef]
- Chen, X.; Cao, G.; Han, A.; Punyamurtula, V.K.; Liu, L.; Culligan, P.J.; Kim, T.; Qiao, Y. Nanoscale fluid transport: Size and rate effects. Nano Lett. 2008, 8, 2988–2992. [Google Scholar] [CrossRef]
- Abbas, W.; Magdy, M.M. Heat and Mass Transfer Analysis of Nanofluid Flow Based on Cu, Al2O3, and TiO2 over a Moving Rotating Plate and Impact of Various Nanoparticle Shapes. Math. Probl. Eng. 2020, 2020, 9606382. [Google Scholar] [CrossRef]
- Yang, R. Nanoscale Heat Conduction with Applications in Nanoelectronics and Thermoelectrics. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005; 217p. [Google Scholar]
- Kaneez, H.; Qureshi, M.A.; Alharbi, S.O.; Aziz, T.; Nawaz, M. Role of hybrid nano-structures and dust particles on transportation of heat energy in fluid with memory effects. Ain. Shams Eng. J. 2021, 12, 2171–2180. [Google Scholar] [CrossRef]
- Sivashanmugam, P. Application of Nanofluids in Heat Transfer. In An Overview of Heat Transfer Phenomena; InTech: Rijeka, Croatia, 2012; pp. 411–440. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.S.; Patel, H.E. Heat transfer in nanofluids—A review. Heat Transf. Eng. 2006, 27, 3–19. [Google Scholar] [CrossRef]
- Rashid, U.; Lu, D.; Iqbal, Q. Nanoparticles impacts on natural convection nanofluid flow and heat transfer inside a square cavity with fixed a circular obstacle. Case Stud. Therm. Eng. 2023, 44, 102829. [Google Scholar] [CrossRef]
- Ajeeb, W.; Murshed, S.M.S. Nanofluids in compact heat exchangers for thermal applications: A State-of-the-art review. Therm. Sci. Eng. Prog. 2022, 30, 101276. [Google Scholar] [CrossRef]
- Sobhan, C.B.; Peterson, G.P. Microscale and Nanoscale Heat Transfer Fundamentals and Engineering Applications, 1st ed.; Peterson, G.P., Ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Li, X.; Yuan, F.; Tian, W.; Dai, C.; Yang, X.; Wang, D.; Du, J.; Yu, W.; Yuan, H. Heat Transfer Enhancement of Nanofluids with Non-Spherical Nanoparticles: A Review. Appl. Sci. 2022, 12, 4767. [Google Scholar] [CrossRef]
- Maitra, T.; Zhang, S.; Tiwari, M.K. Thermal Transport in Micro- and Nanoscale Systems; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Chen, G. Non-Fourier phonon heat conduction at the microscale and nanoscale. Nat. Rev. Phys. 2021, 3, 555–569. [Google Scholar] [CrossRef]
- Gupta, R.; Bera, C. Effect of nanoinclusions on the lattice thermal conductivity of SnSe. Nano Express 2020, 1, 030035. [Google Scholar] [CrossRef]
- Zhang, H.; Qing, S.; Gui, Q.; Zhang, X.; Zhang, A. Effects of surface modification and surfactants on stability and thermophysical properties of TiO2/water nanofluids. J. Mol. Liq. 2022, 349, 118098. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, P.; Zhang, Q.; Wu, J.; Dai, Y.; Hu, W.; Wereley, N.M. Effects of surface modification on the stability of suspension and thermal conductivity enhancement of composite fe nanofluids. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Beck, J.; Palmer, M.; Inman, K.; Wohld, J.; Cummings, M.; Fulmer, R.; Scherer, B.; Vafaei, S. Heat Transfer Enhancement in the Microscale: Optimization of Fluid Flow. Nanomaterials 2022, 12, 3628. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.H.; Ahn, H.S. A comprehensive review on micro/nanoscale surface modification techniques for heat transfer enhancement in heat exchanger. Int. J. Heat Mass Transf. 2021, 178, 121601. [Google Scholar] [CrossRef]
- Souayeh, B.; Bhattacharyya, S. Turbulent Heat Transfer Augmentation in a Square Channel by Augmenting the Flow Pattern with Novel Arc-Shaped Ribs. Mathematics 2023, 11, 1490. [Google Scholar] [CrossRef]
- Ghadimi, A.; Saidur, R.; Metselaar, H.S.C. A review of nanofluid stability properties and characterization in stationary conditions. Int. J. Heat Mass Transf. 2011, 54, 4051–4068. [Google Scholar] [CrossRef]
- Yarmand, H.; Gharehkhani, S.; Shirazi, S.F.S.; Goodarzi, M.; Amiri, A.; Sarsam, W.S.; Alehashem, M.S.; Dahari, M.; Kazi, S.N. Study of synthesis, stability and thermo-physical properties of graphene nanoplatelet/platinum hybrid nanofluid. Int. Commun. Heat Mass Transf. 2016, 77, 15–21. [Google Scholar] [CrossRef]
- Goswami, A.; Pillai, S.C.; McGranaghan, G. Micro/Nanoscale surface modifications to combat heat exchanger fouling. Chem. Eng. J. Adv. 2023, 16, 100519. [Google Scholar] [CrossRef]
- Hsu, H.Y.; Lin, M.C.; Popovic, B.; Lin, C.R.; Patankar, N.A. A numerical investigation of the effect of surface wettability on the boiling curve. PLoS ONE 2017, 12, e0187175. [Google Scholar] [CrossRef]
- Heidarshenas, A.; Azizi, Z.; Peyghambarzadeh, S.M.; Sayyahi, S. Experimental investigation of heat transfer enhancement using ionic liquid-Al2O3 hybrid nanofluid in a cylindrical microchannel heat sink. Appl. Therm. Eng. 2021, 191, 116879. [Google Scholar] [CrossRef]
- Shahmardi, A.; Tammisola, O.; Chinappi, M.; Brandt, L. Effects of surface nanostructure and wettability on pool boiling: A molecular dynamics study. Int. J. Therm. Sci. 2021, 167, 106980. [Google Scholar] [CrossRef]
- Lee, J.Y.; Kim, M.H.; Kaviany, M.; Son, S.Y. Bubble nucleation in microchannel flow boiling using single artificial cavity. Int. J. Heat Mass Transf. 2011, 54, 5139–5148. [Google Scholar] [CrossRef]
- Chakraborty, P.; Ma, T.; Cao, L.; Wang, Y. Significantly enhanced convective heat transfer through surface modification in nanochannels. Int. J. Heat Mass Transf. 2019, 136, 702–708. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; Ziegenhein, T. Two-phase bubble columns: A comprehensive review. ChemEngineering 2018, 2, 13. [Google Scholar] [CrossRef]
- Chen, J.; Ahmad, S.; Cai, J.; Liu, H.; Lau, K.T.; Zhao, J. Latest progress on nanotechnology aided boiling heat transfer enhancement: A review. Energy 2021, 215, 119114. [Google Scholar] [CrossRef]
- Lu, Y.W.; Kandlikar, S.G. Nanoscale surface modification techniques for pool boiling enhancementa—A critical review and future directions. Heat Transf. Eng. 2011, 32, 827–842. [Google Scholar] [CrossRef]
- Yuan, D.; Chen, D.; Yan, X.; Xu, J.; Lu, Q.; Huang, Y. Bubble behavior and its contribution to heat transfer of subcooled flow boiling in a vertical rectangular channel. Ann. Nucl. Energy 2018, 119, 191–202. [Google Scholar] [CrossRef]
- Kancheva, M.; Aronson, L.; Pattilachan, T.; Sautto, F.; Daines, B.; Thommes, D.; Shar, A.; Razavi, M. Bubble-Based Drug Delivery Systems: Next-Generation Diagnosis to Therapy. J. Funct. Biomater. 2023, 14, 373. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, G.; Moghtaderi, B.; Doroodchi, E. A review of microreactors based on slurry Taylor (segmented) flow. Chem. Eng. Sci. 2022, 247, 117040. [Google Scholar] [CrossRef]
- Shahid, M.; Ahmed, W.; Zhan, Y.; Hongtao, Z.; Kaewsaneha, C.; Opaprakasit, P. Nanosolar Cell Technologies; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar] [CrossRef]
- Allen, J.J.; Smits, A.J. Energy Harvesting eel. J. Fluids Struct. 2001, 15, 629–640. [Google Scholar] [CrossRef]
- Biswas, P.K.; Uddin, M.; Islam, M.U.; Sarkar, M.I.; DeSa, V.; Khan, M.; Huq, A. Icme09-Am-29 Harnessing Raindrop Energy in Bangladesh. Int. Conf. Mech. Eng. 2009, 2009, 26–28. [Google Scholar]
- Ilyas, M.A.; Swingler, J. Piezoelectric energy harvesting from raindrop impacts. Energy 2015, 90, 796–806. [Google Scholar] [CrossRef]
- Viola, F.; Romano, P.; Miceli, R.; Acciari, G. On the harvest of rainfall energy by means of piezoelectric transducer. In Proceedings of the 2013 International Conference on Renewable Energy Research and Applications, Madrid, Spain, 20–23 October 2013; pp. 1133–1138. [Google Scholar] [CrossRef]
- Valentini, L.; Bon, S.B.; Kenny, J. Liquid droplet excitation of freestanding poly(methyl methacrylate)/ graphene oxide films for mechanical energy harvesting. J. Polym. Sci. Part B Polym. Phys. 2013, 51, 1028–1032. [Google Scholar] [CrossRef]
- Lai, Y.C.; Hsiao, Y.C.; Wu, H.M.; Wang, Z.L. Waterproof-Fabric-Based Multifunctional Triboelectric Nanogenerator for Universally Harvesting Energy from Raindrops, Wind, and Human Motions and as Self-Powered Sensors. Adv. Sci. 2019, 6, 1801883. [Google Scholar] [CrossRef]
- Le, A.T.; Ahmadipour, M.; Pung, S.Y. A review on ZnO-based piezoelectric nanogenerators: Synthesis, characterization techniques, performance enhancement and applications. J. Alloys Compd. 2020, 844, 156172. [Google Scholar] [CrossRef]
- Soin, N.; Shah, T.H.; Anand, S.C.; Geng, J.; Pornwannachai, W.; Mandal, P.; Reid, D.; Sharma, S.; Hadimani, R.L.; Bayramol, D.V.; et al. Novel “3-D spacer” all fibre piezoelectric textiles for energy harvesting applications. Energy Environ. Sci. 2014, 7, 1670–1679. [Google Scholar] [CrossRef]
- Kang, L.; An, H.L.; Park, J.Y.; Hong, M.H.; Nahm, S.; Lee, C.G. La-doped p-type ZnO nanowire with enhanced piezoelectric performance for flexible nanogenerators. Appl. Surf. Sci. 2019, 475, 969–973. [Google Scholar] [CrossRef]
- Tinaikar, A. Harvesting Energy from Rainfall. Int. J Renew. Sustain. Energy 2013, 2, 130. [Google Scholar] [CrossRef][Green Version]
- Adhikari, A.; Sengupta, J. Nanogenerators: A New Paradigm in Blue Energy Harvesting; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex TE meterials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Rowe, D.M. CRC Handbook of Thermoelectrics; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Heremans, J.P.; Dresselhaus, M.S.; Bell, L.E.; Morelli, D.T. When thermoelectrics reached the nanoscale. Nat. Nanotechnol. 2013, 8, 471–473. [Google Scholar] [CrossRef] [PubMed]
- Chen, G. Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons, 1st ed.; Christensen, D., Ed.; Oxford Universty Press: Oxford, UK, 2005. [Google Scholar]
- Sui, J.; Li, J.; He, J.; Pei, Y.L.; Berardan, D.; Wu, H.; Dragoe, N.; Cai, W.; Zhao, L.D. Texturation boosts the thermoelectric performance of BiCuSeO oxyselenides. Energy Environ. Sci. 2013, 6, 2916–2920. [Google Scholar] [CrossRef]
- Minnich, A.J.; Dresselhaus, M.S.; Ren, Z.F.; Chen, G. Bulk nanostructured thermoelectric materials: Current research and future prospects. Energy Environ. Sci. 2009, 2, 466–479. [Google Scholar] [CrossRef]
- Shakouri, A. Recent developments in semiconductor thermoelectric physics and materials. Annu. Rev. Mater. Res. 2011, 41, 399–431. [Google Scholar] [CrossRef]
- Venkatasubramanian, R.; Siivola, E.; Colpitts, T.; O’Quinn, B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature 2001, 413, 597–602. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Kanatzidis, M.G.; Dravid, V.P. High performance bulk thermoelectrics via a panoscopic approach. Mater. Today 2013, 16, 166–176. [Google Scholar] [CrossRef]
- Zhao, L.D.; Lo, S.H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 2014, 508, 373–377. [Google Scholar] [CrossRef]
- Alahmad, M.; El-Aleem, F.A. Heat Transfer Challenges in Semiconductors Processing and the Applications of Heat Pipes for Efficient Heat Removal. J. King. Saud. Univ.-Eng. Sci. 2003, 15, 141–154. [Google Scholar] [CrossRef]
- Simons, R.E.; Antonetti, V.W.; Nakayama, W.; Oktay, S. Heat Transfer in Electronic Packages. In Microelectronics Packaging Handbook; Springer: New York, NY, USA, 1997; Volume 6, pp. 314–403. [Google Scholar] [CrossRef]
- Gurrum, S.P.; Suman, S.K.; Joshi, Y.K.; Fedorov, A.G. Thermal Issues in Next-Generation Integrated Circuits. IEEE Trans. Device Mater. Reliab. 2004, 4, 709–714. [Google Scholar] [CrossRef]
- Kumar, J.P.S.; Sankaranarayanan, R.; Sujana, J.A.J.; Hynes, N.R.J. Advantages and disadvantages of nanodevices. In Nanomedicine Manufacturing and Applications; Elsevier: Amsterdam, The Netherlands, 2021; pp. 163–171. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Ke, C.; Pugno, N. Nanoelectromechanical Systems: Experiments and Modeling. In Encyclopedia of Materials: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1–9. [Google Scholar] [CrossRef]
- Lei, S.; Su, N.; Li, M. Thermal-Resistance Effect of Graphene at High Temperatures in Nanoelectromechanical Temperature Sensors. Micromachines 2022, 13, 2078. [Google Scholar] [CrossRef] [PubMed]
- Shikida, M.; Hasegawa, Y.; Farisi, M.S.; Al Matsushima, M.; Kawabe, T. Advancements in MEMS technology for medical applications: Microneedles and miniaturized sensors. JPN J. Appl. Phys. 2022, 61, SA0803. [Google Scholar] [CrossRef]
- Nemec, D.; Janota, A.; Hrubos, M.; Simak, V. Intelligent Real-Time MEMS Sensor Fusion and Calibration. IEEE Sens. J. 2016, 16, 7150–7160. [Google Scholar] [CrossRef]
- Li, J. Micro-/Nano-Fiber Sensors and Optical Integration Devices. Sensors 2022, 22, 7673. [Google Scholar] [CrossRef]
- Jiao, P.; Matin Nazar, A.; Egbe, K.J.I.; Barri, K.; Alavi, A.H. Magnetic capsulate triboelectric nanogenerators. Sci. Rep. 2022, 12, 89. [Google Scholar] [CrossRef]
- Macenić, M.; Kurevija, T.; Medved, I. Novel geothermal gradient map of the Croatian part of the Pannonian Basin System based on data interpretation from 154 deep exploration wells. Renew. Sustain. Energy Rev. 2020, 132, 110069. [Google Scholar] [CrossRef]
- Jiang, X.; Kazarin, P.; Sinanis, M.D.; Darwish, A.; Raghunathan, N.; Alexeenko, A.; Peroulis, D. A non-invasive multipoint product temperature measurement for pharmaceutical lyophilization. Sci. Rep. 2022, 12, 12010. [Google Scholar] [CrossRef] [PubMed]
- Takács, G.; Bognár, G.; Bándy, E.; Rózsás, G.; Szabó, P.G. Fabrication and characterization of microscale heat sinks. Microelectron. Reliab. 2017, 79, 480–487. [Google Scholar] [CrossRef]
- Sundén, B.; Fu, J. Heat Pipes for Aerospace Application. In Heat Transfer in Aerospace Applications; Elsevier: Amsterdam, The Netherlands, 2017; pp. 117–144. [Google Scholar] [CrossRef]
- Reay, D.A.; Kew, P.A.; McGlen, R.J. Cooling of electronic components. In Heat Pipes; Elsevier: Amsterdam, The Netherlands, 2014; pp. 207–225. [Google Scholar] [CrossRef]
- Jouhara, H. 4.3 Heat Pipes. In Comprehensive Energy Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 70–97. [Google Scholar] [CrossRef]
- Faghri, A.; Zhang, Y. Introduction to transport phenomena. In Transport Phenomena in Multiphase Systems; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1–106. [Google Scholar] [CrossRef]
- Chen, X.; Shen, S.; Guo, L.; Mao, S.S. Semiconductor-based photocatalytic hydrogen generation. Chem. Rev. 2010, 110, 6503–6570. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.F.; Sun, T.; Cao, F.; Liu, Q.; Ren, Z. Metallic nanostructures for light trapping in energy-harvesting devices. Light. Sci. Appl. 2014, 3, e161. [Google Scholar] [CrossRef]
- Lee, J.; Mubeen, S.; Ji, X.; Stucky, G.D.; Moskovits, M. Plasmonic photoanodes for solar water splitting with visible light. Nano Lett. 2012, 12, 5014–5019. [Google Scholar] [CrossRef]
- Won, D.H.; Shin, H.; Koh, J.; Won, D.H.; Shin, H.; Koh, J.; Chung, J.; Lee, H.S.; Kim, H.; Woo, S.I. Highly Efficient, Selective, and Stable CO2 Electroreduction on a Hexagonal Zn Catalyst. Angew. Chem.-Int. Ed. 2016, 55, 9297–9300. [Google Scholar] [CrossRef]
- Du, J.; Li, F.; Sun, L. Metal-organic frameworks and their derivatives as electrocatalysts for the oxygen evolution reaction. Chem. Soc. Rev. 2021, 50, 2663–2695. [Google Scholar] [CrossRef] [PubMed]
- Pak, J.; Jang, J.; Cho, K.; Kim, T.Y.; Kim, J.K.; Song, Y.; Hong, W.K.; Min, M.; Lee, H.; Lee, T. Enhancement of photodetection characteristics of MoS2 field effect transistors using surface treatment with copper phthalocyanine. Nanoscale 2015, 7, 18780–18788. [Google Scholar] [CrossRef]
- Hu, H.; Xu, C.; Zhao, Y.; Ziegler, K.J.; Chung, J.N. Boiling and quenching heat transfer advancement by nanoscale surface modification. Sci. Rep. 2017, 7, 6117. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Bhaumik, S. Enhancement of Nucleate Pool Boiling Heat Transfer on Titanium Oxide Thin Film Surface. Arab. J. Sci. Eng. 2014, 39, 7385–7395. [Google Scholar] [CrossRef]
- Bongarala, M.; Hu, H.; Weibel, J.A.; Garimella, S.V. Microlayer evaporation governs heat transfer enhancement during pool boiling from microstructured surfaces. Appl. Phys. Lett. 2022, 120, 221602. [Google Scholar] [CrossRef]
- Hu, H.; Chakraborty, M.; Allred, T.P.; Weibel, J.A.; Garimella, S.V. Multiscale Modeling of the Three-Dimensional Meniscus Shape of a Wetting Liquid Film on Micro-/Nanostructured Surfaces. Langmuir 2017, 33, 12028–12037. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Weibel, J.A.; Garimella, S.V. Role of nanoscale roughness in the heat transfer characteristics of thin film evaporation. Int. J. Heat Mass Transf. 2020, 150, 119306. [Google Scholar] [CrossRef]
- Hasan, M.N.; Shavik, S.M.; Rabbi, K.F.; Mukut, K.M.; Alam, M.M. Thermal transport during thin-film argon evaporation over nanostructured platinum surface: A molecular dynamics study. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2018, 232, 83–91. [Google Scholar] [CrossRef]
- Plawsky, J.L.; Fedorov, A.G.; Garimella, S.V.; Ma, H.B.; Maroo, S.C.; Chen, L.; Nam, Y. Nano-and microstructures for thin-film evaporation—A review. Nanoscale Microscale Thermophys Eng. 2014, 18, 251–269. [Google Scholar] [CrossRef]
- Davoodabadi, A.; Ghasemi, H. Evaporation in nano/molecular materials. Adv. Colloid Interface Sci. 2021, 290, 102385. [Google Scholar] [CrossRef] [PubMed]
- Ward, C.A. Liquid-Vapour Phase Change Rates and Interfacial Entropy Production. J. Non-Equilibrium Thermodyn. 2002, 27, 289–303. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, L.; Liu, Q.; Yu, J.; Wang, H. Nanoscale View of Dewetting and Coating on Partially Wetted Solids. J. Phys. Chem. Lett. 2016, 7, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Ciraci, S.; Buldum, A.; Batra, I.P. Quantum effects in electrical and thermal transport through nanowires. J. Phys. Condens Matter. 2001, 13, R537–R568. [Google Scholar] [CrossRef]
- Sun, T.; Wang, J.; Kang, W. Van der Waals interaction-tuned heat transfer in nanostructures. Nanoscale 2013, 5, 128–133. [Google Scholar] [CrossRef] [PubMed]
- Laliotis, A.; de Silans, T.P.; Maurin, I.; Ducloy, M.; Bloch, D. Casimir–Polder interactions in the presence of thermally excited surface modes. Nat. Commun. 2014, 5, 4364. [Google Scholar] [CrossRef]
- Xu, L.; Molinero, V. Liquid–Vapor Oscillations of Water Nanoconfined between Hydrophobic Disks: Thermodynamics and Kinetics. J. Phys. Chem. B 2010, 114, 7320–7328. [Google Scholar] [CrossRef] [PubMed]
- Maroo, S.C.; Chung, J.N. Nanoscale liquid-vapor phase-change physics in nonevaporating region at the three-phase contact line. J. Appl. Phys. 2009, 106, 064911. [Google Scholar] [CrossRef]
- Pekur, D.V.; Sorokin, V.M.; Nikolaenko, Y.E. Thermal characteristics of a compact LED luminaire with a cooling system based on heat pipes. Therm. Sci. Eng. Prog. 2020, 18, 100549. [Google Scholar] [CrossRef]








| Parameters | TIP4P | SPC/E |
|---|---|---|
| r(OH), Å | 0.9572 | 1 |
| <HOH, ° | 104.52 | 109.47 |
| A × 10−3, kcal Å12/mol | 600 | 629.4 |
| C, kcal Å6/mol | 610 | 625.5 |
| q(O) | 0 | −0.8476 |
| q(H) | 0.52 | 0.4238 |
| q(M) | −1.04 | 0 |
| r(OM), Å | 0.15 | 0 |
| Advantages | Disadvantages |
|---|---|
|
|
| Application | Key Parameter | References |
|---|---|---|
| Microfluidic devices |
| Ref. [159] |
| Micro/nano heat exchanger |
| Ref. [173] |
| Microprocessors and integrated circuits |
| Ref. [218] |
| Nano-electromechanical systems (NEMS) |
| Ref. [221] |
| Microscale heat pipes |
| Ref. [230] |
| Microscale heat sinks |
| Ref. [256] |
| Thermoelectric energy conversion |
| Refs. [207,208] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, S.; Paras; Hu, H.; Chakraborty, M. A Review of Nano and Microscale Heat Transfer: An Experimental and Molecular Dynamics Perspective. Processes 2023, 11, 2769. https://doi.org/10.3390/pr11092769
Chatterjee S, Paras, Hu H, Chakraborty M. A Review of Nano and Microscale Heat Transfer: An Experimental and Molecular Dynamics Perspective. Processes. 2023; 11(9):2769. https://doi.org/10.3390/pr11092769
Chicago/Turabian StyleChatterjee, Samyabrata, Paras, Han Hu, and Monojit Chakraborty. 2023. "A Review of Nano and Microscale Heat Transfer: An Experimental and Molecular Dynamics Perspective" Processes 11, no. 9: 2769. https://doi.org/10.3390/pr11092769
APA StyleChatterjee, S., Paras, Hu, H., & Chakraborty, M. (2023). A Review of Nano and Microscale Heat Transfer: An Experimental and Molecular Dynamics Perspective. Processes, 11(9), 2769. https://doi.org/10.3390/pr11092769







