Research on Downhole Throttling Characteristics of Gas Wells Based on Multi-Field and Multi-Phase
Abstract
:1. Introduction
2. Construction of Wellbore Temperature and Pressure Field Model with Multi-Field and Multi-Phase Coupling
2.1. Basic Assumptions of the Model
- (1)
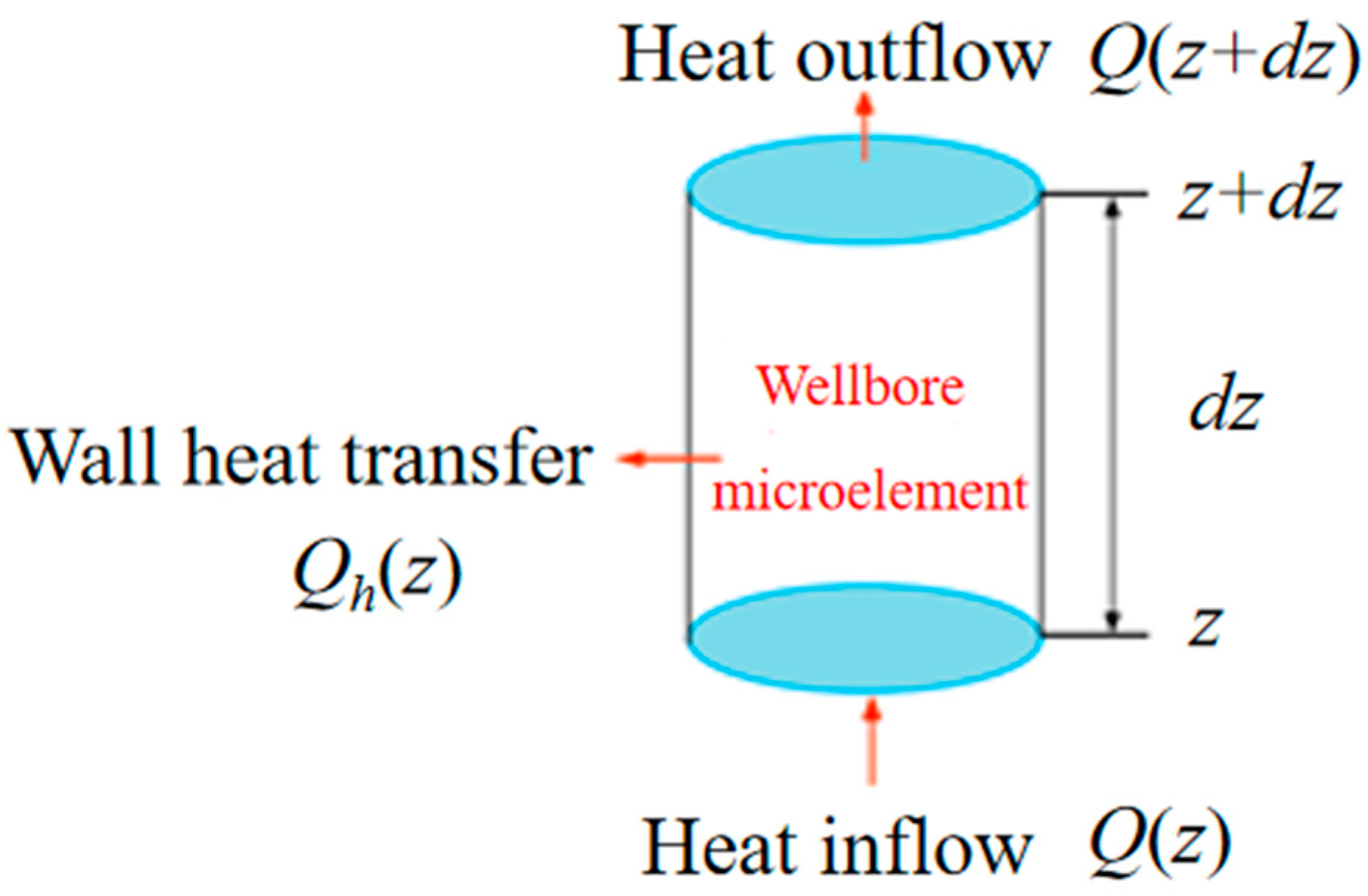
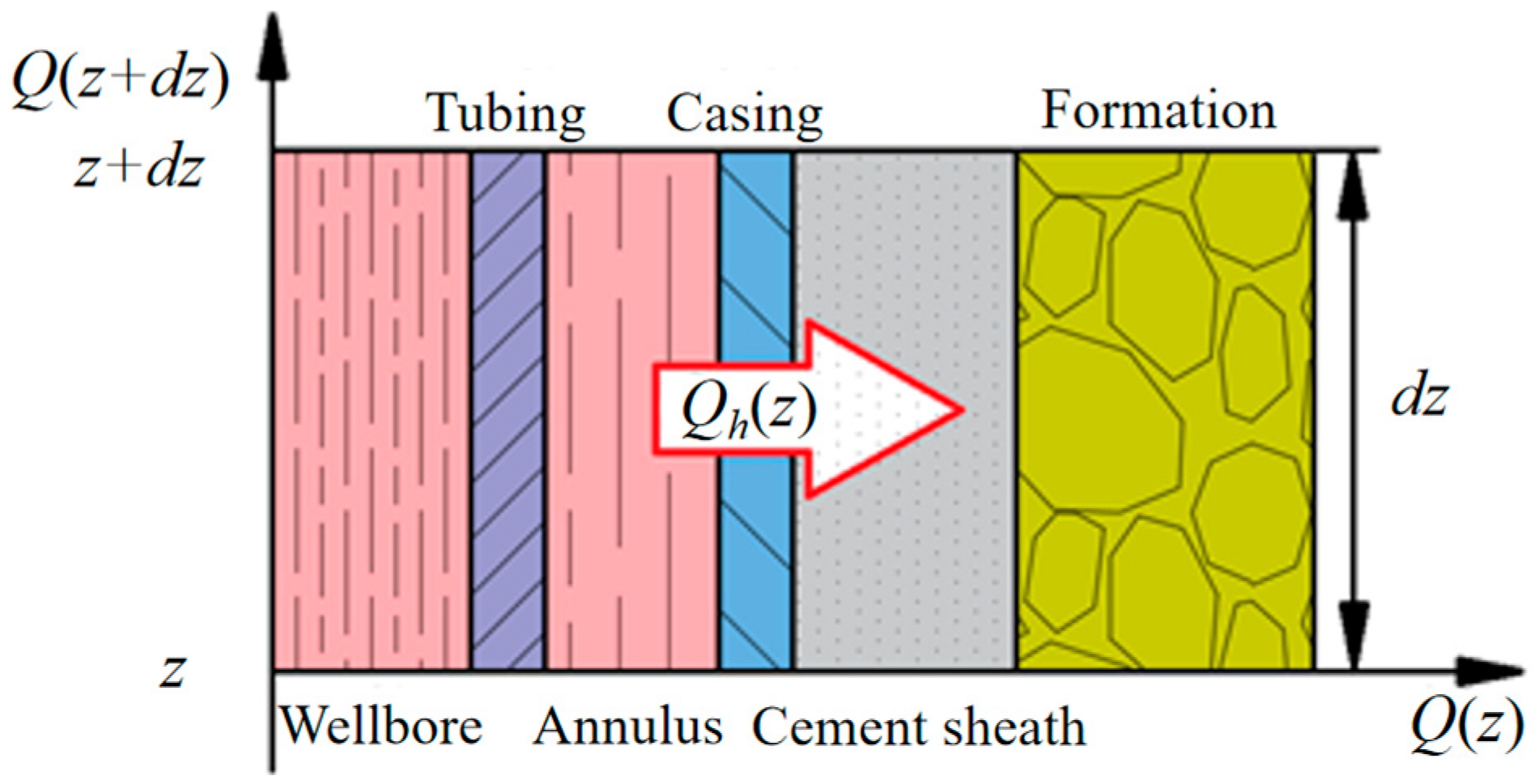
- It is assumed that the heat transfer from the wellbore to the formation around the wellbore is radial.
- (2)
- It is assumed that the conduction process of heat from the wellbore to the formation is unsteady and that the heat transfer in the wellbore is steady state.
- (3)
- There is only radial heat loss in the wellbore micro-elements.
- (4)
- The gas–water/gas–solid two-phase transient in the wellbore satisfies the thermal equilibrium [22].
- (5)
- During the flow process, the fluid and the outside world do not perform work on each other.
- (6)
- The proportion of the gas phase in the fluid is much higher than that of other phases [23].
- (7)
- Each phase in the fluid is composed of continuous particles and conforms to the theory of continuous media, which can be averaged in time and space.
- (8)
- There is no mass transfer between the components.
- (9)
- The fluid flow in the wellbore is regarded as a one-dimensional flow along the wellbore axis.
- (10)
- All components on the same cross-section are in thermal equilibrium, and all components have the same pressure and temperature.
2.2. Multi-Phase Coupling Method
2.3. Judgment of Multi-Phase Flow Pattern and Establishment of Flow Friction Gradient Equation
- (1)
- Bubble flow
- (2)
- Slug flow
- (3)
- Foam flow
- (4)
- Annular flow
2.4. Multi-Field Coupling Model Construction
- (1)
- Temperature field
- (2)
- Pressure field
- (3)
- Density field
- (4)
- Velocity field
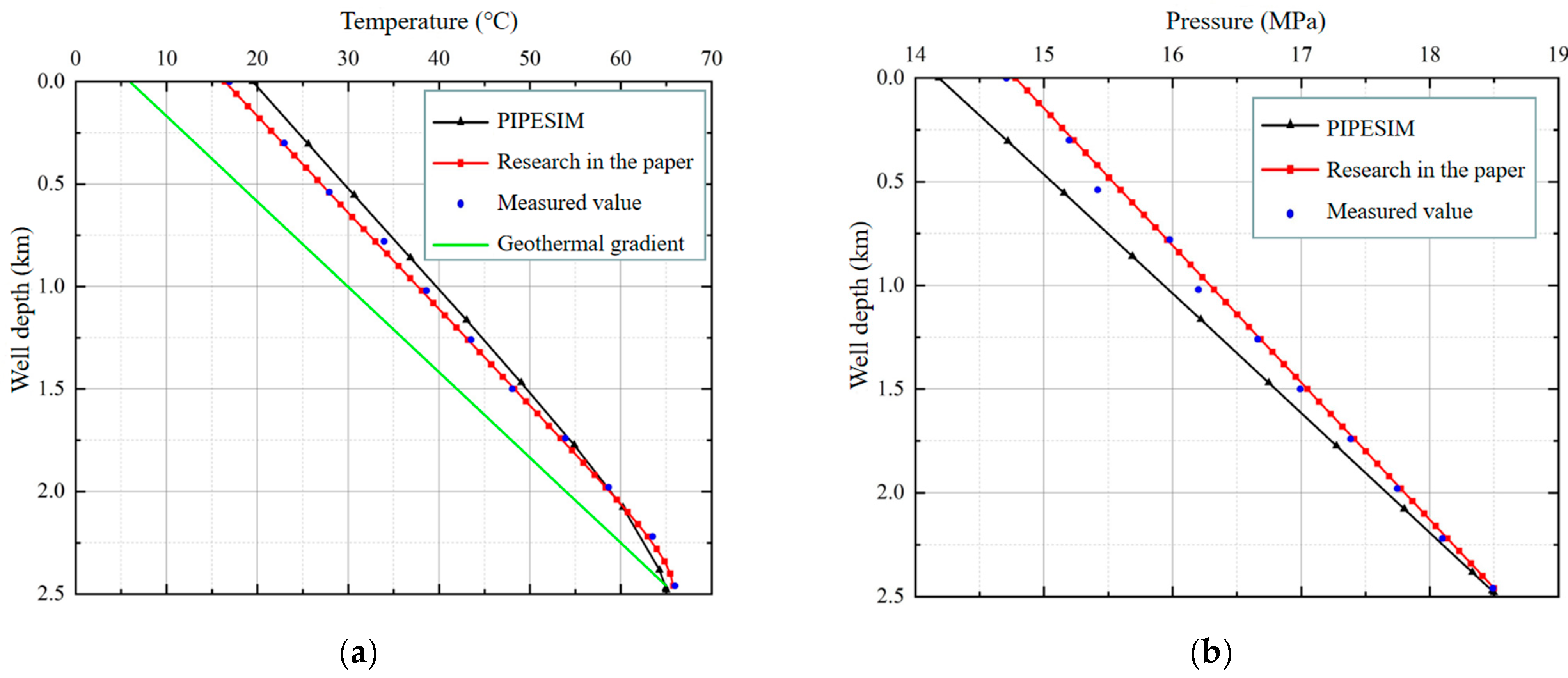
3. Case Study of Wellbore Temperature and Pressure Field Model with Multi-Field and Multi-Phase Coupling
- (1)
- Example calculation
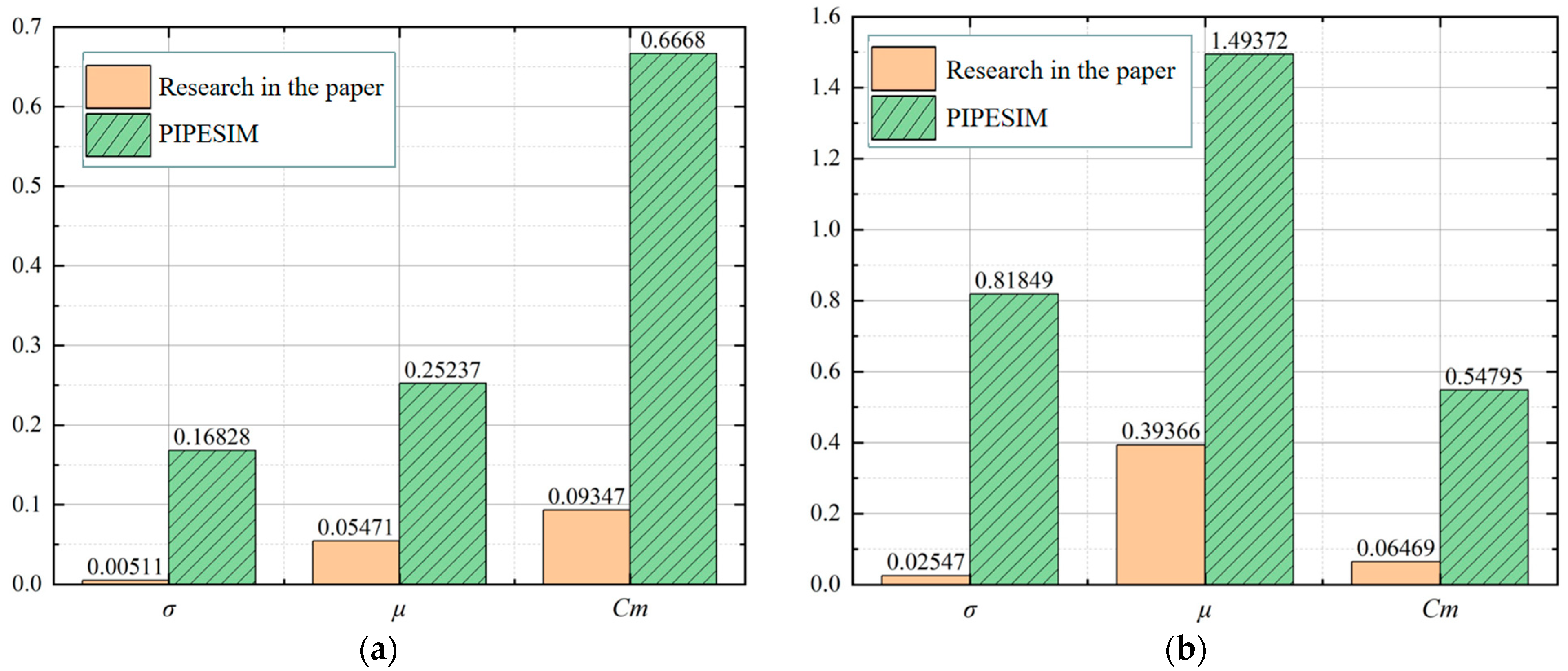
- (2)
- Error analysis
4. Application of Multi-Field and Multi-Phase Coupling
4.1. Temperature and Pressure Changes before and after Throttling
- (1)
- Temperature drop
- (2)
- Pressure drop
- (3)
- Calculation of minimum throttle nozzle diameter
- (4)
- Calculation of minimum depth of entry
4.2. Comparative Analysis of Gas Well Throttling Examples
5. Conclusions
- (1)
- Based on the study of the wellbore temperature and pressure field model, the velocity field and density field of the gas well are considered, and the multi-phase correction coefficient of the gas well is introduced. Based on the multi-phase flow pattern judgment equation, the friction gradient equation of multi-phase flow is obtained, and a multi-field and multi-phase coupling wellbore temperature and pressure field model is established.
- (2)
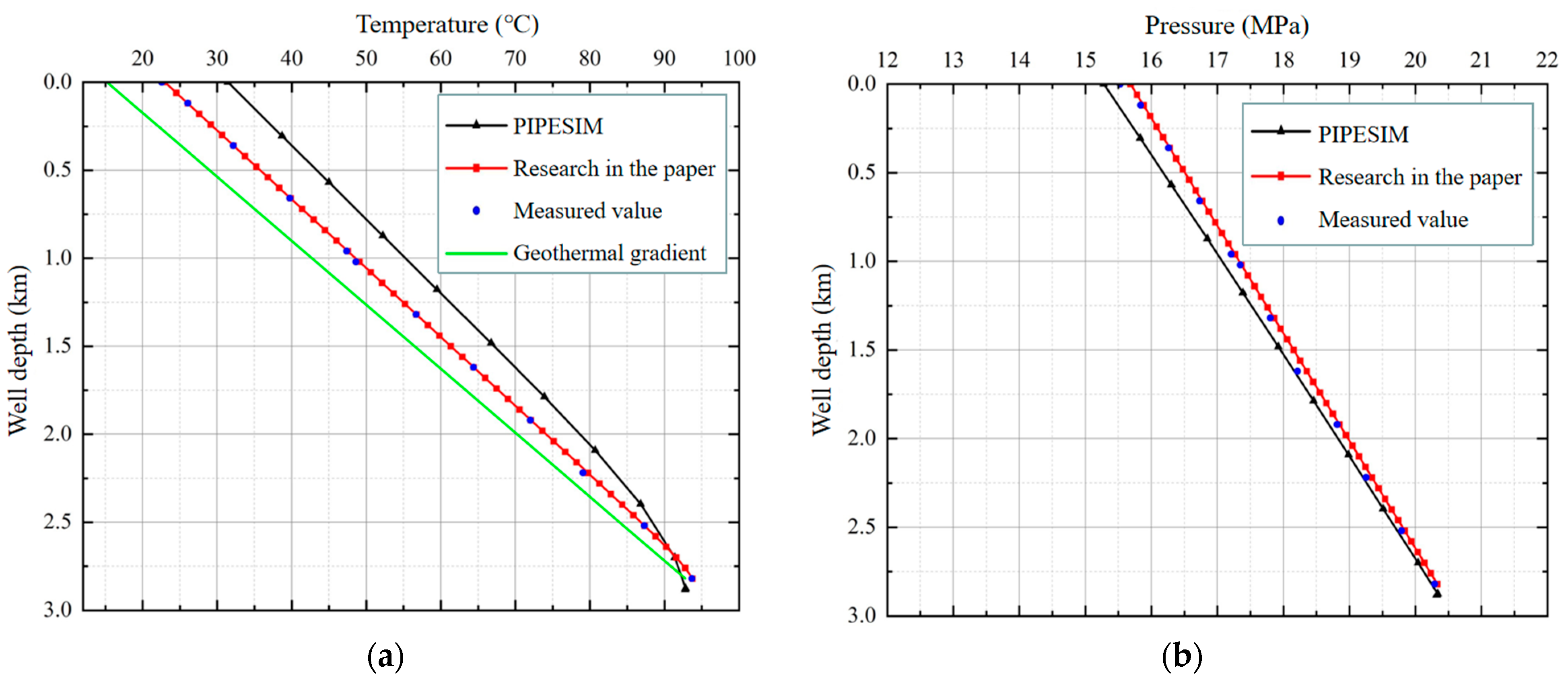
- The multi-field and multi-phase coupling wellbore temperature and pressure field model were applied to wells K1 and K2, and the calculation results of this research model were analyzed and compared with the PIPESIM simulation results and measured values. We evaluated the mean μ, variance σ, and coefficient of variation Cm of the difference between the calculation results of the proposed model and those of the PIPESIM simulation results, and the measured values. The results show that the variation coefficients of the calculation results of the model proposed in this study are all less than 15%, which is more accurate than the PIPESIM simulation results.
- (3)
- Considering the problems of gas well liquid carrying, sand production, and gas hydrate clogging the wellbore, the design method of depth of entry of the throttle device and throttle nozzle diameter is optimized. Taking well K2 as an example and applying the downhole throttling technology, it was calculated that a throttle device with a nozzle diameter of 4 mm can be installed at a depth of 1688 m to solve the problem of hydrate formation, and at the same time, a prediction of hydrate formation can be obtained with the data of the temperature and pressure field after throttling. The results show that hydrates will not form in the wellbore of well K2 after throttling.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X.K.; Liu, L.M.; Yu, Z.C.; Zhang, L.; Zhou, L.; Zhang, Z.; Guo, F. Study on the Coupling Model of Wellbore Temperature and Pressure During the Production of High Temperature and High Pressure Gas Well. Energy Rep. 2022, 8, 1249–1257. [Google Scholar] [CrossRef]
- Zheng, J.; Li, J.H.; Wu, J.; Li, Z.; Zhang, Y. Review of Downhole Throttle Failure in Oil and Gas Wells. J. Fail. Anal. Prev. 2023, 23, 609–621. [Google Scholar] [CrossRef]
- Ramecy, H. Wellbore Heat Transmission. J. Pet. Technol. 1962, 1, 427–435. [Google Scholar] [CrossRef]
- Tragesser, A.; Crawford, P.; Crawford, H. A Method for Calculating Circulating Temperatures. J. Pet. Technol. 1967, 19, 1507–1512. [Google Scholar] [CrossRef]
- Hu, Z.M. Engineering Method for Determining the Total Heat Transfer Coefficient of A Steam Injection (Hot Water) Well Shaft. Oil Drill. Prod. Technol. 1985, 1, 55–62. [Google Scholar]
- Raymond, L. Temperature Distribution in a Circulating Drilling Fluid. J. Pet. Technol. 1969, 21, 333–341. [Google Scholar] [CrossRef]
- Han, C.; Chen, W.; Ding, L.; Zhang, Q. A New Two-dimensional Transient Forecast Model of Wellbore Temperature Based on Precise Time Step Integration Method. J. Pet. Sci. Eng. 2022, 215, 110708. [Google Scholar] [CrossRef]
- Fu, Y.R.; Dou, Q.G.; Liu, W.D.; Sun, M.Q.; Sun, B.; Hu, J.P. Coupling Model for Calculating Wellbore Temperature Distribution of Thermal Insulation Tubing. Pet. Geol. Eng. 2023, 37, 103–106. [Google Scholar]
- Duns, H.; Ros NC, J. Vertical Flow of Gas and Liquid Mixtures in Wells. In Proceedings of the 6th World Petroleum Congress, Frankfurt am Main, Germany, 19 June 1963; pp. 451–465. [Google Scholar]
- Hagedorn, A.R.; Brown, K.E. Experimental Study of Pressure Gradients Occurring During Continuous Two-phase Flow in Small-diameter Vertical Conduits. J. Pet. Technol. 1965, 17, 475–484. [Google Scholar] [CrossRef]
- Bhagwat, S.M.; Chajar, A.J. A Flow Pattern Independent Drift Flux Model Based Void Fraction Correlation for a Wide Range of Gas-liquid Two Phase Flow. Int. J. Multiph. Flow 2014, 59, 186–205. [Google Scholar] [CrossRef]
- Zhang, H.; Shen, R.C.; Qimin, L. Coupling Analysis of Temperature and Pressure Distribution of Underground Gas Storage Injection-production Wellbore. Sci. Technol. Eng. 2017, 17, 66–73. [Google Scholar]
- Hasan, A.R.; Kabir, C.S.; Lin, D. Analytic Wellbore Temperature Model for Transient Gas-well Testing. SPE Reserv. Eval. Eng. 2005, 8, 240–247. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S.; Wang, X. A Robust Steady-State Model for Flowing-fluid Temperature in Complex Wells. SPE Prod. Oper. 2009, 24, 269–276. [Google Scholar] [CrossRef]
- Xu, B.; Kabir, C.S.; Hasan, A.R. Nonisothermal reservoir/wellbore flow modeling in gas reservoirs. J. Nat. Gas Sci. Eng. 2018, 57, 89–99. [Google Scholar] [CrossRef]
- Onur, M.; Cinar, M. Modeling and Analysis of Temperature Transient Sandface and Wellbore Temperature Data from Variable Rate Well Test Data. In Proceedings of the SPE Europe Featured at 79th EAGE Conference and Exhibition, Paris, France, 12 June 2017. [Google Scholar]
- Wang, H.Y. A Non-isothermal Wellbore Model for High Pressure High Temperature Natural Gas Reservoirs and Its Application in Mitigating Wax Deposition. J. Nat. Gas Sci. Eng. 2019, 72, 103016. [Google Scholar] [CrossRef]
- Zhang, P.Y.; Wen, B.; Wang, L.J.; Haojie, L.; Min, T. Study on Wellbore Temperature Field of Shale Gas Horizontal Well Drilling in Y101 Block. Drill. Prod. Technol. 2022, 45, 1–7. [Google Scholar]
- Zheng, J.; Dou, Y.; Li, Z.; Yan, X.; Zhan, Y.; Bi, C. Investigation and Application of Wellbore Temperature and Pressure Field Coupling with Gas–liquid Two-phase Flowing. J. Pet. Explor. Prod. Technol. 2021, 12, 753–762. [Google Scholar] [CrossRef]
- Dastkhan, Y.; Kazemi, A. An Efficient Numerical Model for Nonisothermal Fluid Flow Through Porous Media. Can. J. Chem. Eng. 2021, 99, 2789–2799. [Google Scholar] [CrossRef]
- Dastkhan, Y.; Kazemi, A.; Al-Maamari, R. Well and Reservoir Characterization Using Combined Temperature and Pressure Transient Analysis: A Case Study. Results Eng. 2022, 15, 100488. [Google Scholar] [CrossRef]
- Huang, X.L.; Qi, Z.L.; Li, S.N.; Li, S.; Xiao, Q.; Mo, F.; Fang, F. Study on Prediction Model about Water Content in High Temperature and High Pressure Water Soluble Gas Reservoirs. J. Energy Resour. Technol. 2021, 143, 023501. [Google Scholar] [CrossRef]
- Jiang, D.L.; Liu, S.J.; Huang, Y.; Meng, W.; Diao, H.; Gan, B.; Zou, F. Wellbore Temperature-Pressure Coupling Model Under Deep-Water Gas Well Intervention Operation. Adv. Transdiscipl. 2022, 23, 293–305. [Google Scholar]
- Liu, J.J.; Wu, W.L.; Qian, P.; Wang, S. A Temperature-Pressure Coupling Model for Predicting Gas Temperature Profile in Gas Drilling. Therm. Sci. 2021, 25, 3493–3503. [Google Scholar] [CrossRef]
- An, J.T.; Li, J.; Huang, H.L.; Liu, G.; Chen, S.; Zhang, G. Numerical Study of Temperature Pressure Coupling Model for the Horizontal Well with a Slim Hole. Energy Sci. Eng. 2023, 11, 1060–1079. [Google Scholar] [CrossRef]
- Zhang, S.L.; Ma, F.M. Gas Downhole Throttling Technology; Petroleum Industry Press: Beijing, China, 2015; pp. 58–62. [Google Scholar]
- Huo, G.Y.; Dian, S.Y.; Xu, X. Finite Element Analysis of New Downhole Throttle Based on Orifice Value. IOP Conf. Ser. Mater. Sci. Eng. 2018, 428, 012016. [Google Scholar] [CrossRef]
- Fu, Y.; Ma, H.; Yu, C.; Dong, L.; Yang, Y.; Zhu, X.; Sun, H. Analysis of Effective Operation Performance of Wireless Control Downhole Choke. Shock. Vib. 2020, 2020, 7831819. [Google Scholar] [CrossRef]
- Furukawa, T.; Sekogchi, K. Phase Distribution for Air-Water Two Phase in Annuli. Bull. JSME 1986, 29, 3007–3014. [Google Scholar] [CrossRef]

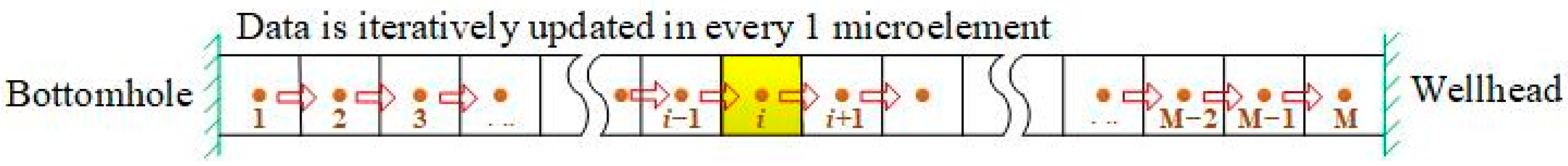




| Basic Parameters | K1 | K2 |
|---|---|---|
| Inner diameter of tubing (mm) | 62 | 76 |
| Tubing wall thickness (mm) | 7 | 6.5 |
| Tubing steel grade | N80 | J55 |
| Inner diameter of surface casing (mm) | 157.08 | 226.62 |
| Surface casing wall thickness (mm) | 10.36 | 8.94 |
| Setting depth of surface casing (m) | 567.74 | 554.64 |
| Inner diameter of gas layer casing (mm) | 108.62 | 121.36 |
| Gas layer casing wall thickness (mm) | 9.19 | 9.17 |
| Setting depth of gas layer casing (m) | 2874.59 | 2486.47 |
| Casing grade | P110 | P110 |
| Roughness of tubing casing wall (mm) | 0.0254 | 0.0254 |
| Wellbore diameter (mm) | 431.8 | 445.6 |
| Artificial bottom hole (m) | 2867.08 | 2472.3 |
| Gas production (m3/d) | 3.3562 × 104 | 5.122 × 104 |
| Water production (m3/d) | 2.4 | 64.025 |
| Sand production (m3/d) | 1.2 | 0.8 |
| Oil production (m3/d) | 0.2 | 0.04 |
| Bottom hole pressure (MPa) | 20.332 | 18.5 |
| Bottom hole temperature (°C) | 92.776 | 65 |
| Geothermal gradient (°C/m) | 0.0275 | 0.024 |
| Total heat transfer coefficient (J/(m2·s·°C)) | 11.356 | 10.564 |
| Formation thermal diffusion coefficient (m2/s) | 7.5 × 10−7 | 7.5 × 10−7 |
| Formation thermal conductivity (J/(m·s·°C)) | 1.7307 | 1.7297 |
| Relative density of natural gas | 0.5756 | 0.5916 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Li, J.; Dou, Y.; Hu, Z.; Yang, X.; Zhang, Y. Research on Downhole Throttling Characteristics of Gas Wells Based on Multi-Field and Multi-Phase. Processes 2023, 11, 2670. https://doi.org/10.3390/pr11092670
Zheng J, Li J, Dou Y, Hu Z, Yang X, Zhang Y. Research on Downhole Throttling Characteristics of Gas Wells Based on Multi-Field and Multi-Phase. Processes. 2023; 11(9):2670. https://doi.org/10.3390/pr11092670
Chicago/Turabian StyleZheng, Jie, Jiahui Li, Yihua Dou, Zhihao Hu, Xu Yang, and Yarong Zhang. 2023. "Research on Downhole Throttling Characteristics of Gas Wells Based on Multi-Field and Multi-Phase" Processes 11, no. 9: 2670. https://doi.org/10.3390/pr11092670
APA StyleZheng, J., Li, J., Dou, Y., Hu, Z., Yang, X., & Zhang, Y. (2023). Research on Downhole Throttling Characteristics of Gas Wells Based on Multi-Field and Multi-Phase. Processes, 11(9), 2670. https://doi.org/10.3390/pr11092670





