Mass and Heat Transfer of Pressure Swing Adsorption Oxygen Production Process with Small Adsorbent Particles
Abstract
:1. Introduction
2. Mathematical Models
2.1. Governing Equations
2.2. Model Parameters
2.3. Cycle Description
2.4. Initial and Boundary Conditions
2.5. Method of Solution
3. Experimental Section
4. Results and Discussions
4.1. Model Verification
4.2. Gas Concentration, Temperature Distributions at the End of Cycle Step
4.3. Effect of Mass Transfer Resistance
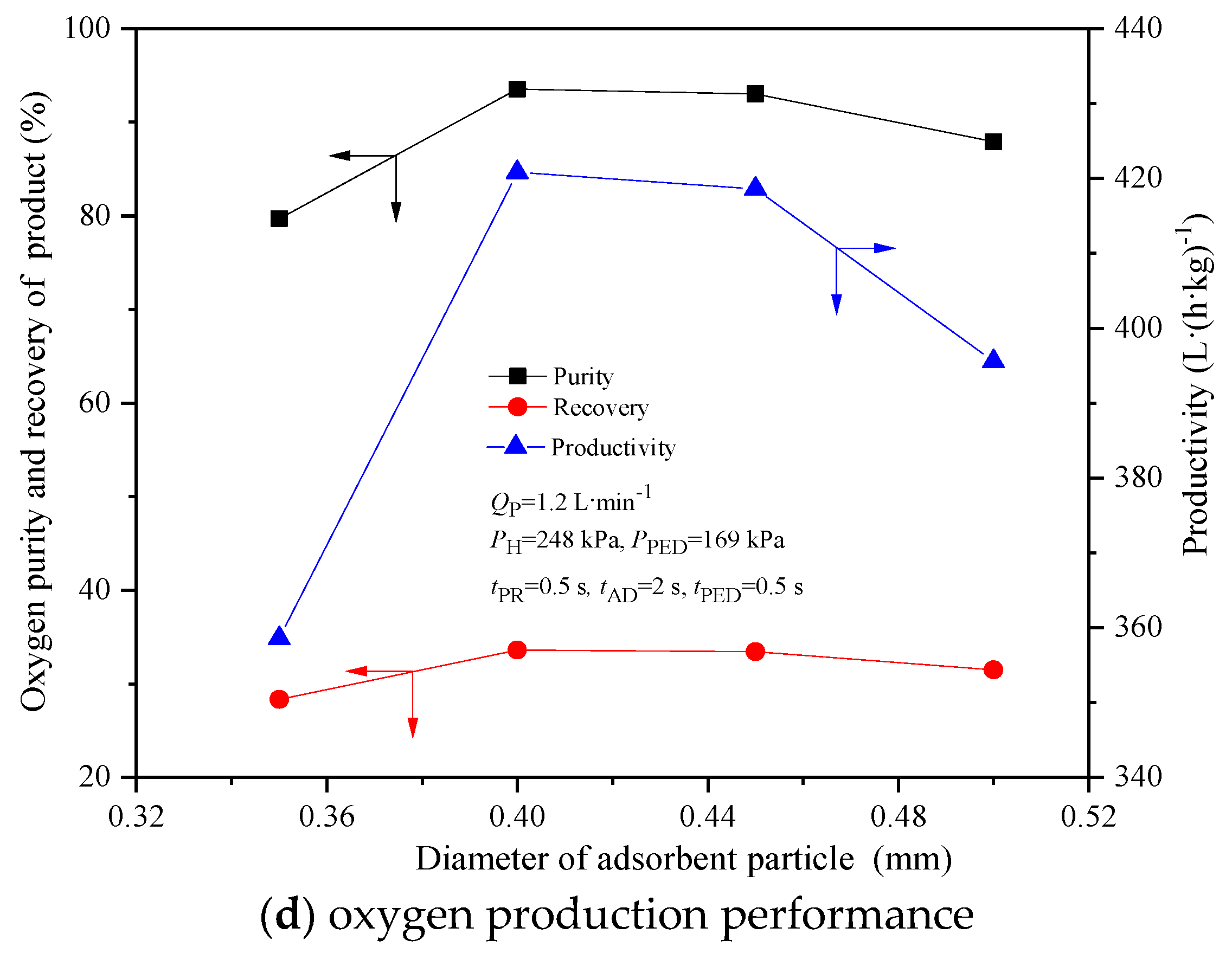
4.4. Effect of Particle Size
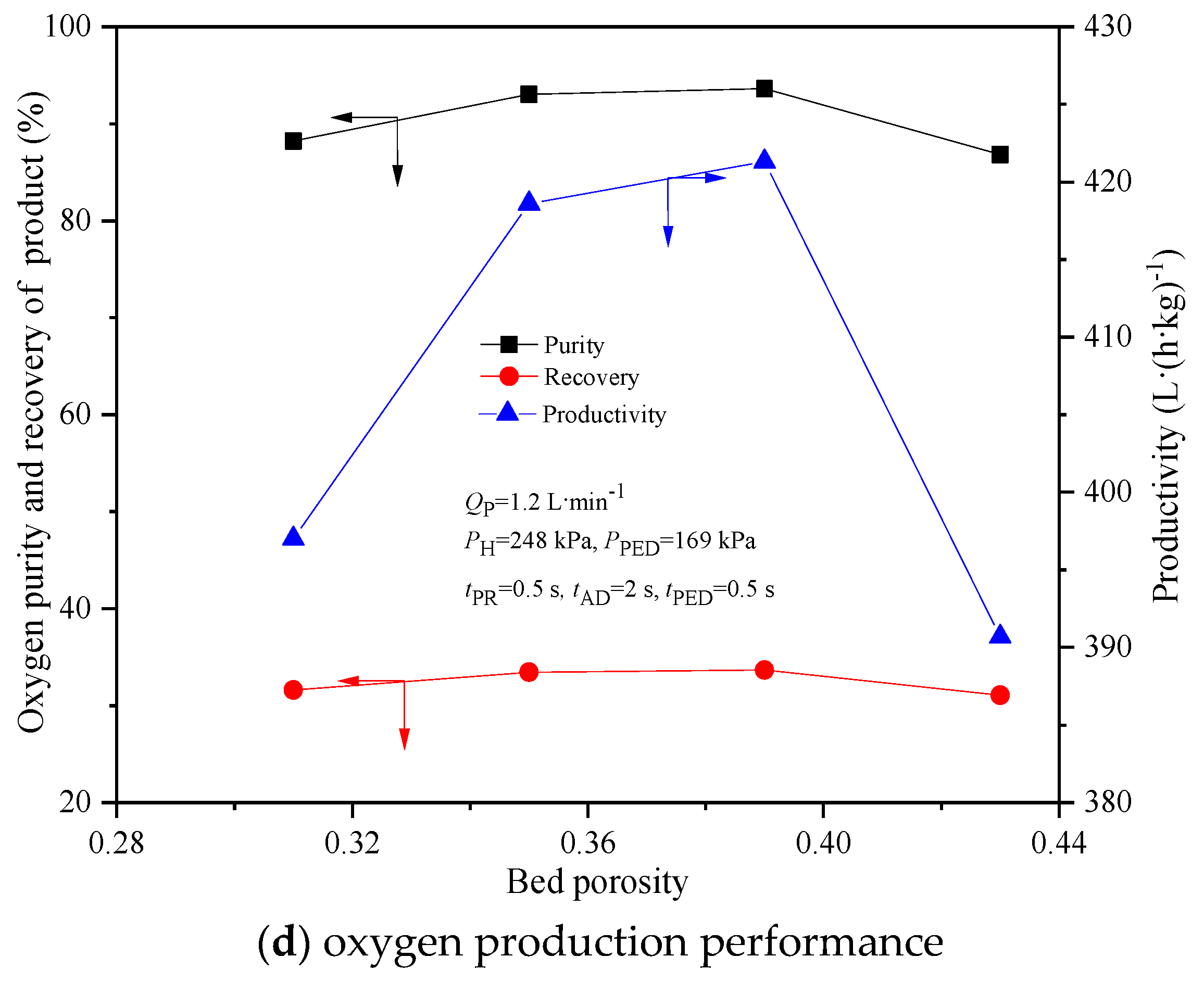
4.5. Effect of Bed Porosity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin letters | |||
| bi | Langmuir parameter (kPa−1) | QF | feed flowrate (L·min−1) |
| bi0 | Langmuir parameter (kPa−1) | QP | product flowrate (L·min−1) |
| c | molar concentration (mol·m−3) | Rg | gas constant (J·mol−1·K−1) |
| ci | component i molar concentration (mol·m−3) | t | time (s) |
| Cf | gas heat capacity (J·kg−1·K−1) | tAD | duration of AD step (s) |
| Cs | solid heat capacity (J·kg−1·K−1) | tBD | duration of BD step (s) |
| dp | particle diameter (m) | tPED | duration of PED step (s) |
| din | bed diameter (m) | tPR | duration of PR step (s) |
| DL | axial dispersion coefficient(m2·s−1) | tPEU | duration of PEU step (s) |
| L | N2 adsorbents loading height (m) | tPU | duration of PU step (s) |
| m | amount of adsorbents (kg) | Tf | gas temperature (K) |
| Nu | Nusselt number | TF | feed temperature (K) |
| hf | gas-solid heat transfer coefficient (W·m−2·K−1) | TPU | purge gas temperature (K) |
| hw | internal gas-wall convective heat transfer coefficient (W·m−2·K−1) | Ts | solid temperature (K) |
| ki | mass transfer coefficient for adsorbate i (s−1) | Tw | wall temperature (K) |
| Kf | gas thermal dispersion coefficient (W·m−1·K−1) | u | interstitial gas velocity (m·s−1) |
| Ks | solid phase thermal conductivity (W·m−1·K−1) | uin | feed velocity (m·s−1) |
| P | pressure (kPa) | y | oxygen purity of gas |
| Pi | gas partial pressure (kPa) | yF | oxygen purity of feed gas |
| PH | adsorption pressure (kPa) | yPU | oxygen purity of purge gas |
| PL | desorption pressure (kPa) | z | axial position (m) |
| PPED | pressure at end of PED step (kPa) | Greek letters | |
| PPEU | pressure at end of PEU step (kPa) | μ | dynamic viscosity (Pa·s) |
| PPR | pressure at end of PR step (kPa) | ρf | gas density (kg·m−3) |
| Pr (=μCf/Kf) | Prandtl number | ρp | apparent density (kg·m−3) |
| qi | adsorbed concentration of the component i (mol·kg−1) | ρb | bulk density (kg·m−3) |
| qi* | equilibrium adsorption concentration of the component i, mol·kg−1 | εb | inter-particle porosity |
| qis | saturation adsorbed concentration of the component i, mol·kg−1 | εp | particle porosity |
| qis | saturation adsorbed concentration of the component i, mol·kg−1 | εp | particle porosity |
References
- Zhang, R.; Shen, Y.; Tang, Z.; Li, W.; Zhang, D. A Review of Numerical Research on the Pressure Swing Adsorption Process. Processes 2022, 10, 812. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, C.; Wang, H.; Li, Z.; Liu, Y. Airflow Distributions in a Z Type Centripetal Radial Flow Reactor: Effects of Opening Strategy and Opening Rate. Processes 2022, 10, 1250. [Google Scholar] [CrossRef]
- Zhu, X.; Sun, Y.; Liu, Y.; Sun, X.; Shi, J. Experimental performance analysis of vacuum pressure swing adsorption air separation process under plateau special conditions. Sep. Sci. Technol. 2022, 18, 2885–2893. [Google Scholar] [CrossRef]
- Vemula, R.R.; Urich, M.D.; Kothare, M.V. Experimental design of a “snap-on” and standalone single-bed oxygen concentrator for medical applications. Adsorption 2021, 27, 619–628. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.S.; Li, Z.; Xiao, P.; Liu, W.; Yang, X.; Fu, Y.; Zhao, C.; Yang, R.T.; Webley, P.A. Experimental study on oxygen concentrator with wide product flow rate range: Individual parametric effect and process improvement strategy. Sep. Purif. Technol. 2021, 274, 118918–118928. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Wang, X.W. Experimental study of a rotary valve multi-bed rapid cycle pressure swing adsorption process based medical oxygen concentrator. Adsorption 2020, 26, 1267–1274. [Google Scholar] [CrossRef]
- Zhu, X.; Sun, Y.; Liu, Y.; Li, Z.; Feng, F.; Ma, J.; Li, S. Correlation analysis between working conditions and the performance of a small-scale pressure swing adsorption oxygen production process. Ind. Eng. Chem. Res. 2022, 61, 14962–14972. [Google Scholar] [CrossRef]
- Rama Rao, V.; Wu, C.W.; Kothare, M.V.; Sircar, S. Comparative performances of two commercial samples of LiLSX zeolite for production of 90% oxygen from air by a novel rapid pressure swing adsorption system. Sep. Sci. Technol. 2015, 50, 1447–1452. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Liu, Y.S.; Yang, R.T. Effects of operating temperature on the performance of small-scale rapid cycle pressure swing adsorption air separation process. Adsorption 2021, 27, 205–212. [Google Scholar] [CrossRef]
- Qadir, S.; Li, D.; Gu, Y.; Yuan, Z.; Zhao, Y.; Wang, S. Experimental and numerical analysis on the enhanced separation performance of a medical oxygen concentrator through two-bed rapid pressure swing adsorption. Ind. Eng. Chem. Res. 2021, 60, 5903–5913. [Google Scholar] [CrossRef]
- Zhong, G.; Rankin, P.J.; Ackley, M.W. High Frequency PSA Process for Gas Separation. U.S. Patent 7,828,878 B2, 9 November 2010. [Google Scholar]
- Wu, C.W.; Kothare, M.V.; Sircar, S. Column dynamic study of mass transfer of pure N2 and O2 into small particles of pelletized LiLSX zeolite. Ind. Eng. Chem. Res. 2014, 53, 17806–17810. [Google Scholar] [CrossRef]
- Moran, A.; Patel, M.; Talu, O. Axial dispersion effects with small diameter adsorbent particles. Adsorption 2018, 24, 333–344. [Google Scholar] [CrossRef]
- Moran, A.; Talu, O. Limitations of portable pressure swing adsorption processes for air separation. Ind. Eng. Chem. Res. 2018, 57, 11981–11987. [Google Scholar] [CrossRef]
- Rama Rao, V.; Farooq, S. Experimental study of a pulsed pressure swing adsorption process with very small 5A zeolite particles for oxygen enrichment. Ind. Eng. Chem. Res. 2014, 53, 13157–13170. [Google Scholar] [CrossRef]
- Zheng, X.G.; Liu, Y.S.; Liu, W.H. Two-dimensional modeling of the transport phenomena in the adsorber during pressure swing adsorption process. Ind. Eng. Chem. Res. 2010, 49, 11814–11824. [Google Scholar] [CrossRef]
- Ogawa, K.; Inagaki, Y.; Ohno, A. Numerical analysis of O2 concentration, gas-zeolite temperatures in two zeolite columns for an oxygen concentrator. Int. J. Heat. Mass Transfer. 2019, 129, 238–254. [Google Scholar] [CrossRef]
- Moran, A.; Talu, O. Role of pressure drop on rapid pressure swing adsorption performance. Ind. Eng. Chem. Res. 2017, 56, 5715–5723. [Google Scholar] [CrossRef]
- Rumbo Morales, J.Y.; López, G.L.; Alvarado Martínez, V.M.; Sorcia Vázquez, F.J.; Brizuela Mendoza, J.A.; García, M.M. Parametric study and control of a pressure swing adsorption process to separate the water-ethanol mixture under disturbances. Sep. Purifi. Technol. 2020, 236, 116214–116224. [Google Scholar] [CrossRef]
- Rumbo Morales, J.Y.; Ortiz-Torres, G.; Domínguez García, R.O.; Torres Cantero, C.A.; Rodriguez, M.C.; Sarmiento-Bustos, E.; Oceguera-Contreras, E.; Flores Hernández, A.A.; Rodríguez Cerda, J.C.; Molina, Y.A.; et al. Review of the Pressure Swing Adsorption Process for the Production of Biofuels and Medical Oxygen: Separation and Purification Technology. Adsorpt. Sci. Technol. 2022, 2022, 3030519. [Google Scholar] [CrossRef]
- Khamseh, A.A.G.; Ghorbanian, S.A.; Amini, Y.; Shadman, M.M. Investigation of kinetic, isotherm and adsorption efcacy of thorium by orange peel immobilized on calcium alginate. Sci. Rep. 2023, 13, 8393–8403. [Google Scholar] [CrossRef]
- Zhu, X.; Sun, Y.; Dong, L.; Sun, X.; Li, S.; Chen, H.; Zhang, J.; Chen, J. Comprehensive performance and numerical analysis of pressure swing adsorption process based medical oxygen concentrator under various operating conditions. Sep. Sci. Technol. 2023. [Google Scholar]
- Rege, S.U.; Yang, R.T. Limits for air separation by adsorption with LiX zeolite. Ind. Eng. Chem. Res. 1997, 36, 5358–5365. [Google Scholar] [CrossRef]
- Langmuir, I.; Amer, J. The adsorption of gases on plane surfaces of glass, mica and platinum. JACS 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Gleuckauf, E.; Coates, J.I. The Influence of Incomplete Equilibrium on the Front Boundary of Chromatograms and the Effectiveness of Separation. J. Chem. Soc. 1947, 78, 1315–1321. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Ruthven, D.M.; Farooq, S.; Knaebel, K.S. Pressure Swing Adsorption; VCH Publisher: New York, NY, USA, 1994. [Google Scholar]
- Wakao, N.; Kaguei, S.; Funazkri, T. Effect of fluid dispersion coefficients on particle to fluid heat transfer coefficients in packed beds. Chem. Eng. Sci. 1979, 34, 325–336. [Google Scholar] [CrossRef]
- Lopes, F.V.S.; Grande, C.A.; Rodrigues, A.E. Fast-cycling VPSA for hydrogen purification. Fuel 2012, 93, 510–523. [Google Scholar] [CrossRef]
- Yang, R.T. Adsorbents: Fundamentals and Applications; JohnWiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Zhu, X.Q.; Liu, Y.S.; Yang, X.; Liu, W.H. Study of a novel rapid vacuum pressure swing adsorption process with intermediate gas pressurization for producing oxygen. Adsorption 2017, 23, 175–184. [Google Scholar] [CrossRef]
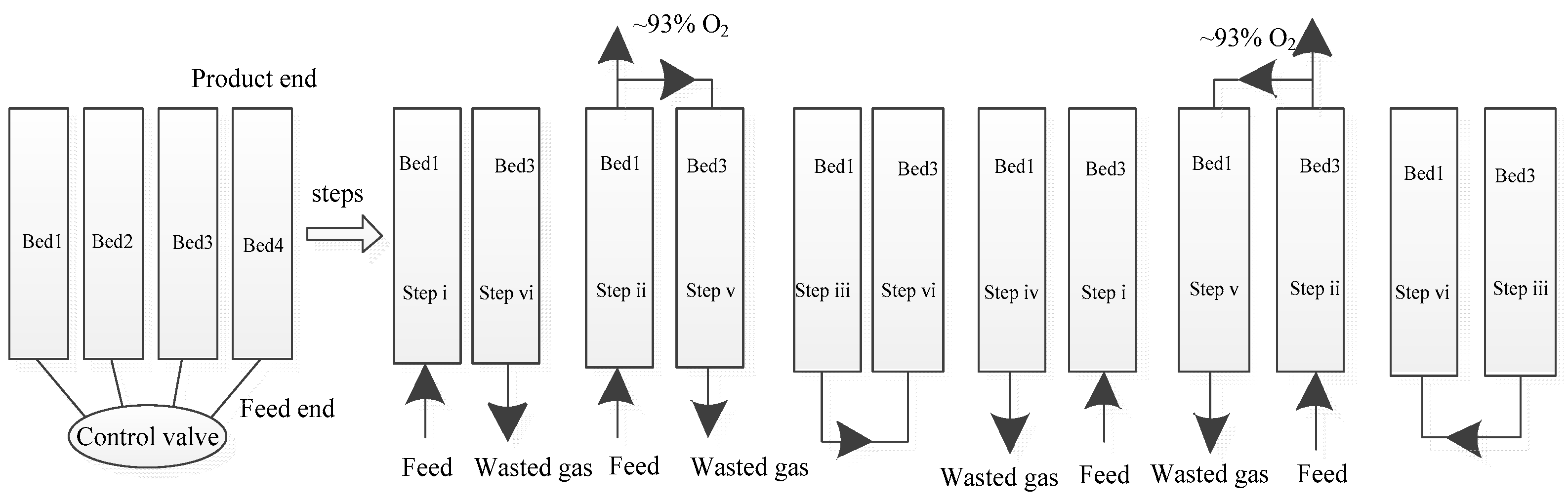
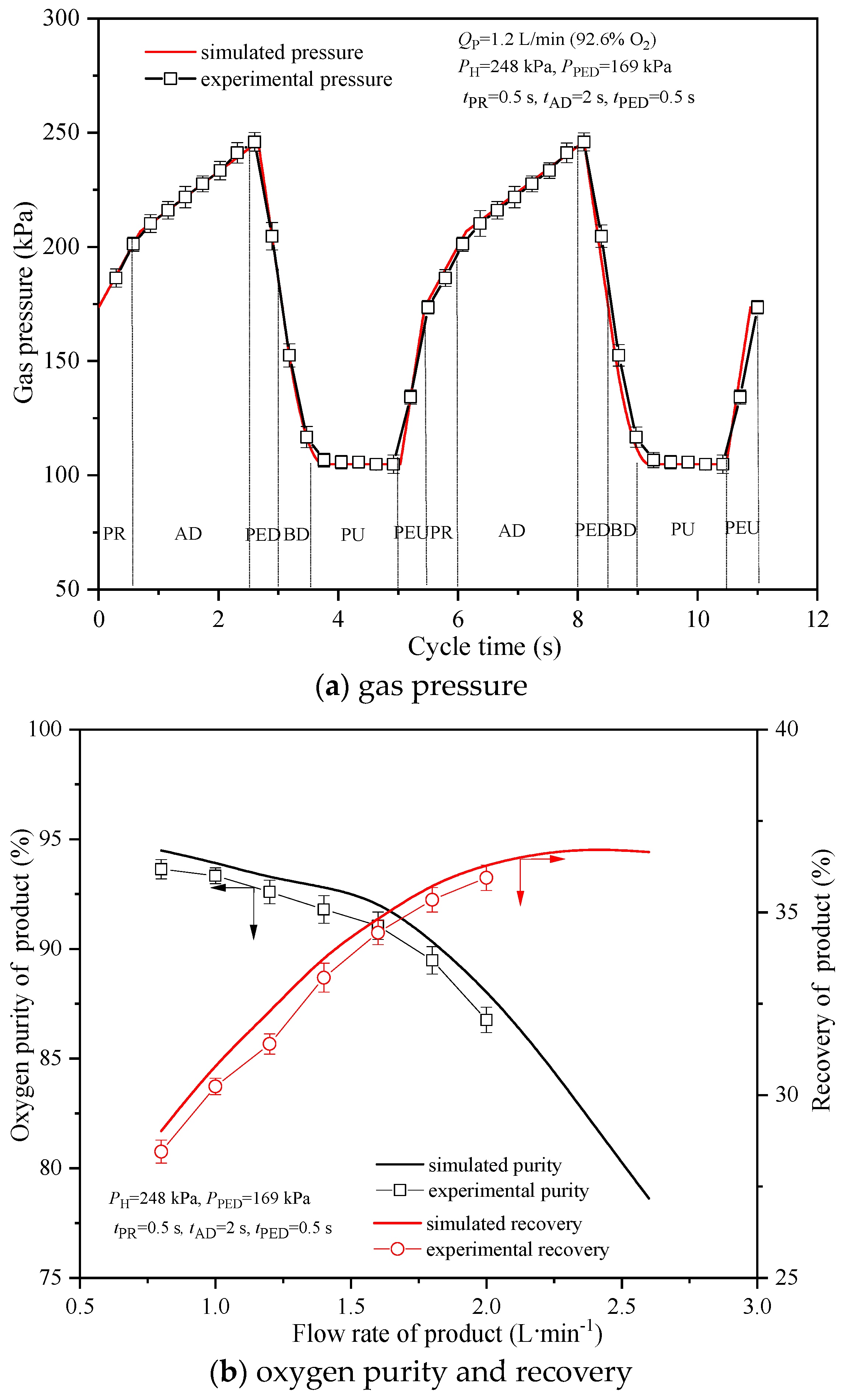
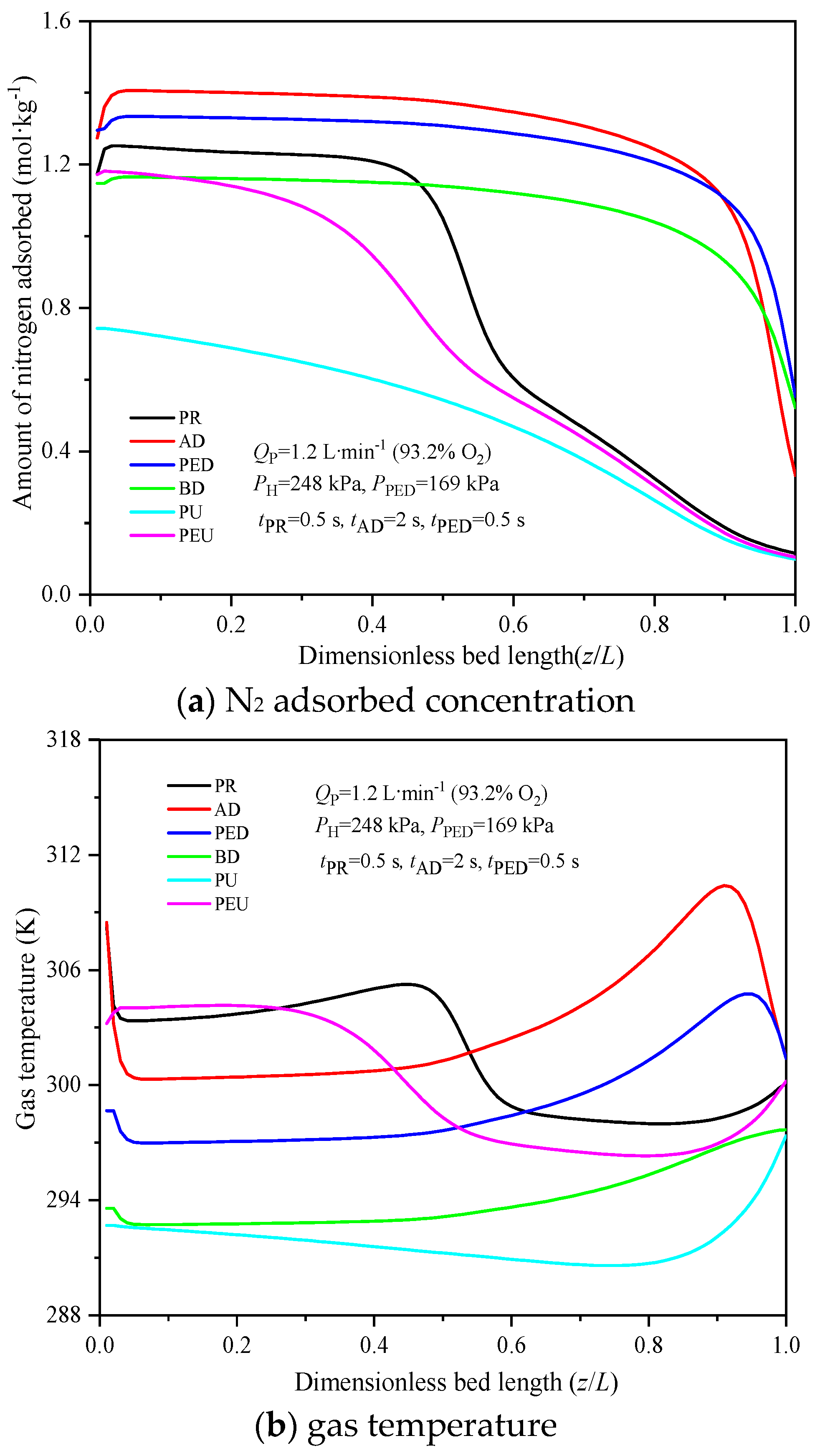
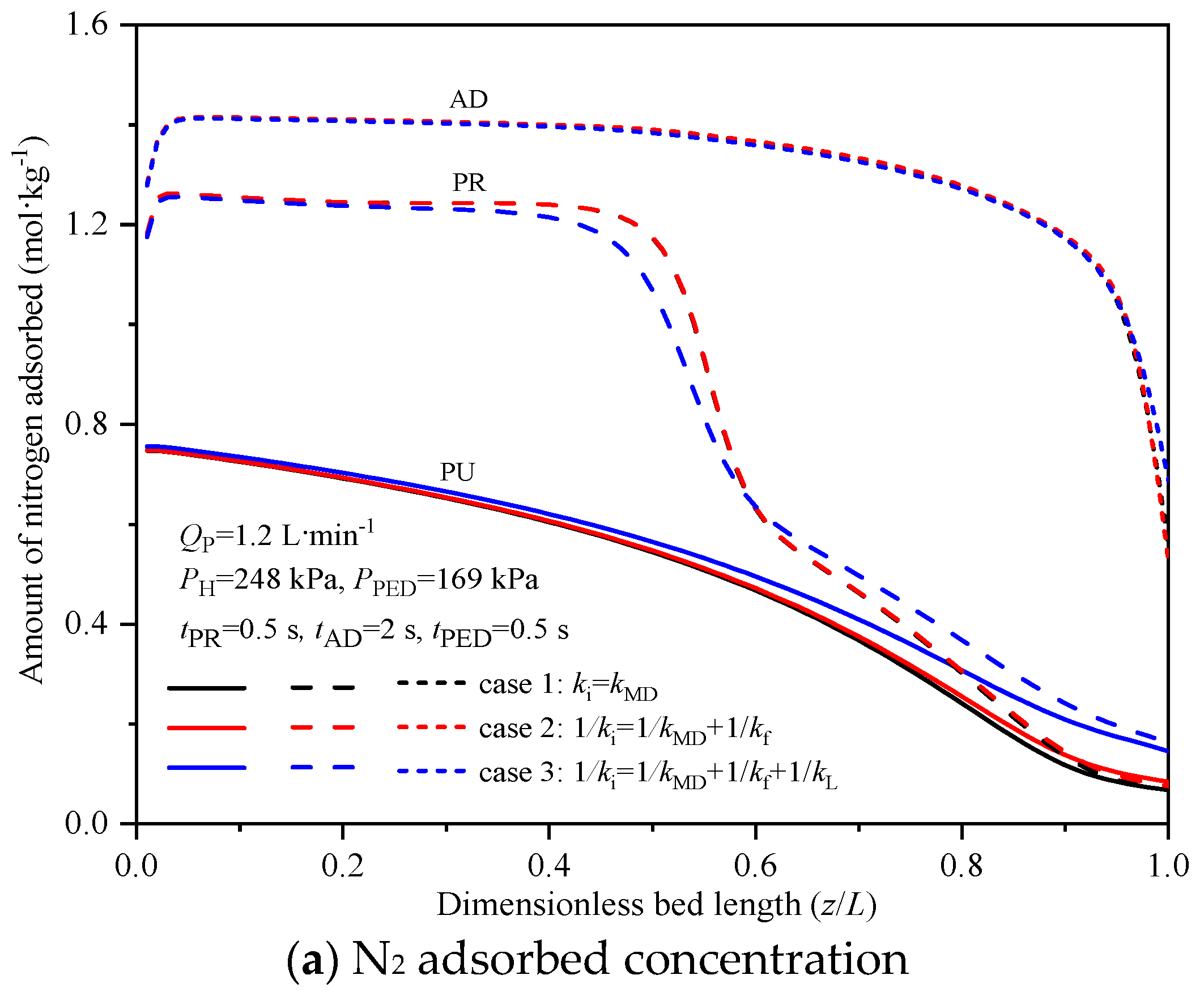



| Case | ki [7,11,12,13,14,27] | Model of Dominant Resistance [7,11,12,13,14,27] |
|---|---|---|
| 1 | , , | |
| 2 | , | |
| 3 | , |
| Bed | Zeolite | Fluid | |||
|---|---|---|---|---|---|
| PH/kPa | ~250 | Cs/J·kg−1·K−1 | 1172 | Feed | 21% O2, 79% N2 |
| PL/kPa | 101~103 | dp/mm | 0.35~0.5 | M1/kg·mol−1 | 0.032 |
| yF | 0.21 | ρp/kg·m−3 | 1035 | M2/kg·mol−1 | 0.028 |
| din/m | 0.026 | ρb/kg·m−3 | 625~630 | ρf/kg·m−3 | 1.743 |
| L/m | 0.12 | εb | 0.31~0.43 | Cf/J·kg−1·K−1 | 1005 |
| TF/K | 310.15 | εp | 0.33 | Kf/W·m−1·K−1 | 0.2624 |
| TPU/K | 298.15 | Ks/W·m−1·K−1 | 0.3 | ||
| TW/K | 298.15 | ||||
| Initial Conditions y(z) = 0.21; P(z) = 101.325 kPa; Tf(z) = Ts(z) = 298.15 K | ||
|---|---|---|
| Step | z = 0 (Feed End) | z = L (Product End) |
| i | , , | |
| ii | , | , |
| iii | , | , , |
| iv | , | , , |
| v | , , | , |
| vi | , | , , |
| Adsorbate | qs (mol·kg−1) | bi0 (kPa−1) | (J·mol−1) |
|---|---|---|---|
| O2 | 2.29 | 2.8901 × 10−6 | 14,071.54 |
| N2 | 2.29 | 6.6988 × 10−7 | 23,638.76 |
| Case | 1 | 2 | 3 | Experimental Results |
|---|---|---|---|---|
| Purity (%) | 96.3 | 95.7 | 93.2 | 92.6 |
| Recovery (%) | 34.7 | 34.6 | 32.4 | 31.4 |
| Productivity (L·(h·kg)−1) | 433.4 | 430.8 | 420.3 | 416.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhang, C.; Zhu, X.; Dong, L.; Sun, X. Mass and Heat Transfer of Pressure Swing Adsorption Oxygen Production Process with Small Adsorbent Particles. Processes 2023, 11, 2485. https://doi.org/10.3390/pr11082485
Sun Y, Zhang C, Zhu X, Dong L, Sun X. Mass and Heat Transfer of Pressure Swing Adsorption Oxygen Production Process with Small Adsorbent Particles. Processes. 2023; 11(8):2485. https://doi.org/10.3390/pr11082485
Chicago/Turabian StyleSun, Yuan, Chuanzhao Zhang, Xianqiang Zhu, Liang Dong, and Xianhang Sun. 2023. "Mass and Heat Transfer of Pressure Swing Adsorption Oxygen Production Process with Small Adsorbent Particles" Processes 11, no. 8: 2485. https://doi.org/10.3390/pr11082485
APA StyleSun, Y., Zhang, C., Zhu, X., Dong, L., & Sun, X. (2023). Mass and Heat Transfer of Pressure Swing Adsorption Oxygen Production Process with Small Adsorbent Particles. Processes, 11(8), 2485. https://doi.org/10.3390/pr11082485






