Development of Ultrasound Piezoelectric Transducer-Based Measurement of the Piezoelectric Coefficient and Comparison with Existing Methods
Abstract
1. Introduction
- The various purposes for measuring piezoelectric coefficients are listed, and the importance of accurate coefficients is emphasized.
- The theory behind the coefficient is mentioned, and the practical ways to measure it are discussed, including the quasi-static method, dynamic method, interferometric technique, and acoustic method.
- The drawbacks and suitability of each measurement method to specific materials in energy harvesting are discussed and compared with other related works.
- We developed a new measurement method for the coefficient, experiment setup, and methodology. These are explained in detail, and the applications of this method are suggested within the evaluation of other manufacturing processes. The advantages and challenges presented by the method are discussed.
- The proposed method is compared with other existing methods based on the direct and indirect effect, the accuracy, the repeatability, the frequency range, etc.
2. Longitudinal Piezoelectric Coefficient
3. Practical Methods to Determine Longitudinal
3.1. Quasi-Static Method
3.2. Dynamic Method
3.3. Interferometric Method
3.4. Acoustic Method
4. Proposed Measurement Device
4.1. Experiment Setup
4.2. Methodology and Result
5. Discussion
- Non-Destructive Testing: Ultrasound transducers enable non-destructive testing, allowing measurements to be taken without damaging the sample. This advantage is particularly useful when evaluating the coefficient in piezoelectric materials, as it ensures the material’s integrity is preserved.
- Wide Frequency Range: Ultrasound transducers can operate over a broad frequency range, making them suitable for measuring the coefficient in various materials with different resonance frequencies. This versatility allows for the comprehensive characterization of piezoelectric materials across different applications.
- Real-Time Measurements: Ultrasound transducers provide real-time measurements, enabling immediate feedback on the coefficient. This real-time capability facilitates prompt adjustments or modifications during material development or quality control processes.
- High Sensitivity: Ultrasound transducers offer high sensitivity, making them capable of detecting small variations in the coefficient. This sensitivity allows for precise measurements, crucial in applications that require accurate characterization and optimization of piezoelectric materials.
- Problems with Electrode Contact: Measurements are affected by the acoustic junction between the sample and the electrode while in contact. If there is an air gap between the electrode and sample, the ultrasound signal can be reflected away from the sample due to the three big differences between the air impendence and the acoustic impedance. Hence, the use of any kind of liquid layer such as oil on the electrode is necessary.
- Coupling Issues: Achieving effective coupling between the ultrasound transducer and the sample surface can be challenging. Proper coupling is necessary to ensure efficient transmission and reception of ultrasound waves, which directly affects the accuracy of the coefficient measurement.
- Reflections and Interference: Ultrasound waves can encounter reflections and interference, leading to inaccuracies in the measured coefficient. These issues arise when ultrasound waves encounter boundaries or interfaces within the material, causing signal distortion and potential measurement errors.
- Calibration Requirements: Calibration is crucial for an accurate coefficient measurement using ultrasound transducers. Calibration ensures that the transducer response is well-characterized and properly accounted for during measurements. However, calibration procedures can be time-consuming and require careful attention to detail.
6. Conclusions
- Laser interferometry and quasistatic methods can be used to estimate the piezoelectric charge or voltage constants quickly. To investigate the sensitivity of piezoelectricity to mechanical fatigue and static stresses, the dynamic method is preferred. Whereas, when a clear understanding of the frequency response of piezoelectricity is needed, then the acoustical method is suitable.
- The development of an ultrasound piezoelectric transducer was performed to estimate the coefficient with a reference value. The purpose of the method was mainly to measure the values of piezoelectric materials in order to measure the efficiency of the poling method which will be presented in future works. The investigation of the proposed ultrasound piezoelectric transducer is yet in the preliminary stage, and future work will aim to calibrate the device and to eliminate the other challenges discussed in the previous section.
- The test setup described in this study allowed for the effective measurement of the factor of piezoelectric materials using a 1.4 MHz PZT ultrasonic piezoelectric transducer. The arrangement of the components, including the use of organic glass, copper, and aluminum electrodes, ensured accurate and reliable measurements. This setup can be valuable for various applications requiring the characterization of piezoelectric materials and understanding their behavior under specific conditions.
- We put forward a comparative review to investigate the behavior of piezoelectric polymers under different pressure and temperature conditions. The piezoelectric capacity of these harvesters is crucial in predicting their service life and determining the maximum safe operating temperature range. This information is critical for storage and final applications, as it can help reduce device failures and promote a more efficient use of existing materials.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, D.; Jeong, D.-Y.; Fu, Z.; Chu, B. Flexoelectric Effect of Ferroelectric Materials and Its Applications. Actuators 2023, 12, 114. [Google Scholar] [CrossRef]
- Pal, S.; Sarath, N.V.; Priya, K.S.; Murugavel, P. A review on ferroelectric systems for next generation photovoltaic applications. J. Phys. D Appl. Phys. 2022, 55, 283001. [Google Scholar] [CrossRef]
- Ben Dali, O.; Pondrom, P.; Sessler, G.M.; Zhukov, S.; von Seggern, H.; Zhang, X.; Kupnik, M. Cantilever-based ferroelectret energy harvesting. Appl. Phys. Lett. 2020, 116, 243901. [Google Scholar] [CrossRef]
- Gerard, M.; Bowen, C.R.; Osman, F.H. Processing and Properties of PTFE-FEP-PTFE Ferroelectret Films. Ferroelectrics 2011, 422, 59–64. [Google Scholar] [CrossRef]
- Zhang, Y.; Phuong, P.T.T.; Roake, E.; Khanbareh, H.; Wang, Y.; Dunn, S.; Bowen, C. Thermal Energy Harvesting Using Pyroelectric-Electrochemical Coupling in Ferroelectric Materials. Joule 2020, 4, 301–309. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, X. Low cost electrostatic vibration energy harvesters based on negatively-charged polypropylene cellular films with a folded structure. Smart Mater. Struct. 2017, 26, 085001. [Google Scholar] [CrossRef]
- Klimiec, E.; Królikowski, B.; Machnik, M.; Zaraska, W.; Dzwonkowski, J. Increase of Piezoelectric Constant and Thermal Durability of Polypropylene Electret by Introducing SiO2 and Kaolin Filler and Creating a Cellular Structure. J. Electron. Mater. 2015, 44, 2283–2291. [Google Scholar] [CrossRef]
- Wang, J.; Lou, J.; Wang, J.F.; Qu, S.B.; Du, H.L.; Cui, T.J. Ferroelectric composite artificially-structured functional material: Multifield control for tunable functional devices. J. Phys. D Appl. Phys. 2022, 55, 303002. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y.; Xu, J.; Zhang, M.; Yu, P.; Zhao, Q. Frequency domain analysis of mechanical properties and failure modes of PVDF at high strain rate. Constr. Build. Mater. 2019, 235, 117506. [Google Scholar] [CrossRef]
- Kivirand, T. Method for Measuring Piezoelectric Charge Coefficients. Master’s Thesis, Tallin University of Technology, Tallin, Estonia, 2015; pp. 1–66. [Google Scholar]
- Stewart, M.; Battrick, W.; Cain, M. Measuring Piezoelectric d 33 co-efficients using the Direct Method Measuring Piezoelectric d 33 coefficients using the Direct Method Contents. In Measurement Good Practice Guide No. 44; Materials Centre National Physical Laboratory: Teddington, UK, 2001. [Google Scholar]
- Hillenbrand, J.; Sessler, G.M.; Zhang, X. Verification of a model for the piezoelectric d33 coefficient of cellular electret films. J. Appl. Phys. 2005, 98, 064105. [Google Scholar] [CrossRef]
- Gusarov, B.; Gusarova, E.; Viala, B.; Gimeno, L.; Cugat, O. PVDF piezoelectric voltage coefficient in situ measurements as a function of applied stress. J. Appl. Polym. Sci. 2015, 133, 43248. [Google Scholar] [CrossRef]
- Guo, Q.; Cao, G.Z.; Shen, I.Y. Measurements of Piezoelectric Coefficient d33 of Lead Zirconate Titanate Thin Films Using a Mini Force Hammer. J. Vib. Acoust. 2013, 135, 011003. [Google Scholar] [CrossRef]
- Finot, E.; Passian, A.; Thundat, T. Measurement of Mechanical Properties of Cantilever Shaped Materials. Sensors 2008, 8, 3497–3541. [Google Scholar] [CrossRef]
- Yang, K.; Li, Z.; Jing, Y.; Chen, D.; Ye, T. Research on the resonant frequency formula of V-shaped cantilevers. In Proceedings of the 2009 4th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Shenzhen, China, 5–8 January 2009; pp. 59–62. [Google Scholar] [CrossRef]
- Fang, P.; Holländer, L.; Wirges, W.; Gerhard, R. Piezoelectric d33 coefficients in foamed and layered polymer piezoelectrets from dynamic mechano-electrical experiments, electro-mechanical resonance spectroscopy and acoustic-transducer measurements. Meas. Sci. Technol. 2012, 23, 035604. [Google Scholar] [CrossRef]
- Shetty, S.; Yang, J.I.; Stitt, J.; Trolier-McKinstry, S. Quantitative and high spatial resolution d33 measurement of piezoelectric bulk and thin films. J. Appl. Phys. 2015, 118, 174104. [Google Scholar] [CrossRef]
- Zhang, X.; Hillenbrand, J.; Sessler, G.M. Ferroelectrets with improved thermal stability made from fused fluorocarbon layers. J. Appl. Phys. 2007, 101, 054114. [Google Scholar] [CrossRef]
- Kos, T.; Slabki, M.; Petrovcic, J.; Vrancic, D.; Dolanc, G.; Koruza, J. Measurement System for Piezoelectric Resonance Impedance Spectroscopy Under Combined AC and High-Voltage DC Loading. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2022, 69, 3137–3144. [Google Scholar] [CrossRef]
- Kelley, T. Effect of temperature on the pulse-echo performance of ultrasonic transducers fabricated with PVDF film. IET Sci. Meas. Technol. 2019, 13, 370–374. [Google Scholar] [CrossRef]
- Mahbub, I.; Wang, H.; Islam, S.K.; Pullano, S.A.; Fiorillo, A.S. A low power wireless breathing monitoring system using piezoelectric transducer. In Proceedings of the 2016 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Benevento, Italy, 15–18 May 2016. [Google Scholar] [CrossRef]
- Jiang, L.; Wu, B.; Wei, X.; Lv, X.; Xue, H.; Lu, G.; Zeng, Y.; Xing, J.; Wu, W.; Wu, J. Flexible lead-free piezoelectric arrays for high-efficiency wireless ultrasonic energy transfer and communication. Mater. Horizons 2022, 9, 2180–2190. [Google Scholar] [CrossRef]
- Lu, H.; Cui, H.; Lu, G.; Jiang, L.; Hensleigh, R.; Zeng, Y.; Rayes, A.; Panduranga, M.K.; Acharya, M.; Wang, Z.; et al. 3D Printing and processing of miniaturized transducers with near-pristine piezoelectric ceramics for localized cavitation. Nat. Commun. 2023, 14, 054114. [Google Scholar] [CrossRef]
- Wu, N.; Cheng, X.; Zhong, Q.; Zhong, J.; Li, W.; Wang, B.; Hu, B.; Zhou, J. Cellular Polypropylene Piezoelectret for Human Body Energy Harvesting and Health Monitoring. Adv. Funct. Mater. 2015, 25, 4788–4794. [Google Scholar] [CrossRef]
- Zhang, X.; Sessler, G.M.; Wang, Y. Fluoroethylenepropylene ferroelectret films with cross-tunnel structure for piezoelectric transducers and micro energy harvesters. J. Appl. Phys. 2014, 116, 074109. [Google Scholar] [CrossRef]
- Hillenbrand, J.; Sessler, G. Quasistatic and dynamic piezoelectric coefficients of polymer foams and polymer film systems. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 72–79. [Google Scholar] [CrossRef]
- Neugschwandtner, G.S.; Schwödiauer, R.; Vieytes, M.; Bauer-Gogonea, S.; Bauer, S.; Hillenbrand, J.; Kressmann, R.; Sessler, G.M.; Paajanen, M.; Lekkala, J. Large and broadband piezoelectricity in smart polymer-foam space-charge electrets. Appl. Phys. Lett. 2000, 77, 3827–3829. [Google Scholar] [CrossRef]
- Mohebbi, A.; Mighri, F.; Ajji, A.; Rodrigue, D. Cellular Polymer Ferroelectret: A Review on Their Development and Their Piezoelectric Properties. Adv. Polym. Technol. 2016, 37, 468–483. [Google Scholar] [CrossRef]
- Fialka, J.; Benes, P. Comparison of methods of piezoelectric coefficient measurement. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference Proceedings, Graz, Austria, 13–16 May 2012; pp. 37–42. [Google Scholar] [CrossRef]
- Longbiao, H.; Xiujuan, F.; Triantafillos, K.; Feng, N.; Bo, Z.; Ping, Y. Comparison between Methods for the Measurement of the d33 Constant of Piezoelectric Materials. In Proceedings of the ICSV25, Horoshima, Japan, 9–12 July 2018; pp. 77–84. [Google Scholar]
- Hillenbrand, J.; Sessler, G. Foamed and solid polymer electrets with high piezoelectric constants. In Proceedings of the Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Cancun, Mexico, 20–24 October 2002; pp. 287–290. [Google Scholar] [CrossRef]
- Hillenbrand, J.; Sessler, G. Piezoelectricity in cellular electret films. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 537–542. [Google Scholar] [CrossRef]
- Zhang, X.; Hillenbrand, J.; Sessler, G. Thermally stable fluorocarbon ferroelectrets with high piezoelectric coefficient. Appl. Phys. A 2006, 84, 139–142. [Google Scholar] [CrossRef]
- Zabek, D.; Bowen, C.R.; Taylor, J. Electrical capacitance with meshed electrodes for piezo- and pyro-electric energy harvesting applications. In Proceedings of the 2015 Joint IEEE International Symposium on the Applications of Ferroelectric (ISAF), International Symposium on Integrated Functionalities (ISIF), and Piezoelectric Force Microscopy Workshop (PFM), Singapore, 24–27 May 2015; pp. 83–86. [Google Scholar] [CrossRef]
- Basso, H.; Neto, L.G.; Lima, L.; Altafim, R.; de Aquino, C. Piezoelectricity in multi-air voids electrets. In Proceedings of the CEIDP ‘05. 2005 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Nashville, TN, USA, 16–19 October 2005; pp. 669–672. [Google Scholar] [CrossRef]
- Bernard, C.A.; Correia, J.P.M.; Ahzi, S.; Bahlouli, N. Numerical implementation of an elastic-viscoplastic constitutive model to simulate the mechanical behaviour of amorphous polymers. Int. J. Mater. Form. 2016, 10, 607–621. [Google Scholar] [CrossRef]
- Pardo, L.; Jiménez, R.; García, A.; Brebøl, K.; Leighton, G.; Huang, Z. Impedance measurements for determination of the elastic and piezoelectric coefficients of films. Adv. Appl. Ceram. 2010, 109, 156–161. [Google Scholar] [CrossRef]
- Gusarov, B. PVDF Piezoelectric Polymers: Characterization and Application to Thermal Energy Harvesting. Available online: https://theses.hal.science/tel-01241414 (accessed on 9 August 2023).
- Zhang, Y.; Bowen, C.R.; Ghosh, S.K.; Mandal, D.; Khanbareh, H.; Arafa, M.; Wan, C. Ferroelectret materials and devices for energy harvesting applications. Nano Energy 2018, 57, 118–140. [Google Scholar] [CrossRef]
- Anton, S.R.; Farinholt, K.M. An evaluation on low-level vibration energy harvesting using piezoelectret foam. Act. Passive Smart Struct. Integr. Syst. 2012, 8341, 83410G. [Google Scholar]
- Ma, X.; Von Seggern, H.; Sessler, G.M.; Zhukov, S.; Ben Dali, O.; Kupnik, M.; Zhang, X. High performance fluorinated polyethylene propylene ferroelectrets with an air-filled parallel-tunnel structure. Smart Mater. Struct. 2020, 30, 015002. [Google Scholar] [CrossRef]
- Chiu, F.-C.; Chuang, Y.-C.; Liao, S.-J.; Chang, Y.-H. Comparison of PVDF/PVAc/GNP and PVDF/PVAc/CNT ternary nanocomposites: Enhanced thermal/electrical properties and rigidity. Polym. Test. 2018, 65, 197–205. [Google Scholar] [CrossRef]
- Qiu, X.; Groth, F.; Wirges, W.; Gerhard, R. Cellular polypropylene foam films as DC voltage insulation and as piezoelectrets—A comparison. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 829–834. [Google Scholar] [CrossRef]
- Guo, Y.; Bao, C.; Song, L.; Yuan, B.; Hu, Y. In Situ Polymerization of Graphene, Graphite Oxide, and Functionalized Graphite Oxide into Epoxy Resin and Comparison Study of On-the-Flame Behavior. Ind. Eng. Chem. Res. 2011, 50, 7772–7783. [Google Scholar] [CrossRef]

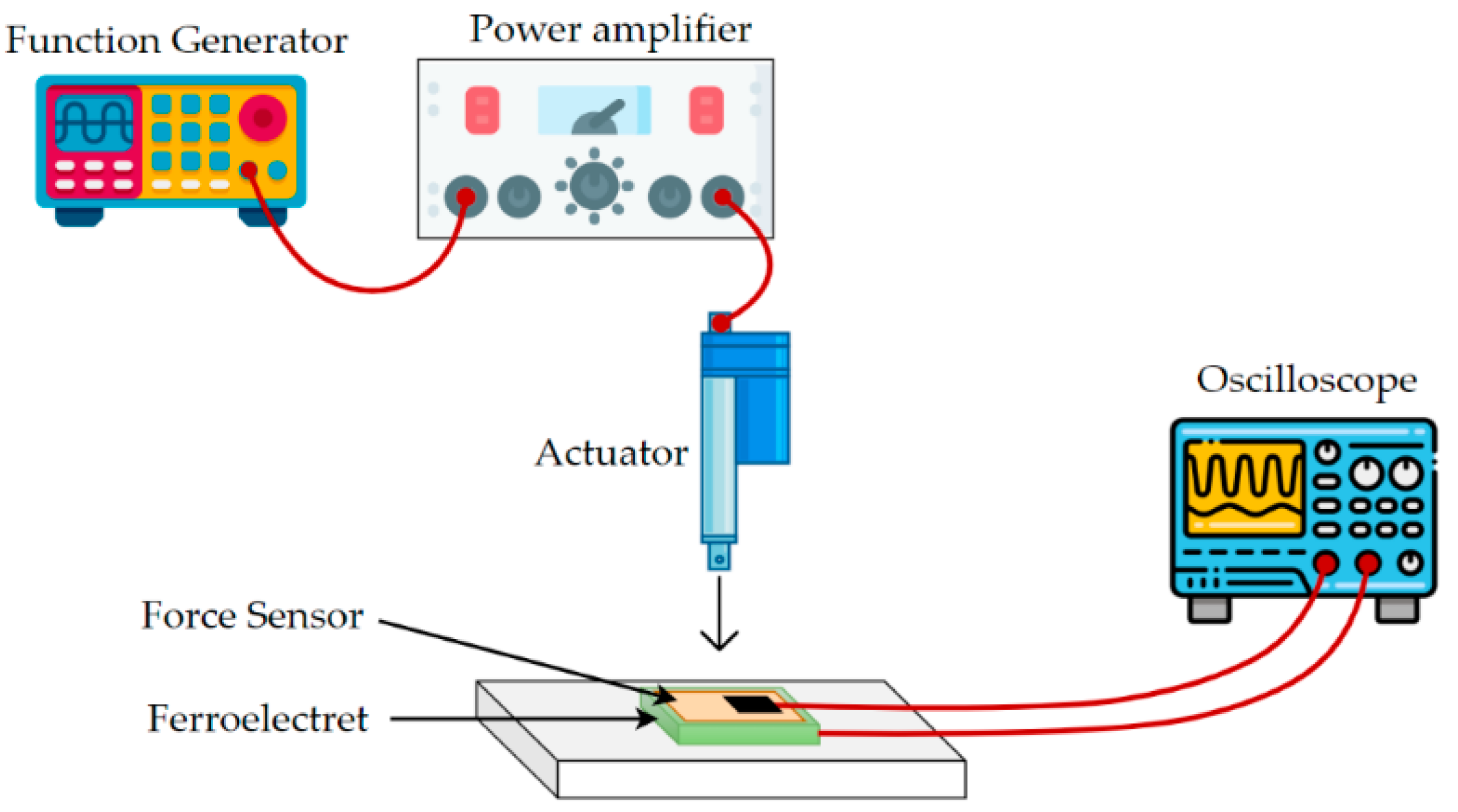

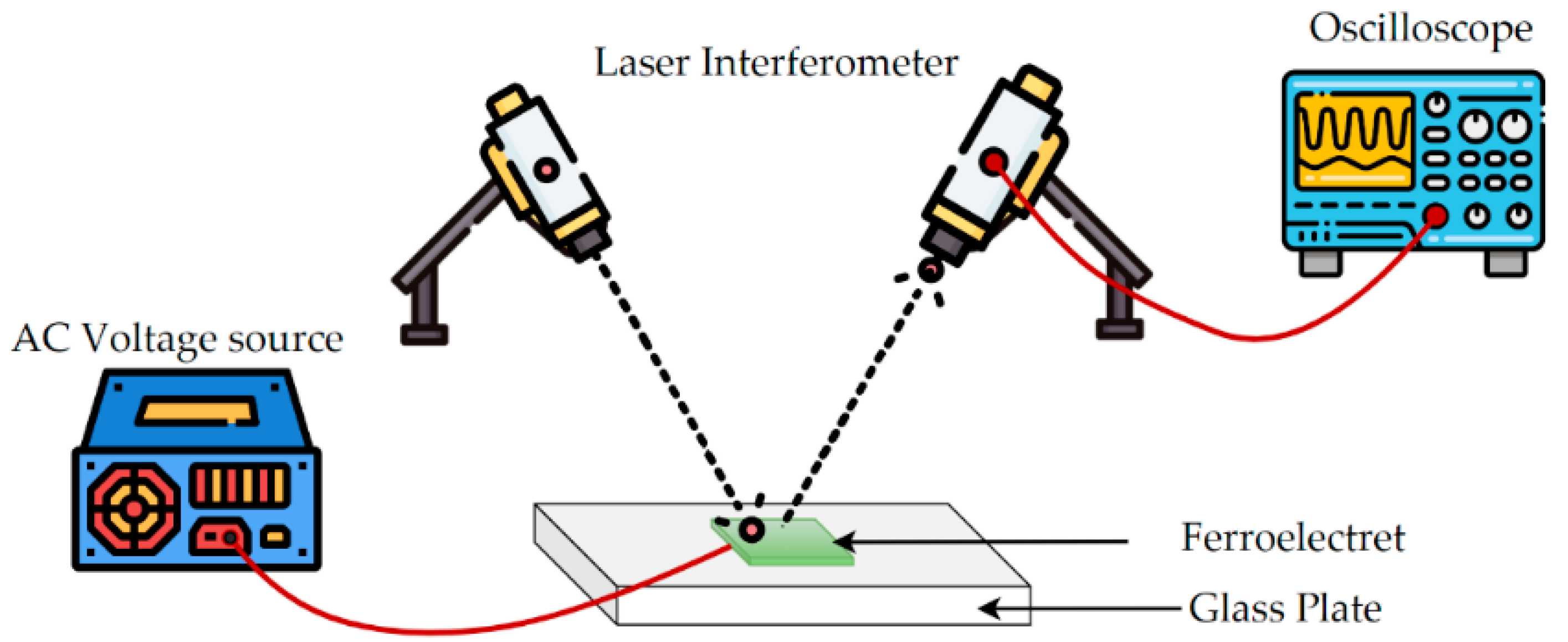
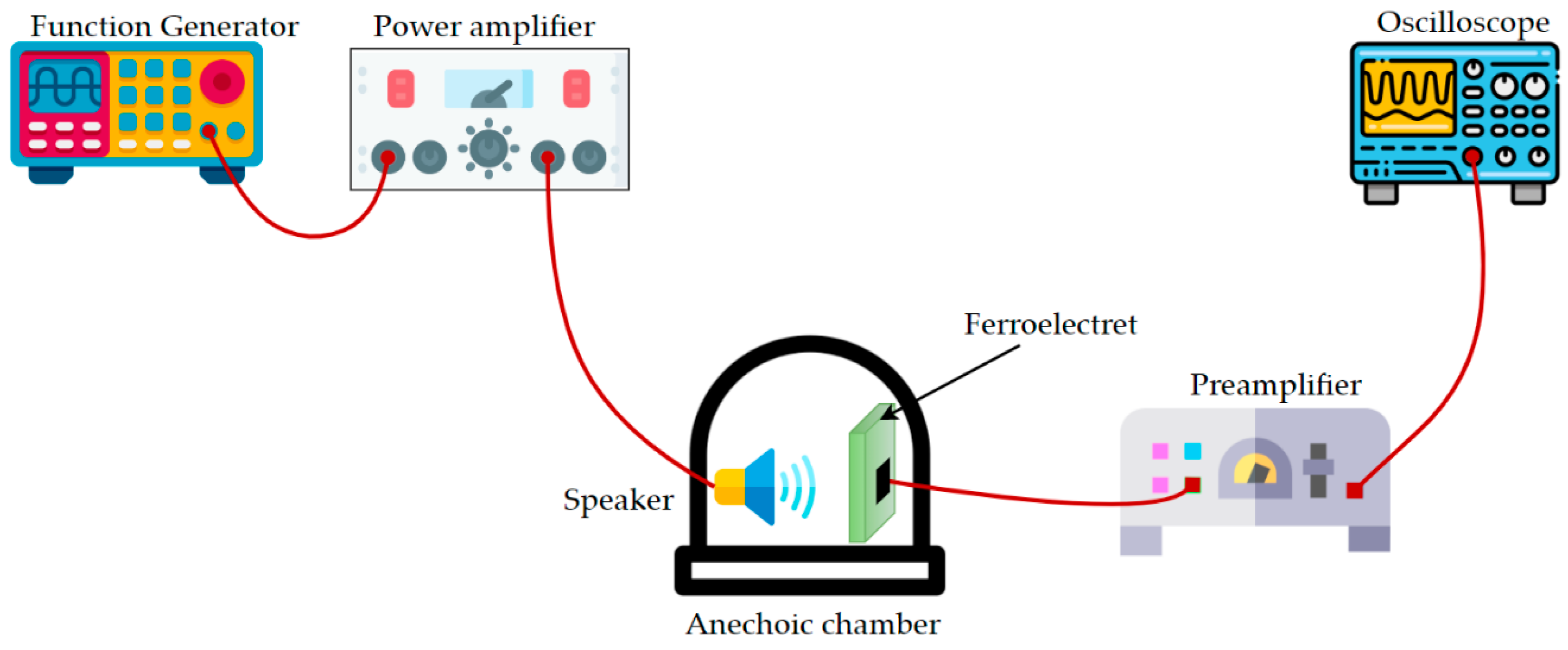


| No. | Features | Quasi-Static | Dynamic | Interferometric | Acoustic | Proposed Method |
|---|---|---|---|---|---|---|
| 1 | Procedure | Direct | Direct | Indirect | Indirect | Direct |
| 3 | coefficient(pC/N) | 1000–2500 | 1200–1300 | 150–700 | 300–350 | All values |
| 4 | Accurate | No | No | Yes | Yes | Moderate accuracy |
| 5 | Repeatable | No | No | Yes | Yes | Yes |
| 6 | Time-consuming | Yes | Yes | Yes | Yes | no |
| 7 | Special equipment needed | No | No | Yes | Yes | yes |
| 8 | Wide frequency range | No | No | Yes | Yes | yes |
| 9 | Non-destructive | No | No | Yes | Yes | yes |
| 10 | Independent of geometry, electrode contact | No | No | Yes | Yes | Depends on electrode conatct |
| 11 | Suitable for the highly viscoelasticand resistive material | No | No | Yes | Yes | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ravikumar, C.; Markevicius, V. Development of Ultrasound Piezoelectric Transducer-Based Measurement of the Piezoelectric Coefficient and Comparison with Existing Methods. Processes 2023, 11, 2432. https://doi.org/10.3390/pr11082432
Ravikumar C, Markevicius V. Development of Ultrasound Piezoelectric Transducer-Based Measurement of the Piezoelectric Coefficient and Comparison with Existing Methods. Processes. 2023; 11(8):2432. https://doi.org/10.3390/pr11082432
Chicago/Turabian StyleRavikumar, Chandana, and Vytautas Markevicius. 2023. "Development of Ultrasound Piezoelectric Transducer-Based Measurement of the Piezoelectric Coefficient and Comparison with Existing Methods" Processes 11, no. 8: 2432. https://doi.org/10.3390/pr11082432
APA StyleRavikumar, C., & Markevicius, V. (2023). Development of Ultrasound Piezoelectric Transducer-Based Measurement of the Piezoelectric Coefficient and Comparison with Existing Methods. Processes, 11(8), 2432. https://doi.org/10.3390/pr11082432







