CFD-DEM Simulation of Fast Fluidization of Fine Particles in a Micro Riser

Abstract

In recent years, the discrete element method (DEM) has gradually been applied to the traditional fluidization simulation of fine particles in a micro fluidized bed (MFB). The application of DEM in the simulating fast fluidization of fine particles in MFB has not yet received attention. This article presents a drag model that relies on the surrounding environment of particles, namely the particle circumstance-dependent drag model or PCDD model. Fast fluidization in an MFB of fine particles is simulated using DEM based on the PCDD model. Simulations indicate that the local structure in an MFB exhibits particle aggregation, which is a natural property of fast fluidization, forming a structure where a continuous dilute phase and dispersed concentrated phase coexist. There exists a strong effect of solid back-mixing in an MFB, leading to relatively low outlet solid flux. The gas back-mixing effect is, however, not so distinct. The axial porosity shows a monotonically increasing distribution with the bed height but does not strictly follow the single exponential distribution. The solid volume fraction at the bottom of the bed is significantly lower than the correlated value in CFB. The axial heterogeneous distribution of the cross-sectional average porosity in the lower half of the bed is also weakened. The radial porosity shows a higher distribution pattern in the central region and a lower one in the sidewall region.

1. Introduction

Gas–solid fluidized beds are widely used in environmental, energy, chemical and other process engineering fields [1]. Numerical simulation has become an indispensable means of studying gas–solid two-phase fluid dynamics for the cognition of a fluidized bed. The discrete element method [2,3,4,5], or DEM, providing particle-level information has been a tool needed to guide process design and operation in the field of fluidization engineering. The particle and device sizes simulated with DEM show a wide range. With the development of computer technology, high-performance algorithms and modeling capabilities, DEM has been able to simulate laboratory-scale coarse particle reactors. This method is gradually recognized by the industry and will inevitably be widely used [6]. On the other hand, with the improvement of the model and the calculation accuracy, the particle size used in DEM simulation gradually turns refined. Yu’s research group once simulated and analyzed different fluidization types of particle systems with particles as small as 30 μm [7].

In order to distinguish the particles in the gas–solid system with practical significance, Geldart [8] divided the particles into four classes: A, B, C and D. This is a widely accepted particle classification method in academia. Class C particles or ultra-fine particles are usually considered difficult to be fluidized; Class D particles or ultra-coarse particles have been used in numerous DEM simulation studies but are limited to fewer operations such as spout and slugging in practice; Class B particles are fluidized materials with a relatively small size in previous DEM simulations but still classified as coarse particles; and Class A particles or fine particles have a more smaller size (30–100 μm) and density (less than 1400 kg/m³). Fine particles are rarely used in DEM simulation, but they are widely used in engineering. For example, the catalytic cracking catalyst (FCC) particles, as a typical fine fluidized material, show advantages and characteristics different from other types of particles, such as a high gas–solid mass transfer rate, high bed expansion ratio and high heat transfer rate; they significantly expand before bubbling. Moreover, their cohesion is stronger, and the van der Waals force should not be ignored in many cases.

Ye et al. [9] modeled the fluidization of class A particles using DEM in 2004. The next year, Potic et al. [10] from the same study group proposed the concept of a micro fluidized bed (MFB), which is far small than an experimental circulating fluidized bed (CFB). They also studied the micro fluidized bed experimentally and theoretically. Han et al. [11] indicated that MFB has the advantages of convenience, safety, low cost and high efficiency. As an ideal isothermal reactor, it can be used as a reaction analyzer. As a small high selectivity module reactor, it can be used to produce high-value fine chemicals. Since only a few coarse particles side by side can fill the whole bed diameter, it is inevitable to abandon the use of class D particles or even class B particles. One has to choose Class A particles as fluidized materials in MFB experiments and DEM simulations. Therefore, the DEM simulation of class A particle fluidization in an MFB may become a hot research field.

Due to the lack of experimental data and simulation research, it is difficult to find reference literature. The existing DEM simulation results are mainly limited to fixed, uniform expansion, bubbling, slugging and turbulence fluidized beds [12,13,14,15,16,17]. Taking additional research in the past two years as examples, Guo et al. [18] presented a study of the solid-like and fluid-like states in the homogeneous fluidization regime of Class A particles. Li et al. [19] also performed a detailed analysis of bed hydrodynamics for polydisperse gas–solid flow of Class A particles. Both of the recent works implemented 3-D simulations. It is currently imperative to carry out the DEM simulation study of unconventional fast fluidization in MFB, even if it is a 2-D simulation study.

One difficult problem is how to reasonably simulate the flow structures, especially the macroscopic structure in an MFB. The local flow structure of particle agglomeration could be well simulated in [20]. However, the gas–solid back-mixing behavior could not be reasonably simulated, leading to the macroscopic structure seriously not insistent with the well-known core-annulus theoretical model. Can DEM reasonably simulate the fast fluidization of fine particles in MFB? Looking at the problem, this paper proposes a drag force model considering the surrounding particle environment and tries to solve the problem by reasonably calculating the drag force.

2. Drag Model

The drag model formally adopts the drag formula of a single particle in the particle group

$$F_{\mathrm{d}i}=\frac{1}{8}\pi d_{\mathrm{p}}{C}_{\mathrm{d}i}{\rho }_{\mathrm{g}}|u_i-v_i|(u_i-v_i){\epsilon }_i^2.$$

(1)

where $d_{\mathrm{p}}$ is the particle diameter, $C_{\mathrm{d}i}$ is the apparent drag coefficient of the particle group around particle $i$, ${\rho }_{\mathrm{g}}$ is the gas density, $u_i$ is the local gas velocity, $v_i$ is the local gas velocity and ${\epsilon }_i$ is the local porosity. A gird-independent calculation method for ${\epsilon }_i$ is given in the following.

A neighborhood of the target particle is firstly determined to consider the influence of each surrounding particle in the neighborhood on the target particle. The influence of each surrounding particle is distinguished according to the different distances from the surrounding particle. This grid-independent calculation method is similar to the kernel approximation method in smooth particle dynamics (SPH) [21]. In this way, Xu et al. [22] calculated ${\epsilon }_i$ as

$${\epsilon }_i=1-{\displaystyle \sum _{j=1}^{N_i}W(\left|r_i-r_j\right|,h)}\cdot \frac{1}{6}\pi d_{\mathrm{p}}{}^2$$

(2)

where $N_i$ is the number of particles in the neighborhood, $h$ is the characteristic radius or smooth length of the neighborhood, $\left|r_i-r_j\right|$ is the distance between particle $i$ and $j$ and $W(d,h)$ is the normalized kernel function which is calculated as

$$W(d,h)=\frac{7}{478\pi h^2}\left\{\begin{array}{l}{(3-d/h)}^5-6{(2-d/h)}^5+15{(1-d/h)}^5,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\le d/h<1,\\ {(3-d/h)}^5-6{(2-d/h)}^5,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} 1\le d/h<2,\\ {(3-d/h)}^5,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}2\le d/h<3,\\ 0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \hspace{0.33em}d/h\ge 3,\end{array}\right.$$

(3)

However, the anomalies close to the boundary have been addressed for the above Equations (2) and (3). The local porosity close to the boundary is effectively improved by adding boundary virtual particles in a previous study [23]. Figure 1 shows the diagram of the neighborhood, real particles and virtual particles in the kernel approximation method.

In ref. [23], $h$ is set to be 2.5 $d_{\mathrm{p}}$. In fact, the accurate tune is difficult even in SPH simulations. On the other hand, in Equation (2), the contribution of each particle $j$ for the local solid volume fraction of particle $i$ is $W(\left|r_i-r_j\right|,h)\cdot \pi d_{\mathrm{p}}{}^2/6$. However, this contribution is formally not three-dimensional but two-dimensional. Moreover, the contribution should not be fixed for different particle systems. Thirdly, the basis for the correction is that the global mean values of local porosity cannot deviate from the global mean values of grid porosity. This problem is solved by introducing a solid volume fraction multiplier as

$${\epsilon }_i=1-\lambda {\displaystyle \sum _{j=1}^{N_i}W(\left|r_i-r_j\right|,h)}\cdot \frac{1}{6}\pi d_{\mathrm{p}}{}^2$$

(4)

In order to avoid parameter testing, $\lambda$ is determined by the following equation as

$${\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^{N_i}W(\left|r_i-r_j\right|,h)}\cdot \frac{\lambda }{6N}\pi d_{\mathrm{p}}{}^2}={\epsilon }_{\mathrm{ts}}$$

(5)

where ${\epsilon }_{\mathrm{ts}}$ is the particle filling ratio of the bed, i.e., the total solid volume fraction and $N$ is the total number of real particles that are randomly distributed throughout the bed.

Combined with the apparent drag coefficient proposed by Wen and Yu [24] and the single-particle drag coefficient proposed by Schiller and Naumann [25], the apparent drag coefficient is calculated as

$$C_{\mathrm{d}i}=\frac{24{\mu }_{\mathrm{g}}{\epsilon }_i^{-3.7}}{{\rho }_{\mathrm{g}}|u_{\mathrm{g}}-v_{\mathrm{p}}|d_{\mathrm{p}}}+\frac{3.6{\mu }_{\mathrm{g}}^{0.313}{\epsilon }_i^{-4.387}}{{({\rho }_{\mathrm{g}}|u_{\mathrm{g}}-v_{\mathrm{p}}|d_{\mathrm{p}})}^{0.313}}$$

(6)

where ${\epsilon }_i$ is calculated according to Equation (4). Thus, the particle circumstance-dependent drag (PCDD) model is constructed according to Equations (1) and (6).

3. Simulation Method

The Navier–Stokes equations of the gas phase motion are expressed as Equations (7) and (8),

$$\frac{\partial \left({\epsilon }_{\mathrm{g}}{\rho }_{\mathrm{g}}\right)}{\partial t}+\nabla \cdot ({\epsilon }_{\mathrm{g}}{\rho }_{\mathrm{g}}u)=0$$

(7)

$$\frac{\partial \left({\epsilon }_{\mathrm{g}}{\rho }_{\mathrm{g}}u\right)}{\partial t}+\nabla \cdot ({\epsilon }_{\mathrm{g}}{\rho }_{\mathrm{g}}uu)=-{\epsilon }_{\mathrm{g}}\nabla p-S_{\mathrm{p}}-\nabla \cdot ({\epsilon }_{\mathrm{g}}{\tau }_{\mathrm{g}})+{\epsilon }_{\mathrm{g}}{\rho }_{\mathrm{g}}g$$

(8)

where ${\epsilon }_{\mathrm{g}}$ is the mean porosity, $p$ is the pressure, $u$ is the gas velocity, $t$ is the time, ${\tau }_{\mathrm{g}}$ is the stress tensor and $S_{\mathrm{p}}$ is the momentum exchange source term. $S_{\mathrm{p}}$ is calculated as

$$S_{\mathrm{p}}=\frac{{\displaystyle {\sum }_{i=1}^{N_k}{A}_i{F}_{\mathrm{d}i}}}{AV}$$

(9)

where $N_k$ is the number of particles that overlap with grid $k$, $A$ is the particle disc area, $A_i$ is the overlap area of particle $i$ with grid $k$ and $V$ is the grid volume, which is calculated as if the grid had a thickness of $d_{\mathrm{p}}$.

The exact area fraction model is used [26] to calculate the 2-D porosity, and the following conversion formula [3] is used to convert ${\epsilon }_{2\mathrm{D}}$ to the 3-D porosity ${\epsilon }_{3\mathrm{D}}$ as

$${\epsilon }_{3D}=1-\frac{2}{\sqrt{\pi \sqrt{3}}}{(1-{\epsilon }_{2D})}^{\frac{3}{2}}$$

(10)

The finite volume method is used for discretizing the Navier–Stokes equations, using the consistent velocity inlet, pressure outlet and wall impenetrable conditions as boundary conditions and using the SIMPLER method [27] to solve the discretized algebraic equations.

The particle translation is described according to the Newton’s Second Law as

$${\rho }_{\mathrm{p}}{V}_i\frac{d{v}_i}{dt}={\rho }_{\mathrm{p}}{V}_{\mathrm{p}}g+F_{\mathrm{d}i}+F_{\mathrm{v}i}+F_{\mathrm{c}i}-V_i\Delta p_i$$

(11)

where $F_{\mathrm{c}i}$ is the sum of contact force on particle $i$, $F_{\mathrm{v}i}$ is the sum of van der Waals force on particle $i$, $V_i$ is the volume of the particle, $p_i$ is the local pressure. The soft sphere method is used to handle the particle–particle and particle–wall collision. The mass of the wall is infinite. The drag force $F_{\mathrm{d}i}$ is calculated using the PCDD model. The van der Waals force between particles is calculated as

$$F_{\mathrm{v}ij}=\frac{H_{\mathrm{a}}{d}_{\mathrm{p}}{e}_{ij}}{24{(d_{ij}-d_{\mathrm{p}})}^2}$$

(12)

where $H_{\mathrm{a}}$ is the Hamaker constant, $e_{ij}$ is the unit vector from particle $i$ to particle $j$ and $d_{ij}$ is the distance between particle $i$ and particle $j$. The van der Waals force of the wall applied to particle $i$ is calculated as

$$F_{\mathrm{v}i\mathrm{w}}=\frac{H_{\mathrm{a}}{d}_{\mathrm{p}}{e}_{i\mathrm{w}}}{12{(d_{i\mathrm{w}}-d_{\mathrm{p}})}^2}$$

(13)

where $e_{i\mathrm{w}}$ is the unit vector from the particle to the wall, and $d_{i\mathrm{w}}$ is the distance between the particle and the wall. Moreover, to calculate the non-contact van der Waals force according to Equations (12) and (13), one needs to set the cutoff distance $H_0$, i.e., the lower bound of $d_{ij}-d_{\mathrm{p}}$ and $d_{i\mathrm{w}}-d_{\mathrm{p}}$. The current simulations take $H_0$ = 0.4 nm.

The particle rotation is described as

$$I\frac{d{\omega }_i}{dt}=T_{\mathrm{c}i}$$

(14)

where ${\omega }_i$ is the particle angular velocity, I is the inertia of the particle and $T_{\mathrm{c}i}$ is the torque of the collision.

In the present two-dimensional simulations, the size of the micro riser is D × H = 2.5 mm × 40 mm. The number of grids discretizing the corresponding flow field is 10 × 160. The maximal particle number used is 11,452. Initially, 8230 real particles are set static and randomly distributed throughout the whole bed, which determines $\lambda$ = 0.948 according to Equation (5). The particle feed way follows the import-and-export balance.

Table 1. Fixed parameters for particle and gas.

Particle	Gas
Density ρp = 930 kg·m−3	Viscosity μg = 1.7 × 10−5 N·s·m−2
Particle diameter dp = 54 μm	Density ρg = 1.28 kg·m−3
Porosity at minimum fluidization εmf = 0.45	Inlet gas velocity u0 = 1.7 m·s−1
Stiffness Coef. κ = 10 N·m−1	CFD time step Δ tg = 2 × 10−6 s
Restitution Coef. ξ = 0.9
DEM time step Δ tp = 2.5 × 10−7 s

shows the other fixed parameters of the gas–solid phases in the simulations.

4. Results and Discussion

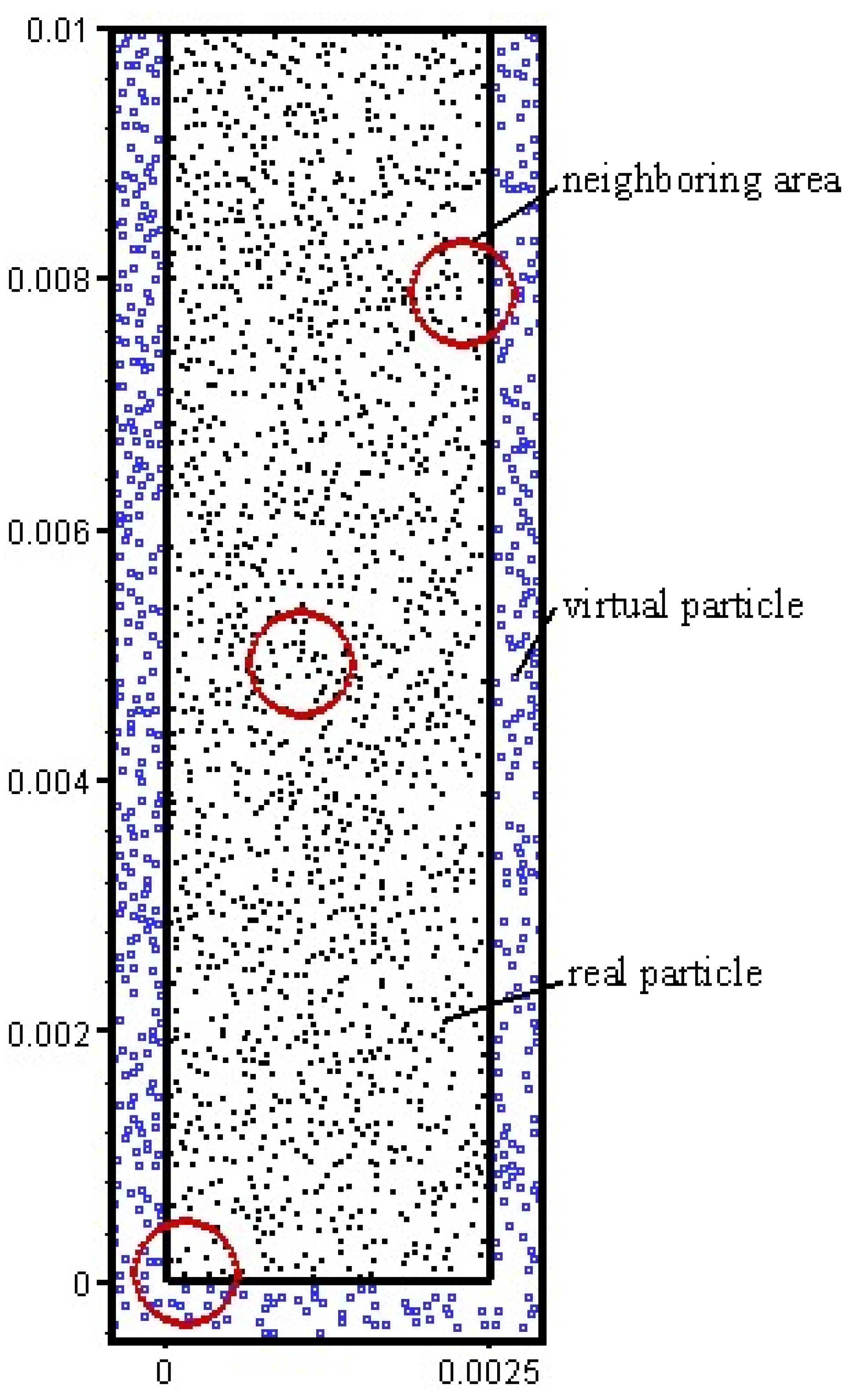
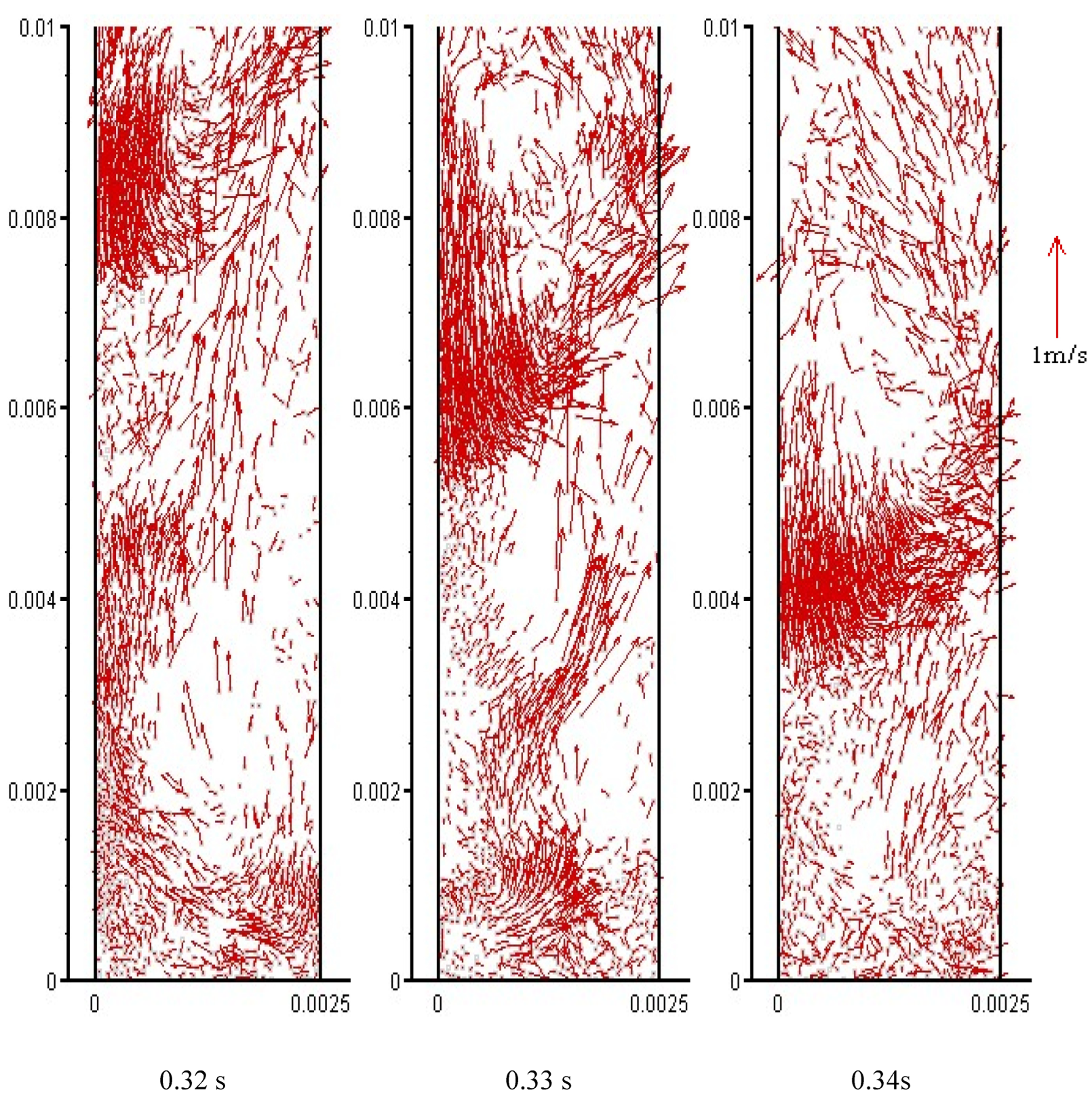
4.1. Particle Agglomeration

The transient particle and porosity distribution are given in Figure 2. The coexisting structures of the dilute phase as disperse particles and the dense phase as granular aggregates are consistently presented in the MFB. Kuipers et al. [28] recommended using the porosity of 0.85 as a standard to distinguish the emulsion phase and the bubble phase in a bubbling fluidized bed. Figure 2 also uses this standard to distinguish the dense phase and the dilute phase. As can be seen from the porosity distribution, the dilute phase is continuous while the dense phase is dispersed. In different areas of the bed, the boundaries of the two phases are sometimes blurred and sometimes clear. With the change of time and space, clusters show the dynamic behaviors of continuous formation and fragmentation, and they vary in shape and size.

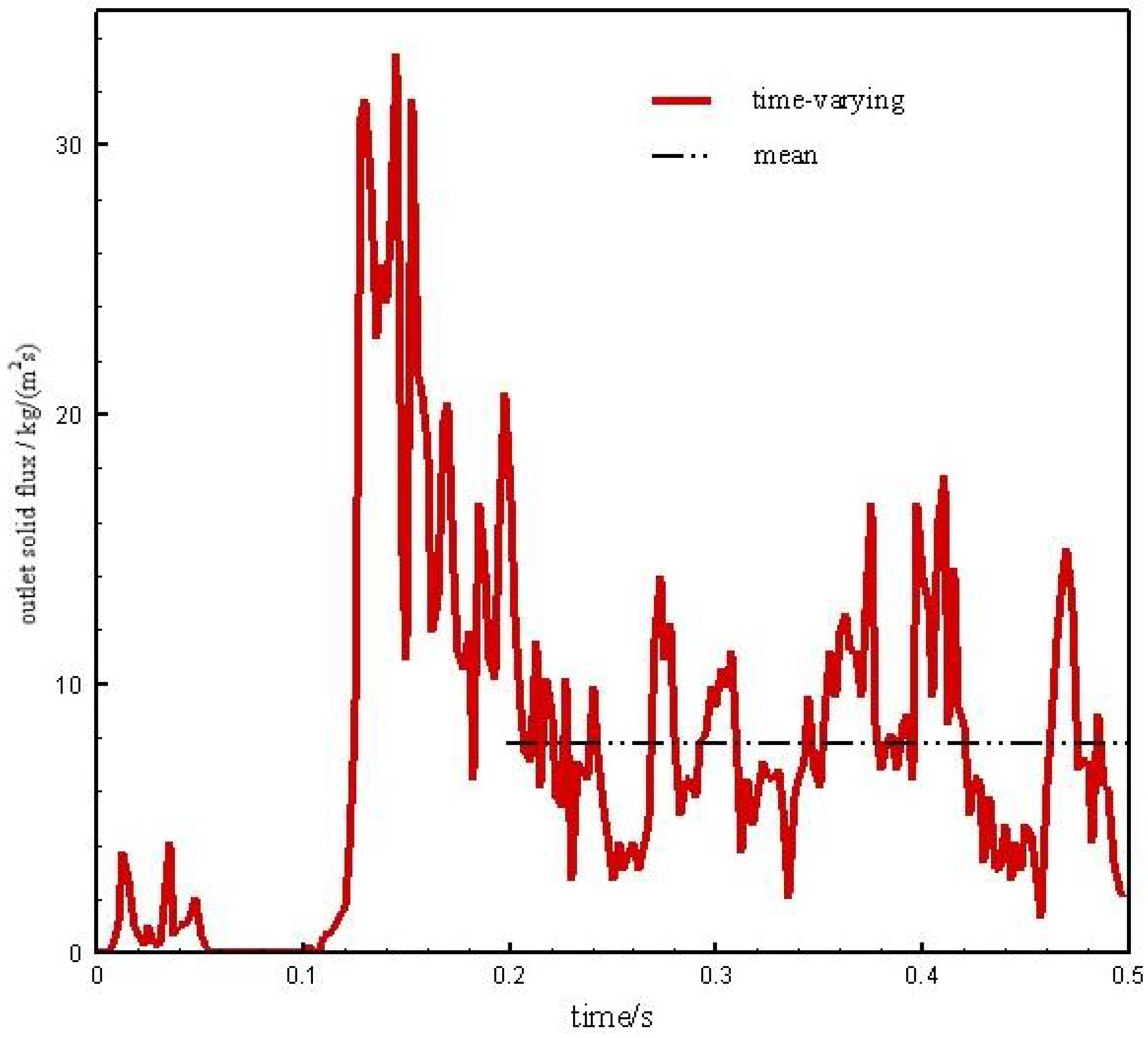
4.2. Gas–Solid Back-Mixing

Figure 3 presents the instantaneous distribution of the particle velocity within the 0.01 m height range in the bed. As shown in the figure, there is a serious back-mixing effect of the particles. The large cluster forms near the wall and then moves down along the wall. The radial velocity of the particles inside the cluster is small, and the axial velocity is large. Where the cluster passes, a strong tail vortex is formed to attract the tail particles to follow down. At the same time, a part of the peripheral particles begins to break away from the cluster due to the large radial velocity. Eventually, the cluster disintegrates due to the penetration of the fluid. At the bottom of the bed, the newly entering particles have not been fully accelerated, and the upper particles are in frequent contact. This results in a low radial and axial velocity of the particles in this area and also in a disorder orientation. In addition to the concentrated phase area, the particle velocity near the wall is relatively small, while the velocity in the central area is relatively large. Moreover, for the particles in the central area, whether they are the dispersed particles or particle groups, the axial velocity is mainly upward. As also indicated in Figure 3, the positive and negative velocity might be detected in almost all radial and axial positions.

Figure 4 shows the instantaneous distribution of the gas velocity in the 0.01 m height range, which corresponds to time in Figure 3. The gas tends to bypass the large cluster, around which the gas has a high radial velocity. In the interior of the cluster, both the radial and axial gas velocity are greatly reduced. Although the orientation of the radial velocity becomes chaotic, the larger part of the axial velocity is negative. Only in this area, the gas shows a sign of back-mixing. This proves that the back-mixing of the gas phase is mainly caused by the back-mixing of particles, i.e., the solid phase flow dominates. Except for the dense phase area, the gas velocity tends to be evenly distributed. Gas flow is mainly axially upward, and the radial velocity is small. That is to say, the dilute phase area is generally dominated by the upward gas flow. Thus, most of the dispersed particles can be continuously transported upward.

Figure 5 shows the outlet solid flux over time. After about 0.2 s, the two-phase flow within the MFB reaches a relatively stable state. In the relatively stable state, the outlet solid flux still has large fluctuations. The average value is about 7.8 kg/(m²·s), and it is much smaller than in the literature [20], which is 90~110 kg/(m²·s). This significant difference indicates that the overall drag force calculated with the PCDD model is largely reduced in the current simulations.

The saturated entrainment rate of the particle $G_{\mathrm{s}}^{\ast }$ can be calculated using the following correlation formula of Bai and Kato [29] as

$$\frac{G_{\mathrm{s}}^{\ast }{d}_{\mathrm{p}}}{{\mu }_{\mathrm{g}}}=0.125F{r}^{1.85}A{r}^{0.63}{(\frac{{\rho }_{\mathrm{p}}-{\rho }_{\mathrm{g}}}{{\rho }_{\mathrm{g}}})}^{-0.44}$$

(15)

where $Fr$ is the Frodes number and $Ar$ is the Archimedes number. When the operating gas velocity is 1.52 m/s, the correlated $G_{\mathrm{s}}^{\ast }$ is 16.18 kg/(m²·s). The experimental result given by Li and Kwauk [30] and the simulation result presented by Yang et al. [31] are both approximately 14.3 kg/(m²·s), indicating that the correlation formula has good predictive power. The correlation value at the current gas operating velocity 1.7 m/s is 19.9 kg/(m$G_{\mathrm{s}}^{\ast }$·S). Therefore, due to the failure to reasonably simulate the back-mixing behavior of particles, the outlet solid flux is overestimated in [20], which is even much higher than the saturation entrainment rate of particles. The currently selected gas–solid properties are basically the same as those in Yang et al. In this work the operating gas velocity is slightly higher, and the particle filling ratio is slightly lower. However, the simulated average outlet solid flux is much lower than the simulated and correlated values in CFB. The authors speculate that the most direct reason might be the geometry effect. In MFB compared with CFB, the bed diameter is very small, and thus for the wall, the relative area of contact with particles significantly enlarges [11]. The strong wall friction force causes the particles near the wall to be unable to be transported upward, which through particle collisions, gradually passed to the surrounding particles and even the central area. And the gas phase needs to consume a lot of energy or pressure drop for suspended particles, which seriously hinders the transport of the particles.

4.3. Axial Structure

Figure 6 shows the distribution of the mean porosity at the bottom and top sections of the bed. It shows that the top of the bed is a dilute phase area, and the fluctuation range of the mean porosity is small or even close to 1. At the bottom of the bed, the porosity is greatly reduced, and the fluctuation range is large. The lowest value can descend to below 0.8, which indicates that the dense phase can continuously form in different radial positions of the bottom.

Figure 7 shows the instantaneous and time averaging cross-sectional porosity between 0.2–0.5 s, with the height 0.000125 m, 0.005125 m, 0.015125 m, 0.025125 m, 0.035125 m and 0.039875 m, respectively. In CFB, the axial porosity distribution of fast fluidized bed is usually a monotonically increasing exponential distribution unless the outlet solid flux reaches the saturated entrainment rate of the particles. The current simulated axial distribution, although a monotonically increasing function of height, does not strictly obey the simple exponential distribution. It appears to have an inflection point between 0.015125 m and 0.025125 m. Because the parameters of the simple exponential function given by the vast majority of experimental studies are not uniform, it is difficult to compare the current simulated distribution of axial porosity with the results of the literature. Consider the solid phase volume fraction at the bottom of the bed ${\epsilon }_{\mathrm{sd}}$. As $G_{\mathrm{s}}^{}$ < $G_{\mathrm{s}}^{\ast }$; the correlation formula of Bai and Kato [29] is used as

$$\frac{{\epsilon }_{\mathrm{sd}}{\rho }_{\mathrm{p}}(u_{\mathrm{g}}-u_{\mathrm{t}})}{G_{\mathrm{s}}}=1+0.00614{(\frac{{\rho }_{\mathrm{p}}{u}_{\mathrm{g}}}{G_{\mathrm{s}}})}^{-0.23}{(\frac{{\rho }_{\mathrm{p}}-{\rho }_{\mathrm{g}}}{{\rho }_{\mathrm{g}}})}^{1.21}{(\frac{u_{\mathrm{g}}}{\sqrt{gD}})}^{-0.383}$$

(16)

where $u_{\mathrm{t}}$ represents the terminal velocity of the particles. In the moderate Reynolds number condition, the formula of Lewis et al. [32] can be used to calculate $u_{\mathrm{t}}$. From (16) the correlated ${\epsilon }_{\mathrm{sd}}$ is 0.22, while the presently simulated value is 0.136. The simulated value is far below the correlated value. The possible reasons for such a deviation include the following. The two-dimensional simulation cannot reach the reality of the three-dimensional simulation; the simple set import and export boundary conditions cannot simulate the real complex import and export effects. Additionally, it should be more inclined to think that the relative area of wall-particle contacts increase significantly in the MFB, resulting in a large decrease of the outlet solid flux. It is not difficult to analyze according to Formula (16), and ${\epsilon }_{\mathrm{sd}}$ decreases with the decrease in the outlet solid flux. Due to the low level of ${\epsilon }_{\mathrm{sd}}$, the heterogeneous distribution of cross-sectional porosity in the bottom area of the bed is weakened. This may be the main reason why the simulated axial voidage does not strictly obey the simple exponential distribution.

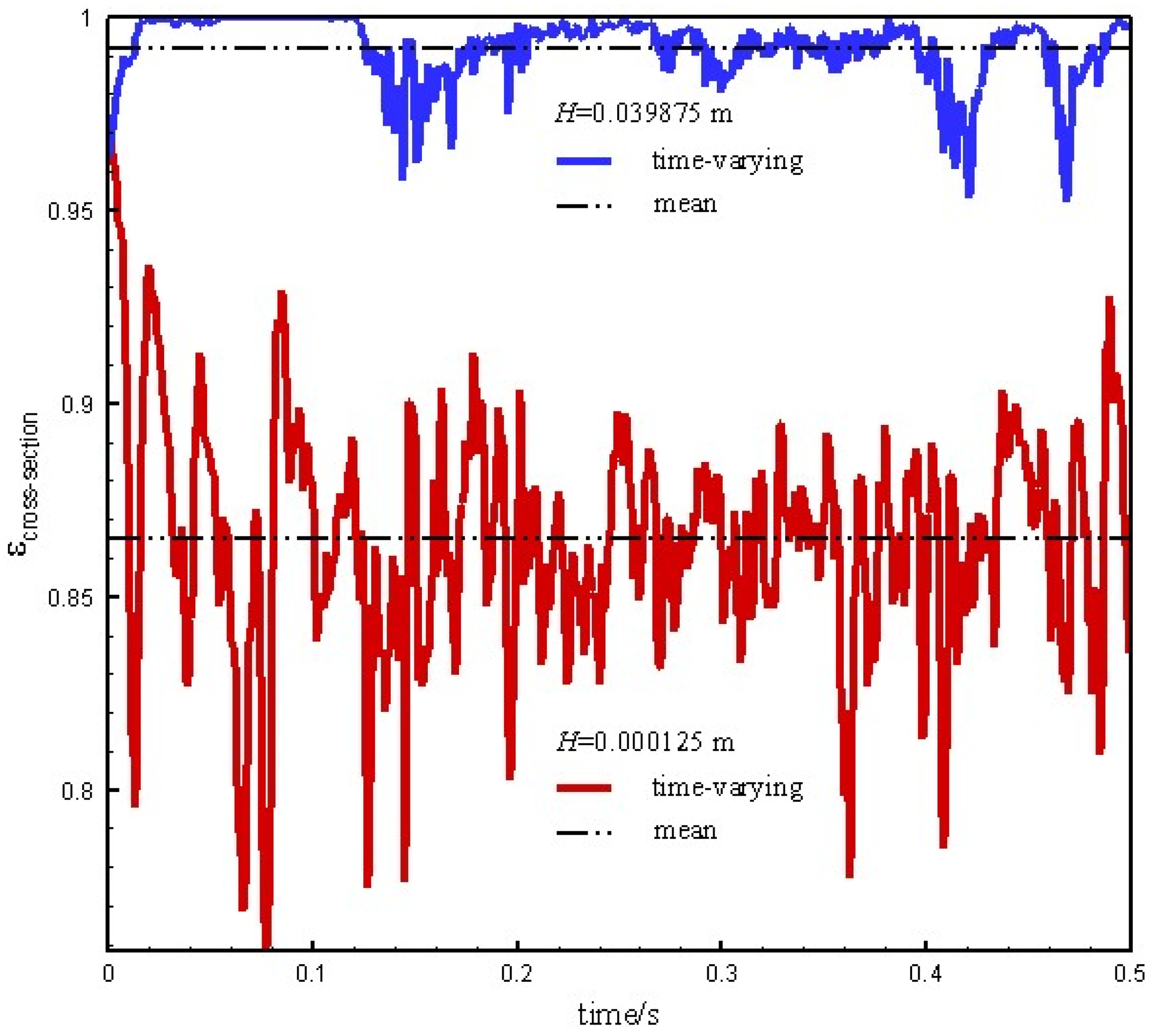
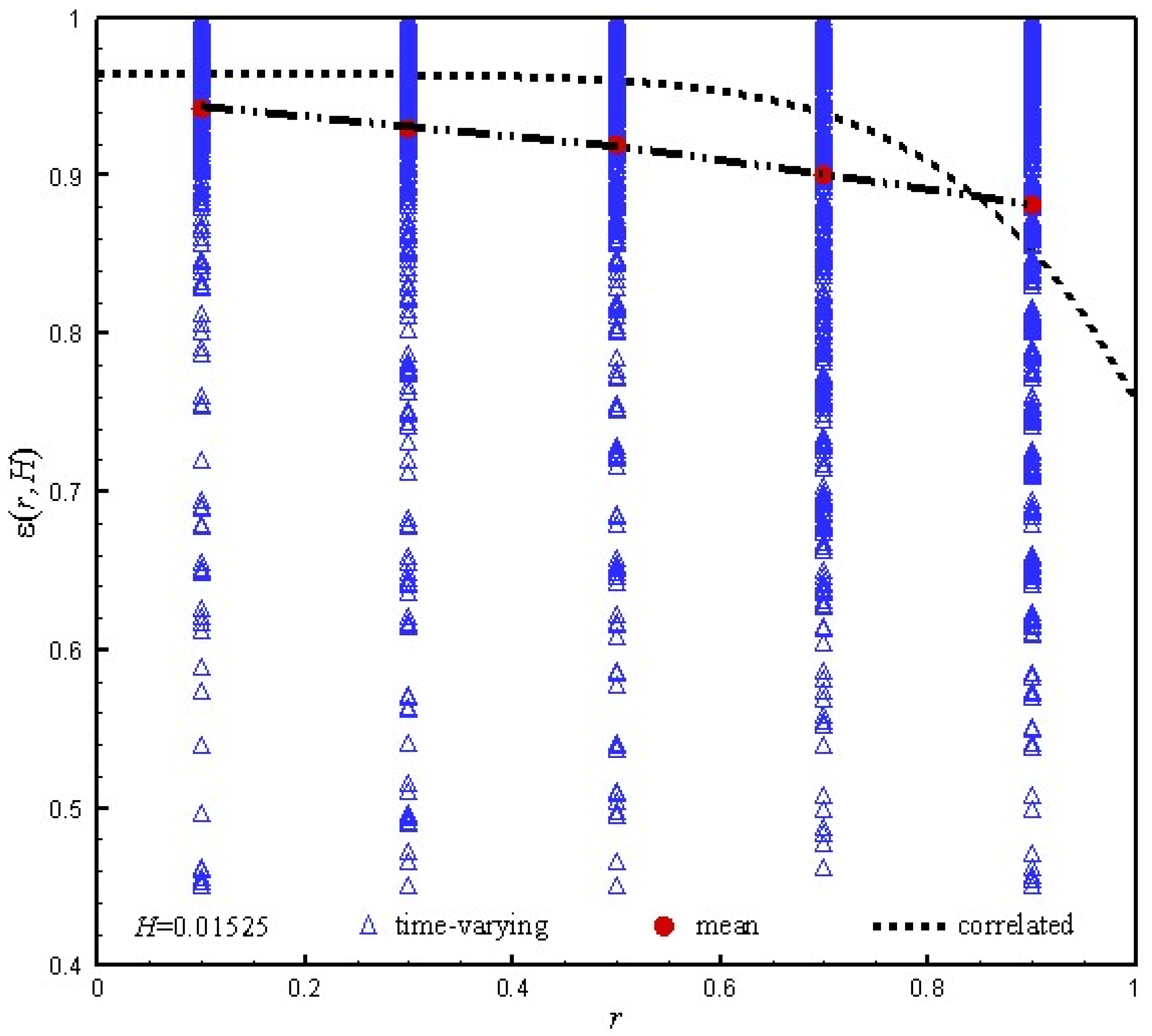
4.4. Radial Structure

The radial flow law of gas–solid phases in the fast fluidized bed is extremely important. The results of extensive experimental analysis show that as long as the cross-sectional porosity is determined, the radial distribution of the porosity is only a function of the radial position, i.e., the dimensionless radius, regardless of the operating conditions. The cross-sectional porosity at the height 0.015125 m is 0.912. The correlation formula of Patience and Chaouki [33] can be used as the following

$$\frac{{\overline{\epsilon }}^{0.4}-\epsilon }{{\overline{\epsilon }}^{0.4}-\epsilon }=4r^6.$$

(17)

The correlation result of the radial porosity in CFB is then obtained.

Figure 8 shows the radial distribution of the porosity at the height 0.015125 m. $r$ can be the dimensionless radius of the bed, and only the results from the right of the MFB can be selected. The simulation results in Figure 8 and the correlation results both show the high porosity in the central and the low porosity in close the wall, which follows the typical core-annulus distribution in the trend. The difference between the correlated and the simulated lies in the relatively low porosity in the central area and the relatively high porosity in the close wall in the simulated results, indicating a weak core-annulus effect. This significant difference lies in the amplification effect of wall friction in the MFB. The narrow bed diameter itself is easy to cause material slug, which can easily fill most of the bed diameter. As has also been stated, there exists the trace of clusters in the central area of the bed. Therefore, the heterogeneity of the radial distribution is also weakened.

5. Conclusions

In this paper, we give a drag model considering the particle environment, which is heterogeneous and complex. This model is implanted into CFD-DEM for simulation of fast fluidization in the MFB of fine particles. Simulations show that gas–solid two-phase flow in the MFB satisfies the common law of fast fluidization to some extent. Because the geometric size of the container is much smaller than that of a CFB, the relative area of the wall-particle contact is large. The wall friction factor becomes very significant, and thus, simulations exhibit a special rule of a large difference with those in CFB. The specific conclusions are drawn as follows:

(1)

The local structure in the MFB satisfies the natural property of fast fluidized particle agglomeration, forming a disperse dilute phase and continuous dense phase;

(2)

There is serious gas–solid back-mixing in the MFB, and the dense phase is the main area of gas–solid back-mixing. The wall friction factor aggravates the particle remixing effect, resulting in a relatively low outlet solid flux;

(3)

The axial porosity presents an increasing distribution with the bed height but does not strictly satisfy the monotonic exponential distribution. The solid volume fraction at the bottom of the bed is much lower than the correlated results for a CFB;

(4)

The radial porosity exhibits a weak core-annulus structure with a higher central region and lower side region. Compared with the correlated results for a CFB, the central region in the MFB is relatively dense, while the side region is relatively dilute;

(5)

All distinct variation results of the present simulation can be successfully explained using the relatively strong friction factor. Thus, the present drag model and simulation are both validated and effective, at least in the sense of a qualitative trend.