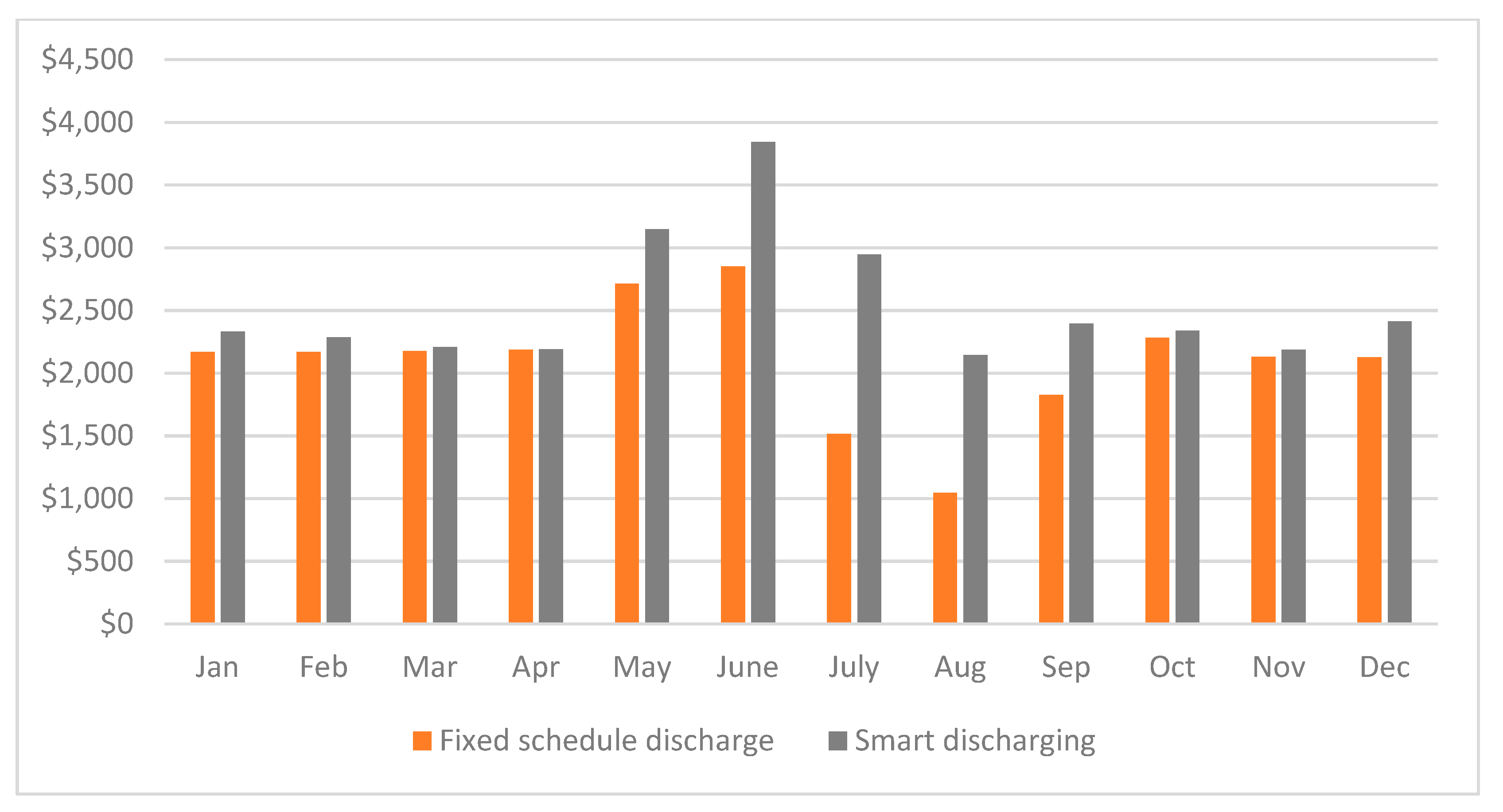1. Introduction
Every industrial facility has an electric demand profile that represents its power usage. Manipulation of the industrial facilities’ electric demand profile has earned the interest of industry pioneers, especially in recent years due to the initiatives and new developments that help in providing various strategies and applications to reduce power demand charges. Many studies have worked on strategies to achieve power and energy savings such as that by Lee and Cheng [
1] and another study about a review on energy saving strategies by Abdelaziz et al. [
2]. Some researchers focused on increasing the facility’s energy efficiency such as the studies by Aflaki et al. [
3] and Laitner [
4]. There is a specific case in California where the aggregate demand of the entire system using electricity minus the load generated by renewable energy has a demand curve resembling the shape of a duck, and that is why it was named “The duck curve” [
5]. Several researchers have conducted studies on how to manage the duck curve to achieve energy savings. For example, Krietemeyer et al. [
6] published a paper in 2021 explaining a local energy management program with the potential to flatten the duck curve.
Energy assessments are critical to study the capability of facilities to achieve energy and power savings. Patterson et al. [
7] focused on the current practices and recommendations of the Industrial Energy Assessments Centers (IACs) sponsored by the U.S. Department of Energy (DOE). Some energy assessments provide recommendations on how to manipulate the facility’s power profile to achieve demand charge savings. Most of these strategies involve a process called demand side management. Demand side management strategies provide saving mechanisms for industrial facilities by manipulating their demand profile [
8,
9,
10]. One promising strategy for demand side management is energy storage, which is one of the core pillars of this study.
Energy storage has caught the attention of many researchers, especially regarding the industrial sector, owing to the potential savings provided by the various applications of energy storage. Schmalensee [
11] explained how competitive energy storage is in manipulating the duck curve, while Zhang et al. [
12] presented a study about the recent developments regarding thermal energy storage (TES) and Alva et al. [
13] gave an overview of TES systems and their potential in providing demand charge savings. Kosowatz [
14] conducted research on the energy storage contribution in smoothing the duck curve, which is similar to the study of flattening the duck curve [
6]. Chen et al. [
15] performed a case study on the effect of smart pumping and water storage, battery storage, and solar panels on the demand profile, similar to the objective of this paper but with different applications. Recently, new applications have combined renewable energy forms with energy storage systems. Saffari et al. [
16] and Pitra et al. [
17] have published papers involving studies of energy storage integrated with renewable energy, specifically solar PV. Powell and Edgar [
18] presented dynamic simulation results of adding thermal energy storage with advanced control techniques to concentrating solar power. Immonen et al. [
19] performed a case study about dynamic optimization with flexible heat integration of solar energy with TES for industrial process heat, while Howlader et al. [
20] introduced pumped storage hydroelectricity. The high interest of the researchers in the field of thermal energy storage applications shows how promising these applications are, especially the applications of integrating thermal energy storage with renewable energy forms.
The main objective of this case study is to highlight the potential savings from the implementation of real-time demand response control strategies using TES for an industrial facility. The main addition of the paper to TES applications is having a smart controller that maintains the power usage of industrial facilities at a given setpoint using the flexible charging and discharging of TES.
The core points discussed in the paper are
Incorporating TES with the modeling of a stratified TES tank;
Using TES in two possible scenarios of process simulation;
Presenting the potential savings from employing the two scenarios utilizing TES and highlighting the novelty of the paper, which is the application of the smart controller integrated with TES, which has a given setpoint to maintain the power usage of industrial facilities.
Looking at the literature of the optimization applications utilizing TES, Powell et al. [
21] published a paper about the optimal loading of a system with a chiller integrated with TES. McLaughlin and Choi [
22] published a paper about estimating energy savings by utilizing machine learning models in industrial energy systems. Chen et al. [
23] examined the case of using intelligent control strategies with built-in storage of renewable energy, while Palensky and Dietrich [
24] implemented intelligent control strategies for demand side management. Jo and Park [
25] examined the strategy of demand side management with energy storage integrated with a smart grid. Powell et al. [
26] tackled the topic of dynamic optimization of a campus cooling system with TES. Industrial facilities also considered stochastic optimization to be implemented with TES tanks for energy savings [
27,
28,
29], where these three case studies explained the potential of stochastic optimization with energy storage. The difference between stochastic optimization and the application of this case study is that this case study has a controller with an optimized setpoint to control the power usage of an industrial facility. Looking at the literature and the published papers, this paper provides a new optimization method that maintains the power usage of industrial facilities at a specific setpoint to achieve optimum electric demand charge savings. Electric demand charges are the charges that any industrial facility incurs due to power consumption (
Section 2.3). This paper conducts the case study using real data from a facility that uses chillers for process cooling purposes. An added TES tank will store the chilled water and provide the cooling load to the process during necessary periods. The chillers have variable-frequency drives (VFDs), which are considered manipulated variables for the smart controller to meet the process cooling needs. Two papers showed energy savings achieved by applying VFDs on compressors and motors [
30,
31].
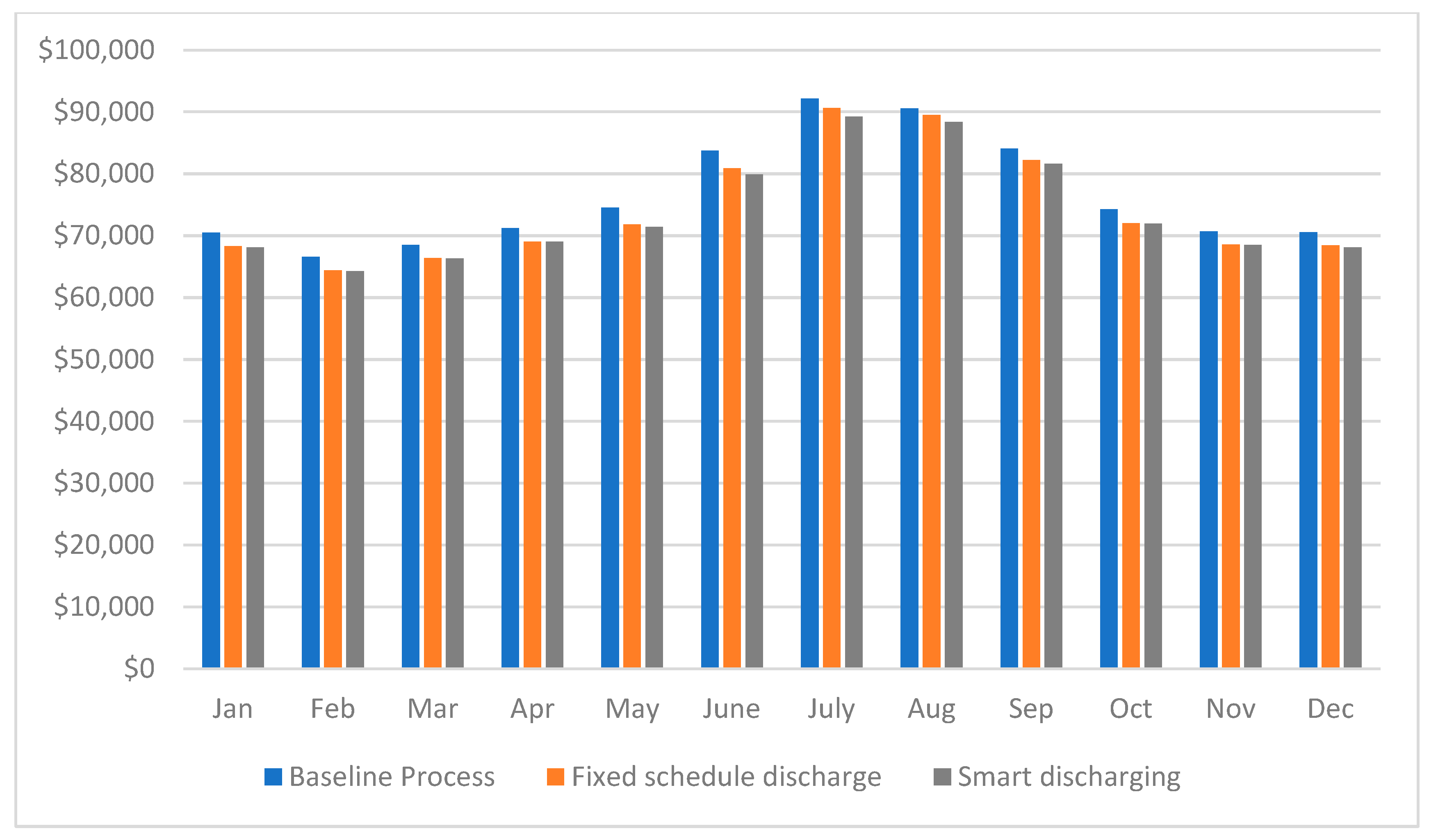
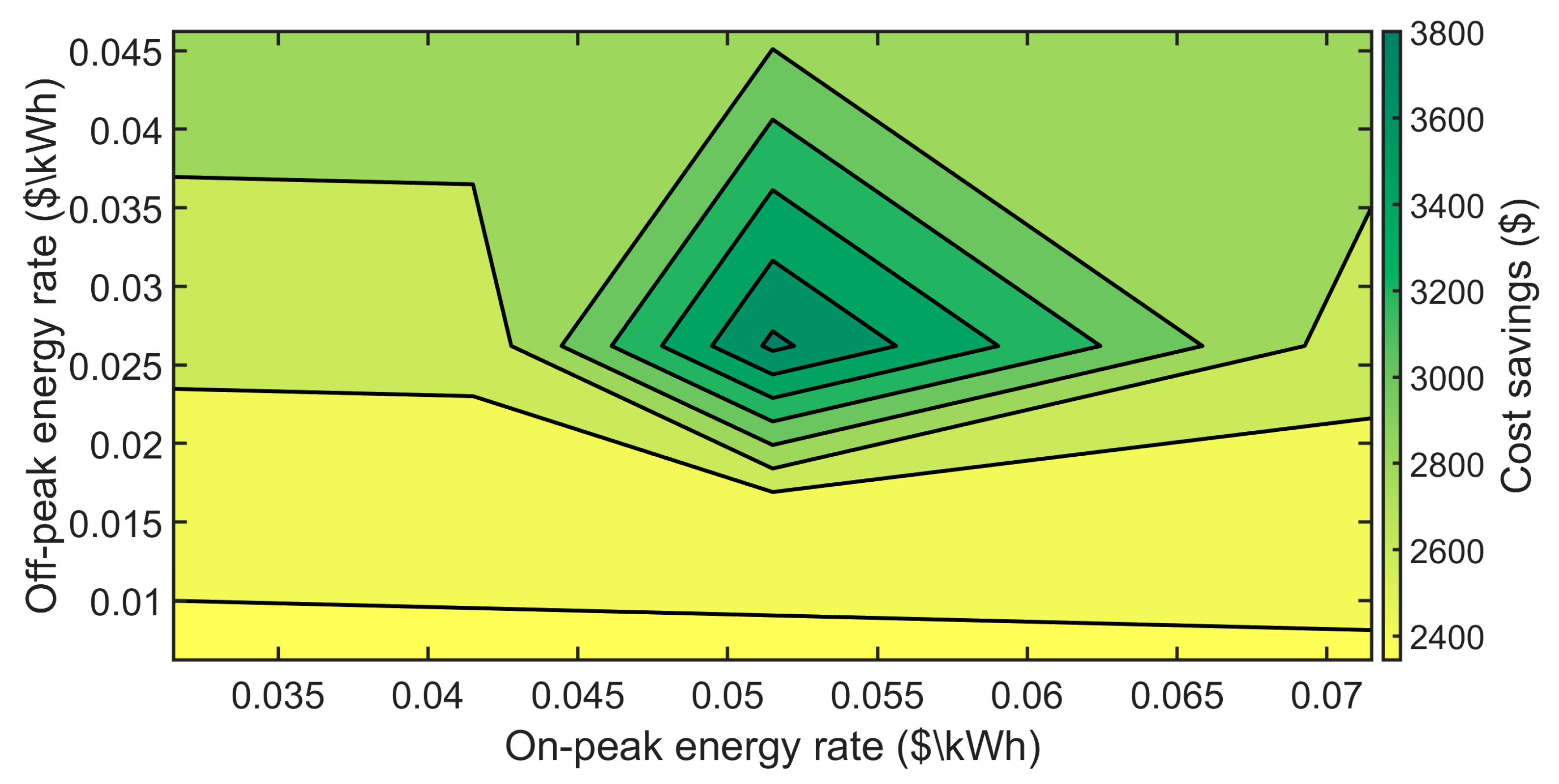
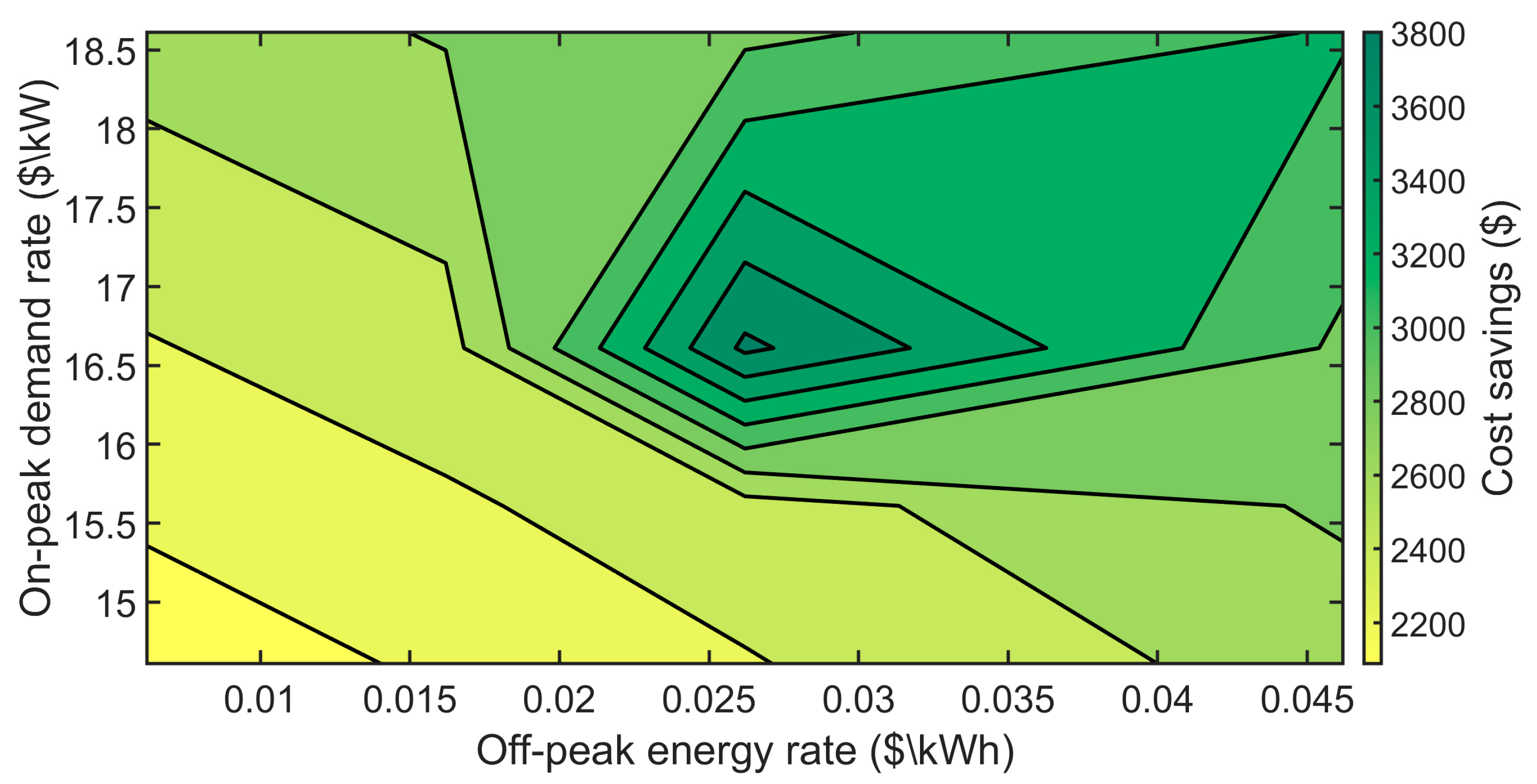
This study shows three scenarios of process implementation and compares the results of demand charges, highlighting the new application of having a smart controller with a given setpoint that maintains the power usage of an industrial facility using TES and VFDs of the chillers. The setpoint is chosen to achieve optimum energy savings for the facility, but the estimation of the setpoint should consider two points. Firstly, the setpoint could be so low that the tank would be over-discharged. In this case, the process will be forced to follow the ordinary process scheme and the chillers will charge the tank during the times when they are not supposed to. The second point is that choosing a high setpoint could lead to the facility losing potential savings that could be provided by the tank. The two proposed scenarios can contribute to the utility grid production problem and cooperate with the utility provider to have a flexible demand usage based on the grid [
32]. The three implemented scenarios are listed in
Table 1.
2. Methods
2.1. Process Scenarios
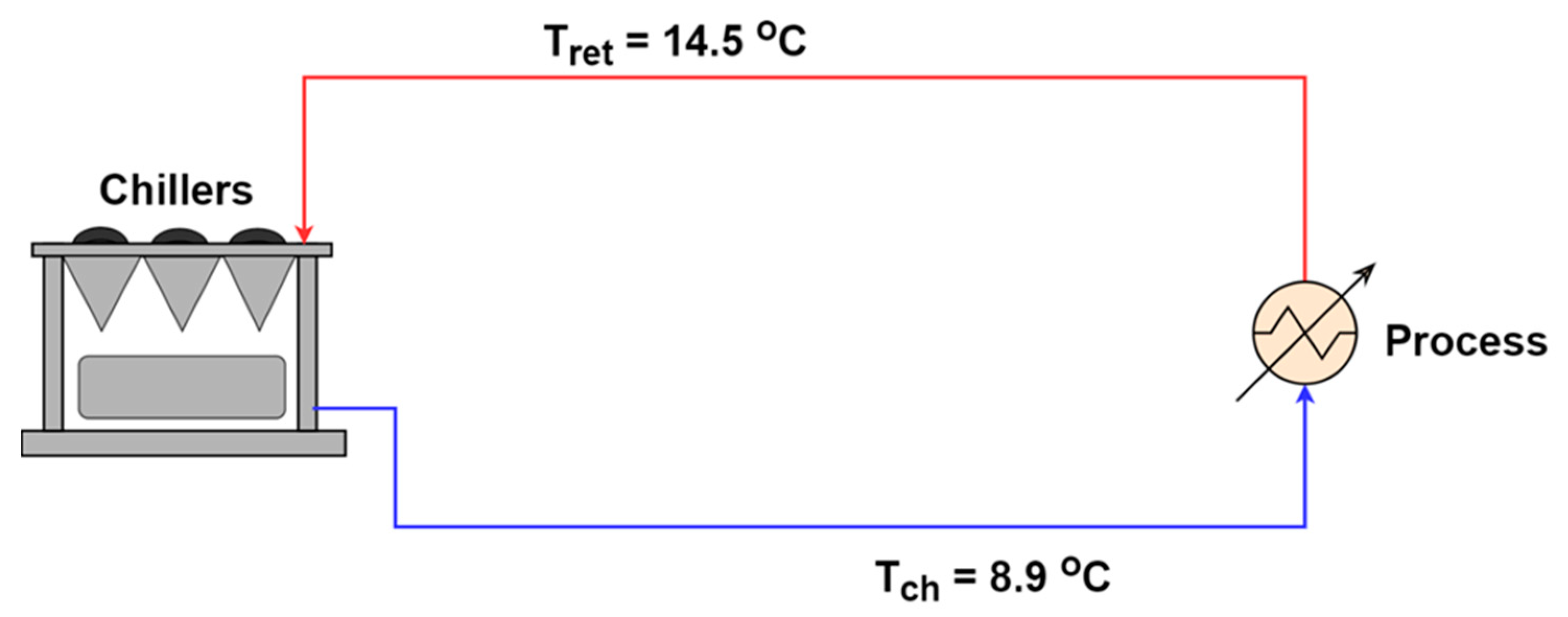
The facility uses air-cooled chillers to provide a continuous cooling load to the manufacturing process every day. The chillers provide chilled water at a temperature of 8.9 °C and a flowrate of 37.4 kg/s. The temperature difference across the chillers is ∆T = 5.6 °C and the return water temperature is 14.5 °C. This study compares three different scenarios for the process scheme with two of them having TES employed.
In the first scenario, “Baseline process”, the chillers provide the required cooling load (kWth) to the process. It is assumed that the process cooling load is constant and the chillers directly match the cooling load by varying their VFDs throughout the day as shown in
Figure 1.
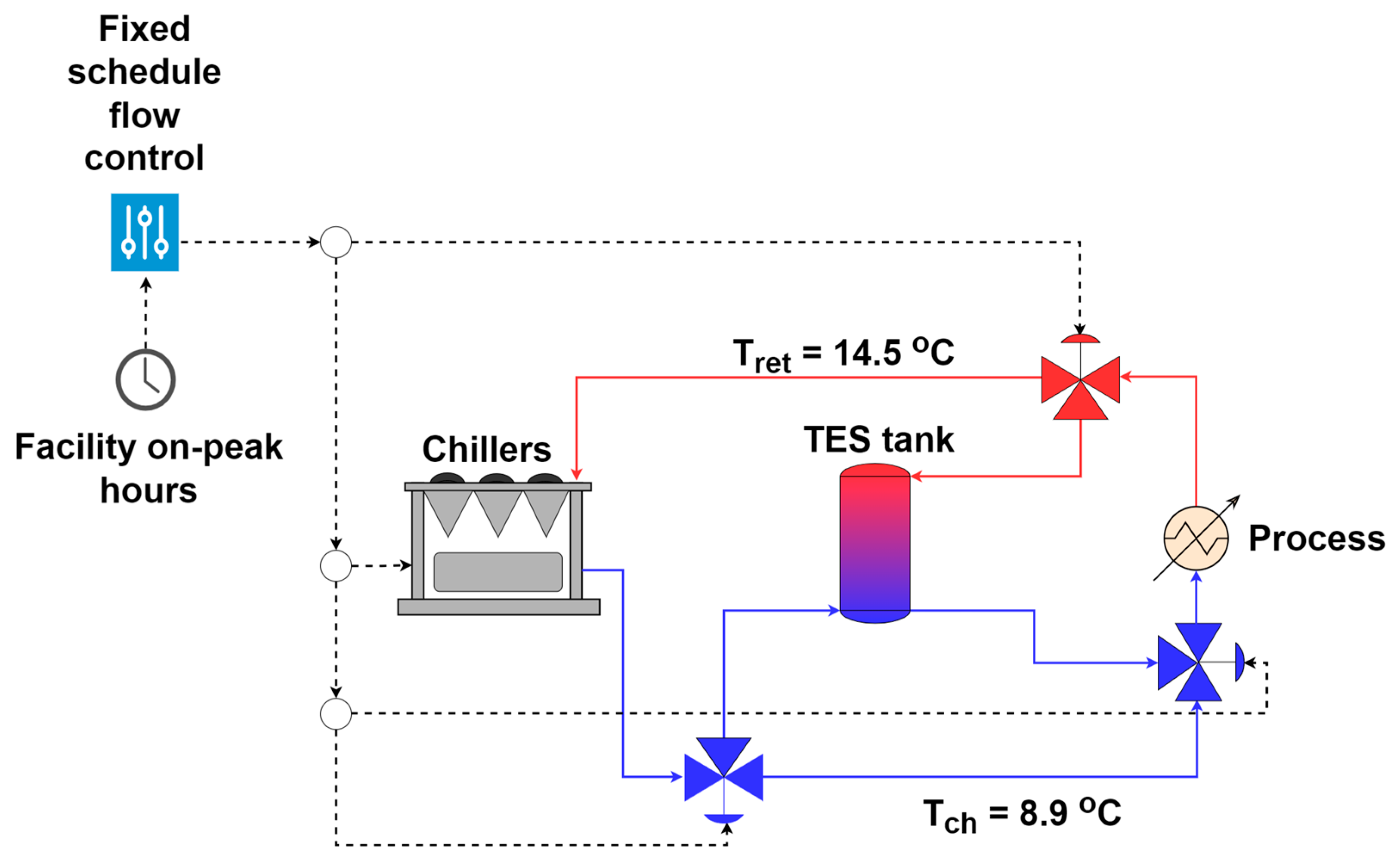
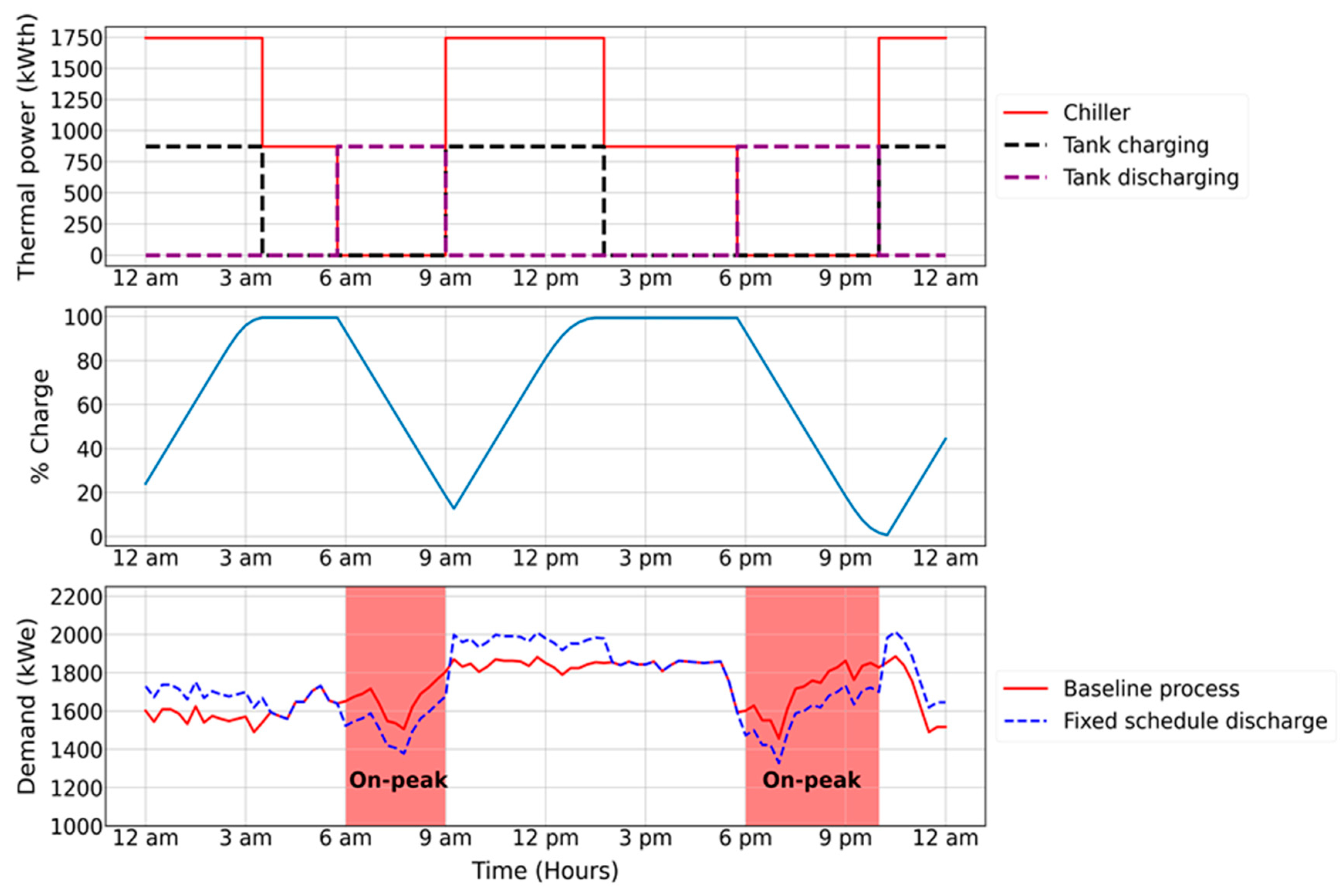
The second scenario, “Fixed schedule discharge”, utilizes TES to provide the cooling load (kWth) during on-peak hours. During off-peak hours, the chillers charge the tank and provide the required cooling to the process in which the chillers are using more electric load (kWe) to do both.
The fixed schedule of discharging and charging varies based on the electric rate schedule of the facility, which is set by the electric utility provider (as described in
Section 2.3). Different rate schedules determine when facilities undergo schedules for on-peak and off-peak hours. For the facility studied in this paper, their rate schedule has on-peak hours occurring for seven hours divided into two different periods (from 6 a.m. to 9 a.m. and from 6 p.m. to 10 p.m.) during the months from October to May referred to as the winter schedule. During the months from June to September, the on-peak hours occur as seven continuous hours from 3 p.m. to 10 p.m. and this schedule is referred to as the summer schedule. During the winter schedule, the tank can serve the cooling load (kWth) to the process during the two different on-peak hour periods. During the summer schedule, the tank provides 60% of the required cooling load (kWth) to the process and the rest is provided by the chillers. The “Fixed schedule discharge” scenario has a logic controller as shown in
Figure 2 that changes its action according to the fixed schedule discussed above. The controller charges the tank during off-peak hours in which the chillers use around double the usual electric load (kWe) to charge the tank and provide the cooling load (kWth) to the process.
The controller discharges the tank and turns off the chillers during on-peak hours of the winter schedule and relies solely on the tank to provide the cooling load (kWth) to the process. During the summer schedule, the controller ramps down the chillers to provide 40% of the cooling load (kWth) and the rest is supplied by the tank to meet the required cooling load of the process.
If the tank is fully charged, the controller will operate the process under the baseline process scenario during off-peak hours.
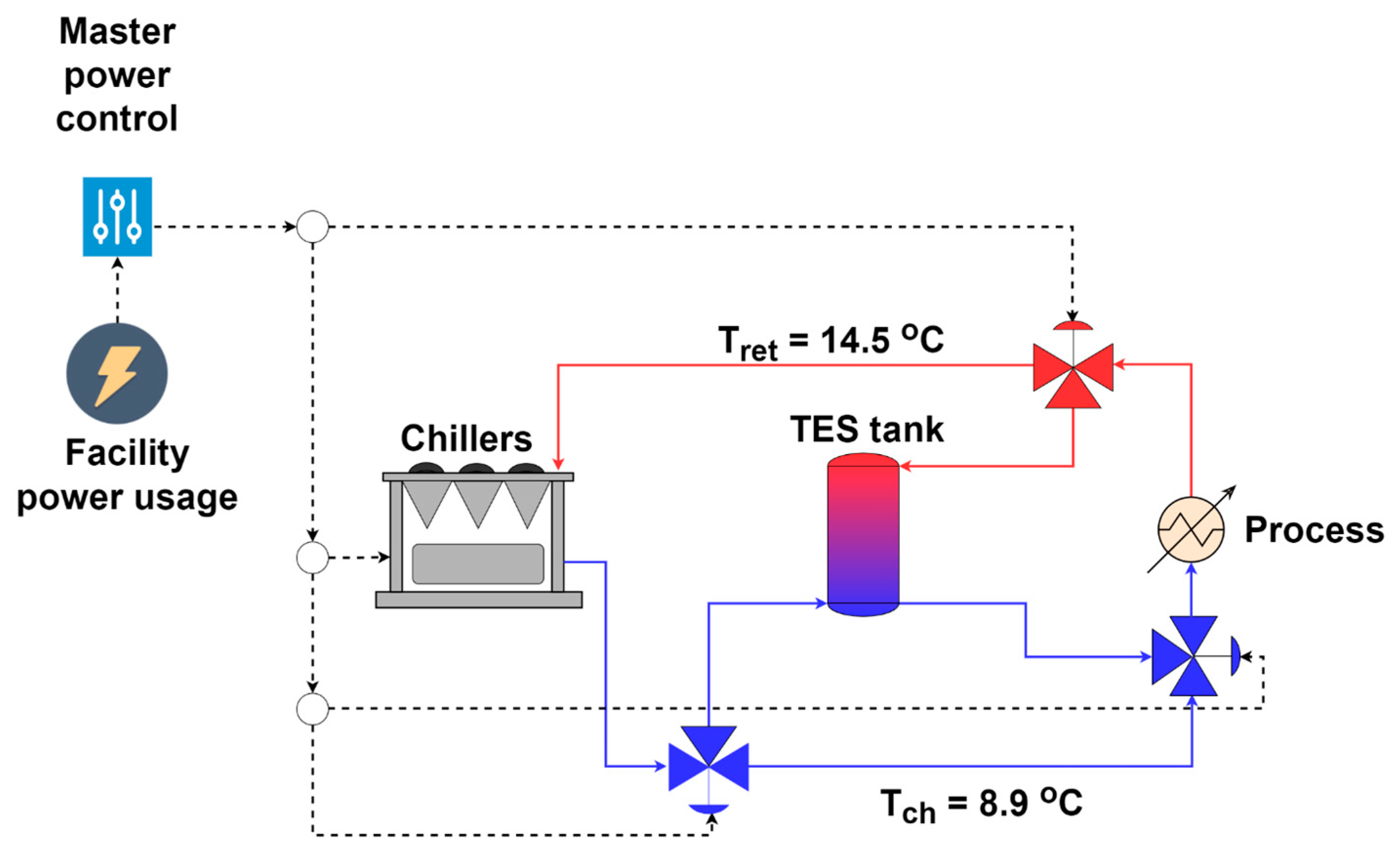
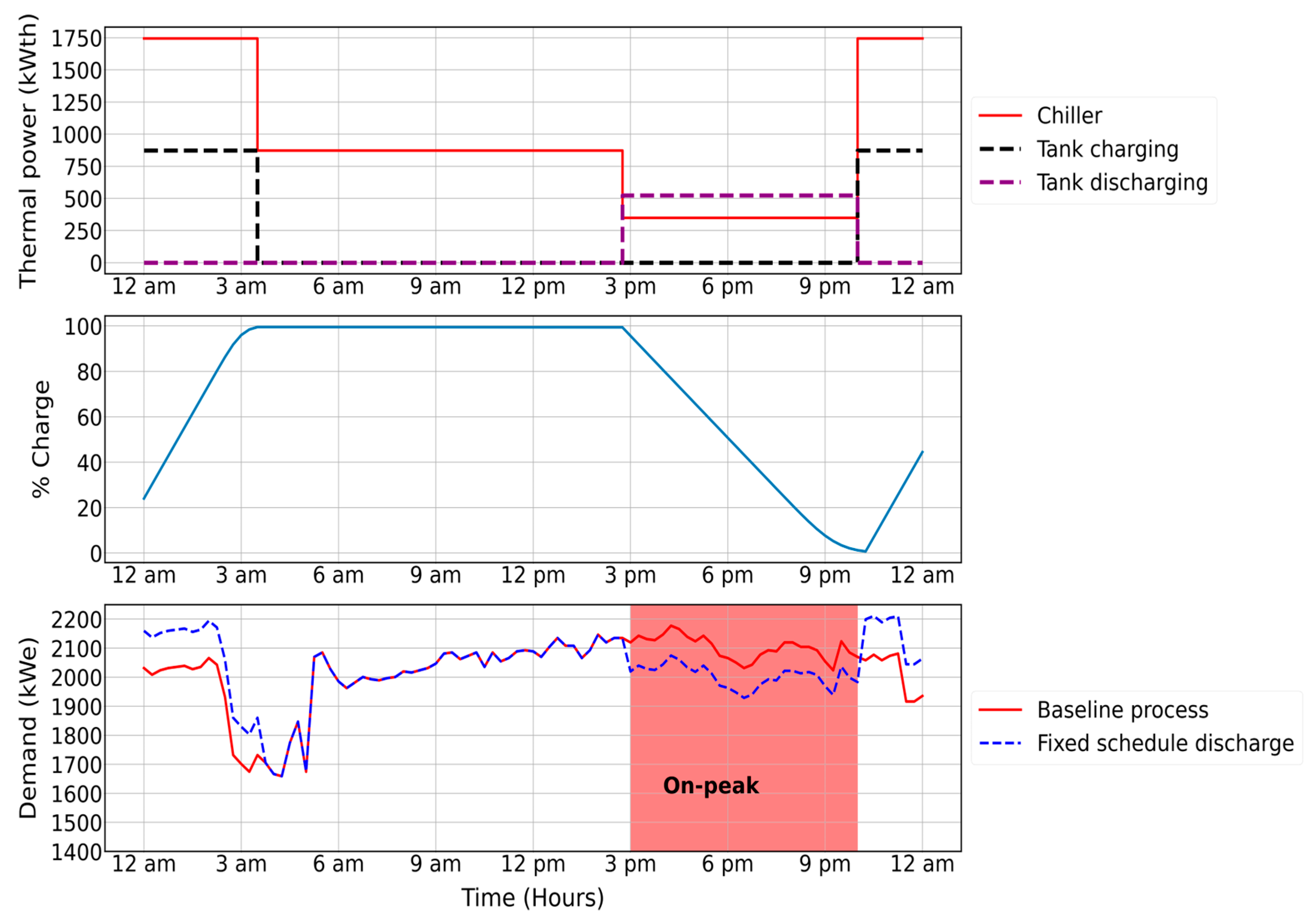
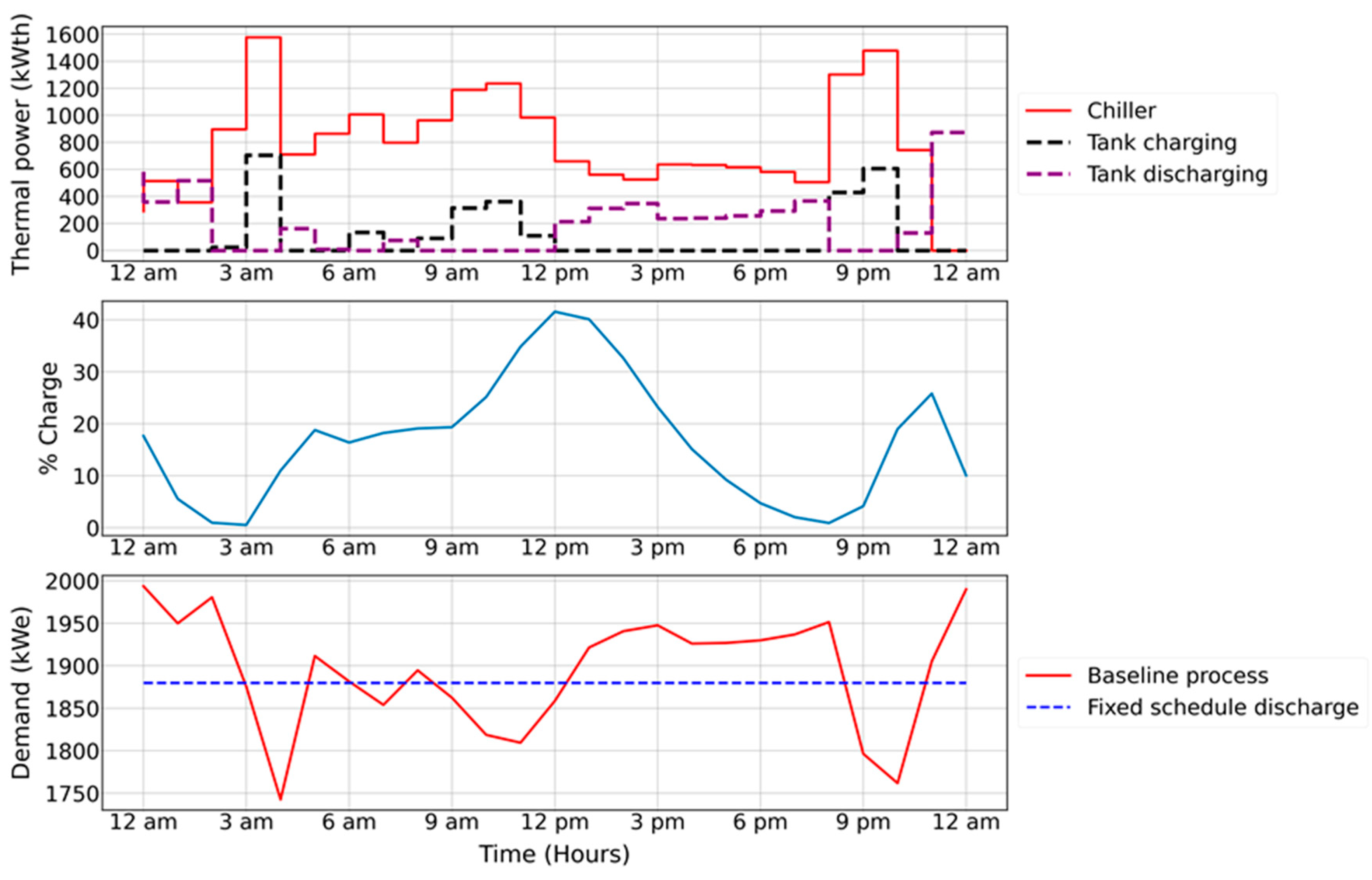
“Smart discharging” employs a smart controller as shown in
Figure 3 to manipulate the VFDs of the chillers based on the facility’s real-time demand and the setpoint given to the controller, allowing for flexible charging and discharging of the tank. The control actions in this scenario differ from the “Fixed schedule discharge” scenario. The charging and discharging rates are not constant and can be adjusted based on the current power usage of the facility and the deviation from the setpoint.
Charging of the tank occurs when the facility’s power consumption is less than the setpoint of the controller; in this case, the chillers are using more load to charge the tank and provide the required cooling load (kWth) to the process. The electric load (kWe) used to charge the tank is equal to the difference between the setpoint and the transmitter reading.
Discharging of the tank occurs when the facility’s power consumption is higher than the setpoint and the difference between them is high enough that the controller will turn off the chillers and utilize the tank to provide the required cooling load (kWth) to the process.
Smart discharging occurs when the difference between the transmitter reading and the setpoint is not high enough. To meet the setpoint, the controller will ramp down the chiller load and discharge the tank with the difference between the transmitter reading and the setpoint to provide the required cooling load (kWth) to the process using both the chillers and the tank.
If the facility power consumption is equal to the setpoint or the tank is fully charged, the smart controller will employ the baseline process scenario.
The setpoints are chosen based on the historical data provided by the facility, with each month having its setpoint. The setpoint is chosen so that it avoids the over-discharge of the tank and, in this case, the chillers will use more electric load (kWe) to charge the tank, which will increase the facility’s power usage, or the process will be forced to follow the baseline scheme because the tank cannot provide the required cooling load (kWth). In the instance of choosing a high setpoint, this will lead to losing some potential savings from using the tank to achieve demand charge savings.
2.2. TES Tank Modeling
TES tank modeling has been studied by various researchers and different modeling approaches have been proposed using a varying number of nodes [
33,
34,
35,
36]. The accuracy of temperature profiles and the issue of numerical diffusion are greatly influenced by the number of nodes used. An increase in the number of nodes reduces the numerical diffusion effect but also leads to longer simulation times [
33,
34]. To investigate the impact of numerical diffusion, researchers have employed various numbers of nodes and observed the effect on the temperature profiles. In our study, a one-dimensional model equation with 100 nodes is used in this study to simulate the temperature variations at each node of the TES tank and generate a temperature profile. Equation (1) is used to model the temperature of the tank at each node:
The energy rate of change for each node is represented by the term on the left hand side of the equation, which depends on several factors, including the density of water at node (i) denoted as
[
37] in which the density varies with the temperature; the specific heat capacity of water denoted as C
p [
37]; the incremental height ∆z, which is the height of each node calculated using the tank height Z and the number of nodes N, also plays a role in this term and is calculated in
Appendix A. On the right-hand side of the equation, the first term represents the heat loss to the ambient air, where U is the overall heat transfer coefficient to the ambient air [
19] and P is the perimeter of the node. The second term represents heat transfer by conduction, with k representing the thermal conductivity coefficient [
37]. The last two terms represent the energy of charging and discharging the chilled water going to the process. These two energies are calculated based on upwind energy balance calculations. The (i − 1) node appears in the charging term because the flow is upward, so the upwind node here is (i − 1) with reference to (i), while (i + 1) is used for discharging because of the downward flow, so the upwind node is (i + 1) with reference to (i). Equations (2) and (3) calculate the temperatures at the bottom and top nodes, respectively, which are the boundaries of the tank. The coefficient
arises from the assumption that the wall temperature is equal to the water temperature, with the wall being located at a distance of
, leading to the usage of the mentioned coefficient [
34].
The parameters used in the three equations are listed in
Appendix A. The tank model uses N = 100 nodes in which the numerical diffusion does not have a significant impact and, at the same time, the simulation time is about 15 min. For further clarifications and comparisons of results obtained by varying node numbers, refer to previous studies [
33,
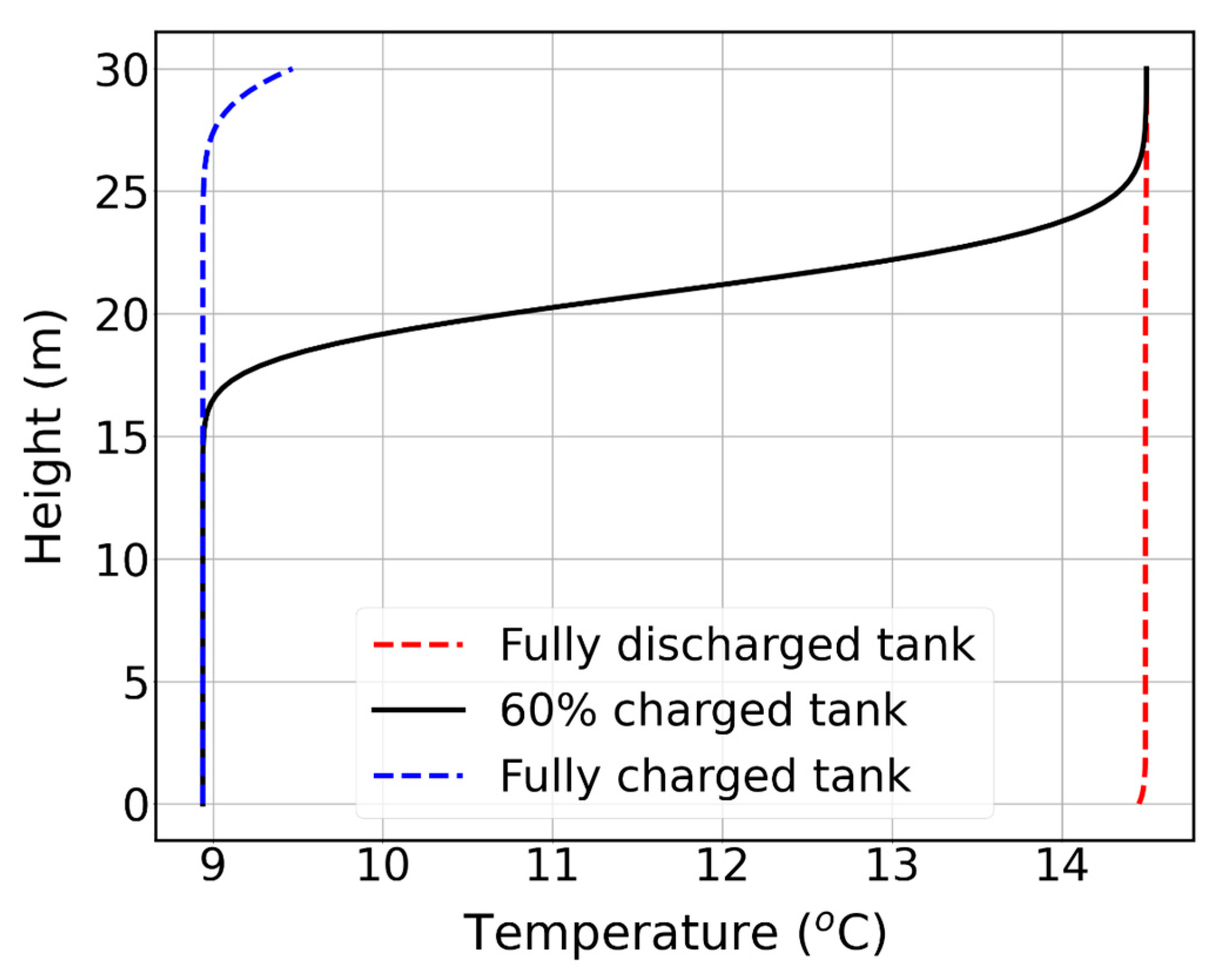
34]. A graphical representation of the tank temperature profile as a function of height is shown in
Figure 4 and
Figure 5.
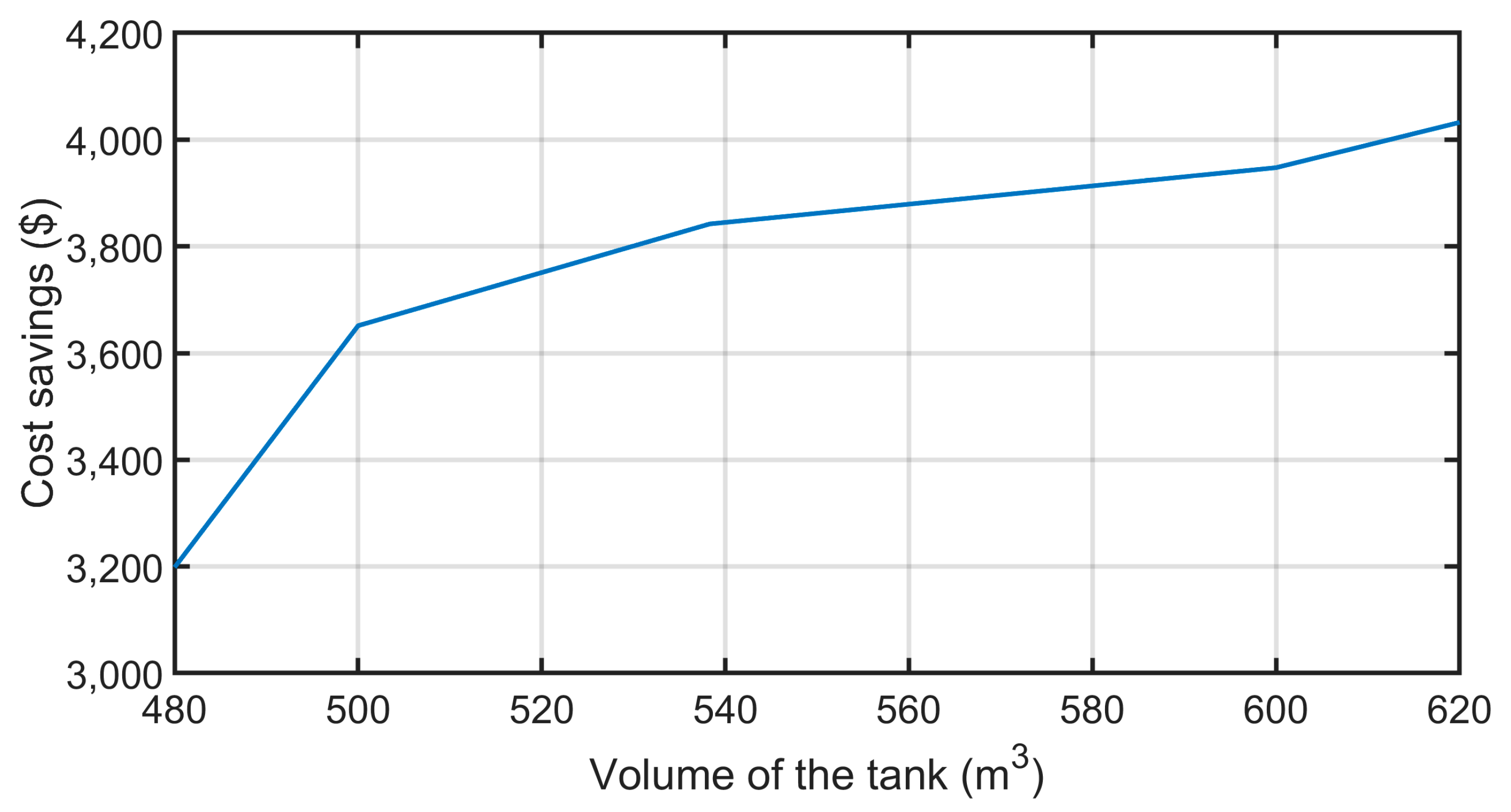
The charging temperature of the tank is 8.9 °C while the return temperature from the process to the tank is 14.5 °C. The tank is designed to meet the process cooling requirements for a duration of 4 h, which are the on-peak hours (
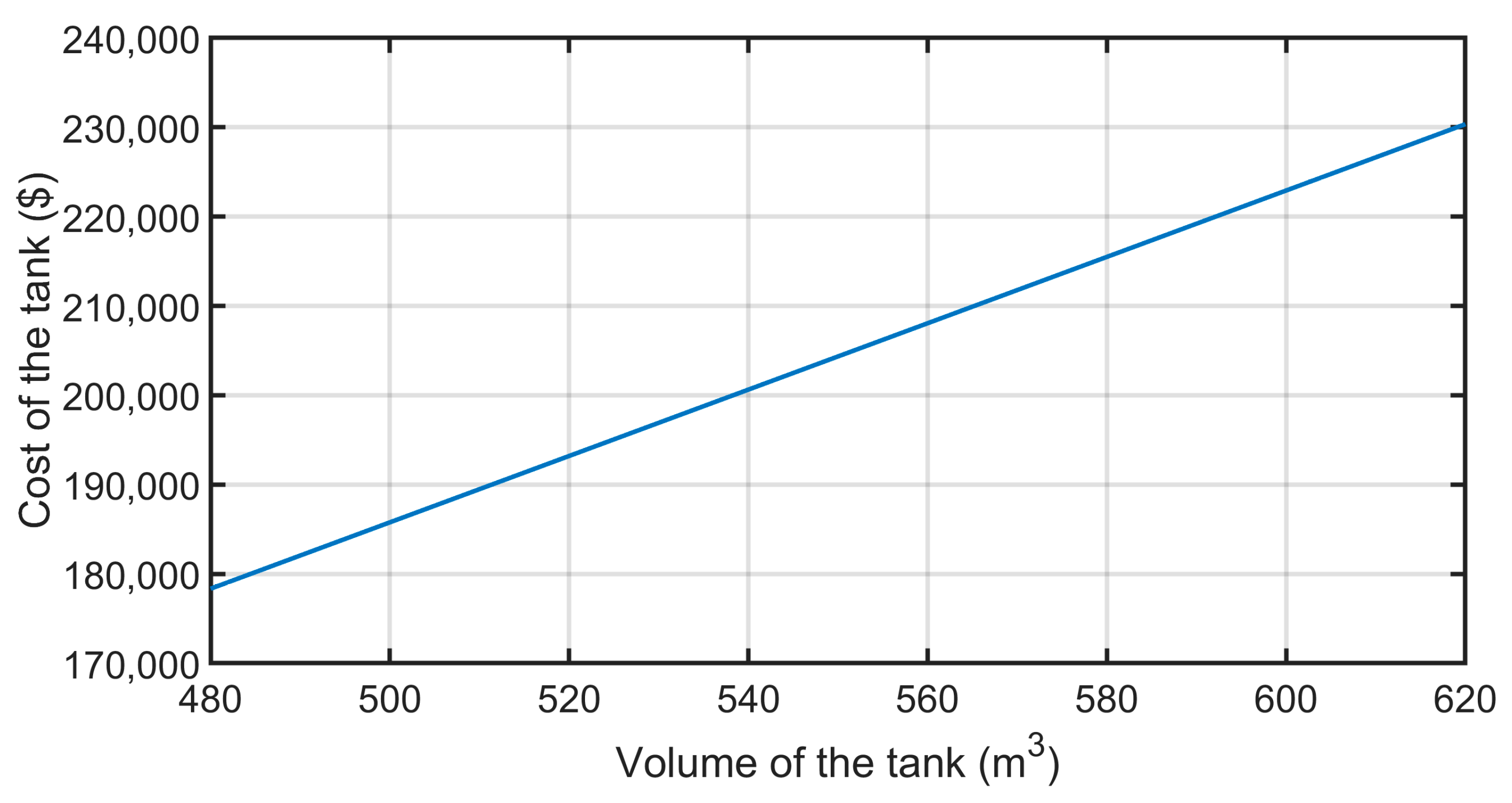
Section 2.3). As a result, it has a height of 21.5 m and a diameter of 5.7 m. The height and diameter are determined using the typical industrial aspect ratio AR = 3.8, which is the ratio between the height and the diameter [
38].
2.3. Facility Data
This study utilizes utility data obtained from the facility for 2022 year total energy usage. The data provided by the facility include the electricity usage in kilowatt-hours (kWh) totaled every 15 min. The specific charges for each category according to the facility’s rate schedule are presented in
Table 2. The cooling load (kWth) required for the facility’s process is estimated to be 873 kW, based on on-site data collection.
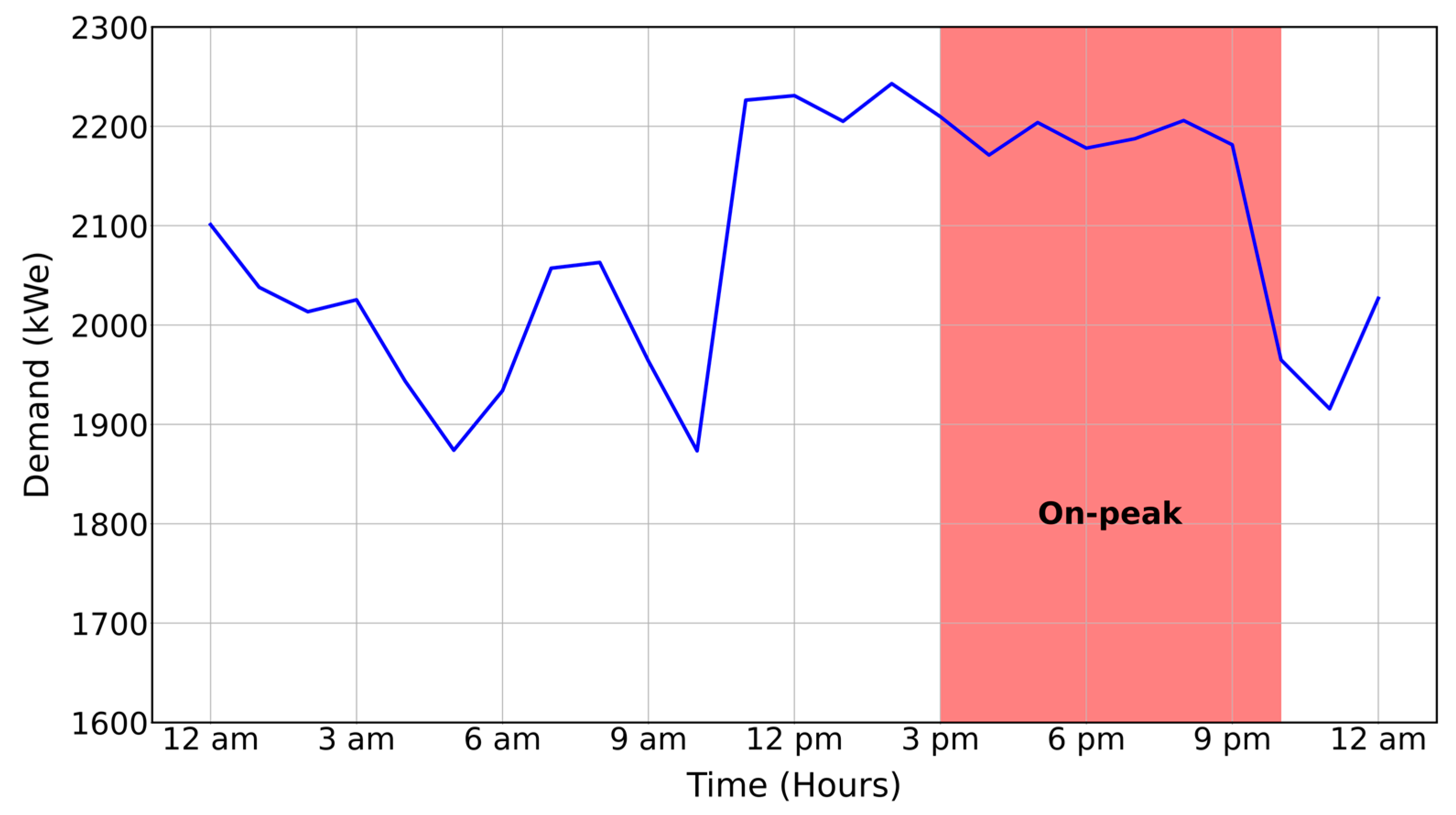
Figure 6 provides an example of a facility demand profile on a representative day in the summer schedule, with the shaded area representing the kW values for on-peak hours, and the area under the curve here would be kWh usage during on-peak hours. Using the same means, off-peak kWh usage can be calculated. On-peak demand charges are calculated using the peak kW usage during on-peak hours multiplied by the charges of the facility, which are listed in
Table 2.
2.4. Chiller Model
The chillers in this facility are air-cooled chillers with VFDs on their compressors. In this study, the chiller model is created based on the chiller datasheet provided by the facility (
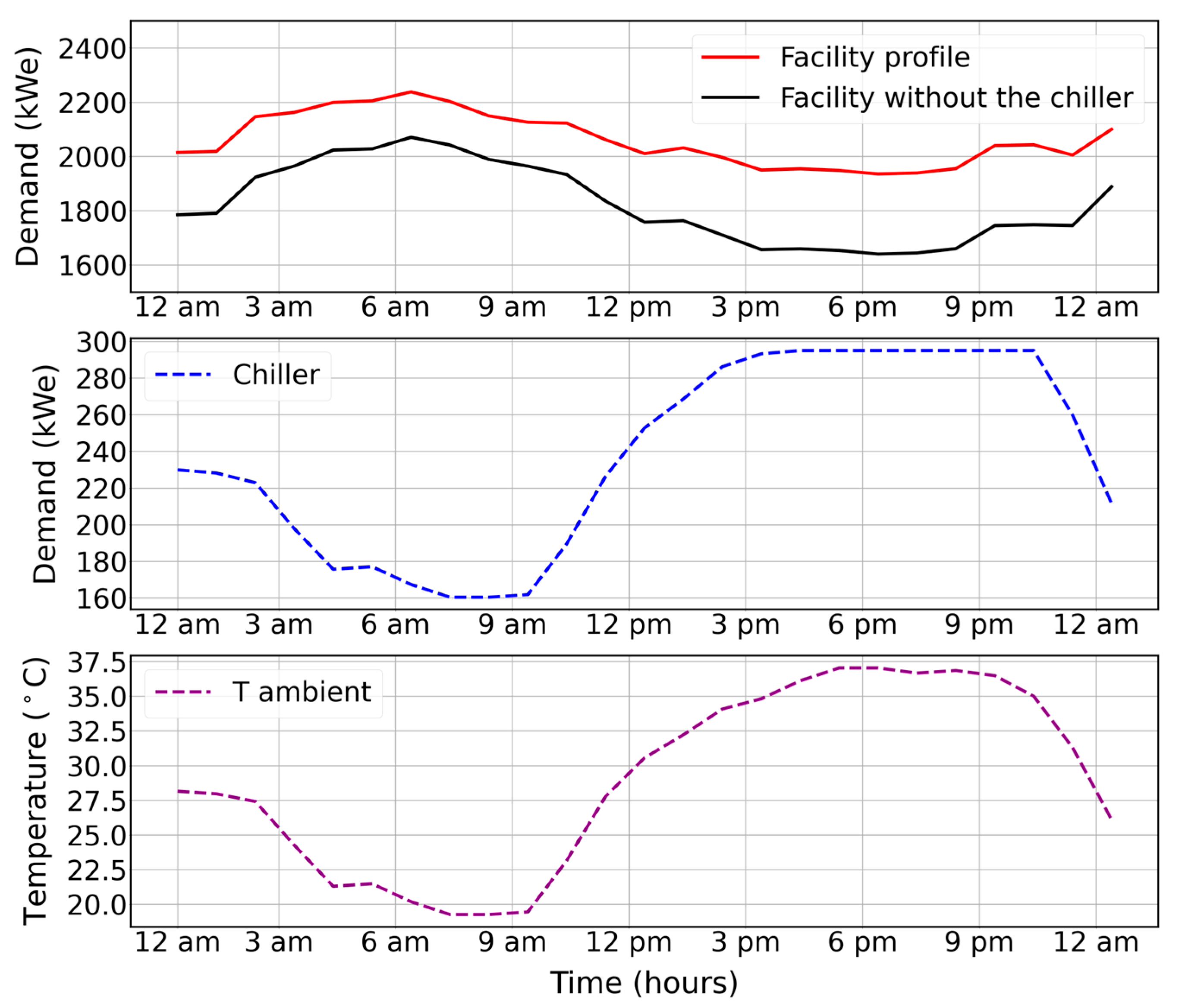
Table 3). The model utilizes ambient air temperature as an independent variable to calculate the electric load in (kWe) required by the chiller based on the cooling needs (kWth) of the facility. The chiller’s electric load (kWe) and thermal load (kWth) are directly proportional to ambient air temperature, with higher temperatures requiring more electric power (kWe) from the chiller to meet the cooling load (kWth).
The chiller model is created using a 2D interpolation function to generate a load profile for the chiller based on the ambient air temperature and the required cooling load for the process, as shown in
Figure 7. The model provides upper and lower limits for kWe usage, regardless of variations in ambient air temperature. This model is a critical parameter in achieving results and savings for the case study, as the chillers use more kWe during off-peak hours to charge the tank and less power during on-peak hours when the tank provides the necessary cooling load (kWth) to the process. The chiller model plays a crucial role in both the “Fixed schedule discharge” and “Smart discharging” process schemes discussed in
Section 2.1. After creating the chiller model and generating a load profile for the entire study period, a baseline is established by subtracting the chiller load profile from the facility profile data to be used in the two proposed scenarios calculations, as demonstrated in
Figure 8. The three process scenarios along with the TES tank are simulated using Simulink in MATLAB with solver ode23s.