Pseudopotential Lattice Boltzmann Model for Immiscible Multicomponent Flows in Microchannels

Abstract

To investigate droplet formation in a microchannel with different walls, simulations were conducted based on a pseudopotential model using the exact difference method force scheme. The variable surface tension was obtained using Laplace’s law, and the static contact angle was estimated using a first-order linear equation of the corresponding control parameter of the model. The droplet motion in microchannels was simulated using our model, and the effects of surface wettability and the Bond number on the droplet motion were investigated. The droplet motion for the intermediate microchannel wall took a significantly shorter time than that for the hydrophilic wall, and the wet length also depended on the contact angle. As the Bond number increased, the wet length of the droplet decreased on the hydrophilic surface. The droplet formation in a T-junction device was also simulated using the proposed model, and the effects of the capillary number and viscosity ratio on droplet formation were discussed in detail, and some empirical correlations between the capillary number and dimensionless droplet length are presented according to different viscosity ratios. The three flow patterns of droplet formation were categorized by the different capillary numbers as the dripping–squeezing, jetting–shearing, and threading regimes. In the dripping–squeezing regime, the droplet volume was nearly independent of the viscosity ratio, but the viscous effect was more prone to occur in the jetting–shearing regime. In the jetting–shearing regime, as the capillary number increased, the effect of the viscosity ratio on droplet formation became more significant.

1. Introduction

Liquid–liquid multicomponent flows in microchannels exist widely in many fields, including chemical synthesis, oil recovery [1,2,3,4,5], lab-on-chip microfluidic applications [6,7,8,9,10], and microchemical reactions [11,12,13,14]. Many conventional computational fluid dynamics (CFD) approaches have been used to simulate multicomponent flows in microchannels by solving the macroscopic Navier–Stokes equations [15]. These methods are based on interface tracking, such as the front tracking method [16], and interface capturing, such as the volume of fluid (VOF) [17] and level set methods [18]. These methods can be used to simulate multicomponent flows, but it is difficult to track complex flows between molecules [19]. The Lattice Boltzmann method, a mesoscopic method, is very powerful in solving multicomponent flows due to its statistical representation of kinetic theory, easy implementation, and low computational cost [20,21]. The LB method of multiphase flows is usually classified into four types: pseudopotential [22,23,24], free-energy [25], color-gradient [26], and kinetic-theory-based models [27,28]. Since the deformation of interfaces is more accurate and simulation is more effective [29] in the pseudopotential model, it is suitable for modeling multicomponent flows in microchannels. To avoid unphysical slip boundary condition, an external force is considered to improve this boundary condition in LBM [30]. In addition, the heat transfer has also been focused since it is important to microfluidic devices, i.e., heat exchangers. The heat transfer and Pseudoplastic flow of non-Newtonian fluid in a microchannel were investigated using LBM, and the slip velocity enhances the convection heat transfer [31]. The mixed convection of water/nanofluid in a two dimensional microchannel was studied using LBM considering the effects of buoyancy forces on nanofluid slip velocity, and the most heat transfer rate is obtained under higher amounts of nanoparticles mass fraction and small slip coefficient [32]. Furthermore, a uniform magnetic field was applied to investigate the conjugate heat transfer of water/Ag nanofluids in a microchannel with the hydrophobic surface, and when Hartmann number is 30, the Nusselt number increases up to 20% [33]. In addition, the geometric size also influences the heat transfer and flow characteristics [34], and open microchannel has better thermal performance than closed one [35]. Instabilities of flow in microchannels are also important features, and different to macro channels, flow in microchannels is more likely to form instabilities [36]. To investigate the instabilities of flow, Yogesh etc. [37] conducted a series of experiments and found that they reduced significantly in segmented finned channels due to easy passage of bubbles.

Despite significant research progress, multicomponent flows in microchannels provide major challenges to the modeling approach. Many methods, such as the free-energy and color-gradient models, are mainly adopted to model droplet formation. In addition, the pseudopotential LB model is usually applied to investigate the impingement of droplets on the liquid film near the wall [38,39]. However, to the best of the authors’ knowledge, the pseudopotential model of the Lattice Boltzmann method has not yet been applied to investigate droplet formation in microchannels. In this study, the pseudopotential model based on the exact difference method (EDM) force scheme is used to model droplet motion and droplet formation in microchannels. The rest of this study is organized as follows: In Section 2, the pseudopotential model and EDM force scheme are discussed in detail. In Section 3, the present model is validated, and some simulations are represented. Laplace’s law is used to determine the surface tension. A droplet in two flat plates is applied to analyze the interrelation between the static contact angle and relevant parameters in the LB model. Two-component Poiseuille flow is employed to validate the viscous effect. In Section 4, the droplet motion and formation are investigated in detail. In Section 5, we summarize our main findings as conclusions.

2. Numerical Method

2.1. Pseudopotential Lattice Boltzmann Model for Immiscible Fluids

Using the pseudopotential LB model with an interaction force, the particle distribution evolution was obtained by the following equation:

$$f_i^{\alpha }(x+e_i\Delta t,t+\Delta t)=f_i^{\alpha }(x,t)+{\Omega }_i^{\alpha }+K_i^{\alpha }$$

(1)

where $f_i^{\alpha }$ is the density distribution function of the αth component fluid at lattice node x; ${\Omega }_i^{\alpha }$ is the αth component fluid collision term, which describes the relaxation of density distribution functions towards the equilibrium states; $K_i^{\alpha }$ is the interaction force, which includes both the fluid–fluid and fluid–solid interaction forces; and α is an index for components, which is set as α = {1, 2} for simplicity. We used the classical lattice BGK collision operator owing to its simplicity and low computational cost:

$${\Omega }_i^{\alpha }=-\frac{1}{{\tau }_{\alpha }^{}}\left(f_i^{\alpha }-f_i^{\alpha ,eq}\right)$$

(2)

where τ_α is the αth component relaxation time.

For simplicity, we used the D2Q9 lattice model on a uniform square 2D lattice to analyze the multicomponent flow when Δx = Δt = 1 [40,41]. This model has nine velocities and is widely applied in 2D simulations [42,43]. Although the D2Q9 lattice model with eighth-order isotropy could not reduce the spurious current enough [44], when the droplet moves quickly in microchannels, the spurious currents may have a limit influence on the droplet dynamics. The lattice velocity was obtained as

$$e=\left[\begin{array}{ccccccccc}0& 1& 0& -1& 0& 1& -1& -1& 1\\ 0& 0& 1& 0& -1& 1& 1& -1& -1\end{array}\right],$$

(3)

The equilibrium density distribution function was obtained as

$$f_i^{\alpha ,eq}\left({\rho }^{\alpha }(x),u^{\alpha ,eq}\right)={\rho }^{\alpha }(x)w_i\left[1+3e_i\cdot u^{\alpha ,eq}+\frac{9}{2}(e_i\cdot u^{\alpha ,eq})-\frac{3}{2}{(u^{\alpha ,eq})}^2\right],$$

(4)

where w_i is the weigh factor in the D2Q9 model and is defined as

$$w_i=\{\begin{array}{c}4/9\\ 1/9\\ 1/36\end{array}\begin{array}{cc}& \end{array}\begin{array}{c}i=0\\ i=1,\dots ,4\\ i=5,\dots ,8\end{array},$$

(5)

The density ${\rho }^{\alpha }$ and velocity u^α of the αth component fluid and mixture flow velocity u can be obtained from the following equations

$${\rho }^{\alpha }={\displaystyle \sum _i{f}_i^{\alpha }}, u^{\alpha }={\displaystyle \sum _i{e}_i\cdot f_i^{\alpha }/{\rho }^{\alpha }}, \mathrm{and} u={\displaystyle \sum _{\alpha }{u}^{\alpha }},$$

(6)

The relaxation time τ_α is related to the kinematic viscosity of the αth component fluid by

$${\nu }_{\alpha }=\frac{1}{3}\left({\tau }_{\alpha }-\frac{1}{2}\right),$$

(7)

To achieve better accuracy of the multicomponent flow, Guo’s force scheme [45] and the EDM [46] are usually used to incorporate the fluid–fluid interaction force of other component fluids and fluid–solid interaction force of solid nodes acting on the αth component fluid and body force. The equations of Guo’s force term and the EDM are written as

$$K_i^{\alpha }=\left(1-\frac{1}{2{\tau }_{\alpha }}\right)w_i\left(3(e_i-u_{\alpha }^{eq})+9(e_i\cdot u_{\alpha }^{eq})e_i\right)\cdot F_{\alpha },$$

(8)

$$K_i^{\alpha }=f_i^{\alpha ,eq}({\rho }_{\alpha },u_{\alpha }^{eq}+\Delta u_{\alpha })-f_i^{\alpha ,eq}({\rho }_{\alpha },u_{\alpha }^{eq}),$$

(9)

The macroscopic equilibrium velocity $u^{\alpha ,eq}$ was computed to be

$${\rho }_{\alpha }{u}^{\alpha ,eq}={\displaystyle \sum _i{e}_i{f}_i^{\alpha }(x,t)+\frac{\Delta t{F}_{\alpha }}{2}},$$

(10)

The pseudopotential LBM was first mentioned by Shan and Chen [47] and is widely used for multicomponent flows. Compared with the original force term of the Shan–Chen model, both Guo’s force scheme and the EDM offer better features. Although Guo’s force term can be totally derived from the Boltzmann equation using the Chapman–Enskog expansion, the prediction of the EDM is more stable than that of Guo’s force scheme [24]. Therefore, we chose the EDM to incorporate forces.

2.2. Interaction Force for Immiscible Fluids

In Lattice Boltzmann methods, all the different components are simulated using the same collision and streaming process. Therefore, the interfaces between different fluids are represented by several lattice nodes, wherein the density varies smoothly from one to another and is controlled by the interaction force. The fluid–fluid interaction force [47,48] between a central node and its surrounding nodes was deduced to be

$$F_{\alpha ,int}=-G_c{\psi }_{\alpha }(x,t){\displaystyle \sum _{i}w(\left|e_i\right|){\psi }_{\overline{\alpha }}}(x+e_i\Delta t,t)e_i,$$

(11)

where α and $\overline{\alpha }$ denote the different components. G_c is a parameter controlling the interaction strength between the different components and determining attractive or repulsive interactions. ψ is the effective density and is defined as

$$\psi =\rho ,$$

(12)

Spurious currents occur due to the insufficient isotropy of the discrete gradient in Equation (11) [47]. Therefore, higher-order isotropy is used to compute the discrete gradient term. However, this leads to using more surrounding nodes to calculate the fluid–fluid interaction force, which increases computational cost and reduces the parallel level. In this study, we chose the eighth-order scheme for the pseudopotential multicomponent model.

The fluid–solid interaction force acting on the αth component fluid determined fluid wetting, spreading properties, and the contact angle and was deduced to be

$$F_{\alpha ,ads}=-G_{\alpha }{\psi }_{\alpha }(x,t){\displaystyle \sum _{i}w(\left|e_i\right|)s}(x+e_i\Delta t)e_i,$$

(13)

where s (x + e_iΔt) is an indicator, which either equals to 1 for solid nodes or 0 for fluid nodes. G_α can adjust the strength between the fluid and solid nodes. A non-wetting fluid requires G_α < 0, while a wetting fluid requires G_α > 0. In this study, the sign of G_α varies in a two-component flow, wherein one fluid is non-wetting, and the other fluid is wetting.

Moreover, the body force was deduced to be

$$F_{\alpha ,b}={\rho }^{\alpha }g,$$

(14)

where g is the body force per unit mass.

Lastly, the total force was deduced to be

$$F_{\alpha }=F_{\alpha ,int}+F_{\alpha ,ads}+F_{\alpha ,b},$$

(15)

3. Model Validation

3.1. Validation of Surface Tension Using Laplace’s Law

Laplace’s law states that the pressure difference P_in − P_out between the inside and outside of a static droplet is linearly proportional to the inverse of the droplet radius r, and the coefficient is the surface tension σ. Laplace’s law is defined as

$$P_{in}-P_{out}=\frac{\sigma }{r},$$

(16)

In this section, we present a droplet (second component fluid) surrounded by the first component fluid and validate the current pseudopotential multicomponent model with different viscosity ratios using Laplace’s law. The grid size was 100 × 100 l.u.², the boundary condition was set to be periodic, and there was no body force application. The parameter G_c determined the surface tension in the LB model. In this simulation, four values of G_c (1.4, 1.5, 1.9, and 2.0) were used to obtain four values of surface tension. The densities both inside and outside of the droplet were initialized as one, and the viscosities inside and outside of the droplet were set to be 0.3 and 0.0712, respectively. After a steady droplet state was achieved, the interface width was approximately 4–5 lattices. The final radius of the droplet was measured, and the corresponding pressure was calculated using

$$P=c_s^2{\displaystyle \sum {\rho }_{\alpha }+\frac{1}{2}}{c}_s^2{\displaystyle \sum _{\alpha \ne \overline{\alpha }}{G}_c{\psi }_{\alpha }{\psi }_{\overline{\alpha }}},$$

(17)

where c_s is the lattice sound speed. The pressures inside (P_in) and outside (P_out) the droplet were calculated on the lattices that were away from the interface to avoid pressure variations. The radius was measured between the two centerlines of the interface, where the density was 0.5 (ρ₁ + ρ₂) along the central horizontal line. The corresponding results are shown in Figure 1, wherein the solid lines fit the simulation data well. The slopes of the linear fit lines are 0.041, 0.050, 0.092, and 0.101 (i.e., the surface tension) for G_c = 1.4, 1.5, 1.9, and 2.0, respectively. Thus, the surface tension increased as the value of G_c increased, and a variable surface tension was obtained, as shown in

Table 1. Parameter G_c vs. surface tension.

Value of Gc	1.4	1.5	1.9	2.0
Surface tension	0.041	0.050	0.092	0.101

.

3.2. Estimation of Static Contact Angle with a Droplet in Two Flat Plates

The contact angle is an important feature of both wetting and non-wetting fluids and can be predicted using the pseudopotential multicomponent model [38]. We used a static droplet near a flat plate to simulate its contact angle and set parameter G₂ = −G₁ to achieve a more accurate relationship of G₂ and the contact angle [38]. The grid size was 100 × 100 l.u.², and the second component of a 40 × 40 l.u.² rectangle near the wall was surrounded by the first. The no-slip boundary condition was applied for the top and bottom walls, while the periodic boundary condition was set for the left and right surfaces. The wet length, where the droplet touches the wall, and the height of the droplet are crucial to describe its formation. Therefore, after a stable state was achieved, the wet length (b) and height (h) of a semicircular droplet were measured. The semicircular radius was deduced to be

$$R=\frac{4h^2+b^2}{8h},$$

(18)

The contact angle of the droplet was then obtained to be

$$\theta =\{\begin{array}{cc}arcsin(\frac{b}{2R}),\hfill & \theta <{90}^{\circ }\hfill \\ \pi -arcsin(\frac{b}{2R}),\hfill & \theta \ge {90}^{\circ }\hfill \end{array},$$

(19)

As shown in Figure 2, the contact angle is adjusted by changing G₂ under different G_c values, and the relationship of G₂ and the contact angle with the viscosity ration is written by a first-order linear equation with G₂ ranging from −0.5 to 0.5; however, we must note that the contact angle ranges from ~30°–150° and cannot be measured accurately beyond this range. As G_c increases, the slope of the fit line decreases, but all fit lines have almost the same intercept, which is approximately 90°, indicating that the contact angle is 90° with G₂ being 0, regardless of G_c, as presented in

Table 2. Slopes and intercepts of linear fit lines of G₂ and the contact angle.

Value of Gc	1.4	1.5	1.9	2.0
Slope	108.99563	98.66357	60.73874	50.25828
Intercept	90.36321	90.74755	89.45507	89.82452

.

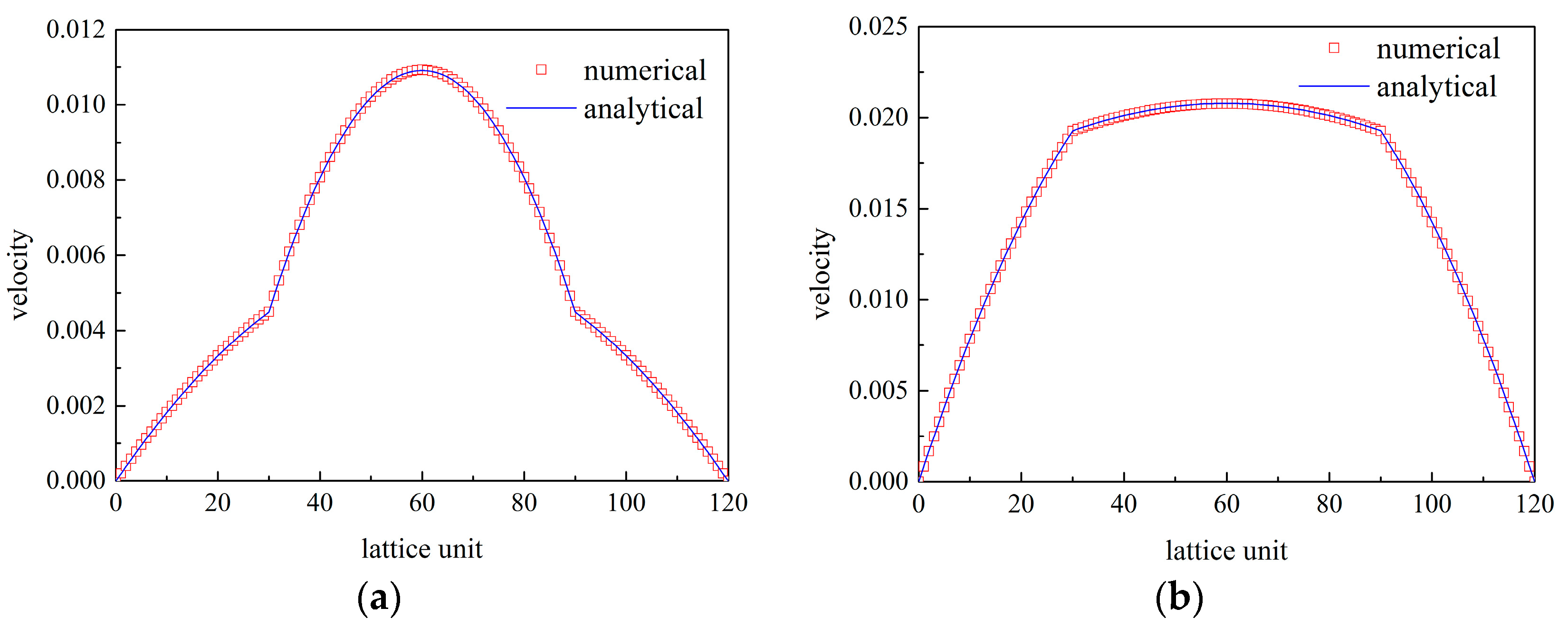
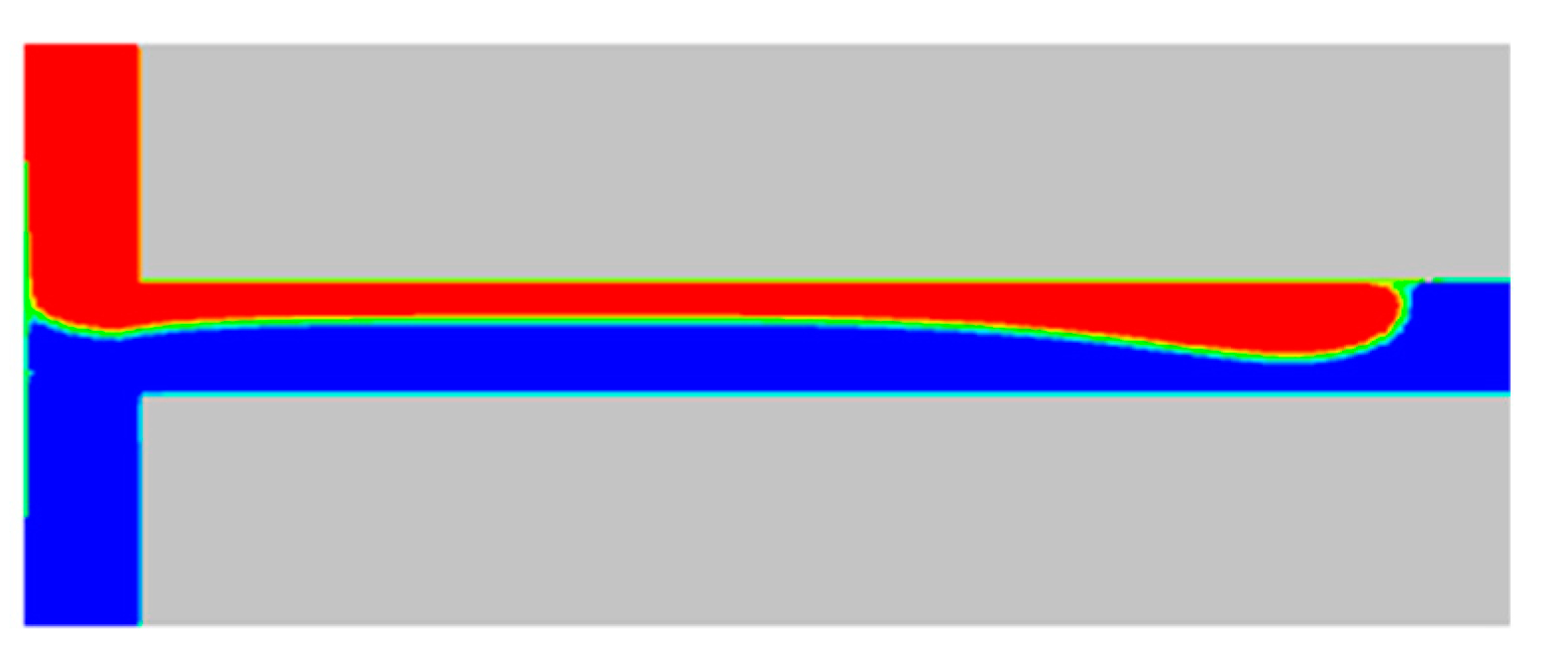
3.3. Two-Component Poiseuille Flow

A two-component Poiseuille flow driven by the pressure gradient was used to validate the viscous effect. The non-wetting fluid was near the wall, while the wetting fluid was in the central region. The non-wetting fluid was more viscous than the wetting fluid in the first case but was less viscous than the wetting fluid in the second case. In either case, a periodic boundary condition was applied at the inlet and outlet boundaries. The no-slip boundary condition was applied to the upper and lower surfaces. The viscosity ratio λ was 4.21. The viscosity of the more viscous fluid was 0.3, while that of the less viscous fluid was 0.0712. The channel width and driving force were set to be 120 Lu and 1.0 × 10⁻⁶, respectively. The corresponding simulations and analytical results are shown in Figure 3. In Figure 3, the two-component LB model results agree with the analytical solutions.

4. Results and Discussion

4.1. Droplet Motion in Microchannels

The droplet motion plays a vital role in the microfluidics within the microchannel [49]. In this section, we use our model to predict the droplet motion in microchannels and discuss the influence of the contact angle and Bond number on this motion. A rectangular geometry was applied to simulate this motion, and the computational domain was taken as L × W = 600 × 100 l.u.². Periodic boundary conditions were applied at the left and right sides, and the no-slip boundary condition (i.e., bounce-back scheme) was applied at the top and bottom sides. This motion was driven by a volume force (i.e., pressure force). Some simulations were performed under different contact angles and Bond numbers, and the density of the second component fluid was initialized by the l₀ × w₀ = 80 × 40 l.u.² rectangle near the bottom wall, surrounded by first component fluid. The volume force F = 1.0 × 10⁻⁶ was applied in the x-direction. The characteristic velocity, dimensionless time, and dimensionless ratio (usually referred to as the Bond number) (pressure force/surface force) were defined as u = ρ₂aLH/μ₂, t* = tu/H, and Bo = ρ₂aLH/σ, respectively, where ρ₂, μ₂, t, and σ are the density and viscosity of the second fluid, time step, and surface tension, respectively.

To quantitively analyze the droplet motion in the microchannel, the dimensionless centroid of the droplet was defined as x* = x/L and y* = y/H, representing its position in the x- and y-directions, respectively, and it was described by x = ∫_A xdx/∫_A dx and y = ∫_A ydy/∫_A dy, where A is the region of the droplet. The dimensionless height and wet length of the droplet were computed as h* = h/h₀ and l* = l/l₀, respectively.

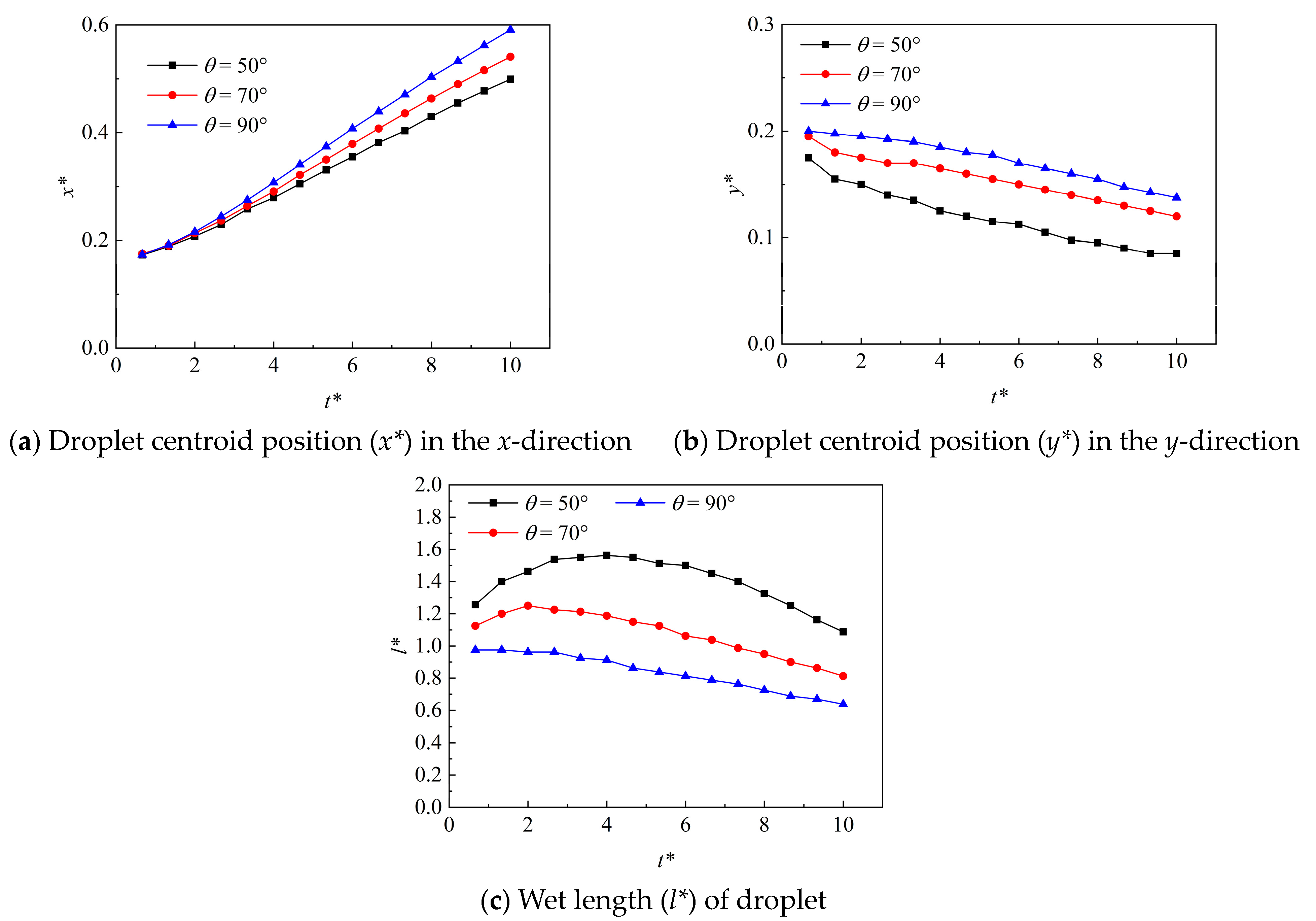
4.1.1. Effect of Contact Angle

As shown in Figure 4, microchannels with different surface wettabilities (θ = 50° and 90°) are considered, and the same Bo number is applied in this simulation. The droplet motion under different contact angles is different: when θ = 50° and 90°, the droplet always attaches to the wall, but the wet length in the former condition is larger than that in the latter condition. Overall, the velocity in a microchannel is similar to the flow without droplets. In addition, the velocity over on the droplet is higher than that in other places since the existence of droplet results in the decrease in cross-area of the flow microchannel.

As shown in Figure 5, different G₂ values are applied in this simulation to achieve different contact angles (50°, 70°, and 90°), and G_c is set as 1.5. In Figure 5a, when the contact angles (θ) are 50°, 70°, and 90°, the three curves are close to each other, and the increase in x* at θ = 50° is the sharpest. On comparing x* under different contact angles, the droplet motion in the x-direction for the hydrophilic microchannel wall takes a longer time than that for the intermediate wall. In Figure 5b, y* decreases with droplet motion when the droplet attaches to the wall. As the contact angle increases (increasing the wall wettability), y* increases. In Figure 5c, the curves of wet length (l*) have similar change tendencies regardless of the curve at θ = 50°. On comparing the different wettabilities from the hydrophilic to the intermediate wall, the wet length depends on the contact angle.

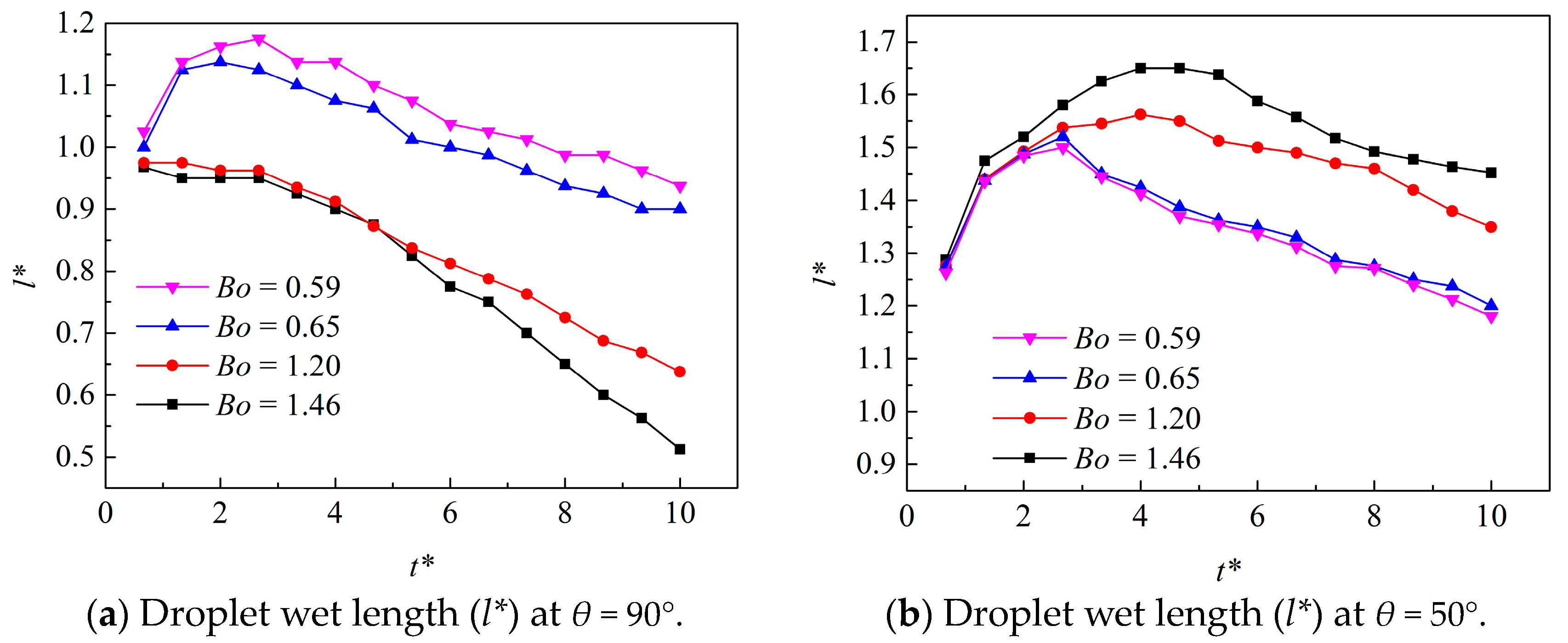
4.1.2. Effect of Bond Number

As mentioned earlier, the Bond number represents the ratio of pressure and surface forces. In this LB multiphase model, different surface tension values were obtained by changing the G_c values (1.4, 1.5, 1.9, and 2.0) that were then used to achieve different Bond numbers (1.46, 1.20, 0.65, and 0.59), as described in the following. The wall was categorized into intermediate (neutral) (θ = 90°) and hydrophilic surfaces (θ = 50°), and they all exhibited different properties.

In Figure 6a, as the Bond number increases, the droplet wet length increases on the on the neutral surface. However, as the Bond number increases, the droplet wet length decreases on the hydrophilic surface, as shown in Figure 6b.

4.2. Droplet Formation in Microchannels

In recent years, many researchers have focused on the process of droplet formation in a T-junction because of the simplicity and easy control of the break-up of droplets [50,51]. The regimes of flow in a T-junction are affected by the shear stress caused by the continuous fluid. Thorsen et al. [52] initially investigated droplet formation within a T-junction. Several fluid properties (i.e., velocities of disperse fluid u_d and continuous fluid u_c, viscosities of disperse fluid µ_d and continuous fluid µ_c, densities of disperse fluid ρ_d and continuous fluid ρ_c, and surface tension σ) and dimensional parameters (i.e., widths of the channels of disperse fluid w_d and continuous fluid w_c) affect the slug flow in microchannels [25,26,27]. Moreover, the viscosity ratio λ = µ_d/µ_c, capillary number Ca = µ_c u_c/σ, flow rate ratio ϕ = (u_d w_d)/(u_c w_c), and Г = w_d/w_c are usually used to analyze slug flow. As shown in Figure 7, l and w denote the main channel length and width, respectively, and L represents the droplet length.

4.2.1. Unit Conversion and Boundary Conditions in LB Simulation

To validate our LB model, the experimental data in [53] were compared with the simulation results. In the experiments presented in [53], a T-junction microfluidic device was used to investigate a droplet formation consisting of the inlets of the disperse and continuous fluids and main and wide outlet channels. For simplicity, we built a T-junction comprising the inlets of the disperse and continuous fluids and a main channel. In the experiment in [53], the constriction channel width was 20 μm, and the main channel length was 500 μm. Unit conversion was used to link both the LB simulations and physical phenomenon, which is an important factor that significantly affects the efficiency, accuracy, and stability of the LB model [54]. In this study, a 20 × 500 l.u² computational domain corresponded to a 20 × 500 μm² microchannel, implying the length scale C_l to be 1 μm. The properties of oil and water in the experiment in [53] are listed in

Table 3. Physical properties of oil (hexadecane) and water components.

Parameter	Value
Density of oil (hexadecane)	773.4 kg·m−3
Density of water	998.2 kg·m−3
Dynamic viscosity of oil	3.28 mPa·s
Dynamic viscosity of water	1.005 mPa·s
Interfacial tension	0.01 N·m−1
Static contact angle	130°

. The kinematic viscosity scale C_ν was 1.41 × 10⁻⁵ m²/s. Therefore, the relaxation times of oil (continuous fluid) and water (disperse fluid) were chosen as 1.4 and 0.0712, respectively, to satisfy the viscosity ratio requirement. The velocity scale C_u was 14.14 m/s, and time scale C_t was 7.09 × 10⁻⁸ s. The densities of both the fluids were assumed to be in unity, and the interfacial tension was set to be 0.05 by setting G_c = 1.5 to obtain the physical value of interfacial tension, and the value of G₂ was set to be 0.3978 to correspond to the static contact angle.

The velocity and pressure boundaries, based on the study by He et al. [54], were easily implemented in the inlet and outlet surfaces, and no-slip boundary conditions were applied at the walls (i.e., bounce-back scheme). This multicomponent flow was assumed to be a pressure-driven fully developed channel flow.

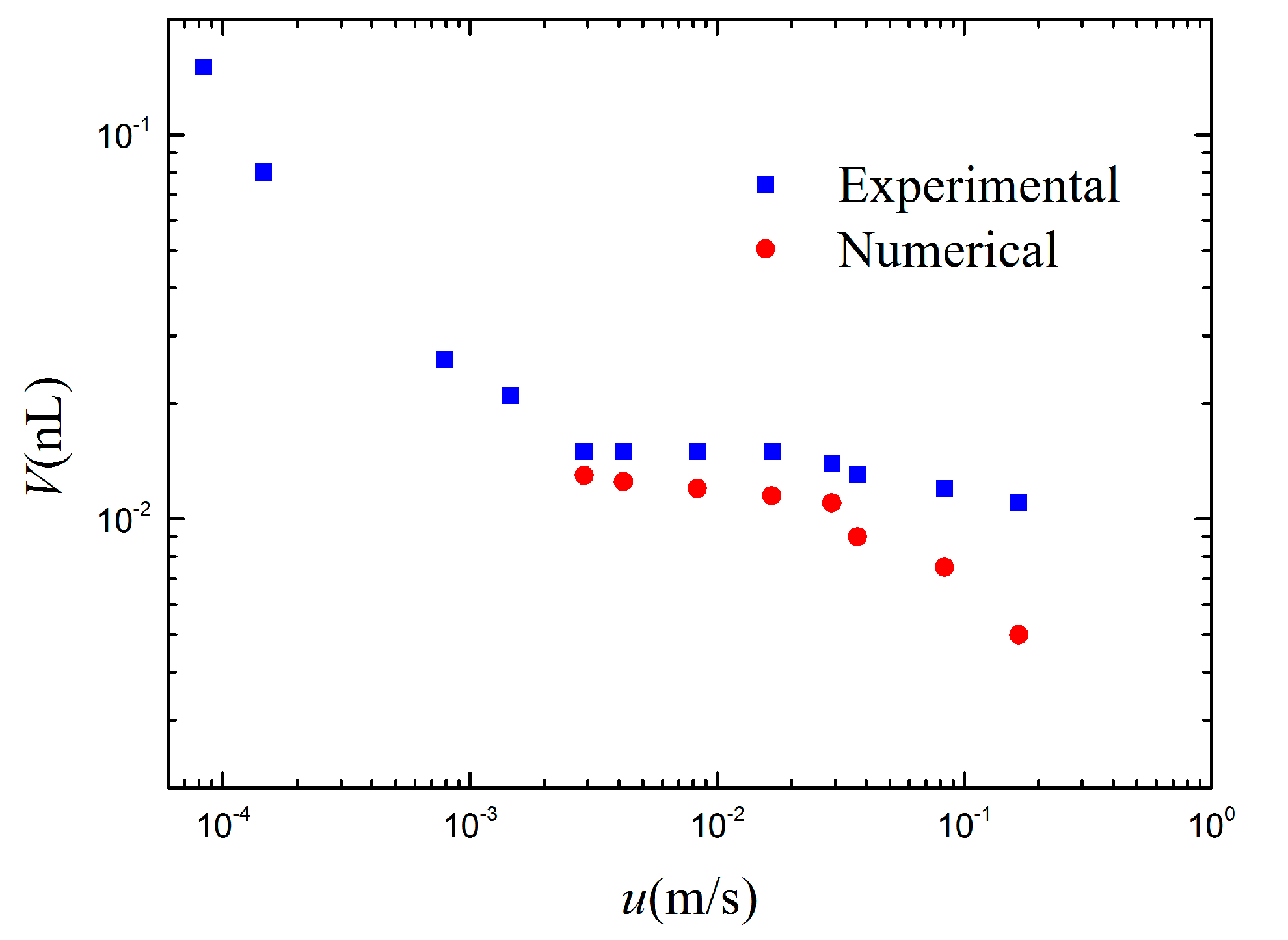
4.2.2. Validation of Droplet Formation in Microchannels

Figure 8 shows the relationship between the fluid velocity and droplet volume, and the red solid circle and blue diamond denote the numerical and experimental results, respectively. The droplet volume in the simulation results agrees well with that in the experimental results, implying that our application of the LB model to this research is reasonable.

4.2.3. Formation Regime and Critical Capillary Number

The formation regime of a droplet or bubble in microchannels has been widely investigated [55,56,57,58,59,60], and the formation patterns have been classified into three categories based on the droplet shape [14,53]. (1) The dripping–squeezing regime occurs at a low capillary number; the droplet breakup is mainly caused by pressure difference, and the breakup occurs at the T-junction corner. (2) In the jetting-shearing regime, when the capillary number is relatively high, shearing occurs; unlike in the dripping–squeezing regime, the shearing stress caused by the continuous fluid dominates in the breakup, and the breakup point evidently moves downstream. (3) In the threading regime, when the shearing stress is adequately large, the breakup does not happen, and both the fluids flow parallel to each other in the main channel. These regimes were simulated using the improved pseudopotential LBM. The corresponding details are discussed later.

Many experimental and numerical studies focus on the critical capillary number (Ca_c), which can distinguish between the dripping–squeezing and jetting–shearing regimes, but the critical capillary number varies [53,55,56]. This is because of the difficulty to distinguish the droplet breakup point when it is close to the corner of the downstream T-junction. In our simulation, the critical capillary number is ~0.002, and this value is independent of the viscosity ratio, as shown in Figure 9. The capillary number significantly affects the droplet length in the jetting–shearing regime, but this effect is minimal in the dripping–squeezing regime. The dimensionless droplet length is expressed as: $\overline{L}=L/w$. If Ca < Ca_c, the viscosity ratio has a limit influence on droplet length, and it is found that the droplet length almost has a relationship with the capillary number, which the empirical correlation can be written as $\stackrel{-}{L}=1.13-0.54log(Ca)$. If Ca > Ca_c, as the viscosity ratio increases, the droplet length also increases, and the empirical correlations between capillary number and droplet length are given by $\stackrel{-}{L}=-15.54-13.62\mathit{log}\left(Ca\right)-2.56{log}^2(Ca)$, $\stackrel{-}{L}=-18.85-15.05\mathit{log}\left(Ca\right)-2.64{log}^2(Ca)$, and $\stackrel{-}{L}=-22.26-16.81\mathit{log}\left(Ca\right)-2.84{log}^2(Ca)$ for λ = 4.21, 3.00, and 1.00, respectively.

4.2.4. Effect of Viscosity Ratio on Droplet Formation

In the simulations, the flow rate ratio ϕ was fixed at 1. As shown in Figure 9, the critical capillary number Ca_c is ~0.002, which is independent of the viscosity. However, the viscosity still affects the droplet formation, especially in the jetting–shearing regime. Since the pressure difference is dominated in the dripping–squeezing regime, the droplet length is almost independent of the viscosity. On the contrary, the droplet length in the jetting–shearing regime is significantly affected by the viscosity due to shear stress. As the viscosity ratio increases, the droplet length decreases, implying that the shear stress leads to the generation of smaller droplets.

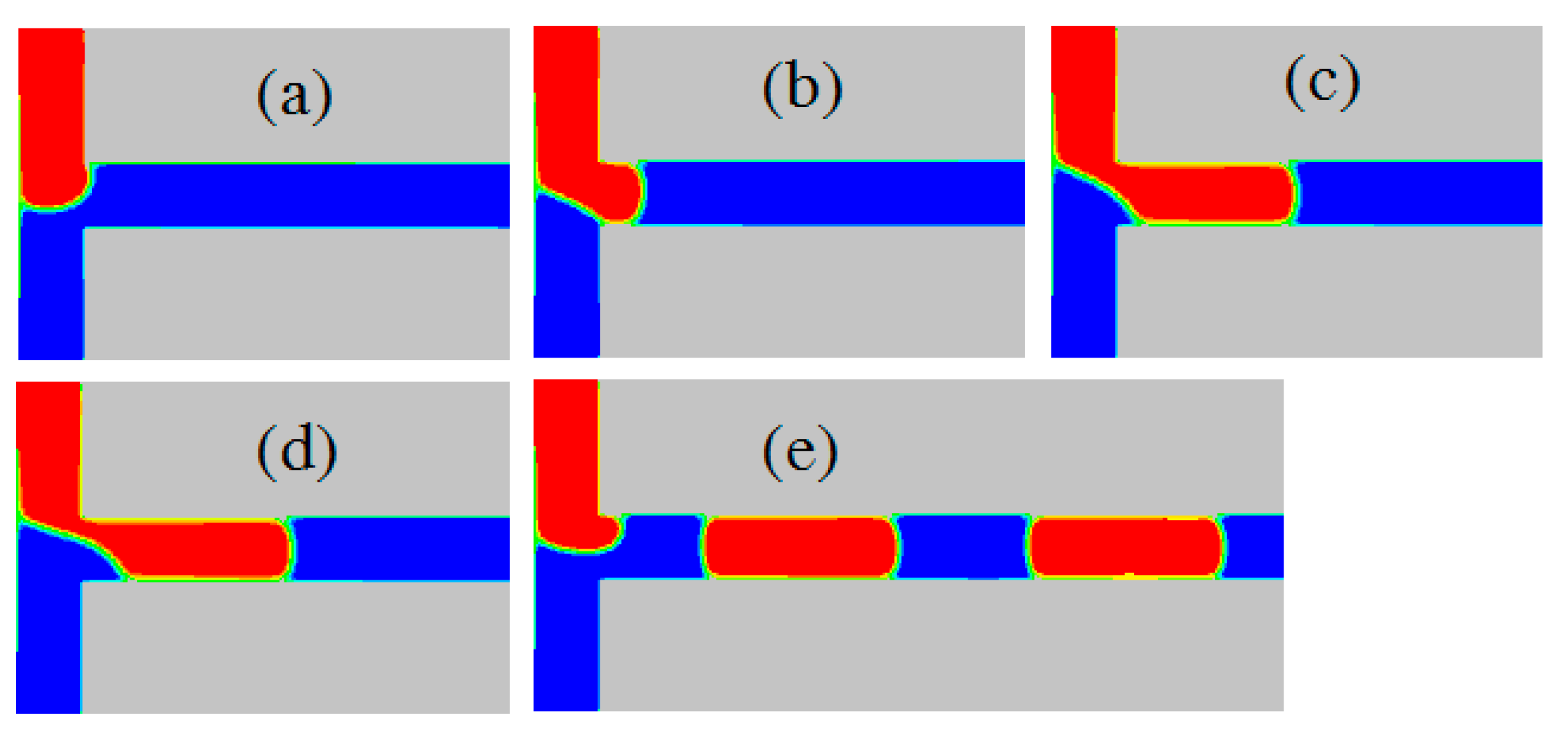
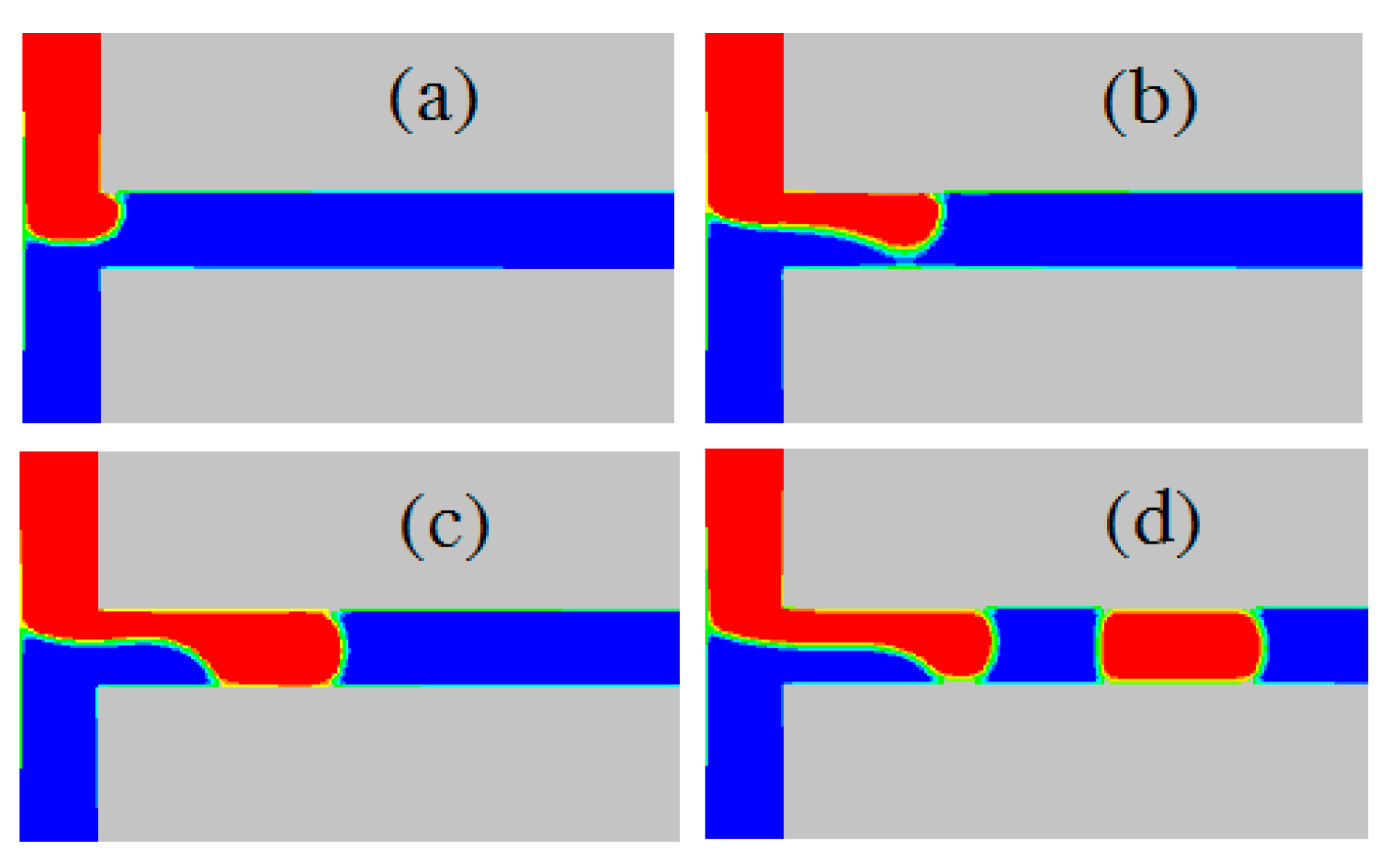
4.2.5. Dripping–Squeezing, Jetting–Shearing, and Threading Regimes

The dripping–squeezing regime is dominated by pressure difference, and uniform droplets are generated. Five stages are used to describe the droplet formation in this regime [50,60], as shown in Figure 10: (a) the disperse fluid begins to enter the main channel, (b) the disperse fluid tip gradually becomes larger and plugs up the whole main channel, (c) the continuous fluid squeezes the disperse fluid, (d) the disperse fluid breaks up, and (e) a droplet finally forms in the main channel.

The jetting–shearing process driven by the shearing stress and droplet generation occurs in four steps: (1) as shown in Figure 11a, the tip of the disperse fluid first enters the main channel, and the disperse and continuous fluids flow parallel to each other; (2) a round occurs at the tip of the disperse fluid, as shown in Figure 11b; (3) the round eventually attaches to the wall, as shown in Figure 11c; and (4) afterwards, the continuous fluid squeezes the disperse fluid until the breakup occurs and a droplet forms, as shown in Figure 11d. After a cycle of the above steps, droplets occur in the main channel, as shown in Figure 11d. This jetting–shearing process is also described by Shui [50].

When the flow rates of the disperse and continuous fluids increase, the former can not block the main channel, and a layered flow occurs. This is because the pressure difference is more than the surface tension. As shown in Figure 12, in the threading regime, the disperse and continuous fluids both flow in the main channel and are parallel to each other.

5. Conclusions

In this study, an improved pseudopotential model was used to simulate droplet motion and formation in microchannels, and some conclusions were drawn as follows:

(1)

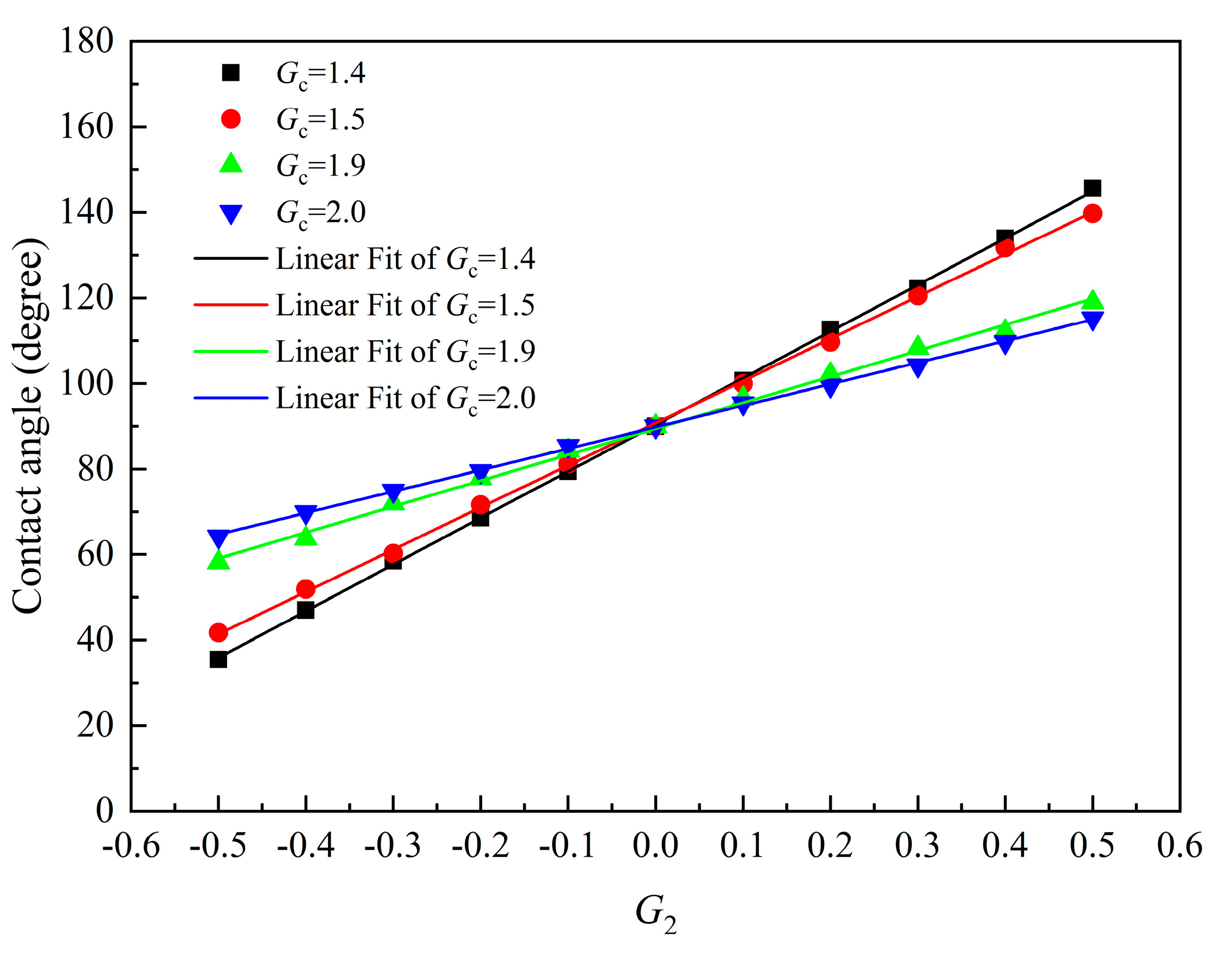
In this model, the variable surface tension was obtained by varying the parameter G_c. The relationship between the static contact angle and relevant parameter G₂ was represented by a linear equation.

(2)

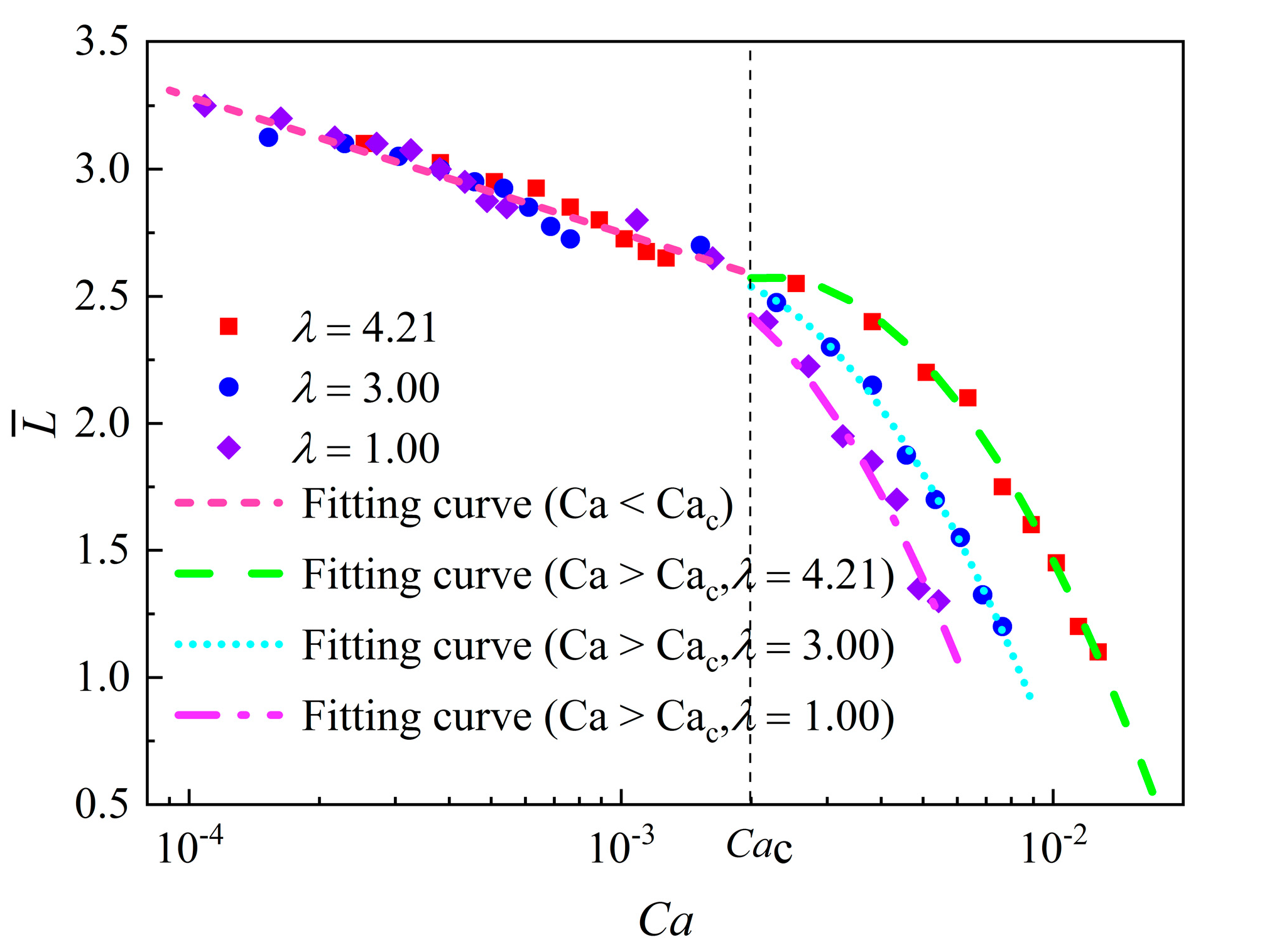
The droplet motion is crucial to understand multi-component flow in a microchannel. The surface wettability and Bond number significantly affected the droplet motion. When contact angles (θ) were 50°, 70°, and 90°, the dimensionless positions in the x-direction (x*) and y-direction (y*) exhibited a similar variation trend, and the increase in x* at θ = 50° was the sharpest. However, the droplet motion in the x-direction of the intermediate microchannel wall took a shorter time than that for the hydrophilic wall. Thus, the wet length also depended on the contact angle. As the Bond number increases, the droplet wet length increases on the neutral surface. However, as the Bond number increases, the droplet wet length decreases on the hydrophilic surface. It is found that the droplet length almost has a relationship with the capillary number (Ca < Ca_c), written as $\stackrel{-}{L}=1.13-0.54log(Ca)$. As the viscosity ratio increases and Ca > Ca_c, the droplet length also increases, and the empirical correlations between capillary number and droplet length are given by $\stackrel{-}{L}=-15.54-13.62\mathit{log}\left(Ca\right)-2.56{log}^2(Ca)$ , $\stackrel{-}{L}=-18.85-15.05\mathit{log}\left(Ca\right)-2.64{log}^2(Ca)$ , and $\stackrel{-}{L}=-22.26-16.81\mathit{log}\left(Ca\right)-2.84{log}^2(Ca)$ for λ = 4.21, 3.00, and 1.00, respectively.

(3)

The droplet formation patterns were classified into three categories based on the droplet shape: dripping–squeezing, jetting–shearing, and threading regimes. These regimes were simulated using the improved pseudopotential LBM. In our simulation, the critical capillary number, which distinguishes the dripping–squeezing and jetting–shearing regimes, was ~0.002, and this value was independent of the viscosity ratio. The viscosity ratio affected the droplet formation, especially in the jetting–shearing regime. Since the pressure difference was dominant in the dripping–squeezing regime, the droplet length was almost independent of the viscosity. In contrast, the droplet length in the jetting–shearing regime was significantly affected by viscosity due to shear stress. As the viscosity ratio increased, the droplet length decreased, implying that the shear stress led to generation of smaller droplets.

Dynamics of the multiple droplets (i.e., translocation [61], coalescence, and permeation [62]) in microchannels are usually related to many engineering applications, i.e., cell migration, chemical mini-reactions, and porous materials. In addition, lab-on-chip microfluidic devices may be key components of high-performance computers (HPCs). The LB methods in the present work are appropriate to deal with these research subjects due to their easy implementation and robustness, and then the related studies need to be investigated in the future.