Abstract
Mixed-mode fracture toughness refers to the ability of a material to withstand loads and expand under multiple modes of loading. It is usually tested by a semi-circular bend (SCB) to investigate the shale fracture toughness under combined modes of loading, such as tension and shear. When shale samples contain vein fractures, the dimensionless parameters Y1 and Y2 used in the SCB test method can be affected. The finite element method (FEM) was used to conduct a study investigating the impact of the natural fracture angle on the dimensionless parameters Y1 and Y2. The research findings indicate that as the vein fracture angle increases, Y1 and Y2 gradually increase. A construction was made to simulate the propagation path of a mixed-mode crack and compare it under various experimental conditions, utilizing the cohesive zone method (CZM). The results indicate that as the thickness of the vein fracture increases, the propagation path of the fracture becomes more tortuous. When the fracture encounters a vein with lower fracture strength, it will extend the vein fracture propagation. On the other hand, when the fracture encounters a vein with higher fracture strength, it will cross the vein fracture. This research considers the magnitude of the dimensionless stress intensity factor under different vein angles, simulating the crack propagation for varying vein widths and strengths.
1. Introduction
Shale gas reservoirs are characterized as unconventional reservoirs and have bitter contrasting properties due to the layered rocks and ubiquitously distributed vein fractures and weak interfaces, which are critical factors that control the fracture propagation pathway. Fracture toughness is indeed a fundamental mechanical property that defines the crack propagation resistance of a material. It is a critical parameter that governs the initiation and growth of cracks within a material. Therefore, the impact of fracture toughness on hydraulic fracturing is significant. Materials with high fracture toughness can better resist crack propagation, control crack propagation direction, resist brittle fracture, and reduce permeability during hydraulic fracturing treatment [1,2].
It is common for shale gas reservoirs to contain various types of disruptions, including natural fractures, cracks, and bedding planes, which make them largely anisotropic material both mechanical and petrol physical characteristic. The vein fractures in shale commonly occur, as it has a weak bonding strength. It is indeed true that the nature of natural fractures in shale systems can vary, and some studies have shown that these fractures can contain mineral fillings. Gale’s study [3], which investigated several typical shale systems in North America, identified that shale formations contain fractures filled with minerals such as quartz, calcite, and others. In addition to that, vein fracture can be obtained in the Longmaxi Formation shale.
In shale rocks with discontinuities, hydraulic fractures require excessively high pressure to propagate, and fracture propagation takes place in mixed mode, causing change in their trajectories and directions. Previous studies have examined the criteria for fracture interactions [4,5,6,7,8]. Hydraulic fracture propagation in anisotropic shale rocks may take place in three possible scenarios: the fracture may cross, be arrested by, or propagate along the discontinuity. Taking natural fracture as an example, as the natural fracture’s mechanical properties are different from that of the shale matrix, when a hydraulic fracture approaches the frictional nature fracture, the local tensile and shear stresses will cause the propagation path to change. Due to its importance in hydraulic fracture treatments of shale gas reservoirs, recently, many researchers have studied the fracture interaction problems by means of experiments [5,9,10,11,12] and numerical simulations [13,14,15,16].
The understanding of the natural fracture growth phenomenon is critical as it experiences initiation, propagation, and fracture branching when hydraulic pressure is induced. Numerical simulation is an effective method for the understanding of complex fracture propagation. Numerical techniques for studying the fracture toughness of rocks include the discrete element method (DEM) [15], displacement discontinuity method (DDM) [17], finite element method (FEM) [18], extended finite element Method (XFEM) [19,20,21] and boundary element method (BEM). In this study, the FEM and XFEM are used in the numerical simulation. Indeed, the International Society of Rock Mechanics (ISRM) has proposed four methods for measuring fracture toughness in mode I (tensile opening mode) failure. These methods include the cut notched bend (CB) [22], short rod (SR) [22], cracked chevron notched Brazilian disc (CCNBD) [23,24], and semi-circular curved (SCB) [20,25,26,27,28] specimens. Among these test configurations, the SCB test is particularly suitable for characterizing fracture toughness under mixed-mode loading conditions The SCB test attracted considerable attention for different materials such as sedimentary rocks [27,28,29], asphalt mixtures [30], and PMMA24. In the study conducted by Lee et al. [12], they conducted SCB tests on samples of Marcellus shale that included natural fractures or veins. The tests conducted on shale specimens with induced fractures and veins have revealed that the approach angle of the induced fracture and the thickness of the veins play a significant role in fracture propagation and fracture toughness. In the case of oblique approach angles and thicker veins, there is a higher probability of diversion or propagate into the vein occurring in the induced fracture rather than continuing along its original path within the surrounding shale material. The fracture toughness of Marcellus Shale samples with calcite veins has been observed to vary in the range of 0.24 to 0.83 MPa∙m1/2. Comparatively, the fracture toughness of unfractured Marcellus Shale is measured to be 0.47 MPa∙m1/2. Chandler et al. [31] studied the fracture toughness of the Mancos shale when affected by bedding layers. The study found that the highest fracture toughness value, 0.72 MPa∙m1/2, was obtained when the initial crack plane was normal (perpendicular) to the bedding. The lowest fracture toughness value, 0.21 MPa∙m1/2, was observed when the initial crack plane was aligned with the bedding. The study also noted that cracks propagating non-parallel to the bedding have a tendency to deviate toward a bedding-parallel orientation. In the research conducted by Zuo et al. [29], a series of tests were conducted on SCB sandstone samples to examine the propagation of fractures under mixed-mode conditions. The findings from the study unveiled an exponential increase in the peak load of the specimen as the crack inclination angle rises. Meanwhile, the mode I stress intensity factor KI exhibited a gradual decrease with the increase in the crack inclination angle. This implies a diminishing resistance to mode I crack propagation with a higher inclination angle. Conversely, the mode II stress intensity factor KII initially displayed an increase followed by a decrease, suggesting a more intricate relationship between the crack inclination angle and the behavior of mode II crack propagation. Notably, the research focused on sandstone samples devoid of any bedding layers or pre-existing fractures. When it comes to estimating fracture toughness through the SCB test, it heavily depends on obtaining anisotropic shale rock samples and ensuring the repeatability of experimental data. Although the SCB method has been extensively utilized to determine fracture toughness in materials that demonstrate pure mode I and mixed-mode fractures, the investigation specifically targeting mixed mode fracture propagation in heterogeneous shale samples is notably scarce.
Many scholars have also made corresponding research on the criterion of destruction. Wu [32] conducted numerical simulations on cement concrete edge-notched specimens subjected to three-point bending at different inclinations based on the maximum tensile stress criterion (MTS). The study analyzed the variations of the stress intensity factor. Li et al. [33] elucidated the applicability of defining failure criteria for rocks using strain energy density (SED) under combined dynamic and static loading conditions. They employed dynamic and static loading experiments to validate the strain energy density criterion and achieved good agreement between theoretical and experimental results. Hou et al. [34] used the modified maximum tensile stress criterion (MMTS) to predict the crack initiation angle and fracture resistance of concrete specimens with different crack types. They solved theoretical formulas simultaneously to obtain the predicted values and compared and analyzed them with experimental values. The experimental results showed good consistency with the predictions. This paper adopts the MTS criterion.
In this study, the shale sample containing vein fractures is tested to investigate the mixed-mode fracture toughness. The extended finite element method (XFEM) is used to analyze mixed-mode crack propagation behavior. The numerically simulated fracture propagation path and propagation pressure are compared with experimental results. The different vein fracture effects on crack initiation and propagation are discussed.
2. Experimental Procedure and Results
2.1. Sample Preparation
The Longmaxi Formation shale samples were collected from the southwest region of China for the purpose of this study. X-ray diffraction (XRD) and X-ray fluorescence (XRF) are common analytical techniques used to determine the mineral composition and elemental content of geological samples, including shale samples. Based on the XRD pattern shown in Figure 1, the main constituents identified in the shale samples from the Longmaxi Formation were quartz, calcite, dolomite, and illite. These mineral phases are commonly found in shale formations. The presence of quartz, a hard and brittle mineral, suggests that the shale samples have a relatively higher brittleness compared to average shale compositions.
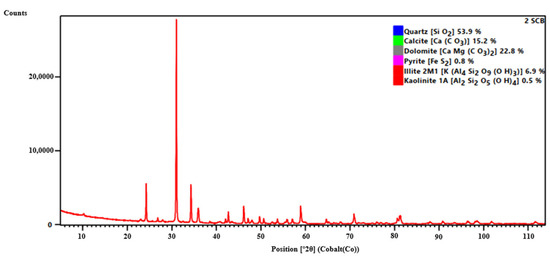
Figure 1.
XRD spectrum.
According to Figure 2, the SCB specimen preparation process involves extracting a cylindrical shale sample with a diameter of 76 mm and a length of 250 mm by drilling from a shale outcrop, as shown in Figure 2a. From the drilled shale plug, 30 mm thick disks are cut to ensure consistent thickness, as depicted in Figure 2b. Each shale disk is then divided into two equal halves, as illustrated in Figure 2c. According to the experimental requirements, the size of the gap is determined at the center of the sample’s width. The gap is then machined by milling, which is followed by adjustments and polishing to ensure the accuracy and smoothness of the sample gap. A notch is created at the center of each semi-circular sample, as shown in Figure 2d, with the notch angle varying within the range of 30° to determine the mixed-mode loading condition for fracture toughness testing. The SCB shale specimens are prepared following the guidelines provided by the ISRM. The sample has a radius of 38 mm, a thickness of 30 mm, and an initial crack length of 11 mm.

Figure 2.
The sample preparation process. (a) Outcrop core pillars. (b) Standard shale disk. (c) Semi-circular specimen. (d) Sample with crack.
2.2. Experimental Method
In Figure 3, the diagram illustrates the geometric configuration of an SCB specimen with a vein fracture. The specimen consists of a semi-circular disk with a radius denoted as R. The disk has a certain thickness indicated as B. Additionally, a notch of length a is present in the center of the specimen. During the SCB test, a loading force was denoted as P. The sample is positioned with the assistance of two lower rollers. The two lower rollers are positioned at a separation distance of 2S. The notch angles (β) are varied from 0° to 55°. When the notch angle β is 0°, the configuration represents a pure mode I loading condition. As the notch angle (β) increases in the SCB test configuration, the mode II stress intensity factor (KII) also increases; however, the mode I stress intensity factor (KI) decreases as the notch angle increases. When the notch angle β is 55°, the configuration represents a pure mode II loading condition. By varying the notch angles, it is possible to achieve three distinct failure modes in the SCB specimens: pure mode I when the notch angle β is 0°, pure mode II when β is 55°, and mixed-mode when the notch angle falls between 0° and 55°; 55° to 90° is a pure type II fracture. α refers to the vein fracture angle.
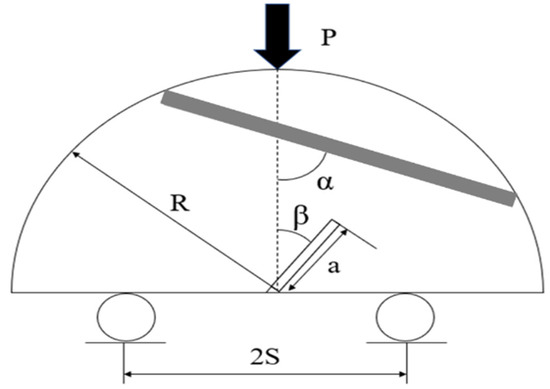
Figure 3.
Semi-circular bend (SCB) geometry.
The formula for calculating the fracture toughness of SCB specimen type I and type II is as follows [34]:
where P represents the load applied on the sample at the point of failure, and B represents the thickness of the sample. The stress intensity factors, KI and KII, represent the magnitudes of stress near the crack tip that control crack propagation. Y1 and Y2 are dimensionless parameters that represent the normalized stress intensity factors in the SCB test. They (Y1 and Y2) are dependent on the specimen geometry parameters, specifically a/R (notch length to radius ratio), S/R (support span to radius ratio), and β (notch angle). These values can be calculated using numerical procedures [30].
The maximum tensile stress criterion (MTS) is used to simulate the crack propagation. The maximum tensile stress criterion takes the direction of the crack initiation as the direction of the annular maximum tensile stress. The expression of the stress component of the crack tip in the polar coordinate system is as follows [32]:
The circumferential stress can be expressed as:
Let . Based on Equations (1) and (2), the stress intensity factor can be used to calculate the crack angle, so as to obtain the crack propagation.
As per the research conducted by Lim et al. [35], it is advantageous to have shorter crack lengths in the semi-circular bend (SCB) specimen for fracture testing. This is attributed to the fact that a shorter crack length helps achieve a lower sensitivity of the stress intensity factor to variations in specimen geometry [32]. Consequently, for the SCB tests, an a/R value of 0.29 and an S/R value of 0.66 were selected. The WAW-1500B servo-controlled rock mechanics test system, depicted in Figure 4, was utilized to perform the SCB tests.

Figure 4.
Test equipment.
In the uniaxial compression test, the WAW-1500B electrohydraulic servo rock mechanics test system was utilized for the testing of the shale specimens, and the loading rate is set at 0.18 mm/min. During the uniaxial compression test on shale samples, the stress and displacement are recorded to determine the uniaxial compression strength of the samples. The polishing process is carefully controlled to maintain an error within a range of 0.02 mm. The stress–strain curve is shown in Figure 5. The average UCS value of the shale samples is determined to be 112.5 MPa, and the Young’s modulus is measured to be 28.6 GPa. The experiment results are used in the following numerical simulations in this paper.
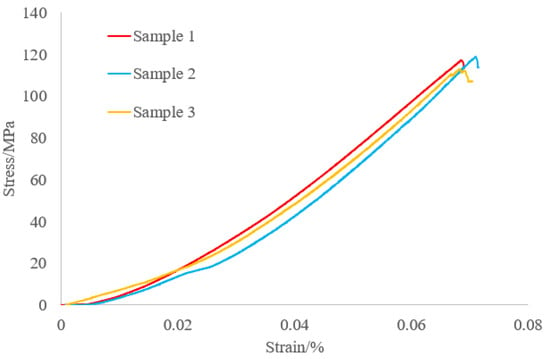
Figure 5.
Stress–strain curve for shale sample.
3. Numerical Method
Setting up a semi-circular bend (SCB) 2D model involves defining the geometry, material properties, boundary conditions, and loading conditions based on the specifications of the testing specimens. In this section, the basic parameters of the model were investigated. Based on the geometry model, the calculation of Y1 and Y2 can be determined [36]. Indeed, when the SCB specimen contains bedding layers or vein fractures, the presence of these features can affect the values of Y1 and Y2. In this study, a numerical model is established for computing Y1 and Y2 for specimens containing bedding layers or fractures. The SCB specimen’s typical model with bedding layers or fractures in an ABAQUS setup is depicted in Figure 6. Quadratic elements were employed to mesh the crack tip region in the numerical model. Quadratic elements have a higher order of interpolation compared to linear elements, allowing for a more accurate representation of the stress and strain fields near the crack tip. Quadratic elements utilize more nodes and shape functions, enabling them to better approximate complex stress and strain distributions. Near the crack tip, stress and strain fields often exhibit significant gradients, which linear elements may not fully capture due to their limited interpolation capabilities.

Figure 6.
The mesh for semi-circular bend (SCB). (a) The mesh for SCB model. (b) The mesh for SCB model with vein fracture.
Figure 6a illustrates the mesh configuration of a homogeneous SCB specimen, whereas Figure 6b demonstrates the mesh of the SCB specimen incorporating a vein fracture. The J-integral method was employed to directly extract the stress intensity factor.
In the numerical simulations conducted in this study, the SCB specimen with varying notch angles was modeled to calculate the normalized stress intensity factors, Y1 and Y2. In Figure 7, the values of Y1 and Y2 for the SCB specimen without bedding layer or natural fracture are presented. These values were obtained through numerical simulations, and it is noted that the results are consistent with the findings reported by Xie et al., 2017 [19]. From Figure 7, the relationship becomes evident that as the notch angle β increases, there is a consistent decrease in the normalized stress intensity factor (Y1) for mode I, while the normalized stress intensity factor (Y2) for mode II initially increases as the notch angle β increases until reaching a peak value at around 40 degrees. Afterward, Y2 starts to decrease with further increases in the notch angle. By comparing the values of Y1 and Y2 in the mixed mode, it is observed that Y1 is higher than Y2. To conduct a sensitivity analysis of the notch length, the following procedure was employed. Y1 and Y2 can also be calculated for different values of a/R, such as 0.4 and 0.5. The results of these calculations can be presented in Figure 7 alongside the existing data for a/R = 0.3. The analysis of Y1 and Y2 for different notch angles at different a/R ratios reveals that both Y1 and Y2 are less sensitive to changes in notch angles when the a/R value is lower.
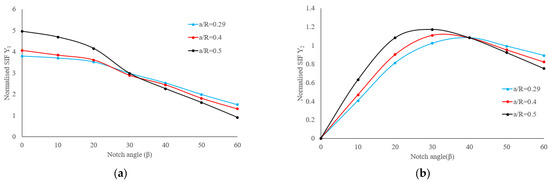
Figure 7.
Variations of Y1 and Y2 (a) Y1. (b) Y2.
The numerical model setup shown in Figure 6b is specifically designed to compute the values of Y1 and Y2 for a specimen containing a bedding layer or vein fracture. In our model, we assume a fixed notch angle (β) of 30° and a notch length-to-radius ratio (a/R) of 0.29. Additionally, we vary the bedding layer/vein fracture angle from 30° to 90° degrees. Figure 8 shows the Y1 and Y2 values with the change in bedding layer/vein fracture angle. It is shown that the Y1 and Y2 both decreased when the SCB specimen contains a bedding layer/vein fracture. The observed increase in Y1 and Y2, with an increase in the angle of the bedding layer/vein fracture, suggests that as the angle of the bedding layer/vein fracture becomes more inclined to the loading direction, there is a corresponding increase in the mode I and mode II stress intensity factors. The corrected Y1 and Y2 values obtained from the numerical simulation were incorporated into the subsequent determination of fracture toughness. The direct calculation is Y1 = 3.49 and Y2 = 1.27. Comparing the experimentally calculated Y1 and Y2 with the simulated values of Y1 and Y2, it is found that the dimensionless stress intensity factor obtained by direct calculation is approximately 17% higher than the simulated value.
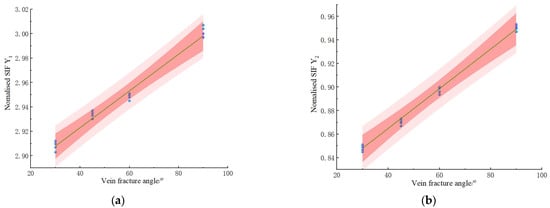
Figure 8.
Y1 and Y2 are obtained at different vein fracture angles. (a) Y1 range with vein fracture angle; (b) Y2 range with vein fracture angle.
4. Experiment Results
4.1. Laboratory for Mixed Mode with Homogenous Shale
Different notch angles will lead to different failure modes. Figure 9 illustrates the fracture propagation path for homogeneous SCB specimens with varying initial approach angles. Figure 9 shows the result of an approach angle of 30° where the loading displays a condition for mixed-mode fracture propagation. Initially, the fracture propagates along the notch direction a small distance (few millimeters, mixed mode); then, it turns into the loading direction and propagates (mode I) until it intersects the vein fracture. Following the intersection, it begins to propagate along the vein fracture (mixed mode). Figure 9b presents the numerical simulation result for notch angle β = 30° (30° approach angle), which is in agreement with the experiment result. With an increase in the notch angle (β), mode II fracture becomes more prominent. Consequently, the fracture propagates along a curved path, ultimately aligning with the load direction of the SCB specimen. Table 1 shows the facture toughness KI and KII value when the notch angle is 30°.

Figure 9.
Compare experiment result and simulation of fracture path with different approach angle. (a) Experiment result β = 30°. (b) Numerical simulation result β = 30°.

Table 1.
The fracture toughness of homogenous shale sample.
4.2. Experiment Results for Mixed Mode with Vein Fracture
In the experiment, the SCB shale samples containing vein fractures are used in the experiment. Figure 10 displays the fracture toughness results for specimens containing vein fractures under mixed-mode loading conditions. The fracture angles α were varied at 30°, 45°, and 60°, while a constant notch angle of 30° was maintained. For the mode I fracture toughness, the low value is 0.5 MPa·m1/2 in the 30° vein fracture angle, and the highest fracture toughness is 0.62 MPa·m1/2 in the 60° vein fracture angle. For the mode II fracture toughness, the lowest value is 0.17 MPa·m1/2 in the 30° vein fracture angle and the highest fracture toughness is 0.21 MPa·m1/2 in the 60° vein fracture angle. The increase in fracture angle is accompanied by an observable rise in fracture toughness. This means that specimens with larger fracture angles exhibit higher resistance to crack propagation and are more resistant to failure. Based on Figure 10c, it can be observed that the direction of the crack initiation angle is consistent with the vein fracture angle, and the results obtained from the MTS criterion calculation show good agreement with the experimental results. Figure 11a illustrates the post-test failure pattern of a separate specimen exhibiting a fracture angle of 60°. The examined specimen exhibits a partial vein fracture located on the right-hand side of the notch. The obtained results indicate that the fracture initiation occurs at the notch tip and propagates toward the vein fracture, eventually extending along the vein surface. Upon reaching the vein section of the fracture, it can be observed that the fracture branches in the direction of the applied load, following a curved trajectory. This branching behavior is replicated in the numerical simulation, as depicted in Figure 11b, effectively capturing the path of fracture propagation.
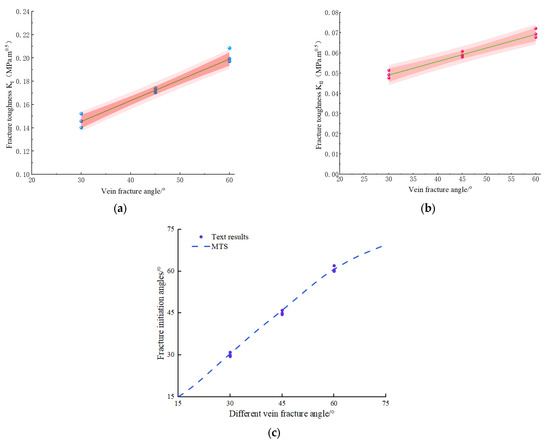
Figure 10.
Experiment results of mixed mode at different vein fracture angle. (a) KI at different vein fracture angle. (b) KII at different vein fracture angle. (c) Experimental values and MTS criteria for initial crack propagation angle at different vein fracture angle.

Figure 11.
Failure pattern of specimen containing vein fracture (α = 60°). (a) Experiment result for vein fracture angle = 30°. (b) Numerical simulation for vein fracture angle = 30°.
5. Numerical Simulation
In this section, vein fracture is numerically studied to compare with the experimental results. Based on the previous experimental results, the 2D numerical model is set up and the specimen diameter is 38 mm. The Young’s modulus E is 28.6 GPa, which comes from the UCS result. The Poisson ratio set as 0.25, and the tensile strength is 5 MPa. The loading pressure is applied on the top roller, and the vein fracture properties are obviously different from the shale sample. The vein fracture is set to our numerical simulation. The numerical simulation natural facture is also set to 30°. We assume that the vein fracture has a Young’s modulus of 10 GPa, and it is much lower than the shale sample when the tensile strength is 1 MPa. The numerical simulation results are as follows.
5.1. Vein Fracture Thickness Effect on Mixed-Mode Fracture Propagation
The influence of different vein fracture thicknesses on fracture propagation was explored through the data obtained from the above simulation verification. Figure 12 shows the fracture paths of samples with different vein fracture thicknesses. The vein fracture paths running through the entire sample are shown in Figure 12a. The small thickness of the vein fracture has almost no effect on the fracture propagation, and the fracture directly passes through the small thickness of the vein fracture. In Figure 12b, the normal fracture passes through the vein fracture, but an obvious path zigzag occurs before passing through the vein fracture, and an obvious turn occurs after passing through the vein fracture. In Figure 12c, the thickness of the vein fracture further increases, and the propagation path is similar to Figure 12b, but there is a certain deviation. The thickness between the three types of vein fracture in Figure 12 shows that different inter-bedding thicknesses have a certain influence on fracture propagation, and a small vein fracture thickness has little influence on the crack growth path. Increasing the vein fracture thickness will affect the zigzagging degree of the fracture propagation path, and the fracture propagation path will turn after passing through the vein fracture.

Figure 12.
Vein fracture thickness effect on mixed-mode fracture propagation (α = 60°). (a) Vein fracture thickness = 2.5 mm. (b) Vein fracture thickness = 5 mm. (c) Vein fracture thickness = 7.5 mm.
5.2. Vein Fracture Strength Effect on Mixed-Mode Fracture Propagation
Figure 13 shows the effect of different vein fracture strengths on crack propagation by changing the vein fracture thickness to 5 mm. The stratification strength is divided into 0.5 shale strength, 0.25 shale strength, and 0.1 shale strength. In Figure 13a, the fracture propagates through the lower vein fracture, and the propagation path is basically unchanged when it reaches the upper vein fracture. After intersecting with the upper vein fracture, the crack propagates through the upper vein fracture for a certain distance to the sample fracture. Figure 13b shows the 0.25 shale strength of the vein fracture; when the fracture extends to the lower vein fracture, it extends a certain distance, and the length of the extension distance is longer than that of the 0.5 shale strength. After that, it continues to extend through the vein fracture. When the fracture encounters vein fracture, the expansion path takes obvious twists, but it does not extend the vein fracture. As shown in Figure 13c, the 0.1 shale strength has been set very low. When the fracture propagation intersects the lower vein fracture, the vein fracture propagation is extended to the lower vein fracture. It cannot cross the whole vein fracture, which only propagates along the lower vein. As shown in the three bedding strengths in Figure 13, the longer propagation distance will result if the fracture extends to the vein fracture as well as has lower strength. Moreover, the fracture will extend to the lower vein fracture if the bedding strength is low to a certain level.

Figure 13.
Vein fracture strength effect on mixed-mode fracture propagation (α = 60°). (a) 0.4 shale strength. (b) 0.25 shale strength. (c) 0.1 shale strength.
6. Conclusions
- (1)
- The experimental study focused on a comprehensive set of results for mixed-mode fracture using the SCB shale sample with vein fractures.
- (2)
- Tests conducted on specimens without vein fractures under mixed-mode loading conditions show that as the notch angle increases, KI reduces while KII increases.
- (3)
- By conducting numerical simulations based on the finite element method (FEM), the modified Y1 and Y2 by FEM were determined to calculate the fracture toughness of vein fracture shale specimens. The crack growth angle is predicted by MTS criterion, and the predicted result is more accurate.
- (4)
- The presence of naturally occurring vein fractures has a significant impact on both fracture toughness and crack propagation paths. As the thickness of the vein fracture increases, the path of crack propagation has some deviation. It will extend the vein fracture and propagate when the fracture has lower vein fracture strength. It will cross the vein fracture when the fracture encounters a higher vein fracture strength.
Author Contributions
Methodology, Q.R. and J.D.; Validation, M.X.; Investigation, D.R. and R.L.; Writing—original draft, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [Key Core Technology Research Projects of PetroChina Company Limited] grant number [2020B-4911]. And the APC was funded by [Research Institute of Petroleum Exploration and Development].
Data Availability Statement
The data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- Jiang, M.; Li, Z.Q.; Duan, G.F.; Yang, J.J.; Shi, Y.Z.; Shi, H.Q. Effect of hydraulic fracture conductivity on deep shale gas production. Xinjiang Oil Gas 2023, 19, 35–41. [Google Scholar]
- Luo, Y.; Kong, H.; Xu, K.S.; Mamuti, T.E.X.J.; Zheng, H. Numerical simulation for vertical propagation pattern of hydraulic fractures in sand-shale interbedded reservoirs. Xinjiang Oil Gas 2023, 19, 49–56. [Google Scholar]
- Gale, J.F.W.; Reed, R.M.; Holder, J. Natural fractures in the Barnett Shale and their importance for hydraulic fracture treatments. AAPG Bull. 2007, 91, 603–622. [Google Scholar] [CrossRef]
- Sarmadivaleh, M.; Rasouli, V. Modified Reinshaw and Pollard Criteria for a Non-Orthogonal Cohesive Natural Interface Intersected by an Induced Fracture. Rock Mech. Rock Eng. 2014, 47, 2107–2115. [Google Scholar] [CrossRef]
- Blanton, T.L. An experimental study of interaction between hydraulically induced and pre-existing fractures. In Proceedings of the SPE Unconventional Gas Recovery Symposium, Pittsburgh, PA, USA, 16–18 May 1982; Society of Petroleum Engineers: Richardson, TX, USA, 1982. [Google Scholar]
- Gu, H.; Weng, X.; Lund, J.B.; Mack, M.G.; Ganguly, U.; Suarez-Rivera, R. Hydraulic Fracture Crossing Natural Fracture at Non-orthogonal Angles, A Criterion, Its Validation and Applications. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 24–26 January 2011; Society of Petroleum Engineers: Richardson, TX, USA, 2011. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, W.; Keer, L.M. An energy based analytical method to predict the influence of natural fractures on hydraulic fracture propagation. Eng. Fract. Mech. 2018, 189, 232–245. [Google Scholar] [CrossRef]
- Xu, W.; Zhao, J.; Rahman, S.S.; Li, Y.; Yuan, Y. A Comprehensive Model of a Hydraulic Fracture Interacting with a Natural Fracture: Analytical and Numerical Solution. Rock Mech. Rock Eng. 2019, 52, 1095–1113. [Google Scholar] [CrossRef]
- Chuprakov, D.; Melchaeva, O.; Prioul, R. Injection-Sensitive Mechanics of Hydraulic Fracture Interaction with Discontinuities. Rock Mech. Rock Eng. 2014, 47, 1625–1640. [Google Scholar] [CrossRef]
- Zhou, J.; Jin, Y.; Chen, M. Experimental investigation of hydraulic fracturing in random naturally fractured blocks. Int. J. Rock Mech. Min. Sci. 2010, 47, 1193–1199. [Google Scholar] [CrossRef]
- Olson, J.E.; Bahorich, B.; Holder, J. Examining Hydraulic Fracture—Natural Fracture Interaction in Hydrostone Block Experiments. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 6–8 February 2012; Society of Petroleum Engineers: Richardson, TX, USA, 2012. [Google Scholar] [CrossRef]
- Lee, H.P.; Olson, J.E.; Holder, J.; Gale, J.F.W.; Myers, R.D. The interaction of propagating opening mode fractures with preexisting discontinuities in shale. J. Geophys. Res. Solid Earth 2015, 120, 169–181. [Google Scholar] [CrossRef]
- Dahi-Taleghani, A.; Olson, J.E. Numerical Modeling of Multistranded-Hydraulic-Fracture Propagation: Accounting for the Interaction Between Induced and Natural Fractures. SPE J. 2011, 16, 575–581. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, X.; Zhu, H.; Zhang, X.; Pan, R. Numerical simulation of interaction of hydraulic fracture and natural fracture based on the cohesive zone finite element method. J. Nat. Gas Sci. Eng. 2015, 25, 180–188. [Google Scholar] [CrossRef]
- Lee, H.P.; Olson, J.E.; Schultz, R.A. Interaction analysis of propagating opening mode fractures with veins using the Discrete Element Method. Int. J. Rock Mech. Min. Sci. 2018, 103, 275–288. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, H.; Zhao, Z.; Chen, Z. DEM Modeling of Interaction Between the Propagating Fracture and Multiple Pre-existing Cemented Discontinuities in Shale. Rock Mech. Rock Eng. 2019, 52, 1993–2001. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, J.; Guo, Q.; Wei, J.; Li, J. Miscibility, morphology and fracture toughness of epoxy resin/poly(styrene-co-acrylonitrile) blends. Polymer 1996, 37, 4667–4673. [Google Scholar] [CrossRef]
- Wang, W.; Olson, J.E.; Prodanović, M.; Schultz, R.A. Interaction between cemented natural fractures and hydraulic fractures assessed by experiments and numerical simulations. J. Pet. Sci. Eng. 2018, 167, 506–516. [Google Scholar] [CrossRef]
- Xie, Y.; Cao, P.; Jin, J.; Wang, M. Mixed mode fracture analysis of semi-circular bend (SCB) specimen: A numerical study based on extended finite element method. Comput. Geotech. 2017, 82, 157–172. [Google Scholar] [CrossRef]
- Suo, Y.; Su, X.; Wang, Z.; He, W.; Fu, X.; Feng, F.; Pan, Z.; Xie, K.; Wang, G. A study of inter-stratum propagation of hydraulic fracture of sandstone-shale interbedded shale oil. Eng. Fract. Mech. 2022, 275, 108858. [Google Scholar] [CrossRef]
- Suo, Y.; Chen, Z.; Rahman, S.S.; Song, H. Experimental and Numerical Investigation of the Effect of Bedding Layer Orientation on Fracture Toughness of Shale Rocks. Rock Mech. Rock Eng. 2020, 53, 3625–3635. [Google Scholar] [CrossRef]
- Ouchterlony, F. Extension of the Compliance and Stress Intensity Formulas for the Single Edge Crack Round Bar in Bending. In Fracture Mechanics for Ceramics, Rocks, and Concrete; ASTM International: West Conshohocken, PA, USA, 1981. [Google Scholar]
- Fowell, R.; Hudson, J.; Xu, C.; Zhao, X. Suggested method for determining mode I fracture toughness using cracked chevron notched Brazilian disc (CCNBD) specimens. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 7, 322A. [Google Scholar] [CrossRef]
- Amrollahi, H.; Baghbanan, A.; Hashemolhosseini, H. Measuring fracture toughness of crystalline marbles under modes I and II and mixed mode I–II loading conditions using CCNBD and HCCD specimens. Int. J. Rock Mech. Min. Sci. 2011, 48, 1123–1134. [Google Scholar] [CrossRef]
- Suo, Y.; Zhao, Y.; Fu, X.; He, W.; Pan, Z. Mixed-mode fracture behavior in deep shale reservoirs under different loading rates and temperatures. Pet. Sci. 2023. [Google Scholar] [CrossRef]
- Suo, Y.; Dong, M.; Wang, Z.; Gao, J.; Fu, X.; Pan, Z.; Xie, K.; Qi, T.; Wang, G. Characteristics of mixed-mode Ⅰ-Ⅱ fracture of bedding mud shale based on discrete element method. J. Pet. Sci. Eng. 2022, 219, 111135. [Google Scholar] [CrossRef]
- Ayatollahi, M.; Aliha, M.; Hassani, M. Mixed mode brittle fracture in PMMA—An experimental study using SCB specimens. Mater. Sci. Eng. A 2006, 417, 348–356. [Google Scholar] [CrossRef]
- Kuruppu, M.D.; Chong, K.P. Fracture toughness testing of brittle materials using semi-circular bend (SCB) specimen. Eng. Fract. Mech. 2012, 91, 133–150. [Google Scholar] [CrossRef]
- Zuo, J.-P.; Yao, M.-H.; Li, Y.-J.; Zhao, S.-K.; Jiang, Y.-Q.; Li, Z.-D. Investigation on fracture toughness and micro-deformation field of SCB sandstone including different inclination angles cracks. Eng. Fract. Mech. 2019, 208, 27–37. [Google Scholar] [CrossRef]
- Ameri, M.; Mansourian, A.; Pirmohammad, S.; Aliha, M.; Ayatollahi, M. Mixed mode fracture resistance of asphalt concrete mixtures. Eng. Fract. Mech. 2012, 93, 153–167. [Google Scholar] [CrossRef]
- Chandler, M.R.; Meredith, P.G.; Brantut, N.; Crawford, B. Fracture toughness anisotropy in shale. J. Geophys. Res. Solid Earth 2016, 121, 1706–1729. [Google Scholar] [CrossRef]
- Wu, M.Q. Numerical Simulation of Three—Point Bending of Hydraulic Concrete Side Slotting Specimen Based on MTS. Water Conserv. Sci. Technol. Econ. 2020, 26, 32–37. [Google Scholar]
- Li, X.B.; Zuo, Y.J.; Ma, C.D. Failure criterion of strain energy density and catastrophe theory analysis of rock subjected to static-dynamic coupling loading. Chin. J. Rock Mech. Eng. 2005, 24, 2814–2824. [Google Scholar]
- Hou, C.; Wang, Z.Y.; Wang, Z.H. Fracture behaviors of concrete CSTBD specimens by the modified MTS criterion under the condition of compression loading. Sci. Sin. Technol. 2016, 46, 377–386. [Google Scholar]
- Lim, I.L.; Johnston, I.W.; Choi, S.K.; Boland, J.N. Fracture testing of a soft rock with semi-circular specimens under three-point bending. Part 2—Mixed-mode. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 199–212. [Google Scholar] [CrossRef]
- Ayatollahi, M.; Aliha, M. Wide range data for crack tip parameters in two disc-type specimens under mixed mode loading. Comput. Mater. Sci. 2007, 38, 660–670. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).