Multi-Time Scale Economic Dispatch of Integrated Electricity and Natural Gas Systems with Flexibility Constraints Based on Chance-Constrained Programming
Abstract
1. Introduction
- (1)
- A mathematical model for the energy production, conversion, and storage of an IENGS is established, and a quasi-steady-state model of the natural gas pipeline network is built. Then, the obtained nonlinear optimization model is transformed into a linear model to facilitate the application of the powerful software tool CPLEX.
- (2)
- A multi-time scale economic dispatching model of an IENGS is proposed. According to the difference in prediction errors under different time scales, two different decision-making objectives are presented for two different scheduling periods.
- (3)
- Considering the flexibility in energy supply and load demand of the coupled system, the flexibility constraints are adjusted according to different time scales, and the chance-constrained programming is applied to the economic dispatch problem of an IENGS.
- (4)
- The chance-constrained programming is linearized by the sample average approximation approach (SAA).
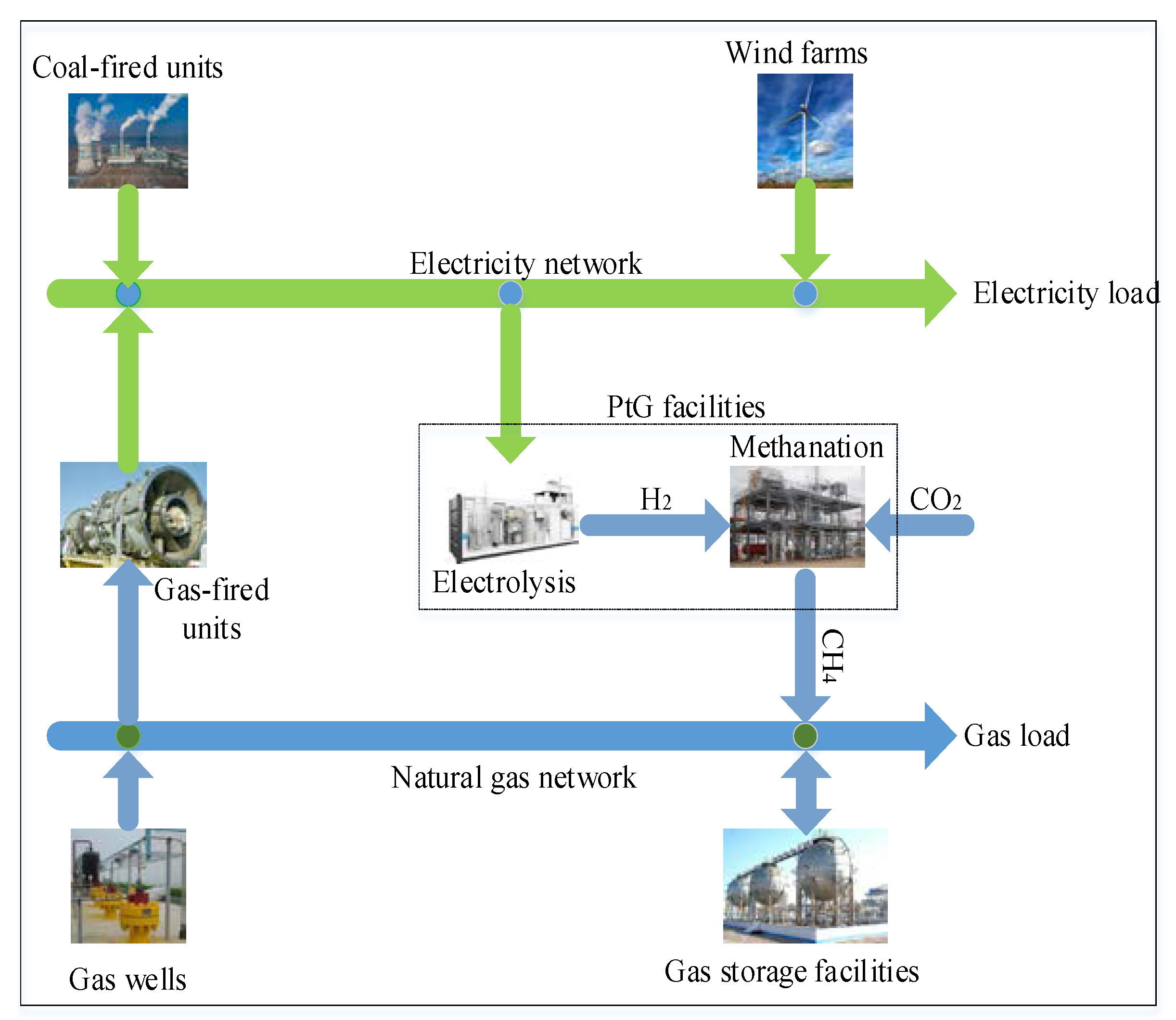
2. Multi-Energy Flexibility Model of the IENGS
2.1. Equipment Model
2.1.1. Power Generation Equipment
- (1)
- Thermal power unit
- (2)
- Wind power generation
2.1.2. Coupling Equipment
2.1.3. Gas Storage Facility
2.1.4. Power Flow
- (1)
- Power grid flow
- (2)
- Gas grid flow
2.2. Multi-Energy Flexibility
2.2.1. The Flexibility of Power Grid
2.2.2. The Flexibility of Gas Grid
2.3. Flexibility Constraints Based on Chance-Constrained Programming
2.3.1. Mathematical Expression of Flexibility Constraints
2.3.2. Transformation to Deterministic Problem
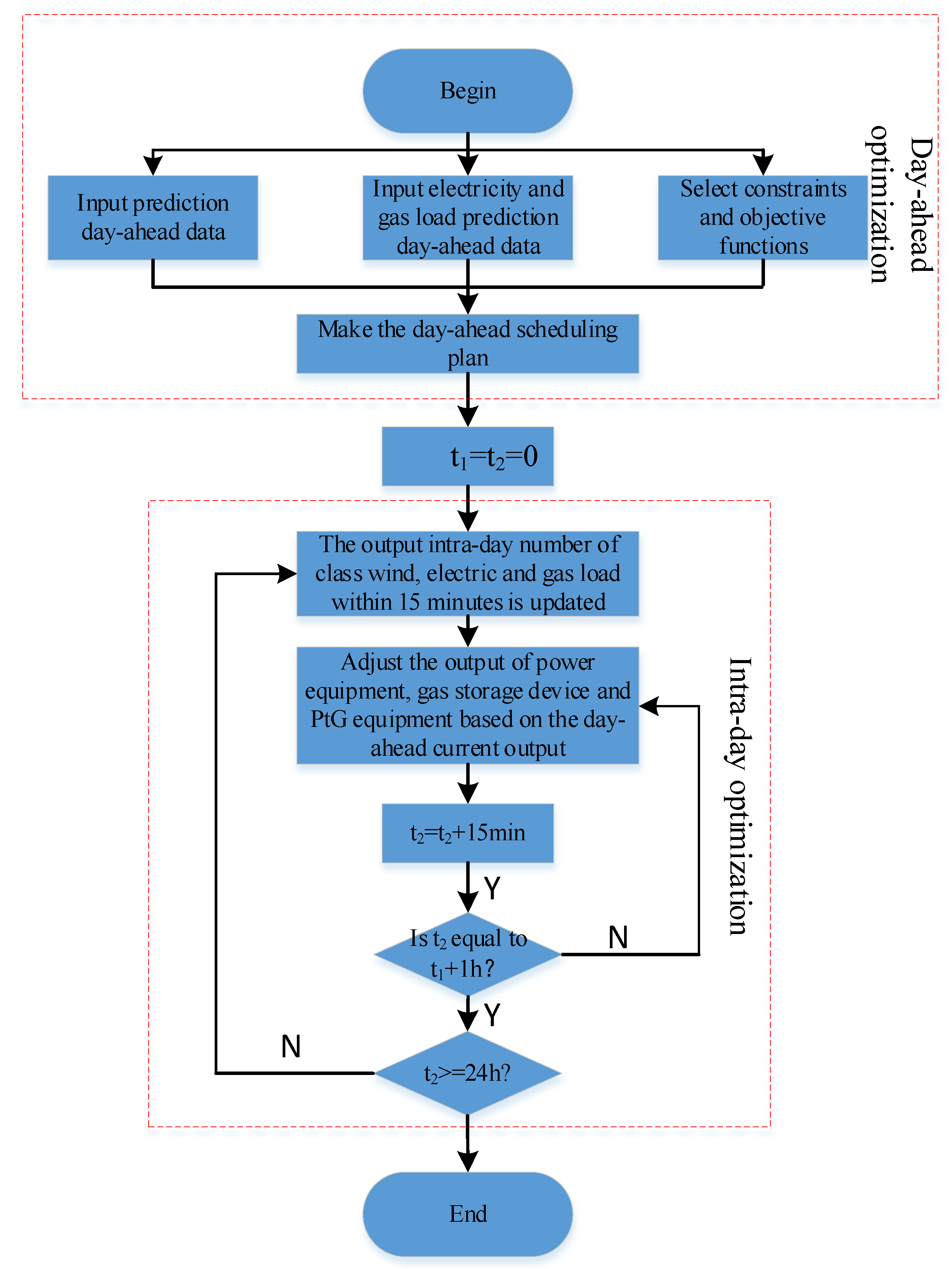
3. Multi-Time Scale Optimal Scheduling Strategy
3.1. Day-Ahead Optimization Model
3.1.1. Objective Function
3.1.2. Constraints
- (1)
- Equipment constraints are given by Equations (1)–(15).
- (2)
- The power balance constraints of the power grid and gas grid are given by Equations (16)–(33).
- (3)
- The multi-functional flexibility constraints are given by Equations (34)–(48).
3.2. Intra-Day Optimization Model
3.2.1. Objective Function
3.2.2. Constraints
- (1)
- The operation status of the equipment shall comply with the day-ahead operation plan:
- (2)
- The storage capacity of the heat supply network pipes at the beginning and end of each scheduling cycle is consistent with the day-ahead scheduling results.
3.3. Solution Method for Model
4. Case Studies
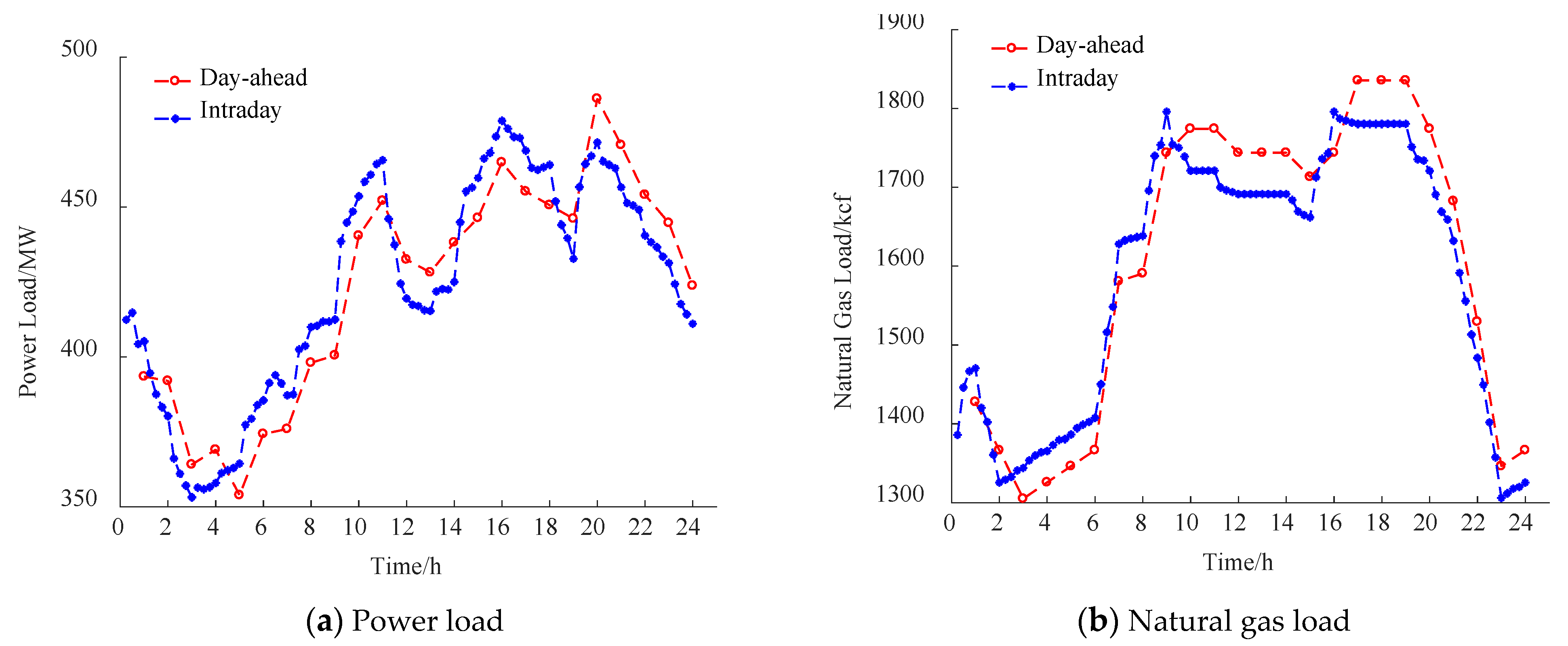
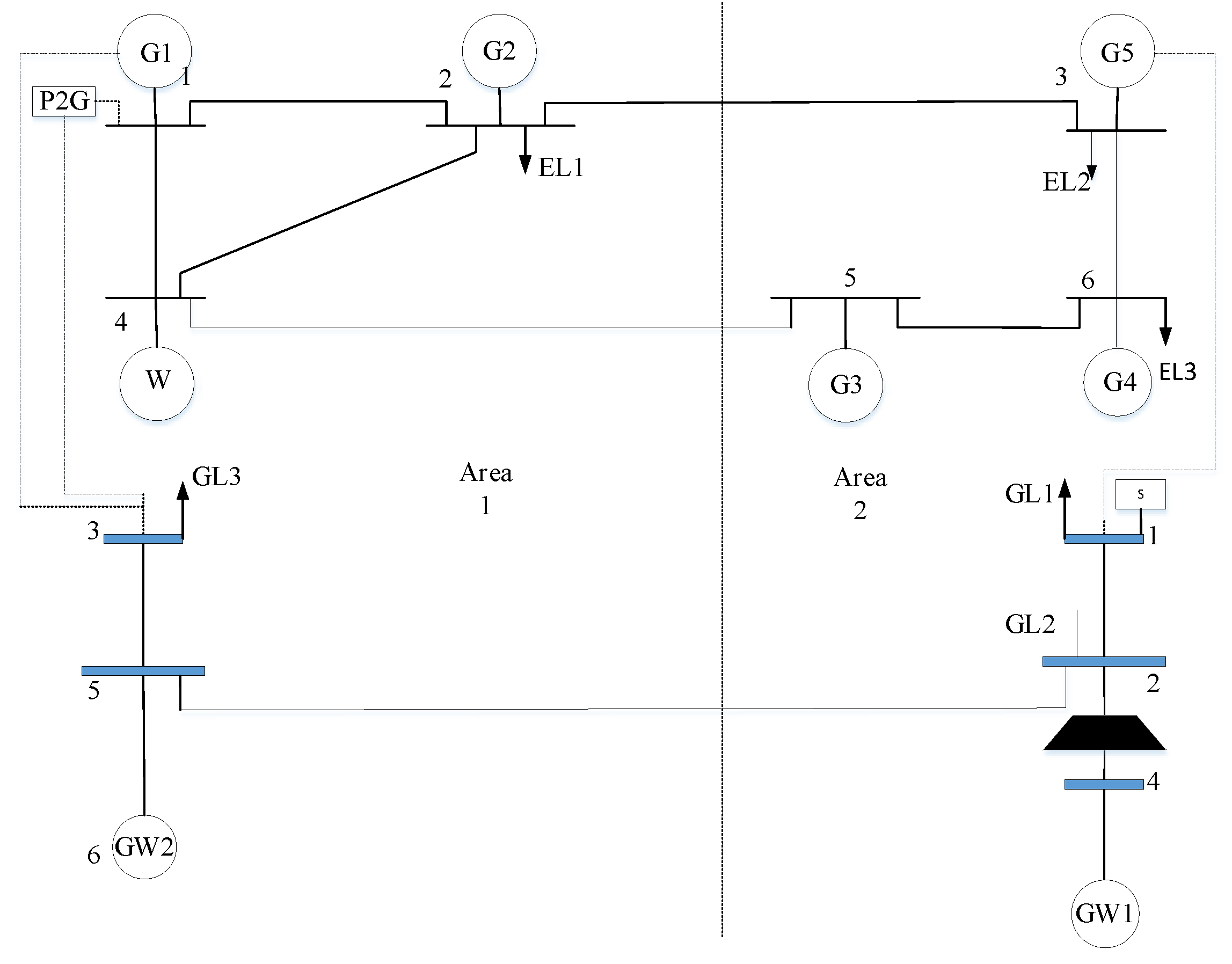
4.1. A Six-Node Power System Coupled with a Seven-Node Natural Gas System
4.2. Results and Analysis
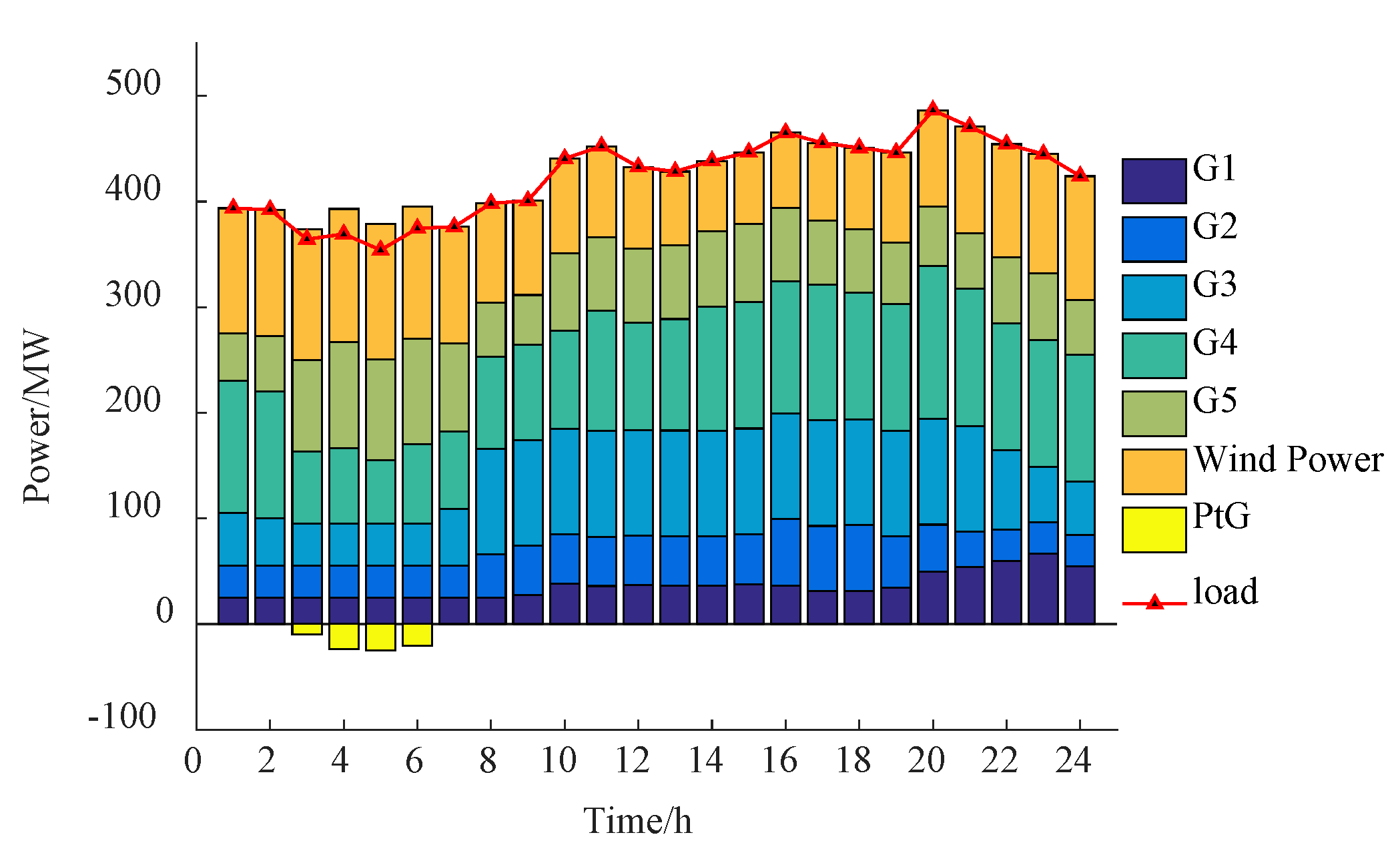
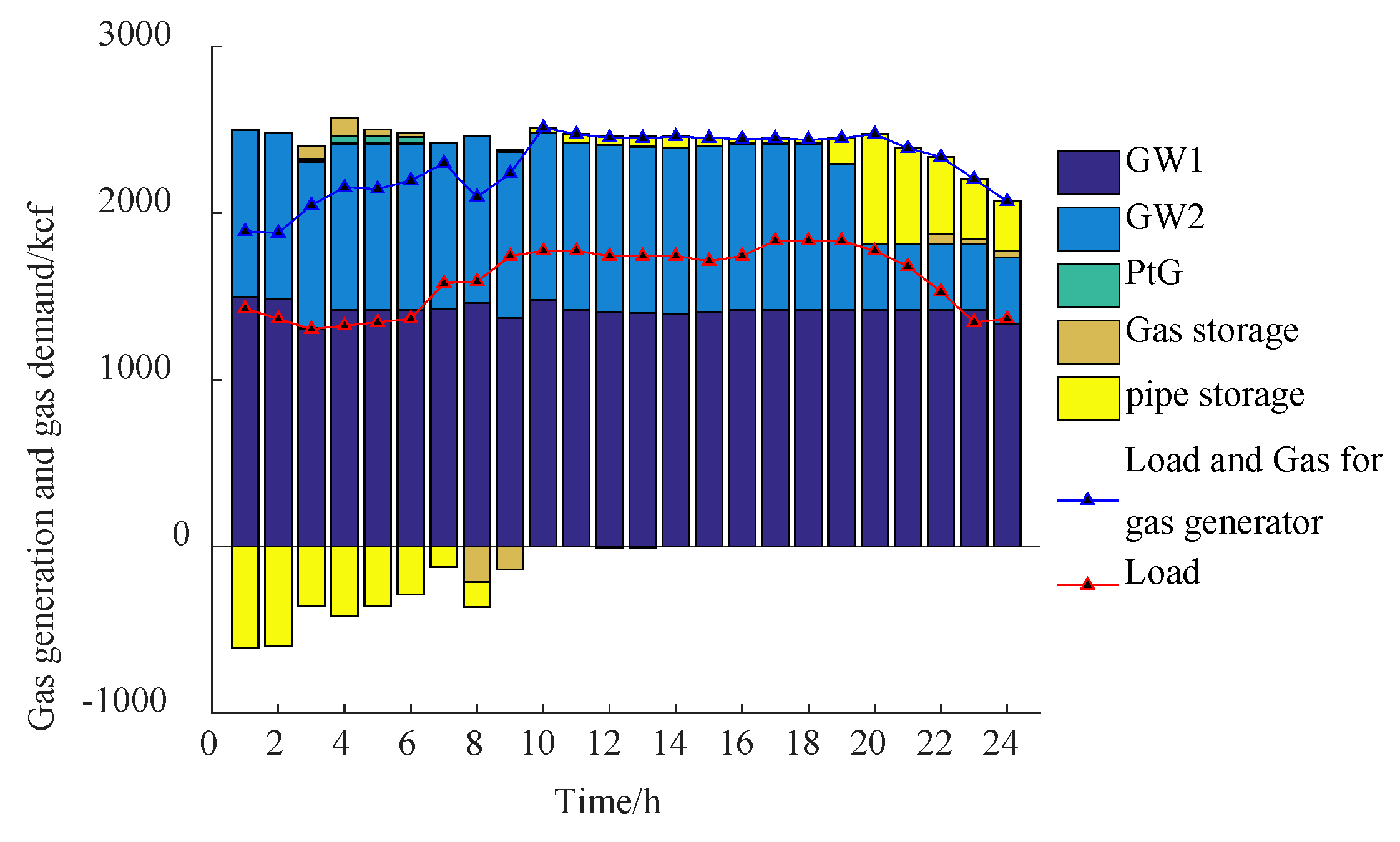
- (1)
- Power balance of the IENGS in Case 3
- (2)
- Analysis for flexibility constraints of Case2
- (3)
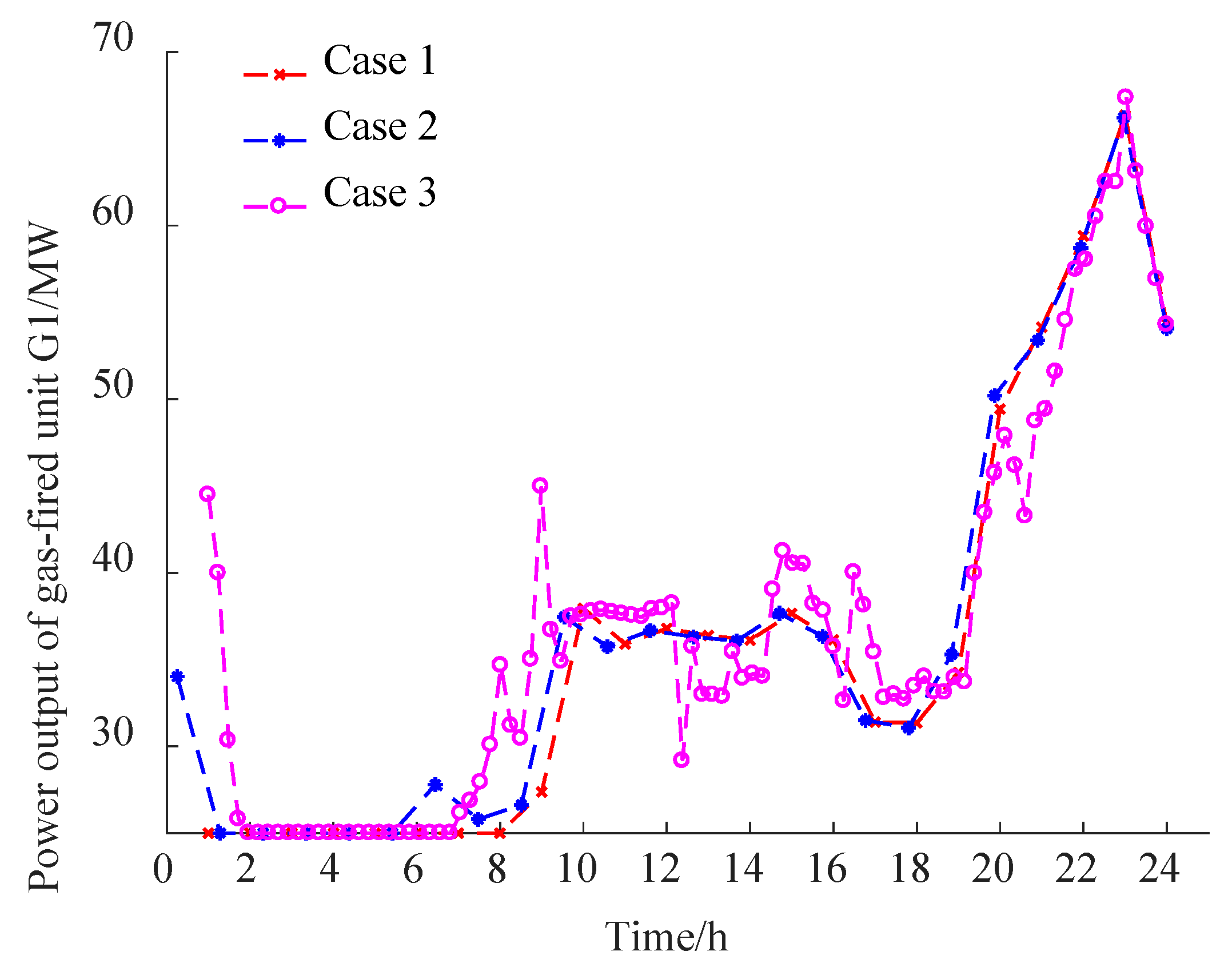
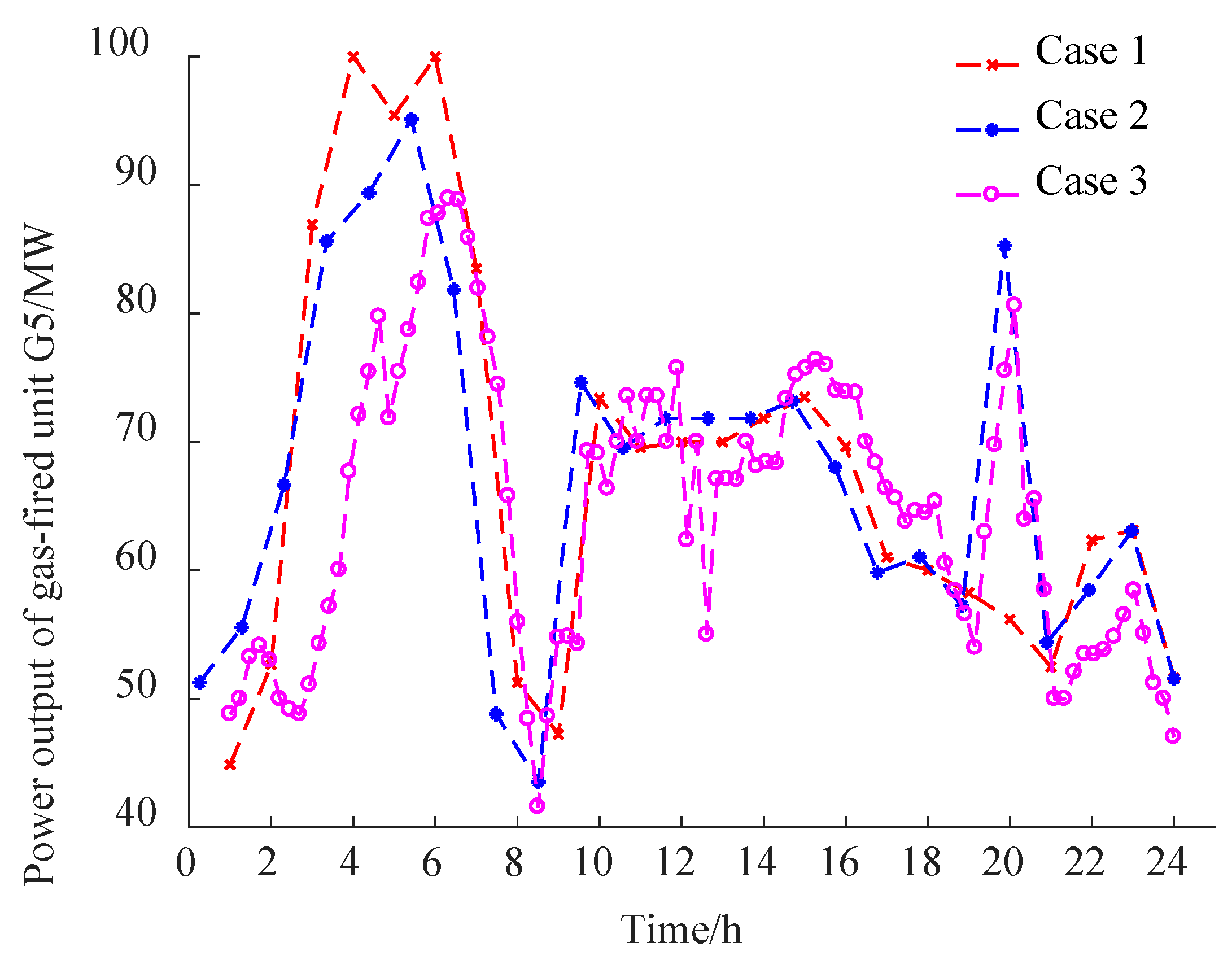
- Analysis for multi-time scale optimal scheduling strategy of Case 3
4.3. The 118-Bus Power System Coupled with 12-Node Natural Gas System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices and Sets | |
| Buses of the electric network and nodes of the gas network, respectively | |
| Indexes for thermal generation units, PtG (power to gas), and wind farms | |
| Transmission lines, buses of the line head and tail | |
| Gas pipelines, nodes of the pipeline head and tail | |
| Storage facilities and wells of the natural gas system | |
| Scheduling scale (hours, 15 min) | |
| ,, | Sets of time, coal-fired units and gas wells, respectively |
| , | Sets of PtG facilities and gas storage unit |
| , | Sets of generators and lines, respectively |
| Variables | |
| Fuel consumption of unit f at time t | |
| Natural gas produced by well w at time t (kcf) | |
| , | Unit prices of energy and natural gas, respectively |
| Input power of power-to-gas equipment (MW) and the level of natural gas storage equipment (kcf) at time t | |
| Bus voltage angle at time t (rad) | |
| Maximum power flow of line l (MW) | |
| Wind farm output, PtG converted power, node load, and power flow of line l at time t | |
| Pressure of pipe at time t | |
| Average flow, output flow, and input flow of pipeline p in time t (kcf/h) | |
| Average pressure of pipeline p at time t | |
| The gas storage capacity of pipeline p at time t and t-1 (kcf/h) | |
| The gas storage capacity of pipeline p at initial time and | |
| Gas well gas production flow, gas storage device, gas discharge flow (kcf/h) | |
| The conversion flow of PtG facilities, the consumption flow of gas unit f, the discharge and inflation flow of pipeline p (kcf/h) | |
| Gas load flow of node n | |
| Output power of unit f at time t and t-1 (MW) | |
| Power outputs of wind farm w at time t (MW) | |
| Net fluctuation value of wind farm w at time t (MW) | |
| Electrical energy is converted to an equivalent thermal coefficient | |
| Gas storage of gas storage device (kcf) | |
| The flow rate injected and released by the gas storage device (kcf/h) | |
| Flexibility provided by the unit i (MW) | |
| Flexibility provided by PtG facilities ptg (MW) | |
| The confidence level of the upward and downward flexibility | |
| Constants | |
| , | Unit costs for electric power consumed (USD/kWh) and natural gas released (USD) |
| Maximum and minimum unit output | |
| Gas turbine power generation efficiency and PtG conversion efficiency | |
| High calorific values of natural gas and hydrogen | |
| Maximum ramp down and up power of unit f | |
| The flexibility provided by unit f at time t | |
| Floor function of a real number | |
| sorting function to sort a vector in ascending order | |
| Power fluctuation penalty and energy storage penalty coefficient | |
| Actual output power and actual state of energy storage in actual operation | |
| Unit output power and energy storage status obtained by day-ahead scheduling | |
| Upper and lower limits of gas storage capacity | |
| The correlation matrix of wind power, PtG facilities, unit, and line | |
| Storage constant of pipe p | |
| Minimum and maximum compression ratios of compressors in pipeline p | |
| Fuel curve coefficients of coal-fired units f | |
Appendix A

References
- Karimi, M.; Rahimpour, M.R.; Rafiei, R.; Jafari, M.; Iranshahi, D.; Shariati, A. Reducing environmental problems and increasing saving energy by proposing new configuration for moving bed thermally coupled reactors. J. Nat. Gas Sci. Eng. 2014, 17, 136–150. [Google Scholar] [CrossRef]
- Lynch, M.; Devine, M.T.; Bertsch, V. The role of power-to-gas in the future energy system: Market and portfolio effects. Energy 2019, 185, 1197–1209. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, C.; Zhao, M. Coordination of integrated natural gas and electrical systems in day-ahead scheduling considering a novel flexible energy-use mechanism. Energy Convers. Manag. 2019, 196, 117–126. [Google Scholar] [CrossRef]
- Zhang, D.; Zhu, H.; Zhang, H.; Hui, H.; Liu, H.; Wu, T. An optimized design of residential integrated energy system considering the power-to-gas technology with multi-functional characteristics. Energy 2022, 238, 121774. [Google Scholar] [CrossRef]
- Zhong, J.; Li, Y.; Cao, Y.; Tan, Y.; Peng, Y.; Zeng, Z.; Cao, L. Stochastic optimization of integrated energy system considering network dynamic characteristics and psychological preference. J. Clean. Prod. 2020, 275, 122992. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, C.; Yan, S.; Yan, Y.; Guo, Y.; Shao, T.; Li, T.; Jia, X.; Hao, J. Dynamic modeling and characteristic analysis of natural gas network with hydrogen injections. Int. J. Hydrogen Energy 2022, 78, 33209–33223. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y. Environment-friendly and economical scheduling optimization for integrated energy system considering power-to-gas technology and carbon capture power plant. J. Clean. Prod. 2020, 276, 123348. [Google Scholar] [CrossRef]
- Chen, F.; Deng, H.; Chen, Y.; Wang, J.; Jiang, C.; Shao, Z. Distributed robust cooperative scheduling of multi-region integrated energy system considering dynamic characteristics of networks. Int. J. Electr. Power Energy Syst. 2023, 145, 108605. [Google Scholar] [CrossRef]
- Tang, J.; Ding, M.; Lu, S. Operational flexibility constrained intraday rolling dispatch strategy for CHP microgrid. IEEE Access 2019, 7, 96639–96649. [Google Scholar] [CrossRef]
- Clegg, S.; Mancarella, P. Integrated electrical and gas network flexibility assessment in low carbon multi-energy systems. IEEE Trans. Sustain. Energy 2016, 7, 718–731. [Google Scholar] [CrossRef]
- Su, X.; Bai, X.; Zheng, Y. Data-driven Robust Dispatch of Integrated Electricity-gas Energy Systems Considering Uncertainty of Wind Power. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Mu, Y.; Xu, Y.; Cao Yan Chen, W.; Jia, H.; Yu, X.; Jin, X. A two-stage scheduling method for integrated community energy system based on a hybrid mechanism and data-driven model. Appl. Energy 2022, 323, 119683. [Google Scholar] [CrossRef]
- Hamza, A.; Woan-Ho, P.; Mark, B.; Yun-Su, K. Two-Stage stochastic optimization for operating a Renewable-Based Microgrid. Appl. Energy 2022, 325, 119848. [Google Scholar]
- Firmansyah, N.; Makbul, A.; Ahmad, H.; Houssem, R.; Muhyaddin, R.; Rifqi, F.; Mustafa, M. Stochastic optimization for the scheduling of a grid-connected microgrid with a hybrid energy storage system considering multiple uncertainties. Energy Rep. 2022, 8, 7444–7456. [Google Scholar]
- Arsalan, N.; Mahdi, P.; Michal, J.; Matti, L.; Zbigniew, L. A max–min–max robust optimization model for multi-carrier energy systems integrated with power to gas storage system. J. Energy Storage 2022, 48, 103933. [Google Scholar]
- Arsalan, N.; Mahdi, P.; Michal, J.; Matti, L.; Zbigniew, L. A medium-term hybrid IGDT-Robust optimization model for optimal self scheduling of multi-carrier energy systems. Energy 2022, 238, 121661. [Google Scholar]
- Wang, H.; Xing, H.; Luo, Y.; Zhang, W. Optimal scheduling of micro-energy grid with integrated demand response based on chance-constrained programming. Int. J. Electr. Power Energy Syst. 2023, 144, 108602. [Google Scholar] [CrossRef]
- Liang, W.; Lin, S.; Liu, M. Stochastic economic dispatch of regional integrated energy system considering the pipeline dynamics using improved approximate dynamic programming. Int. J. Electr. Power Energy Syst. 2022, 141, 108190. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Chen, S.; Zhao, Y.; Dong, X.; Han, X. Multitime Scale Co-Optimized Dispatch for Integrated Electricity and Natural Gas System Considering Bidirectional Interactions and Renewable Uncertainties. IEEE Trans. Ind. Appl. 2022, 58, 5317–5327. [Google Scholar] [CrossRef]
- Yi, Z.; Xu, Y.; Gu, W.; Wu, W. A Multi-Time-Scale Economic Scheduling Strategy for Virtual Power Plant Based on Deferrable Loads Aggregation and Disaggregation. IEEE Trans. Sustain. Energy 2020, 11, 1332–1346. [Google Scholar] [CrossRef]
- Cheng, Z.; Jia, D.; Li, Z.; Si, J.; Xu, S. Multi-time scale dynamic robust optimal scheduling of CCHP microgrid based on rolling optimization. Int. J. Electr. Power Energy Syst. 2022, 139, 107957. [Google Scholar] [CrossRef]
- Wu, G.; Xiang, Y.; Liu, J.Y. Decentralized day-ahead scheduling of multi-area integrated electricity and natural gas systems considering reserve optimization. Energy 2020, 198, 117271. [Google Scholar] [CrossRef]
- Correa-Posada, C.; Sánchez-Martın, P. Integrated power and natural gas model for energy adequacy in short-term operation. IEEE Trans. Power Syst. 2015, 30, 3347–3355. [Google Scholar] [CrossRef]
- Liu, H.; Fan, Z.; Xie, H.; Wang, N. Distributionally Robust Joint Chance-Constrained Dispatch for Electricity–Gas–Heat Integrated Energy System Considering Wind Uncertainty. Energies 2022, 15, 1796. [Google Scholar] [CrossRef]
- Tran, T.H.; Frenc, S.; Ashman, R. Linepick planning models for gas transmission network under uncertainty. Eur. J. Oper. Res. 2018, 268, 688–702. [Google Scholar] [CrossRef]
- MacKinnon, L.; Li, H.; Swartz, C.L.E. Robust model predictive control with embedded multi-scenario closed-loop prediction. Comput. Chem. Eng. 2021, 149, 107283. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Y.; Wang, J. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar] [CrossRef]
- Soliman, M.S.; Belkhier, Y.; Ullah, N.; Achour, A.; Alharbi, Y.M.; Al Alahmadi, A.A.; Abeida, H.; Khraisat, Y.S.H. Supervisory energy management of a hybrid battery/PV/tidal/wind sources integrated in DC-microgrid energy storage system. Energy Rep. 2021, 7, 7728–7740. [Google Scholar] [CrossRef]
- Sahri, Y.; Belkhier, Y.; Tamalouzt, S.; Ullah, N.; Shaw, R.N.; Chowdhury, S.; Techato, K. Energy management system for hybrid PV/wind/battery/fuel cell in microgrid-based hydrogen and economical hybrid battery/super capacitor energy storage. Energies 2021, 14, 5722. [Google Scholar] [CrossRef]
- He, L.C.; Lu, Z.G.; Geng, L.J. Low-carbon economic dispatch for electricity and natural gas systems considering carbon capture systems and power-to-gas. Appl. Energy 2018, 224, 357–370. [Google Scholar] [CrossRef]
- He, L.C.; Lu, Z.G.; Geng, L.J. Environmental economic dispatch of integrated regional energy system considering integrated demand response. Int. J. Electr. PowerEnergy Syst. 2020, 116, 105525. [Google Scholar] [CrossRef]







| Authors | Studied Issues | System Settings | Solution Method | Contribution |
|---|---|---|---|---|
| [4] | Modeling of equipment in IENGS | CHP, Fr, AC, PV | MILP, GAMS/CPLEX | The electrolytic cell and the methanation reactor in P2G are discussed in detail |
| [5] | 54-node IENGS network | MILP, GAMS/CPLEX | The IENGS model considering the dynamic characteristics of the gas network is proposed | |
| [6] | 14-node gas network | dynamic simulation | Dynamic model of the natural gas network is established | |
| [7] | PV, GT, ES, PtG, CCS | MILP | P2G is extended into the IENGS with a high wind power penetration level | |
| [8] | CHP, WP, GT | MISOCP | The dynamic transmission model of the gas network can converge reliably and provide a flexible scheduling scheme for the IENGS | |
| [9] | Flexibility of the IENGS | a hypothetical microgrid in North China | GUROBI | Propose an operational flexibility metric to quantify the ability of the microgrid |
| [10] | 29 busbar network | DC OPF | A novel metric using zonal linepack is introduced to assess the IENGS flexibility | |
| [11] | CHP, WP, GT, DR | MILP | Flexibility is described by a probability distribution | |
| [12] | Dealing with uncertain problems | EPS, DHS, NGS | two-stage stochastic | A two-stage stochastic scheduling scheme is proposed for the IENGS |
| [13] | PV, ESS, UPS, ATS | two-stage stochastic | A two-stage stochastic optimization for a renewable-based microgrid is proposed | |
| [14] | ORNL-DESS | stochastic scheduling | Stochastic scheduling of a hybrid energy storage system is proposed. | |
| [15] | CHP, PtG, ESS, WT | robust scheduling | Proposing a new approach to robust max–min–max self-scheduling of the IENGS | |
| [16] | CHP, DA, PtG, ESS | IGDT-Robust | Proposing a linear hybrid IGDT-robust optimization model for operation of the IENGS | |
| [17] | EV, CHP, PtG, IDR | MILP | Proposing a chance-constrained programming model in the background of renewable uncertainty | |
| [18] | 54-node IENGS network | ADP method | An SMES model of the IENGS considering the pipeline dynamics is proposed | |
| [19] | Multi-time scale | IEEE118-GAS40 | MISOCP | Presenting a multi-time scale dispatch for the IENGS considering the interactions |
| [20] | DGs, RES, ESS, DL | MILP | Proposing a multi-time scale economic scheduling strategy for a virtual power plant | |
| [21] | CCHP MG | MATLAB/YALMIP | Proposes a multi-time scale scheduling of CCHP microgrid based on rolling optimization |
| Case | Total Operational Cost (USD) | Fuel Cost of Coal-Fired Units (USD) | Gas Production Cost of Gas Wells (USD) | PtG Operating Costs (USD) | Operational Cost of Gas Storage Facility (USD) |
|---|---|---|---|---|---|
| 1 | 471,135.24 | 240,537.60 | 229,934.61 | 287.61 | 375.42 |
| 2 | 474,366.36 | 243,859.15 | 229,891.37 | 262.37 | 353.47 |
| 3 | 471,524.99 | 243,818.82 | 226,972.06 | 109.48 | 624.63 |
| Case | Total Operational Cost (USD) | Fuel Cost of Coal-fired Units (USD) | Gas Production Cost (USD) | PtG Operating Cost (USD) | Gas Storage Cost (USD) |
|---|---|---|---|---|---|
| 1 | 5,705,800.24 | 3,449,438.71 | 2,252,534.56 | 3102.81 | 724.16 |
| 2 | 5,730,908.70 | 3,465,589.73 | 2,261,325.91 | 3156.30 | 836.76 |
| 3 | 5,714,642.46 | 3,452,225.73 | 2,257,681.68 | 3415.17 | 1319.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Cheng, H.; Liu, Z.; Zhang, J.; He, L.; Liu, Y.; Lu, Z. Multi-Time Scale Economic Dispatch of Integrated Electricity and Natural Gas Systems with Flexibility Constraints Based on Chance-Constrained Programming. Processes 2023, 11, 1987. https://doi.org/10.3390/pr11071987
Yang P, Cheng H, Liu Z, Zhang J, He L, Liu Y, Lu Z. Multi-Time Scale Economic Dispatch of Integrated Electricity and Natural Gas Systems with Flexibility Constraints Based on Chance-Constrained Programming. Processes. 2023; 11(7):1987. https://doi.org/10.3390/pr11071987
Chicago/Turabian StyleYang, Peng, Huilin Cheng, Zhenyu Liu, Jing Zhang, Liangce He, Yujie Liu, and Zhigang Lu. 2023. "Multi-Time Scale Economic Dispatch of Integrated Electricity and Natural Gas Systems with Flexibility Constraints Based on Chance-Constrained Programming" Processes 11, no. 7: 1987. https://doi.org/10.3390/pr11071987
APA StyleYang, P., Cheng, H., Liu, Z., Zhang, J., He, L., Liu, Y., & Lu, Z. (2023). Multi-Time Scale Economic Dispatch of Integrated Electricity and Natural Gas Systems with Flexibility Constraints Based on Chance-Constrained Programming. Processes, 11(7), 1987. https://doi.org/10.3390/pr11071987





