Optimization of Levenberg Marquardt Algorithm Applied to Nonlinear Systems
Abstract
1. Introduction
2. Related Work
3. Optimization and Identification of NS Model Based on LM-BPNN
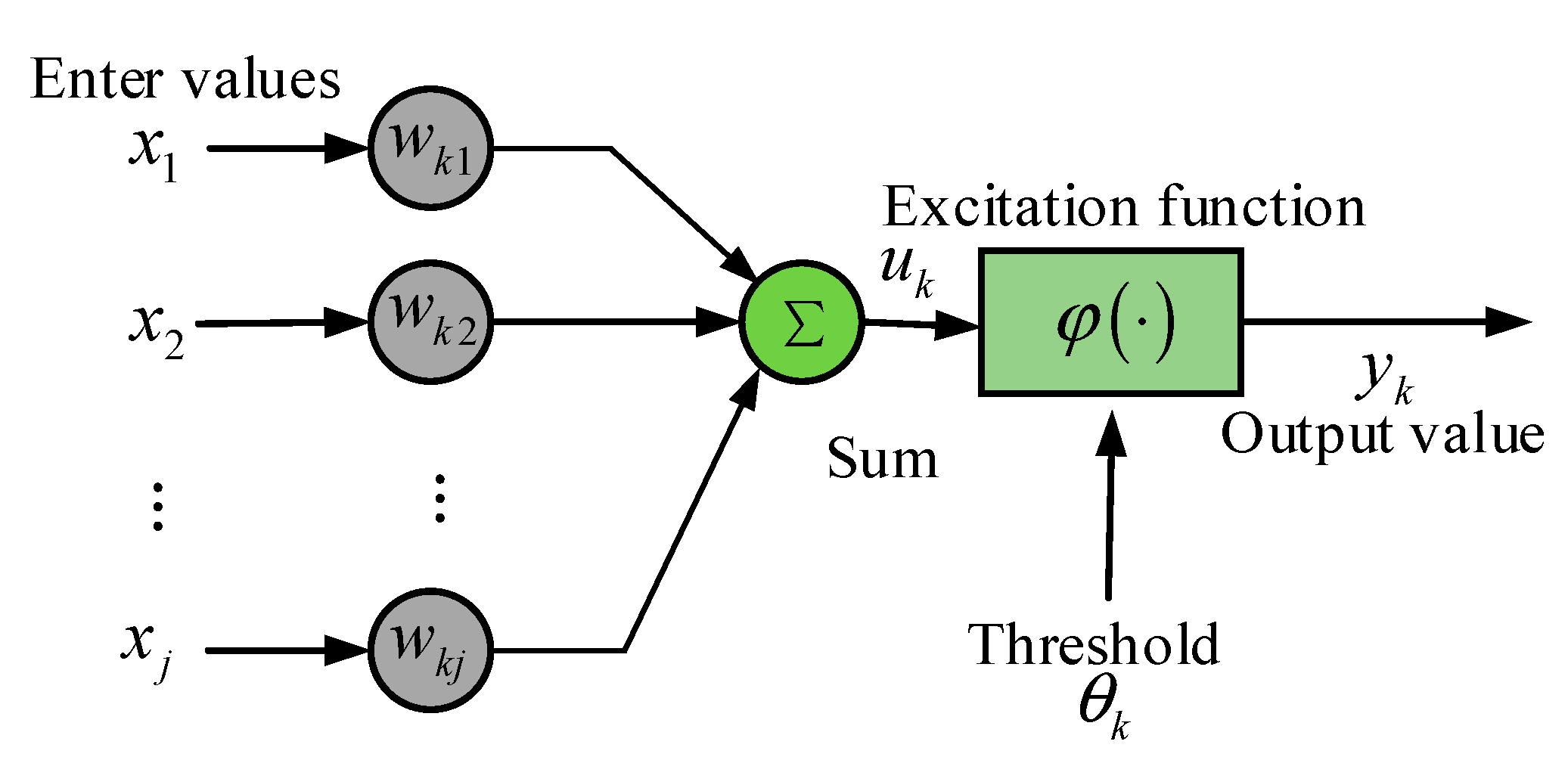
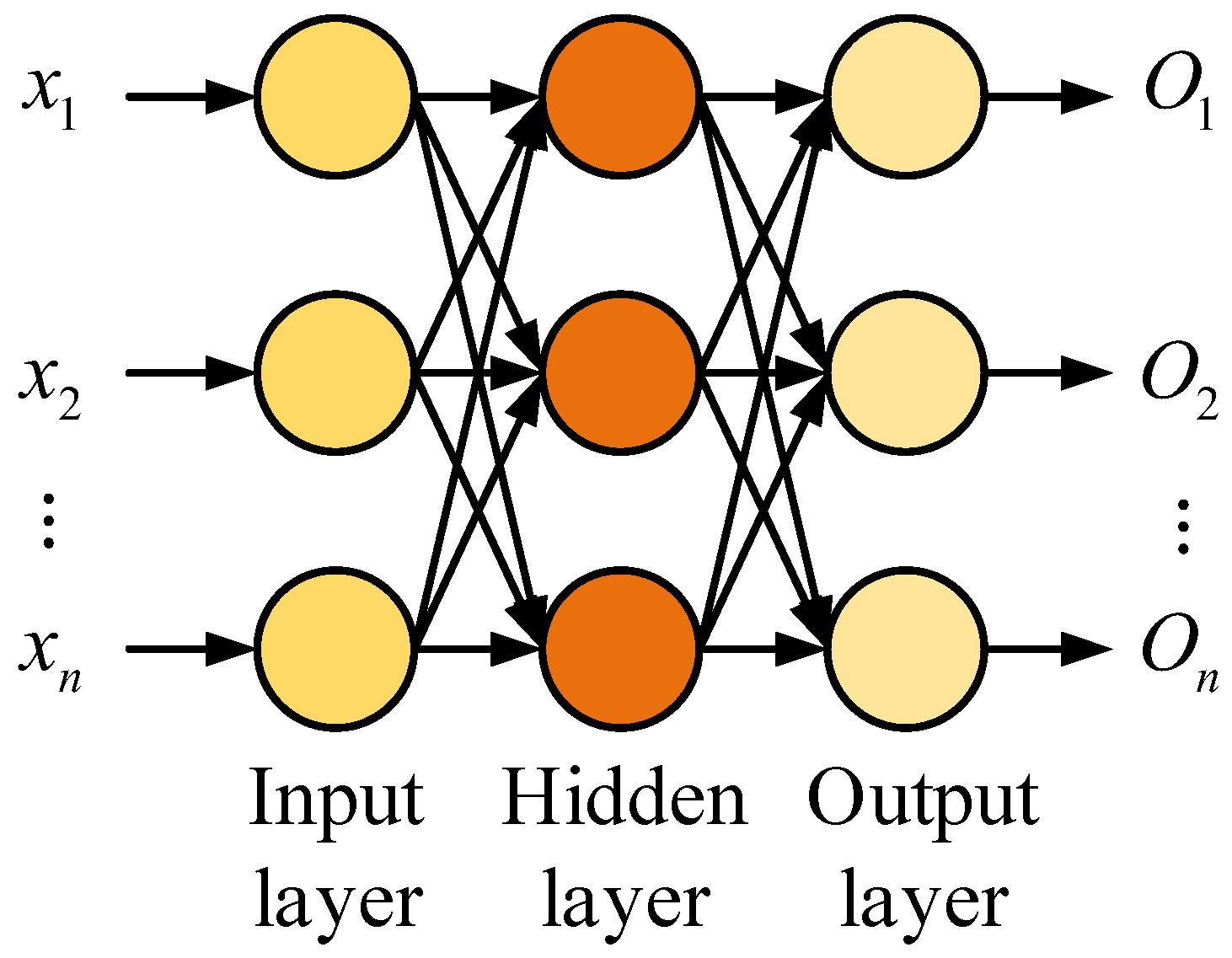
3.1. Construction of NS Strategic Control Method Based on BPNN
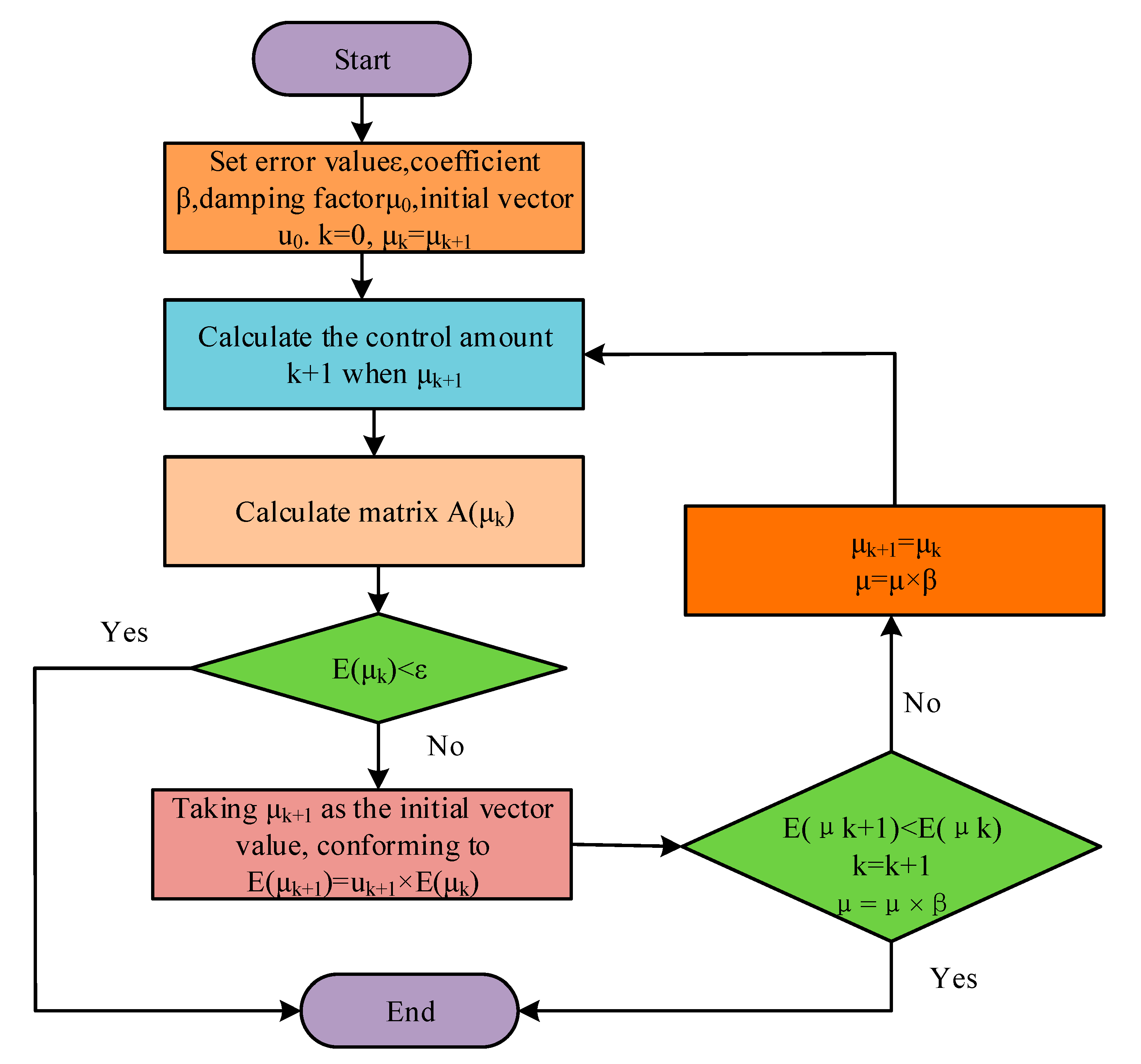
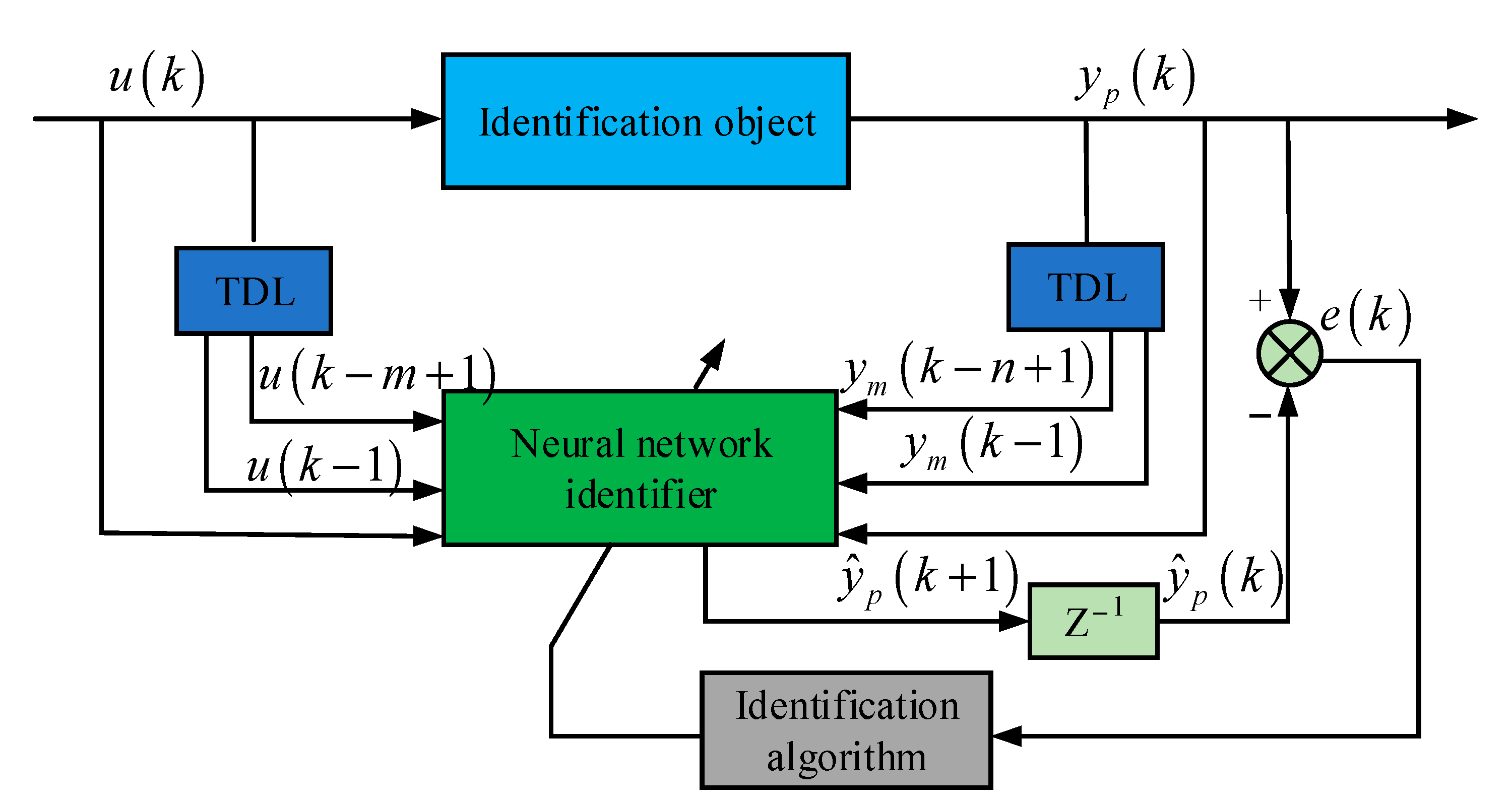
3.2. Construction of NS Strategic Control Method Based on Optimized BPNN
4. Simulation Analysis Based on LM-BP Optimization Algorithm in Nss
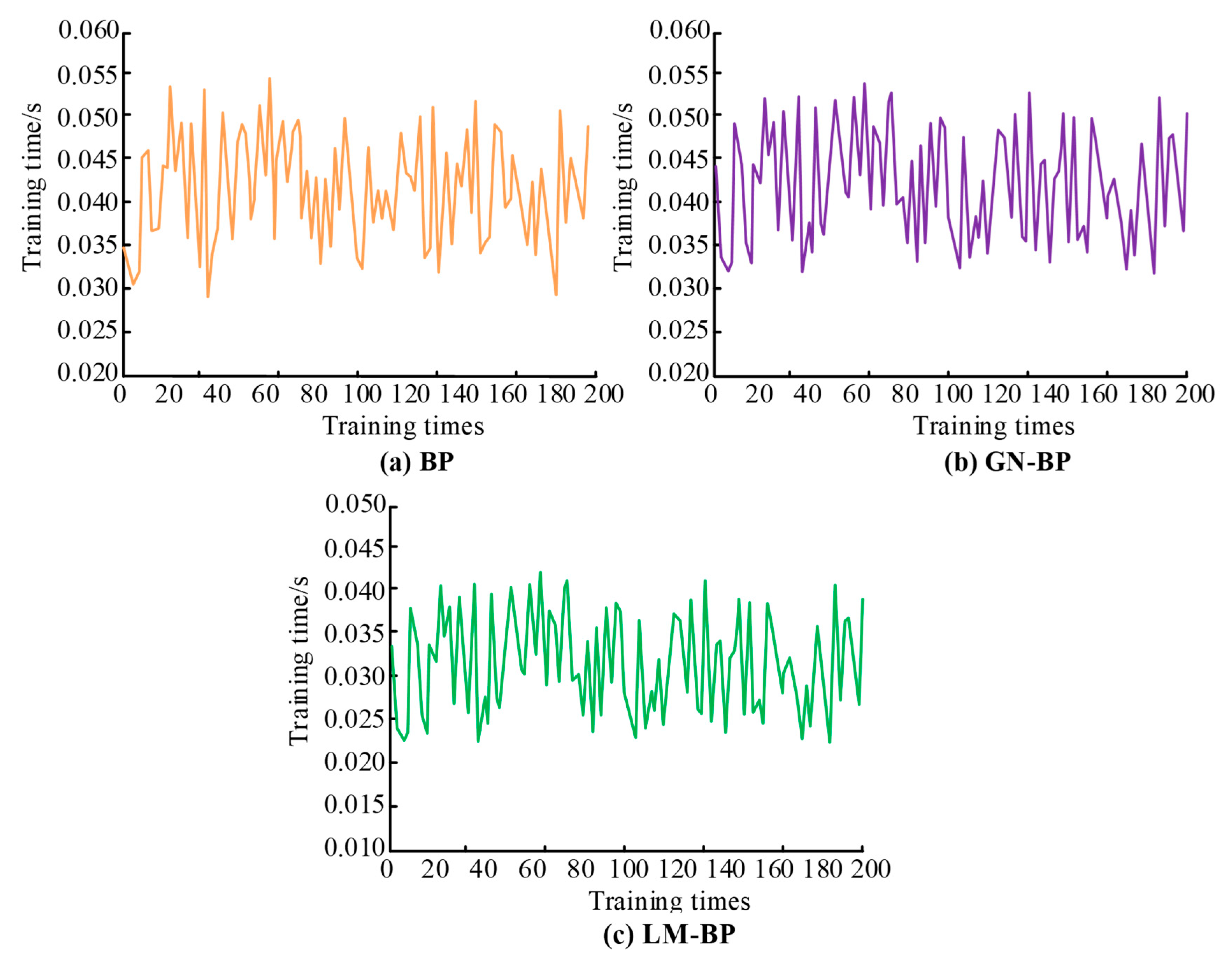
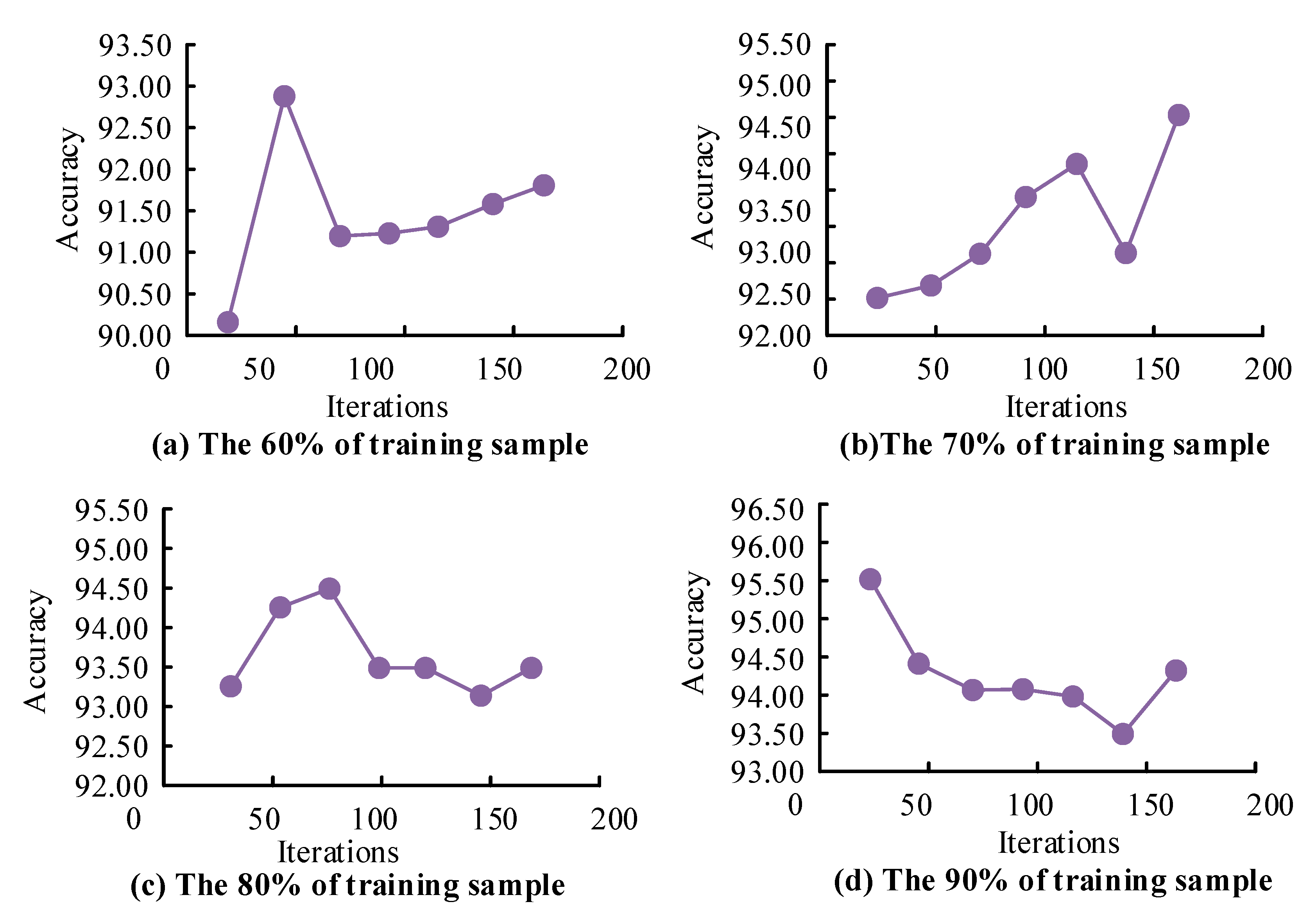
4.1. Performance Analysis of LM-BP-Based Optimization Algorithms
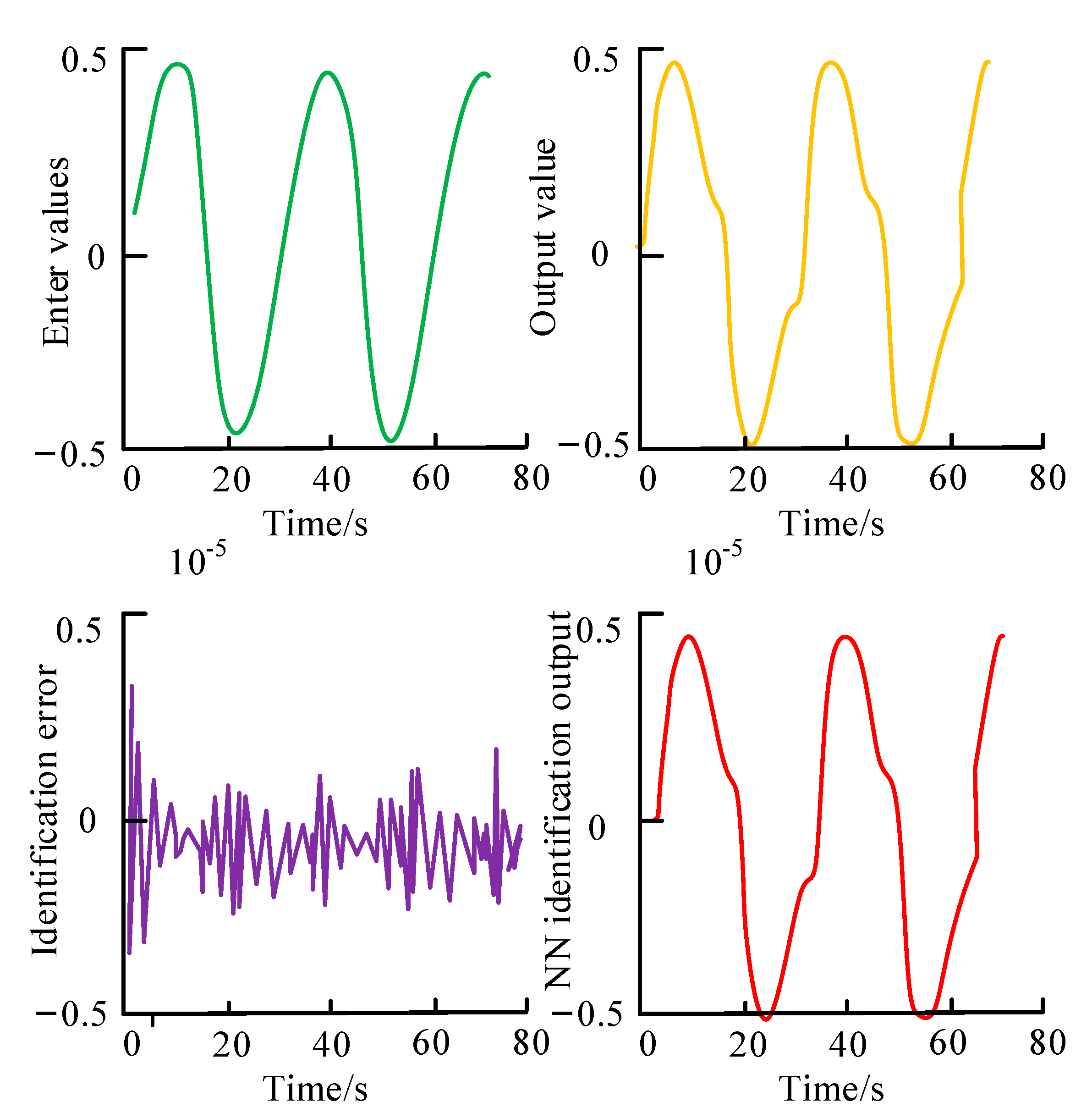
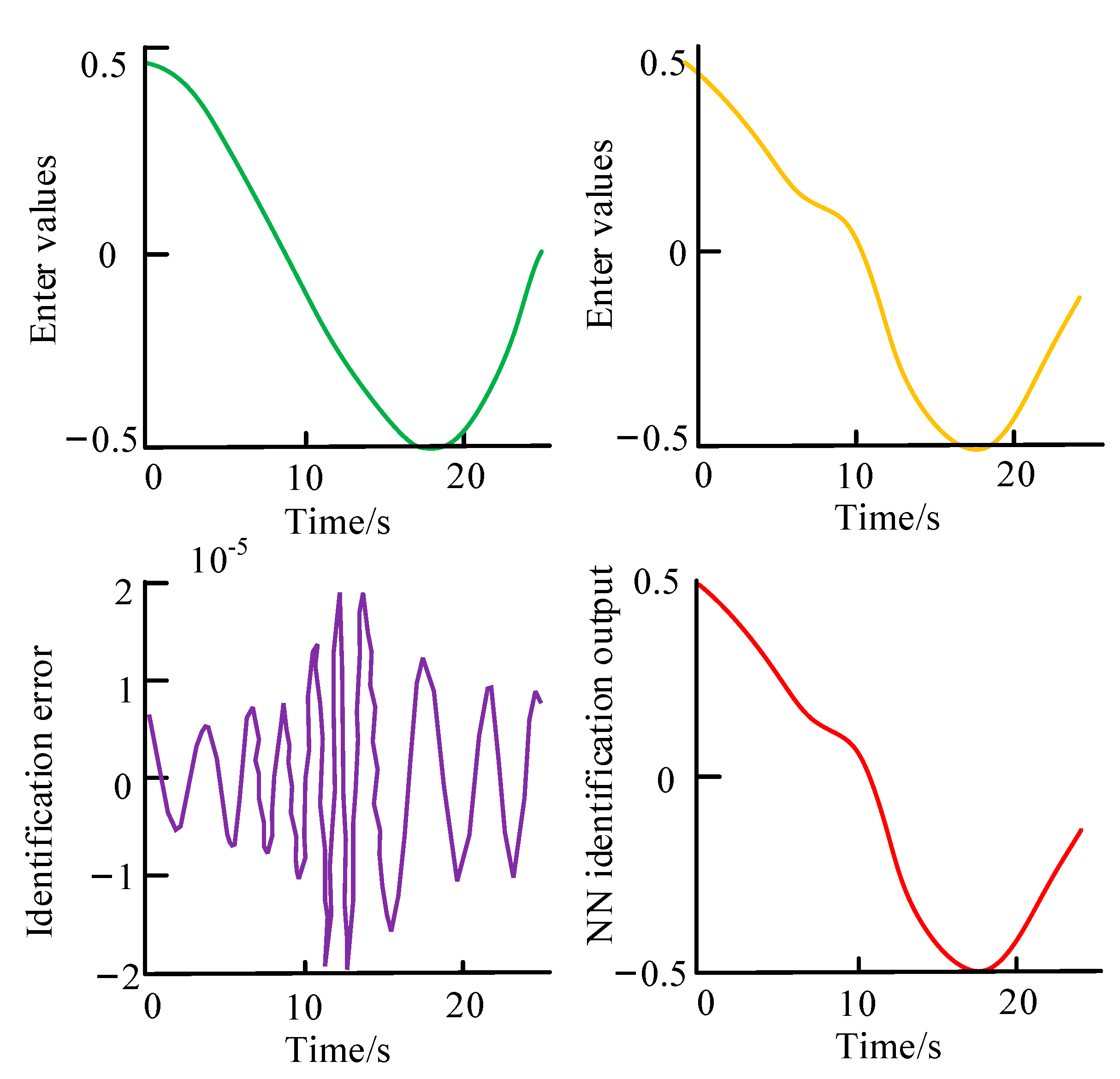
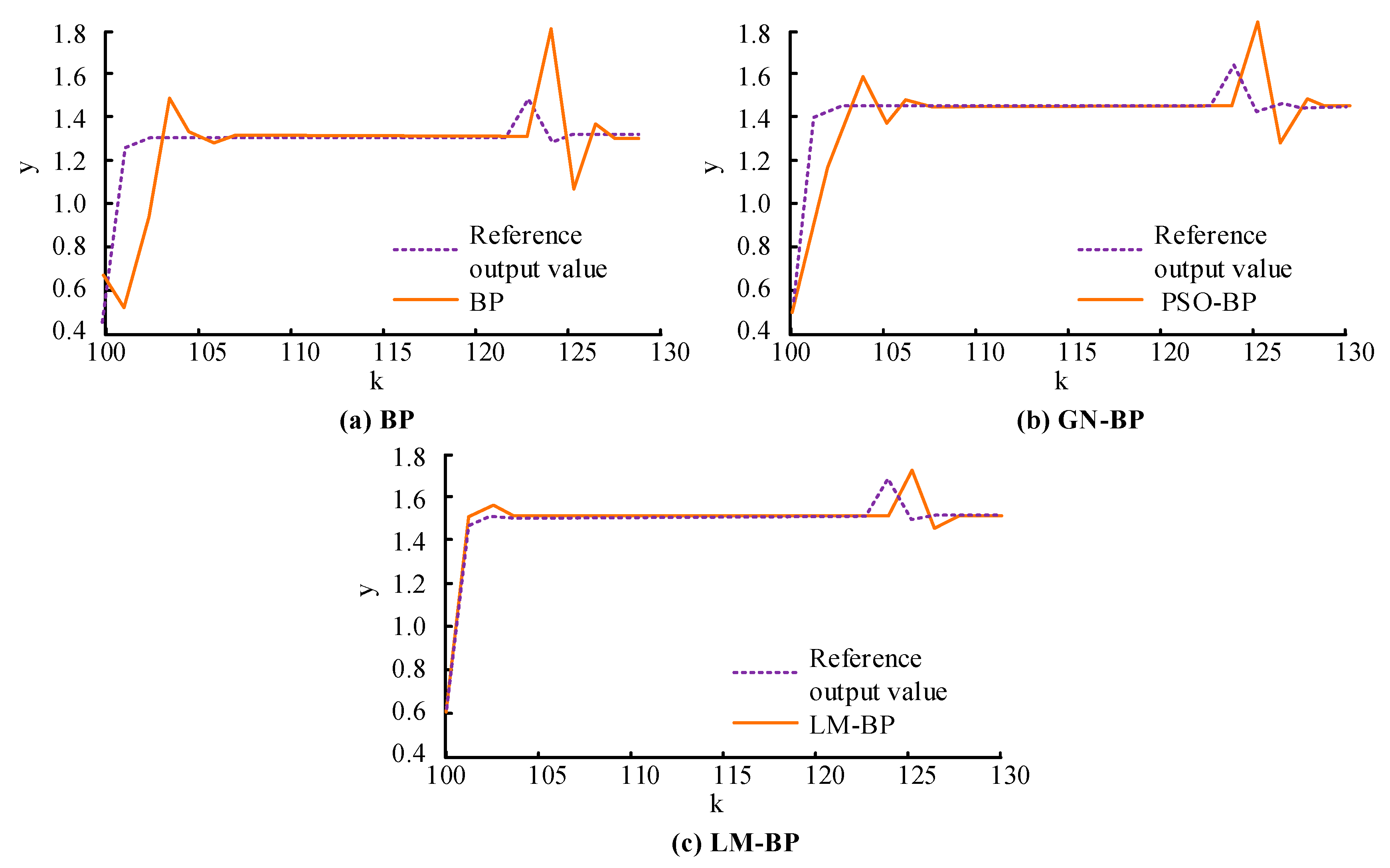
4.2. Application Analysis of LM-BP Optimization Algorithm in NSs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mariappan, M.; Tamilselvan, A. An efficient numerical method for a nonlinear system of singularly perturbed differential equations arising in a two-time scale system. J. Appl. Math. Comput. 2022, 68, 1069–1086. [Google Scholar] [CrossRef]
- Alabedalhadi, M. Exact travelling wave solutions for nonlinear system of spatiotemporal fractional quantum mechanics equations. Alex. Eng. J. 2022, 61, 1033–1044. [Google Scholar] [CrossRef]
- Jin, H.Y.; Wang, Z.A. Global stabilization of the full attraction-repulsion Keller-Segel system. Discret. Contin. Dyn. Syst. -Ser. A 2020, 40, 3509–3527. [Google Scholar] [CrossRef]
- Mazumdar, S.; Gangopadhyay, G. Centre manifold analysis of 3-d nonlinear system and kinetic stability of protein assembly. J. Appl. Nonlinear Dyn. 2022, 11, 139–152. [Google Scholar] [CrossRef]
- Kandel, S.; Maddali, S.; Nashed, Y.S.G.; Hruszkewycz, S.O.; Jacobsen, C.; Allain, M. Efficient ptychographic phase retrieval via a matrix-free Levenberg-Marquardt algorithm. J. Opt. Express 2021, 29, 23019–23055. [Google Scholar] [CrossRef] [PubMed]
- Gan, H.; Xu, C.; Hou, W.; Guo, J.F.; Liu, K.; Xue, Y.J. Spatiotemporal graph convolutional network for automated detection and analysis of social behaviours among pre-weaning piglets. J. Biosyst. Eng. 2022, 217, 102–114. [Google Scholar] [CrossRef]
- Almaiah, M.A.; Zahrani, M.A. Multilayer neural network based on mimo and channel estimation for impulsive noise environment in mobile wireless networks. Int. J. Adv. Trends Comput. Sci. Eng. 2020, 9, 315–321. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Y.; Lu, T.; Dang, S.L.; Kong, Z.M. Metering equipment running error estimation model based on genetic optimized LM algorithm. J. Comput. Methods Sci. Eng. 2022, 22, 197–205. [Google Scholar] [CrossRef]
- Shi, Q.; Xu, Q.; Zhang, J. Amended DV-hop scheme based on N-gram model and weighed LM algorithm. Electron. Lett. 2020, 56, 247–250. [Google Scholar] [CrossRef]
- Deb, N.; Pal, N. Interaction behavior and load sharing pattern of piled raft using nonlinear regression and LM algorithm-based artificial neural network. Front. Struct. Civ. Eng. 2021, 15, 1181–1198. [Google Scholar] [CrossRef]
- Niu, Y.; Zhou, Y.Q.; Luo, Q. Optimize star sensor calibration based on integrated modeling with hybrid WOA-LM algorithm. J. Intell. Fuzzy Syst. 2020, 38, 2691–2693. [Google Scholar] [CrossRef]
- Bilski, J.; Kowalczyk, B.; Marchlewska, A.; Zurada, J.M. Local levenberg-marquardt algorithm for learning feedforwad neural networks. J. Artif. Intell. Soft Comput. Res. 2020, 10, 299–316. [Google Scholar] [CrossRef]
- Li, X.; Sun, Y. Stock intelligent investment strategy based on support vector machine parameter optimization algorithm. Neural Comput. Appl. 2020, 32, 1765–1775. [Google Scholar] [CrossRef]
- Li, K.; Ji, L.; Yang, S.; Li, H.; Liao, X. Couple-group consensus of cooperative–competitive heterogeneous multiagent systems: A fully distributed event-triggered and pinning control method. IEEE Trans. Cybern. 2022, 52, 4907–4915. [Google Scholar] [CrossRef]
- Li, B.; Tan, Y.; Wu, A.; Duan, G. A distributionally robust optimization based method for stochastic model predictive control. IEEE Trans. Autom. Control. 2021, 67, 5762–5776. [Google Scholar] [CrossRef]
- He, D.; Wang, H.; Tian, Y. An α-variable model-free prescribed-time control for nonlinear system with uncertainties and disturbances. Int. J. Robust Nonlinear Control. 2022, 32, 5673–5693. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, R.; Kaiping, Y.U.; Bowen, Z. Nonlinear system identification framework of folding fins with freeplay using backbone curves. Chin. J. Aeronaut. 2022, 35, 183–194. [Google Scholar] [CrossRef]
- Kien, C.V.; Anh, H.; Son, N.N. Adaptive inverse multilayer fuzzy control for uncertain nonlinear system optimizing with differential evolution algorithm. Appl. Intell. 2021, 51, 527–548. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Wang, C. Parameter identification of nonlinear system via a dynamic frequency approach and its energy harvester application. Acta Mech. Sin. 2020, 36, 606–617. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, S.; Zheng, W.; Dong, H.R. Fuzzy adaptive event-triggered control for uncertain nonlinear system with prescribed performance: A combinational measurement approach. J. Frankl. Inst. 2022, 359, 371–391. [Google Scholar] [CrossRef]
- Chen, H.X.; Liu, M.M.; Chen, Y.T.; Li, S.Y.; Miao, Y.Z. Nonlinear lamb wave for structural incipient defect detection with sequential probabilistic ratio test. Secur. Commun. Netw. 2022, 9851533. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, Z. Failure analysis of corroded high-strength pipeline subject to hydrogen damage based on FEM and GA-BP neural network. Int. J. Hydrog. Energy 2022, 47, 4741–4758. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, L.; Gai, T.; Xu, P.; Wei, Y. Aberration analysis and compensate method of a BP neural network and sparrow search algorithm in deep ultraviolet lithography. Appl. Opt. 2022, 61, 6023–6032. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Wang, L.; Li, W. Forecasting of solar radiation in photovoltaic power station based on ground-based cloud images and BP neural network. IET Gener. Transm. Distrib. 2022, 16, 333–350. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y.; Zhang, W. A composite adaptive fault-tolerant attitude control for a quadrotor uav with multiple uncertainties. J. Syst. Sci. Complex. 2022, 35, 81–104. [Google Scholar] [CrossRef]
- Mule, G.M.; Kulkarni, S.; Kulkarni, A.A. An assessment of a multipoint dosing approach for exothermic nitration in CSTRs in series. React. Chem. Eng. 2022, 7, 1671–1679. [Google Scholar] [CrossRef]
- Mukherjee, D.; Raja, G.L.; Kundu, P.; Ghosh, A. Design of optimal fractional order lyapunov based model reference adaptive control scheme for CSTR. IFAC-Pap. 2022, 55, 436–441. [Google Scholar] [CrossRef]


| Term | Definition |
|---|---|
| CSTR | Continuous stirred tank reactor |
| LM | Levenberg–Marquardt |
| BPNN | Back Propagation Neural Network |
| NN | Neural Network |
| PI | Proportional-Integral |
| Ca | Reactant concentration |
| RMSE | Root mean square error |
| MAE | Maximum absolute error |
| AAE | Average absolute error |
| GN-BP | Gauss–Newton-Back Propagation |
| ANN | Artificial neural network |
| NS | Nonlinear system |
| Test Conditions | Parameter Value |
|---|---|
| Input signal | |
| Output signal | |
| Training function | Trainlm function |
| Number of hidden layer nodes | 7 |
| Learning Rate | θ = 0.5 |
| Maximum Number of Iterations | 500 |
| Target error accuracy | 10−4 |
| Inertial coefficient | 0.05 |
| Input reference trajectory | 10 Hz square wave signal |
| Model Type | RMSE | MAE | AAE |
|---|---|---|---|
| LM-BPNN | 0.0451 | 0.0958 | 0.0351 |
| BPNN | 0.0744 | 0.1775 | 0.0536 |
| GN-BPNN | 0.0539 | 0.1108 | 0.0443 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Cao, H.; Jia, B. Optimization of Levenberg Marquardt Algorithm Applied to Nonlinear Systems. Processes 2023, 11, 1794. https://doi.org/10.3390/pr11061794
Huang X, Cao H, Jia B. Optimization of Levenberg Marquardt Algorithm Applied to Nonlinear Systems. Processes. 2023; 11(6):1794. https://doi.org/10.3390/pr11061794
Chicago/Turabian StyleHuang, Xinyi, Hao Cao, and Bingjing Jia. 2023. "Optimization of Levenberg Marquardt Algorithm Applied to Nonlinear Systems" Processes 11, no. 6: 1794. https://doi.org/10.3390/pr11061794
APA StyleHuang, X., Cao, H., & Jia, B. (2023). Optimization of Levenberg Marquardt Algorithm Applied to Nonlinear Systems. Processes, 11(6), 1794. https://doi.org/10.3390/pr11061794







