Abstract
Hybrid grid-connected renewable energy systems have gained significant importance in sustainably responding to an increased electrical energy demand. These are time-varying nonlinear dynamical plants, where the value of their parameters depends on changing weather conditions and the alternating grid voltage with randomly fluctuating amplitude. This paper proposes a robust cascade MRAC for nonlinear plants representing a class of these systems, which includes n renewable energy converts and a DC/AC single-phase full bridge inverter. The proposal reduces commissioning time by avoiding linearization and knowledge of the plant parameters. Moreover, it includes specific formulas for tuning the controller parameters that decrease their adjustments based on trial and error. Finally, it uses a direct adaptive method with adaptive laws having modification and an inner loop at least five times faster than the outer loop. The proposition validation includes the theoretical stability proof based on the Lyapunov stability method and Barbalat’s Lemma. Furthermore, it presents comparative simulation results with quoted cascade PI controllers for a monophasic system, including two renewable energy sources and injection. Both techniques effectively track setpoint changes of the energy sources’ currents and direct current bus voltage, showing the proposal similar or reduced ripple. At the same time, both ensure robustness against decreased photovoltage panels irradiance, increased fuel cells voltage, and grid voltage amplitude random fluctuations. However, the proposal does these things while avoiding prior linearization and unknowing the plant parameters.
1. Introduction
The use of hybrid grid-connected renewable energy systems has risen over the last years to respond to an increasing electrical energy demand more sustainably. It injects electrical power generated by renewable energy sources and could avoid the expense of electric batteries as storage devices [1,2].
Several technical aspects improved this technology advancement, such as power electronics [3,4], economic issues [5,6], dispatching management [2,7], and control strategies [1,8]. This paper focuses on improving the control strategy for a class of power system.
According to the review [9], a Hybrid Renewable Energy System is “a combination of two or more renewable/non-renewable energy sources”. As essential components, it has energy sources, power electronic converters, and loads [9,10,11]. Moreover, it could be grid-connected or not. It could use isolated or nonisolated converters [12,13], using transformers or coupling inductors, respectively, for instance. Finally, the system can supply power constantly despite the intermittent nature of renewable energy sources or not. For this last case, it would not have storage components, such as batteries, fly-wheels, or superconducting magnetic energy storage (SMES) [9].
This manuscript’s research focuses on a novel controller for the Hybrid Grid-Connected Renewable Energy System class studied in [1,14]. This way, it meets the Funders’ requirements. This type includes renewable energy sources, intermittent power supplies such as [12,13,14,15,16,17,18,19,20,21,22,23], and coupling inductors as in [16,17,18,19,20]. Moreover, it uses a DC-DC boost converter for each renewable energy source and a DC/AC single-phase full-bridge inverter and grid. Similar to [13,14,15,16,17,18,19,20,21,22,23,24], it does not consider a storage component.
Regarding this science area, different studies of control algorithms aim to improve hybrid grid-connected renewable energy systems. The work [25] uses PI controllers adjusted without considering the dynamical model. It assumes the plant has a generic linear behavior and applies this controller, adjusting its control parameters based on trial and error. After making a steady state analysis [26], proposes open-loop controllers. As a result, it does not ensure stability for the different operation conditions. In contrast [27], describes obtaining dynamical equations and uses linear controllers based on small-signal analysis. However, these research works apply to non-grid-connected renewable systems.
Moreover [28], employs a nonadaptive backstepping nonlinear controller, assuming all parameters are known. The works [29,30] propose nonadaptive sliding mode controllers (SMC). Here [29], details how the power and current injection versus the voltage of photovoltage panels (PVP) depend on their characteristics curves depending on the irradiance and temperature changes. Then, the designed SMC ensures robustness despite these variations. On the other hand, the SMC from [30] works for a more extensive system, considering batteries, wind turbines, and fuel cells (FC). All these studies [28,29,30] have a complete theoretical analysis, again for non-grid-connected renewable systems. These describe the dynamical model, controller design, and stability proof. However, these studies treat the DC-DC converter and the inverter as separate and not interconnected subsystems.
The DC and AC subsystems are interconnected and dynamically coupled, as detailed in [31] (Chapter 8). The work [32] considers this DC/AC coupling effect and proposes adaptive SMC instead of the nonadaptive SMC from [29,30]. As a result, it improves robustness under parameter variations. However [33], suggests using a cascade model reference adaptive control (MRAC) to eliminate the undesired chattering issues associated with the SMC technique. This last study considers a linearized hybrid grid-connected renewable energy system. Moreover, it applies to only one renewable energy source, considerably simplifying the dynamical model. Finally, it exhibits a trial-and-error controller adjustment. Therefore, this paper aims to improve the proposal [33] after expanding the MRAC for nonlinear plants given in [34] (Section 3.3.2).
Adaptive control interest grew in the 1950s, as described in the survey [35] and book [36]. In 1958 [35], described and characterized several adaptive techniques already used to ensure robustness despite plant parameters, structure, inputs, and others changes. Later, the book [36] deeper describes some of these techniques. MRAC is one of the adaptive control central techniques, significantly developed during the 1980s, as detailed in the book [34]. Today, it has rigorous mathematical solutions and guaranteed convergence for robust stabilization, regulation, and tracking control of nonlinear systems. The work [37] has recently improved some tuning issues for adaptive passivity-based control (APBC). Moreover [38], extends this result for parameters estimate using model reference adaptive systems (MRAS), while this paper develops it for MRAC.
The main contribution of this paper is proposing a cascade MRAC for time-varying nonlinear systems representing hybrid grid-connected renewable energy systems. It assumes unknown parameters diminishing the controller commissioning time by avoiding testing and computing for the plant parameters finding. The authors present the stability proof of the overall design, using the second Lyapunov stability method and Barbalat’s Lemma [34] (Section 4.5.2) to validate the proposal theoretically. Moreover, the manuscript shows simulation results as in [15,16,17,22,23]. These show the proposal ensures robustness in front of the plant´s time-varying parameter changes, in contrast to [29,30,32]. Finally, the paper has the following specific novelties:
- 1.
- It starts by finding the dynamic model of hybrid grid-connected renewable energy systems with renewable energy sources. Then, it expands the dynamical model with only two renewable energy sources described in [1] by detailing its finding, taking elements from [31] (Chapter 8). In contrast with the mathematical models studied in [28,29,30], this paper’s DC and AC subsystems are interconnected and dynamically coupled to better represent the plant.
- 2.
- In contrast to [29,30], and similar to [32], this paper uses an adaptive controller. However, it proposes a cascade MRAC instead of an SMC avoiding the undesired SMC chattering [33]. The proposal applies to nonlinear systems encompassing hybrid grid-connected renewable energy systems after expanding the MRAC theories from [34] (Section 3.3.2) and avoiding linearizing the model as in [33]. The proposed robust cascade MRAC has a SISO outer loop setting the set point, through a nonlinear interface, of a MIMO inner loop. Moreover, this paper presents the stability proof of the overall design, not exhibited in [33].
- 3.
- Finally, this paper gives specific formulas to tune the controller parameters, which differ from the MRAC theories presented in [33,34]. These last only define positive controller gains adjusted via trial-and-error. Our proposal expands the adjustments proposed for MRAS in [37,38] for the proposed cascade MRAC. As a result, it decreases commissioning time, minimizing the trial-and-error adjustment.
Section 2 of the paper describes the preliminaries of a hybrid grid-connected renewable energy system. It considers two types of renewable energy sources, including the power and control schemes. Later, the MRAC basis is depicted. Then, in Section 3, the authors propose the cascade MRAC, including the stability proof. Moreover, Section 4 presents the comparative simulation results, proving the proposal’s effectiveness compared to results from [1]. Finally, Section 5 contains the conclusions.
2. Preliminaries
2.1. Hybrid Grid-Connected Renewable Energy System
Figure 1 shows the power and control general diagram of a hybrid grid-connected renewable energy system based on [1]. It considers renewable energy generated from two sources, PVP delivering the voltage and the current . Moreover, it has a FC giving the voltage and the current . There are two DC-DC buck-boost converters, commanded by the IGBTs and . These have the coupling inductors and and diodes and interconnecting the PVP and FC, respectively, to the DC link at node and producing the current [1]. Furthermore, an inverter and the coupling inductor interconnect the DC link to the power grid generating the voltage and the current towards the grid with a voltage . Here, the control inputs of the buck-boost converters and the inverter are , , and , regulating the variables of currents , , , and the DC voltage , respectively.
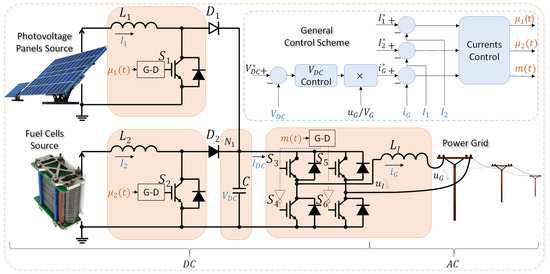
Figure 1.
Power and control general diagram of the hybrid grid-connected renewable energy system, based on [1].
Regarding the system dynamical model described in [1], it starts by applying Kirchhoff´s voltage laws for the PVP, FC, and AC circuits. Furthermore, it applies Kirchhoff´s current Node 1 () rule, treating the DC-DC buck-boost converters as detailed in [31] (Chapter 8). Finally, considering the amplitude modulation index () relationship where the inverter voltage equals , it gives the following equations:
After reorganizing the Equation (1), it takes the form:
where the generated voltages are , . The coupling inductors are , , and . The injected currents are , , and and are desirable these tend to their references , , and . The DC circuits control inputs and , equal one minus the corresponding duty cycles. Finally, , , and are the DC bus’s capacitor, current, and voltage, respectively. Here, the should approach the references . The grid voltage is , and the inverter amplitude modulation index is .
The generated power of PVP and the FC depends on their rated variables, characteristic curves, environmental conditions, and dynamic behavior. The work [29] (Figures 1–4) presents the PVP dependence on temperature and irradiance, which in the model (2) impacts the values of and . The study [39] (Figures 8, 9, and 11) describes how FC injection depends on the temperature, reflected in the values of and . Hence, this paper designs a general method to deal with these PVP and FC time-varying parameters in Section 3. Moreover, Section 4 describes specific PVP and FC models used to validate the design experimentally.
Furthermore, several authors, such as [1,3,4], make the following considerations to obtain an expression for the term of the fourth equation of (2)
- Obtains from the relationships ,
- Computes the remaining from , after neglecting , and
- Relates the maximum grid Voltage with the nominal grid voltage with a ratio .
As a result, the dynamical model of this hybrid grid-connected renewable energy system gives:
with the identity matrix of order 3.
Remark 1:
Readers may notice in (3) and (4) that hybrid grid-connected renewable energy systems have the nonlinearity . To apply linear nonadaptive controllers like the proposal [1], designers starts by linearizing (3) and (4) around an operating point. Later, they develop a test to find its parameters around the operation point. On the other hand, the linear adaptive controller [33] avoids testing but still needs linearizing. In contrast, nonlinear and nonadaptive controllers avoid linearizing but still make testing to find the parameters of (3) and (4). Finally, the proposed nonlinear control methodology does not linearize (3) and (4). Moreover, it is an adaptive technique that works properly without the plant parameters knowledge.
Remark 2:
These systems (3) and (4) have the time-varying parameters , , , , , and . Here, is an alternating grid voltage, having a variable voltage amplitude that randomly changes its value around its nominal value as reflected in parameter . Moreover, and depend on weather conditions that may change from sunny to cloudy and rainy, for instance (due to the irradiance and temperature changes for the PVP [29] and the temperature changes for the FC [39]). Finally, has an associated ripple. The proposed control methodology avoids prior feedback linearization; thus, it directly deals with the variation of these parameters that change even for a given current operating point.
Remark 3:
The hybrid grid-connected renewable energy systems (2) [1] have grid injection and two renewable energy sources (from PVP and FC). However, it may increase this quantity to sources, including different types such as wind turbines and batteries. Thus, controller design should consider a more general model.
The following section describes the basis of MRAC for nonlinear systems extended in this manuscript to control hybrid grid-connected renewable energy systems solving these issues.
2.2. Basis of MRAC for Nonlinear Systems
MRAC theory [34] (Section 3.3.2) considers nonlinear plants of the form:
where the variable to control is , the nonlinear function is , and the input (control) variable is . All system parameters are assumed to be unknown. Moreover, it assumed that with known [34] (Section 3.3.2, case ii) and [40] (Section 7.3). The time-varying plant parameters and their first-time derivatives are also bounded [34] (Section 8.6.1 case ii).
The following MRAC ensures the output of the system (5) tends asymptotically to its desired value [34] (Sections 3.3.2 and 8.3.3) [37,38]:
where is the reference model output, is the uniformly continuous bounded reference, and is the control input. The reference model parameters are defined as in [37], and the control error is . The adaptive controller parameter is , and is the adaptive law fixed-gain, according to [38]. Here, the control information vector is . The adaptive control law modification parameter to ensure robustness in front of time-varying parameters is . Finally, adjustment depends on the rated values of the output and the setpoint . are fine-tuning factors, with values between 0 and 10. is the required stabilization time.
| Reference model | (6) | |
| Control law | (7) | |
| Control adaptive law | (8) | |
| Adaptive law fixed-gain | (9) | |
| Reference model parameters | (10) |
Remark 4:
The MRAC (6)–(10) is robust and applies to nonlinear systems. However, it does not directly apply to hybrid grid-connected renewable energy systems (3), (4) with inner and outer control loops running with different response times and needing non-identical reference models for the inner and outer loops.
Based on the previous background, this paper extends the MRAC (6)–(10) for hybrid grid-connected renewable energy systems, as the following section describes.
3. Proposal
This section describes the proposal of a robust cascade MRAC for the nonlinear dynamical plants representing hybrid grid-connected renewable energy systems with renewable energy sources.
3.1. Dynamical Model of Hybrid Grid-Connected Renewable Energy Systems
The following nonlinear dynamical system represents hybrid grid-connected renewable energy systems, like those in (3) and (4) but with renewable energy sources.
The outer-loop variable (13) represents Equation (4) where is the outer loop to control. Here, compared to (4) , , , and the term extending (4) to nth sources. The inner-outer variables interface (12) clear the variable from the expression obtained from (4).
The AC injection row of the inner-loop variables (11) corresponds to the last row of (3). Here, , , and .
Finally, the nth DC sources row of the inner-loop variables (11) expands Equation (3) first two rows to nth sources. It considers and . Moreover, the time-varying parameters are , . Here, the renewable energy sources having a voltage and a current are interconnected via the corresponding coupling inductors and diode , where .
Hence, is the inner loop vector output to control. Furthermore, it considers the grid injection current , and the vector of renewable energy generated currents evaluating sources. Therefore, the internal loop control input is , which includes the inverter modulation index , and the vector composed by the DC circuits control inputs. Moreover, the external loop control input is , which allows obtaining the desired after using the inner-outer interface expression (12).
It is important to notice that the nonlinear dynamical system (11)–(13) fulfills assumptions made by MRAC in Section 2.2. The following Remarks detail it:
Remark 5:
This work considers nonlinear dynamical system (11)–(13) has bounded, time-varying, and unknown plant parameters ,. Furthermore, these also have a bounded first-time derivative. Remark 2 describes the nature of these variations.
Remark 6:
Moreover, nonlinear dynamical system (11)–(13) has that , where is the unknown matrix composed by the modulus of each element of the diagonal matrix , and is the known matrix composed by the sign of each element of . Finally, we have that with unknown and known . It follows:
However, two different MRAC (11)–(13) would have to apply for the inner and outer variables, each one with the proper dimension. Moreover, the inner reference model would have to be faster than the outer one. The following section presents the proposed cascade CMRAC.
3.2. Cascade MRAC
Figure 2 and Theorem 1 detail the proposed cascade MRAC.
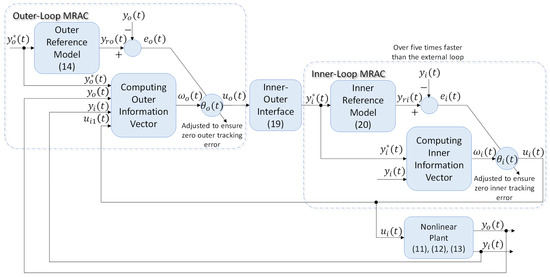
Figure 2.
Proposed robust cascade MRAC block diagram.
Theorem 1:
For MIMO dynamical systems (11)–(13), the following cascade MRAC assures the systems outputs and tracks the model reference outputs and , which tends to the desired outputs and , respectively:
Outer-loop MRAC
| Outer reference model | (14) | |
| Outer control law based outer information vector | (15) | |
| Outer adaptive law | (16) | |
| Ideal outer controller parameter | (17) | |
| Controller tuning parameters | (18) |
Inner-outer loop interface
| Inner-outer interface | (19) |
Inner-loop MRAC
| Inner reference model | (20) | |
| Inner control law based inner information vector | (21) | |
| Inner adaptive law | (22) | |
| Ideal inner controller parameter | (23) | |
| Adaptive law fixed-gain, with inner loop tuning parameters | (24) |
This way, the outer tracking error and the inner tracking error . Here, for the quantity of renewable energy sources; , are the outer and inner reference model outputs. The set points are and . The reference model parameters are and made equal ( and ) for an exact set point tracking without scaling. The adaptive external and internal controllers and depend on their adaptive parameters and and their corresponding information vectors and . The ideal adaptive parameters are and . The term refers to a vector with all its components equaling one. Besides the model reference parameters, the cascade MRAC has the following tuning parameters: adaptive law fixed-gains and adaptive law modification factors and , model reference time-constant factors , and the adaptive law fixed-gain factors , .
These tuning parameters depend on the plant required establishment times , the maximum operating range of output variables , input variable , and setpoints .
Proof of Theorem 1.
Let us first obtain the closed-loop dynamical equations and then verify their sta bility.
First, subtract the reference models (14) and (20) from the subsystems’ dynamical Equations (13) and (11), respectively. Later, add and subtract the terms and to the right side. Moreover, applying controllers (15) and (21), and regrouping the terms, considering the definitions (17), (23), the outer tracking error and the inner tracking error , we obtain the following tracking errors dynamical equations:
Here, the inner information vector (21), where (19), fulfills the condition due to this internal loop is over five times faster than the external loop ensuring the set point equals the designed .
Obtaining now the first-time derivative of the control parameters errors , and , considering the definitions given in Theorem 1 for (16), (17) and (22), (23), the control parameters errors dynamical equations give:
These closed-loop dynamical Equations (25) and (26) have the following associated Lyapunov function, which is an extension of the function given in [40] (Section 11.2.2):
where represents the matrix containing the modulus of each element of .
Taking the first-time derivative of (27), considering the derivative property of the product in the trace, and replacing the tracking errors dynamical Equation (25), we obtain:
Moreover, using the vector property we can write the term . Employing the vector property we write the term . Finally, considering that and (due to is diagonal), it gives the following expression:
Here, replacing the control parameters errors dynamical Equation (26), canceling terms, and taking into account the expressions and , the Lyapunov function first-time derivative becomes:
Here, we have that , , , , , . Moreover, the plant parameters and their first-time derivatives are bounded as described in Remarks 2 and 5. However, although the first terms of (28) are negatives, there is nothing we can say about the sign of the last fourth terms at a glance. Therefore, we reexpress Equation (28) using some modulus and norm properties.
Using the vector and matrix norm property, the fourth term of (28) takes the form as and are positive scalar numbers [41] (Lemma 10.2 (ii)), where is the norm of matrix called Frobenius norm. Later, using the scalar property the last two terms becomes and [40] (Section 11.2.2).
For the case of the terms with a trace, the authors use similar properties of the Frobenius norm and the Cauchy–Schwarz inequality where [40] (Section 11.2.2). Here, considering a positive , and the third term becomes . Moreover, the other two trace terms become and . Finally, using the property [40] (Section 11.2.2), these last take the forms and .
As a result, Equation (28) becomes:
which equals a hyper elliptical paraboloid of parameter :
Therefore, only outside the region , which is the following instability hyper elliptical paraboloid that is compact, closed, and includes the origin:
Hence, using Lyapunov’s second method, it can be concluded that the variables of the closed-loop dynamical Equations (25) and (26) are bounded outside . In case the errors take small enough values that result in (inside the instability compact and closed region , including the origin); these will be pushed back to a stable boundary. In practice, the values of , are chosen so the permanent errors are smaller as possible, as can be seen in the following section.
Thus, are bounded outside , i.e., . Since and are bounded, it implies that and are bounded, as and are bounded references. As and are bounded, and we have bounded plant parameters, then the adaptive parameters and are bounded, since and . Having all these bounded signals outside , and that , from (25) and (26), we have that .
Integrating both sides of in the interval , it gives
as is bounded outside , from the right-hand side of this last equation; we have that outside .
Furthermore, as and , and and , all outside , using Barbalat’s Lemma [34] (Section 4.5.2) we have that and , both tend asymptotically to zero outside . Hence, and outside . We do not ensure parameter convergence. This concludes the proof. □
The following Section applies the proposed cascade MRAC, and also describes and discusses the results.
4. Simulation Results and Discussion
This section applies the proposed cascade MRAC to the hybrid grid-connected renewable energy system of Figure 1 [1], having two renewable energy sources. It runs on a personal computer, in Simulink 10.3, MATLAB R2021a. The modeling settings are: stopping time of 1 s, solver Ode8 (Dorman-Prince) with fixed-step, and using power toolbox components set with a powergui relative tolerance of 1 × 10−6.
The authors use the “PV Array” block from the Simulink library path Simscape/Electrical/Specialized Power Systems/Sources. It was set as user-defined with the PVP information of Table 1. Table 1 depicts the PVP parameters, model BP585 PV from [1], used in simulations for comparison purposes.

Table 1.
PVP parameters [1].
On the other hand, the simulation uses the block “Fuel Cell Stack” from the same Simulink library path. It was also configured as user-defined, with the FC information of Table 2 based on model 6 kW–45 V, PEMFC stack (the NedStack PS63) from [42].

Table 2.
FC Module parameters [1].
Finally, Table 3 lists the employed power circuit parameters [1], and Table 4 presents the based controller parameters [1] and the proposal ones.

Table 3.
Nominal parameters of the power circuit [1].

Table 4.
Base and proposed controller parameters.
Figure 3 describes the given set points and obtained results after applying these two controllers for comparison purposes.
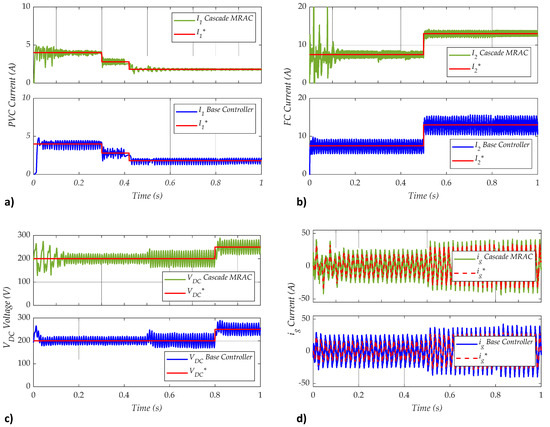
Figure 3.
Comparative results, from left to right and top to bottom: (a) PVP current; (b) FC current; (c) voltage; and (d) current.
Cascade MRAC (14)–(24) tuning considers n = 2 and for () and (). Furthermore, for () and () it uses:
The considered set points in Figure 2 are: that changes from to at and decreases to at ; which varies from to at ; and voltage increases from to at . Furthermore, the saturation for and is [0, 1], and the levels of saturation for are [−311, 311].
Moreover, we verify robustness against the following situations: PVP irradiance decreases from to 500 W/m2 at 0.4 s; FC voltage changes (from to at ; and the grid voltage amplitude fluctuates randomly between +6% and −6%.
However, Figure 2 depicts that both controllers have good results. Both effectively regulate the inner currents of the PVP (), FC (), and grid (). In addition, the base and the proposed controllers adequately regulate the voltage, with robustness in front of the different voltage changes introduced, as previously described.
At the beginning of the simulation, the proposed controller shows more oscillations than the based one [1], while adapting its parameters for all cases. However, it improves its performance later by describing the following:
- The proposal has the lowest current ripple in Figure 2a. At 0.4 s after the PVP irradiance decreased, the controller got saturated, and the PVP could not feed the required current, reducing the set point at 0.42 s. Moreover, it is robust against the FC set point changes at 0.5 s and grid voltage amplitude fluctuations.
- Cascade MRAC has the lowest current ripple in Figure 2b. There is robustness when the PVP set point varies at 0.3 s, and the grid voltage amplitude fluctuates.
- The proposition has a similar voltage ripple in Figure 2c with more robustness. Several variations impact the due to changing PVP and FC current setpoints change and the random fluctuations of the grid voltage amplitude. However, both controllers are robust, and the proposal has the best results.
- Figure 2d shows similar injection current results. Here, the injected current amplitude and frequency are similar between the proposed and the base controllers, depicting all previously described changes. Signal TDH is also similar.
The following section presents the conclusions.
5. Conclusions
This paper generalized the dynamic hybrid grid-connected renewable energy systems model class studied in [1,14], including n renewable energy sources, intermittent power supplies, coupling inductors, a DC-DC boost converter for each renewable energy source, a DC/AC single-phase full-bridge inverter and grid, and without storage components. Later, the manuscript proposed a robust cascade MRAC for nonlinear plants representing these time-varying nonlinear systems. It used:
- A direct adaptive method,
- Adaptive laws modifications, and
- Specific tuning controller formulas to decrease trial-and-error adjustments and ensure the inner loop is at least five times faster than the outer loop.
The author presented the stability proof of the overall closed-loop system based on the Lyapunov stability method and Barbalat’s Lemma.
Furthermore, the proposition was designed and applied for a monophasic system, including two renewable energy sources and injection. Comparative simulation tests with cascade PI controllers [1] showed its effectiveness:
- Both tracked set points changes for the energy sources’ currents and direct current bus voltage with similar or reduced ripple.
- Both ensured robustness against decreased photovoltage panels irradiance, increased fuel cells output voltage, and grid voltage amplitude random fluctuations.
However, in contrast to the base algorithm used for the comparisons [1], the proposed robust cascade MRAC does not need prior linearizing and runs without knowledge of the plant parameters.
6. Patents
There are no patents resulting from the work reported in this manuscript.
Author Contributions
J.C.T.-T. conducted the conceptualization, investigation, formal analysis, funding acquisition, project administration, supervision, and writing the original draft preparation. A.R.-M. led the software, methodology, investigation, and visualization. A.V.-T. and F.L.-S. managed the support software, methodology, investigation, and visualization. All authors have read and agreed to the published version of the manuscript.
Funding
Author A.R.-M. has received support from the research grant 2022 of the Industrial Technologies Department, USACH. Author A.V.-T. has received support from the research grant 2022 of the Technological Faculty, USACH. Authors J.C.T.-T. and F.L.-S. have received support from the research grant FONDEF ID17I20338, ANID.
Data Availability Statement
This manuscript has no associated data.
Acknowledgments
The National Research and Development Agency supported this work through the research grant FONDEF ID17I20338. Also, the University of Santiago of Chile via the research grant 2022 of the Industrial Technologies Department and the research grant 2022 of the Technological Faculty.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Salimi, M.; Radmand, F.; Firouz, M.H. Dynamic Modeling and Closed-loop Control of Hybrid Grid-connected Renewable Energy System with Multi-input Multi-output Controller. J. Mod. Power Syst. Clean Energy 2021, 9, 94–103. [Google Scholar] [CrossRef]
- Luo, Z.; Zhu, Z.; Zhang, Z.; Qin, J.; Wang, H.; Gao, Z.; Yang, Z. Multi-Time-Scale Rolling Optimal Dispatch for Grid-Connected AC/DC Hybrid Microgrids. Processes 2019, 7, 961. [Google Scholar] [CrossRef]
- Zare, M.H.; Mohamadian, M.; Beiranvand, R. A Single-Phase Grid-Connected Photovoltaic Inverter Based on a Three-Switch Three-Port Flyback With Series Power Decoupling Circuit. IEEE Trans. Ind. Electron. 2016, 64, 2062–2071. [Google Scholar] [CrossRef]
- Elaheh, H.; Yazdian, V.A.; Demba, D. A Dual-Function Power Decoupling Circuit for Single-Stage Grid-Connected PV Inverter. IEEE Trans. Power Electron. 2022, 37, 7422–7431. [Google Scholar]
- Türkay, B.E.; Ali, Y.T. Economic analysis of standalone and grid connected hybrid energy systems. Renew. Energy 2011, 36, 1931–1943. [Google Scholar] [CrossRef]
- Vakili, S.; Schönborn, A.; Ölçer, A.I. Techno-economic feasibility of photovoltaic, wind and hybrid electrification systems for stand-alone and grid-connected shipyard electrification in Italy. J. Clean. Prod. 2022, 366, 132945. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Ye, L.; Fang, J. A coordinated dispatch method with pumped-storage and battery-storage for compensating the variation of wind power. Prot. Control. Mod. Power Syst. 2018, 3, 2. [Google Scholar] [CrossRef]
- Arul, P.; Ramachandaramurthy, V.K.; Rajkumar, R. Control strategies for a hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2015, 42, 597–608. [Google Scholar] [CrossRef]
- Krishna, K.S.; Kumar, K.S. A review on hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2015, 52, 907–916. [Google Scholar] [CrossRef]
- Khan, F.A.; Pal, N.; Saeed, S.H. Stand-alone hybrid system of solar photovoltaics/wind energy resources: An eco-friendly sustainable approach. Renew. Energy Syst. 2021, 687–705. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. Renewable energy based off-grid rural electrification in Uttarakhand state of India: Technology op-tions, modelling method, barriers and recommendations. Renew. Sustain. Energy Rev. 2015, 51, 662–681. [Google Scholar] [CrossRef]
- Cao, D.; Jiang, S.; Yu, X.; Peng, F.Z. Low-Cost Semi-Z-source Inverter for Single-Phase Photovoltaic Systems. IEEE Trans. Power Electron. 2011, 26, 3514–3523. [Google Scholar] [CrossRef]
- Freddy, T.K.S.; Rahim, N.A.; Hew, W.-P.; Che, H.S. Comparison and Analysis of Single-Phase Transformerless Grid-Connected PV Inverters. IEEE Trans. Power Electron. 2013, 29, 5358–5369. [Google Scholar] [CrossRef]
- Okundamiya, M. Integration of photovoltaic and hydrogen fuel cell system for sustainable energy harvesting of a university ICT infrastructure with an irregular electric grid. Energy Convers. Manag. 2021, 250, 114928. [Google Scholar] [CrossRef]
- Hasanien, H.M. An adaptive control strategy for low voltage ride through capability enhancement of grid-connected photovoltaic power plants. IEEE Trans. Power Syst. 2015, 31, 3230–3237. [Google Scholar] [CrossRef]
- Radwan, A.A.; Mohamed, Y.A.R.I. Grid-connected wind-solar cogeneration using back-to-back voltage-source converters. IEEE Trans. Sustain. Energy 2019, 11, 315–325. [Google Scholar] [CrossRef]
- Khan, O.; Xiao, W. An Efficient Modeling Technique to Simulate and Control Submodule-Integrated PV System for Single-Phase Grid Connection. IEEE Trans. Sustain. Energy 2015, 7, 96–107. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, W.; Zhao, P.; Zhao, J. A Transformerless Grid-Connected Photovoltaic System Based on the Coupled Inductor Single-Stage Boost Three-Phase Inverter. IEEE Trans. Power Electron. 2013, 29, 1041–1046. [Google Scholar] [CrossRef]
- Kim, K.; Cha, H.; Kim, H.-G. A New Single-Phase Switched-Coupled-Inductor DC–AC Inverter for Photovoltaic Systems. IEEE Trans. Power Electron. 2016, 32, 5016–5022. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiang, X.; Li, C.; Gu, Y.; Li, W.; He, X. Single-Phase High Step-up Converter With Improved Multiplier Cell Suitable for Half-Bridge-Based PV Inverter System. IEEE Trans. Power Electron. 2013, 29, 2807–2816. [Google Scholar] [CrossRef]
- Khan, M.N.H.; Forouzesh, M.; Siwakoti, Y.P.; Li, L.; Kerekes, T.; Blaabjerg, F. Transformerless inverter topologies for single-phase photovoltaic systems: A comparative review. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 805–835. [Google Scholar] [CrossRef]
- Liu, S.; Liu, P.X.; Wang, X. Stochastic Small-Signal Stability Analysis of Grid-Connected Photovoltaic Systems. IEEE Trans. Ind. Electron. 2015, 63, 1027–1038. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Han, H.; Liu, Z.; Yuan, W.; Su, M. A fully decentralized control of grid-connected cascaded inverters. IEEE Trans. Sustain. Energy 2018, 10, 315–317. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A.; Haque, M.H.H. Optimal Capacity of Solar PV and Battery Storage for Australian Grid-Connected Households. IEEE Trans. Ind. Appl. 2020, 56, 5319–5329. [Google Scholar] [CrossRef]
- Ajami, A.; Shayan, P.A. Soft switching method for multiport DC/DC converters applicable in grid connected clean energy sources. IET Power Electron. 2015, 8, 1246–1254. [Google Scholar] [CrossRef]
- Lo, K.-Y.; Chen, Y.-M.; Chang, Y.-R. Bidirectional Single-Stage Grid-Connected Inverter for a Battery Energy Storage System. IEEE Trans. Ind. Electron. 2016, 64, 4581–4590. [Google Scholar] [CrossRef]
- Dasika, J.D.; Bahrani, B.; Saeedifard, M.; Karimi, A.; Rufer, A. Multivariable Control of Single-Inductor Dual-Output Buck Converters. IEEE Trans. Power Electron. 2014, 29, 2061–2070. [Google Scholar] [CrossRef]
- Martin, A.D.; Cano, J.M.D.; Silva, J.F.A.; Vázquez, J.R. Backstepping Control of Smart Grid-Connected Distributed Photovoltaic Power Supplies for Telecom Equipment. IEEE Trans. Energy Convers. 2015, 30, 1496–1504. [Google Scholar] [CrossRef]
- Ahmed, S.; Adil, H.M.M.; Ahmad, I.; Azeem, M.K.; e Huma, Z.; Khan, S.A. Supertwisting Sliding Mode Algorithm Based Nonlinear MPPT Control for a Solar PV System with Artificial Neural Networks Based Reference Generation. Energies 2020, 13, 3695. [Google Scholar] [CrossRef]
- Mehdi, H.M.; Azeem, M.K.; Ahmad, I. Artificial intelligence based nonlinear control of hybrid DC microgrid for dynamic stability and bidirectional power flow. J. Energy Storage 2022, 58, 106333. [Google Scholar] [CrossRef]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics: Converters, Applications, and Design; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Neisarian, S.; Arefi, M.M.; Vafamand, N.; Javadi, M.; Santos, S.F.; Catalao, J.P.S. Finite-time Adaptive Sliding Mode Control of DC Microgrids with Constant Power Load. In Proceedings of the IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021. [Google Scholar]
- Bhunia, M.; Subudhi, B.; Ray, P.K. Design and Real-Time Implementation of Cascaded Model Reference Adaptive Controllers for a Three-Phase Grid-Connected PV System. IEEE J. Photovolt. 2021, 11, 1319–1331. [Google Scholar] [CrossRef]
- Narendra, K.; Annaswamy, A. Stable Adaptive Systems; Courier Corporation: Mineola, NY, USA, 2012; Volume 32, pp. 134–145. [Google Scholar]
- Aseltine, J.; Mancini, A.; Sarture, C. A survey of adaptive control systems. IRE Trans. Autom. Control. 1958, 6, 102–108. [Google Scholar] [CrossRef]
- Eveleigh, V. Adaptive Control and Optimization Techniques; McGraw-Hill Electrical and Electronic Engineering Series; McGraw-Hill: New York, NY, USA, 1967; p. 434. [Google Scholar]
- Travieso-Torres, J.C.; Vilaragut-Llanes, M.; Costa-Montiel, Á.; Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Contreras-Jara, C.; Álvarez-Gracia, A. New Adaptive High Starting Torque Scalar Control Scheme for Induction Motors Based on Passivity. Energies 2020, 13, 1276. [Google Scholar] [CrossRef]
- Véliz-Tejo, A.; Travieso-Torres, J.C.; Peters, A.A.; Mora, A.; Leiva-Silva, F. Normalized-Model Reference System for Parameter Estimation of Induction Motors. Energies 2022, 15, 4542. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I.; Rosen, M.A. Transient thermal performance assessment of a hybrid solar-fuel cell system in Toronto, Canada. Int. J. Hydrogen Energy 2015, 40, 7846–7854. [Google Scholar] [CrossRef]
- Lavretsky, E.; Wise, K.A. Robust and Adaptive Control: With Aerospace Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Phillips, G.M.; Taylor, P.J. Theory and Applications of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Tremblay, O.; Louis-A, D. Dessaint A generic fuel cell model for the simulation of fuel cell vehicle. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 1722–1729. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).