Effect of Flexible Operation on Residual Life of High-Temperature Components of Power Plants
Abstract
1. Introduction
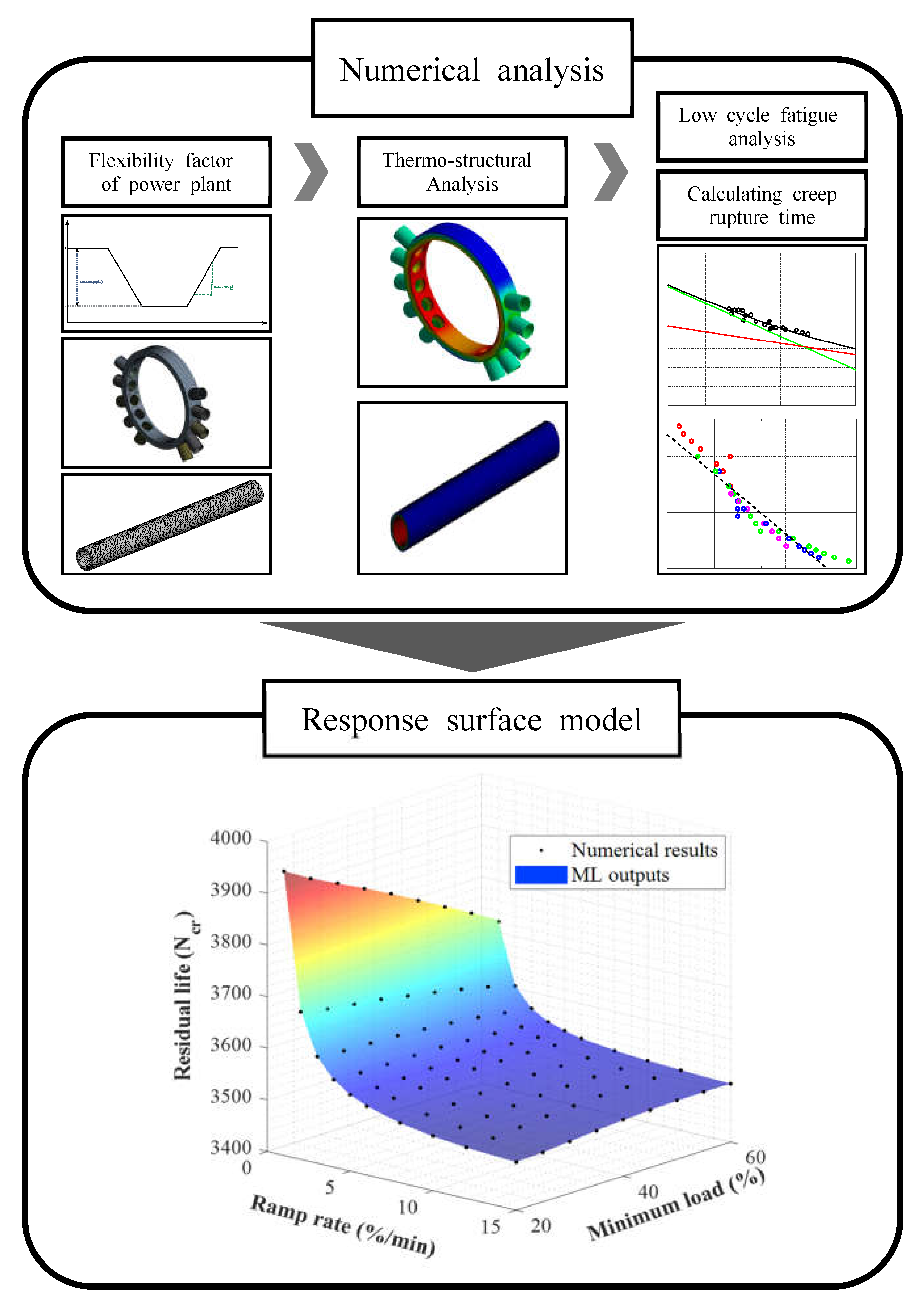
2. Methodology
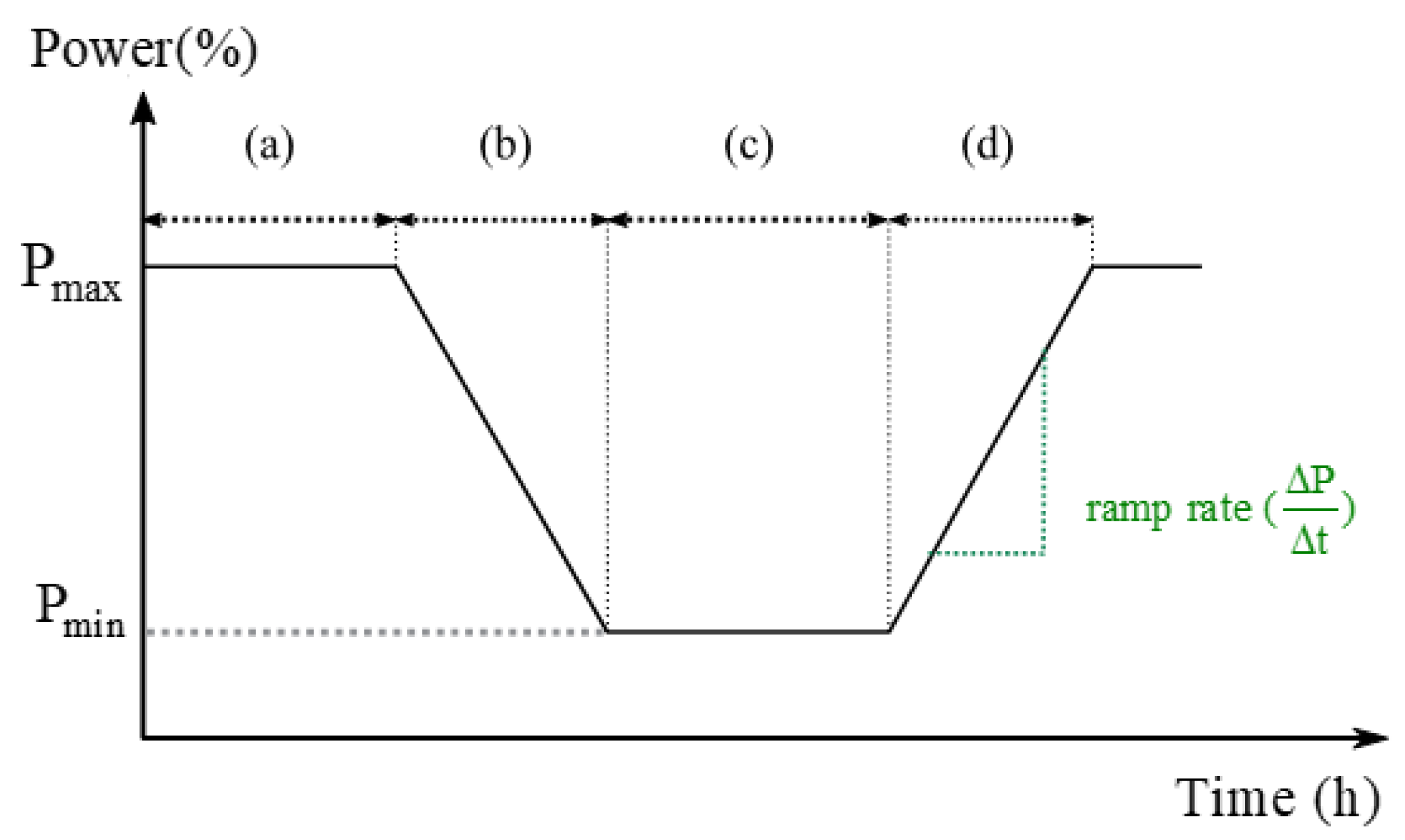
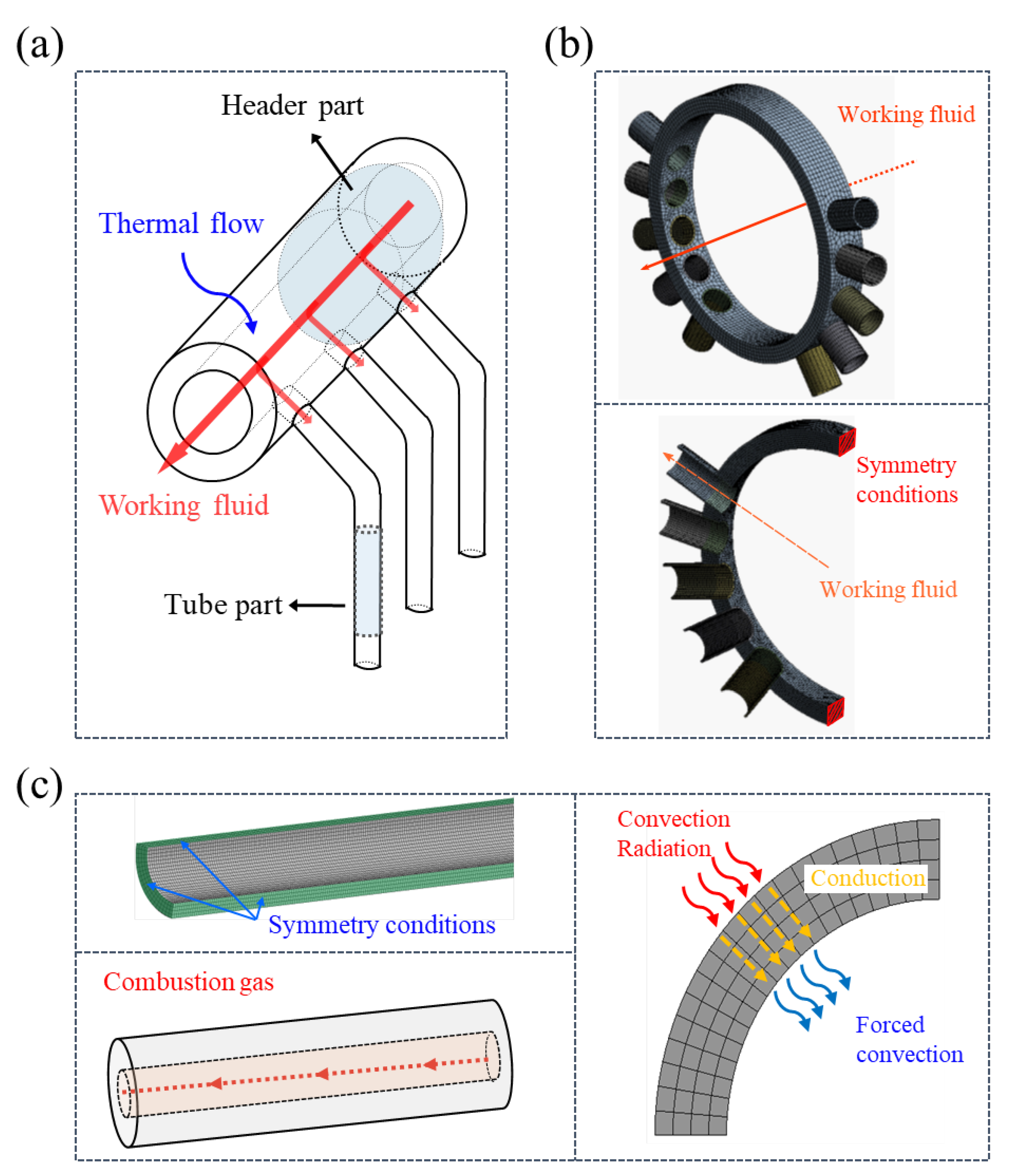
2.1. Thermo-Structural Analysis for Evaluation of Strain Range during Flexible Operation
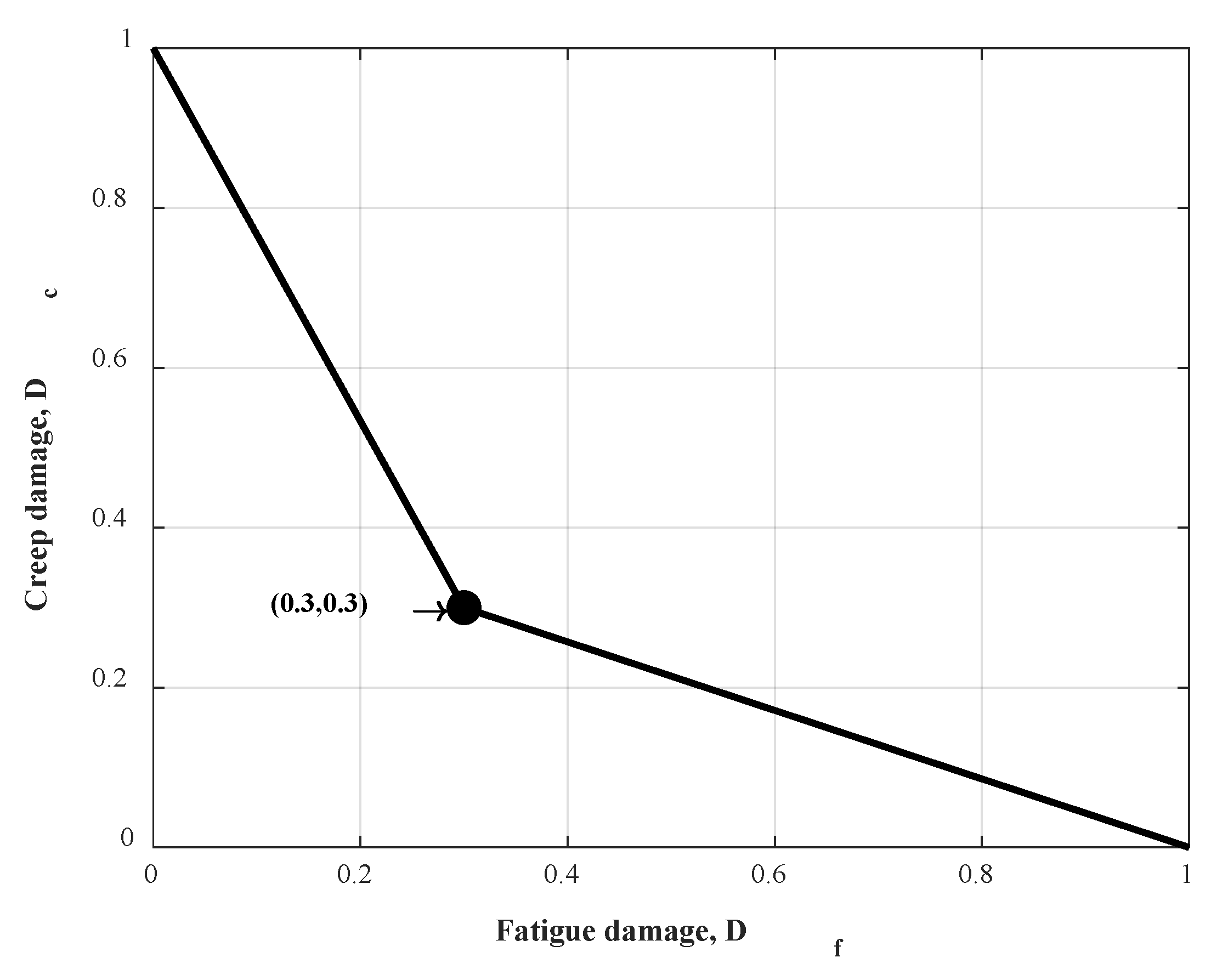
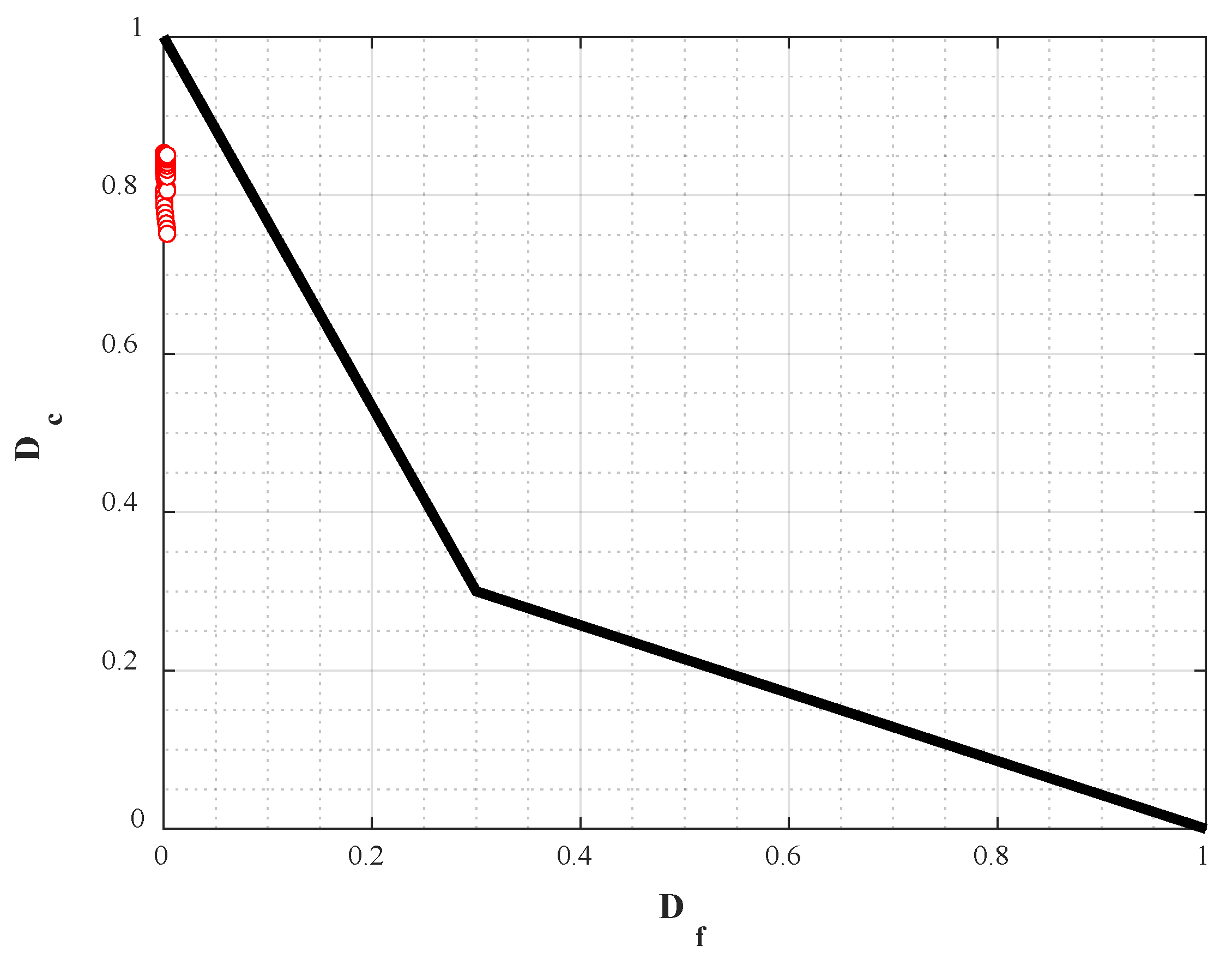
2.2. Creep–Fatigue Damage Theory
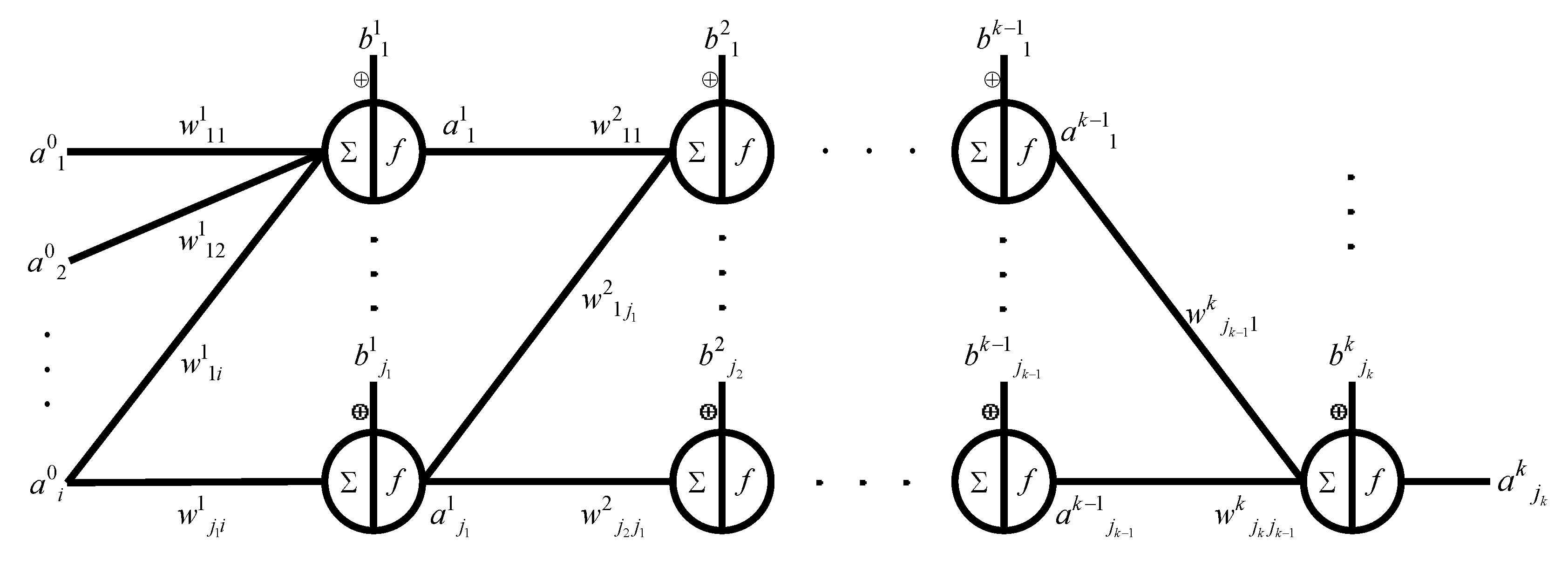
2.3. Machine Learning Techniques
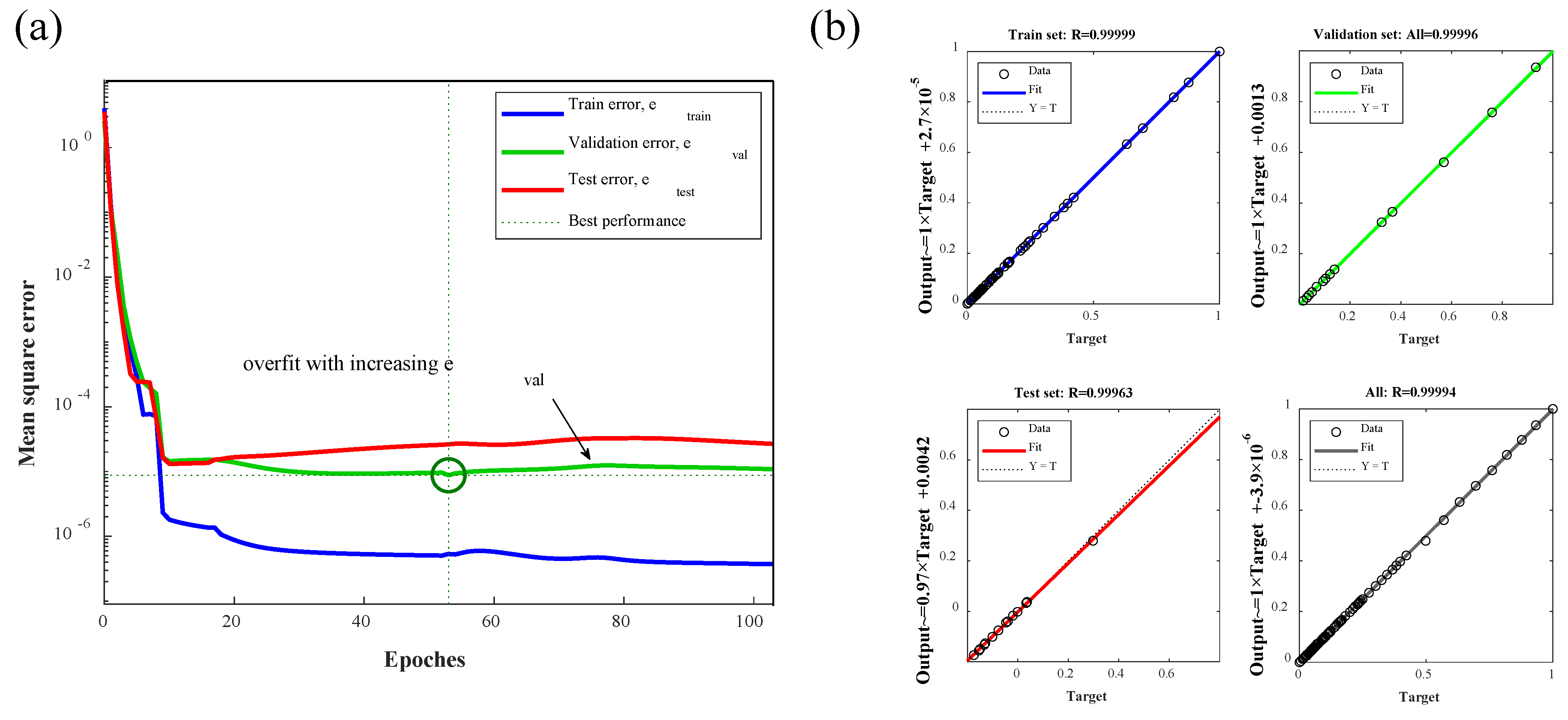
2.3.1. Feedforward Neural Network Model
2.3.2. Hyperparameter Optimization Using Random Search
3. Numerical Examples
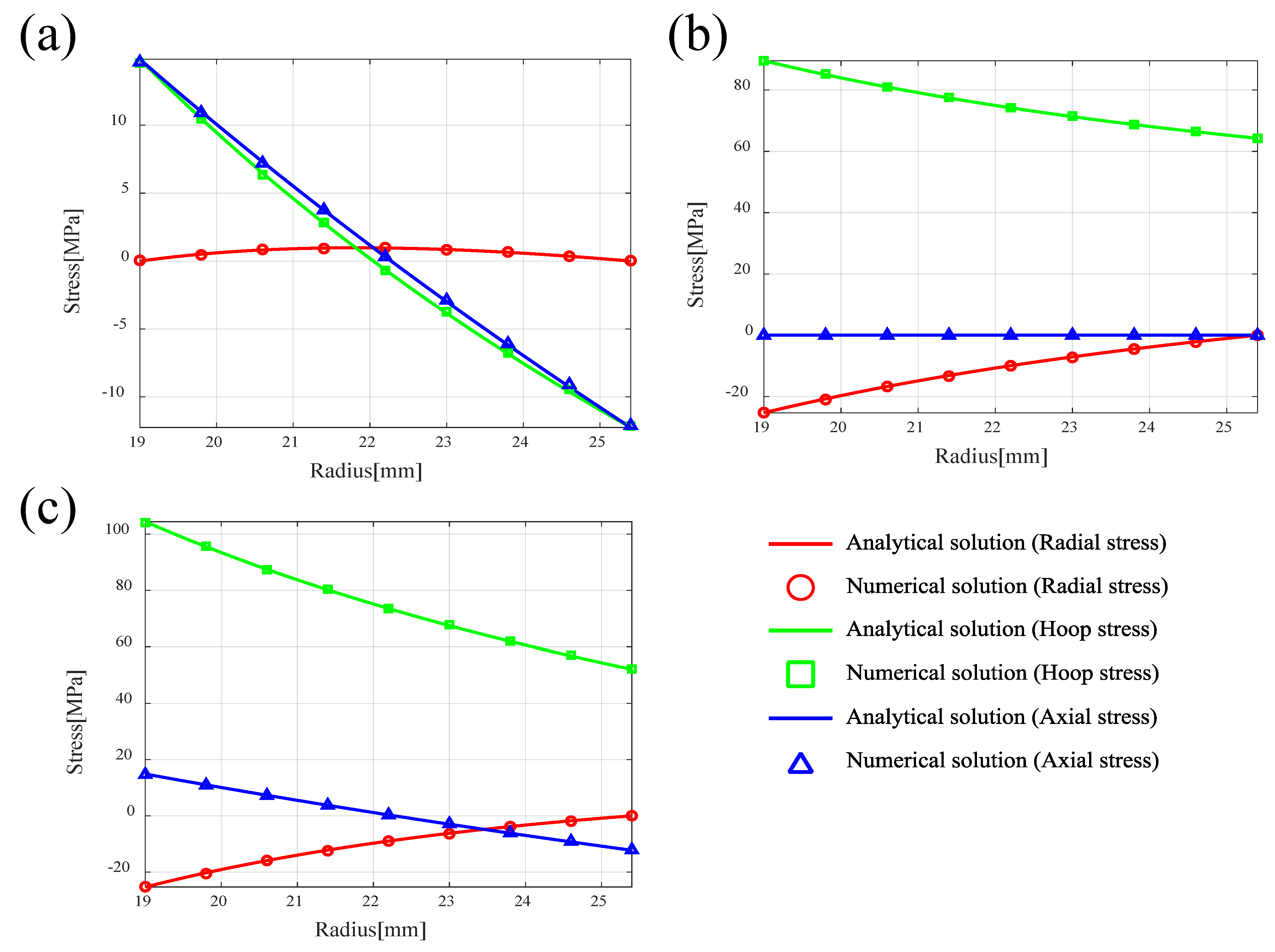
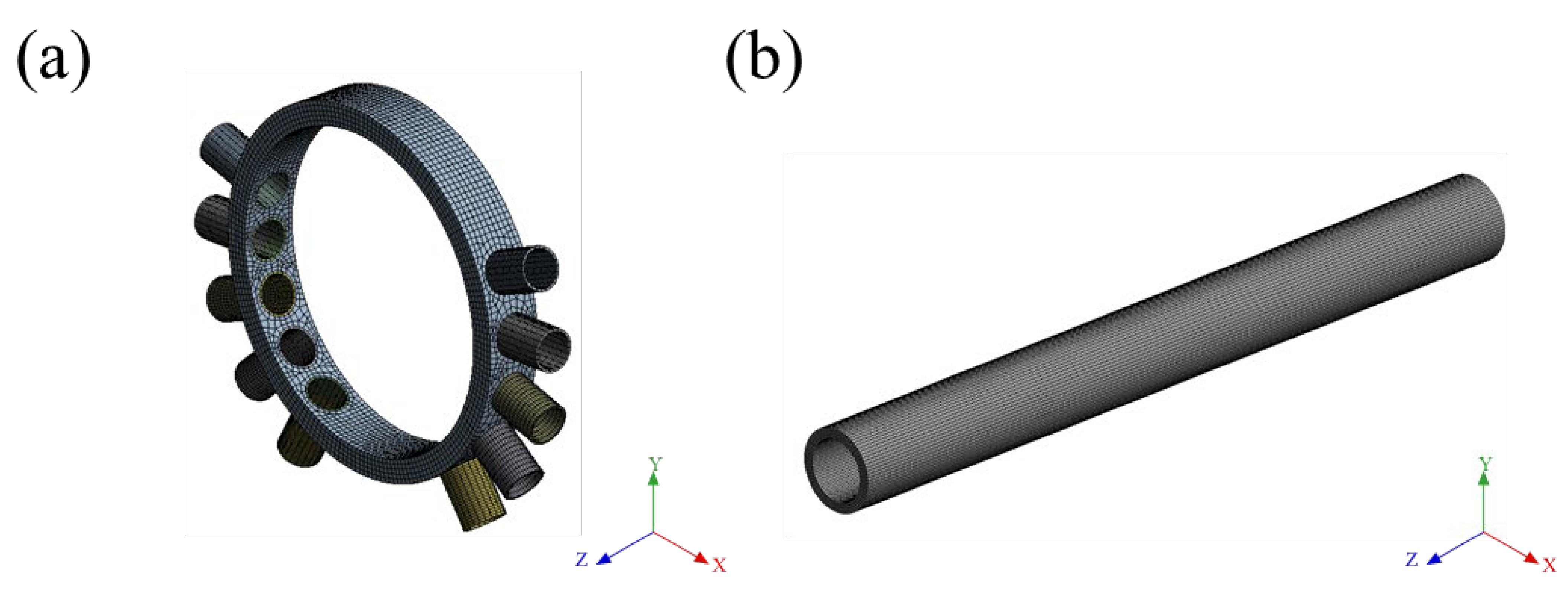
3.1. Validation for Thermo-Structural FE Model
- (a)
- Radiant and convective heat transfer from combustion gas at the outer wall;
- (b)
- Conduction in the tube wall;
- (c)
- Convection at the inner wall of the working fluid.
3.2. Estimation of Fatigue Life under Cyclic Thermal Loads
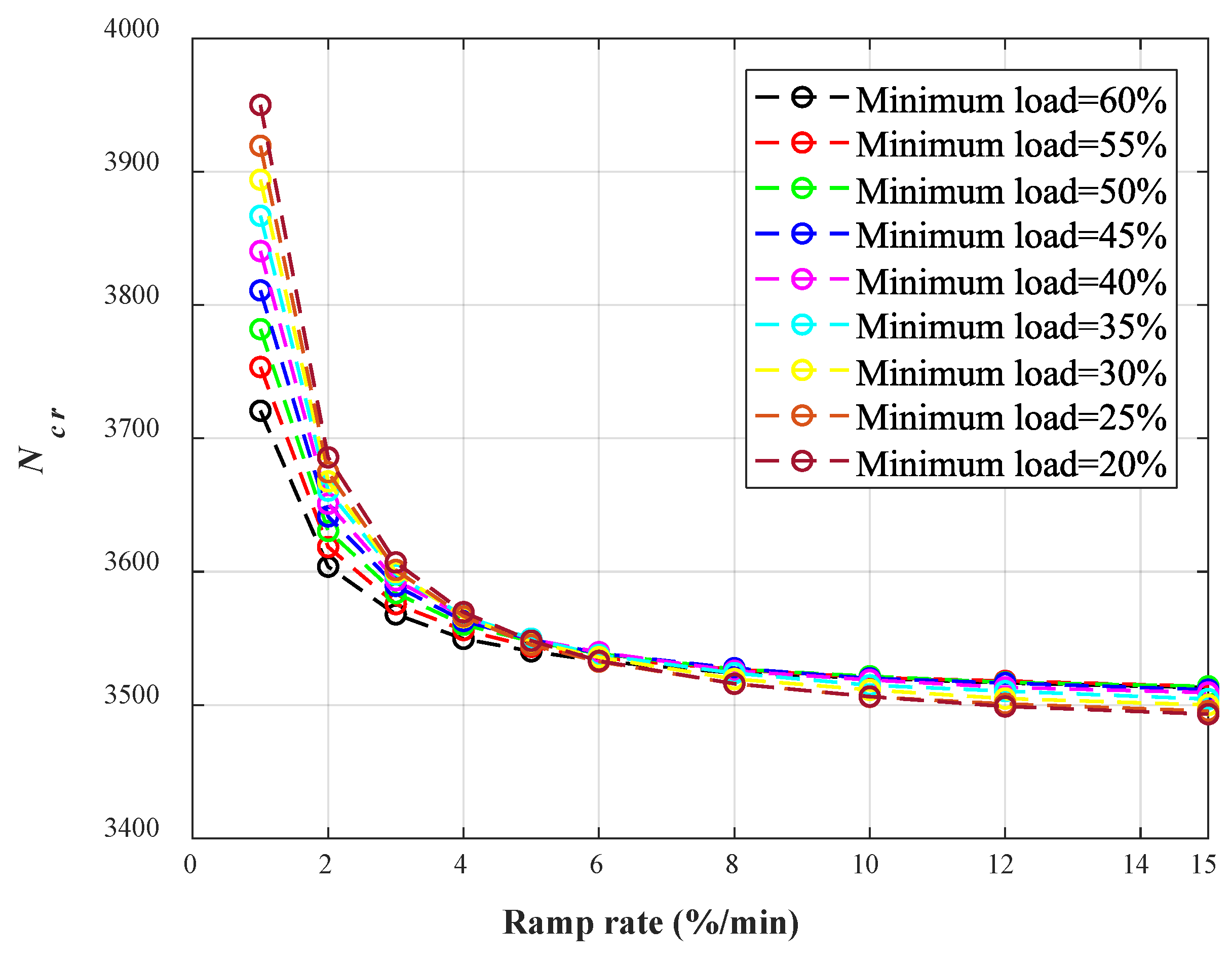
3.3. Creep and Fatigue Life of the Header
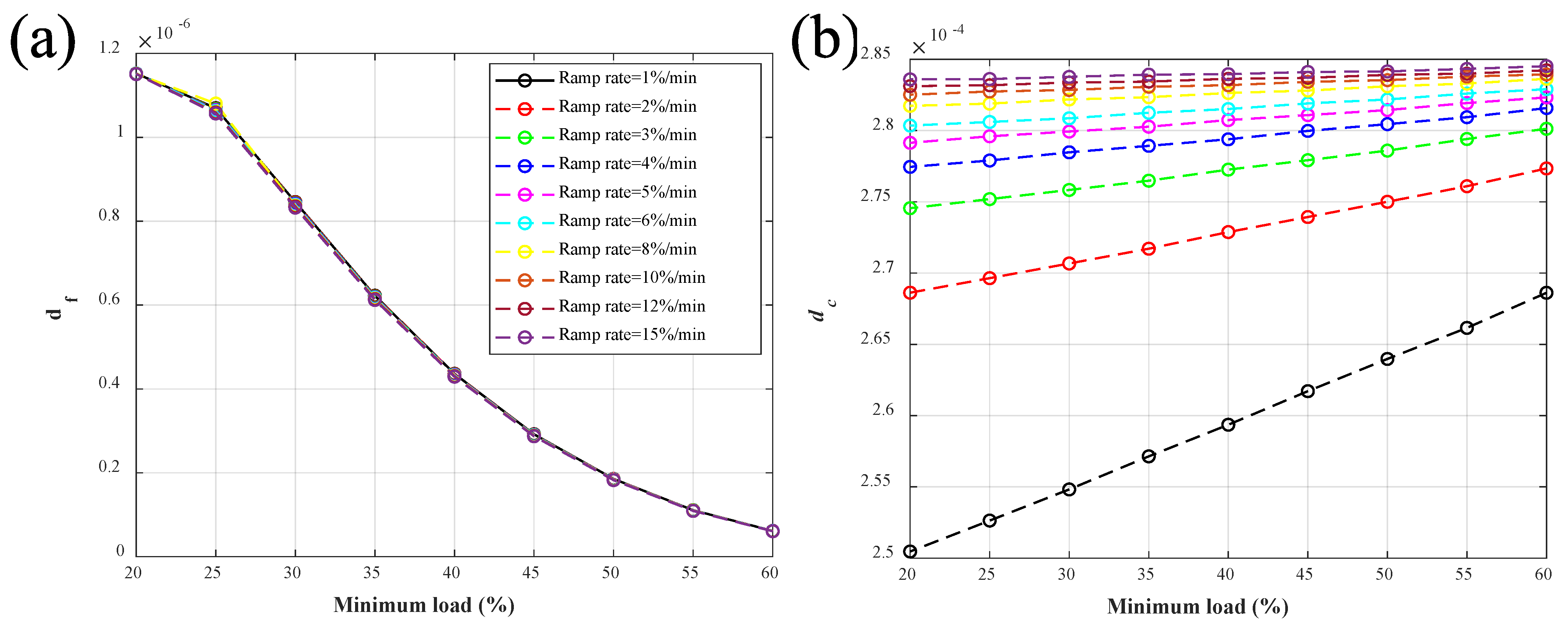
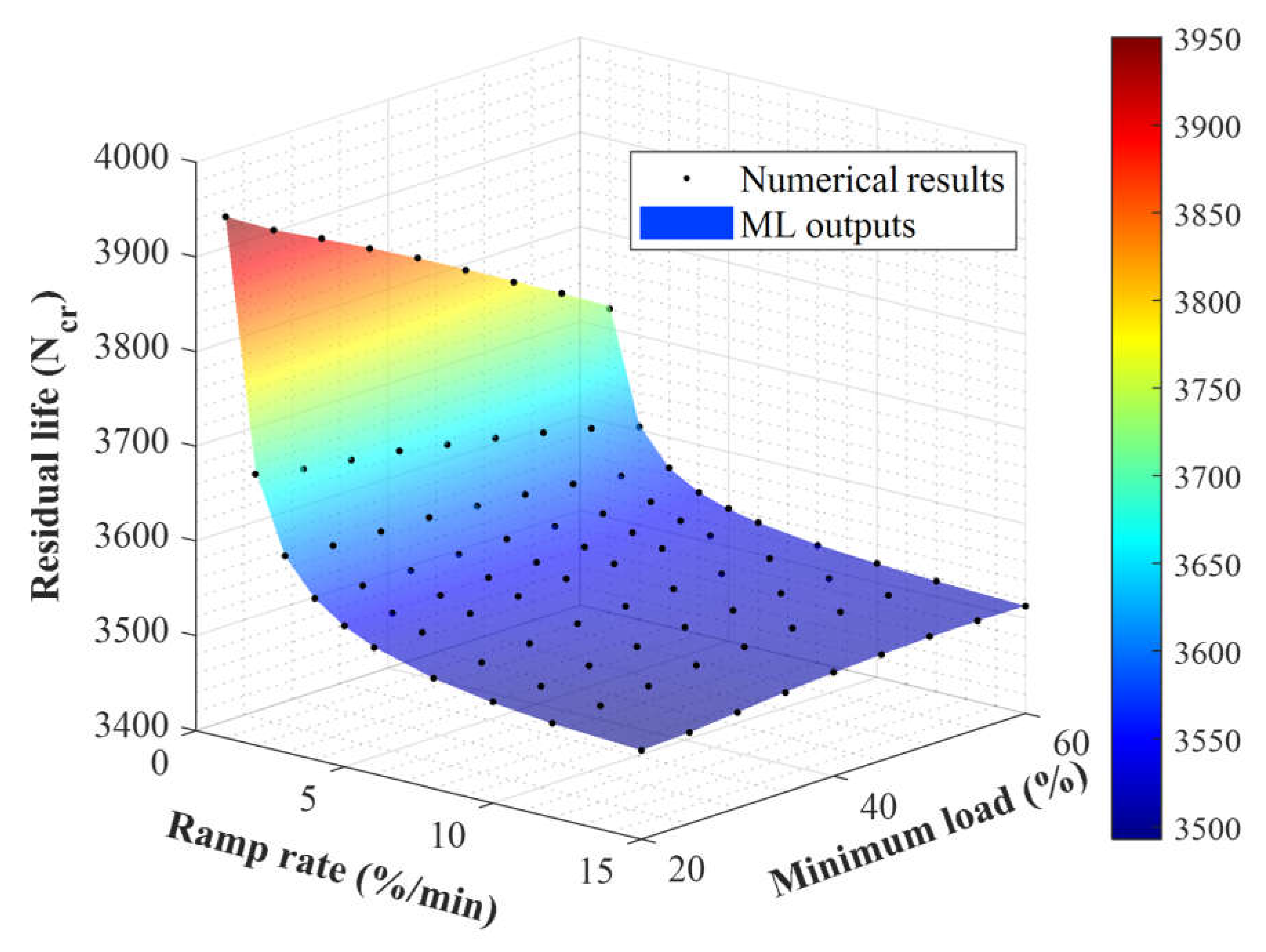
3.4. Response Surface Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Belbute, J.M.; Pereira, A.M. An alternative reference scenario for global CO2 emissions from fuel consumption: An ARFIMA approach. Econ. Lett. 2015, 136, 108–111. [Google Scholar] [CrossRef]
- Alam, M.M.; Murad, M.W.; Noman, A.H.; Ozturk, I. Relationships among carbon emissions, economic growth, energy consumption and population growth: Testing Environmental Kuznets Curve hypothesis for Brazil, China, India and Indonesia. Ecol. Indic. 2016, 70, 466–479. [Google Scholar] [CrossRef]
- Hanif, I. Impact of fossil fuels energy consumption, energy policies, and urban sprawl on carbon emissions in East Asia and the Pacific: A panel investigation. Energy Strategy Rev. 2018, 21, 16–24. [Google Scholar] [CrossRef]
- Energy-Charts. Average Net Electricity Generation during One Week in Germany 2021. 2021. Available online: https://www.energy-charts.info/ (accessed on 12 December 2022).
- Papadopoulou, A.G.; Vasileiou, G.; Flamos, A. A comparison of dispatchable RES technoeconomics: Is there a Niche for concentrated solar power? Energies 2020, 13, 4768. [Google Scholar] [CrossRef]
- Alobaid, F.; Mertens, N.; Starkloff, R.; Lanz, T.; Heinze, C.; Epple, B. Progress in dynamic simulation of thermal power plants. Prog. Energy Combust. Sci. 2017, 59, 79–162. [Google Scholar] [CrossRef]
- Bethmont, M. Damage and lifetime of fossil power plant components. Mater. High Temp. 1998, 15, 231–238. [Google Scholar] [CrossRef]
- Ray, A.; Tiwari, Y.; Sinha, R.; Chaudhuri, S.; Singh, R. Residual life prediction of service exposed main steam pipe of boilers in a thermal power plant. Eng. Fail. Anal. 2000, 7, 359–376. [Google Scholar] [CrossRef]
- Roy, H.; Ghosh, D.; Roy, P.; Saha, A.; Shukla, A.K.; Basu, J. Failure investigation of platen superheater outlet header. J. Manuf. Sci. Prod. 2009, 10, 17–24. [Google Scholar] [CrossRef]
- Al-Kayiem, H.; Albarody, T. Numerical investigation of superheater tube failure. WIT Trans. Eng. Sci. 2016, 106, 1–10. [Google Scholar]
- Li, M.; Benaarbia, A.; Morris, A.; Sun, W. Assessment of potential service-life performance for MarBN steel power plant header under flexible thermomechanical operations. Int. J. Fatigue 2020, 135, 105565. [Google Scholar] [CrossRef]
- Okrajni, J. Thermo-mechanical fatigue conditions of power plant components. J. Achiev. Mater. Manuf. Eng. 2009, 33, 53–61. [Google Scholar]
- Daga, R.; Samal, M.K. Creep Fatigue Damage Assessment of an In-service Superheater Outlet Header. In Proceedings of the International Conference on Fatigue Durability and Fracture Mechanics, Bangalore, India, 28–30 May 2015. [Google Scholar]
- Avagianos, I.; Rakopoulos, D.; Karellas, S.; Kakaras, E. Review of process modeling of solid-fuel thermal power plants for flexible and off-design operation. Energies 2020, 13, 6587. [Google Scholar] [CrossRef]
- Ali, U.; Akram, M.; Font-Palma, C.; Ingham, D.B.; Pourkashanian, M. Part-load performance of direct-firing and co-firing of coal and biomass in a power generation system integrated with a CO2 capture and compression system. Fuel 2017, 210, 873–884. [Google Scholar] [CrossRef]
- Haryanto, A.; Hong, K.-S. Modeling and simulation of an oxy-fuel combustion boiler system with flue gas recirculation. Comput. Chem. Eng. 2011, 35, 25–40. [Google Scholar] [CrossRef]
- Shuaeib, F.; Benyounis, K.; Hashmi, M. Material Behavior and Performance in Environments of Extreme Pressure and Temperatures; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Goyal, S.; Mariappan, K.; Shankar, V.; Sandhya, R.; Laha, K.; Bhaduri, A. Studies on creep-fatigue interaction behaviour of Alloy 617M. Mater. Sci. Eng. A 2018, 730, 16–23. [Google Scholar] [CrossRef]
- Bauerbach, K.; Grammenoudis, P. Fundamental considerations of the effects of flexible operation on the fatigue of power plant components. Mater. High Temp. 2021, 38, 252–261. [Google Scholar] [CrossRef]
- Impram, S.; Nese, S.V.; Oral, B. Challenges of renewable energy penetration on power system flexibility: A survey. Energy Strategy Rev. 2020, 31, 100539. [Google Scholar] [CrossRef]
- Farragher, T.; Scully, S.; O’Dowd, N.; Leen, S. Development of life assessment procedures for power plant headers operated under flexible loading scenarios. Int. J. Fatigue 2013, 49, 50–61. [Google Scholar] [CrossRef]
- Kandil, A.; El-Kady, A.; El-Kafrawy, A. Transient thermal stress analysis of thick-walled cylinders. Int. J. Mech. Sci. 1995, 37, 721–732. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 1996; Volume 6. [Google Scholar]
- Yoshiyuki, F.; Hideaki, N.; Hisashi, H.; Nobuo, N.; Etsuo, T. Data Sheets On Elevated-Temperature, Time-Dependent Low-Cycle Fatigue Properties Of Sus304-Hp (18cr-8ni) Hot Rolled Stainless Steel Plate. National Institute for Materials Science: Tsubaka, Japan, 1985. [Google Scholar]
- Xia, Z.; Kujawski, D.; Ellyin, F. Effect of mean stress and ratcheting strain on fatigue life of steel. Int. J. Fatigue 1996, 18, 335–341. [Google Scholar] [CrossRef]
- Nihei, M.; Heuler, P.; Boller, C.; Seeger, T. Evaluation of mean stress effect on fatigue life by use of damage parameters. Int. J. Fatigue 1986, 8, 119–126. [Google Scholar] [CrossRef]
- Dowling, N. Mean stress effects in strain–life fatigue. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 1004–1019. [Google Scholar] [CrossRef]
- Palmgren, A. Ball and Roller Bearing Engineering; SKF Industries Inc.: Philadelphia, PA, USA, 1959. [Google Scholar]
- Miner, M.A. Cumulative damage in fatigue. ASME J. Appl. Mech. 1945, 3, A159–A164. [Google Scholar] [CrossRef]
- Sawada, K.; Kimura, K.; Abe, F.; Taniuchi, Y.; Sekido, K.; Nojima, T.; Ohba, T.; Kushima, H.; Miyazaki, H.; Hong, H.; et al. Data Sheets on the Elevated-Temperature Properties of 18cr-9ni-3cu-nb-n Stainless Steel Tube for Power Boilers (KA-SUS 304 J1 HTB); National Institute for Materials Science: Tsubaka, Japan, 2018. [Google Scholar]
- Song, L.-K.; Bai, G.-C. Multi-surrogate collaboration approach for creep-fatigue reliability assessment of turbine rotor. IEEE Access 2020, 8, 39861–39874. [Google Scholar] [CrossRef]
- Robinson, E. Effect of temperature variation on the creep strength of steels. Trans. ASME 1938, 60, 253–259. [Google Scholar] [CrossRef]
- Taira, S. Lifetime of structures subjected to varying load and temperature. In Creep in Structures: Colloquium Held at Stanford University, California 11–15 July 1960; Springer: Berlin/Heidelberg, Germany, 1962. [Google Scholar]
- Rodriguez, P.; Mannan, S.; Rao, K.B.S. Life prediction methods for creep-fatigue conditions. Trans. Indian Inst. Met. 1987, 42, 25–43. [Google Scholar]
- Jetter, R.; Rao, K. Subsection nh-Class 1 Components in Elevated Temperature Service; American Society of Mechanical Engineers: New York, NY, USA, 2002; pp. 369–404. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Foresee, F.D.; Hagan, M.T. Gauss-Newton approximation to Bayesian learning. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 9–12 June 1997. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13. [Google Scholar]
- Andradóttir, S. An overview of simulation optimization via random search. Handb. Oper. Res. Manag. Sci. 2006, 13, 617–631. [Google Scholar]
- Karnopp, D.C. Random search techniques for optimization problems. Automatica 1963, 1, 111–121. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chu, H.H. Correlating equations for laminar and turbulent free convection from a vertical plate. Int. J. Heat Mass Transf. 1975, 18, 1323–1329. [Google Scholar] [CrossRef]
- Taler, D.; Taler, J. Simplified analysis of radiation heat exchange in boiler superheaters. Heat Transf. Eng. 2009, 30, 661–669. [Google Scholar] [CrossRef]
- Otsuka, N. Fireside corrosion. Shreir’s Corros. 2010, 1, 457–481. [Google Scholar]
- Cengel, Y.A.; Boles, M.A.; Kanoğlu, M. Thermodynamics: An Engineering Approach; McGraw-Hill: New York, NY, USA, 2011; Volume 5. [Google Scholar]
- Dowling, N.E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue–International Edition; Pearson: London, UK, 2013. [Google Scholar]
- Klaus-Jürgen, B. Finite Element Procedures in Engineering Analysis; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1982; Volume 7632. [Google Scholar]



| Elements | C | Mn | Si | Cr | Ni | N | Nb | P |
|---|---|---|---|---|---|---|---|---|
| Composition (wt%) | 0.07–0.13 | 1.00 | 0.010 | 17.0–19.0 | 7.5–10.5 | 0.05–0.12 | 0.30–0.60 | 0.040 |
| Material Property | Value at 300 °C | Value at 500 °C | Value at 700 °C |
|---|---|---|---|
| Density, ρ ) | 7790 | 7700 | 7610 |
| Thermal expansion coefficient, α | 9.7 | 10.05 | 10.3 |
| Elastic modulus E | 164.78 | 148.93 | 132.38 |
| Poisson’s ratio ν | 0.2874 | 0.2946 | 0.3018 |
| Thermal conductivity, k | 21.461 | 24.923 | 30.98 |
| Specific heat, c | 542.62 | 579.71 | 616.81 |
| Boundary Condition | Under 100% Condition | Under 30% Condition | ||
|---|---|---|---|---|
| Tube | Inlet | 501.71 | 474.22 | |
| Outlet | 502.29 | 475.32 | ||
| Inlet | 1057.89 | 1066.17 | ||
| Outlet | 843.19 | 857.56 | ||
| Internal pressure p | Inlet | 25.303 | 9.787 | |
| Outlet | 25.298 | 9.786 | ||
() | 8.582 | 8.216 | ||
| 5436.24 | 1620.95 | |||
| Emissivity | 0.8 | |||
| 0.281 | ||||
| Header | 596 | 572 | ||
| Convective film coefficient, () | 2403.8 | 980.54 | ||
| Internal pressure, p () | 4.599 | 1.483 | ||
| Part | Num. of Nodes | Num. of Elements |
|---|---|---|
| Tube | 31,648 | 24,021 |
| Header | 24,324 | 17,527 |
| Value | At Header Component | At Tube Component |
|---|---|---|
| Maximum temperature over time (°C) | 595.52 ° | 527.70 ° |
| Minimum temperature over time (°C) | 566.20 ° | 513.34 ° |
| Maximum von Mises stress over time (MPa) | 228.09 | 113.61 |
| Minimum von Mises stress over time (MPa) | 13.169 | 74.761 |
| Maximum strain range |
| Value | |||
|---|---|---|---|
| Max | 2 | 50 | 0.1 |
| Min | 1 | 5 | 0.000001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heo, J.; Park, M.; Kim, J.-M.; Jang, D.-W.; Han, J.-H. Effect of Flexible Operation on Residual Life of High-Temperature Components of Power Plants. Processes 2023, 11, 1679. https://doi.org/10.3390/pr11061679
Heo J, Park M, Kim J-M, Jang D-W, Han J-H. Effect of Flexible Operation on Residual Life of High-Temperature Components of Power Plants. Processes. 2023; 11(6):1679. https://doi.org/10.3390/pr11061679
Chicago/Turabian StyleHeo, Jun, Mingyu Park, Jeong-Myun Kim, Dong-Won Jang, and Ji-Hoon Han. 2023. "Effect of Flexible Operation on Residual Life of High-Temperature Components of Power Plants" Processes 11, no. 6: 1679. https://doi.org/10.3390/pr11061679
APA StyleHeo, J., Park, M., Kim, J.-M., Jang, D.-W., & Han, J.-H. (2023). Effect of Flexible Operation on Residual Life of High-Temperature Components of Power Plants. Processes, 11(6), 1679. https://doi.org/10.3390/pr11061679






