Numerical and Experimental Simulation of Hydraulic Fracture Propagation Mechanism in Conglomerate Formation Based on Hybrid Finite-Discrete Element Method
Abstract
:1. Introduction
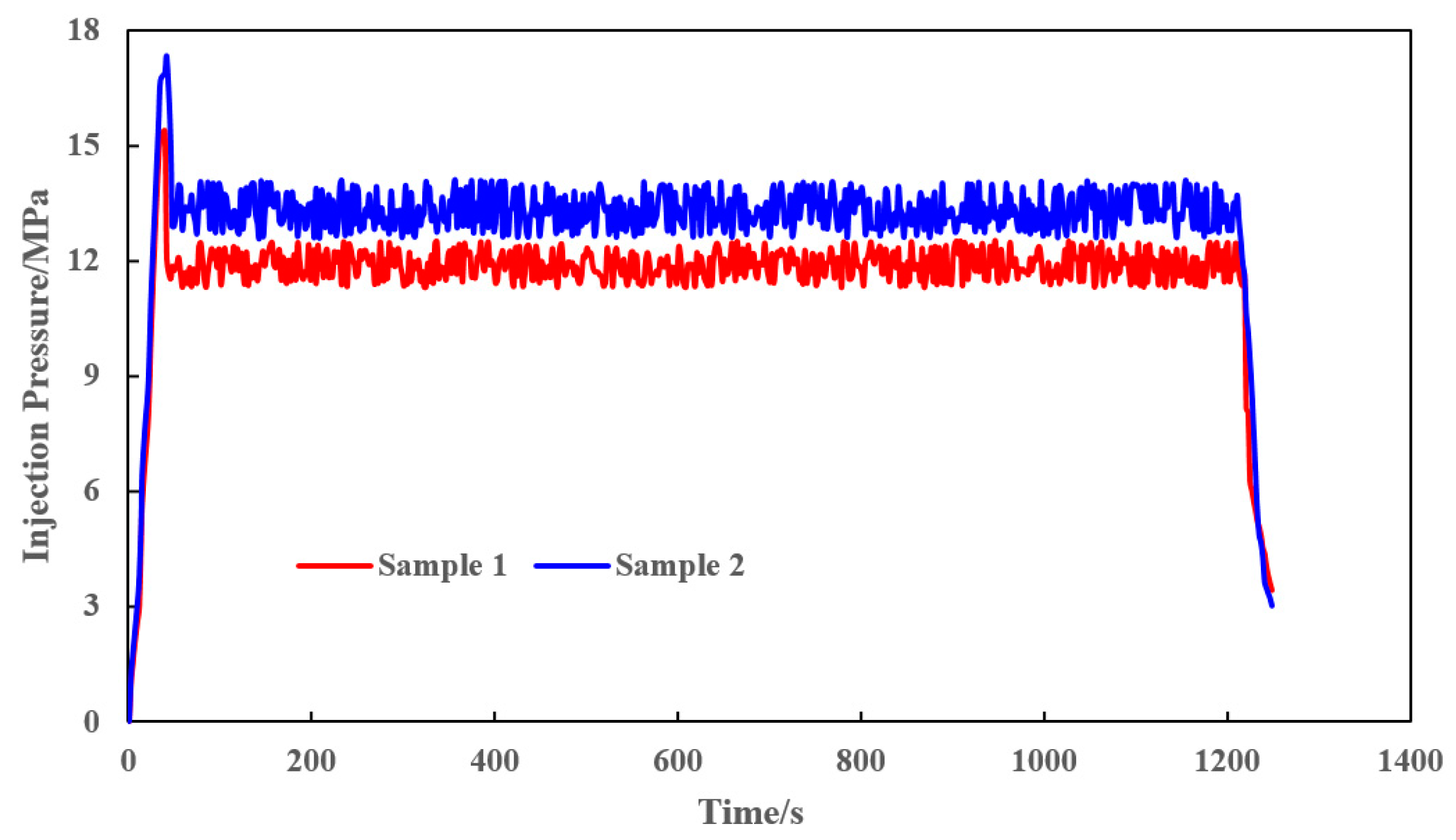
2. Experiment
3. Numerical Simulation
3.1. Governing Equation
3.2. Simulation Results and Discussion
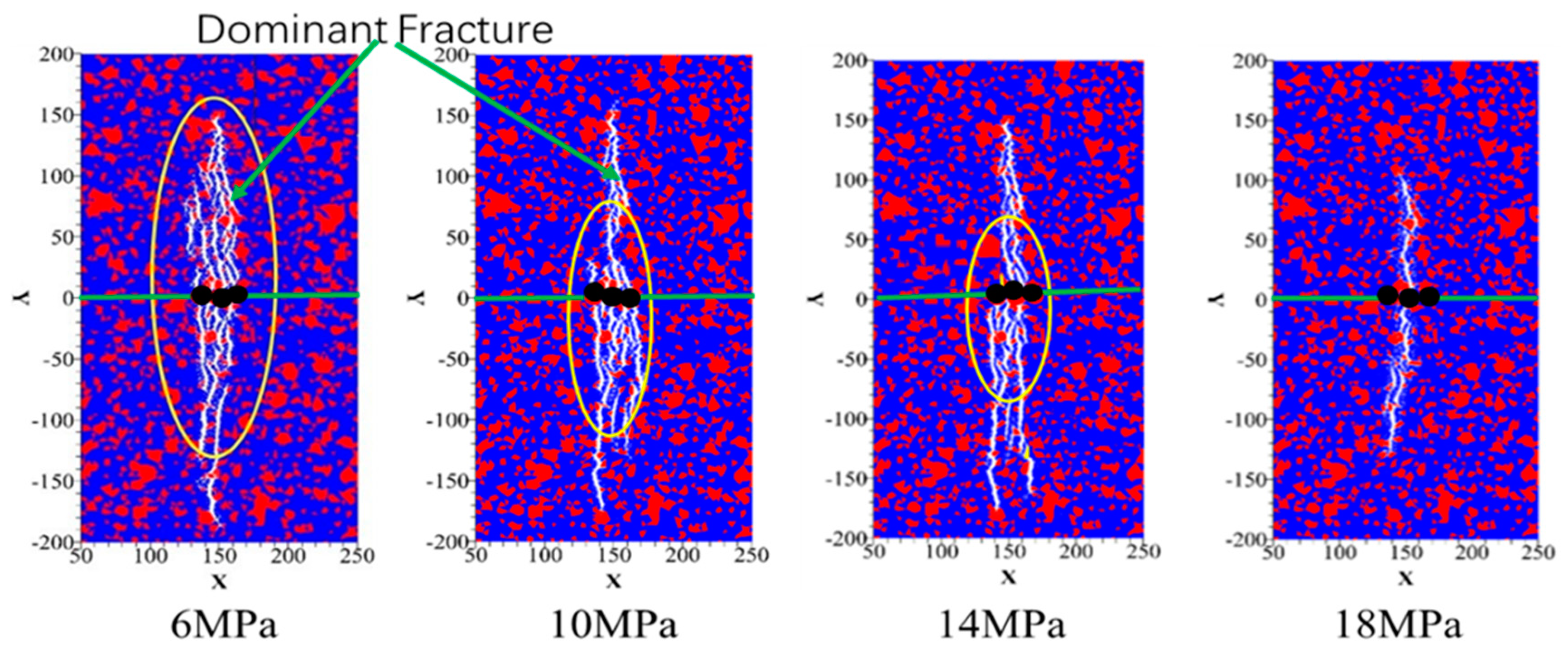
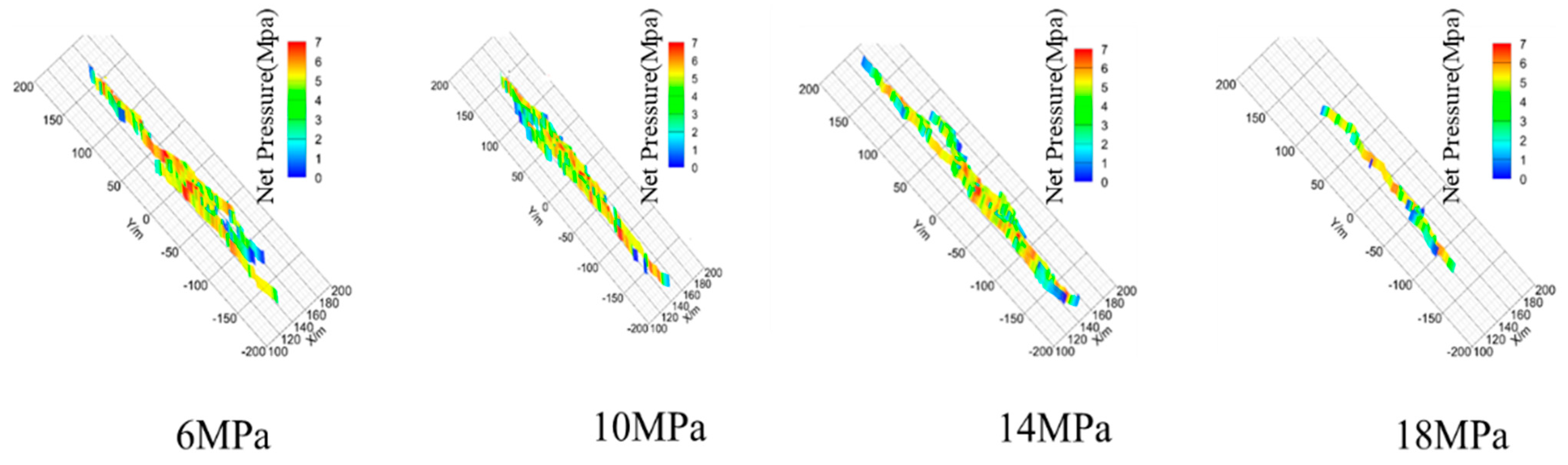
3.2.1. Horizontal Stress Difference
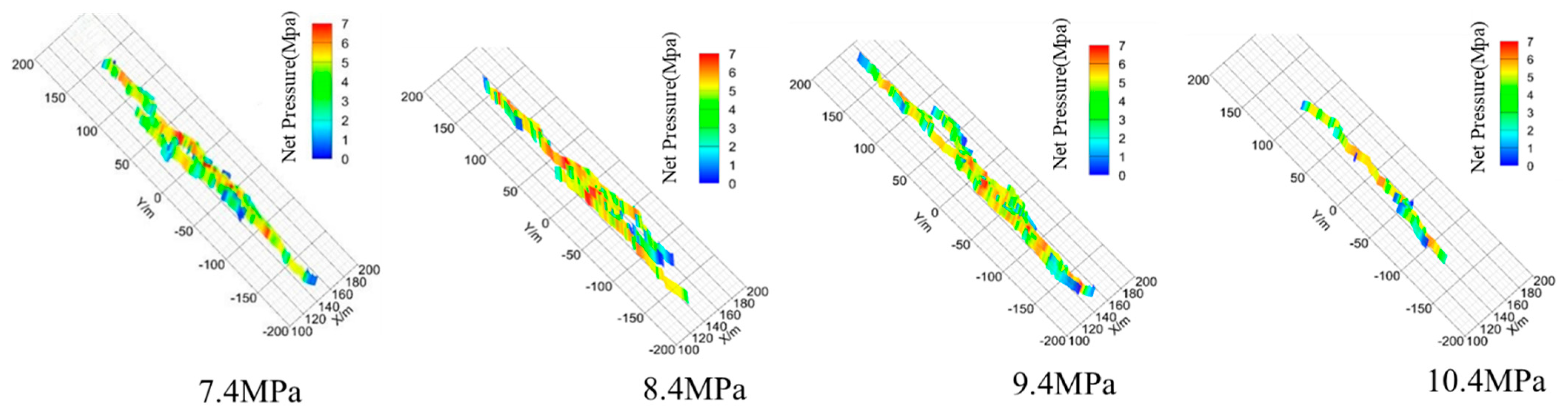
3.2.2. Tensile Strength
3.2.3. Pumping Rate
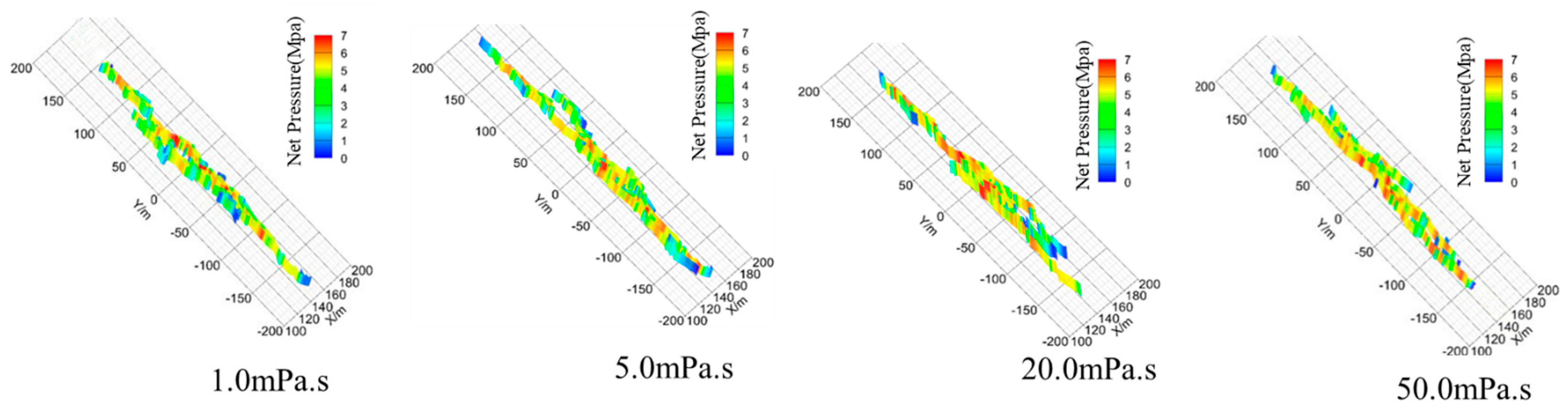
3.2.4. Viscosity of Fracturing Fluid
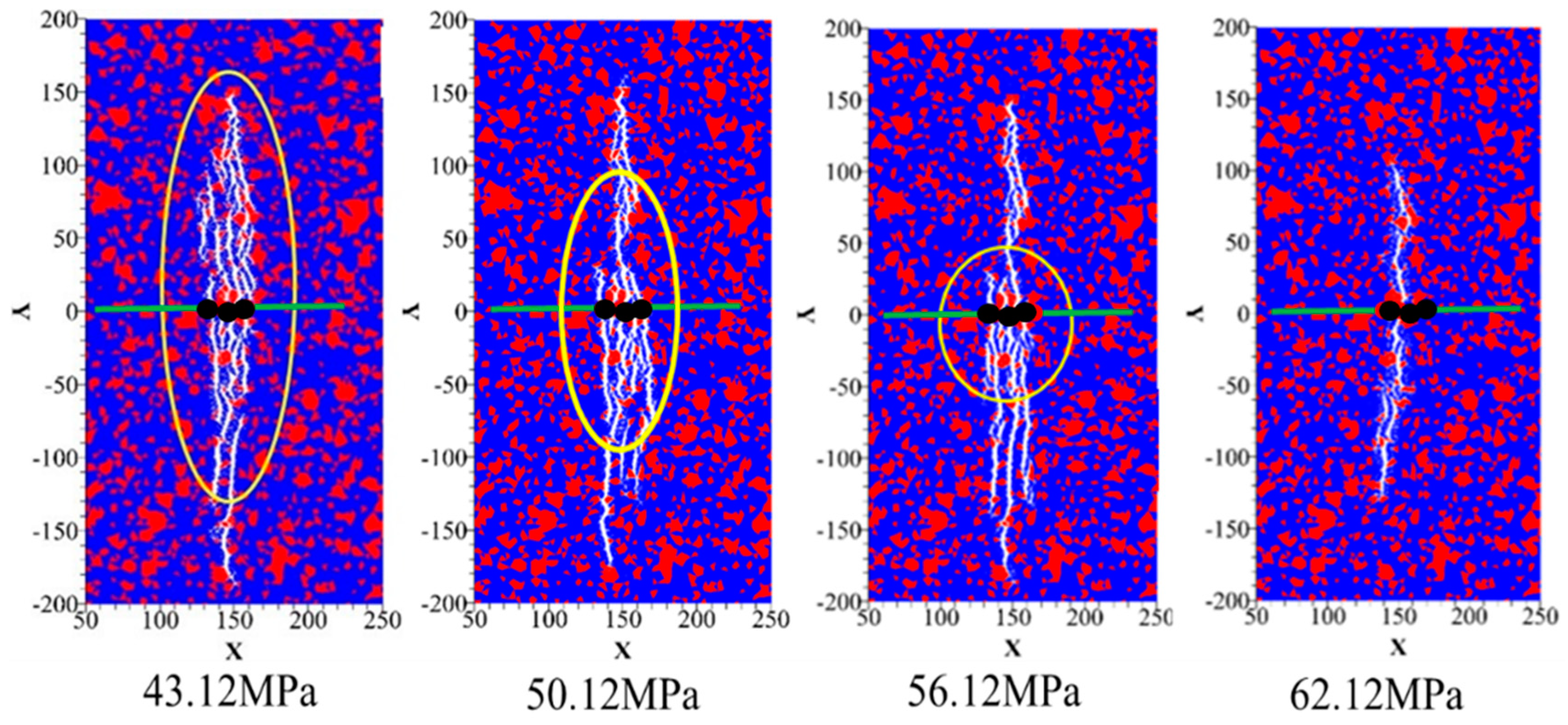
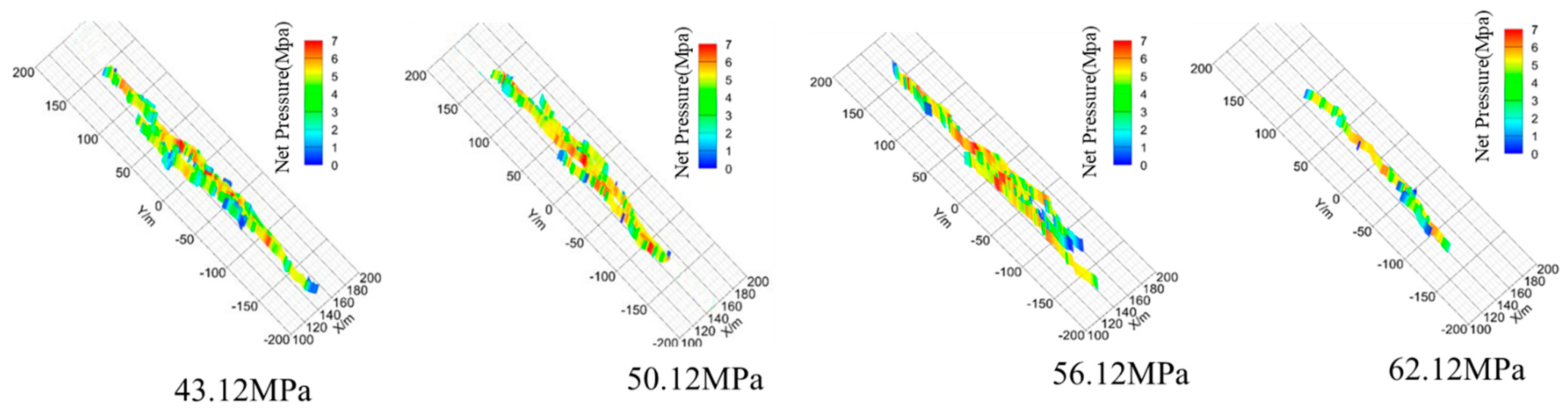
3.2.5. Cohesion Strength
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al-Rubaye, A.; Ben Mahmud, H.K. A numerical investigation on the performance of hydraulic fracturing in nat-urally fractured gas reservoirs based on stimulated rock volume. J. Pet. Explor. Prod. Technol. 2020, 10, 3333–3345. [Google Scholar] [CrossRef]
- Cheng, W.; Jin, Y.; Chen, M. Reactivation mechanism of natural fractures by hydraulic fracturing in naturally fractured shale reservoirs. J. Nat. Gas. Sci. Eng. 2015, 27, 1357–1365. [Google Scholar] [CrossRef]
- Dehghan, A.N. An experimental investigation into the influence of pre-existing natural fracture on the behavior and length of propagating hydraulic fracture. Eng. Fract. Mech. 2020, 240, 107330. [Google Scholar] [CrossRef]
- Guo, T.; Wang, Y.; Du, Z.; Chen, M.; Liu, D.; Liu, X.; Rui, Z. Evaluation of Coated Proppant Unconventional Performance. Energy Fuels 2021, 35, 9268–9277. [Google Scholar] [CrossRef]
- Heng, S.; Liu, X.; Li, X.; Zhang, X.; Yang, C. Experimental and numerical study on the non-planar propagation of hydraulic fractures in shale. J. Pet. Sci. Eng. 2019, 179, 410–426. [Google Scholar] [CrossRef]
- Hou, B.; Chen, M.; Cheng, W.; Diao, C. Investigation of Hydraulic Fracture Networks in Shale Gas Reservoirs with Random Fractures. Arab. J. Sci. Eng. 2016, 41, 2681–2691. [Google Scholar] [CrossRef]
- Liu, B.; Jin, Y.; Chen, M. Influence of vugs in fractured-vuggy carbonate reservoirs on hydraulic fracture propagation based on laboratory experiments. J. Struct. Geol. 2019, 124, 143–150. [Google Scholar] [CrossRef]
- Wei, C.; Zhang, B.; Li, S.; Fan, Z.; Li, C. Interaction between Hydraulic Fracture and Pre-Existing Fracture under Pulse Hydraulic Fracturing. SPE Prod. Oper. 2021, 36, 553–571. [Google Scholar] [CrossRef]
- Liu, X.; Qu, Z.; Guo, T.; Sun, Y.; Wang, Z.; Bakhshi, E. Numerical simulation of non-planar fracture propagation in multi-cluster fracturing with natural fractures based on Lattice methods. Eng. Fract. Mech. 2019, 220, 106625. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, X.; Peng, X.; Zhang, Y.; Chen, H.; He, J. Influence of natural fractures on propagation of hydraulic fractures in tight reservoirs during hydraulic fracturing. Mar. Pet. Geol. 2022, 138, 105505. [Google Scholar] [CrossRef]
- Luege, M.; Orlando, A. A variational asymmetric phase-field model of quasi-brittle fracture: Energetic solutions and their computation. Int. J. Solids Struct. 2021, 225, 110940. [Google Scholar] [CrossRef]
- Ren, L.; Su, Y.; Zhan, S.; Hao, Y.; Meng, F.; Sheng, G. Modeling and simulation of complex fracture network propa-gation with SRV fracturing in unconventional shale reservoirs. J. Nat. Gas Sci. Eng. 2016, 28, 132–141. [Google Scholar] [CrossRef]
- Zhang, F.; Dontsov, E.; Mack, M. Fully coupled simulation of a hydraulic fracture interacting with natural fractures with a hybrid discrete-continuum method. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1430–1452. [Google Scholar] [CrossRef]
- Zheng, H.; Pu, C.; Sun, C. Study on the interaction between hydraulic fracture and natural fracture based on ex-tended finite element method. Eng. Fract. Mech. 2020, 230, 106981. [Google Scholar] [CrossRef]
- Zheng, H.; Pu, C.; Xu, E.; Sun, C. Numerical investigation on the effect of well interference on hydraulic fracture propagation in shale formation. Eng. Fract. Mech. 2020, 228, 106932. [Google Scholar] [CrossRef]
- Zou, J.; Jiao, Y.-Y.; Tan, F.; Lv, J.; Zhang, Q. Complex hydraulic-fracture-network propagation in a naturally fractured reservoir. Comput. Geotech. 2021, 135, 104165. [Google Scholar] [CrossRef]
- Zou, Y.; Gao, B.; Zhang, S.; Ma, X.; Sun, Z.; Wang, F.; Liu, C. Multi-fracture nonuniform initiation and vertical propagation behavior in thin interbedded tight sandstone: An experimental study. J. Pet. Sci. Eng. 2022, 213, 110417. [Google Scholar] [CrossRef]
- Zou, Y.; Shi, S.; Zhang, S.; Yu, T.; Tian, G.; Ma, X.; Zhang, Z. Experimental modeling of sanding fracturing and conductivity of propped fractures in conglomerate: A case study of tight conglomerate of Mahu sag in Junggar Basin, NW China. Pet. Explor. Dev. 2021, 48, 1383–1392. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Stolle, D.F.; Liang, L.; Shi, Y. Modeling hydraulic fracture in heterogeneous rock materials using permeability-based hydraulic fracture model. Undergr. Space 2020, 5, 167–183. [Google Scholar] [CrossRef]
- Pakzad, R.; Wang, S.Y.; Sloan, S.W. Numerical Simulation of Hydraulic Fracturing in Low-/High-Permeability, Quasi-Brittle and Heterogeneous Rocks. Rock. Mech. Rock. Eng. 2018, 51, 1153–1171. [Google Scholar] [CrossRef]







| Item | Parameter | Unit | Value |
|---|---|---|---|
| Stress field | Maximum horizontal principal stress | MPa | 80 |
| Minimum horizontal principal stress | MPa | 70 | |
| Pore pressure | MPa | 30 | |
| Vertical stress | MPa | 107 | |
| Properties of rock matrix | Young’s modulus | GPa | 25.4 |
| Poisson’s rate | Dimensionless | 0.261 | |
| Permeability | mD | 0.14 | |
| Tensile strength | MPa | 6.29 | |
| Cohesion strength | MPa | 43.12 | |
| Internal friction angle | ° | 16.9 | |
| Porosity | % | 7.2 | |
| Properties of gravel | Young’s modulus | GPa | 64.2 |
| Poisson’s rate | Dimensionless | 0.217 | |
| Tensile strength | MPa | 9.41 | |
| Cohesion strength | MPa | 56.12 | |
| Internal friction angle | ° | 18.9 | |
| Injection parameters | Injection rate | m3/min | 3.0 |
| Viscosity of fracturing fluid | mPa·s | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wang, M. Numerical and Experimental Simulation of Hydraulic Fracture Propagation Mechanism in Conglomerate Formation Based on Hybrid Finite-Discrete Element Method. Processes 2023, 11, 1645. https://doi.org/10.3390/pr11061645
Wang L, Wang M. Numerical and Experimental Simulation of Hydraulic Fracture Propagation Mechanism in Conglomerate Formation Based on Hybrid Finite-Discrete Element Method. Processes. 2023; 11(6):1645. https://doi.org/10.3390/pr11061645
Chicago/Turabian StyleWang, Linsheng, and Mingxing Wang. 2023. "Numerical and Experimental Simulation of Hydraulic Fracture Propagation Mechanism in Conglomerate Formation Based on Hybrid Finite-Discrete Element Method" Processes 11, no. 6: 1645. https://doi.org/10.3390/pr11061645
APA StyleWang, L., & Wang, M. (2023). Numerical and Experimental Simulation of Hydraulic Fracture Propagation Mechanism in Conglomerate Formation Based on Hybrid Finite-Discrete Element Method. Processes, 11(6), 1645. https://doi.org/10.3390/pr11061645







