Abstract
The unreasonable development and pollution of groundwater have caused damage to the groundwater system and environmental problems. To prevent this, the concept of “groundwater vulnerability” was proposed, and various evaluation methods were developed for groundwater protection. However, with changing climatic conditions and human activities, groundwater vulnerability is now emphasizing physical processes. This study aims to review and analyze the principles and applications of process-based groundwater vulnerability methods to achieve the source protection of groundwater resources. It introduces the assessment method and elaborates on pollutant migration processes and numerical simulation technology. Relevant articles from the past 30 years are reviewed to show the evolution of process-based groundwater vulnerability assessment. The study also discusses current research trends and proposes future development paths. It concludes that process-based groundwater vulnerability assessment will become the mainstream method, and modern technologies such as artificial intelligence will be necessary to solve challenges and achieve sustainable development.
1. Introduction
Environmental and development issues are the most pressing issues facing humanity today [1,2,3]. For a long time, people have focused only on the development and utilization of natural resources, ignoring the finiteness and non-renewability of resources as well as the environmental damage caused by development [4,5,6]. This has led to the continuous deterioration of the ecological environment and has restricted the sustainable development of the economy and society [7,8,9]. Nearly half of the world’s population uses groundwater as a source of drinking water making it an indispensable valuable resource in countries’ economic development [10,11,12,13]. With the rapid development of industry and agriculture and the continuous increase in population, the unreasonable exploitation and utilization of groundwater and groundwater pollution have become increasingly serious, causing varying degrees of damage to groundwater systems, resulting in a series of ecological and environmental problems such as declining groundwater levels, reduced water volume, and deteriorating water quality [14,15,16,17,18]. This has proved that groundwater pollution has characteristics such as accumulation, lagging behind, potentiality, etc., and is often related to land pollution [19,20,21]. Once the groundwater system is damaged, especially when the water quality deteriorates, the difficulty and cost of its treatment and restoration are extremely huge, rendering it almost impossible in a short time [22,23]. Therefore, how to protect groundwater resources from pollution or minimize pollution is a very important research topic.
Due to the concealment of underground aquifers and the complexity of their distribution, as well as characteristics such as slow flow rate and poor self-purification ability compared to surface water, once groundwater is polluted, it is much more difficult and costly to manage than surface water. Some pollution may even be impossible to completely eradicate [24,25,26]. In karst areas, the lack of natural sealing or filtering layers makes it easy for surface water and all pollutants to directly enter the aquifer or underground rivers through karst forms such as caves, funnels, and sinkholes. Moreover, the karst aquifer has the characteristics of a triple medium, including voids, fractures, and conduits. Pollutants have a short retention time in the karst system and limited reaction with the aquifer; thus, the attenuation of pollutants and chemical and biological decay is often ineffective [27,28]. Therefore, based on hydrogeological conditions and the layout of industrial and agricultural production, we should scientifically divide the scope of groundwater protection zones and adopt strict protective measures to ensure that groundwater is not polluted. To this end, conducting vulnerability zoning evaluations of groundwater and delimiting water source protection zones has become a major means of protecting aquifers [29]. This is of great significance for maintaining harmony between natural resources and the ecological environment and realizing the sustainable development and utilization of groundwater resources. The concept of groundwater vulnerability mainly refers to pollution and focuses on water quality while ignoring water quantity [28,30]. Authors of this article believe that the meaning of groundwater vulnerability should be fully understood from the following two aspects: (1) The meaning of groundwater vulnerability should include both water quality and water quantity. It is manifested as groundwater pollution problems in terms of water quality and a series of negative effects on the water environment caused by changes in water quantity. The evaluation scope needs to include not only the vadose zone but also the corresponding saturated zone. The combination of water quality and water quantity, and the combination of the saturated zone and the vadose zone, form a complete vulnerability evaluation framework for the groundwater system. (2) Groundwater vulnerability refers to the possibility of pollution occurring and is a relative concept. In areas with high groundwater vulnerability, the situation of the groundwater may not necessarily be poor; on the contrary, in areas with low groundwater vulnerability, when there are strong sources of pollution or human activities that cause damage, the groundwater system will be damaged and become vulnerable.
At present, there are many methods for evaluating groundwater vulnerability, and the mainstream methods include the overlay index method, statistical method, and process simulation method [25,31]. Among them, the process-based simulation method is based on the water and pollutant transport model, using deterministic physical and chemical equations to simulate the transport and transformation process of pollutants, establishing a vulnerability evaluation formula, and quantifying each evaluation factor to obtain a comprehensive index that can evaluate vulnerability [32]. This method can describe the physical, chemical, and biological processes that affect groundwater vulnerability and can estimate the spatial and temporal distribution of pollutants, thus becoming the mainstream trend in groundwater vulnerability evaluation. However, although significant progress has been made in the process-based groundwater vulnerability assessment method, there is still a lack of systematic sorting of methods. Most of them are still focused on the transport of pollutants in the vadose zone and have not systematically evaluated groundwater vulnerability from the perspective of sources and sinks by treating the vadose zone-saturated zone as a whole.
This study aims to provide a comprehensive analysis of process-based vulnerability evaluation principles and mathematical calculation methods of physical and chemical processes during pollutant transport in soil. Additionally, we will summarize the commonly used numerical simulation methods for pollutant transport in vadose and saturated zones and review the development of groundwater vulnerability evaluation methods in the past 30 years. Based on this foundation, our study aims to identify bottlenecks and provide innovative solutions for the development of process-based groundwater vulnerability evaluation. This will provide a basis for rational development and utilization of regional groundwater resources, prevention of groundwater pollution, and effective protection of groundwater resources. The innovative aspect of our study lies in its focus on process-based vulnerability evaluation and its emphasis on the identification of bottlenecks and provision of solutions. By doing so, our study will contribute to the advancement in groundwater vulnerability evaluation methods and provide a more comprehensive understanding of the protection and utilization of groundwater resources.
2. The Methodology of the Process-Based Groundwater Vulnerability Assessment
2.1. The Principles of the Process-Based Groundwater Vulnerability Assessment
The process-based method entails constructing a vulnerability assessment mathematical formula based on groundwater flow and contaminant transport models. Various evaluation factors are quantified to obtain a comprehensive regional vulnerability index. The term “process” encompasses the flow of recharge water sources and the movement of pollutants through the soil, unsaturated zone, and saturated zone, as well as the transport and transformation of pollutants in the unsaturated and saturated zones [31]. Multiphase vertical flow exists in the surface soil and unsaturated zone, with physical, chemical, and biological processes predominating, which delays the arrival of pollutants in the groundwater table, with the reaction intensity in the surface soil being higher than that in the unsaturated zone [33,34,35]. Water flow in the saturated zone is primarily horizontal, and the attenuation of pollutant concentration relies mainly on dilution by groundwater flow and secondarily on various reactions. These processes can be attributed to the groundwater flow system and the geochemical action system, which determine the vulnerability of groundwater to pollution [36]. Factors that control the groundwater flow system, such as groundwater supply, runoff and drainage conditions, and the properties of the aquifer itself (porosity, hydraulic conductivity, thickness, etc.), directly affect the intrinsic vulnerability of groundwater resources. The conceptual model is depicted in Figure 1. The important mechanism controlling the transport and transformation of pollutants in the groundwater flow system is the process of diffusion and dispersion. The primary processes responsible for altering the pollutant concentration in groundwater include adsorption–desorption, dissolution–precipitation, oxidation–reduction, and complexation.
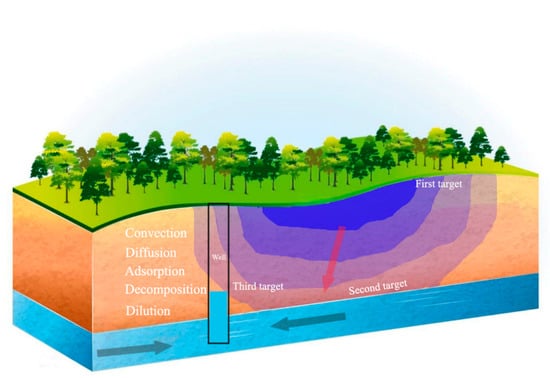
Figure 1.
Conceptual diagram of groundwater pollutant transport based on the “source-sink” process.
The process-based method can be used to evaluate both the intrinsic vulnerability of groundwater and the specific vulnerability to a particular pollutant, and is generally applied at large scales. Understanding the sources and movement of groundwater is crucial in studying the intrinsic vulnerability of groundwater using the process-based method, while the focus of evaluating specific vulnerability is on the sources, transport, and transformation of pollutants. However, the method is primarily limited by the availability of long-term observations of groundwater flow and solute transport.
Simulation is a tool for investigating groundwater vulnerability through “process”, and the establishment of groundwater flow and solute transport transformation models is key to implementing process-based methods for studying groundwater vulnerability. By identifying and validating these models, the accuracy and reliability of groundwater vulnerability assessment results based on modeling can be ensured to a certain extent. Thus, process-based methods are not only a means of evaluating groundwater vulnerability, but also a process for verifying the results of such assessments.
The transport behavior of solutes in unsaturated zones is constantly changing, as various natural and human factors influence groundwater flow. As solutes move from the unsaturated zone into the saturated zone with groundwater, their transport behavior is not only affected by factors such as infiltration and evaporation, but also by the physical and chemical properties of the solutes themselves and the matrix potential of the soil. In groundwater mixed within soil and rock fissures, solutes are displaced due to differences in the concentration of different solutions in the water flow, and solute transport is mainly achieved through processes such as convection, dispersion, and adsorption. The process-based groundwater vulnerability assessment method is shown in Figure 2. Based on the entire transport path of pollutants entering from the ground surface and flowing through the vadose zone and saturated zone, the main control targets of process-based groundwater vulnerability assessment are selected at the groundwater surface and pumping wells. The evaluation scope is, respectively, the vadose zone and saturated zone, and the groundwater system, as shown in Figure 1. In summary, it mainly includes the following calculation positions:
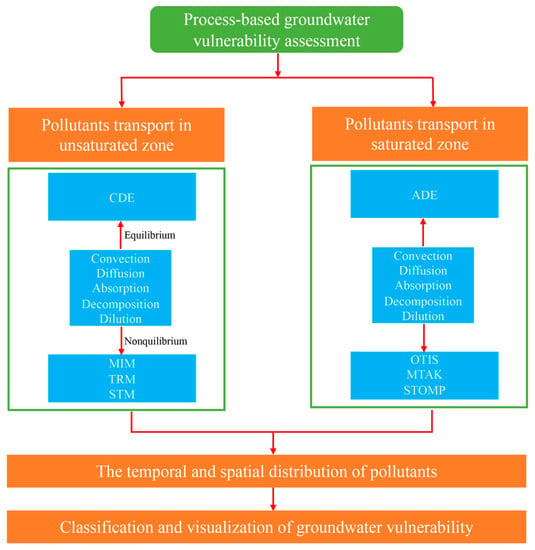
Figure 2.
Process-based groundwater vulnerability assessment process.
First position: Calculate the actual infiltration amount and total amount of pollutants entering the ground based on rainfall, evaporation, runoff, and pollutant sources.
Second position: Use a simulation model to calculate the total amount of pollutants passing through vadose zone soil layers and entering the groundwater system.
Third position: Use a process-based method to obtain water flux and pollutant concentration entering the saturated zone from the vadose zone. This information serves as the boundary condition for a 2D or 3D groundwater flow and pollutant migration model to study changes in pollutant concentration in the pumping well.
2.2. The Physical and Chemical Processes Involved in Process-Based Groundwater Vulnerability Assessment
2.2.1. Convection
The process of solute movement through groundwater flow in soil is known as convection. The formation of convection requires two fundamental elements: fluid flow and the existence of a pore system, which leads to the transport of solutes. Convection typically occurs in the saturated–unsaturated zone of stable or unstable water flow regimes [37,38]. The strength of the convection effect is generally represented by the convection flux, which denotes the amount of material or mass of solute that passes through a unit area of unsaturated groundwater in a given time. It can be expressed as follows [39]:
where Jc represents the convective flux of solute, also known as solute transport density, measured in mol/(m2·s); q denotes the water flux, which represents the amount of water passing through a unit area in the vertical direction per unit time, measured in m/s; and c represents the relative concentration of the solute, measured in kg/m3. If expressed in terms of soil water content θ or pore velocity v, Equation (1) can be written as follows:
where v represents the average pore flow velocity (m/s) and θ represents the volumetric water content of the soil.
2.2.2. Hydrodynamic Dispersion
Hydrodynamic dispersion is caused by the mechanical dispersion and molecular diffusion of solutes in porous media. Mechanical diffusion and molecular diffusion occur simultaneously and act together to cause mixing and dispersion of solute concentration.
- (1)
- Molecular diffusion
Molecular diffusion is a phenomenon of material transport caused by the uneven concentration of solutes in a liquid. Concentration gradients cause the material to move from areas of high concentration to areas of low concentration, in order to achieve a uniform concentration. Therefore, molecular diffusion occurs even in stationary liquids. In free solutions, molecular diffusion follows Fick’s law, which states that [40,41]:
where Js represents the diffusion flux of the solute (mol/m2·s); dc/dx represents the concentration gradient; and represents the diffusion coefficient of the solute in units (m2/s). Due to factors such as soil moisture content and pore tortuosity, the diffusion coefficient of molecules in soil is lower than that in free water. It is generally believed that the solute diffusion coefficient is independent of soil solute concentration and is instead represented as a function of soil water content:
where a and b are empirical constants. Unsaturated groundwater is connected to the air, and some pores are filled with air. It does not fill the entire aquifer, but only fills part of the pore system of the aquifer. Therefore, for the description of the diffusion process of solute molecules mixed in soil, the following equation is often used:
- (2)
- Mechanical diffusion
Due to the existence of pores of different sizes and shapes in the soil, the flow velocity and direction of the aqueous solution in each pore is different, which disperses the solute and expands the transport range, causing mechanical dispersion of the solute. The solute migration flux caused by mechanical dispersion can be expressed as [42,43]:
where represents the mechanical dispersion flux of the solute (mol/m2·s) and represents the mechanical dispersion coefficient (m2/s). By combining Equations (3) and (6), we can obtain the advection–dispersion equation:
By combining Equations (5) and (6),
where represents the solute hydraulic dispersion flux, and and D are the effective hydraulic dispersion coefficient and hydraulic dispersion coefficient, respectively. These coefficients are functions of water content and average pore velocity. One-dimensional hydraulic dispersion can be expressed as follows:
Researchers [44,45,46,47] have determined the hydrodynamic dispersion coefficient D through extensive experimentation:
where v represents the average pore velocity, and d represents the characteristic length scale of the porous medium, which could be either the average particle size or some other relevant length scale.
2.2.3. Adsorption
After pollutants enter the unsaturated zone, solutes are transferred from the liquid phase to the solid phase under specific conditions. This process significantly affects solute transport from the unsaturated zone to the saturated zone, with factors such as soil solution composition, pH value, mineral properties, ionic strength, and organic matter content playing important roles. The adsorption of solutes occurs through two mechanisms: specific and non-specific adsorption, with specific adsorption being the predominant mechanism in variable charge soils. The adsorption equilibrium equation is [48,49,50]:
where b represents the adsorption constant, q represents the amount of solute adsorbed on the soil solid framework, and represents the maximum adsorption capacity relative to the soil framework.
2.3. The Influence Factors of Solute Transport in Vadose Zone
2.3.1. Initial Concentration
The initial concentration is used to indicate the existing level of pollution in the study area and to predict the potential degree of contamination to groundwater under current conditions. The value of the initial concentration can be determined through experimentation.
2.3.2. Boundary Conditions
- (1)
- The constant concentration boundary condition
The constant concentration boundary condition can be conceptualized as a pollutant source where a known concentration of the pollutant is introduced into the study area. Under certain circumstances, this boundary condition can also serve as a sink, removing solutes from the simulation zone. The solute concentration values at the boundary of the study area can be determined through measurements.
- (2)
- The recharge concentration
The recharge concentration can be defined as the concentration of solutes that are released into the study area over a specified time frame.
- (3)
- The evapotranspiration
The boundary conditions for evapotranspiration concentration indicate the concentration of various types of solutes resulting from the evapotranspiration process specified in the solute transport model.
- (4)
- The point source
The point source boundary condition represents the concentration of various solutes under the influence of water flow boundary conditions.
2.3.3. The Component Parameters
The component parameters are used to represent the solute transport parameters that consider the interaction and adsorption effects among solutes, typically expressed as the decomposition coefficient. If the transport simulation does not consider adsorption and reaction effects, this parameter is not taken into account.
2.3.4. The Dispersion Coefficient
Dispersion arises from the tortuosity of groundwater flow as it percolates through interconnected soil voids. This physical phenomenon serves to disperse contaminants in the X, Y, and Z directions along solute transport pathways, leading to a reduction in solute concentration. The dispersion coefficient [51] can be calculated using the following equation:
where D represents the dispersion coefficient (L2/T); denotes the longitudinal dispersivity, (L); denotes the longitudinal flow velocity along the solute transport path (L/T); represents the transverse dispersivity (L); denotes the transverse flow velocity along the solute transport path (L/T); denotes the vertical dispersivity (L); denotes the vertical flow velocity along the solute transport path, measured in units of L/T; D* represents the diffusion coefficient (L2/T); and |v| represents the magnitude of the seepage velocity, measured in units of L/T.
3. The Commonly Used Method for Numerical Simulation
The numerical simulation methods involved in the process-based groundwater vulnerability assessment are mainly divided into unsaturated zone solute simulation and saturated zone solute transport simulation. Table 1 presents a classification and summary of commonly used models, and detailed introductions are provided in the following text.

Table 1.
Equilibrium models for chemicals retention and release in soil.
3.1. The Vadose Zone Models
The vadose zone models for pollutants in the vadose zone can be broadly classified into three categories: geometric models, convection–diffusion transport models, and stochastic models. These models facilitate the study of pollutant transport theory and the integration of laboratory and practical issues, providing a quantitative and systematic approach for pollutant transport in soil and essential raw data for environmental monitoring and management agencies.
3.1.1. The Geometric Model
The geometric model is the earliest model used to study water and salt movement, and it is established by fully simplifying the process of sudden solute transport.
- (1)
- The leaching model
The “piston flow” leaching model [52] is a physical model for solute transport that is idealized and developed from water movement in soil. Its basic assumptions are:
- I.
- The soil pores are cylindrical tubes with a diameter of D;
- II.
- The solute and water flow at the same speed v, without considering flow velocity distribution and reactions between soil and solutes;
- III.
- Molecular diffusion is not considered;
- IV.
- Changes in soil structure are not taken into account.
This model is based on the assumption that when a solution infiltrates downwards, it displaces another solution in the soil pores, similar to a piston moving in a cold cylinder. The formula for this model is:
where represents the depth of the solute infiltration front, is the quantity of the dissolved solution, and is the soil moisture content.
This model is applicable to the infiltration of non-adsorbing solutes in sandy soil.
- (2)
- The capillary bundle model
The capillary bundle model regards soil as a combination of capillaries of varying thickness, according to the soil moisture characteristic curve [53,54]. The model assumes that:
- I.
- Soil is composed of a series of capillaries of varying thickness, with the diameter distribution reflecting the soil moisture characteristics;
- II.
- Solutes primarily move through convection in the soil, with molecular diffusion being negligible and therefore ignored;
- III.
- Soil moisture is divided into two parts, mobile water and immobile water, with mass exchange between them in a transient equilibrium state;
- IV.
- The structure of the soil remains unchanged
3.1.2. The Convection–Diffusion Equation Model (CDE)
- (1)
- Unicomponent solute transport
The CDE model represents the most prevalent and fundamental mathematical model for describing solute transport. It considers the transport of solutes induced by both convection and diffusion, including the accompanying processes of sorption or degradation during convection and diffusion [55,56]. An unsteady one-dimensional advection–diffusion equation for solute transport in soil, which incorporates sorption or degradation, can be expressed as follows [56]:
where C represents the concentration of solutes in soil, denotes the soil moisture content, is the soil bulk density, S represents the concentration of solutes in the adsorption phase, D(θ,q) is the diffusion coefficient, q represents the water flow rate in soil, t is time, z is the depth coordinate in soil, and ψ(z,t) denotes the rate of solute uptake or release induced by plant roots.
The equation for soil water content control is [57]:
where represents the soil hydraulic conductivity, H is the soil water potential, and is the plant root water uptake function. In Equation (14), soil moisture θ is generally treated as a constant to avoid the difficulty in nonlinear equation solving caused by transient changes in soil moisture. However, as field soil moisture is constantly changing, scholars in recent years have recognized that the effect of soil hydraulic conductivity on soil solute transport cannot be ignored. Therefore, in some studies, the artificial assumption of constant soil moisture has been eliminated. Simulation results have also shown that soil hydraulic conductivity characteristics have a significant impact on soil moisture and solute transport. Hence, using the variable coefficient method to study the solute transport in the field has achieved better results.
After simplifying Equation (14), assuming that the dispersion coefficient D is constant and that the water flow is in a steady state, regardless of whether the soil moisture content is saturated or unsaturated, when the moisture content is constant, Equation (5) can be expressed as:
The variable represents the velocity of soil pore water, where . Using Equations (14)–(16) as the governing equation in a model, solute transport can be solved in the presence of ion adsorption or exchange and plant influence. This model can be classified into either analytical equilibrium models or nonequilibrium models, depending on the rate function of solute adsorption and decomposition. The analytical equilibrium model assumes that the reaction rate between chemicals and soil solution or solid phase is rapid and reaches equilibrium instantaneously or within a short period of time, commonly represented by the equilibrium models shown in Table 2.

Table 2.
Classification of methods for the process-based groundwater vulnerability assessment.
The models shown in Table 2 have different ranges of applicability. The specific model should be chosen based on experimental data and conditions, and the best model is determined by selecting the model with the largest regression coefficient. Nonequilibrium models, also known as kinetic models, assume that the reaction between chemicals and soil solution or solid phase is time dependent, which is referred to as a kinetic process. Currently, there are many mathematical simulation studies on adsorption both domestically and internationally. However, due to the complexity of the calculation in Equation (16), the adsorption term is often simplified in applications. In the case of steady state without soil solute adsorption and decomposition, and without plant roots, Equation (14) can be simplified as follows:
Equation (17) is a typical convection–diffusion model used to estimate the dispersion coefficient with the breakthrough curve method. Some scholars [58,59,60] believe that there exist some non-connected water-filled pores in the soil, which can be referred to as dead pores. The water in these pores does not participate in the flow movement, but the solute in them participates in the solute transport through mass exchange, thus proposing the mobile–immobile model (MIM). Its governing equation is [61]:
where m represents the mobile water region, im represents the immobile water region, represents the solute concentration in the mobile water, represents the solute concentration in the immobile water, and represents the Darcy velocity. Due to the significant spatiotemporal variability in soil parameters in the field, simulation results often deviate considerably from field observations. Therefore, current research mainly focuses on the determination of initial values and hydraulic dispersion coefficients in the model.
Therefore, building upon the steady-state water model, some scholars [62,63] have proposed a two-region model (TRM) that divides water in soil into two distinct flow rate zones based on their respective velocities, both of which are non-zero. This model assumes that the fast-flowing zone is designated as Zone A, while the slow-flowing zone is designated as Zone B. The two regions are characterized by their respective water velocities , water content (), solute concentration (), and dispersivity coefficients (). Moreover, solute exchange occurs between the two regions, which can be expressed as follows [62]:
where Γ represents the mass exchange between the two flow regions and α denotes the mass exchange coefficient (h−1) between the two regions. The two-region model can be expressed as follows:
From the basic structure and assumptions of the two models, it can be seen that both the two-region model and the two-layer model divide soil water into two distinct regions. Although the two-region model divides the regions based on the velocity of water flow, while the two-layer model divides them based on the size of soil pores, the size of soil pores is the main factor that determines the velocity of water flow. Therefore, the assumptions of the two models have inherent consistency. Moreover, the mass exchange between the two flow regions in the two-region model has characteristics similar to molecular diffusion between the two layers in the two-layer model. The biggest difference between the two models lies in the fact that both regions in the two-region model have non-zero velocities, while the water velocity in one region of the two-layer model is zero. However, when the velocity of water flow in the slow region = 0 in the two-region model (in fact, Zone A and Zone B are symmetrical, and designating either region as the slow region does not affect the final results), the two-region model evolves into the two-layer model. Additionally, the dispersion coefficient and mass exchange coefficient are included in the model, and it is necessary to analyze whether these parameters are the same in both models. Moreover, since the two-region model is relatively complex, obtaining an analytical solution is generally not feasible and numerical calculations must be used. However, when the velocity of water flow = 0, the convergence of the calculation is reduced, and it is necessary to seek a reasonable transformation method.
- (2)
- Multiple solute transport
The theoretical basis for studying the transport of multiple ions with chemical reactions in soils is the conservation of mass and hydrodynamic dispersion theory. Currently, there are two methods commonly used to solve such problems. The first method assumes no chemical reactions among the various components and uses the convection–dispersion equation (CDE) transport model to separately determine the concentration distribution of each ion, and then adjusts the concentration of each ion based on its chemical equilibrium relationship. The second method, called chromatographic simulation, involves solving the algebraic equations representing the chemical equilibrium relationships and the CDE transport equations simultaneously.
The movement of components in unstable and unsaturated flow can be expressed as follows [64,65]:
for which:
where represents the valence of component , denotes the interconversion quantity of component , stands for the density of the fluid solution, represents the soil moisture content, and denotes the Darcy flow velocity.
The transport of multiple solutes in soil involves diffusion, adsorption/desorption, distribution, and microbial degradation conditions, which are related to various fields of research such as chemistry, thermodynamics, and soil physics. Many unresolved issues in these fields have limited the application of this model in the soil–water environment system. However, scholars have improved the model to investigate the transport of pollutants in soil under specific conditions.
3.1.3. Random Model
Due to the significant variation in the spatial structure of the soil and the velocity of water flow in the soil under field conditions, Jury proposed a stochastic function model. This model considers that when a solute enters a porous medium from a certain point, the solute particles cannot move along the original flow trajectory entirely due to various random factors, leading to deviation. In addition, although solute particles exhibit a trend of flowing along the main direction in the pores, their movement in terms of time and direction also shows a random trend. Therefore, this model does not limit the mechanism of solute migration in soil, and for a specific soil, as long as the probability distribution of the time required for solute particles to reach a certain depth from the surface is known, the model can be used to predict the average concentration process at different depths. The model can be expressed as follows [66,67]:
where represents the probability density function of the transition.
represents the probability of a solute particle, initially located at z = 0 at time t = 0, reaching the position Z = L at time t + dt.
For a solute that does not interact with the medium, instantaneously injected at the surface at t = 0, the solute concentration process at depth Z can be described by the temporal transfer function of the soil, given by:
According to the results of various infiltration experiments, the average concentration process at location Z can be expressed as follows:
The model exhibits remarkable capabilities in describing the infiltration dispersion resulting from “branch-merge” processes during solute transport, thus conferring unique advantages for studying issues such as hydrodynamic dispersion and spatial variability in field experiments. However, since the functional model is approached from a statistical and stochastic perspective for simulating the overall solute transport process, it cannot simulate the transport trajectory of individual molecules or ions, and is subject to various unknown influencing factors. As a result, the utilization of such models to reveal soil solute transport mechanisms is severely limited.
3.2. The Model for Saturated Zone
The basis for solute transport simulation lies in the mathematical model, which includes the governing equations, initial conditions, and boundary conditions. By considering the hydraulic conditions, transport parameters, and source-sink terms, various methods can be used to solve the governing equations and obtain the concentration distribution and temporal evolution of the solute of interest.
The governing equation can be described as follows [68]:
where represents the solute concentration (M·L−3); represents the effective porosity; represents the dispersion coefficient tensor (L2·T−1); represents the Darcy velocity (L·T−1); Cs represents the concentration of the source-sink term (M·L−3); and represents the chemical reaction rate (T−1).
Its initial condition is:
Given the concentration and the model domain , the boundary conditions are as follows:
is the known concentration and is the model boundary.
Currently, methods for obtaining solutions to mathematical models can be roughly divided into two categories: analytical solutions and numerical solutions. As far as the current state of mathematics is concerned, there is still no universal solution for analytical solutions to partial differential equations. Numerical solutions for solute transport modeling can be applied to general cases, and their accuracy can also meet scientific needs. Therefore, they are widely used in practical work. Only under certain simple conditions, such as when simulating isotropic hydraulic parameters in the region, simple geometric shapes, and uniform flow fields, can solute problems be solved using analytical solutions. In most hydrogeological conditions, convection migration is much larger than diffusion migration, and the convection effect dominates in the solute migration process.
Therefore, reliable preliminary results of solute transport processes can be obtained through pure convection calculations. In convection migration simulations, fluids are often considered a collection of infinitely small fluid particles, while solutes in fluids are considered another type of contaminant particle. The convection migration process is simulated based on the movement of representative particles/contaminant particles.
Although particle tracking is a simplified approach to simulating solute migration processes, it can effectively address many issues of concern in process-based simulation, such as determining capture zone boundaries of hydraulic control systems, estimating the time of arrival of contaminants and the duration of cleaning up contaminated aquifers, assessing the sources and residence times of different groundwater portions, and analyzing geochemical evolution. Currently, most numerical methods for solving the advection-diffusion equation are the Euler method, the Lagrange method, and the mixed Euler–Lagrange method.
- (1)
- The Euler method is the earliest method used for solute transport simulation. It is still widely used today, especially in hydraulic simulations, due to its effectiveness [69,70]. Its advantage lies in the use of a fixed grid, which satisfies the law of mass conservation, allowing for precise and efficient handling of migration problems where dispersion is dominant. Additionally, it is easy to implement programmatically. However, in dealing with the prevalent convective dominant problem in field conditions, the Euler method often brings about excessive numerical diffusion and oscillations. Within the Euler method, finite difference and finite element methods each have their own advantages and disadvantages. Finite element methods are more flexible in terms of spatial discretization, whereas finite difference methods have lower numerical complexity and often require less computation.
- (2)
- The Lagrangian method, which abstracts fluid and solutes as a large number of moving particles, is employed to represent convection and diffusion. It can precisely solve migration processes dominated by convection and effectively eliminate numerical diffusion [71]. However, due to the lack of a fixed simulation network, the Lagrangian method can cause numerical instability and computational difficulties. These shortcomings are especially difficult to control when dealing with non-uniform media with multiple sources/sinks and complex boundary conditions, resulting in local conservation errors and anomalies. The representative method in the Lagrangian method is the stochastic walking method, which approximately handles migration caused by convection using particle tracking, and characterizes diffusion processes by adding a random displacement term to the particle position during convection. By adjusting the flow velocity and particle mass, adsorption and decay can be treated.
- (3)
- The mixed Euler–Lagrange method seeks to combine the advantages of the Euler method and the Lagrangian method [72,73]. The Euler method, which employs finite differences and finite element methods, is used to handle dispersion and other terms, while the Lagrangian method, which employs particle tracking, is used to solve convection terms. Currently, the trend in the development of the mixed Euler–Lagrange method is to seek solutions that satisfy mass conservation and are more computationally efficient. The primary approaches for the mixed Euler–Lagrange method are the Method of Characteristics (MOC), Modified Method of Characteristics (MMOC), and Hybrid Method of Characteristics (HMOC). The Method of Characteristics employs conventional particles to solve convection terms, but the particles do not carry mass; they represent the concentration field. Its advantage is that it has very low numerical dispersion, and the concentration obtained is less discrete than that obtained with the Random Walk Method. The Modified Method of Characteristics is similar to the Method of Characteristics, but it differs in how it handles convection terms. The Method of Characteristics requires a large number of particles that move with time and records the concentration and position of each particle during tracking, while the Modified Method of Characteristics only requires one particle at each differential or finite element location. Therefore, the Modified Method of Characteristics, when combined with simple low-order concentration interpolation, is more computationally efficient than the Method of Characteristics. The Hybrid Method of Characteristics attempts to combine the advantages of the Method of Characteristics and the Modified Method of Characteristics, and adjusts the solution method automatically according to the nature of the concentration field. By using appropriate control criteria to switch between the Method of Characteristics and the Modified Method of Characteristics, the solution method can achieve almost no numerical dispersion, while using far fewer particles than the Method of Characteristics.
4. Application and Progress in the Assessment of Process-Based Groundwater Vulnerability
Since the 1950s, with the development of computational tools, mathematical modeling has gradually been introduced into the study of solute transport. Taylor (1953) [74] was the first to quantitatively describe longitudinal dispersion in capillaries, opening a new era of using mathematical models to quantitatively study solute transport processes. Subsequently, Aris (1956) [75] applied Taylor’s method to capillaries with irregular shapes and concluded that the local velocity distribution is not a parabola. According to the theory of hydraulic dispersion [76], the convection–diffusion equation (CDE) derived from the principles of mass and momentum conservation in fluid media has become a classic mechanistic model for studying solute transport processes in porous media, and is widely used in practice. As such, CDE has become one of the primary models for studying contaminant transport in aqueous media. Fariz Mikailsoy [77] argues that the CDE can effectively simulate the transport of salts in soil and can be used to predict the behavior of salt transport under different soil types and environmental conditions. The CDE facilitates a deeper understanding of the physical processes involved in the transport of solutes in porous media, providing a valuable tool for predicting the fate of contaminants in geothermal reservoirs under varying temperature conditions [78]. Further investigation [79] has been conducted on the impact of initial concentration and input flux on the transport of Zinc (Zn) in sand columns, which revealed that the CDE model is more suitable for simulating the transmission of Zn in columns with higher relative concentrations, specifically at 50 and 100 mg L−1 initial concentrations. The CDE equation model exhibits remarkable performance in describing the transport process of solutes in porous media. Based on experimental data and fitted parameters, the results show that an increase in soil bulk density, silt, and clay content leads to a reduction in the average soil pore water velocity and dispersivity coefficient, thereby prolonging the infiltration time of solutes in soil [80].
Many scholars [81,82] have found that the conventional CDE model falls short in explaining the occurrence of early breakthrough and tailing phenomena in the transport of solutes in heterogeneous media. Some scholars [83,84] have discovered that even in soil columns or troughs that are uniformly filled indoors, irregular solute transport phenomena may occur. Furthermore, the CDE model is limited in capturing variations in pollutant concentrations only within the upper layers of soil, and falls short in providing satisfactory simulation results for deeper layers [85].
To better describe the irregular phenomena that occur during solute transport, scholars [62] have proposed various improved models over time. The MIM model has a sound theoretical foundation and is relatively straightforward in its formulation. At the local scale, the MIM transport model provides a better description of the observed early breakthrough and tailing phenomena in BTC compared to the CDE model [86]. When dealing with various forms of solute transport, such as breakthrough curves with multiple peaks, the MIM model exhibits superior performance [87]. In addition, the MIM model demonstrates greater precision compared to the equilibrium model in soils with lower solute concentrations [79].
The TRM model, also known as the two-region model, was introduced by van Genuchten and Wierenga (1976) [88] as a modification of the classical CDE for the purpose of explaining nonequilibrium transport in heterogeneous porous media. TRM has been widely used to simulate the transport of pollutants in soils and aquifers, particularly in cases where nonequilibrium conditions are expected, such as in fractured or layered media [83,89]. When the solute is present in the soil under physical nonequilibrium conditions, the TRM model can effectively simulate experimental breakthrough curves [83].
The two-site model (TSM) is a commonly used model for describing the processes of sorption and desorption of substances in soil or rock pores [90]. It has been applied to a range of pollutants, including heavy metals and organic pollutants [91,92]. When a solute exists in a chemical nonequilibrium state, the TSM model demonstrates high accuracy in simulating its penetration curve [83].
Another common mathematical model used to describe solute transport in heterogeneous media is the continuous-time random walk model (CTRW). Initially developed to describe the theory of electron irregular migration in statistical physics, CTRW [93,94] has also been introduced in geology to address the problem of irregular solute transport in porous and fractured media. After comparing the parameter variations in the CDE, TRM, and CRTW methods, the results indicate that the CTRW modeling method is better suited for determining the concentration of non-reactive pollutants in low-permeability soil media with small depths [95]. However, in simulating the transport of heavy metals in soil, the CTRW model exhibits inferior performance compared to the CDE and MIM [96].
Figure 3 shows the changes in the number of models using the vadose zone equilibrium model, vadose zone nonequilibrium model, saturated zone model, and their coupled models, from 2000 to 2022. It can be seen from the figure that the use of nonequilibrium models for vadose zone solute transport simulation has received more attention, and reflects the importance of nonequilibrium models in vadose zone solute transport simulation. The simulation of the saturated zone and the equilibrium simulation of the vadose zone are relatively low in popularity, reflecting that the related numerical simulation technology is relatively mature. At the same time, it can also be seen that with the development of monitoring and numerical analysis technology, the coupled vadose zone–saturated zone pollutant transport model has gradually received attention, which is the basis for the development of process-based groundwater vulnerability assessment technology and shows that process-based assessment technology is attracting more and more attention. It is the focus and urgent problem of future development.
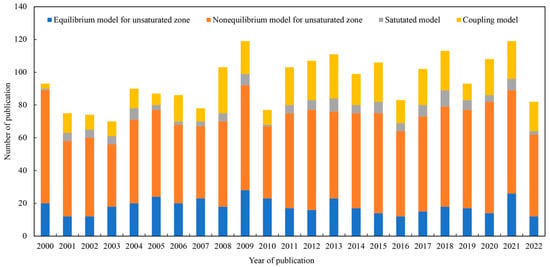
Figure 3.
The histogram for the number of articles using different numerical simulation methods in different years.
From the 1940s to the 1960s, many scholars [97,98] studied the theory of fully penetrating well flow in confined aquifers, further improving the theory of unsteady groundwater flow. In recent decades, a plethora of groundwater numerical simulation software has emerged, with commonly used ones including MODFLOW, FEFLOW, and GMS.
MODFLOW is a software developed by the United States Geological Survey for simulating groundwater flow in porous media. The Canadian company Waterloo Hydrogeologic has added MODPATH and MT3D modules to this software and has also enhanced it with visualization capabilities, resulting in VISUAL MODFLOW. This software can simulate both groundwater flow and solute transport, but it is limited to saturated zones and has some shortcomings in handling irregular boundaries [99].Visual MODFLOW utilizes a visual approach, allowing for the intuitive representation of changes in groundwater quality over time and space, thereby facilitating the assessment and comprehension of complex three-dimensional data [100]. The software has been employed to simulate acid mine drainage in tailings dams, and the simulation results have revealed the migration pathway of heavy metals. The model further predicts that the volume of acidic mine drainage, and the concentration of Zn can be reduced through the installation of a low-permeability barrier downstream of the tailings dam or the utilization of ground-sealing techniques to minimize backfilling [101]. Furthermore, scholars [102] have employed both the MODFLOW and MT3DMS models as simulation models, utilizing genetic algorithms as the optimization algorithm, and encoding the optimization process of the genetic algorithm in MATLAB software, thereby achieving the potential of combining models with algorithms.
The researchers have, for the first time, established an underground water reactive transport model for the study area by utilizing FEFLOW [103]. The transport of pollutants is not only controlled by natural groundwater flow but also by drainage during deep mining operations. Using mathematical models and solute transport models in the FEFLOW system, the migration patterns of multiple pollution sources in mining areas were studied under conditions with and without drainage [104]. Furthermore, upon comparing the MODFLOW, PTC, and FEFLOW models, it was discovered that FEFLOW exhibited the most superior performance in simulating groundwater levels and nitrate distribution [105].
GMS (Groundwater Modeling System) is a software system developed by Aquaveo that enables groundwater flow and water quality simulation, which supports multiple numerical models, such as MODFLOW, MT3DMS, and MODPATH, while also providing diverse data visualization and analysis tools, such as topographic maps, water level maps, stream line maps, and water quality maps. GMS is compatible with a variety of computer operating systems and platforms. However, due to its relatively comprehensive nature, GMS may have certain limitations in certain complex geological conditions [106]. By utilizing T-PROGS in GMS, a three-dimensional stratigraphic model of chlor-alkali contaminated sites was generated based on lithological information obtained from soil drilling. This was then combined with a hydrogeological model and in situ groundwater monitoring to numerically simulate the groundwater flow in the study area and obtain the transport behavior of the contaminant plume in the groundwater [107]. Using MODFLOW and MT3DMS software in the Groundwater Modeling System (GMS), the hydrological and water quality characteristics, as well as the transport trend in ammonia in groundwater, were simulated and analyzed in the study area [108]. Based on the GMS software, an equivalent porous medium model was used to simulate the transport of total nitrogen under different conditions in the study area [109]. GMS was used to predict the concentration and migration range of arsenic, and to verify that sediment release is the main source of heavy metal pollution in groundwater [110].
In order to accurately characterize the spatiotemporal distribution patterns and complex transport and transformation processes of solutes in soil water and groundwater, scholars have conducted a significant amount of research. In the early stages, pollution concentration measurements were mainly taken by collecting in situ samples. However, with the continuous development of computer technology and numerical calculation methods, attention [111,112] has gradually shifted towards numerical simulation studies on the spatiotemporal distribution patterns and transport and transformation processes of water flow and solutes using process-based models. To this end, models that incorporate multiple physical, chemical, and biological processes such as water transport, solute migration, bioreactions, and chemical reactions, are applied to predict the spatiotemporal distribution patterns and transport and transformation processes of solutes in soil water and groundwater. Compared to early in situ sampling experiments, numerical simulation research has higher efficiency and reliability and is able to simulate a wider range of real-world scenarios and complex groundwater systems [113,114,115].
Currently, commonly used models for saturated–unsaturated water flow and solute transport can be roughly divided into three categories: (1) Hydraulic models, such as HYDRUS [116], SWAP [117], FEFLOW [118], MODFLOW [119], RT3D [120], etc. These models establish a set of governing equations based on mass conservation and Darcy’s law to describe the physical transport of water flow and contaminant convection–dispersion in porous media, without considering chemical reactions; (2) Multi-component geochemical models, such as PHREEQC [121], MINTEQA2 [122], EQ3/6 [123], etc. Taking PHREEQC as an example, it employs chemical equilibrium and kinetics to calculate the concentration, solubility, precipitation, dissolution, and chemical reaction rates of ions and compounds in water. It can predict the chemical properties of water by inputting hydrochemical data of groundwater or surface water, or simulate chemical reactions between solid materials and water by inputting the chemical properties of solid materials. The simulated reaction pathway is static and does not consider the influence of hydrodynamics on the spatial distribution of solutes; (3) Coupled models for water flow, solute transport, and chemical reactions. Considering that the spatial and temporal distribution of pollutants in groundwater is influenced by convection, migration, dispersion, and biogeochemical reaction processes, scholars have developed various models that couple hydrodynamic processes and biogeochemical reactions.
A dynamic modeling approach coupling HYDRUSA 1D and MODFLOW is employed to simulate hydraulic heads, achieving a relative error of less than 1%. By coupling hydrogeology and radionuclide transport, a general picture of pollutant migration can be obtained [124]. Shultz et al. [125] researched a physically based finite difference model, RT3D-OTIS, for simulating the fate and transport of selenium (Se) species in coupled groundwater/surface water systems. It considers the impact of NO3 on selenium speciation and migration, as well as the cycling and migration of nitrogen (N) in these systems. The objective of RT3D-OTIS is to simulate the spatial and temporal distribution of selenium and nitrogen in aquifers and their connected streams at a regional scale, building upon existing models for selenium groundwater. The model’s contribution lies in its ability to simulate the spatial and temporal distribution of selenium and nitrogen more accurately in groundwater and surface water systems. Beegum et al. [126] developed an enhanced unsaturated water flow and transport package that is integrated with the 3D groundwater flow model MODFLOW and the 3D groundwater solute transport model MT3DMS. In addition to simulating water flow in the unsaturated zone, this new software package can also simulate solute transport involving a multitude of biogeochemical processes and reactions, including first-order degradation, volatilization, linear or nonlinear sorption, single-center kinetic sorption, dual-site sorption, and dual-site kinetic sorption. Rock and Kupfersberger [127] developed a new HYDRUS package for MODFLOW by switching between the θ and h forms of the Richards equation (RE) at each numerical node. This approach avoids the drawbacks of both h- and θ-type REs and results in higher numerical stability and computational efficiency. Zeng et al. [128] directly coupled the soil water movement and nitrogen transport model SIMWASER/STOTRASIM with the groundwater flow and solute transport model FEFLOW. This coupled model was applied to a partially saturated aquifer in southeastern Austria to investigate the influence of groundwater table depth on the distribution of pore water pressure in the vadose zone. Wei and Bailey [129] conducted a study using a coupled flow model, SWAT-MODFLOW, which includes a groundwater reactive transport model, RT3D, to simulate the groundwater reactions and migration of NO3 and P in the soil–aquifer–river system and their interactions. This study demonstrates that the code for the SWAT-MODFLOW-RT3D model is a useful tool for verifying the migration of NO3 and P, as well as quantifying the best management practices effects on groundwater-driven watersheds. Figure 4 shows several mainstream commercial models used for solute transport in the vadose zone and saturated zone, including Feflow, GMS, Modflow, and Hydrus. From the figure, it can be seen that among the four models, GMS and Hydrus have higher usage rates in the saturated zone and vadose zone, respectively, while Feflow and Modflow have relatively lower usage frequencies. At the same time, the usage frequency of GMS and Hydrus has an increasing trend year by year, reflecting the stability and reliability of the two commercial software in solute transport simulation.
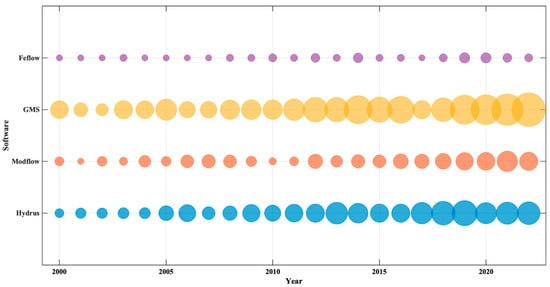
Figure 4.
Bubble chart of the usage of various commercial software in the past 20 years.
5. Challenges and Prospects
The focus of studying the intrinsic vulnerability of groundwater is to understand the sources and movement of groundwater, while the focus of studying special vulnerability is to identify the sources, transport, and transformation of pollutants. The process-based method can provide a mechanistic description of the process based on groundwater flow and solute migration and transformation models, but it also has the following disadvantages:
- (1)
- The operation of the unsaturated zone model requires a large number of parameters and boundary conditions. Existing technologies still have deficiencies in dealing with the heterogeneity of soil parameters at the field scale, which increases the uncertainty of simulation results;
- (2)
- It requires sufficient long-term groundwater level and water quality data;
- (3)
- There is uncertainty in the process-based method in groundwater vulnerability assessment; the reasons include objective uncertainty factors and subjective uncertainty factors. The randomness and complexity of the groundwater system determine the objective uncertainty, while the researcher’s one-sided understanding of the research object causes subjective uncertainty;
- (4)
- There is uncertainty in the transport and transformation rules of characteristic pollutants in the vadose zone and saturated zone and in obtaining quantitative characterization parameters;
- (5)
- This method focuses on simulating the process of surface pollutants entering the vadose zone and saturated zone. The model can quantitatively describe the vulnerability changes caused by the lowering of groundwater levels and the increase in vadose zone thickness due to excessive groundwater exploitation, leading to an extended time for pollutants to enter the saturated zone. However, there are some shortcomings in describing the mechanisms of groundwater quality changes caused by changes in groundwater quantity.
Therefore, future work on the process-based method in solving groundwater vulnerability can be carried out regarding the following aspects:
- (1)
- In evaluating groundwater resource vulnerability, focus on theoretical research on solute migration and transformation in the vadose zone. In evaluating groundwater source vulnerability, how to comprehensively reflect the impact of vadose zone and saturated zone on groundwater vulnerability and coupling of water flow and pollutant migration models in vadose zone and saturated zone deserves further study;
- (2)
- Explore methods to combine the process-based method with stochastic models and various intelligent methods (gray system, BP neural network, projection pursuit, extension theory, etc.) to study groundwater vulnerability;
- (3)
- From a technical perspective of groundwater vulnerability assessment, the combination of GIS technology with various mathematical models will be a major development direction for groundwater vulnerability assessment;
- (4)
- The process-based method has clear physical meaning, high reliability of evaluation results, low subjectivity, and strong practicality in evaluating groundwater vulnerability. However, due to the complex random uncertainty of the groundwater system itself, further research is needed on both the evaluation method and uncertainty analysis of results.
6. Conclusions
The research provides a comprehensive review of the principles and methods of groundwater vulnerability assessment based on the process approach. It considers an assessment framework that includes both the unsaturated and saturated zones. The concept of groundwater vulnerability has been developed since the 1960s–1970s and has been widely applied in the assessment of groundwater vulnerability in many countries worldwide. In the past 30 years, several qualitative, quantitative, and statistical methods have been proposed for vulnerability assessment. The process approach, as a branch of groundwater vulnerability assessment, is based on water and pollutant transport models, and uses deterministic physical and chemical equations to simulate the migration and transformation of pollutants. It establishes a mathematical formula for vulnerability assessment and obtains a comprehensive index for vulnerability by quantifying various evaluation factors. The greatest advantage of this method is that it can describe physical, chemical, and biological processes that affect groundwater vulnerability and estimate the spatial and temporal distribution of pollutants. The process-based simulation method is commonly used to determine the essential vulnerability of aquifers and evaluate the vulnerability of water supply sources to a particular target pollutant. The key to evaluating the essential vulnerability using the process-based mathematical simulation model is to understand the source and movement of groundwater, while the evaluation of special vulnerability mainly focuses on the source, transport, and transformation of pollutants.
From this review, it is apparent that the process-based approach to groundwater vulnerability assessment is a major focus for future development, due to the limitations of existing methods and the differences in hydrogeological and land use conditions in different regions.
However, the main limitations of the process-based approach are its complexity and the limited availability of spatial and temporal datasets required for the simulations. Nevertheless, with the advancement in field monitoring technology and numerical methods, it is becoming a trend to rely more on process-based models to reliably simulate/predict groundwater vulnerability under different hydrogeological conditions.
This approach is a priority for addressing the growing global water quantity and quality issues. The potential of remote sensing (RS), geographic information systems (GIS), and artificial intelligence (AI) should be fully utilized for vulnerability assessment. In addition, emerging tools and technologies should be adopted to develop effective spatial decision support or expert systems to improve decision making in water resource management and land use planning. Considering the lack of field data, in-depth field investigations at the basin/watershed scale should be conducted globally to address the heterogeneity and scale issues in hydrology and the watershed division problem of karst aquifers. Efforts should be made to develop a reliable watershed-scale monitoring network for groundwater level and quality, while regular monitoring of groundwater (level and quality) should be an integral part of watershed management strategies. Due to the inherent complex stochastic uncertainty of groundwater systems, further research is needed to analyze the uncertainty of vulnerability assessment methods and their results.
Author Contributions
Conceptualization, D.L. (Debao Lu) and Z.Y.; methodology, D.L. (Debao Lu); software, C.G.; validation, D.L. (Dongfeng Li) and J.O.; formal analysis, C.G.; investigation, C.G.; resources, C.G.; data curation, C.G.; writing—original draft preparation, C.G.; writing—review and editing, D.L. (Debao Lu) and C.X.; visualization, D.L. (Debao Lu); supervision, D.L. (Debao Lu) and Z.Y.; project administration, D.L. (Debao Lu) and J.Q.; funding acquisition, J.O., C.X. and Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Zhejiang Public Welfare Technology Application Research Project [No. LGF21D020002], Key Technology Research and Development Program of Zhejiang [No. 2021C03019], Zhejiang Provincial Natural Science Foundation [LZJWD22E090001] and [LZJWY22E090009].
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
We appreciate the valuable feedback from the editor and anonymous reviewers, which has helped to improve the quality of the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bai, Y.; Xia, Y.; Geng, N.; Qi, Y.; Huang, D.; Zhao, Y.; Huang, L.; Shen, D.; Sun, G.; Xu, C. Research on Oxygen Transfer in an Aerated Flow with Emergent Vegetation. J. Hydrol. 2023, 617, 128935. [Google Scholar] [CrossRef]
- Machado, M.C.; Vivaldini, M.; de Oliveira, O.J. Production and Supply-Chain as the Basis for SMEs’ Environmental Management Development: A Systematic Literature Review. J. Clean. Prod. 2020, 273, 123141. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Li, Y.P.; Sun, J.; Huang, G.H. Optimizing Water Resources Allocation and Soil Salinity Control for Supporting Agricultural and Environmental Sustainable Development in Central Asia. Sci. Total Environ. 2020, 704, 135281. [Google Scholar] [CrossRef]
- Hsiang, S.; Oliva, P.; Walker, R. The Distribution of Environmental Damages. Rev. Environ. Econ. Policy 2019, 31, 1. [Google Scholar] [CrossRef]
- Liu, C.; Cai, W.; Zhai, M.; Zhu, G.; Zhang, C.; Jiang, Z. Decoupling of Wastewater Eco-Environmental Damage and China’s Economic Development. Sci. Total Environ. 2021, 789, 147980. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Liu, B.; Zhang, B. Embodied Environmental Damage in Interregional Trade: A MRIO-Based Assessment within China. J. Clean. Prod. 2017, 140, 1236–1246. [Google Scholar] [CrossRef]
- Bai, Y.; Xuan, W. Drag Force Coefficient of the Flexible Vegetation Root in an Artificial Floating Bed Channel. Ecol. Eng. 2022, 179, 106619. [Google Scholar] [CrossRef]
- Du Pisani, J.A. Sustainable Development–Historical Roots of the Concept. Environ. Sci. 2006, 3, 83–96. [Google Scholar] [CrossRef]
- Lin, S.-S.; Shen, S.-L.; Zhou, A.; Lyu, H.-M. Sustainable Development and Environmental Restoration in Lake Erhai, China. J. Clean. Prod. 2020, 258, 120758. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, Y.; Luo, K.; Shahid, M.Z. Hydrochemical Characteristics and a Health Risk Assessment of the Use of River Water and Groundwater as Drinking Sources in a Rural Area in Jiangjin District, China. Environ. Earth Sci. 2020, 79, 160. [Google Scholar] [CrossRef]
- Berg, M.; Tran, H.C.; Nguyen, T.C.; Pham, H.V.; Schertenleib, R.; Giger, W. Arsenic Contamination of Groundwater and Drinking Water in Vietnam: A Human Health Threat. Environ. Sci. Technol. 2001, 35, 2621–2626. [Google Scholar] [CrossRef] [PubMed]
- Eschauzier, C.; Raat, K.J.; Stuyfzand, P.J.; De Voogt, P. Perfluorinated Alkylated Acids in Groundwater and Drinking Water: Identification, Origin and Mobility. Sci. Total Environ. 2013, 458, 477–485. [Google Scholar] [CrossRef] [PubMed]
- Nolan, B.T.; Hitt, K.J. Vulnerability of Shallow Groundwater and Drinking-Water Wells to Nitrate in the United States. Environ. Sci. Technol. 2006, 40, 7834–7840. [Google Scholar] [CrossRef] [PubMed]
- Jasechko, S.; Perrone, D. Global Groundwater Wells at Risk of Running Dry. Science 2021, 372, 418–421. [Google Scholar] [CrossRef]
- Giri, S. Water Quality Prospective in Twenty First Century: Status of Water Quality in Major River Basins, Contemporary Strategies and Impediments: A Review. Environ. Pollut. 2021, 271, 116332. [Google Scholar] [CrossRef]
- Nafi’Shehab, Z.; Jamil, N.R.; Aris, A.Z.; Shafie, N.S. Spatial Variation Impact of Landscape Patterns and Land Use on Water Quality across an Urbanized Watershed in Bentong, Malaysia. Ecol. Indic. 2021, 122, 107254. [Google Scholar]
- Yadav, B.; Gupta, P.K.; Patidar, N.; Himanshu, S.K. Ensemble Modelling Framework for Groundwater Level Prediction in Urban Areas of India. Sci. Total Environ. 2020, 712, 135539. [Google Scholar] [CrossRef]
- Lu, D.; Wang, H.; Geng, N.; Xia, Y.; Xu, C.; Hua, E. Imaging and Characterization of the Preferential Flow Process in Agricultural Land by Using Electrical Resistivity Tomography and Dual-Porosity Model. Ecol. Indic. 2022, 134, 108498. [Google Scholar] [CrossRef]
- Kurwadkar, S.; Kanel, S.R.; Nakarmi, A. Groundwater Pollution: Occurrence, Detection, and Remediation of Organic and Inorganic Pollutants. Water Environ. Res. 2020, 92, 1659–1668. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, Z.-H.; Xi, B.-D.; He, X.-S.; Li, Q.-L.; Qi, Y.-J.; Jin, M.-Y.; Guo, Y. Characteristics of Groundwater Pollution in a Vegetable Cultivation Area of Typical Facility Agriculture in a Developed City. Ecol. Indic. 2019, 105, 709–716. [Google Scholar] [CrossRef]
- Pan, Z.; Lu, W.; Chang, Z. Simultaneous Identification of Groundwater Pollution Source Spatial–Temporal Characteristics and Hydraulic Parameters Based on Deep Regularization Neural Network-Hybrid Heuristic Algorithm. J. Hydrol. 2021, 600, 126586. [Google Scholar] [CrossRef]
- Lu, D.; Wang, H.; Huang, D.; Li, D.; Sun, Y. Measurement and Estimation of Water Retention Curves Using Electrical Resistivity Data in Porous Media. J. Hydrol. Eng. 2020, 25, 04020021. [Google Scholar] [CrossRef]
- Yadav, M.K.; Saidulu, D.; Gupta, A.K.; Ghosal, P.S.; Mukherjee, A. Status and Management of Arsenic Pollution in Groundwater: A Comprehensive Appraisal of Recent Global Scenario, Human Health Impacts, Sustainable Field-Scale Treatment Technologies. J. Environ. Chem. Eng. 2021, 9, 105203. [Google Scholar] [CrossRef]
- Kim, G.-B. A Study on the Establishment of Groundwater Protection Area around a Saline Waterway by Combining Artificial Neural Network and GIS-Based AHP. Environ. Earth Sci. 2020, 79, 117. [Google Scholar] [CrossRef]
- Machiwal, D.; Jha, M.K.; Singh, V.P.; Mohan, C. Assessment and Mapping of Groundwater Vulnerability to Pollution: Current Status and Challenges. Earth-Sci. Rev. 2018, 185, 901–927. [Google Scholar] [CrossRef]
- Jiang, T.; Qu, C.; Wang, M.; Sun, Y.; Hu, B.; Chu, J. Analysis on Temporal and Spatial Variations of Groundwater Hydrochemical Characteristics in the Past Decade in Southern Plain of Beijing, China. J. Groundw. Sci. Eng. 2017, 5, 235–248. [Google Scholar]
- Ravbar, N.; Goldscheider, N. Comparative Application of Four Methods of Groundwater Vulnerability Mapping in a Slovene Karst Catchment. Hydrogeol. J. 2009, 17, 725–733. [Google Scholar] [CrossRef]
- Voutchkova, D.D.; Schullehner, J.; Rasmussen, P.; Hansen, B. A High-Resolution Nitrate Vulnerability Assessment of Sandy Aquifers (DRASTIC-N). J. Environ. Manag. 2021, 277, 111330. [Google Scholar] [CrossRef]
- Aslam, R.A.; Shrestha, S.; Pandey, V.P. Groundwater Vulnerability to Climate Change: A Review of the Assessment Methodology. Sci. Total Environ. 2018, 612, 853–875. [Google Scholar] [CrossRef]
- Taghavi, N.; Niven, R.K.; Paull, D.J.; Kramer, M. Groundwater Vulnerability Assessment: A Review Including New Statistical and Hybrid Methods. Sci. Total Environ. 2022, 822, 153486. [Google Scholar] [CrossRef]
- Torkashvand, M.; Neshat, A.; Javadi, S.; Pradhan, B. New Hybrid Evolutionary Algorithm for Optimizing Index-Based Groundwater Vulnerability Assessment Method. J. Hydrol. 2021, 598, 126446. [Google Scholar] [CrossRef]
- Gogu, R.C.; Dassargues, A. Current Trends and Future Challenges in Groundwater Vulnerability Assessment Using Overlay and Index Methods. Environ. Geol. 2000, 39, 549–559. [Google Scholar] [CrossRef]
- French, H.K.; Van der Zee, S.; Leijnse, A. Transport and Degradation of Propyleneglycol and Potassium Acetate in the Unsaturated Zone. J. Contam. Hydrol. 2001, 49, 23–48. [Google Scholar] [CrossRef] [PubMed]
- Koroša, A.; Brenčič, M.; Mali, N. Estimating the Transport Parameters of Propyphenazone, Caffeine and Carbamazepine by Means of a Tracer Experiment in a Coarse-Gravel Unsaturated Zone. Water Res. 2020, 175, 115680. [Google Scholar] [CrossRef] [PubMed]
- Van Genuchten, M.T.; ŠImůnek, J. Evaluation of Pollutant Transport in the Unsaturated Zone. Reg. Approaches Water Pollut. Environ. 1996, 20, 139–172. [Google Scholar]
- Masciopinto, C.; Passarella, G.; Caputo, M.C.; Masciale, R.; De Carlo, L. Hydrogeological Models of Water Flow and Pollutant Transport in Karstic and Fractured Reservoirs. Water Resour. Res. 2021, 57, e2021WR029969. [Google Scholar] [CrossRef]
- Nield, D.A.; Simmons, C.T. A Brief Introduction to Convection in Porous Media. Transp. Porous Media 2019, 130, 237–250. [Google Scholar] [CrossRef]
- Or, D.; Smets, B.F.; Wraith, J.M.; Dechesne, A.; Friedman, S.P. Physical Constraints Affecting Bacterial Habitats and Activity in Unsaturated Porous Media–a Review. Adv. Water Resour. 2007, 30, 1505–1527. [Google Scholar] [CrossRef]
- Tosun, I. Modeling in Transport Phenomena: A Conceptual Approach; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Cui, S.T. Molecular Self-Diffusion in Nanoscale Cylindrical Pores and Classical Fick’s Law Predictions. J. Chem. Phys. 2005, 123, 054706. [Google Scholar] [CrossRef]
- Kim, S.; Kavvas, M.L. Generalized Fick’s Law and Fractional ADE for Pollution Transport in a River: Detailed Derivation. J. Hydrol. Eng. 2006, 11, 80–83. [Google Scholar] [CrossRef]
- Lu, J.; Dai, H.C. Numerical Modeling of Pollution Transport in Flexible Vegetation. Appl. Math. Model. 2018, 64, 93–105. [Google Scholar] [CrossRef]
- Pochai, N.; Tangmanee, S.; Crane, L.J.; Miller, J.J.H. A Mathematical Model of Water Pollution Control Using the Finite Element Method. PAMM: Proc. Appl. Math. Mech. 2006, 6, 755–756. [Google Scholar] [CrossRef]
- Haga, D.; Niibori, Y.; Chida, T. Hydrodynamic Dispersion and Mass Transfer in Unsaturated Flow. Water Resour. Res. 1999, 35, 1065–1077. [Google Scholar] [CrossRef]
- Passioura, J.B. Hydrodynamic Dispersion in Aggregated Media: 1. Theory. Soil Sci. 1971, 111, 339–344. [Google Scholar] [CrossRef]
- Smiles, D.E.; Philip, J.R.; Knight, J.H.; Elrick, D.E. Hydrodynamic Dispersion during Absorption of Water by Soil. Soil Sci. Soc. Am. J. 1978, 42, 229–234. [Google Scholar] [CrossRef]
- Toride, N.; Inoue, M.; Leij, F.J. Hydrodynamic Dispersion in an Unsaturated Dune Sand. Soil Sci. Soc. Am. J. 2003, 67, 703–712. [Google Scholar] [CrossRef]
- Baker, R.; Frydman, S. Unsaturated Soil Mechanics: Critical Review of Physical Foundations. Eng. Geol. 2009, 106, 26–39. [Google Scholar] [CrossRef]
- Meng, Z.; Huang, S.; Xu, T.; Lin, Z.; Wu, J. Competitive Adsorption, Immobilization, and Desorption Risks of Cd, Ni, and Cu in Saturated-Unsaturated Soils by Biochar under Combined Aging. J. Hazard. Mater. 2022, 434, 128903. [Google Scholar] [CrossRef]
- Stanić, F.; Delage, P.; Tchiguirinskaia, I.; Versini, P.-A.; Cui, Y.-J.; Schertzer, D. A New Fractal Approach to Account for Capillary and Adsorption Phenomena in the Water Retention and Transfer Properties of Unsaturated Soils. Water Resour. Res. 2020, 56, e2020WR027808. [Google Scholar] [CrossRef]
- Maciejewski, S. Numerical and Experimental Study of Solute Transport in Unsaturated Soils. J. Contam. Hydrol. 1993, 14, 193–206. [Google Scholar] [CrossRef]
- Amrizal, N.; Chemisana, D.; Rosell, J.I.; Barrau, J. A Dynamic Model Based on the Piston Flow Concept for the Thermal Characterization of Solar Collectors. Appl. Energy 2012, 94, 244–250. [Google Scholar] [CrossRef]
- Dong, M.; Dullien, F.A.; Dai, L.; Li, D. Immiscible Displacement in the Interacting Capillary Bundle Model Part I. Development of Interacting Capillary Bundle Model. Transp. Porous Media 2005, 59, 1–18. [Google Scholar] [CrossRef]
- Watanabe, K.; Flury, M. Capillary Bundle Model of Hydraulic Conductivity for Frozen Soil. Water Resour. Res. 2008, 44, 12. [Google Scholar] [CrossRef]
- Hutson, J.L.; Wagenet, R.J. An Overview of LEACHM: A Process Based Model of Water and Solute Movement, Transformations, Plant Uptake and Chemical Reactions in the Unsaturated Zone. Chem. Equilib. React. Model. 1995, 42, 409–422. [Google Scholar]
- Li, L.; Yin, Z. Numerical Simulation of Groundwater Pollution Problems Based on Convection Diffusion Equation. Am. J. Comput. Math. 2017, 7, 350–370. [Google Scholar] [CrossRef]
- Ogden, F.L.; Allen, M.B.; Lai, W.; Zhu, J.; Seo, M.; Douglas, C.C.; Talbot, C.A. The Soil Moisture Velocity Equation. J. Adv. Model. Earth Syst. 2017, 9, 1473–1487. [Google Scholar] [CrossRef]
- Gao, G.; Zhan, H.; Feng, S.; Fu, B.; Ma, Y.; Huang, G. A New Mobile-Immobile Model for Reactive Solute Transport with Scale-Dependent Dispersion. Water Resour. Res. 2010, 46, 8. [Google Scholar] [CrossRef]
- Schumer, R.; Benson, D.A.; Meerschaert, M.M.; Baeumer, B. Fractal Mobile/Immobile Solute Transport. Water Resour. Res. 2003, 39, 1296. [Google Scholar] [CrossRef]
- Vanderborght, J.; Mallants, D.; Vanclooster, M.; Feyen, J. Parameter Uncertainty in the Mobile-Immobile Solute Transport Model. J. Hydrol. 1997, 190, 75–101. [Google Scholar] [CrossRef]
- Li, X.; Wen, Z.; Zhu, Q.; Jakada, H. A Mobile-Immobile Model for Reactive Solute Transport in a Radial Two-Zone Confined Aquifer. J. Hydrol. 2020, 580, 124347. [Google Scholar] [CrossRef]
- Coats, K.H.; Smith, B.D. Dead-End Pore Volume and Dispersion in Porous Media. Soc. Pet. Eng. J. 1964, 4, 73–84. [Google Scholar] [CrossRef]
- Gao, G.; Feng, S.; Zhan, H.; Huang, G.; Mao, X. Evaluation of Anomalous Solute Transport in a Large Heterogeneous Soil Column with Mobile-Immobile Model. J. Hydrol. Eng. 2009, 14, 966–974. [Google Scholar] [CrossRef]
- Mansell, M.G.; Hussey, S.W. An Investigation of Flows and Losses within the Alluvial Sands of Ephemeral Rivers in Zimbabwe. J. Hydrol. 2005, 314, 192–203. [Google Scholar] [CrossRef]
- Valocchi, A.J.; Street, R.L.; Roberts, P.V. Transport of Ion-Exchanging Solutes in Groundwater: Chromatographic Theory and Field Simulation. Water Resour. Res. 1981, 17, 1517–1527. [Google Scholar] [CrossRef]
- Jury, W.A.; Sposito, G.; White, R.E. A Transfer Function Model of Solute Transport through Soil: 1. Fundamental Concepts. Water Resour. Res. 1986, 22, 243–247. [Google Scholar] [CrossRef]
- White, R.E.; Dyson, J.S.; Haigh, R.A.; Jury, W.A.; Sposito, G. A Transfer Function Model of Solute Transport through Soil: 2. Illustrative Applications. Water Resour. Res. 1986, 22, 248–254. [Google Scholar] [CrossRef]
- Ge, X.; Ren, J.; Li, S.; Rene, E.R.; Zhou, D.; Zhang, P.; Hu, Q.; Ma, W. Prediction of the Impact of Benzo [a] Pyrene on Shallow Groundwater during Natural Infiltration of Reclaimed Water-Receiving Rivers: A Case Study of Liangshui, China. J. Environ. Manag. 2022, 323, 116070. [Google Scholar] [CrossRef]
- Biswas, B.N.; Chatterjee, S.; Mukherjee, S.P.; Pal, S. A Discussion on Euler Method: A Review. Electron. J. Math. Anal. Appl. 2013, 1, 294–317. [Google Scholar]
- Ravat, D. Analysis of the Euler Method and Its Applicability in Environmental Magnetic Investigations. J. Environ. Eng. Geophys. 1996, 1, 229–238. [Google Scholar] [CrossRef]
- Hirt, C.W.; Cook, J.L.; Butler, T.D. A Lagrangian Method for Calculating the Dynamics of an Incompressible Fluid with Free Surface. J. Comput. Phys. 1970, 5, 103–124. [Google Scholar] [CrossRef]
- Adamczyk, W.P.; Klimanek, A.; Białecki, R.A.; Węcel, G.; Kozołub, P.; Czakiert, T. Comparison of the Standard Euler–Euler and Hybrid Euler–Lagrange Approaches for Modeling Particle Transport in a Pilot-Scale Circulating Fluidized Bed. Particuology 2014, 15, 129–137. [Google Scholar] [CrossRef]
- Soward, A.M.; Roberts, P.H. The Hybrid Euler–Lagrange Procedure Using an Extension of Moffatt’s Method. J. Fluid Mech. 2010, 661, 45–72. [Google Scholar] [CrossRef]
- Taylor, G.I. Dispersion of Soluble Matter in Solvent Flowing Slowly through a Tube. Proc. R. Soc. Lond. A 1953, 219, 186–203. [Google Scholar] [CrossRef]
- Aris, R. On the Dispersion of a Solute in a Fluid Flowing through a Tube. Proc. R. Soc. Lond. A 1956, 235, 67–77. [Google Scholar] [CrossRef]
- Bear, J.; Bachmat, Y. Generalized Theory on Hydrodynamic Dispersion in Porous Media. Int. Union Geod. Geophys. Publ. 1967, 72. [Google Scholar]
- Mikailsoy, F.; Pachepsky, Y. Average Concentration of Soluble Salts in Leached Soils Inferred from the Convective–Dispersive Equation. Irrig. Sci. 2010, 28, 431–434. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, L.; Liu, X. Temperature Effect on the Transport of Nitrate and Ammonium Ions in a Loose-Pore Geothermal Reservoir. J. Geochem. Explor. 2013, 124, 59–66. [Google Scholar] [CrossRef]
- Shahmohammadi-Kalalagh, S.; Taran, F. Effect of Initial Concentration and Input Flux on Equilibrium and Non-Equilibrium Transport of Zn in Soil Columns. Int. J. Environ. Sci. Technol. 2018, 16, 7565–7572. [Google Scholar] [CrossRef]
- Zhen, Q.; Ma, W.; Li, M.; He, H.; Zhang, X.; Wang, Y. Reprint of “Effects of Vegetation and Physicochemical Properties on Solute Transport in Reclaimed Soil at an Opencast Coal Mine Site on the Loess Plateau, China”. Catena 2017, 148, 17–25. [Google Scholar] [CrossRef]
- Mallants, D. Field-Scale Solute Transport Parameters Derived from Tracer Tests in Large Undisturbed Soil Columns. Soil Res. 2014, 52, 13. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling Non-Fickian Transport in Geological Formations as a Continuous Time Random Walk. Rev. Geophys. 2006, 44, RG2003. [Google Scholar] [CrossRef]
- Alves, A.T.A.; Coutinho, A.P.; de Oliveira Barros, V.H.; Lassabatere, L.; dos Santos Neto, S.M.; de Sousa Lima, J.R.; Antonino, A.C.D. Transport Behavior of RB5 Dye in Alluvial Soil in the Northeast of Brazil. Water 2022, 14, 1000. [Google Scholar] [CrossRef]
- Khan, S.; Alhazmi, S.E.; Alotaibi, F.M.; Ferrara, M.; Ahmadian, A. On the Numerical Approximation of Mobile-Immobile Advection-Dispersion Model of Fractional Order Arising from Solute Transport in Porous Media. Fractal Fract. 2022, 6, 445. [Google Scholar]
- Gao, G.; Fu, B.; Zhan, H.; Ma, Y. Contaminant Transport in Soil with Depth-Dependent Reaction Coefficients and Time-Dependent Boundary Conditions. Water Res. 2013, 47, 2507–2522. [Google Scholar] [CrossRef]
- Mallants, D.; Bekele, E.; Schmid, W.; Miotlinski, K.; Taylor, A.; Gerke, K.; Gray, B. A Generic Method for Predicting Environmental Concentrations of Hydraulic Fracturing Chemicals in Soil and Shallow Groundwater. Water 2020, 12, 941. [Google Scholar] [CrossRef]
- Moradzadeh, M.; Moazed, H.; Sayyad, G.; Khaledian, M. Transport of Nitrate and Ammonium Ions in a Sandy Loam Soil Treated with Potassium Zeolite—Evaluating Equilibrium and Non-Equilibrium Equations. Acta Ecol. Sin. 2014, 34, 342–350. [Google Scholar] [CrossRef]
- Genuchten, M.T.; Wierenga, P.J. Mass Transfer Studies in Sorbing Porous Media I. Analytical Solutions. Soil Sci. Soc. Am. J. 1976, 40, 473–480. [Google Scholar] [CrossRef]
- Zhou, B.B.; Shao, M.A.; Wang, Q.J.; Yang, T. Effects of Different Rock Fragment Contents and Sizes on Solute Transport in Soil Columns. Vadose Zone J. 2011, 10, 386–393. [Google Scholar] [CrossRef]
- Nkedi-Kizza, P.; Biggar, J.W.; Selim, H.M.; Van Genuchten, M.T.; Wierenga, P.J.; Davidson, J.M.; Nielsen, D.R. On the Equivalence of Two Conceptual Models for Describing Ion Exchange During Transport Through an Aggregated Oxisol. Water Resour. Res. 1984, 20, 1123–1130. [Google Scholar] [CrossRef]
- Fox, G.A.; Heeren, D.M.; Miller, R.B.; Mittelstet, A.R.; Storm, D.E. Flow and Transport Experiments for a Streambank Seep Originating from a Preferential Flow Pathway. J. Hydrol. 2011, 403, 360–366. [Google Scholar] [CrossRef]
- Berkowitz, B.; Kosakowski, G.; Margolin, G.; Scher, H. Application of Continuous Time Random Walk Theory to Tracer Test Measurements in Fractured and Heterogeneous Porous Media. Ground Water 2001, 39, 593–604. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.; Wu, G.-C.; Fu, H. A Note on Function Space and Boundedness of the General Fractional Integral in Continuous Time Random Walk. J. Nonlinear Math. Phys. 2022, 29, 95–102. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, L.; James, S.C.; Chrysikopoulos, C.V. Colloid Transport through a Variable-Aperture Fracture under Unfavorable Attachment Conditions: Characterization with a Continuous Time Random Walk Model. Colloids Surf. A Physicochem. Eng. Asp. 2022, 644, 128822. [Google Scholar] [CrossRef]
- Zaheer, M.; Ullah, H.; Mashwani, S.A.; ul Haq, E.; Ali Shah, S.H.; Manzoor, F. Solute Transport Modelling in Low-Permeability Homogeneous and Saturated Soil Media. MBPB 2021, 36, 25–32. [Google Scholar] [CrossRef]
- Morsali, S.; Babazadeh, H.; Shahmohammadi-Kalalagh, S.; Sedghi, H. Simulating Zn, Cd and Ni Transport in Disturbed and Undisturbed Soil Columns: Comparison of Alternative Models. Int. J. Environ. Res. 2019, 13, 721–734. [Google Scholar] [CrossRef]
- Hantush, M.S.; Jacob, C.E. Non-Steady Radial Flow in an Infinite Leaky Aquifer. Eos Trans. Am. Geophys. Union 1955, 36, 95–100. [Google Scholar] [CrossRef]
- Hantush, M.S.; Jacob, C.E. Steady Three-Dimensional Flow to a Well in a Two-Layered Aquifer. Eos Trans. Am. Geophys. Union 1955, 36, 286–292. [Google Scholar] [CrossRef]
- Papadopoulou, M.P.; Varouchakis, E.A.; Karatzas, G.P. Simulation of Complex Aquifer Behavior Using Numerical and Geostatistical Methodologies. Desalination 2009, 237, 42–53. [Google Scholar] [CrossRef]
- Xie, W.; Ren, B.; Hursthouse, A.; Wang, Z.; Luo, X. Simulation of Manganese Transportin Groundwater Using Visual MODFLOW:A Case Study from Xiangtan ManganeseOre Area in Central China. Pol. J. Environ. Stud. 2021, 30, 1409–1420. [Google Scholar] [CrossRef]
- Tabelin, C.; Sasaki, A.; Igarashi, T.; Tomiyama, S.; Villacorte-Tabelin, M.; Ito, M.; Hiroyoshi, N. Prediction of Acid Mine Drainage Formation and Zinc Migration in the Tailings Dam of a Closed Mine, and Possible Countermeasures. MATEC Web Conf. 2019, 268, 06003. [Google Scholar] [CrossRef]
- Rad, P.R.; Fazlali, A. Optimization of Permeable Reactive Barrier Dimensions and Location in Groundwater Remediation Contaminated by Landfill Pollution. J. Water Process. Eng. 2020, 35, 101196. [Google Scholar] [CrossRef]
- Hu, H.; Mao, X.; Yang, Q. Development of a Groundwater Flow and Reactive Solute Transport Model in the Yongding River Alluvial Fan, China. Front. Earth Sci. 2018, 13, 371–384. [Google Scholar] [CrossRef]
- Zeng, B.; Zhang, Z.; Yang, M. Risk Assessment of Groundwater with Multi-Source Pollution by a Long-Term Monitoring Programme for a Large Mining Area. Int. Biodeterior. Biodegrad. 2018, 128, 100–108. [Google Scholar] [CrossRef]
- Matiatos, I.; Varouchakis, E.A.; Papadopoulou, M.P. Performance Evaluation of Multiple Groundwater Flow and Nitrate Mass Transport Numerical Models. Environ. Model. Assess 2019, 24, 659–675. [Google Scholar] [CrossRef]
- Anderson, M.P.; Woessner, W.W.; Hunt, R.J. Applied Groundwater Modeling: Simulation of Flow and Advective Transport; Academic Press: New York, NY, USA, 2015. [Google Scholar]
- Chen, G.; Sun, Y.; Liu, J.; Lu, S.; Feng, L.; Chen, X. The Effects of Aquifer Heterogeneity on the 3D Numerical Simulation of Soil and Groundwater Contamination at a Chlor-Alkali Site in China. Environ. Earth Sci. 2018, 77, 797. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.; Xie, T.; Wen, N.; Yao, J. A Comprehensive Evaluation Model of Ammonia Pollution Trends in a Groundwater Source Area along a River in Residential Areas. Water 2021, 13, 1924. [Google Scholar] [CrossRef]
- Wan, Z.; Dai, J.; Pan, L.; Han, J.; Li, Z.; Dong, K. Simulation Study on Nitrogen Pollution in Shallow Groundwater in Small Agricultural Watersheds in the Huixian Wetland. Water 2022, 14, 3657. [Google Scholar] [CrossRef]
- Zhong, S.; Geng, H.; Zhang, F.; Liu, Z.; Wang, T.; Song, B. Risk Assessment and Prediction of Heavy Metal Pollution in Groundwater and River Sediment: A Case Study of a Typical Agricultural Irrigation Area in Northeast China. Int. J. Anal. Chem. 2015, 2015, 921539. [Google Scholar] [CrossRef]
- Prommer, H.; Barry, D.A.; Zheng, C. MODFLOW/MT3DMS-Based Reactive Multicomponent Transport Modeling. Ground Water 2003, 41, 247–257. [Google Scholar] [CrossRef]
- Steefel, C.; Depaolo, D.; Lichtner, P. Reactive Transport Modeling: An Essential Tool and a New Research Approach for the Earth Sciences. Earth Planet. Sci. Lett. 2005, 240, 539–558. [Google Scholar] [CrossRef]
- Robock, A.; Vinnikov, K.Y.; Srinivasan, G.; Entin, J.K.; Hollinger, S.E.; Speranskaya, N.A.; Liu, S.; Namkhai, A. The Global Soil Moisture Data Bank. Bull. Amer. Meteor. Soc. 2000, 81, 1281–1299. [Google Scholar] [CrossRef]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil Moisture Measurement for Ecological and Hydrological Watershed-Scale Observatories: A Review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Dorigo, W.; Oevelen, P.; Wagner, W.; Drusch, M.; Mecklenburg, S.; Robock, A.; Jackson, T. A New International Network for in Situ Soil Moisture Data. Eos. Trans. AGU 2011, 92, 141–142. [Google Scholar] [CrossRef]
- Šimůnek, J.; Genuchten, M.T.; Šejna, M. Development and Applications of the HYDRUS and STANMOD Software Packages and Related Codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef]
- Van Dam, J.C.; Huygen, J.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; Van Walsum, P.E.V.; Groenendijk, P.; Van Diepen, C.A. Theory of SWAP Version 2.0; Simulation of Water Flow, Solute Transport and Plant Growth in the Soil-Water-Atmosphere-Plant Environment; DLO Winand Staring Centre: Wageningen, The Netherlands, 1997. [Google Scholar]
- Diersch, H.-J.G. FEFLOW: Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. Geological Survey Modular Ground-Water Model—User Guide to Modularization Concepts and the Ground-Water Flow Process. In US Geological Survey Open-File Report 00–92; US Geological Survey: Reston, VA, USA, 2000. [Google Scholar]
- TP Clement. A Modular Computer Code for Simulating Reactive Multi-Species Transport in 3-Dimensional Groundwater Systems; Pacific Northwest National Lab.: Richland, WA, USA, 1999; p. PNNL-11720, EW4010, 8022.
- Šimůnek, J.; Suarez, D.L.; Šejna, M. The UNSATCHEM Software Package for Simulating One-Dimensional Variably Saturated Water Flow, Heat Transport, Carbon Dioxide Production and Transport, and Multicomponent Solute Transport with Major Ion Equilibrium and Kinetic Chemistry. Res. Rep. 1996, 141, 186. [Google Scholar]
- Allison, J.D. Geochemical Assessment Model for Environmental Systems: Version 3.0, User’s Manual; British Library, Document Supply Centre: London, UK, 1991. [Google Scholar]
- Wolery, T.J.; Daveler, S.A. A Software Package for Geochemical Modeling of Aqueous Systems: Version 7.0, User’s Manual; Lawrence Livermore Natl. Lab.: Livermore, CA, USA, 1992.
- Testoni, R.; Levizzari, R.; De Salve, M. Coupling of Unsaturated Zone and Saturated Zone in Radionuclide Transport Simulations. Prog. Nucl. Energy 2017, 95, 84–95. [Google Scholar] [CrossRef]
- Shultz, C.D.; Bailey, R.T.; Gates, T.K.; Heesemann, B.E.; Morway, E.D. Simulating Selenium and Nitrogen Fate and Transport in Coupled Stream-Aquifer Systems of Irrigated Regions. J. Hydrol. 2018, 560, 512–529. [Google Scholar] [CrossRef]
- Beegum, S.; Šimůnek, J.; Szymkiewicz, A.; Sudheer, K.P.; Nambi, I.M. Implementation of Solute Transport in the Vadose Zone into the “HYDRUS Package for MODFLOW”. Groundwater 2019, 57, 392–408. [Google Scholar] [CrossRef]
- Rock, G.; Kupfersberger, H. Modeling Shallow Groundwater Nitrate Concentrations by Direct Coupling of the Vadose and the Saturated Zone. Environ. Earth Sci. 2019, 78, 283. [Google Scholar] [CrossRef]
- Zeng, J.; Yang, J.; Zha, Y.; Shi, L. Capturing Soil-Water and Groundwater Interactions with an Iterative Feedback Coupling Scheme: New HYDRUS Package for MODFLOW. Hydrol. Earth Syst. Sci. 2019, 23, 637–655. [Google Scholar] [CrossRef]
- Wei, X.; Bailey, R.T. Evaluating Nitrate and Phosphorus Remediation in Intensively Irrigated Stream-Aquifer Systems Using a Coupled Flow and Reactive Transport Model. J. Hydrol. 2021, 598, 126304. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).