Generalized Distribution Feeder Switching with Fuzzy Indexing for Energy Saving
Abstract
1. Introduction
2. Fundamental Theory
- The loss increment ΔP obtained by switching is a quadratic function of the equivalent load current in the corresponding power supply area;
- The increase in loss ΔP is a convex function, so there is an optimal value Iopt to minimize ΔP, and this optimal value Iopt represents the optimal equivalent load current that can be transferred;
- 3.
- All feeders are radially structured;
- 4.
- Closing of a tie switch should be followed by the opening of a sectionalized switch.
3. The Fuzzy Index Feeder Switching
3.1. Tie Switch Strategy
3.1.1. Large Loss to Small Loss
3.1.2. High Voltage to Low Voltage
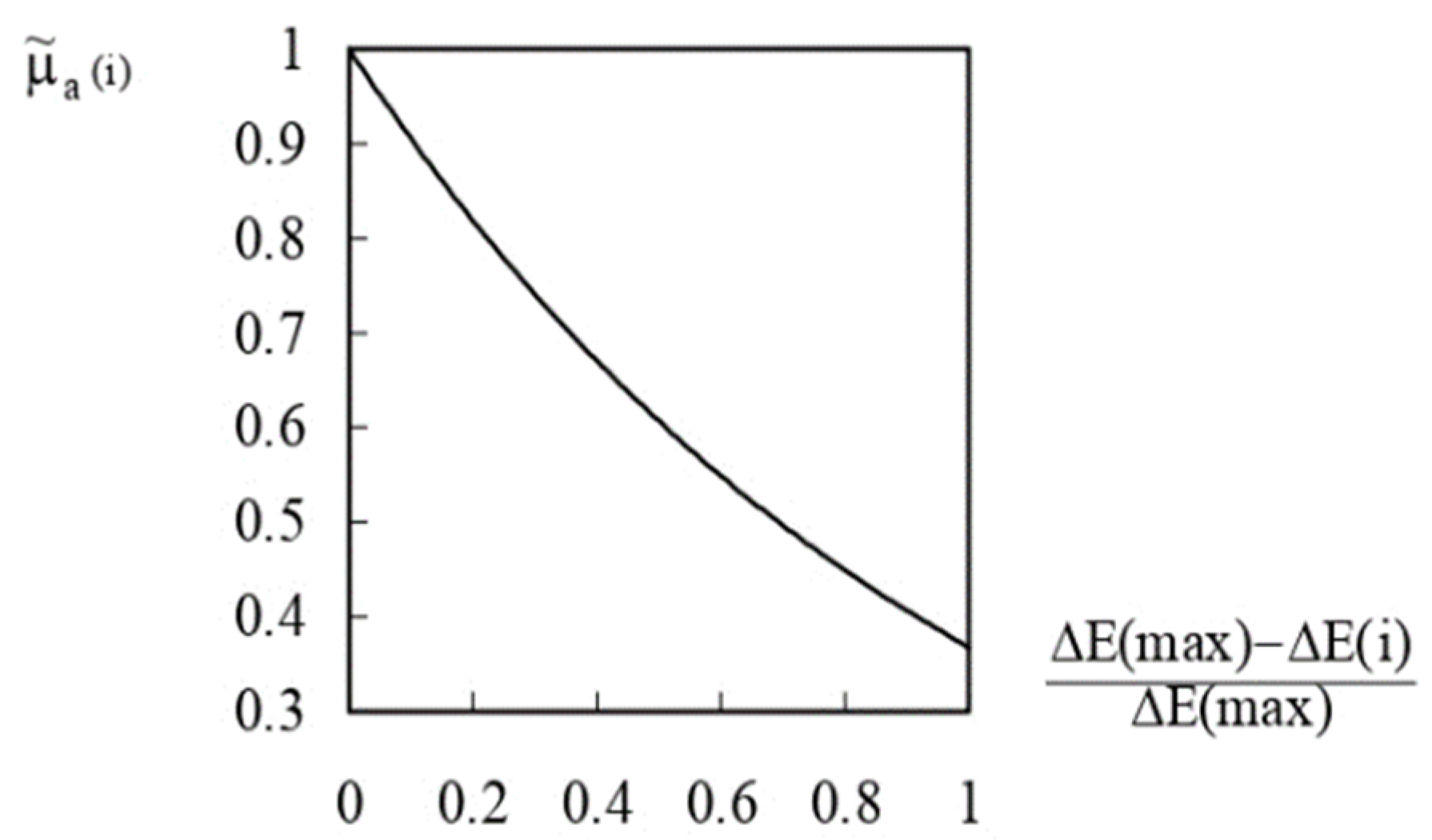
3.1.3. Determination of the Candidate Tie Switch
3.2. Sectionalized Switch Strategy
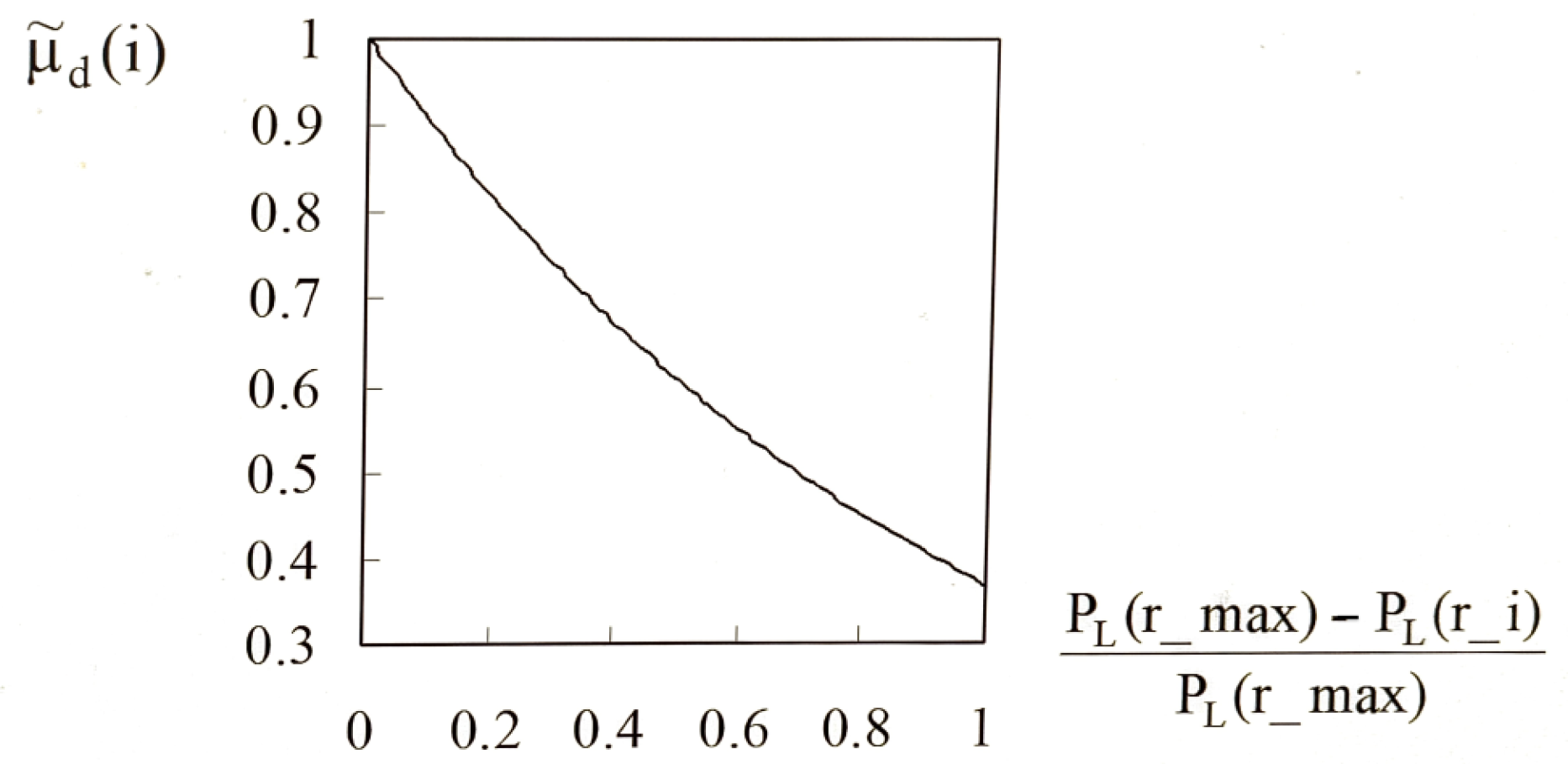
3.2.1. Calculation of Optimal Load
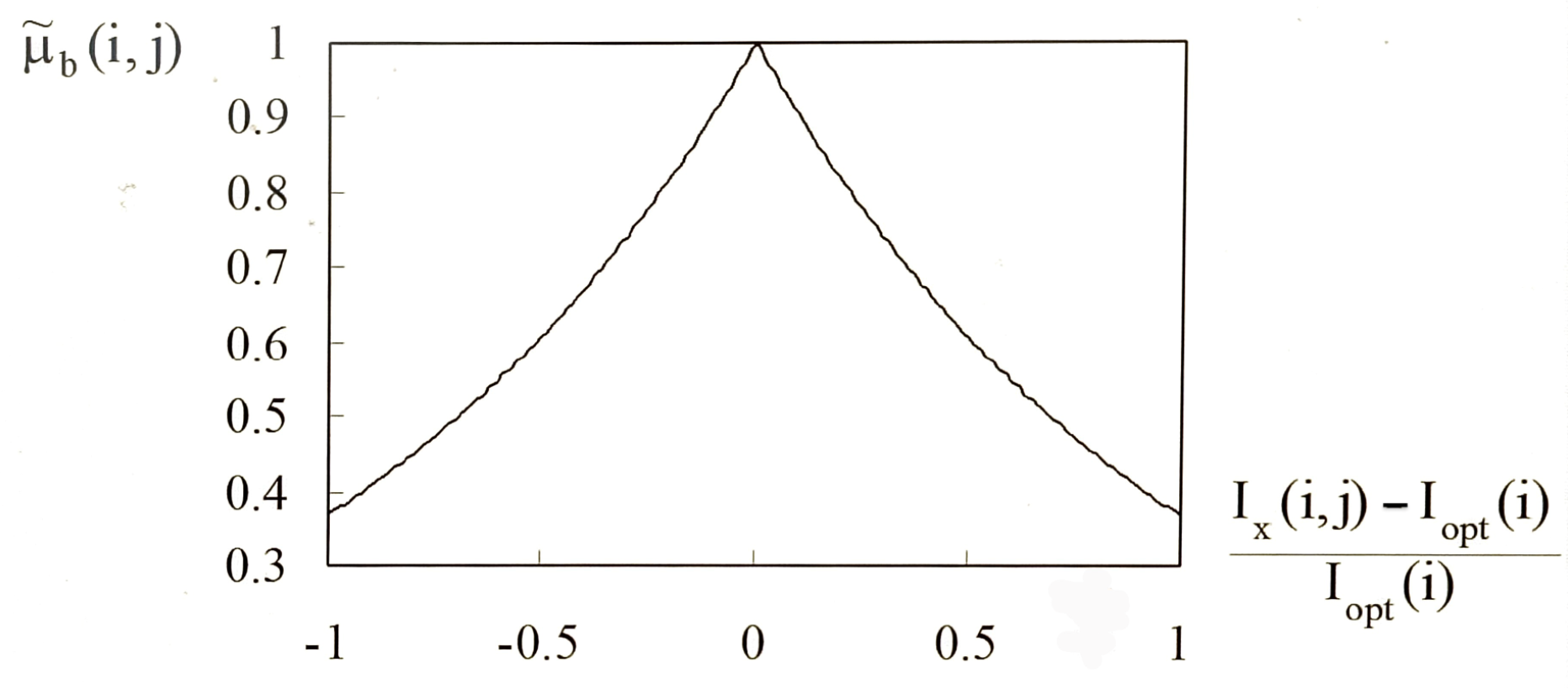
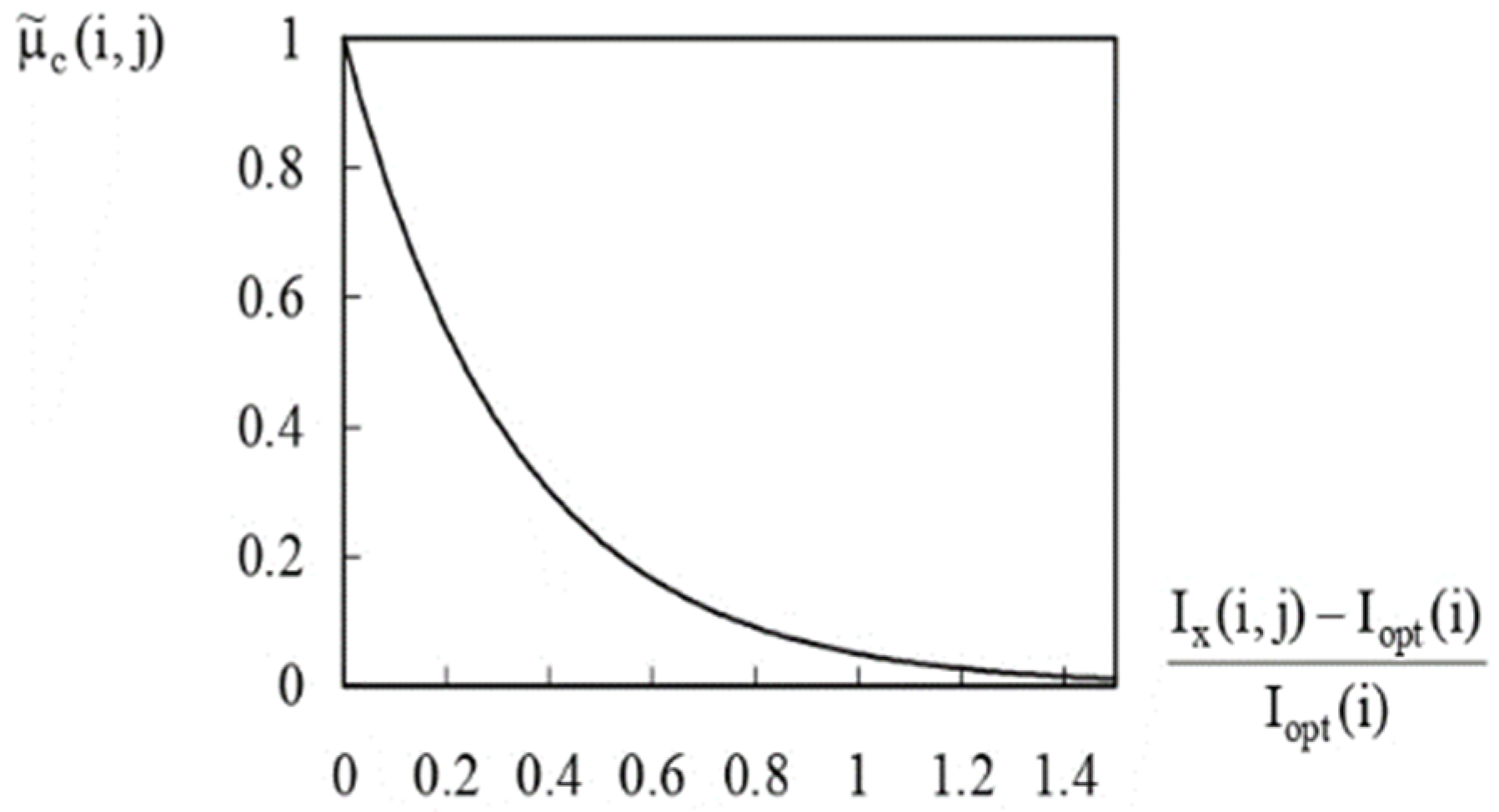
3.2.2. The Effect of Excessive Transfer
3.3. A Complete Switching Strategy
3.3.1. Transfer for Multiple Feeders
3.3.2. Transfer for Single Feeder
4. A Layered Feeder Switching Scheme
4.1. For Multiple Feeders
- Step 1:
- Read system load flow data and compute
- Step 2:
- For layer l, search for the tie switch (i) with (8);
- Step 3:
- Find a sectionalized switch with (11) or (12);
- Step 4:
- Find complete switching strategy with (13);
- Step 5:
- Execute the load flow program.
- Step 6:
- Repeat until the remaining tie switches are 0.
4.2. For a Single Feeder
5. Test Results and Discussion
- The exhausted search enumeration:
- 2.
- del_P loss formula method [2]:
5.1. Multiple Feeder Transfer
5.1.1. Case 1: A Three-Feeder System
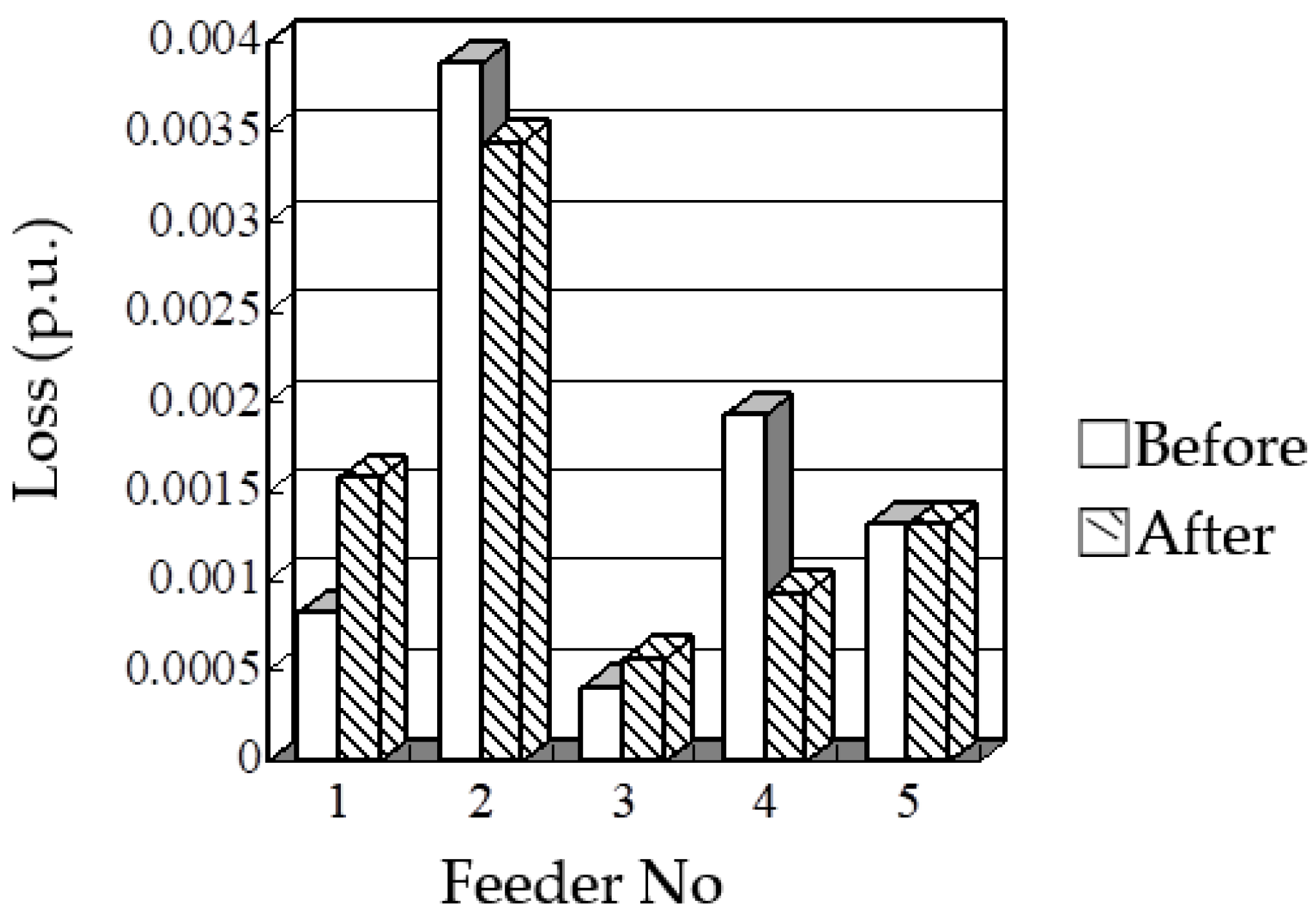
5.1.2. Case 2: Five Feeder System with 33 Switches
5.2. Single Feeder Transfer
Case 3: Single Feeder with 37 Switches
6. Conclusions
- It deals with the large-scale mixed-integer combinatorial problem where conventional techniques would generally fail;
- The fuzzy indexing simplifies the optimization process with easy numeric calculations instead of large-scale sorting or a large amount of computation;
- It executes the load flow only once after finding the switch (i,j); this is a great advantage compared with other methods requiring heavy computation;
- The solution quality is high. It shows that for a small system, the “optimal” results exist and are verifiable by exhausted search. However, for large-scale networks, the solution will be optimal or sub-optimal;
- The method is suitable for real-time applications even for a large distribution system;
- It is applicable to all feeder configurations, including the multiple-feeder and single-feeder systems;
- It can get the best configuration with less switching operations and save on costs;
- The first switching is the most significant to reduce the loss and balance the load;
- Proper switching can solve the transformer load management and terminal voltage problems.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, W.M.; Chen, M.S. An Overall Distribution Aotomation Structure. Electr. Power Syst. Res. 1986, 10, 7–19. [Google Scholar] [CrossRef]
- Civanlar, S.; Grainger, J.J.; Yin, H.; Lee, S.S.H. Distribution Feeder Reconfiguration for Loss Reduction. IEEE Trans. Power Deliv. 1988, 3, 1217–1223. [Google Scholar] [CrossRef]
- Wanger, T.P.; Chikhani, A.Y.; Hackarm, T. Feeder Reconfiguration for Loss Reduction: An Application of Distribution Automation. IEEE Trans. Power Deliv. 1991, 6, 1922–1932. [Google Scholar]
- Chen, C.S.; Cho, M.Y. Determination of Critical Switches in Distribution System. IEEE Trans. Power Deliv. 1992, 7, 1443–1449. [Google Scholar] [CrossRef]
- Kim, H.; Ko, Y.; Jung, K.H. Algorithm of Transferring the Load of the Faulted Substation Transformer Using the Best-First Search Method. IEEE Trans. Power Deliv. 1992, 7, 1434–1441. [Google Scholar]
- Shirmohammadi, D.; Hong, H.W. Reconfiguration of Electric Distribution Networks for Resistive Line Losses Reduction. IEEE Trans. Power Deliv. 1989, 4, 1492–1498. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network Reconfiguration in Distribution System for Loss Reduction and Load Balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Goswami, S.K.; Basu, S.K. A New Algorithm for the Recon-figuration of Distribution Feeders for Loss Minimization. IEEE Trans. Power Deliv. 1992, 7, 1484–1491. [Google Scholar] [CrossRef]
- Rodrigues, F.M.; de Araujo, L.R.; Penido, D.R.R. Optimization of Reliability through Switch Reconfiguration in Distribution Systems. IEEE Lat. Am. Trans. 2019, 17, 972–982. [Google Scholar] [CrossRef]
- Raut, U.; Mishra, S. Power distribution network reconfiguration for loss minimization using a new graph theory based genetic algorithm. In Proceedings of the 2017 IEEE Calcutta Conference (CALCON), Kolkata, India, 2–3 December 2017; pp. 1–5. [Google Scholar]
- Nahman, J.M.; Peric, D.M. Optimal Planning of Radial Distribution Networks by Simulated Annealing Technique. IEEE Trans. Power Syst. 2008, 23, 790–795. [Google Scholar] [CrossRef]
- Cabana, K.; Candelo, J.E.; Castillo, R. Statistical Analysis of Voltage Sensitivity in Distribution Systems Integrating DG. IEEE Lat. Am. Trans. 2016, 14, 4304–4309. [Google Scholar] [CrossRef]
- Tu, H.; Xia, Y.; Iu, H.H.-C.; Chen, X. Optimal Robustness in Power Grids From a Network Science Perspective. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 126–130. [Google Scholar] [CrossRef]
- Borozan, V.; Rajicic, D.; Ackovski, R. Improved Method for Loss Minimization in Distribution Networks. IEEE Trans. Power Syst. 1995, 10, 1420–1425. [Google Scholar] [CrossRef]
- Huang, S.; Wu, Q.; Cheng, L.; Liu, Z. Optimal Reconfiguration-Based Dynamic Tariff for Congestion Management and Line Loss Reduction in Distribution Networks. IEEE Trans. Smart Grid 2016, 7, 1295–1303. [Google Scholar] [CrossRef]
- Momoh, J.A.; Ma, X.W.; Tomsovic, K. Overview and Literature Survey of Fuzzy Set Theory in Power System. IEEE Trans. Power Syst. 1995, 10, 1676–1690. [Google Scholar] [CrossRef]
- Raj, B.N.; Rao, K.S.P. A New Fuzzy Reasoning Approach for Load Balancing in Distribution System. IEEE Trans. Power Syst. 1995, 10, 1426–1431. [Google Scholar]
- Parada, V.; Ferland, A.; Arias, M. Optimization of electrical distribution feeders using simulated annealing. IEEE Trans. Power Syst. 2004, 19, 1135–1141. [Google Scholar] [CrossRef]
- Dashtaki, K.; Haghifam, M.R. A New Loss Estimation Method in Limited Data Electric Distribution Networks. IEEE Trans. Power Syst. 2013, 28, 2194–2200. [Google Scholar] [CrossRef]
- Díaz, P.; Pérez-Cisneros, M.; Cuevas, E.; Camarena, O.; Martinez, F.A.F.; González, A. A Swarm Approach for Improving Voltage Profiles and Reduce Power Loss on Electrical Distribution Networks. IEEE Access 2018, 6, 49498–49512. [Google Scholar] [CrossRef]
- Kumar, P.; Gupta, N.; Niazi, K.R.; Swarnkar, A. A Circuit Theory-Based Loss Allocation Method for Active Distribution Systems. IEEE Trans. Smart Grid 2019, 10, 1005–1012. [Google Scholar] [CrossRef]
- Kaneko, A.; Hayashi, Y.; Anegawa, T.; Hokazono, H.; Kuwashita, Y. Evaluation of an Optimal Radial-Loop Configuration for a Distribution Network With PV Systems to Minimize Power Loss. IEEE Access 2020, 8, 220408–220421. [Google Scholar] [CrossRef]
- Mahdavi, M.; Alhelou, H.H.; Siano, P. Robust Mixed-Integer Programing Model for Reconfiguration of Distribution Feeders Under Uncertain and Variable Loads Considering Capacitor Banks, Voltage Regulators, and Protective Relays. IEEE Trans. Ind. Inform. 2022, 18, 7790–7803. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Li, J.; He, J.; Wang, X. Real Time Optimal Reconfiguration of Multiphase Active Distribution Networks. IEEE Trans. Smart Grid 2018, 9, 6829–6839. [Google Scholar]
- Lin, W.M.; Chin, H.C. Preventive and Corrective Switching for Feeder Contingencies in Distribution Systems with Fuzzy Set Algorithm. IEEE Trans. Power Deliv. 1997, 12, 1711–1716. [Google Scholar] [CrossRef]



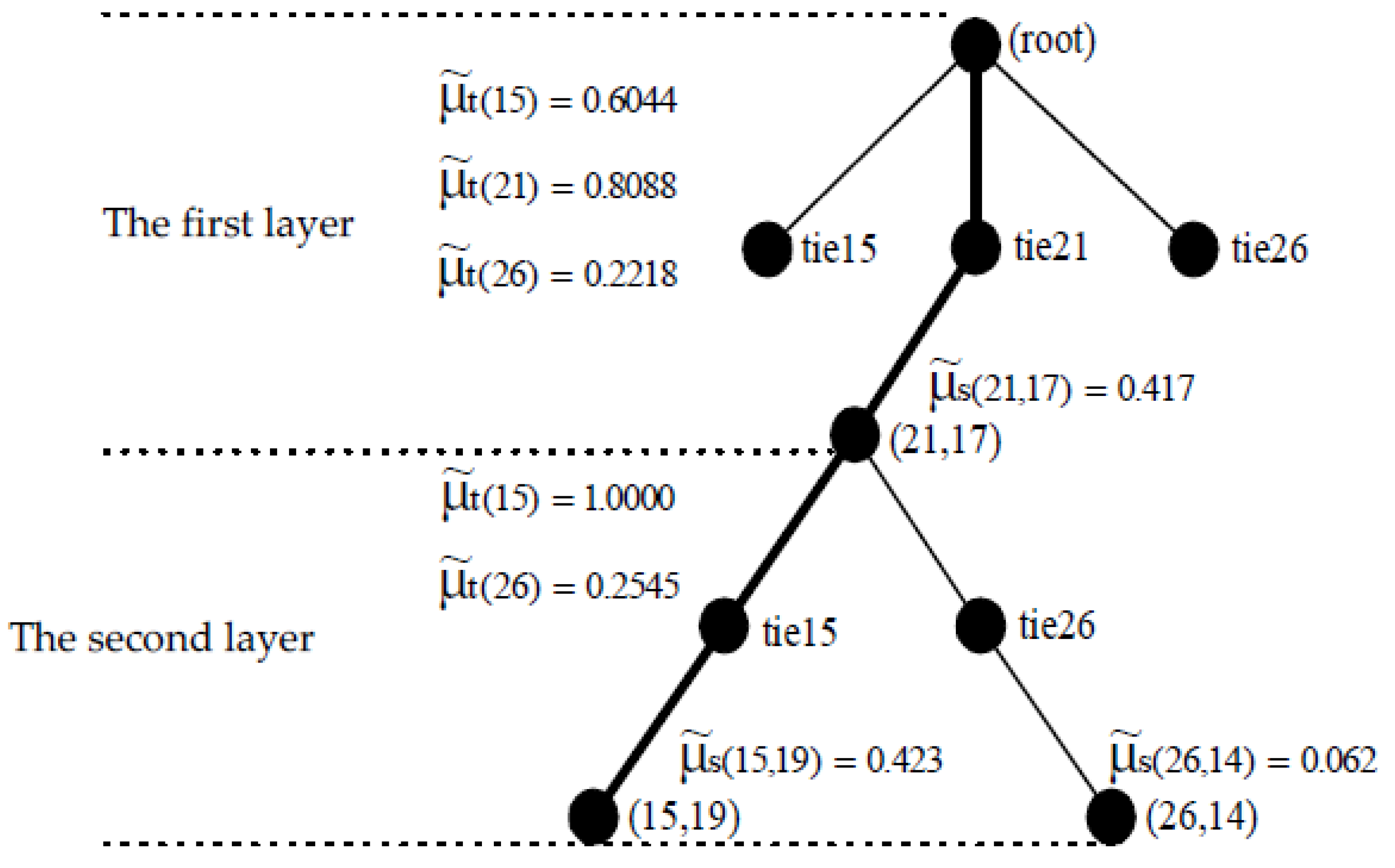

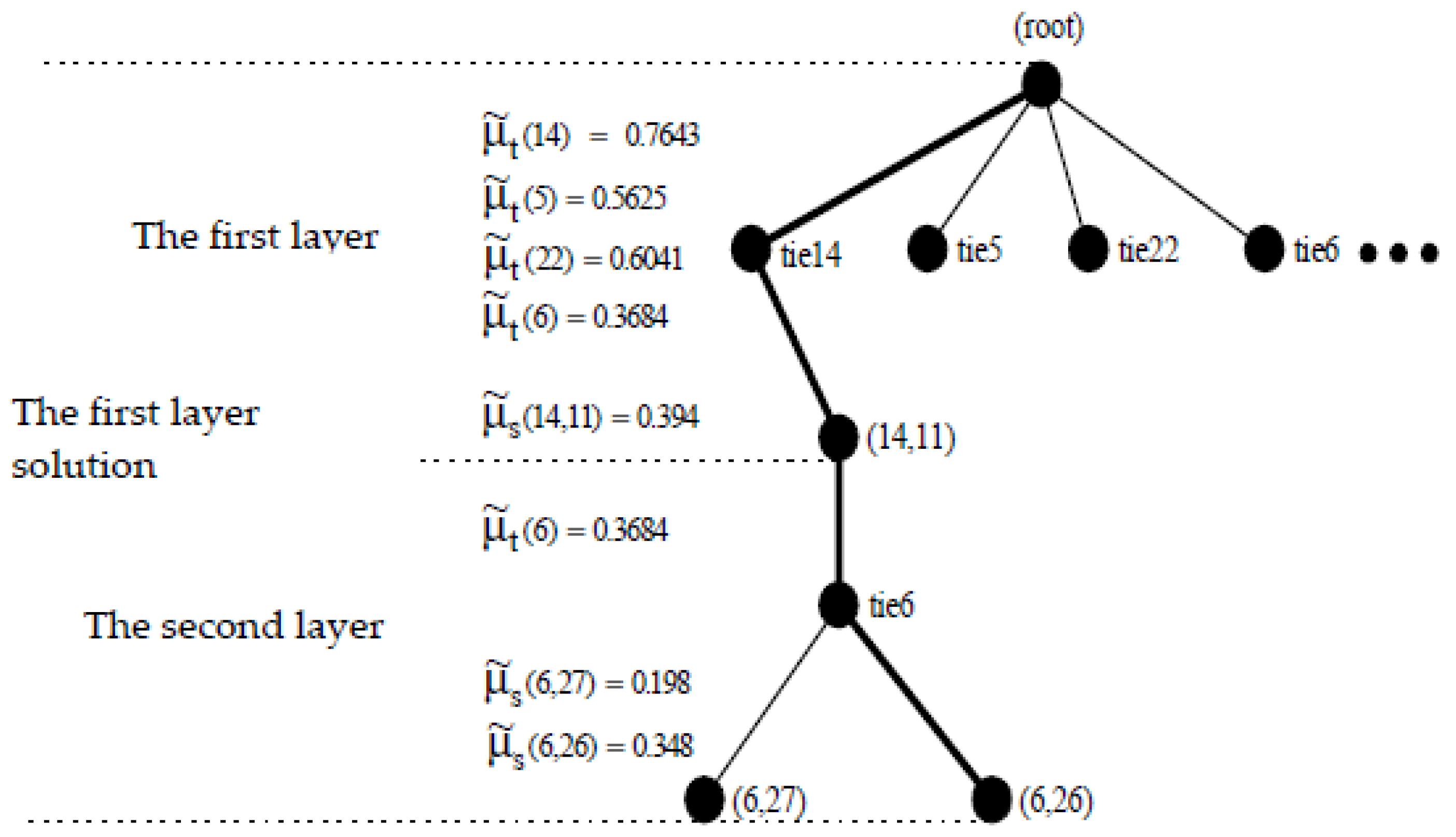
| Layer | Optimal Switch Configuration | del_P Loss Formula | Fuzzy Index Algorithm | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (on,off) | Loss (p.u) | Red (%) | (on,off) | Loss (p.u.) | Red (%) | (on,off) | Loss (p.u) | Red (%) | |
| 1 | (21,17) | 0.004839 | 5.400 | (21,17) | 0.004839 | 5.400 | (21,17) | 0.004839 | 5.400 |
| 2 | (15,19) | 0.004662 | 8.860 | (15,19) | 0.004662 | 8.860 | (15,19) | 0.004662 | 8.860 |
| Original (Tie Switch) | Exhausted Search | del_p Formula | Fuzzy index Algorithm |
|---|---|---|---|
| 5,6,7,8,14,15, 16,21,22,28 | 5,7,8,11,15,16, 21,22,26,28 | 6,7,8,13,14,15, 16,21,26,28 | 5,7,8,11,15,16, 21,22,26,28 |
| Action switch | (14,11),(6,26) | (22,26),(5,13) | (14,11),(6,26) |
| Loss red. (p.u.) | 0.000510 (p.u) | 0.000504 (p.u) | 0.000510 (p.u) |
| Reduction (%) | 6.104% | 6.032% | 6.104% |
| Search Layer | Goswami (Method I) | Goswami (Method II) | Goswami (Method III) | Baran (Method I) | Fuzzy Index Algorithm | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (on,off) | Loss (p.u) | Red. (%) | (on,off) | Loss (p.u) | Red. (%) | (on,off) | Loss (p.u) | Red. (%) | (on,off) | Loss (p.u) | Red. (%) | (on,off) | Loss (p.u) | Red. (%) | |
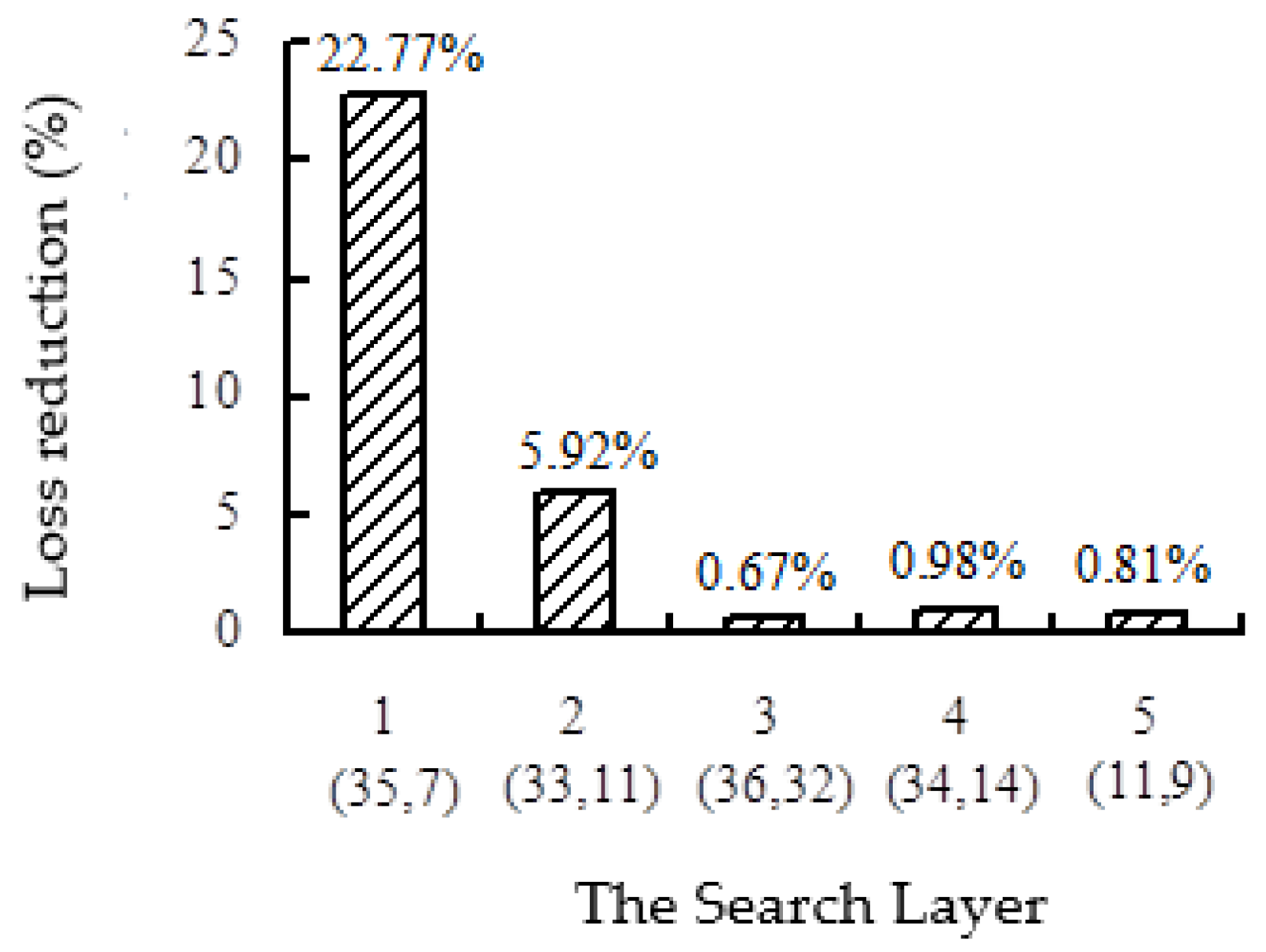
| 1 | (35,8) | 0.01535 | 24.270 | (37,28) | 0.01751 | 13.593 | (33,7) | 0.01584 | 21.852 | (33,6) | 0.01633 | 19.435 | (35,7) | 0.01565 | 22.770 |
| 2 | (37,28) | 0.01477 | 27.107 | (33,7) | 0.01581 | 21.976 | (34,9) | 0.01579 | 22.104 | (35,11) | 0.01450 | 28.439 | (33,11) | 0.01445 | 28.686 |
| 3 | (36,32) | 0.01462 | 27.847 | (35,11) | 0.01443 | 28.809 | (35,14) | 0.01422 | 29.855 | (36,31) | 0.01544 | 23.826 | (36,32) | 0.01432 | 29.352 |
| 4 | (34,14) | 0.01460 | 27.980 | (34,14) | 0.01432 | 29.366 | (36,32) | 0.01396 | 31.148 | (37,28) | 0.01598 | 21.137 | (34,14) | 0.01412 | 30.334 |
| 5 | (8,9) | 0.01446 | 28.666 | (36,32) | 0.01416 | 30.121 | * | * | * | (6,33) | 0.01463 | 27.827 | (11,9) | 0.01396 | 31.148 |
| 6 | (33,7) | 0.01400 | 30.935 | (28,37) | 0.01412 | 30.334 | * | * | * | * | * | * | * | * | * |
| 7 | (28,37) | 0.01396 | 31.148 | (11,9) | 0.01396 | 31.148 | * | * | * | * | * | * | * | * | * |
| Original Tie Switch | Goswami (I) | Goswami (II) | Goswami (III) | Baran. (I) | Baran. (II/III) | Fuzzy Index |
|---|---|---|---|---|---|---|
| 33 | 7 | 7 | 7 | 11 | 6 | 7 |
| 34 | 9 | 9 | 9 | 28 | 11 | 9 |
| 35 | 14 | 14 | 14 | 31 | 31 | 14 |
| 36 | 32 | 32 | 32 | 33 | 34 | 32 |
| 37 | 37 | 37 | 37 | 34 | 37 | 37 |
| Number of operations | 7 | 7 | 4 | 5 | 3 | 5 |
| Loss reduction (%) | 31.148% | 31.148% | 31.148% | 27.83% | 23.83% | 31.148% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.-M.; Tsai, W.-C. Generalized Distribution Feeder Switching with Fuzzy Indexing for Energy Saving. Processes 2023, 11, 1572. https://doi.org/10.3390/pr11051572
Lin W-M, Tsai W-C. Generalized Distribution Feeder Switching with Fuzzy Indexing for Energy Saving. Processes. 2023; 11(5):1572. https://doi.org/10.3390/pr11051572
Chicago/Turabian StyleLin, Whei-Min, and Wen-Chang Tsai. 2023. "Generalized Distribution Feeder Switching with Fuzzy Indexing for Energy Saving" Processes 11, no. 5: 1572. https://doi.org/10.3390/pr11051572
APA StyleLin, W.-M., & Tsai, W.-C. (2023). Generalized Distribution Feeder Switching with Fuzzy Indexing for Energy Saving. Processes, 11(5), 1572. https://doi.org/10.3390/pr11051572







