Fatigue Life and Crack Initiation in Monopile Foundation by Fatigue FE Analysis
Abstract
1. Introduction
2. Material Constant Determination by Experiment
3. FE Welding Analysis Procedure
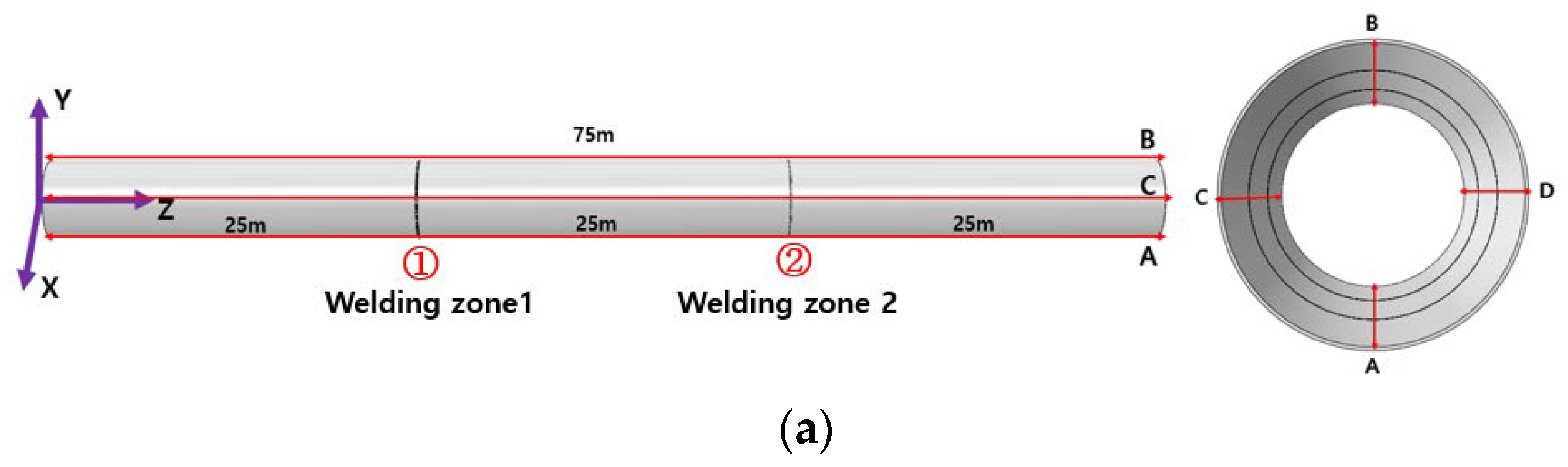
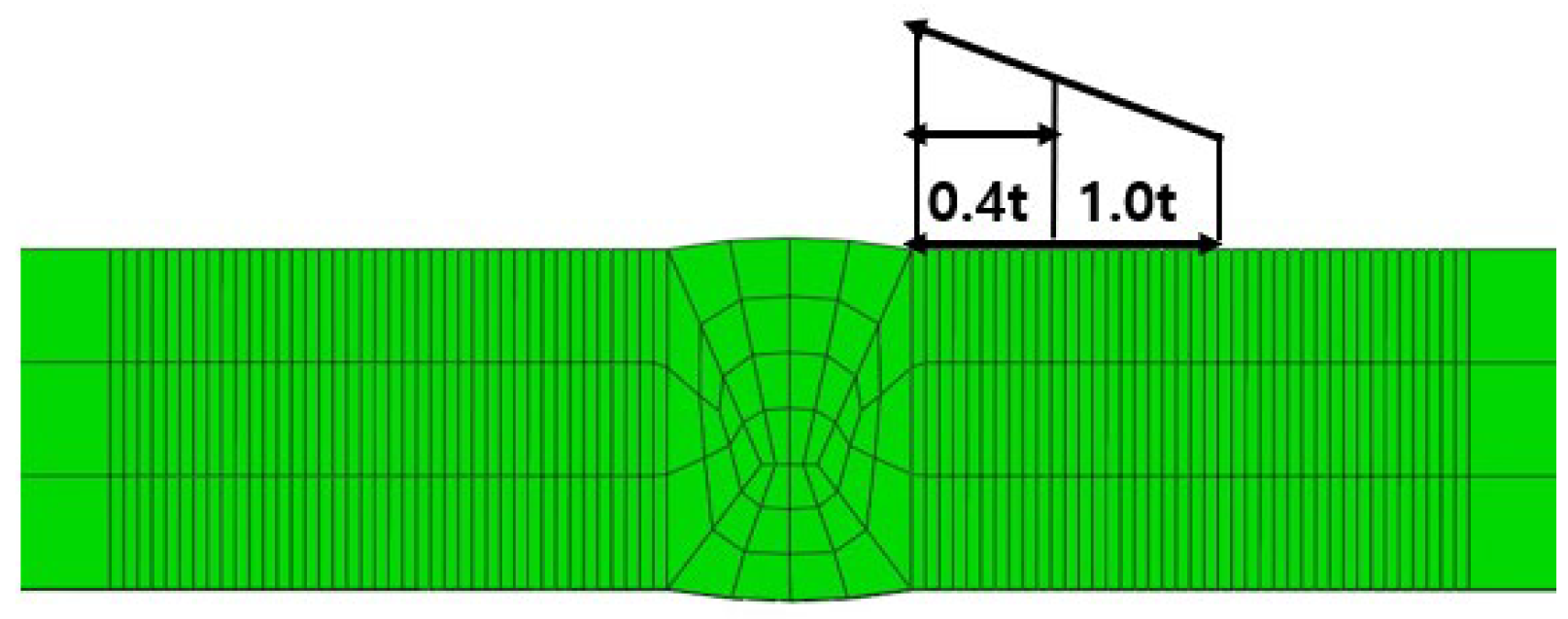
3.1. Model for FE Welding Analysis
3.2. 3D Non-Steady Heat Conduction FE Analysis
3.3. 3D Thermal Elasto-Plastic FE Analysis
4. Fatigue Life Calculation Procedure
4.1. Hot Spot Stress Method
4.2. 3D Fatigue FE Analysis
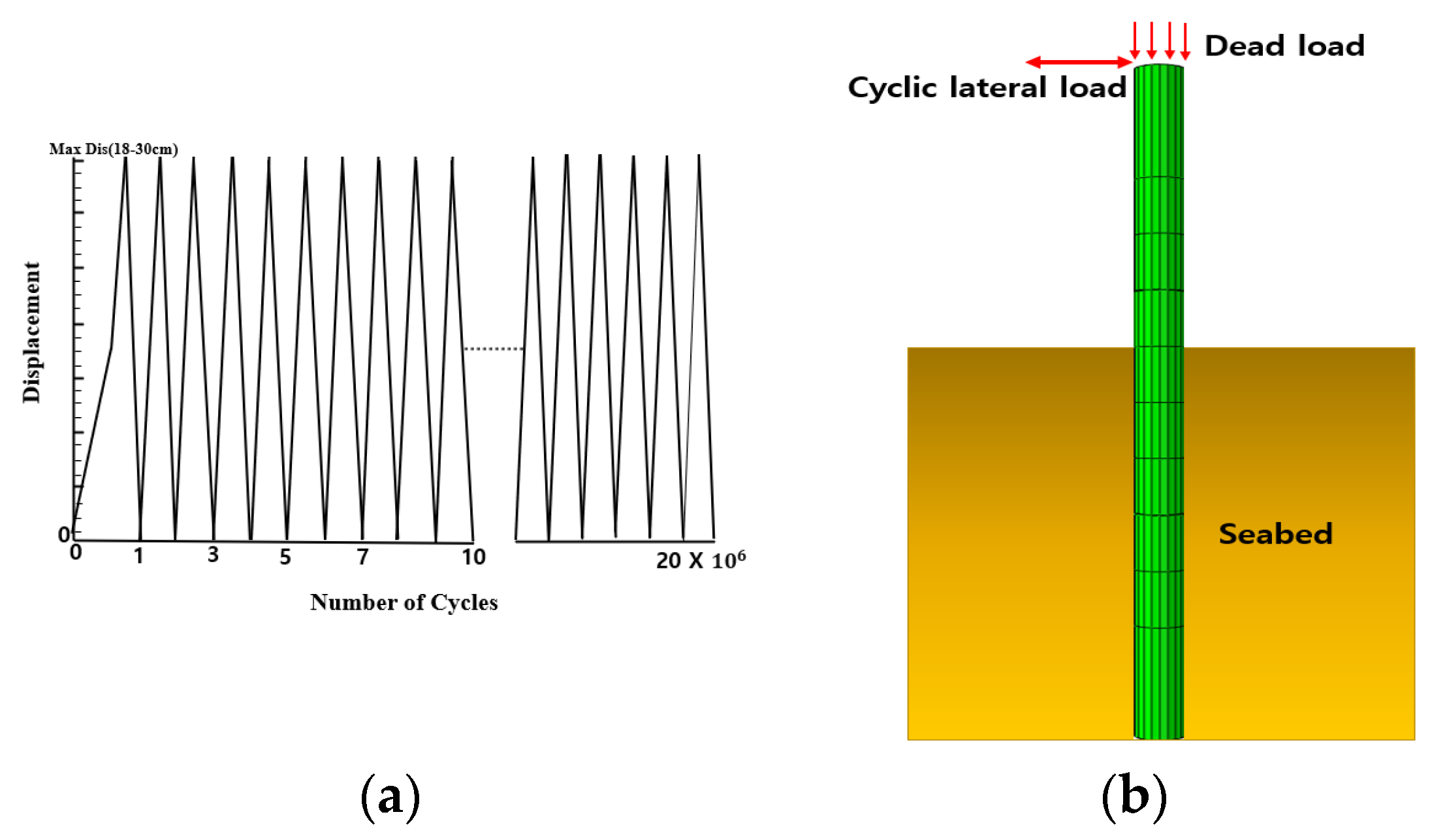
4.3. Boundary Condition of the Monopile Structure
5. Results and Discussion
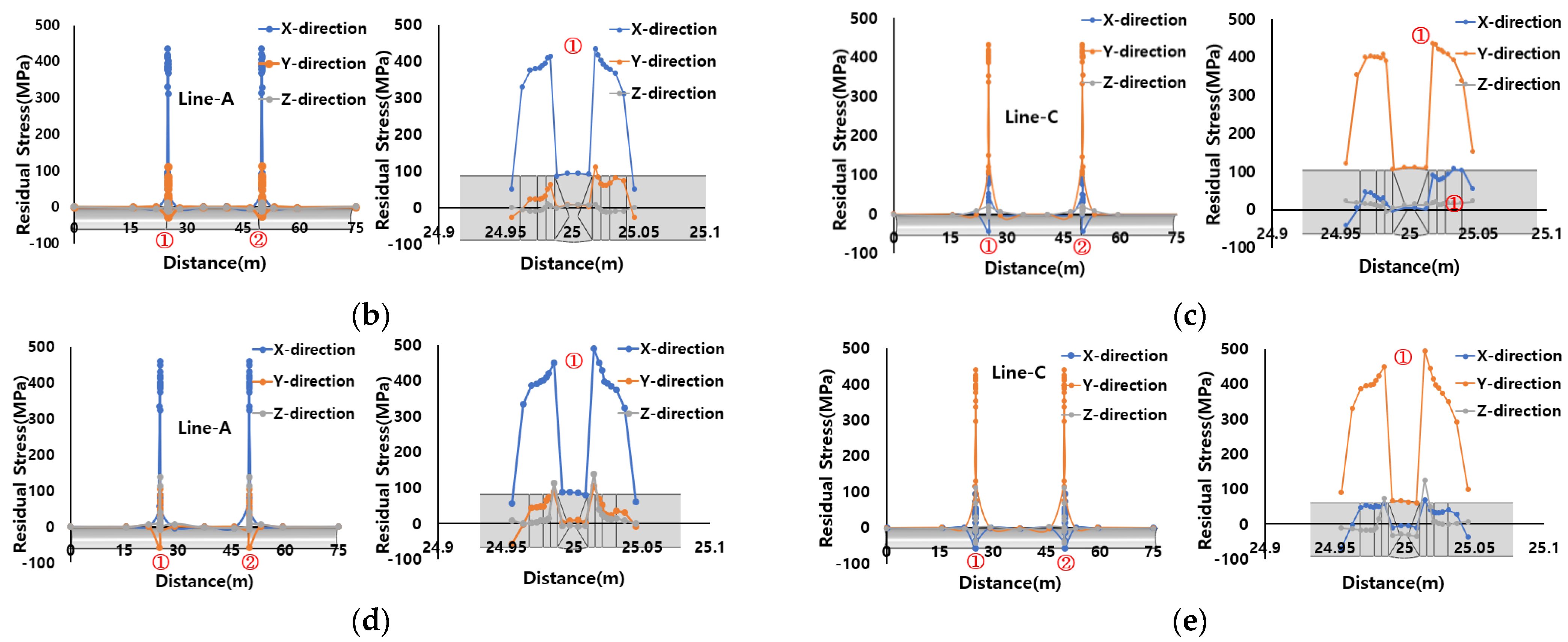
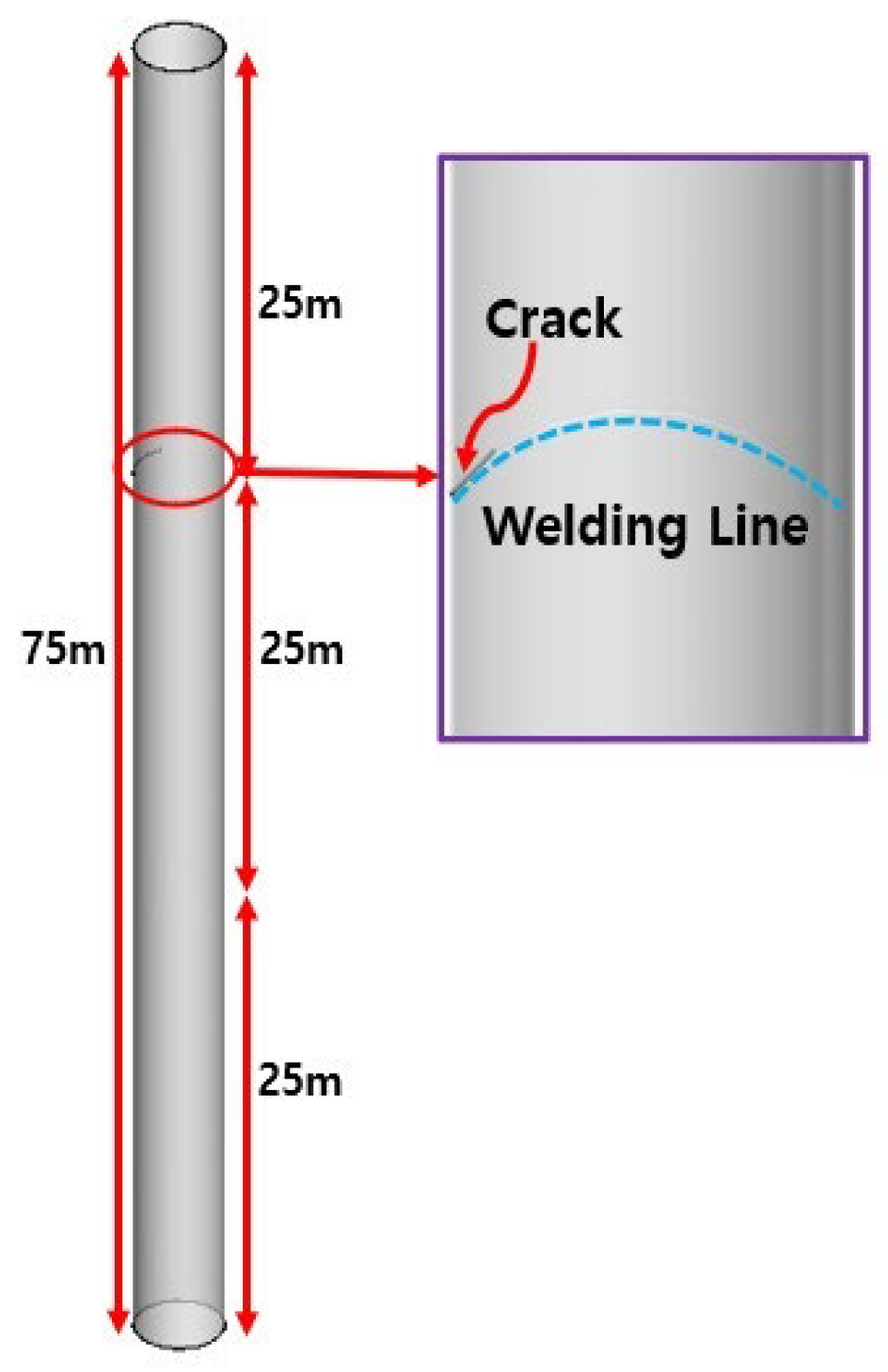
5.1. Crack Initiation
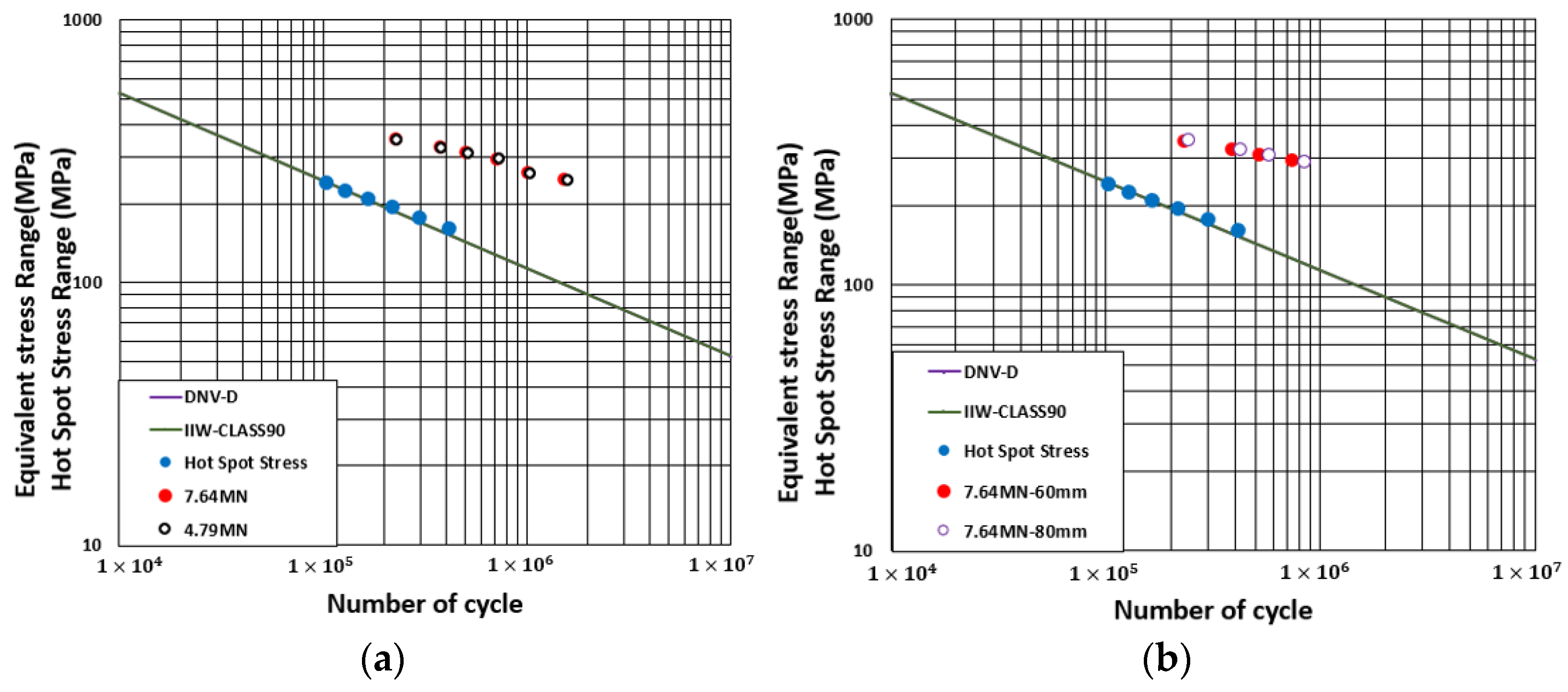
5.2. Comparison of Fatigue FEA Result and IIW DNV Standard
6. Conclusions
- The fatigue life of the monopile structure was analyzed considering the initial state of the weld (residual stress and welding deformation).
- Fatigue FE results were compared with the HSS method and the DNV GL and IIW recommendations, all of which confirmed that the fatigue FE method was a more reliable method of calculating fatigue life and crack initiation than HSS.
- The effect of vertical loads on fatigue life at a higher stress range was about 1.8%, whereas the effect of vertical loads on the fatigue life at a lower stress range increased by about 4.6% for both 7.64 MN and 4.79 MN vertical load types.
- The effect of the thickness of the monopile on fatigue life at a higher stress range was about 6.4%, whereas the effect of vertical loads on the fatigue life at a lower stress range significantly increased by about 15%. Therefore, the effect of thickness was more dominant in the fatigue life of monopile structures than the vertical loading.
- Fatigue FE analysis method is an effective method for calculating the fatigue life.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, M.J.; Yun, J.S.; Choo, Y.W. Effect of Lateral Load-Moment Combination on p-y Curves of Large Diameter Monopile for Offshore Wind Turbine: Centrifuge Model Tests. J. Korean Geotech. Soc. 2020, 2, 29–42. [Google Scholar]
- Nah, D.B.; Shin, H.S.; Na, D.J. Offshore Wind Power, Review. J. Energy Eng. 2011, 2, 143–153. [Google Scholar] [CrossRef]
- Lee, D.Y.; Im, S.W. Technical Aspects for Development of Offshore Wind Power Substructure. Korean Soc. Steel Constr. 2011, 10, 12–16. [Google Scholar]
- Bang, J.-S.; Han, J.-W.; Gil, K. Development of Programs to Analyze Mechanical Load Data of Wind Turbine Generator Systems and Case Studies on Simulation Data. Trans. Korean Soc. Mech. Eng. B 2013, 37, 789–798. [Google Scholar] [CrossRef]
- Jang, H.S.; Kim, H.S.; Eum, H.J.; Kim, M.E. Behavior Analysis by Verticality Error of Monopile Foundation for 5 MW Offshore Wind Turbine. J. Korean Soc. Civ. Eng. 2012, 3, 61–68. [Google Scholar]
- Yoon, G.L.; Kim, K.J.; Kim, H.Y. Reliability Analysis of Monopile for a Offshore Wind Turbine Using Response Surface Method. J. Korean Soc. Civ. Eng. 2013, 33, 2401–2409. [Google Scholar]
- Yoon, G.L.; Kim, H.Y. Case Study on Reliability Analysis of Offshore Wind Turbine Foundation. J. Korean Geo-Environ. Soc. 2012, 13, 91–98. [Google Scholar]
- Kim, S.R.; Lee, J.W.; Kim, B.K.; Lee, J.S. Damage Estimation Method for Monopile Support Structure of Offshore Wind Turbine. Korean Soc. Noise Vib. Eng. 2012, 22, 667–675. [Google Scholar] [CrossRef]
- Jang, H.S.; Kim, H.S.; Kwak, Y.M.; Park, J.H. Analysis of Lateral Behavior of Offshore Wind Turbine Monopile Foundation in Sandy Soil. J. Korean Soc. Steel Constr. 2013, 25, 421–430. [Google Scholar]
- Kim, B.-C.; Jeong, S.-S.; Ko, J.-Y. Proposed Reduction Factor of Cyclic p-y Curves for Drilled Shafts in Weathered Soil. J. Korean Geotech. Soc. 2015, 31, 47–63. [Google Scholar] [CrossRef]
- Romali, B.; Ali, M. Fatigue damage analysis of offshore wind turbine monopile weldments. Procedia Struct. Integr. 2019, 17, 643–650. [Google Scholar]
- Anais, J.; Jeferson, O.; Ali, M.; Foroogh, H.; Joe, K.; Filippo, B. Residual stress measurements in offshore wind monopile weldments using neutron diffraction technique and contour method. Theor. Appl. Fract. Mech. 2018, 96, 418–427. [Google Scholar]
- Khajeian, A.; Mahmoudi, A.; Mehmanparast, A. Shot peening effects on residual stresses redistribution of offshore wind monopile multi-pass weldments. Mar. Struct. 2019, 66, 106–120. [Google Scholar] [CrossRef]
- Ali, M.; Feargal, B.; Isaac, T. Fatigue crack growth rates for offshore wind monopile weldments in air and seawater: SLIC inter-laboratory test results. Mater. Des. 2017, 114, 494–504. [Google Scholar]
- Anais, J.; Ali, M. Crack growth direction effects on corrosion-fatigue behaviour of offshore wind turbine steel weldments. Mar. Struct. 2021, 75, 10288. [Google Scholar]
- Mathieu, B.; Ali, M.; Jarryd, B.; Mahmood, S. New shape function solutions for fracture mechanics analysis of offshore wind turbine monopile foundations. Ocean Eng. 2018, 160, 264–275. [Google Scholar]
- Abdulhakim, A.S.; Ali, M.; Phil, H.; Athanasios, K. Comparative study between S-N and fracture mechanics approach on reliability assessment of offshore wind turbine jacket foundations. Reliab. Eng. Syst. Saf. 2021, 215, 107383. [Google Scholar]
- Joey, V.; Claus, K.; John, D.S.; Gianluca, Z. Fatigue reliability of large monopiles for offshore wind turbines. Int. J. Fatigue 2020, 134, 10548. [Google Scholar]
- Joey, V.; Erin, E.B. Design and fatigue analysis of monopile foundations to support the DTU 10 MW offshore wind turbine. Energy Procedia 2017, 137, 3–13. [Google Scholar]
- Ko, Y.-Y. A simplified structural model for monopile-supported offshore wind turbines with tapered towers. Renew. Energy 2020, 156, 777–790. [Google Scholar] [CrossRef]
- Wang, J.Y.; Sun, G.D.; Chen, G.S.; Yang, X. Finite element analyses of improved lateral performance of monopile when com-bined with bucket foundation for offshore wind turbines. Appl. Ocean Res. 2021, 111, 102647. [Google Scholar] [CrossRef]
- Chen, T.; Wang, X.; Gu, X.; Zhao, Q.; Yuan, G.; Liu, J. Axial compression tests of grouted connections in jacket and monopile offshore wind turbine structures. Eng. Struct. 2019, 196, 109330. [Google Scholar] [CrossRef]
- Chen, T.; Wang, X.; Yuan, G.; Liu, J. Fatigue bending test on grouted connections for monopile offshore wind turbines. Mar. Struct. 2018, 60, 52–71. [Google Scholar] [CrossRef]
- ASTM E606/E606M; Standard Test Method for Strain-Controlled Fatigue Testing. ASTM: West Conshohocken, PA, USA, 2021.
- Shin, W.; Chang, K.-H.; Muzaffer, S. Fatigue analysis of cruciform welded joint with weld penetration defects. Eng. Fail. Anal. 2021, 120, 105111. [Google Scholar] [CrossRef]
- Chang, K.-H.; Kang, S.-U.; Wang, Z.-M.; Muzaffer, S.; Hirohata, M. Fatigue finite element analysis on the effect of welding joint type on fatigue life and crack location of a tubular member. Arch. Appl. Mech. 2019, 89, 927–937. [Google Scholar] [CrossRef]
- Muzaffer, S.; Chang, K.-H.; Wang, Z.-M.; Kang, S.-U. Comparison of stiffener effect on fatigue crack in KT-type pipe joint by FEA. Weld. World 2022, 66, 783–797. [Google Scholar] [CrossRef]
- Van Do, V.N.; Lee, C.-H.; Chang, K.-H. A nonlinear CDM model for ductile failure analysis of steel bridge columns under cyclic loading. Comput. Mech. 2014, 53, 1209–1222. [Google Scholar] [CrossRef]
- Van Do, V.N.; Lee, C.-H.; Chang, K.-H. High cycle fatigue analysis in presence of residual stresses by using a continuum damage mechanics model. Int. J. Fatigue 2015, 70, 51–62. [Google Scholar] [CrossRef]
- Van Do, V.N.; Lee, C.-H.; Chang, K.-H. A constitutive model for uniaxial/multiaxial ratcheting behavior of a duplex stainless steel. Mater. Des. 2015, 65, 1161–1171. [Google Scholar] [CrossRef]
- Wang, Z.-M.; Chang, K.-H.; Muzaffer, S. Fatigue Analysis of the Effects of Incomplete Penetration Defects on Fatigue Crack Initiation Points in Butt-Welded Members. J. Weld. Join. 2020, 38, 543–550. [Google Scholar] [CrossRef]
- Lee, C.H.; Chang, K.H. Prediction of residual stresses in welds of similar and dis-similar steel weldment. J. Mater. Sci. 2007, 42, 6607–6613. [Google Scholar] [CrossRef]
- Chang, K.-H.; Lee, C.-H.; Park, K.-T.; Um, T.-H. Experimental and numerical investigations on residual stresses in a multi-pass butt-welded high strength SM570-TMCP steel plate. Int. J. Steel Struct. 2011, 11, 315–324. [Google Scholar] [CrossRef]
- Chang, K.-H.; Lee, C.-H. Characteristics of High Temperature Tensile Properties and Residual Stresses in Weldments of High Strength Steels. Mater. Trans. 2006, 47, 348–354. [Google Scholar] [CrossRef]
- American Petroleum Institute. API Recommended Practice 2A-WSD (RP 2A-WSD). In Planning, Designing and Constructing Fixed Offshore Platforms—Working Stress Design; API Publishing Services: Sydney, NSW, Australia, 2000. [Google Scholar]
- Lee, S.H. A Study on the Mechanism of the Stress Generated by Replacement Repair Welding and Repair Method of Steel Bridge. Ph.D. Thesis, Chung-Ang University, Seoul, Republic of Korea, 2003. [Google Scholar]
- Park, T.-U.; Jung, D.-H.; Park, J.-H.; Kim, J.-H.; Han, I.-W. Changes in the Mechanical Properties and Microstructure of High Manganese Steel by High Heat Input Welding and General Welding Processes. J. Weld. Join. 2022, 40, 33–39. [Google Scholar] [CrossRef]
- Yi, M.-S.; Seo, J.-K. Residual Stress Study of High Manganese Steel Riser Pipe Manufactured by Longitudinal Butt Welding (1): Residual Stress Measurement and FE Analysis. J. Weld. Join. 2021, 39, 135–143. [Google Scholar] [CrossRef]
- Wu, C.; Wang, C.; Kim, J.-W. Welding Distortion Prediction for Multi-Seam Welded Pipe Structures using Equivalent Thermal Strain Method. J. Weld. Join. 2021, 39, 435–444. [Google Scholar] [CrossRef]
- Kwon, I.K. Derivation of the Mechanical Properties of Structural Steels at High Temperatures. Korean Inst. Fire Sci. Eng. 2007, 21, 47–55. [Google Scholar]
- Hobbacher, A. Recommendations for Fatigue Design of Welded Joints and Components; Doc. XIII-1539-96/XV-845-96; IIW (International Institute of Welding): Paris, France, 2008. [Google Scholar]
- DNVGL-RP-C203; Fatigue Design of Offshore of Steel Structures. Recommended Practice. Det Norske Veritas: Oslo, Norway, 2016.
- Ljjj, L.B.J.; Gravesen, H. Kriegers Flak Offshore Wind Farm—Design Basis Foundations; Version B1 29-01-2008; Vattenfall Vindkraft AB: Solna, Sweden.
- Lee, M.S.; Kim, M.H. Fatigue Crack Growth Evaluation of IMO Type B Spherical LNG Cargo Tank Considering the Effect of Stress Ratio and Load History. J. Weld. Join. 2022, 40, 40–47. [Google Scholar] [CrossRef]
- Kang, S.-K. Crack Propagation Characterization Applying High Manganese Austenitic Steel to Independent Type B Tank. J. Weld. Join. 2022, 40, 9–15. [Google Scholar] [CrossRef]
- Park, S.-Y.; Kang, Y.; Oh, D.; Song, S.; Hong, H.-U. Solidification Cracking Susceptibility of the Weld Metal of Additively Manufactured 316L Stainless Steel. J. Weld. Join. 2021, 39, 45–50. [Google Scholar] [CrossRef]
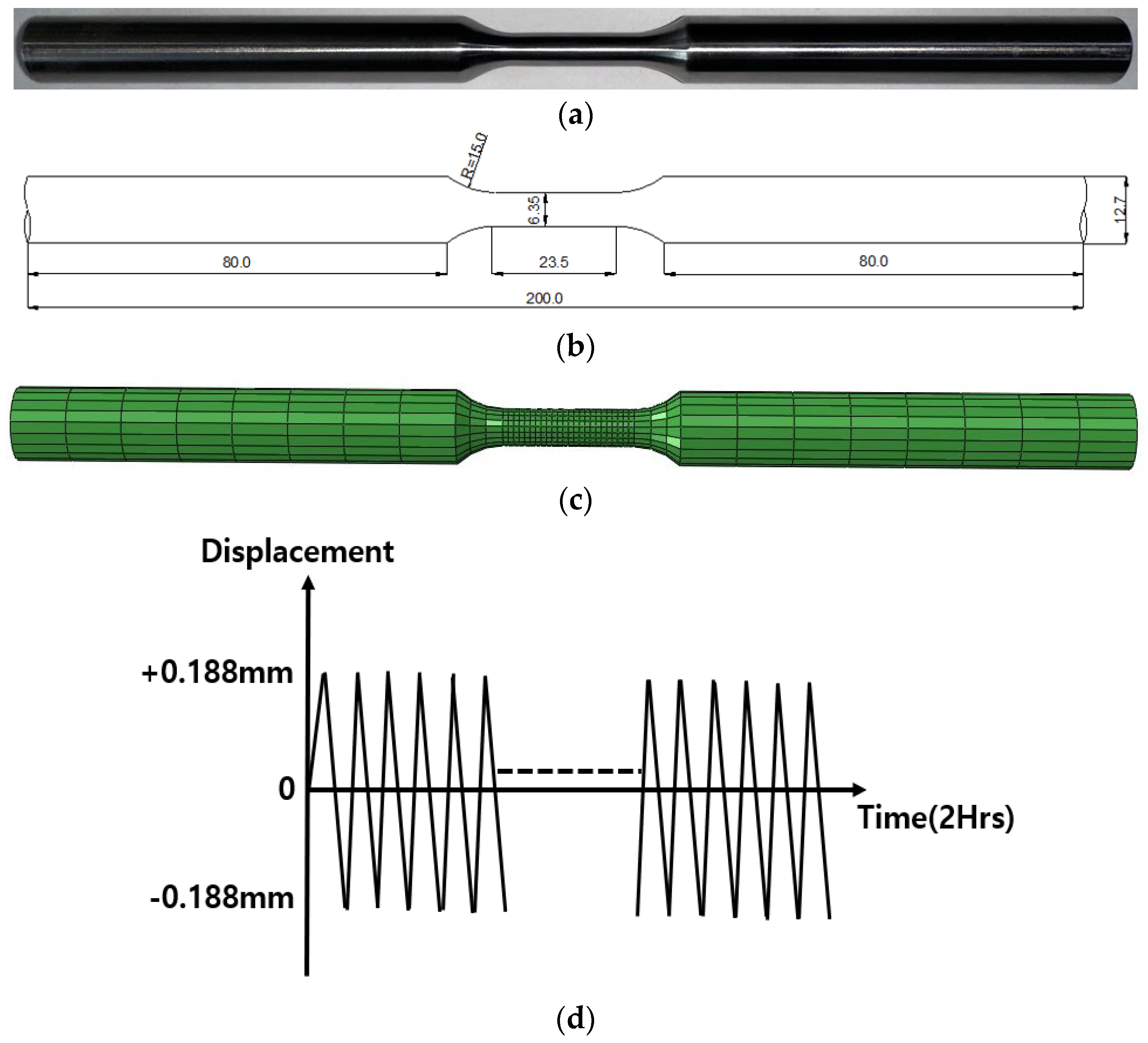


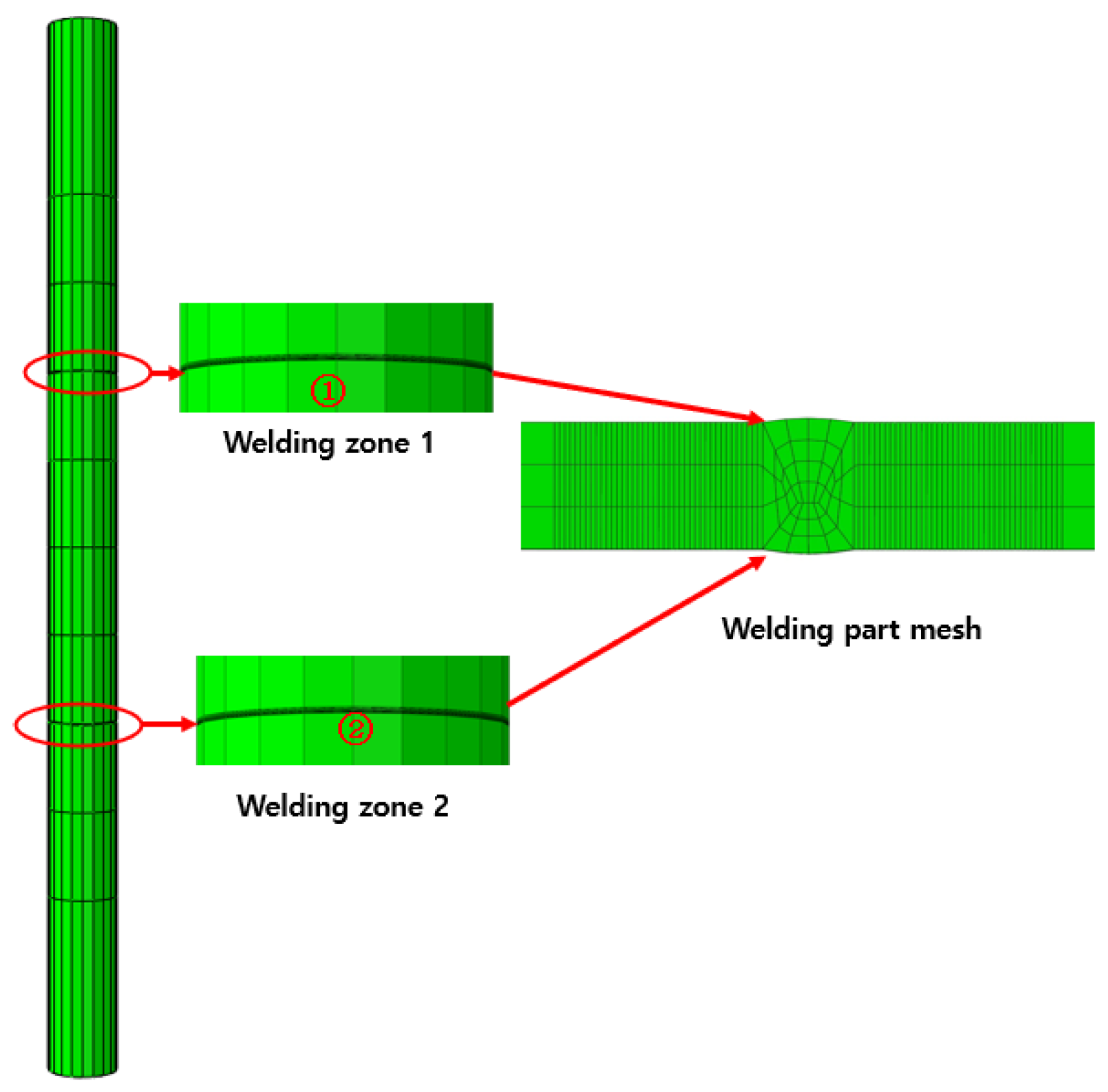
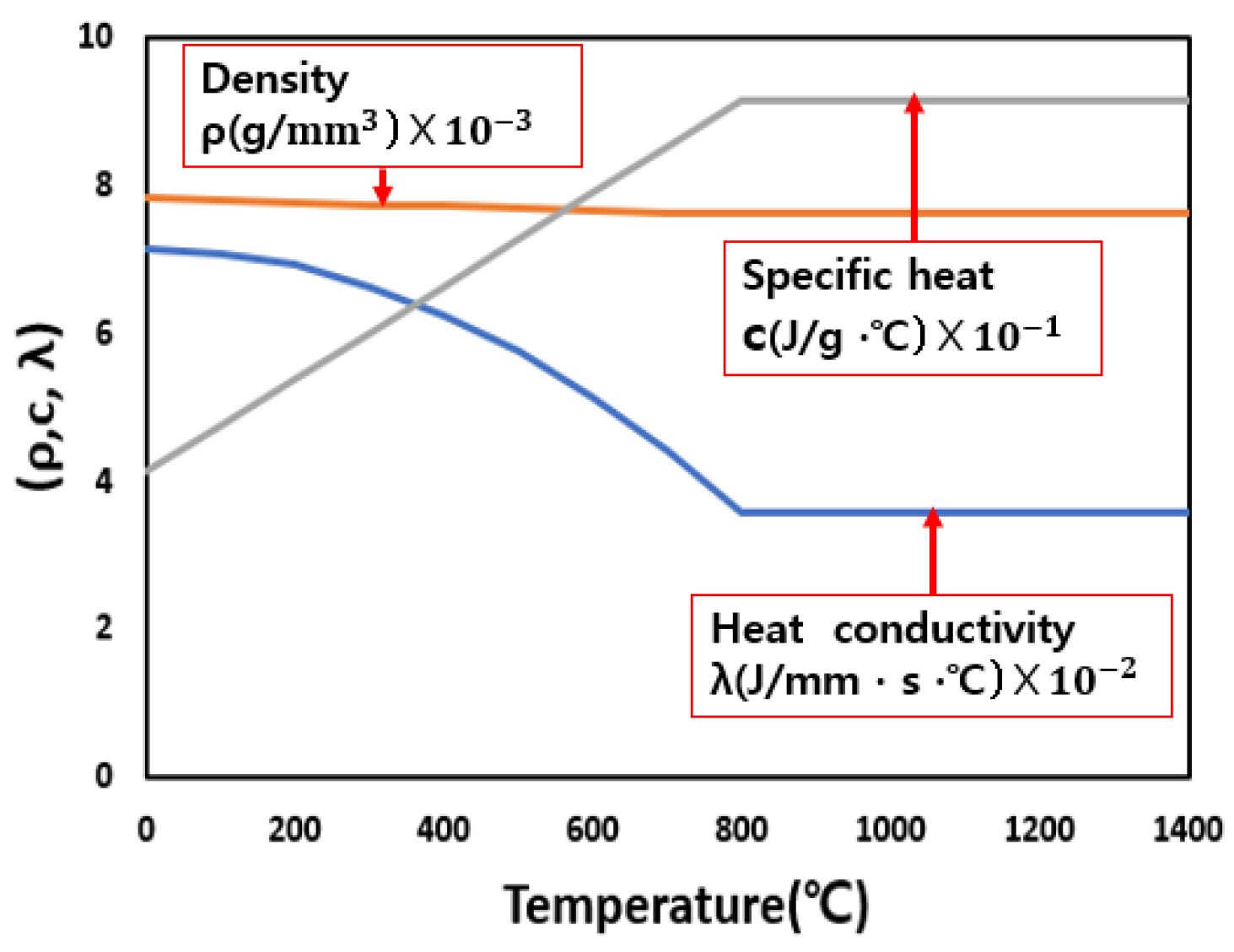
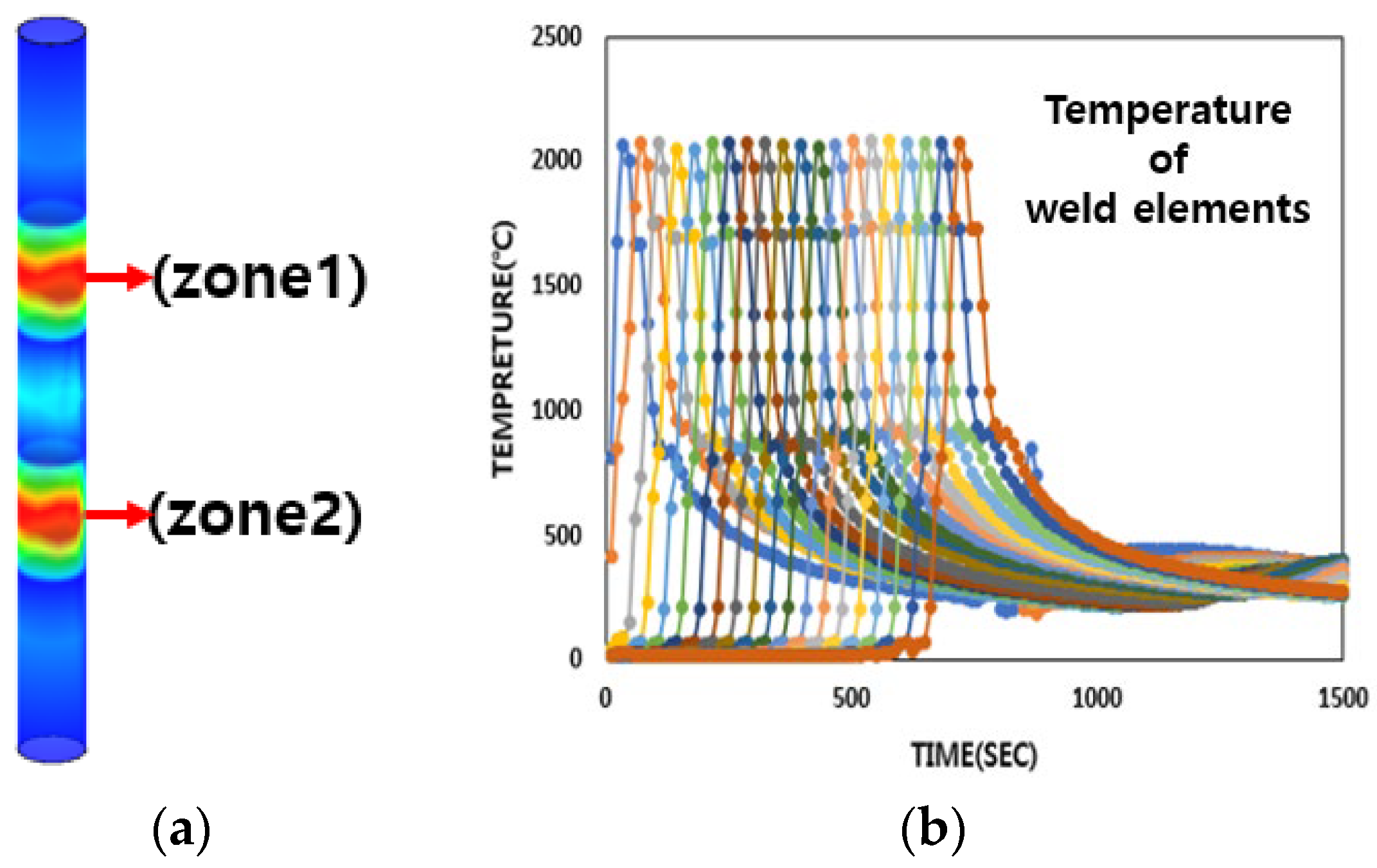
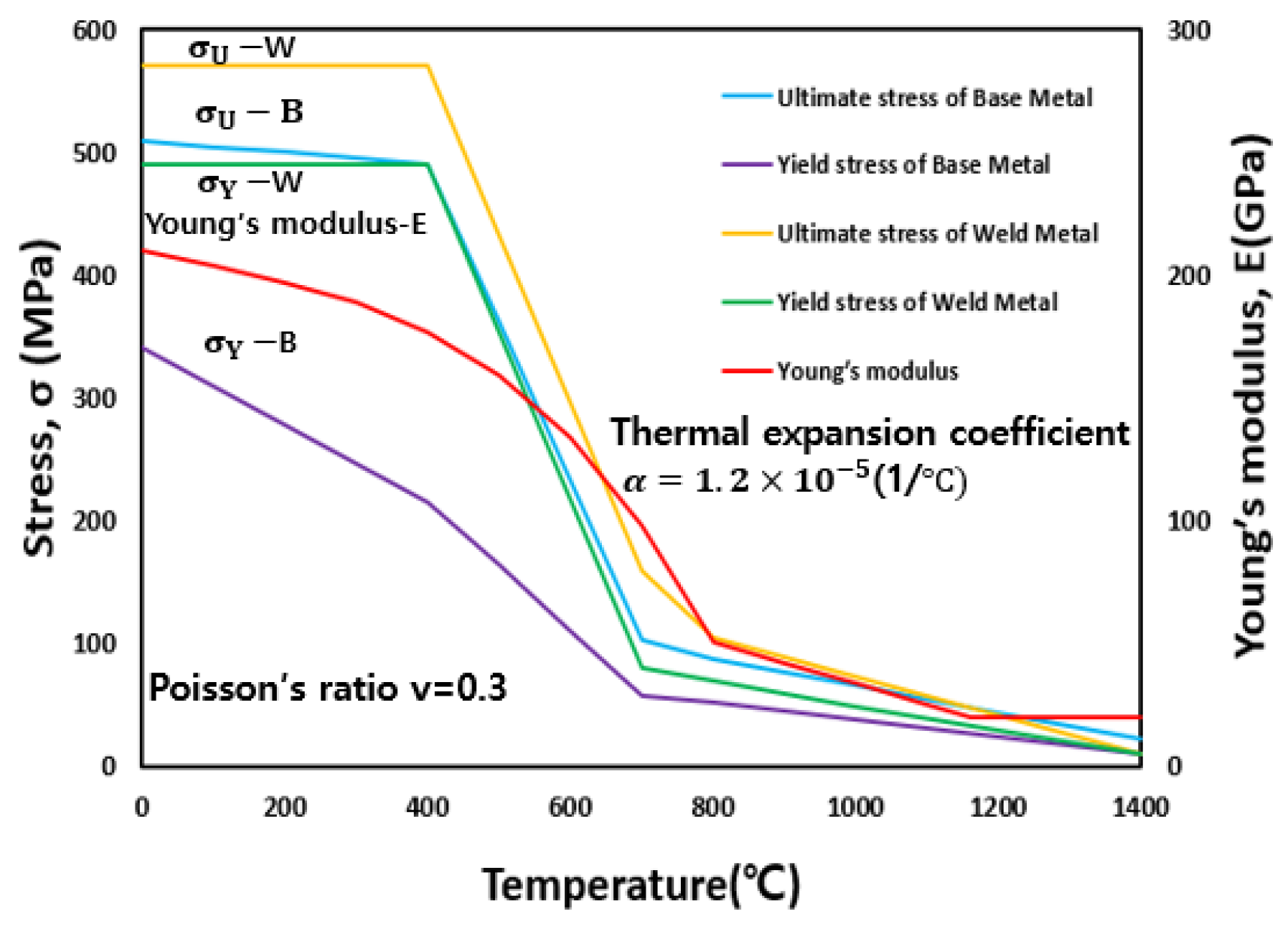

| Material | Young’s Modulus (GPa) | Poisson’s Ratio | Elongation (%) | ||
|---|---|---|---|---|---|
| SM490 | 204 | 0.3 | 344.3 | 580 | 30 |
| Material | Q (MPa) | b | ||||||
|---|---|---|---|---|---|---|---|---|
| SM490 | 130 | 85 | 1.271 | 300 | 56.67 | 1 | 65 | 18.27 |
| Turbine Size | 3.6 MW | 5 MW |
| Nacelle mass incl. rotor | 220 ton | 410 ton |
| Tower mass | 220 ton | 300 ton |
| Blade mass | 39 ton | 54 ton |
| Total mass | 479 ton | 764 ton |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.-M.; Chang, K.-H.; Muzaffer, S.; Hirohata, M. Fatigue Life and Crack Initiation in Monopile Foundation by Fatigue FE Analysis. Processes 2023, 11, 1317. https://doi.org/10.3390/pr11051317
Wang Z-M, Chang K-H, Muzaffer S, Hirohata M. Fatigue Life and Crack Initiation in Monopile Foundation by Fatigue FE Analysis. Processes. 2023; 11(5):1317. https://doi.org/10.3390/pr11051317
Chicago/Turabian StyleWang, Zhen-Ming, Kyong-Ho Chang, Shazia Muzaffer, and Mikihito Hirohata. 2023. "Fatigue Life and Crack Initiation in Monopile Foundation by Fatigue FE Analysis" Processes 11, no. 5: 1317. https://doi.org/10.3390/pr11051317
APA StyleWang, Z.-M., Chang, K.-H., Muzaffer, S., & Hirohata, M. (2023). Fatigue Life and Crack Initiation in Monopile Foundation by Fatigue FE Analysis. Processes, 11(5), 1317. https://doi.org/10.3390/pr11051317








