Multi-Point Flux MFE Decoupled Method for Compressible Miscible Displacement Problem
Abstract
1. Introduction
- The diffusion coefficient D was given by:
2. Problem Formulation and Discretizations
- Then, we could obtain a weak form of the problem (1): , , , from which we could find , as follows:
- In addition, the spaces on partition element E were defined by the following transformations:
- The spaces on were given by:
- For the approximation spaces, there existed a positive constant that was independent of the mesh sizes, such that the following was true:
- We used the time step, let be a positive integer, and set the following:
- The quadrature error of element E was denoted by the following:
- In order to avoid a tedious introduction, please refer to [11] for details about the properties of bijection mapping, mixed-element spaces, quadrature formulas, and quadrature errors.
- In order to facilitate the error analysis, we introduced the projection operator.
- For velocity and pressure, we defined projection such that the following was true:
- For the following approximation properties,
- For the concentration, the projection operator satisfied:
- For the following convergence analysis, we first introduced specific conclusions, which can be found in [11].
3. Convergence Analysis
- Subtracting the n time level and time level of the error equation, dividing that by , and then taking and , as well as adding in the two formulas, we could deduce the following:
- Based on the following:
- We concluded:
- Multiplying the above formula by and then combining Lemma 1 and summing n from 1 to N, we could then obtain the following:
- Next, we estimate the Formula (32), item by item:
- Taking and multiplying on both sides of (40), and then summing for n from 1 to N, we obtained the following:
- The left side of the previous equation could be estimated as follows:
- We estimated the right side of Formula (41) using the Cauchy–Schwarz inequality, and we obtained the following:
- Applying the discrete Gronwall’s Lemma to the previous equation resulted in the following:
4. Numerical Examples
4.1. Test Convergence Rate
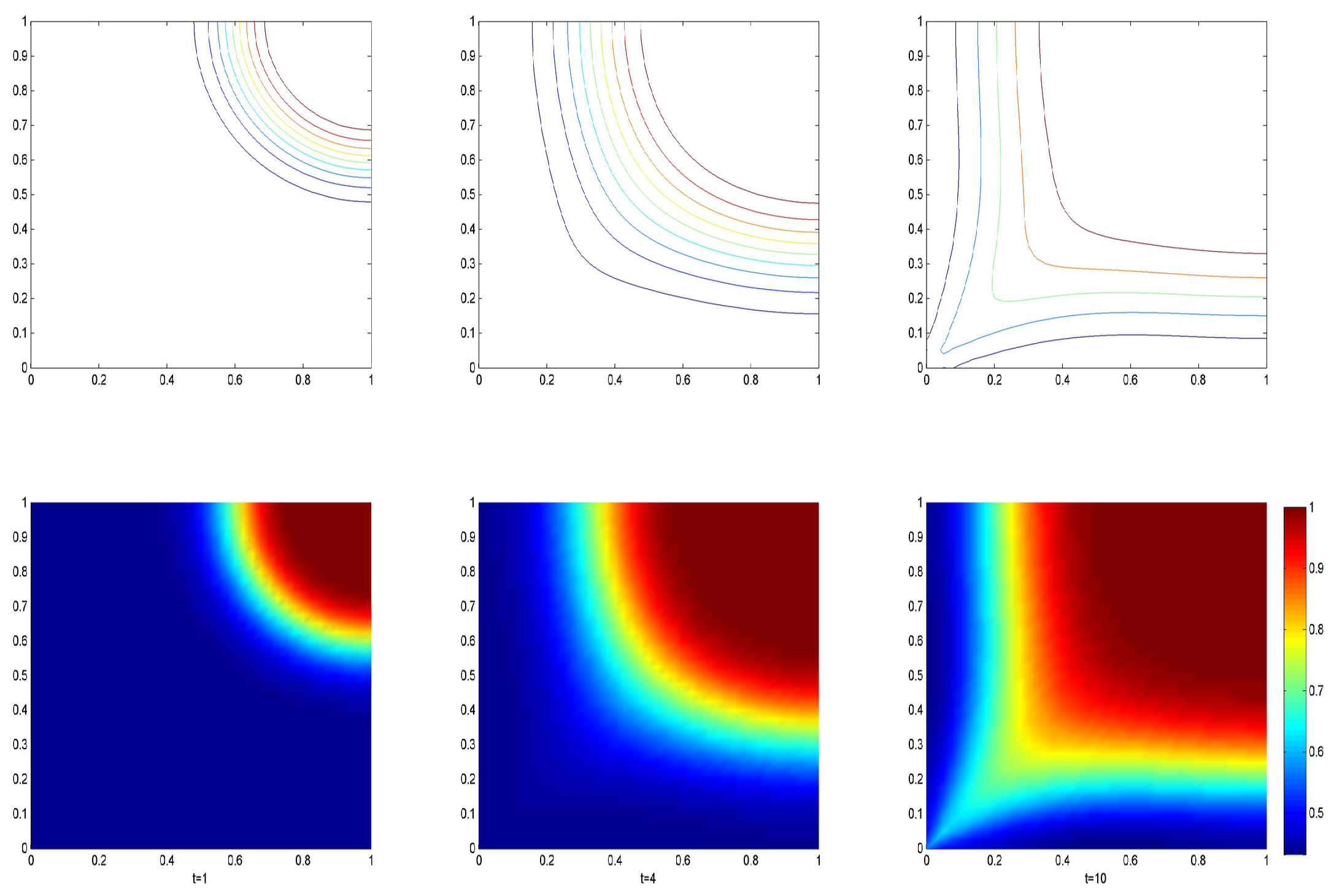
4.2. Single Injection Single Production Case
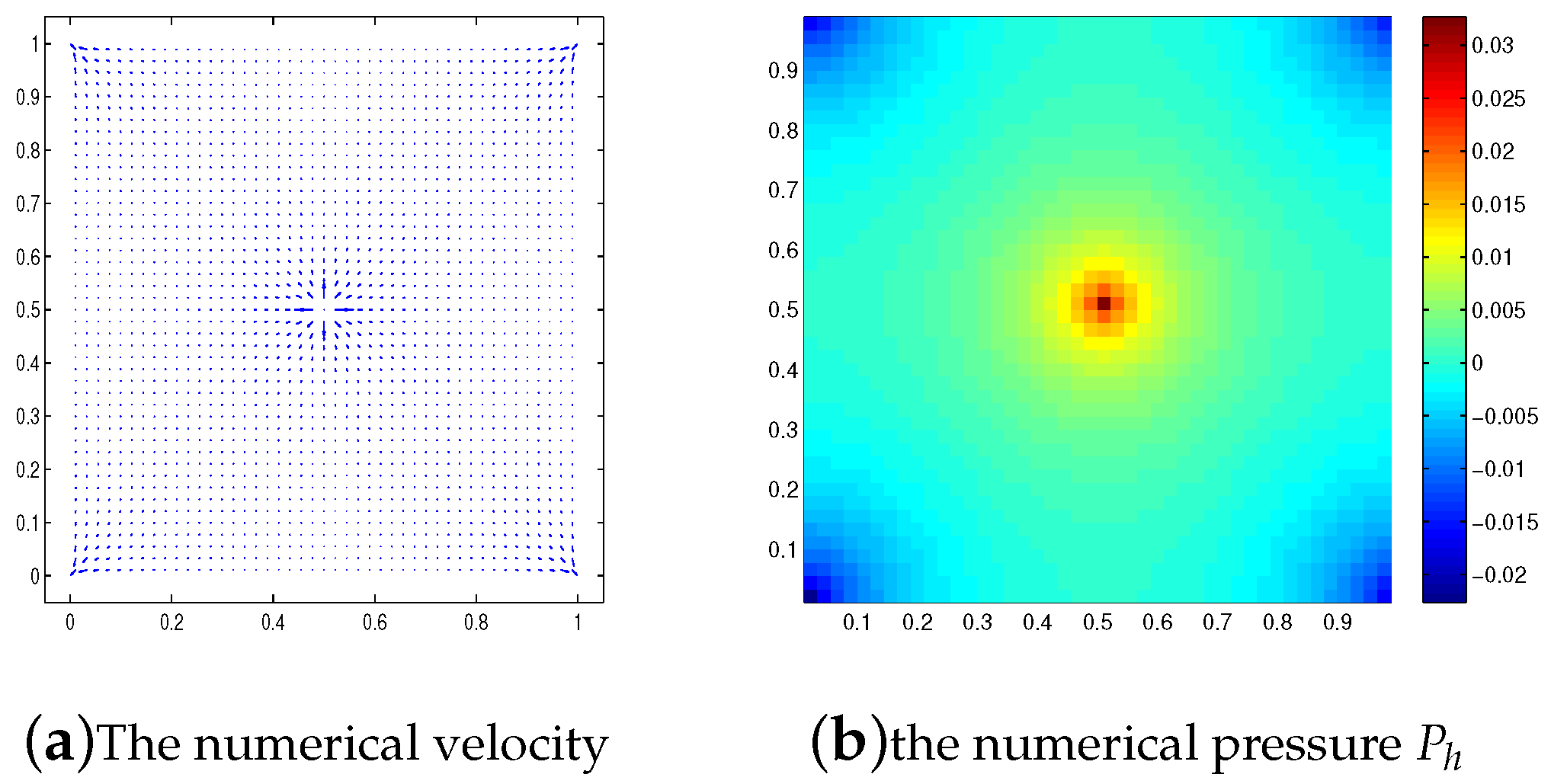
4.3. Five Spot Pattern Case
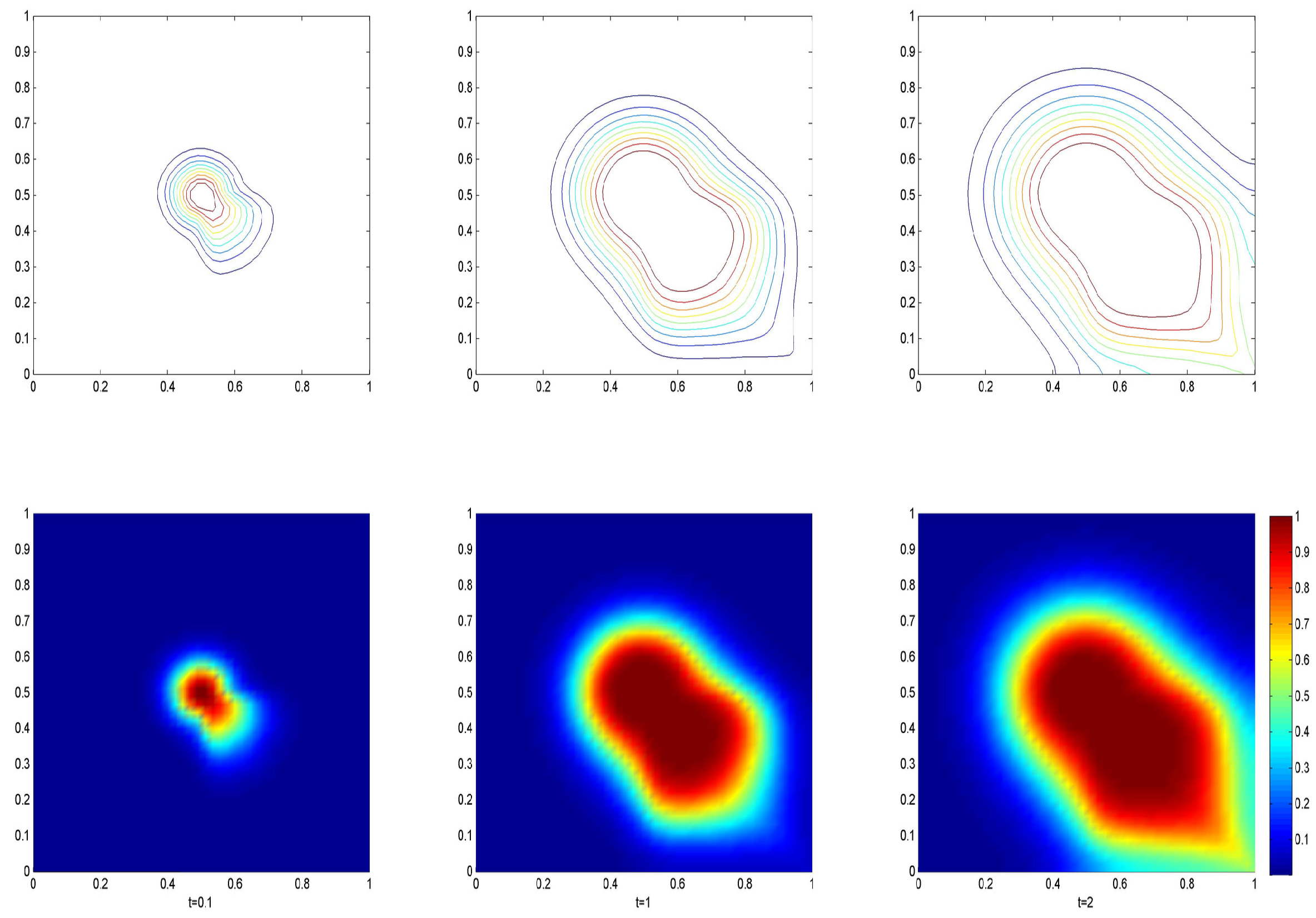
4.4. Five-Spot Pattern with Random Permeability Case
5. Results
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Douglas, J., Jr.; Roberts, J.E. Numerical Methods for a Model for Compressible Miscible Displacement in Porous Media. Math. Comput. 1983, 41, 441–459. [Google Scholar] [CrossRef]
- Feng, W.; Guo, H.; Kang, Y.; Yang, Y. Bound-preserving discontinuous Galerkin methods with second-order implicit pressure explicit concentration time marching for compressible miscible displacements in porous media. J. Comput. Phys. 2022, 463, 111240. [Google Scholar] [CrossRef]
- Guo, H.; Yang, Y. Bound-Preserving Discontinuous Galerkin Method for Compressible Miscible Displacement in Porous Media. SIAM J. Sci. Comput. 2017, 39, A1969–A1990. [Google Scholar] [CrossRef]
- Chuenjarern, N.; Xu, Z.; Yang, Y. High-order bound-preserving discontinuous Galerkin methods for compressible miscible displacements in porous media on triangular meshes. J. Comput. Phys. 2019, 378, 110–128. [Google Scholar] [CrossRef]
- Li, A.; Huang, J.; Liu, W.; Wei, H.; Yi, N. A characteristic block-centered finite difference method for Darcy-Forchheimer compressible miscible displacement problem. J. Comput. Appl. Math. 2022, 413, 114303. [Google Scholar] [CrossRef]
- Li, X.; Rui, H. Characteristic block-centered finite difference method for compressible miscible displacement in porous media. Appl. Math. Comput. 2017, 314, 391–407. [Google Scholar] [CrossRef]
- Li, X.; Rui, H.; Xu, W. A new MCC-MFE method for compressible miscible displacement in porous media. J. Comput. Appl. Math. 2016, 302, 139–156. [Google Scholar] [CrossRef]
- Zhang, J. A new combined characteristic mixed-finite-element method for compressible miscible displacement problem. Numer. Algorithms 2019, 81, 1157–1179. [Google Scholar] [CrossRef]
- Hu, H. Two-grid method for compressible miscible displacement problem by mixed-finite-element methods and expanded mixed-finite-element method of characteristics. Numer. Algorithms 2022, 89, 611–636. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, Y.; Hu, H. Two-grid method for compressible miscible displacement problem by CFEM-MFEM. J. Comput. Appl. Math. 2018, 337, 175–189. [Google Scholar] [CrossRef]
- Wheeler, M.F.; Yotov, I. A multi-point flux mixed-finite-element method. SIAM J. Numer. Anal. 2006, 44, 2082–2106. [Google Scholar] [CrossRef]
- Wheeler, M.F.; Xue, G.; Yotov, I. Coupling multi-point flux mixed-finite-element methods with continuous galerkin methods for poroelasticity. Computat. Geosci. 2014, 18, 57–75. [Google Scholar] [CrossRef]
- Arrarás, A.; Portero, L. Multipoint flux mixed-finite-element methods for slightly compressible flow in porous media. Comput. Math. Appl. 2019, 77, 1437–1452. [Google Scholar] [CrossRef]
- Xu, W.; Liang, D.; Rui, H. A multi-point flux mixed-finite-element method for the compressible Darcy-Forchheimer models. Appl. Math. Comput. 2017, 315, 259–277. [Google Scholar] [CrossRef]
- Xu, W.; Liang, D.; Rui, H.; Li, X. A Multipoint Flux Mixed Finite Element Method for Darcy-Forchheimer Incompressible Miscible Displacement Problem. J. Sci. Comput. 2020, 82, 1–20. [Google Scholar] [CrossRef]
- Adams, R.A.; Fournier, J.J.F. Sobolev Spaces; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Ewing, R.E.; Russell, T.F.; Wheeler, M.F. Convergence analysis of an approximation of miscible displacement in porous media by mixed finite elements and a modified method of characteristics. Comput. Methods Appl. Mech. Eng. 1984, 47, 73–92. [Google Scholar] [CrossRef]
- Brezzi, F.; Douglas, J., Jr.; Marini, L.D. Two families of mixed finite elements for second order elliptic problems. Numer. Math. 1985, 88, 217–235. [Google Scholar] [CrossRef]
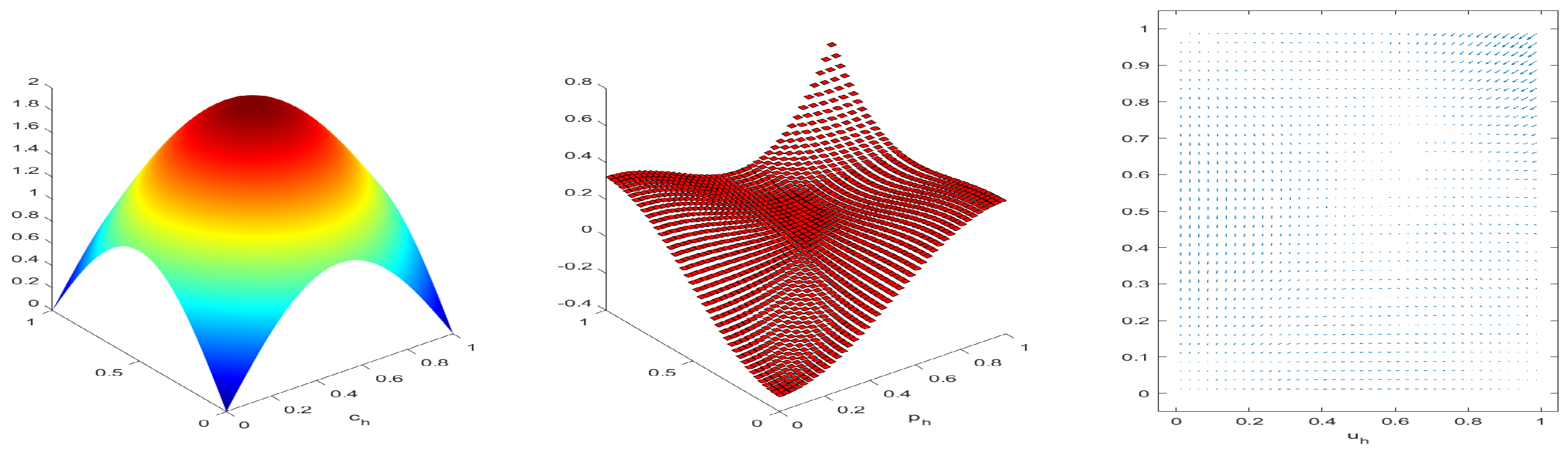

| Norm Type | ||||||||
| mesh | error | rate | error | rate | error | rate | error | rate |
| 5 | — | — | — | — | ||||
| 10 | 1.01 | 1.01 | 0.97 | 0.97 | ||||
| 20 | 0.98 | 0.98 | 0.99 | 0.99 | ||||
| 40 | 0.98 | 0.98 | 1.00 | 1.00 | ||||
| Norm Type | ||||||||
| mesh | error | rate | error | rate | error | rate | error | rate |
| 5 | — | — | — | — | ||||
| 10 | 1.00 | 0.99 | 1.97 | 1.99 | ||||
| 20 | 1.00 | 1.00 | 1.99 | 2.00 | ||||
| 40 | 1.00 | 1.00 | 2.00 | 2.00 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Guo, H.; Li, X.; Ren, Y. Multi-Point Flux MFE Decoupled Method for Compressible Miscible Displacement Problem. Processes 2023, 11, 1244. https://doi.org/10.3390/pr11041244
Xu W, Guo H, Li X, Ren Y. Multi-Point Flux MFE Decoupled Method for Compressible Miscible Displacement Problem. Processes. 2023; 11(4):1244. https://doi.org/10.3390/pr11041244
Chicago/Turabian StyleXu, Wenwen, Hong Guo, Xindong Li, and Yongqiang Ren. 2023. "Multi-Point Flux MFE Decoupled Method for Compressible Miscible Displacement Problem" Processes 11, no. 4: 1244. https://doi.org/10.3390/pr11041244
APA StyleXu, W., Guo, H., Li, X., & Ren, Y. (2023). Multi-Point Flux MFE Decoupled Method for Compressible Miscible Displacement Problem. Processes, 11(4), 1244. https://doi.org/10.3390/pr11041244








