1. Introduction
In order to ensure the safety of industrial production, alarm systems are essential to guarantee the safety and efficiency of operations. Alarms are audible or visual signals that alert operators to equipment failures, process deviations, and other abnormalities, thus preventing equipment damage or even production accidents. With the wide use of industrial control systems (ICSs), on the one hand, the cost of designing and configuring alarms has been reduced; on the other hand, the high degree of correlation and complexity between devices makes it possible for a single point of failure to lead to a failure in a related area or even failures in the whole plant, known as cascaded faults. At the same time, unreasonable alarm thresholds and the low performance of alarm management systems in ICSs pose challenges to the efficient operation of alarm systems [
1,
2], where alarm flooding is the most common and serious problem during the operation of industrial installations. According to EEMUA and ISA 18.2 standards, operators should not receive more than 6 alarms per hour, and alarm flooding is defined as more than 10 alarms per operator per 10 min [
3,
4]. During alarm floods, operators are unable to identify critical information from numerous alarms in a timely manner, resulting in the lack of effective actions to address critical exceptions, which affects product quality and increases production costs and poses a significant risk to process safety as well as personnel safety. For instance, 275 different alarms occurred in the 10.7 min prior to the 2005 hydrocarbon plant explosion at a Texas refinery in the United States [
5,
6]. The operators failed to detect an abnormality in the hydrocarbon fractionation level in its isomerization unit in time, leading to an explosion after the gas-phase component was discharged from the vent stack. Numerous industrial standards and accident analyses have shown that a scientific and reasonable alarm system is important to ensure the safety of industrial processes, to enhance production efficiency, and to guarantee the safety of employees.
Alarm floods have become a common phenomenon in the process industry and pose challenges for alarm systems. To date, extensive studies have been carried out to optimize alarm systems so as to alleviate the effects of alarm floods caused by chattering alarms or reduce the number of these alarm floods. Tulsya et al. [
7] designed a delayed alarm strategy for the desired and worst conditions based on minimizing the missed alarm rate and false alarm rate to ensure robustness to non-smooth industrial processes. Wang et al. [
8] proposed a method to design a dead bandwidth to suppress the number of chattering alarms and mitigate disturbances to the alarm system. Cheng et al. [
9] designed an optimal alarm filter to achieve the best alarm accuracy in the case of the given normal and abnormal statistical distributions.
In the process industry, the switching of some operating states and the propagation of cascaded faults usually generate related alarms. As part of alarm rationalization, alarm flood analysis has also attracted extensive research attention and has become a major branch in handling alarm floods. To date, some modified sequence alignment algorithms have been proposed for the pairwise matching of alarm flood sequences. In Ref. [
10], the similarity index between paired sequences was calculated using an improved Smith–Waterman algorithm (SWA) and clustered similar alarm sequences based on the similarity scores. Lai et al. [
11] proposed an improved basic local alignment search tool (BLAST) by combining the alarm priority information and timestamp. Simulation experiments showed that the improved BLAST has a smaller computational overhead compared to the modified SWA in [
10]. In Ref. [
12], a weighted sequential similarity approach is proposed to extract alarm sequence templates for given faults. Based on the extracted fault templates, an improved Needleman–Wunsch algorithm is proposed to isolate alarms caused by identified alarm patterns [
13].
Alarm flood analysis extracts alarm sequences from alarm logs and identifies alarm patterns based on the similarity indexes or the frequency of alarm occurrences. The extracted alarm patterns can be used in a root cause analysis [
14], alarm display and alarm response improvement [
15], or some advanced methods mentioned in the EEMUA, such as fault prediction, online alarm suppression, and so forth. However, extracting patterns from an alarm database with thousands of alarms is time-consuming and requires fairly accurate process knowledge [
16]. Fortunately, it is common that some events or abnormalities that occur frequently leave a trace in the A&E log. If such a repeated series of alarms can be detected from historical data, it can help to extract alarm patterns.
Although alarm flood analyses with sequence alignment algorithms were implemented in Refs. [
12,
13], these methods focus more on clustering similar alarm flood sequences rather than detecting frequent alarm patterns. The Apriori algorithm and its variants are major methods for extracting frequent patterns [
17]. However, these algorithms need to construct a large number of candidates as well as frequently scan the database to detect patterns, which results in unaffordable computational overhead when applied to industrial alarm databases. In order to reduce the computational cost, Zhou et al. [
18] proposed a modified CloFast algorithm to extract compact alarm patterns in industrial alarm floods.
PrefixSpan (Prefix-Projected Pattern Growth) is an efficient algorithm that generates smaller-sized item databases and provides faster computation [
19]. Niyazamand et al. [
20] proposed a modified PrefixSpan algorithm (M_PrefixSpan) to extract frequent patterns in alarm flood sequences. However, M_PrefixSpan is based on the premise that alarm sequences are sequential, and such a premise is difficult to satisfy in real industrial processes: related alarms occur almost simultaneously and in an uncertain order. When several alarm flood sequences occur with order ambiguities, M_PrefixSpan will sequentially extract alarms as prefixes for expansion. As a result, the frequency of some alarms may not meet the minimum support threshold, making it possible for critical alarms to be neglected, affecting the usability of the extracted patterns. Wang et al. [
21] reduced the computational cost of the PrefixSpan algorithm by applying an incremental mining strategy. However, it still fails to solve the problem of the sequence ambiguity of alarm sequences; at the same time, the existing algorithm outputs a large number of redundant alarm patterns, which makes it difficult for users to find representative alarm patterns.
Motivated by the problems described above, a compressed alarm pattern mining method based on the PrefixSpan algorithm (CAPM_PrefixSpan) is proposed to further facilitate the root cause analysis of the alarm flood.
The main contributions of this paper are as follows:
We propose a pre-matching mechanism based on the similarity scores of pairwise alarm sequences, which can effectively reduce the computational cost when dealing with numerous alarm data.
We modified the method of constructing the projection database in the PrefixSpan algorithm, which can help the algorithm avoid the problem of incomplete patterns due to sequence order ambiguity when mining frequent alarm patterns.
We propose a compression method to merge similar extracted alarm patterns so as to cluster and compress frequent alarm patterns into a compact alarm sequence, which prevents the output of cumbersome alarm patterns.
The rest of this paper is organized as follows.
Section 2 introduces the preliminaries of alarm systems and the PrefixSpan algorithm.
Section 3 presents the proposed CAPM_PrefixSpan algorithm. The effectiveness of CAPM_PrefixSpan is verified based on an industrial case in
Section 4. Finally, the conclusion is given in
Section 5.
2. Preliminaries and Problem Description
This section presents the problem of extracting alarm flood patterns from historical alarm data (A&E log) and describes the relevant definitions and algorithms.
2.1. Alarms and Alarm Floods
Alarms are generated when process variables exceed their predetermined thresholds and are stored as a set of structured texts in the Alarm and Event Log (A&E log). As shown in
Table 1, an alarm contains many attributes, typically including a tag name, an alarm identifier, time information, and an alarm priority [
22]. The tag name is the label corresponding to the alarm, and the alarm identifier denotes the alarm type; e.g., “PVHI” (process variable high) and “PVLO” (process variable low) indicate that an analog variable exceeds the high limit or the low limit of the threshold, respectively. The time label records the time that the alarm happens; the alarm priority indicates the importance of the alarm and is usually determined based on factors such as the consequences of ignoring the alarm and the maximum time allowed to deal with the alarm.
Therefore, in this paper, we represent an alarm with a tuple containing three attributes:
where
is the alarm label, which is a combination of the tag name and the identifier.
and
are the time label and the priority of the alarm, respectively. As a result, these three attributes can define an arbitrary unique alarm
in any alarm sequence
in the A&E log.
Based on the ANSI/ISA 18.2 definition of an alarm flood (more than ten alarms per operator per ten minutes), an alarm flood sequence can be expressed as Equation (2) shows.
where
is the length of the alarm flood sequence and satisfies
according to the definition.
is the alarm flood database, which is a collection of all the alarm flood sequences extracted from the A&E log.
2.2. Chattering Alarms
Chattering alarms are large and single alarm messages due to one alarm variable fluctuating around the alarm threshold over a short period of time. Due to the prevalence of noise and unreasonable alarm designs, chattering alarms are very common in the process industry and account for more than 80% of the total number of alarms [
23]. Chattering alarms are unable to convey interdependent pattern information between alarms and interfere with the extraction of frequent alarm patterns. Therefore, it is important to remove chattering alarms during the data pre-processing phase.
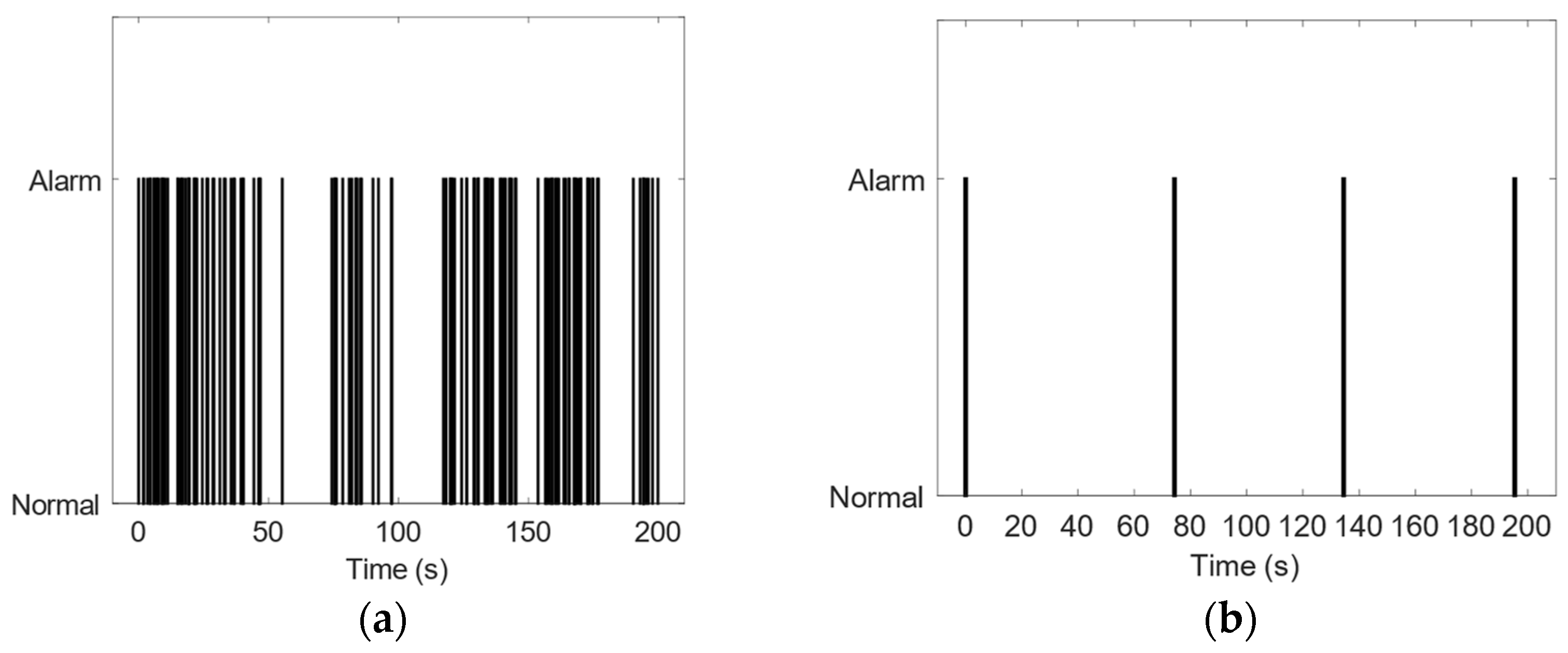
Clustering identical alarms into a single event can eliminate the influence of chattering alarms. We adopt a predefined time window to eliminate chattering alarms: when an alarm is generated, alarms with the same alarm label and the same alarm identifier for the subsequent duration of the alarm are ignored. After this processing, this method ensures that two identical alarms are separated by at least (s).
Figure 1a shows 135 alarms for diesel flow in the atmospheric and vacuum distillation units of the refinery, and
Figure 1b shows the processed alarms by setting the time window
= 120 s. Only four alarms are preserved for further alarm pattern analysis.
2.3. Mining Frequent Alarm Patterns with PrefixSpan
PrefixSpan is a variant of the FreeSpan algorithm, which continuously generates and mines smaller projection databases by recursive mining until all items are lower than the support threshold. In Ref. [
21], a modified PrefixSpan (M-PrefixSpan) is proposed for mining frequent alarm patterns. The relevant definitions of M_PrefixSpan are as follows:
Item: Each alarm label in the alarm flood sequence database. For example, the alarm label “PI251.PVLO” in
Table 1.
Item frequency (marked as ): The total number of alarm sequences in , which contains at least one alarm label.
Support threshold (marked as ): The minimum frequency of an item to be considered a candidate as a frequent item.
Prefix and suffix: Consider three alarm sequences , and with .Alarm sequence is called a prefix of if . The remaining sequence is called a suffix of with regards to prefix .
Projection database: The collection of suffixes for a given prefix in the alarm sequence database.
For instance,
Table 2 shows several alarm sequences from a steam generator in a diesel hydrogenation plant. By setting
, the steps of mining frequent alarm patterns with PrefixSpan are as follows:
Step 1: Scan the database and determine the frequency of each item (alarm) and its frequency: “FI702.PVHI-3”, “LI701.PVHI-3”, “TI702.PVLO-3”, “TI701.PVLO-3”, “TI311.PVLO-2”, “TI407.PVLO-3”, and “PI125.PVHI-1”. Since “PI125.PVHI” does not meet the support threshold , “PI125.PVHI” is excluded. Here, we use “FI702.PVHI” as an example of a prefix to expand its frequency pattern.
Step 2: Create a projection database with each prefix.
Step 3: Determine the frequencies of all suffixes associated with the prefix. The frequency of the suffix with regard to the prefix “FI702.PVHI” is shown in
Table 3.
Step 4: The frequencies of all items in
Table 3 are greater than the support threshold
. The new prefixes are updated to {FI702.PVHI, LI701.PVHI}, FI702.PVHI, TI701.PVLO}, {FI702.PVHI, TI311.PVLO}, and {FI702.PVHI, TI407.PVLO}.
Step 5: Repeat Step 2 to Step 5 until the support values of all items in the projection database are lower than the threshold .
Step 6: Remove alarm patterns that are subsets of other patterns. Finally, the frequent alarm patterns are {FI702.PVHI, LI701.PVHI, TI702.PVLO, TI407.PVLO}, {FI702.PVHI, LI701.PVHI, TI701.PVLO, TI407.PVLO}, {FI702.PVHI, LI701.PVHI, TI701.PVLO, TI702.PVLO}, and {FI702.PVHI, LI701.PVHI, TI311.PVLO, TI407.PVLO}.
2.4. Problem Description
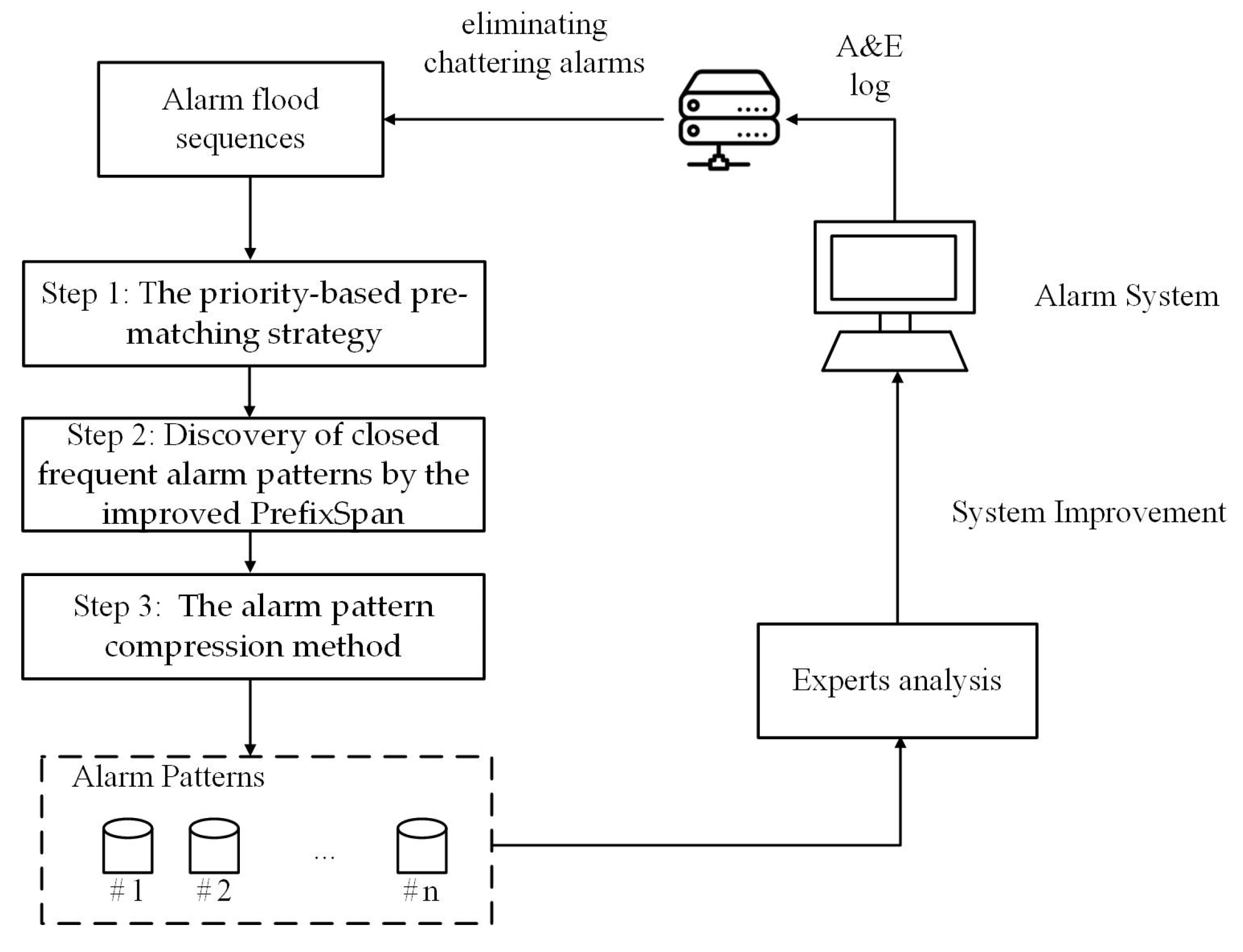
In summary, the major aim of this paper is to extract frequent alarm patterns from the A&E logs of industrial alarm systems. As shown in
Figure 2, after removing chattering alarms, the calculation for extracting alarm patterns from the alarm database
is conducted in the following three steps:
The priority-based pre-matching strategy is used to cluster similar alarm flood sequences so as to reduce the computational overhead.
Closed frequent alarm patterns are discovered to extract typical alarm patterns.
The alarm pattern is compressed to reduce the impact of cumbersome frequent alarm patterns.
The specific calculations and processes for the above steps are described in the following section.
3. Proposed Methods
In this section, we detail the three steps of CAPM_PrefixSpan for mining frequent alarm patterns, including the priority-based pre-matching strategy, the discovery of closed frequent alarm patterns, and the alarm pattern compression method.
3.1. The Priority-Based Pre-Matching Strategy
The pre-matching strategy utilizes the similarity index of alarm sequences or alarm attributes of alarm sequences to cluster similar alarm sequences and thus exclude irrelevant ones. As one of the important attributes of alarms, the alarm priority indicates the importance of the alarm. As shown in
Table 4, there are usually three or four alarm priorities established in industrial alarm systems. According to ISA 18.2, for alarm systems with three levels of alarm priorities, the recommended percentage for each alarm priority from “Low” to “Emergency” should be 80%, 15%, and 5%, respectively. High-priority alarms have a smaller percentage but indicate severe abnormal conditions; on the contrary, lower priorities are typically used to configure most of the less severe alarms. Thus, it is reasonable to cluster alarm flood sequences based on the co-occurrence of alarms with higher priorities.
In order to cluster similar alarm flood sequences in a given database, a binary matrix
is established with each element calculated by Equation (3):
where
represents the element in the i-th row and j-th column of matrix
,
is the similarity index between the i-th and j-th alarm sequences, and
is the threshold for matching similar sequences.
where
is the collection of all identical alarm labels between the i-th and j-th alarm sequences,
represents the length of set
, and
denotes the n-th alarm label in set
. The function
calculates the score based on the priority levels and can be expressed as Equation (5):
where
is the priority level of alarm
,
is the maximum priority level, and
is a positive constant. Therefore,
increases as the alarm priority increases. For instance, given an alarm system with three priority levels, “High”, “Medium”, and “Low”, the scores
are 2, 3.5, and 5, respectively.
Once the binary matrix is finished, alarm flood sequences with are clustered to segment the alarm flood database , denoted as .
In each group , any two sequences and share at least one instance of identical alarm labels. As a result, the algorithm avoids distractions from irrelevant alarm sequences. In the next step, frequent alarm patterns are discovered recursively for each group of alarm sequences by incorporating temporal information.
3.2. Discovering Closed Frequent Alarm Patterns
Definition 1: Alarm pattern is a frequent alarm pattern if the frequency . Notice that if is frequent, all subsets of are also frequent.
Definition 2: Alarm pattern is a closed alarm pattern iff:
- (1)
Alarm pattern is frequent.
- (2)
There is no frequent pattern , such that and .
The PrefixSpan algorithm builds the projection database by counting the frequency of each suffix corresponding to the prefix. In order to reduce interference from the order ambiguity problem in alarm flood sequences, we propose an improved projection database construction method by introducing the temporal information of the alarms.
Without loss of generality, for the arbitrary prefix
with the frequency
, assume that the suffix
has
alarm sequences containing the alarm tag
(
). Let
denote the time information of alarm
corresponding to prefix
, where
is an
column vector. Let
denote the final time of
alarm sequences with respect to prefix
. The time distance matrix
can be calculated by the following equation.
where
and
are the unit vector. The time span
is used to truncate the time distance matrix
, where
is a negative constant, so as to reduce the impact of sequence order ambiguity;
is the time window and a positive constant (usually set to 100 s), which is used to determine the causal relationship between the alarms. To truncate the time distance matrix
by the time span
according to Equation (7), we have
:
where
is an element in the time distance matrix.
indicates that alarm
occurs after prefix
within
seconds;
indicates that alarm
occurs within
seconds before prefix
. Therefore, the frequency of the alarm tag can be calculated as:
where
represents the total frequency of alarm tag
following prefix
. Then, alarm tag
and corresponding frequency
will be recorded in the projection database
. The Pseudocode for constructing the projection database is summarized in Algorithm 1.
If
, alarm tag
is integrated with the current corresponding prefix
to construct a new prefix,
. Further, the average time interval between
and
can be calculated as
and will also be recorded. The prefix extension is recursively performed until no more frequent alarm items can be found in the projection database. The major codes for building the projection database are summarized in Algorithm 1. Finally, a filter is adopted to remove all the subsets of frequent alarm patterns, rendering the final output of the CAPM_PrefixSpan a closed frequent alarm pattern. The main codes for discovering closed frequent alarm patterns are shown in Algorithm 2.
| Algorithm 1 Major codes for building projection database |
| 1 Input: , , |
| 2 Output: |
| 3 =The set of all alarm tags in the suffix with regard to prefix |
| 4 For each alarm tag in . |
| 5 = timestamp of in |
| 6 = timestamp of in |
| 7 Calculate time distance matrix according to Equation (6) |
| 8 = Truncate by time span according to Equation (7) |
| 9 =the frequency of alarm tag with respect to in |
| 10 Add {:} into |
| 11 End For |
| Algorithm 2 Major codes for discovering closed frequent alarm patterns in |
| 1 Input: , , |
| 2 Output: |
| 3 For each in |
| 4 Scan all alarm items in . |
| 5 Remove items with frequencies lower than . |
| 6 the remaining alarm items in . |
| 7 |
| 8 For Each in
|
| 9 = Projection database calculated by Algorithm 1 |
| 10 For each alarm tag in |
| 11 If |
| 12 Update by Assembling with |
| 13 End If |
| 14 End For |
| 15 End For |
| 16 While |
| 17 |
| 18 For each in |
| 19 = projection database with respect to by Algorithm 1 |
| 20 For each in |
| 21 If |
| 22 Update by Assembling with |
| 23 End If |
| 24 End For |
| 25 End For |
| 26 End While |
| 27 remove all subsets of |
| 28
|
| 29 End For |
3.3. Frequent Alarm Pattern Compression Method
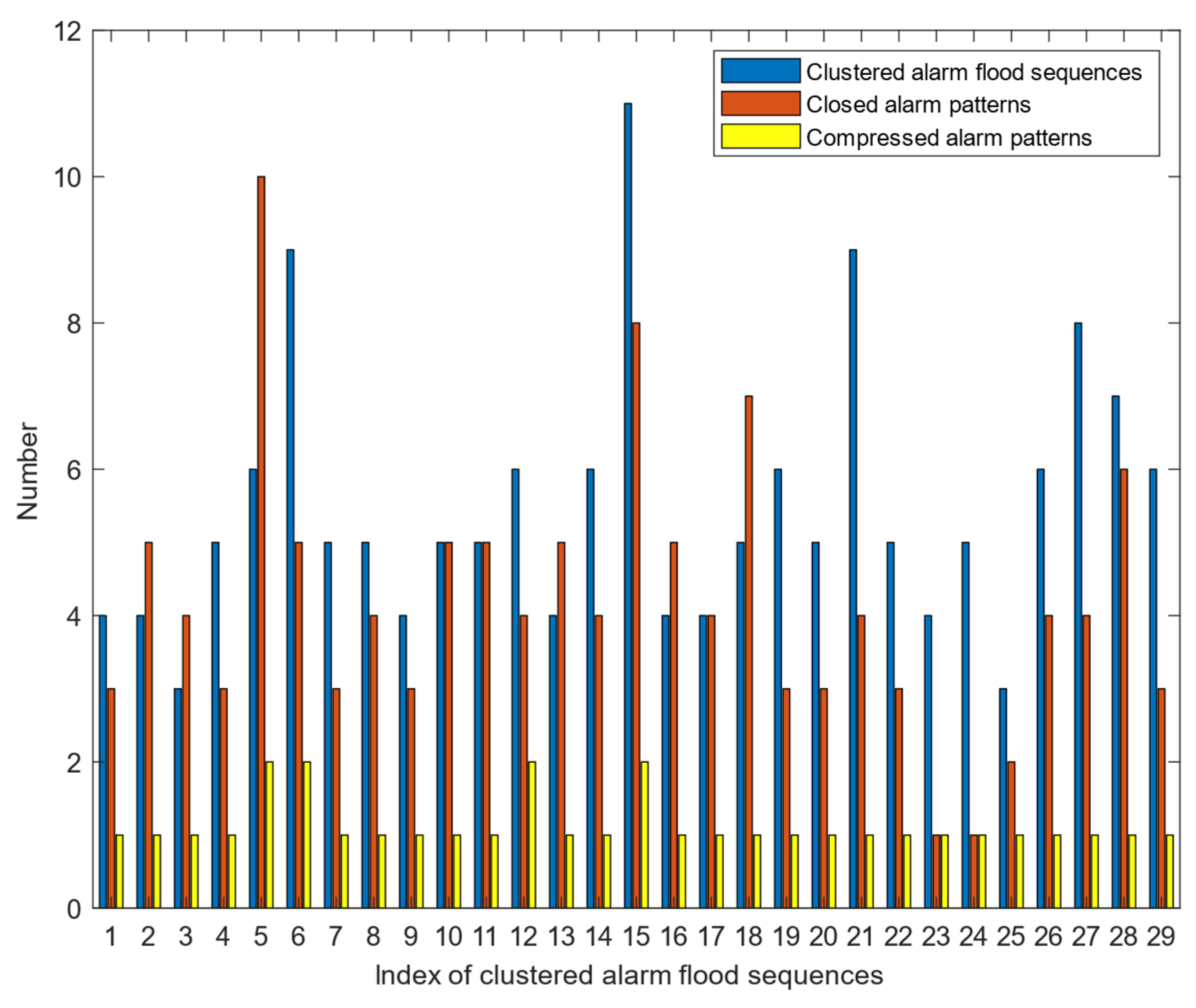
Even if similar alarm flood sequences are clustered by the pre-matching strategy proposed in
Section 3.1, the closed frequent alarm patterns extracted from
are still numerous and redundant. Therefore, the extracted frequent alarm patterns should be further compressed into representative alarm patterns.
For the given closed alarm pattern
extracted from
, a binary matrix
is created by calculating the pairwise similarity index between patterns
and
:
where
is the threshold for pattern compression, and
denotes an element of the i-the column and j-th row in matrix
. The function
calculates the similarity index between
and
. Since the closed alarm patterns extracted from the same collection
usually share identical alarm tags, the similarity index
is calculated based on the optimal alignment of the optimal segment pairs of two alarm patterns. As a result, the Smith–Waterman algorithm is utilized to calculate
as Equation (10) shows.
where
is the similarity index of the segmented pair
. In order to find the best local alignment between
and
, the SW algorithm recursively calculates an index matrix
:
where
is an element of the matrix, and
is the gap penalty. For any
and
,
and
since one or both of the segments of
and
are empty.
is the similarity score function, as Equation (12) shows:
Based on Equation (11), matrix H and the similarity index
can be worked out. Following this, by calculating all alarm patterns in
, the matrix
can be obtained. By clustering the alarm patterns with
, similar closed alarm pattern collections can be recognized for further compression. These collections can be expressed as:
where
is the clustered alarm pattern, and
is the index of the extracted alarm pattern in
.
Finally, the compressed alarm pattern
is distilled from each
in according to Equation (14):
where the operator
indicates the combination of elements in the clustered frequent alarm patterns based on their corresponding average timestamp. The Pseudocode of the frequent alarm pattern compression method is shown in Algorithm 3.
| Algorithm 3 Major codes for compressing alarm patterns in |
| 1 Input: , |
| 2 Output: |
| 3 For each in |
| 4 For i = 1: Length() |
| 5 For j = 1: Length() |
| 6 Calculate the index matrix between and based on Equation (11) |
| 7 Calculate similarity index |
| 8 If |
| 9 |
| 10 Else: |
| 11 |
| 12 End If |
| 13 End For |
| 14 End For |
| 15 Cluster the closed frequent alarm patterns with |
| 16 = the collection of the clustered alarm patterns |
| 17 = compress the alarm patterns in each according to Equation (14) |
| 18 Add into |
| 19 End For |
3.4. Implementation Procedure
The major steps for mining frequent alarm patterns by CAPM_PrefixSpan are summarized in Algorithm 4, where is the alarm flood sequences, are the predefined parameters, and denotes the set of compressed closed alarm patterns. The detailed steps are as follows:
Step 1. Remove chattering alarms by using the time window .
Step 2. Calculate the similarity score of all alarm flood sequences in based on Equation (4) and cluster similar alarm sequences according to Equation (3).
Step 3. Extract closed frequent alarm patterns recursively from the set according to Algorithm 2.
Step 4. Compress the extracted alarm patterns for each collection in
according to Algorithm 3.
| Algorithm 4 Mining closed frequent alarm patterns in |
| 1 Input: , , , , , |
| 2 Output: |
| 3 Remove chattering alarms in . |
| 4 Divide into by using the priority-based pre-matching strategy. |
| 5 For each pattern in in |
| 6 Mining closed frequent alarm patterns according to Algorithm 2 |
| 7 End for |
| 8 Compress the alarm patterns into according to Algorithm 3 |
In the CAPM_PrefixSpan algorithm, several important parameters are involved, including the time window , pre-matching threshold , time span , compress threshold , and minimum support threshold . For the easier implementation of the algorithm for practitioners, the following guidelines can be considered when selecting the parameters of CAPM_PrefixSpan.
In the data processing step,
specifies the minimum time interval between two identical alarm tags. By default,
to filter chattering alarms is widely used in practice [
20].
In the pre-matching stage, specifies the minimum similarity score for the pre-matching strategy. For the alarm system with three levels of priorities, is set because ISA 18.2 considers an alarm flood to be over when the alarm rate is less than five alarms in 10 min; in addition, ISA 18.2 suggests that 80 percent of the alarms should be designated “Low” priority alarms, which have a similarity score of 2 according to Equation (5).
In the closed frequent alarm pattern discovery stage, specifies the minimum occurrence frequency for considering an alarm to be a frequent alarm in the analyzed alarm floods. By default, is set to capture all repeated alarms. specifies the tolerance of order ambiguity in the alarm flood sequences. By default, is set as the tolerance of short-term order ambiguity to discover casualty alarms.
In the alarm pattern compression stage, specifies the threshold for merging similar alarm patterns. The value of can be determined based on user requirements.
5. Conclusions
In the process industry, alarm sequences caused by the same propagation path share different forms because of noise and the randomness of detection delays. In order to facilitate alarm pattern extraction as well as improve alarm systems, an alarm pattern extraction method is proposed, which consists of three main stages: the pre-matching strategy based on alarm priority, the improved PrefixSpan algorithm, and the alarm pattern compression method. To verify the effectiveness of the proposed method, an industrial case study was carried out with alarm data from a complex facility of a refinery. The experimental results show that CAPM_PrefixSpan improves the efficiency of alarm pattern recognition by introducing alarm timestamp information and tolerating short-term order ambiguity. In addition, the effectiveness of the compressed alarm patterns was verified by an expert evaluation.
However, alarm pattern mining based on historical data can only extract alarm patterns from abnormalities that have occurred. Furthermore, as the proposed algorithm is based on the number of occurrences of alarm tags in a particular DCS system, the extracted alarm patterns are still not universal across the same processes at different facilities. Therefore, future work will focus on investigating generalized alarm pattern mining methods.