Disturbing Effect of Intra-Tissue Temperature Sensors in Pre-Clinical Experimental Studies of Radiofrequency Cardiac Ablation: A Computer-Based Modeling Study
Abstract
1. Introduction
2. Methods
2.1. Model Geometry
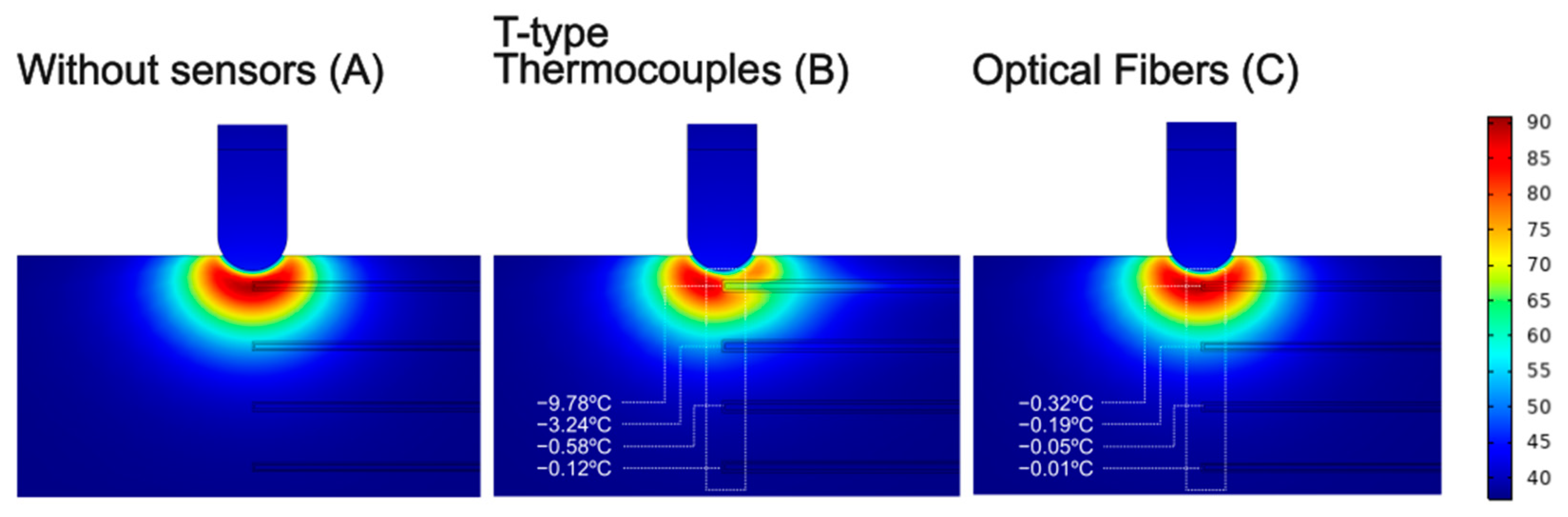
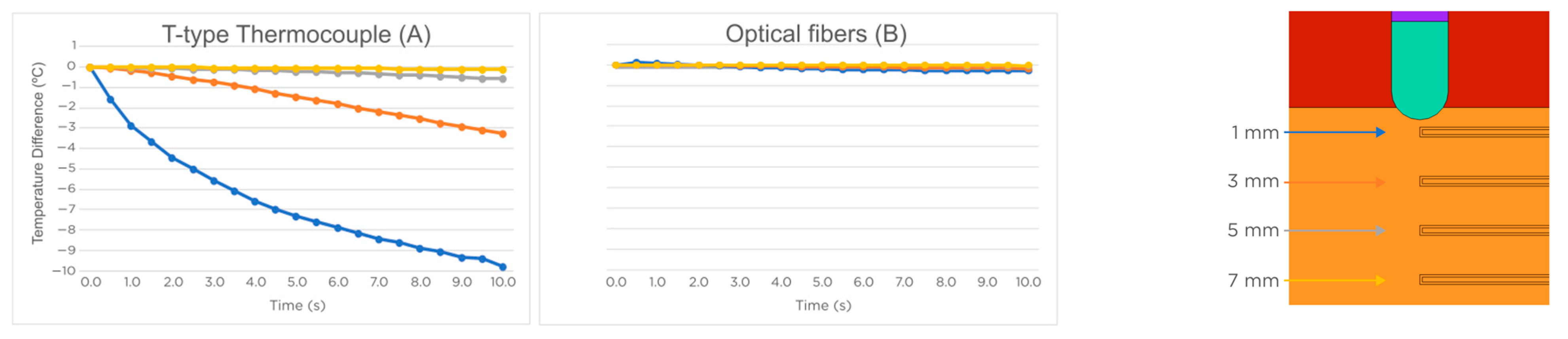
2.2. Modeling of Temperature Sensors
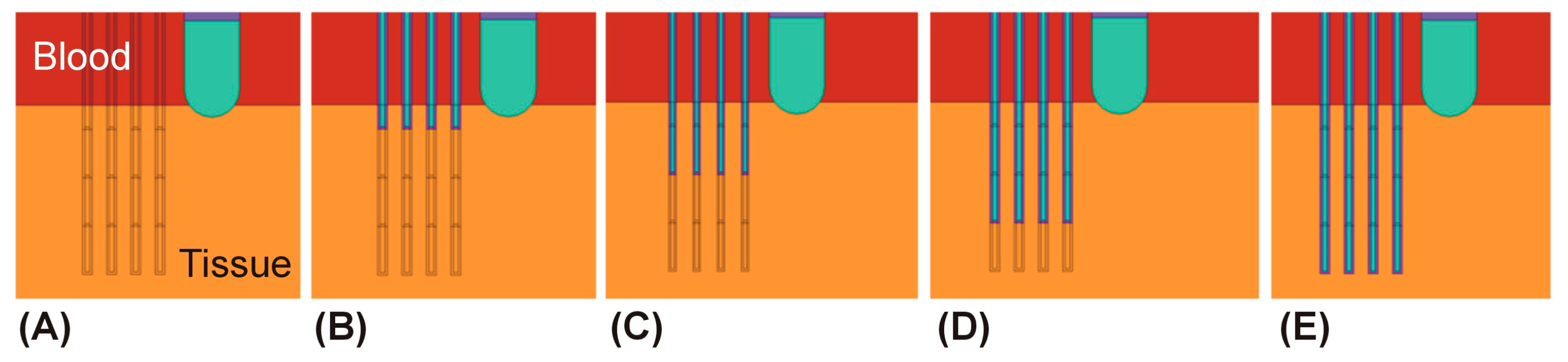
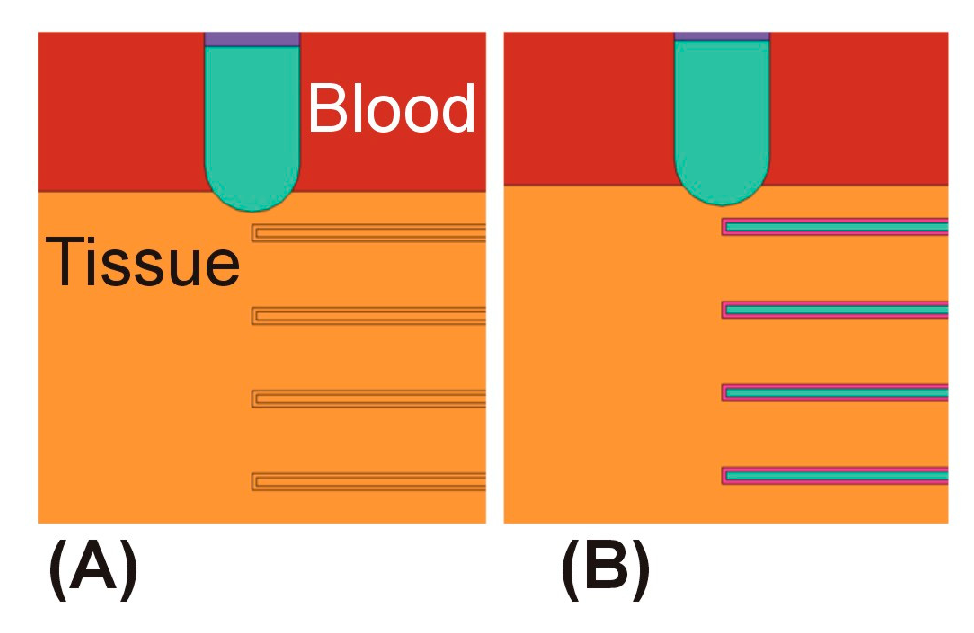
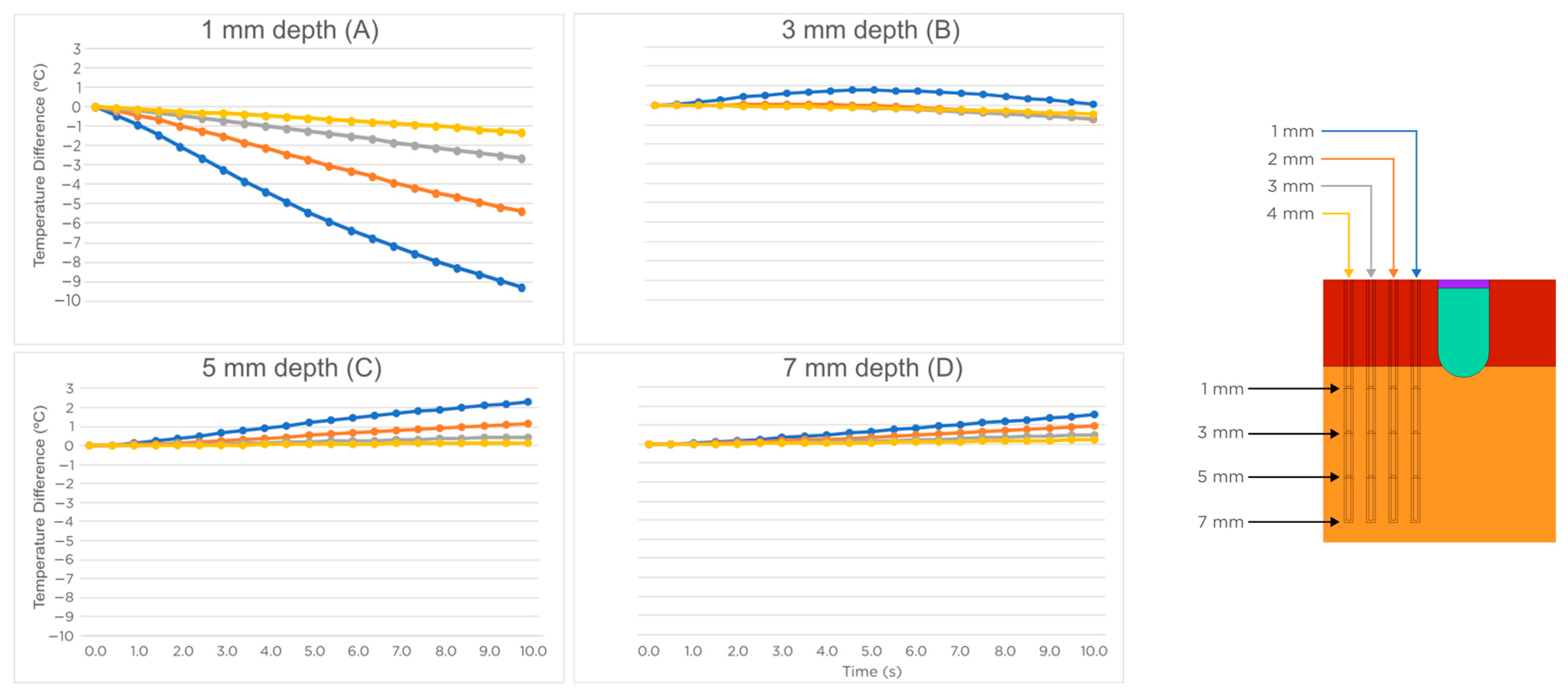
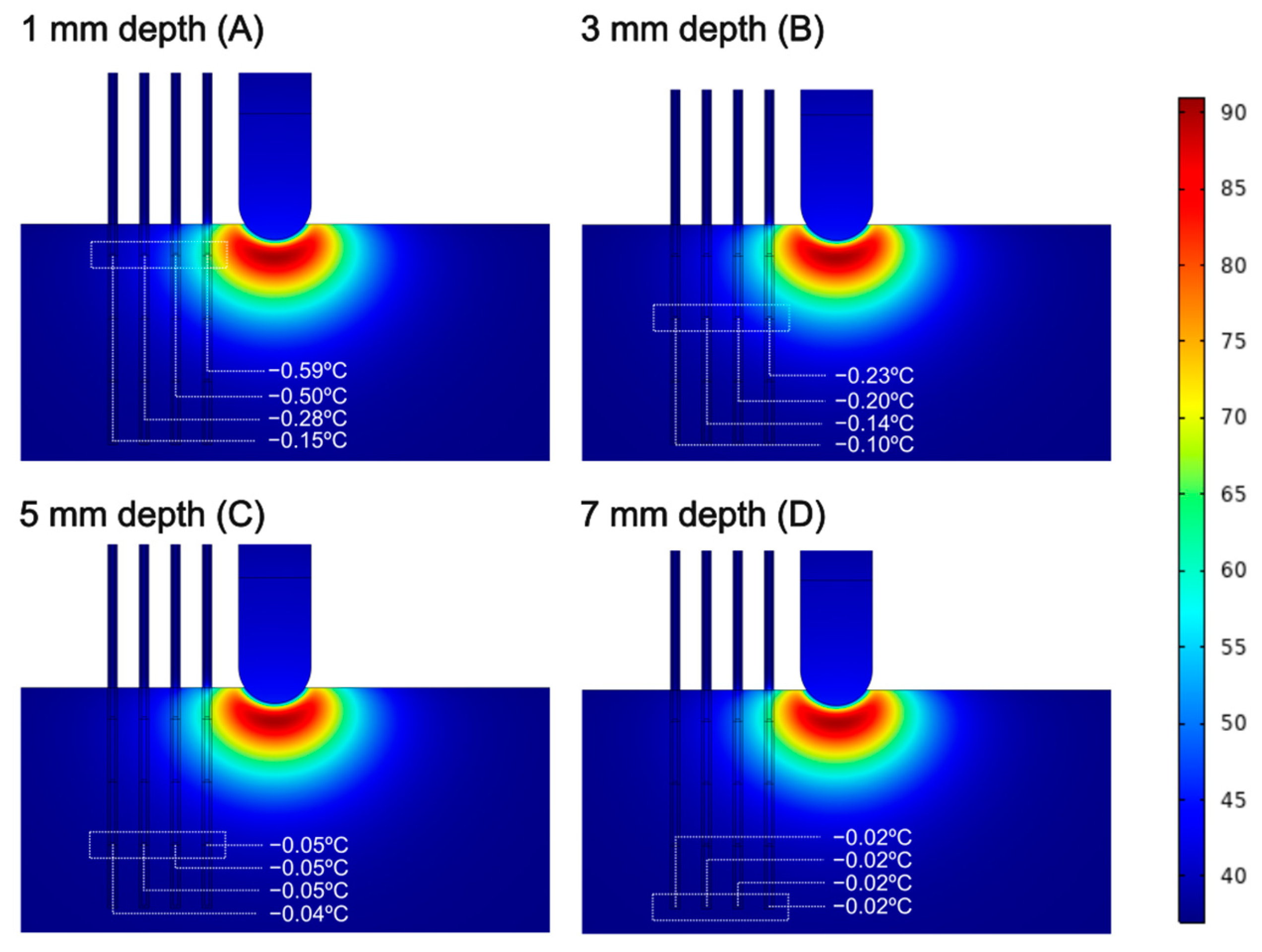
2.3. Spatial Arrangement of the Temperature Sensors
2.4. Properties of Materials and Tissues
2.5. Model Verification
2.6. Governing Equations and Boundary Conditions
3. Results
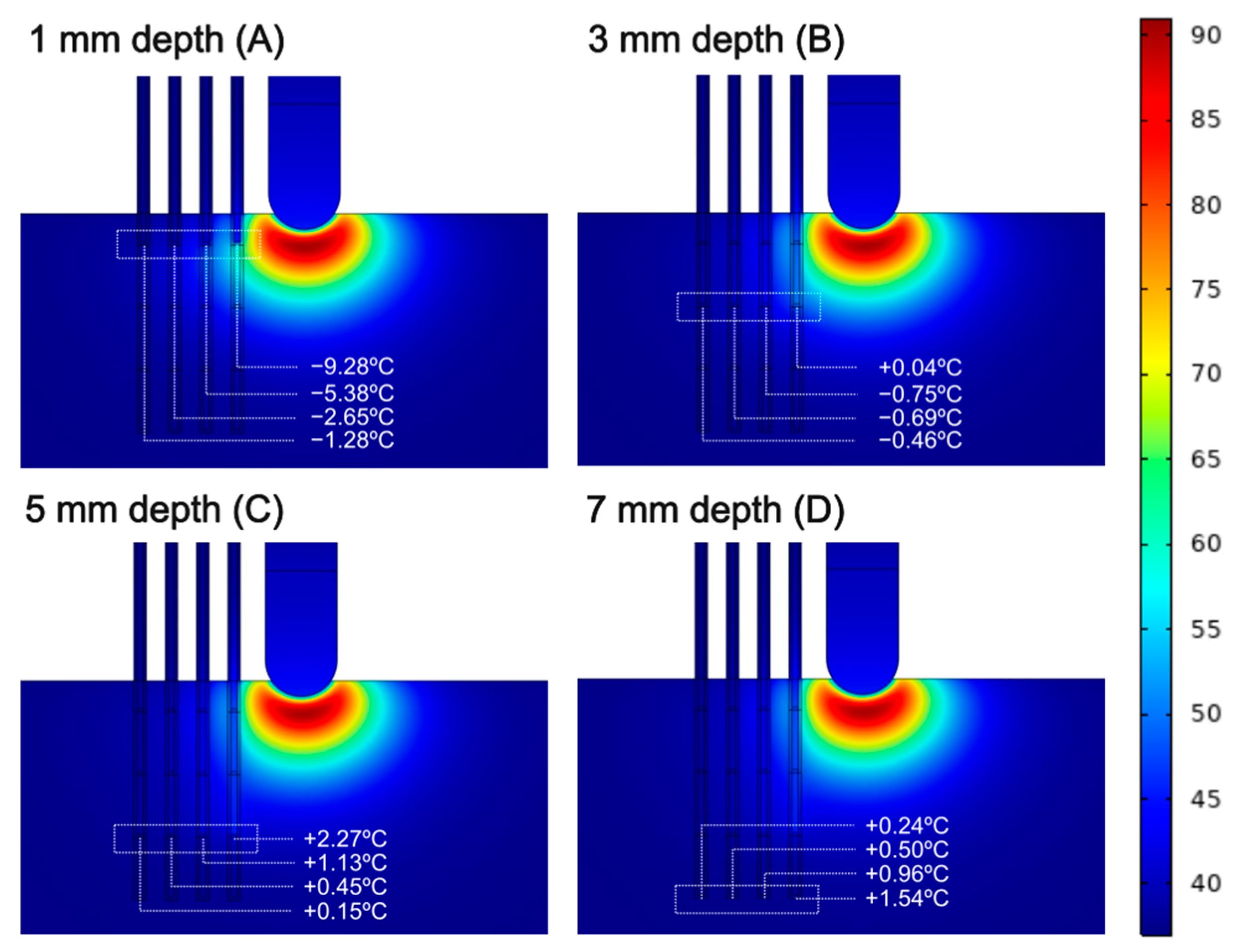
3.1. Sensors Parallel to the Ablation Catheter Axis
3.2. Temperature Sensors Perpendicular to the Ablation Catheter Axis
4. Discussion
4.1. Main Findings
4.2. Practical Implications
4.3. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- González-Suárez, A.; Pérez, J.J.; Irastorza, R.M.; D’Avila, A.; Berjano, E. Computer modeling of radiofrequency cardiac ablation: 30 years of bioengineering research. Comput. Methods Programs Biomed. 2022, 214, 106546. [Google Scholar] [CrossRef] [PubMed]
- Hsu, S.S.; Hoh, L.; Rosenbaum, R.M.; Rosen, A.; Walinsky, P.; Greenspon, A.J. A method for the in vitro testing of cardiac ablation catheters. IEEE Trans. Microw. Theory Tech. 1996, 44, 1841–1847. [Google Scholar] [CrossRef]
- Rossmann, C.; Motamarry, A.; Panescu, D.; Haemmerich, D. Computer simulations of an irrigated radiofrequency cardiac ablation catheter and experimental validation by infrared imaging. Int. J. Hyperth. 2021, 38, 1149–1163. [Google Scholar] [CrossRef] [PubMed]
- Demazumder, D.; Mirotznik, M.S.; Schwartzman, D. Comparison of irrigated electrode designs for radiofrequency ablation of myocardium. J. Interv. Card. Electrophysiol. 2001, 5, 391–400. [Google Scholar] [CrossRef] [PubMed]
- Petersen, H.H.; Chen, X.; Pietersen, A.; Svendsen, J.H.; Haunsø, S. Tissue temperatures and lesion size during irrigated tip catheter radiofrequency ablation: An in vitro comparison of temperature-controlled irrigated tip ablation, power-controlled irrigated tip ablation, and standard temperature-controlled ablation. Pacing Clin. Electrophysiol. 2000, 23, 8–17. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, H.; Ikeda, A.; Sharma, T.; Govari, A.; Ashton, J.; Maffre, J.; Lifshitz, A.; Fuimaono, K.; Yokoyama, K.; Wittkampf, F.H.M.; et al. Comparison of in vivo Tissue Temperature Profile and Lesion Geometry for Radiofrequency Ablation with High Power-Short Duration and Moderate Power-Moderate Duration: Effects of Thermal Latency and Contact Force on Lesion Formation. Circ. Arrhythm. Electrophysiol. 2021, 14, e009899. [Google Scholar] [CrossRef] [PubMed]
- Kovoor, P.; Daly, M.P.; Pouliopoulos, J.; Byth, K.; Dewsnap, B.I.; Eipper, V.E.; Yung, T.; Uther, J.F.; Ross, D.L. Comparison of radiofrequency ablation in normal versus scarred myocardium. J. Cardiovasc. Electrophysiol. 2006, 17, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Pérez, J.J.; Gonzalez-Suárez, A.; Maher, T.; Nakagawa, H.; D’Avila, A.; Berjano, E. Relationship between luminal esophageal temperature and volume of esophageal injury during RF ablation: In silico study comparing low power-moderate duration vs. high power-short duration. J. Cardiovasc. Electrophysiol. 2022, 33, 220–230. [Google Scholar] [CrossRef] [PubMed]
- Irastorza, R.M.; Gonzalez-Suarez, A.; Pérez, J.J.; Berjano, E. Differences in applied electrical power between full thorax models and limited-domain models for RF cardiac ablation. Int. J. Hyperth. 2020, 37, 677–687. [Google Scholar] [CrossRef] [PubMed]
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues, Version 4.1; IT’IS Foundation: Zürich, Switzerland, 2022; Available online: https://itis.swiss/virtual-population/tissue-properties/overview/ (accessed on 5 January 2023). [CrossRef]
- Pérez, J.J.; Ewertowska, E.; Berjano, E. Computer modeling for radiofrequency bipolar ablation inside ducts and vessels: Relation between pullback speed and impedance progress. Lasers Surg. Med. 2020, 52, 897–906. [Google Scholar] [CrossRef] [PubMed]
- Material Property Database. Available online: www.matweb.com (accessed on 5 January 2023).
- Suárez, A.G.; Hornero, F.; Berjano, E.J. Mathematical modeling of epicardial RF ablation of atrial tissue with overlying epicardial fat. Open Biomed. Eng. J. 2010, 4, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Zaltieri, M.; Massaroni, C.; Cauti, F.M.; Schena, E. Techniques for Temperature Monitoring of Myocardial Tissue Undergoing Radiofrequency Ablation Treatments: An Overview. Sensors 2021, 21, 1453. [Google Scholar] [CrossRef] [PubMed]
- Dunscombe, P.B.; Constable, R.T.; McLellan, J. Minimizing the self-heating artefacts due to the microwave irradiation of thermocouples. Int. J. Hyperth. 1988, 4, 437–445. [Google Scholar] [CrossRef] [PubMed]
- Kaatee, R.S.; Crezee, H.; Visser, A.G. Temperature measurement errors with thermocouples inside 27 MHz current source interstitial hyperthermia applicators. Phys. Med. Biol. 1999, 44, 1499–1511. [Google Scholar] [CrossRef] [PubMed]
- Song, C.W.; Rhee, J.G.; Lee, C.K.; Levitt, S.H. Capacitive heating of phantom and human tumors with an 8 MHz radiofrequency applicator (Thermotron RF-8). Int. J. Radiat. Oncol. Biol. Phys. 1986, 12, 365–372. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.P.; Brezovich, I. Error sources affecting thermocouple thermometry in RF electromagnetic fields. J. Microw. Power. 1982, 17, 17–28. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.P.; Brezovich, I. A source of thermocouple error in radiofrequency electric fields. Electron. Lett. 1980, 16, 853–854. [Google Scholar] [CrossRef]





| Element/Material | σ (S/m) | k (W/m·K) | ρ (kg/m3) | c (J/kg·K) |
|---|---|---|---|---|
| Electrode/Pt-Ir | 4.6 × 106 | 71 | 21,500 | 132 |
| Catheter/Polyurethane | 10−5 | 23 | 1440 | 1050 |
| Cardiac Chamber/Blood | 0.748 | -- | -- | -- |
| Myocardium | 0.541 | 0.56 | 1081 | 3686 |
| Optical fiber/Optical fused quartz | 5 × 10−9 | 2 | 2210 | 750 |
| Coating of optical fiber/Polyimide | 1 × 10−8 | 0.12 | 1440 | 1090 |
| T-type thermocouple/Copper-constant | 3.03 × 107 | 206.4 | 8915 | 389 |
| Coating of thermocouple/Teflon | 1 × 10−16 | 0.3 | 2162 | 1350 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuenca-Dacal, L.; Berjano, E.; González-Suárez, A.; Pérez, J.J. Disturbing Effect of Intra-Tissue Temperature Sensors in Pre-Clinical Experimental Studies of Radiofrequency Cardiac Ablation: A Computer-Based Modeling Study. Processes 2023, 11, 1168. https://doi.org/10.3390/pr11041168
Cuenca-Dacal L, Berjano E, González-Suárez A, Pérez JJ. Disturbing Effect of Intra-Tissue Temperature Sensors in Pre-Clinical Experimental Studies of Radiofrequency Cardiac Ablation: A Computer-Based Modeling Study. Processes. 2023; 11(4):1168. https://doi.org/10.3390/pr11041168
Chicago/Turabian StyleCuenca-Dacal, Luis, Enrique Berjano, Ana González-Suárez, and Juan J. Pérez. 2023. "Disturbing Effect of Intra-Tissue Temperature Sensors in Pre-Clinical Experimental Studies of Radiofrequency Cardiac Ablation: A Computer-Based Modeling Study" Processes 11, no. 4: 1168. https://doi.org/10.3390/pr11041168
APA StyleCuenca-Dacal, L., Berjano, E., González-Suárez, A., & Pérez, J. J. (2023). Disturbing Effect of Intra-Tissue Temperature Sensors in Pre-Clinical Experimental Studies of Radiofrequency Cardiac Ablation: A Computer-Based Modeling Study. Processes, 11(4), 1168. https://doi.org/10.3390/pr11041168









