Multi-Objective Multi-Stage Optimize Scheduling Algorithm for Nonlinear Virtual Work-Flow Based on Pareto
Abstract
1. Introduction
2. Related Work
3. Problem Description
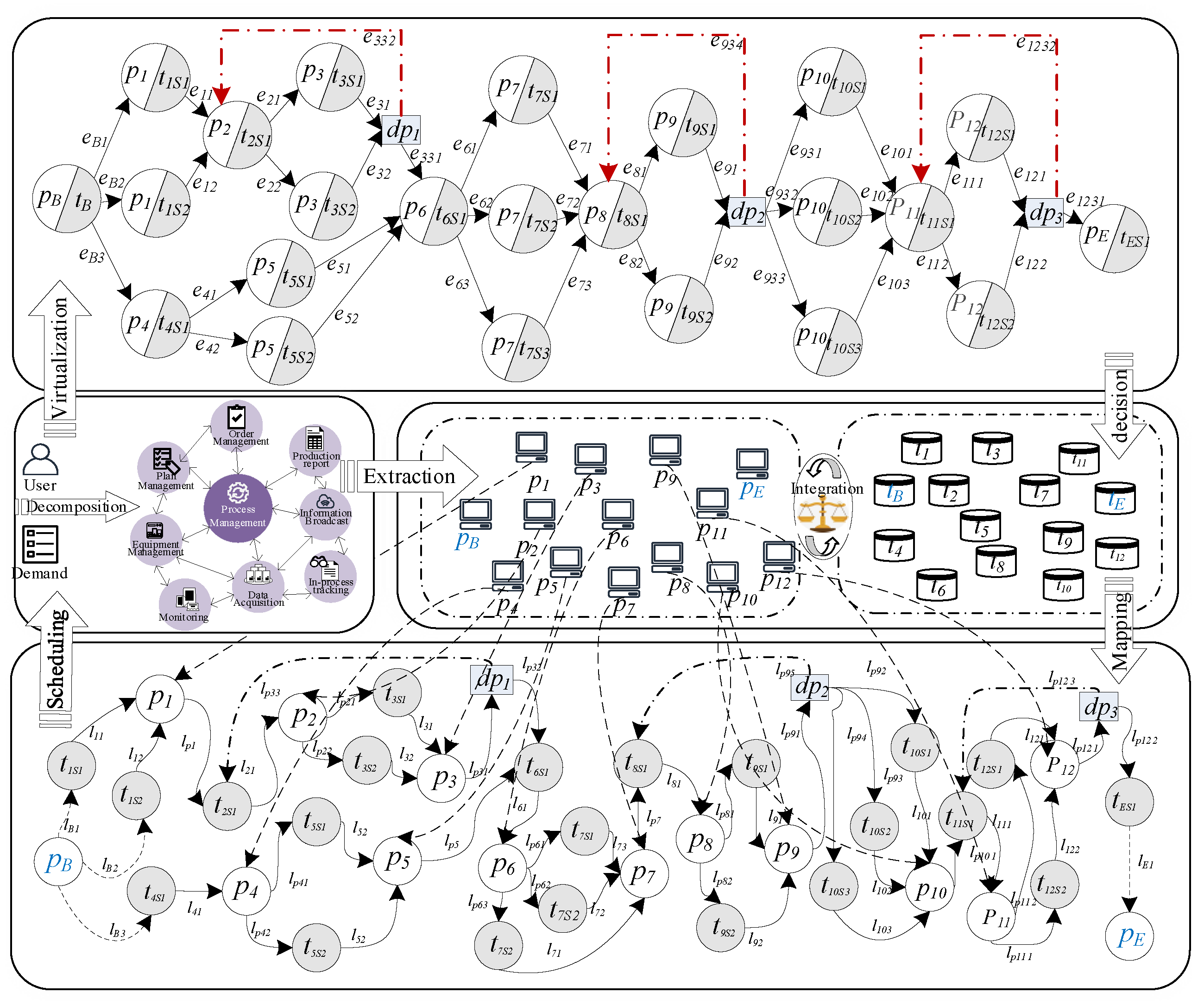
3.1. Work-Flow Definitions
3.2. Nonlinear Virtual Work-Flow Model VWF Generation Algorithm
- Step 1
- Abstract the production as the process node set P and T, the optional resources corresponding to the conversion form as resource set S, and the partial order relationship of each process node as directed edge set L to construct the original work-flow model W.
- Step 2
- Add the set of detection nodes DP and the virtual nodes PB and PE to the work-flow model W and update the set of directed edges L.
- Step 3
- Input process nodes with od or id greater than 1 into the Queue, except for the feedback predecessor structure.
- Step 4
- Output the process node pj with od > 1 in Queue, find the nearest feedback in-degree process node pi, and delete all process nodes between pi and pj from the queue.
- Step 5
- Reconstruct all process nodes between nodes pi and pj, save node pi′ temporarily to the virtual process node set P′, reconstruct the transfer nodes involved in this process as virtual transfer nodes, and save them to the virtual transfer node set T′.
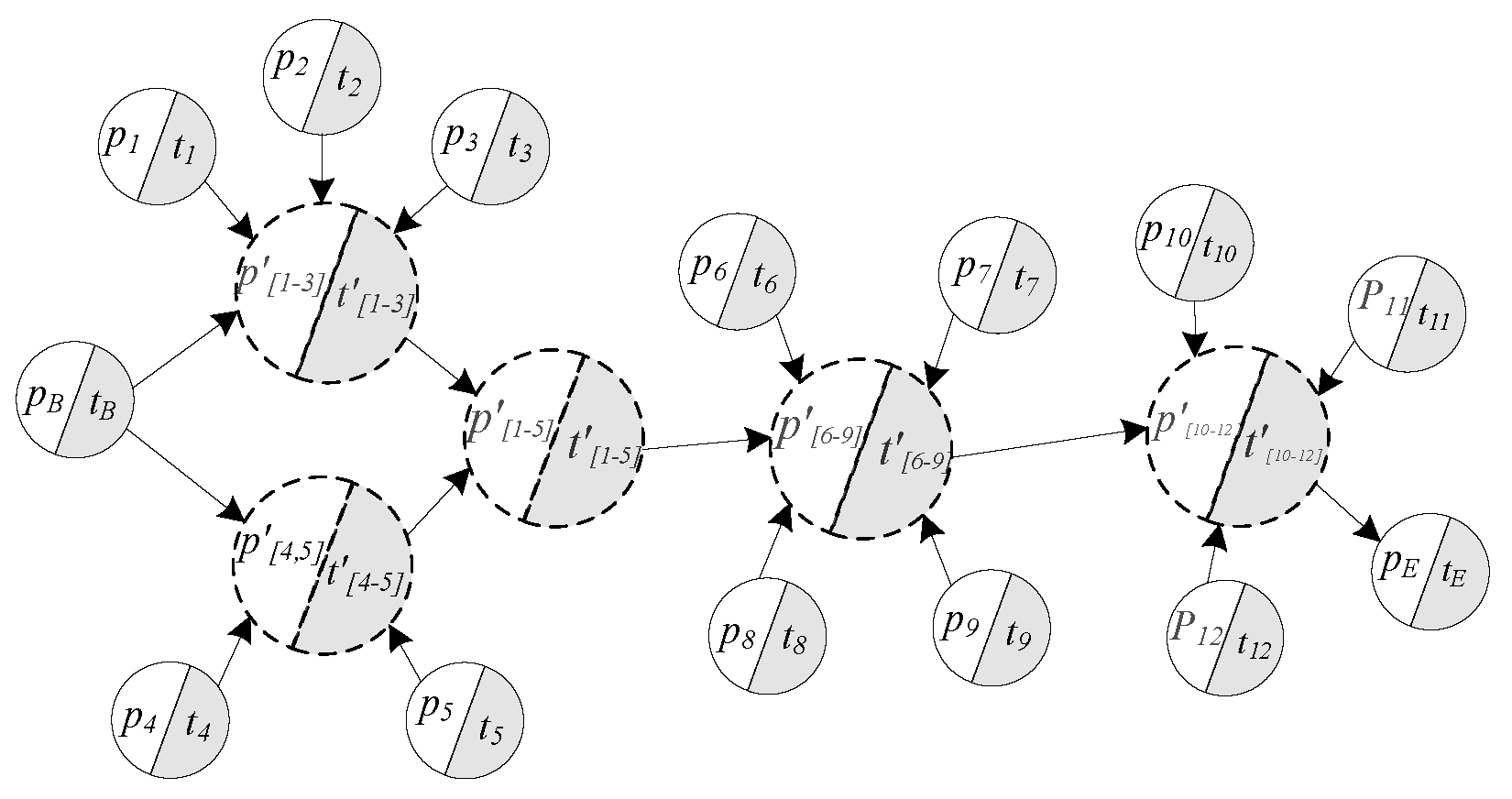
- Step 6
- Iterate virtual process node pi′ in the set P′ and determine whether there is an SDP generated due to virtual reconstruction. If so, divide the virtual process node pi′ and the virtual transfer node ti′ and restore the process nodes and transfer nodes that constitute the virtual node. Otherwise, delete the pi′ and ti′, repeat until the set P′ or T′ is empty, and then output the VW.
- Step 7
- Traverse model VW; count all paths from adjacent process node pi to pj(pi ≠ pj); establish directed edge ejk, where k = 1, 2,…, idpj; calculate the parameters hjk, cjk and qjk of directed edge ejk; and mark these parameters to form a virtual work-flow diagram VG.
3.3. Virtual Work-Flow Example
4. Multi-Objective Nonlinear Virtual Work-Flow Staged Scheduling Algorithm Based on Pareto Optimization
- Step 1
- Invoke the modeling algorithm VWF to process each parameter of the nonlinear manufacturing process and form a nonlinear virtual work-flow model.
- Step 2
- Combine the manufacturing expectations ME and manufacturing characteristics to reverse the work-flow hierarchy, mark the last node of each layer, traverse backwards to the virtual node PB, and analyze and calculate the task interval TFi of each process node pi formed by each layer using Equation (1).
- Step 3
- Compute and mark the ƒw(E0,hE0) and ƒc(E0,hE0) of the process node E0 of the ending layer at each moment within its active interval TFi using Equation (4).
- Step 4
- Traverse the process nodes set P and determine whether there is an SDP. If not, then process the nodes at each stage, combine the process nodes on the serial path as virtual nodes pi, use Equation (4) to calculate the ƒq(pi,hpi) and ƒc(pi,hpi) available to the virtual node at each moment in its execution domain, and record the local feasible solution path. If it exists, however, turn to Step 5.
- Step 5
- If SDP exists, first calculate the execution domain θ of SDP using Equation (2), then calculate ƒq(pi,hpi) and ƒc(pi,hpi) available at different moments for each process node in this domain using Equation (4), and record the local feasible solution path.
- Step 6
- If the cumulative production parameters fail to meet the requirements when executed to detect node dp, a feedback correction is made, and the scheduling results are adjusted according to the dp, and some scheduling strategies are eliminated.
- Step 7
- Using Equation (3) with manufacturing expectation ME as a constraint, fully process the set of marked model process nodes P and deposit the feasible scheduling sequence into the Pareto solution set X according to the stage accumulation rule.
- Step 8
- Determine the dominance relationship based on the manufacturing attributes of each scheduling sequence in the Pareto solution set X and output the optimal scheduling route x*.
5. Algorithm Analysis
5.1. Experimental Environment and Data
5.2. Model Optimization Process
- ƒq(p3,5) = max{0.97} = 0.970; ƒc(p3,5) = 0.3;
- ƒq(p3,4) = max{0.97} = 0.970; ƒc(p3,4) = 0.5;
- ƒq(p3,3) = max{0.97,0.99} = 0.990; ƒc(p3,3) = 0.5.
- ƒq(p2,4) = max{0.98 × ƒq(p3,5)} = 0.951; ƒc(p2,4) = 1.2;
- ƒq(p2,3) = max{0.98 × ƒq(p3,4)} = 0.970; ƒc(p2,26) = 1.2;
- ƒq(p2,2) = max{0.98 × ƒq(p3,3)} = 0.970; ƒc(p2,25) = 1.2.
- ƒq(p1,2) = max{0.94 × ƒq(p2,4)} = 0.894; ƒc(p1,2) = 0.2;
- ƒq(p1,1) = max{0.94 × ƒq(p2,3),0.96׃q (p2,4)} = 0.913; ƒc(p1,1) = 0.3;
- ƒq(p1,0) = max{0.94 × ƒq(p2,2),0.96׃q (p2,3)} = 0.931; ƒc(p1,0) = 0.3.
6. Algorithm Process and Results Analysis
6.1. VWFA Reconstruction Process
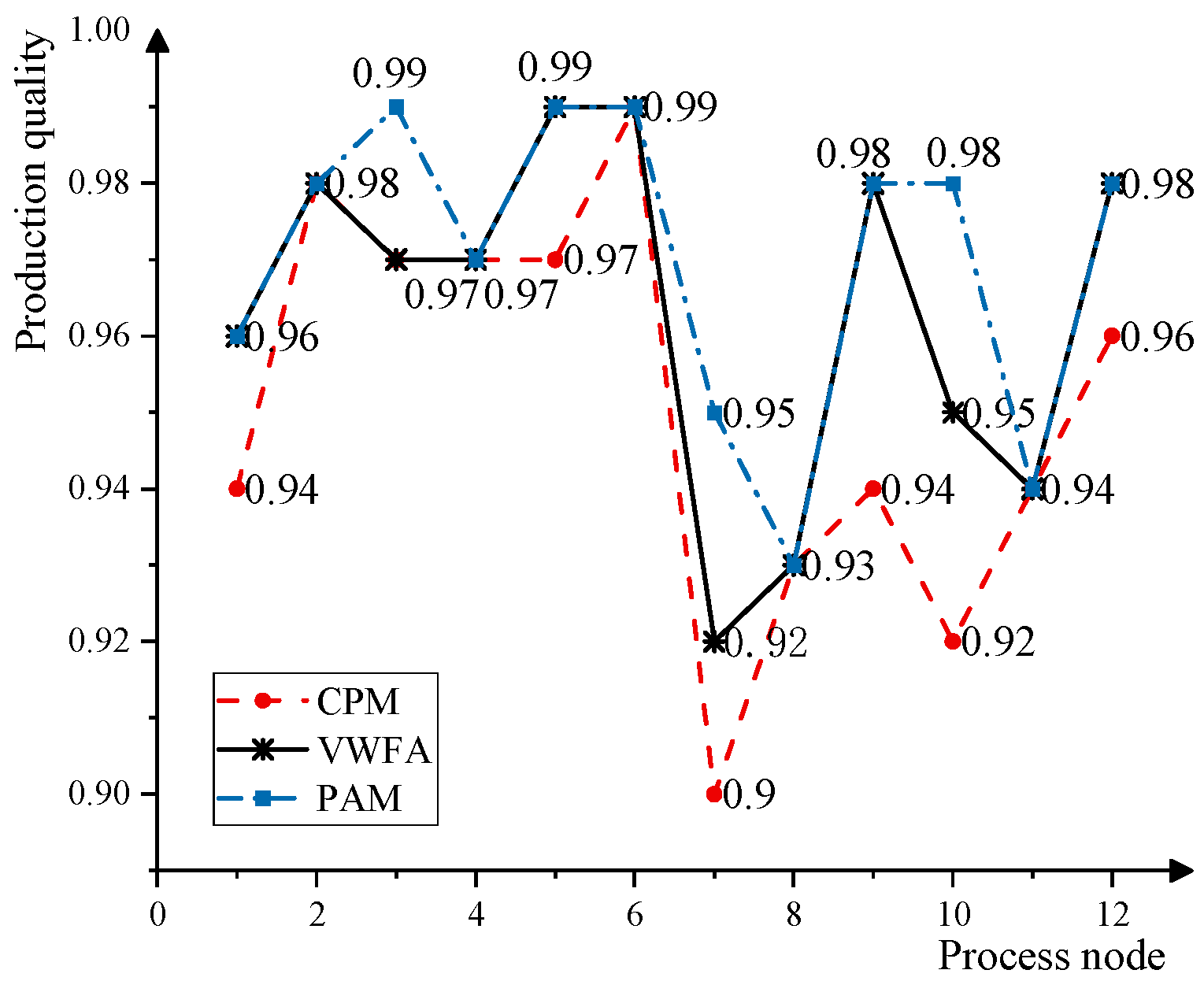
6.2. Results Analyses
7. Impact of Other Parameters on the Performance of VWFA
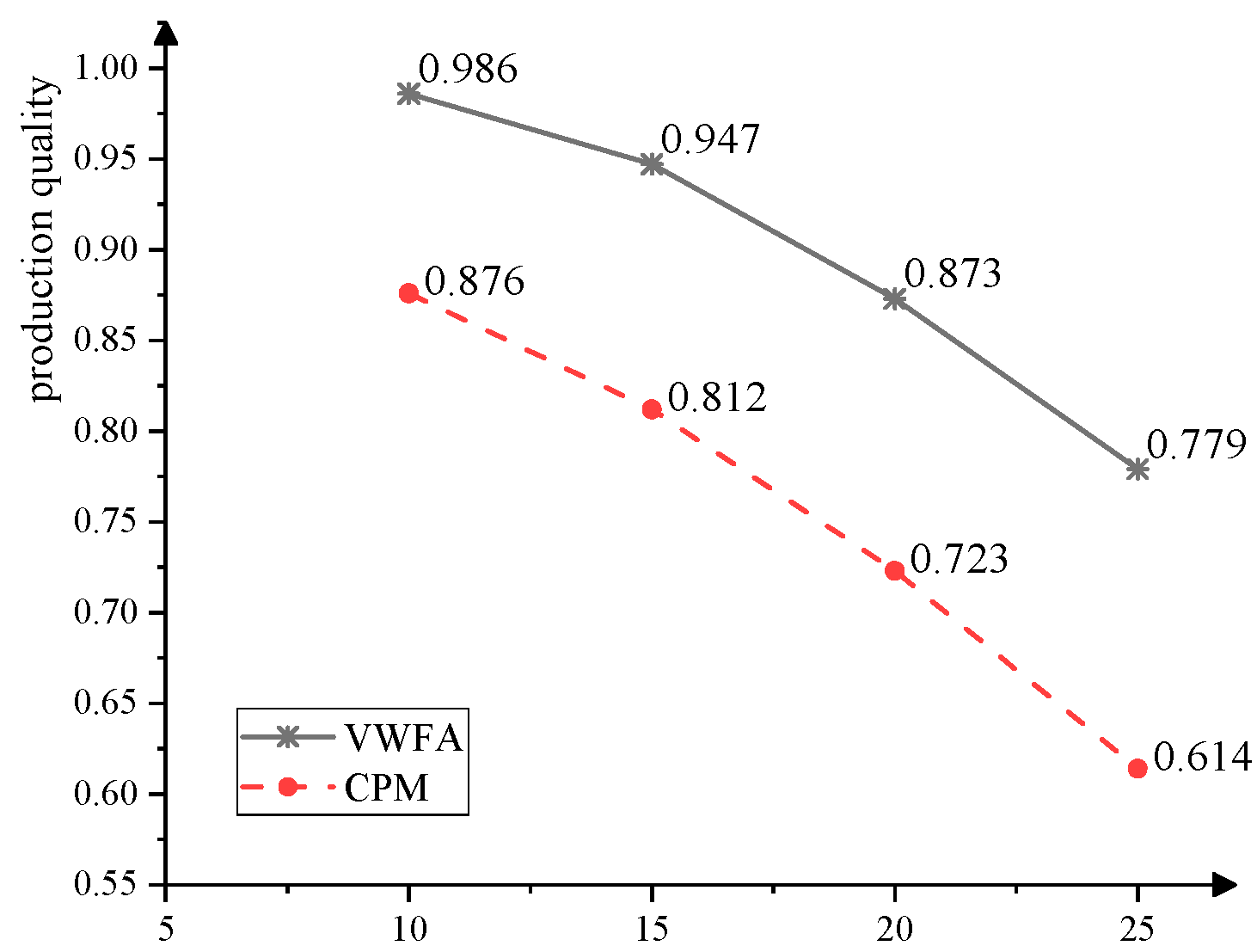
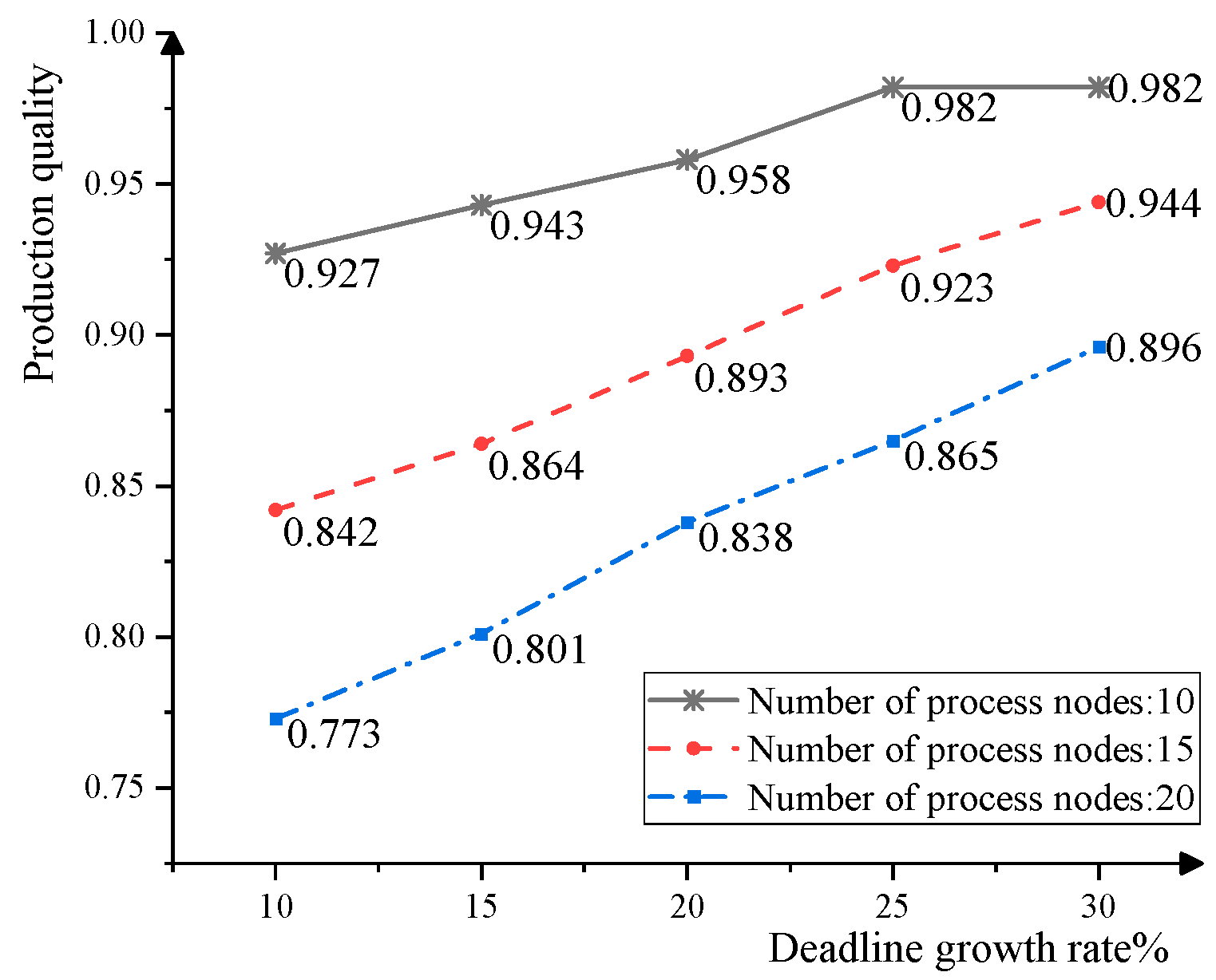
7.1. Impact of the Number of Process Nodes
7.2. Impact of Time Constraints on Algorithm Performance
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, L.; Ren, Y.; Qiu, Q.; Qiu, F. Surveyon Performance Indicators for Multi-Objective Evolutionary Algorithms. Chin. J. Comput. 2021, 44, 1590–1619. [Google Scholar]
- Chao, L.; Fajun, Y.; Lu, Z. Efficient scheduling approaches to time-constrained single-armed cluster tools with condition-based chamber cleaning operations. Int. J. Prod. Res. 2022, 60, 3555–3568. [Google Scholar]
- Lu, R.; Zhu, C.; Cai, H.; Zhou, J.; Jiang, J. Time optimization for work-flow scheduling based on the combination of task attributes. J. Southeast Univ. 2020, 36, 399–406. [Google Scholar]
- Yuan, F.; Huang, B.; Wang, J. A Survey of Modeling and Scheduling of Cluster Tools Based on Petri Nets. Acta Autom. Sin. 2022, 45, 1–20. [Google Scholar]
- Menaka, M.; Kumar, K.S.S. Workflow scheduling in cloud environment–Challenges, tools, limitations & methodologies: A review. Meas. Sens. 2022, 24, 100436. [Google Scholar]
- Song, C. Improved NSGA-II algorithm for hybrid flow shop scheduling problem with multi-objective. Comput. Integr. Manuf. Syst. 2022, 28, 1777–1789. [Google Scholar]
- Luo, Z.Y.; Zhu, Z.H.; You, B.; Liu, J.H. Virtual iterative reduction optimization algorithm of work-flow’s time-accuracy. J. Electron. Inf. Technol. 2018, 40, 2013–2019. [Google Scholar]
- Zhou, W.; Xie, Z. Resource Collaborative Integrated Scheduling Algorithm Considering Multi-process Equipment Weight. J. Electron. Inf. Technol. 2022, 44, 1625–1635. [Google Scholar]
- Liu, C.; Li, J.; Liu, J.; Jiao, L. A Survey on Dynamic Multi-Objective Optimization. Chin. J. Comput. 2020, 43, 1246–1278. [Google Scholar]
- Qiao, Y.; Zhang, S.; Wu, N. Efficient Approach to Failure Response of Process Module in Dual-Arm Cluster Tools with Wafer Residency Time Constraints. IEEE Trans. Syst. Man Cybern. 2021, 51, 1612–1629. [Google Scholar] [CrossRef]
- Stavrinides, G.L.; Karatza, H.D. Multicriteria scheduling of linear work-flows with dynamically varying structure on distributed platforms. Simul. Model. Pract. Theory 2021, 112, 369–377. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Li, L.; Zhao, P.; Zhang, R. Due date assignment scheduling with positional-dependent weights and proportional setup times. Math. Biosci. Eng. 2022, 19, 5104–5119. [Google Scholar] [CrossRef]
- Rama, R.; Ritu, G. Pareto based ant lion optimizer for energy efficient scheduling in cloud environment. Appl. Soft Comput. 2021, 113, 943–962. [Google Scholar]
- Pandey, A.K.; Jadoun, V.K.; Sabhahit, J.N. Real-Time Peak Valley Pricing Based Multi-Objective Optimal Scheduling of a Virtual Power Plant Considering Renewable Resources. Energies 2022, 16, 5970. [Google Scholar] [CrossRef]
- Shirvani, M.H. A hybrid meta-heuristic algorithm for scientific work-flow scheduling in heterogeneous distributed computing systems. Eng. Appl. Artif. Intell. 2020, 90, 501–532. [Google Scholar]
- Zhou, J.; Sun, J.; Zhang, M.; Ma, Y. Dependable Scheduling for Real-Time Work-flows on Cyber–Physical Cloud Systems. IEEE Trans. Ind. Inform. 2021, 17, 7820–7829. [Google Scholar] [CrossRef]
- Saeedizade, E.; Ashtiani, M. DDBWS: A dynamic deadline and budget-aware work-flow scheduling algorithm in work-flow-as-a-service environments. Supercomput 2021, 77, 14525–14564. [Google Scholar] [CrossRef]
- Wang, S.; Wu, R.; Chu, F.; Yu, J. Variable neighborhood search-based methods for integrated hybrid flow shop scheduling with distribution. Soft Comput. 2019, 24, 8917–8936. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, L.; Salah, A. Efficient scientific work-flow scheduling for deadline-constrained parallel tasks in cloud computing environments. Inf. Sci. 2020, 531, 31–46. [Google Scholar] [CrossRef]
- Yang, F.; Qiao, Y.; Gao, K.; Wu, N.; Zhu, Y.; Simon, I.W.; Su, R. Efficient Approach to Scheduling of Transient Processes for Time-Constrained Single-Arm Cluster Tools with Parallel Chambers. IEEE Trans. Syst. Man Syst. 2020, 50, 3646–3657. [Google Scholar] [CrossRef]
- Kumar, K.S.S.; Jaisankar, N. Towards data centre resource scheduling via hybrid cuckoo search algorithm in multi-cloud environment. Int. J. Intell. Enterp. 2017, 4, 21–35. [Google Scholar] [CrossRef]
- Gheisariha, E.; Tavana, M.; Jolai, F.; Rabiee, M. A simulation optimization model for solving flexible flow shop scheduling problems with rework and transportation. Math. Comput. Simul. 2021, 180, 152–177. [Google Scholar] [CrossRef]
- Balszun, M.; Hobbs, C.; Fraccaroli, E.; Roy, D.; Chakraborty, S. Exploiting Process Dynamics in Multi-Stage Schedule Optimization for Flexible Manufacturing. In Proceedings of the 2022 IEEE 27th International Conference on Emerging Technologies and Factory Automation (ETFA), Stuttgart, Germany, 6–9 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–8. [Google Scholar]
- Calzarossa, M.C.; Della Vedova, M.L.; Massari, L.; Nebbione, G.; Tessera, D. Multi-objective optimization of deadline and budget-aware workflow scheduling in uncertain clouds. IEEE Access 2021, 9, 89891–89905. [Google Scholar] [CrossRef]
- Yang, B. Multi-objective optimization of integrated gas–electricity energy system based on improved multi-object cuckoo algorithm. Energy Sci. Eng. 2021, 9, 1839–1857. [Google Scholar] [CrossRef]
- Kusuma, P.D.; Albana, A.S. A Parallel Permutation Flow-Shop Scheduling Model by Using a Two-Step Evolutionary Algorithm to Minimize Intermediate Storage with Tolerable Maximum Completion Time. Int. J. Intell. Eng. Syst. 2021, 14, 464–475. [Google Scholar]
- Geng, K.; Ye, C.; Dai, Z.H.; Liu, L. Bi-objective re-entrant hybrid flow shop scheduling considering energy consumption cost under time-of-use electricity tariffs. Complexity 2020, 2020, 8565921. [Google Scholar] [CrossRef]
- Rui, L.; Chen, X.; Gao, Z.; Li, W.; Qiu, X.; Meng, L. Petri Net-Based Reliability Assessment and Migration Optimization Strategy of SFC. IEEE Trans. Netw. Serv. Manag. 2021, 18, 167–181. [Google Scholar] [CrossRef]
- Alhasnawi, B.N.; Jasim, B.H.; Siano, P.; Guerrero, J.M. A novel real-time electricity scheduling for home energy management system using the internet of energy. Energies 2021, 14, 3191. [Google Scholar] [CrossRef]

| Node | Meaning | Node | Meaning | Node | Meaning |
|---|---|---|---|---|---|
| p1 | Process classification | p2 | Programming | p3 | Machine adjustment |
| p4 | Profile processing | p5 | Material calculation | p6 | Material collection |
| p7 | Cutting | p8 | Bulk processing | p9 | Adjustment |
| p10 | Process allocation | p11 | Batch production | p12 | Warehouse |
| t1 | Category ready | t2 | Program ready | t3 | Machine ready |
| t4 | Processing ready | t5 | Material preparation | t6 | Distribution |
| t7 | Cutting ready | t8 | Processing ready | t9 | Adjustment ready |
| t10 | Allocation ready | t11 | Production ready | t12 | Storage ready |
| Node | Resources Set S | Node | Resources Set S |
|---|---|---|---|
| t1 | (2, 0.94, 0.2), (3, 0.96, 0.3) | t2 | (1, 0.98, 1.2) |
| t3 | (1, 0.97, 0.3), (2, 0.99, 5) | t4 | (1, 0.97,1.4) |
| t5 | (2, 0.97, 0.5), (3, 0.99, 0.7) | t6 | (1, 0.99, 0.6) |
| t7 | (2, 0.90, 0.8), (3, 0.92, 1.0), (4, 0.95, 1.3) | t8 | (15, 0.93, 19) |
| t9 | (2, 0.94, 0.7), (4, 0.98, 1.2) | t10 | (3, 0.92, 0.3), (4, 0.95, 0.5), (6, 0.98, 0.6) |
| t11 | (10, 0.94, 14) | t12 | (2, 0.96, 0.7), (3, 0.98, 1) |
| Deadline | Process |
|---|---|
| 5 | Production quality ƒq = 0.931, production time ƒh = 6 and cost ƒc = 2; because ƒq < σ1q, execute correction processing, then ƒ′q = 0.931 + 0.931 × (1 − 0.931) = 0.995. ƒ′h = 6 + 1 = 7, ƒ′c = 2 + 0.5 = 2.5. Due to ƒ′h exceeds ME.H1, it does not meet the requirements and is discarded. |
| 4 | The maximum production quality is equivalent to the maximum production accuracy of p1 when it begins at time 1, that ƒq = 0.913, production time ƒh = 5 and cost ƒc = 1.8; because ƒq < σ1q, execute correction processing, and ƒ′q = 0.913 + 0.913 × (1 − 0.913) = 0.992, ƒ′h = 5 + 1 = 6, ƒ′c = 1.8 + 0.5 = 2.3. Meets the requirements of dp1. |
| 3 | The maximum production quality is equivalent to the maximum production accuracy of p1 when it begins at time 2, that ƒq = 0.894, production time ƒh = 5 and cost ƒc = 1.7; because ƒq < σ1q, execute correction processing, and ƒ′q(p1,2) = 0.894 + 0.894 × (1 − 0.894) = 0.989, ƒ′h = 5 + 1 = 6, ƒ′c = 1.7 + 0.5 = 2.2. Meets the requirements of dp1. |
| Deadline | Process |
|---|---|
| 23 | Production quality ƒq = 0.857 and production time ƒh = 24; because ƒq < σ2q, execute correction processing, then ƒ′q = 0.857 + 0.857 × (1 − 0.857) = 0.980. ƒ′h = 24 + 2 = 26. Due to ƒ′h exceeds ME.H2, it does not meet the requirements and is discarded. |
| … | … |
| 19 | The maximum production accuracy is equivalent to the maximum production accuracy of p1 when it begins at time 4, that ƒq = 0.796 and production time ƒh = 21; because ƒq < σ2q, execute correction processing, and ƒ′q = 0.796 + 0.796 × (1 − 0.796) = 0.958, ƒ′h = 21 + 2 = 23. Meets the requirements of dp2. |
| 18 | The maximum production accuracy is equivalent to the maximum production accuracy of p1 when it begins at time 5, that ƒq = 0.779 and production time ƒh = 20; because ƒq < σ2q, execute correction processing, and ƒ′q = 0.779 + 0.779 × (1 − 0.779) = 0.951, ƒ′h = 20 + 2 = 22. Meets the requirements of dp2. |
| Deadline | Process |
|---|---|
| 17 | Production quality ƒq = 0.903, production time ƒh = 21 and cost ƒc = 15.6; because ƒq < σ3q, execute correction processing, then ƒ′q = 0.903 + 0.903 × (1 − 0.903) = 0.990. ƒ′h = 21 + 2 = 23, ƒ’c = 18.6. Due to ƒ′h exceeds ME.H3, it does not meet the requirements and is discarded. |
| … | … |
| 14 | The maximum production accuracy is equivalent to the maximum production accuracy of p1 when it begins at time 3, that ƒq = 0.986 ƒh = 18 and ƒc = 15.6; because ƒq < σ3q, execute correction processing, and ƒ′q = 0.860 + 0.860 × (1 − 0.860) = 0.980, ƒ′h = 18 + 2 = 20 and ƒ’c = 18.6. Meets the requirements of dp3. |
| 13 | The maximum production accuracy is equivalent to the maximum production accuracy of p1 when it begins at time 4, that ƒq = 0.823 ƒh = 17 and ƒc = 15.6; because ƒq < σ3q, execute correction processing, and ƒ′q = 0.823 + 0.823 × (1 − 0.823) = 0.969, ƒ′h = 17 + 2 = 19, ƒ’c = 18.6. Meets the requirements of dp3. |
| Segment | Local Solution | Path |
|---|---|---|
| First segment | path11 | pB/tB→p1/t1S2→p2/t2S1→p3/t3S1, B0→p4/t4S1→p5/t5S1 |
| path12 | pB/tB→p1/t1S2→p2/t2S1→p3/t3S1, B0→p4/t4S1→p5/t5S2 | |
| path13 | pB/tB→p1/t1S1→p2/t2S1→p3/t3S2, B0→p4/t4S1→p5/t5S1 | |
| path14 | pB/tB→p1/t1S1→p2/t2S1→p3/t3S2, B0→p4/t4S1→p5/t5S2 | |
| Second segment | path21 | p6/t6S1→p7/t7S2→p8/t3S1→p9/t9S2 |
| path22 | p6/t6S1→p7/t7S3→p8/t3S1→p9/t9S1 | |
| path23 | p6/t6S1→p7/t7S2→p8/t3S1→p9/t9S1 | |
| path24 | p6/t6S1→p7/t7S1→p8/t3S1→p9/t9S2 | |
| Third segment | path31 | p10/t10S2→p11/t11S1→p12/t12S2→pE/tE |
| path32 | p10/t10S2→p11/t11S1→p12/t12S1→pE/tE | |
| path33 | p10/t10S1→p11/t11S1→p12/t12S1→pE/tE |
| Algorithm and Parameter | CPM | PAM | VWFA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ƒq | ƒc | ƒh | ƒq | ƒc | ƒh | ƒq | ƒc | ƒh | |
| First segment | 0.929 | 5.0 | 5 | 0.995 | 7.8 | 6 | 0.989 | 6.2 | 6 |
| Second segment | 0.951 | 26.1 | 22 | 0.969 | 32.1 | 28 | 0.971 | 25.8 | 25 |
| Third segment | 0.970 | 18.0 | 17 | 0.990 | 18.6 | 21 | 0.986 | 18.5 | 19 |
| Cumulative | 0.857 | 50.1 | 44 | 0.955 | 58.5 | 55 | 0.947 | 50.5 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Liu, X.; Tan, S.; Xu, H.; Liu, J. Multi-Objective Multi-Stage Optimize Scheduling Algorithm for Nonlinear Virtual Work-Flow Based on Pareto. Processes 2023, 11, 1147. https://doi.org/10.3390/pr11041147
Luo Z, Liu X, Tan S, Xu H, Liu J. Multi-Objective Multi-Stage Optimize Scheduling Algorithm for Nonlinear Virtual Work-Flow Based on Pareto. Processes. 2023; 11(4):1147. https://doi.org/10.3390/pr11041147
Chicago/Turabian StyleLuo, Zhiyong, Xintong Liu, Shanxin Tan, Haifeng Xu, and Jiahui Liu. 2023. "Multi-Objective Multi-Stage Optimize Scheduling Algorithm for Nonlinear Virtual Work-Flow Based on Pareto" Processes 11, no. 4: 1147. https://doi.org/10.3390/pr11041147
APA StyleLuo, Z., Liu, X., Tan, S., Xu, H., & Liu, J. (2023). Multi-Objective Multi-Stage Optimize Scheduling Algorithm for Nonlinear Virtual Work-Flow Based on Pareto. Processes, 11(4), 1147. https://doi.org/10.3390/pr11041147





