Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—II. Preparative Isolation of Pure Single Homologs
Abstract
1. Introduction
2. Theoretical Background
2.1. Thermodynamic Retention Model
2.2. Column Model Based on Discrete Convolution
2.3. Linear Solvent Strength Theory
3. Experimental
3.1. Materials
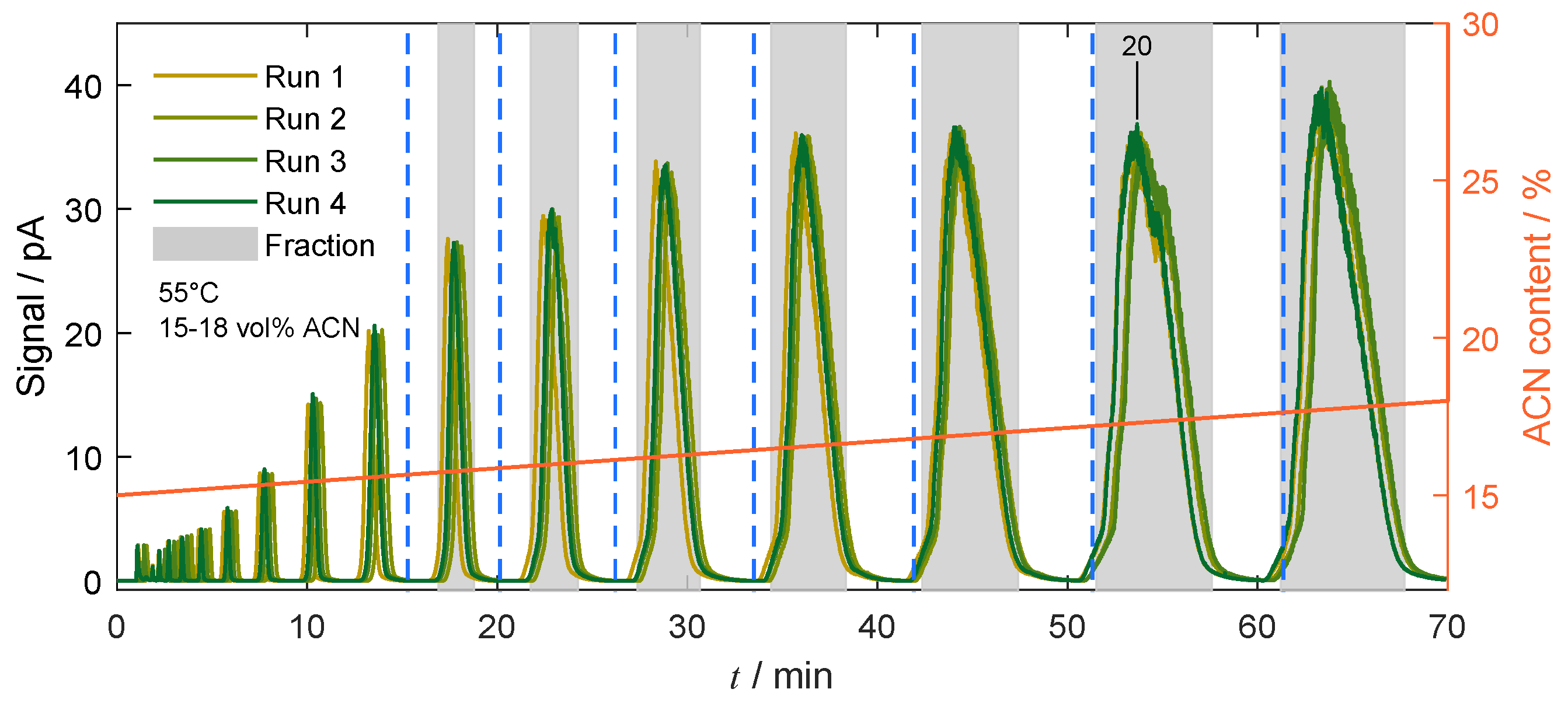
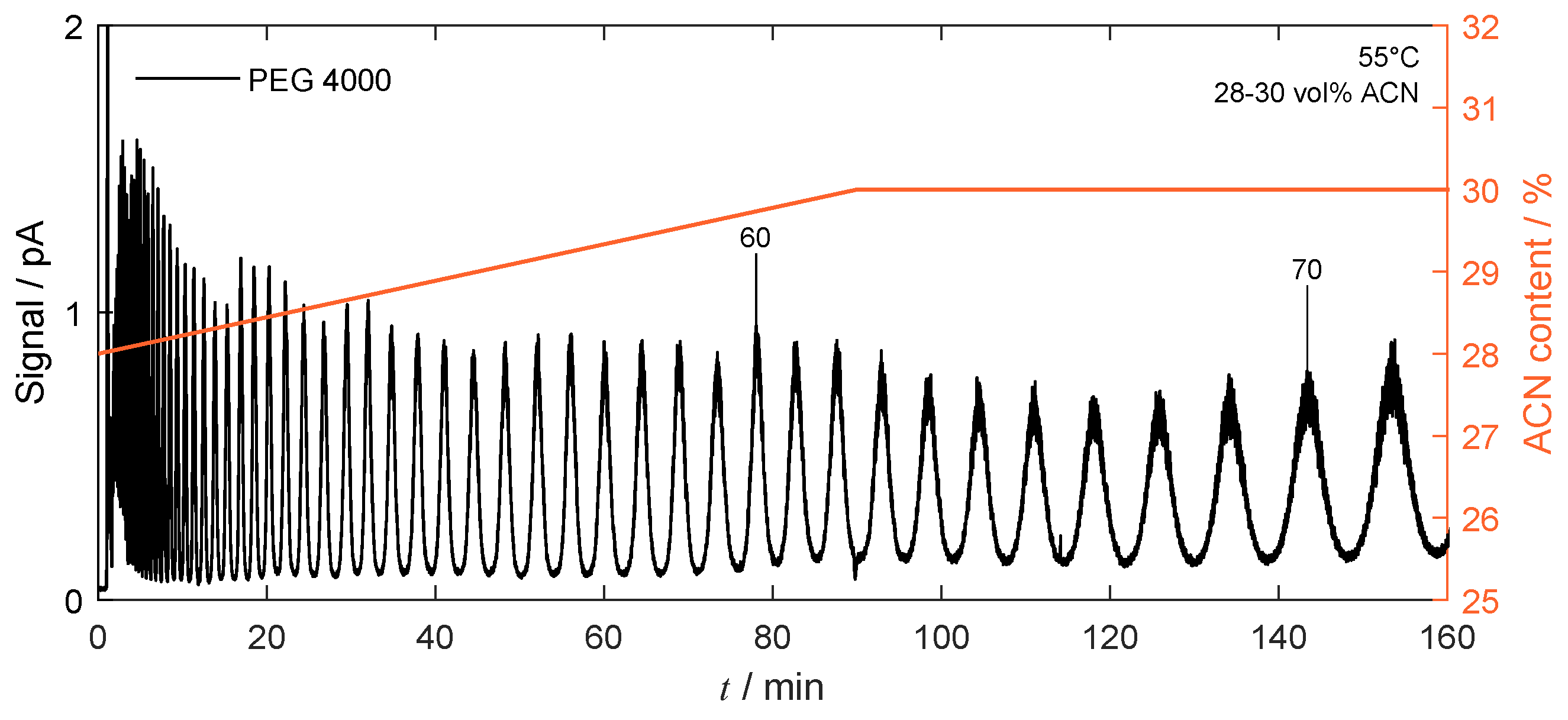
3.2. Preparative Chromatography
3.3. Analytical Chromatography
4. Results and Discussion
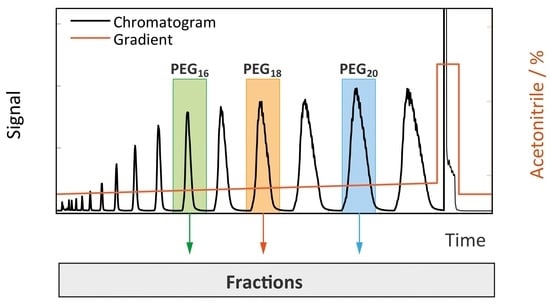
4.1. Separation Problem and Role of Operating Conditions
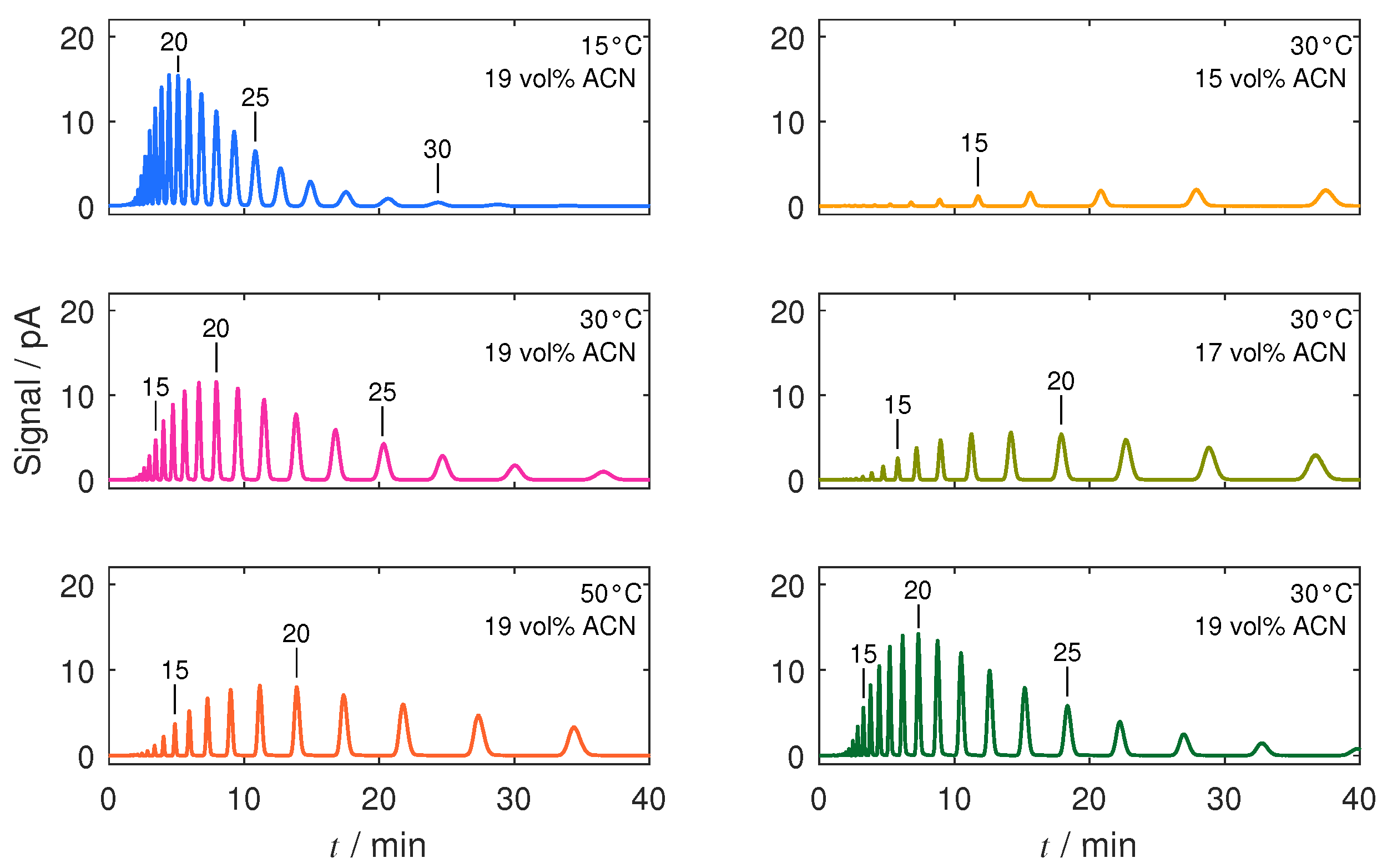
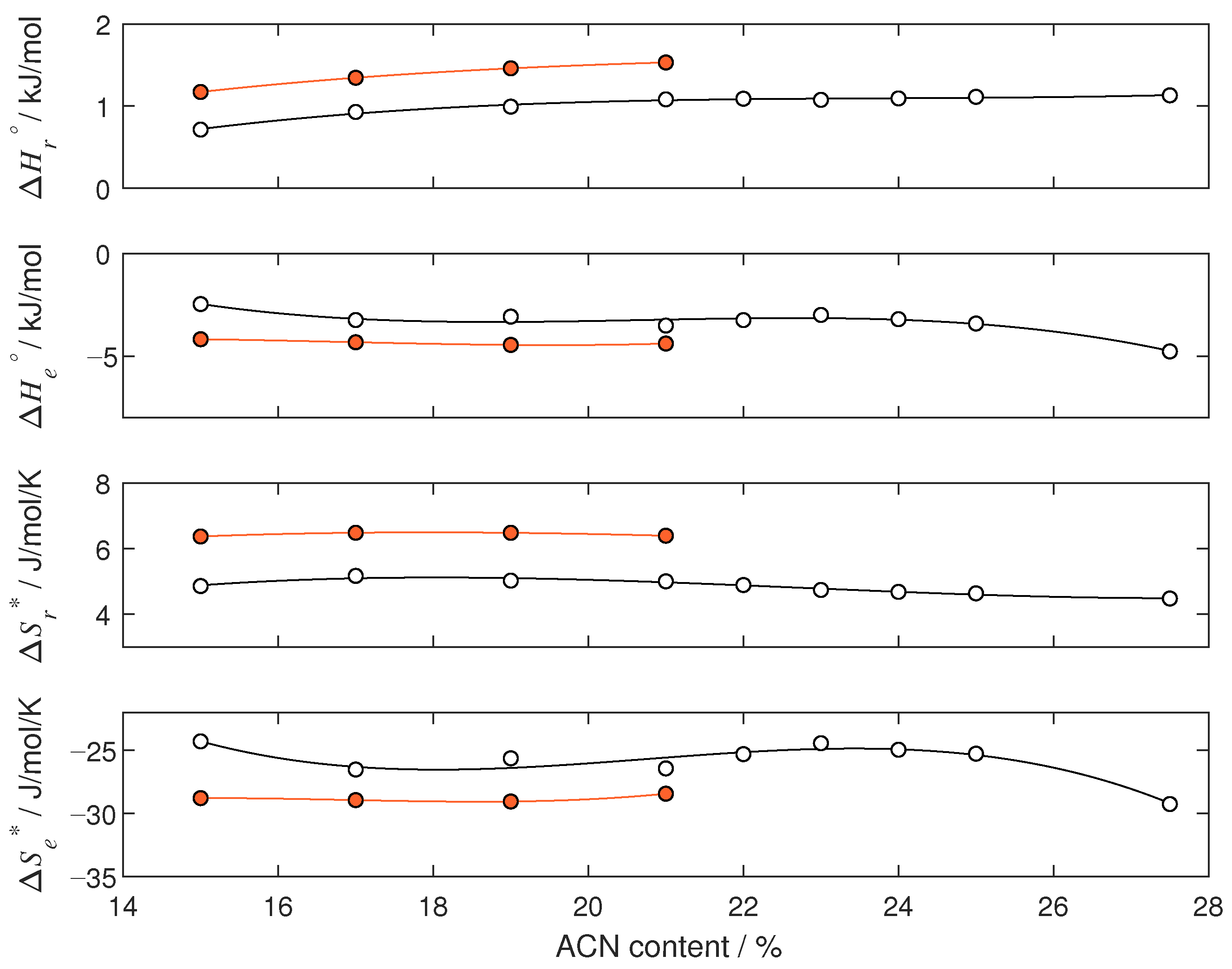
4.2. Thermodynamic Analysis
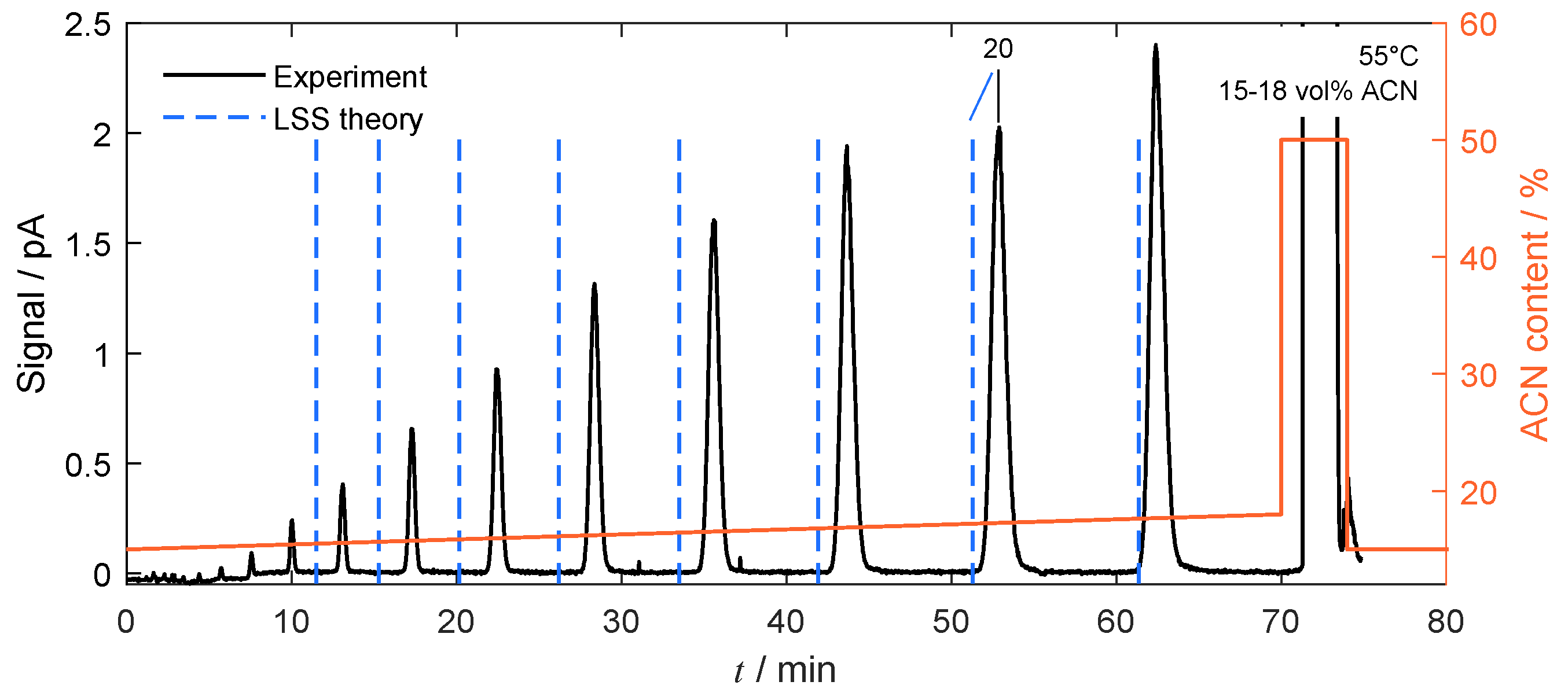
4.3. Separation under Linear Conditions
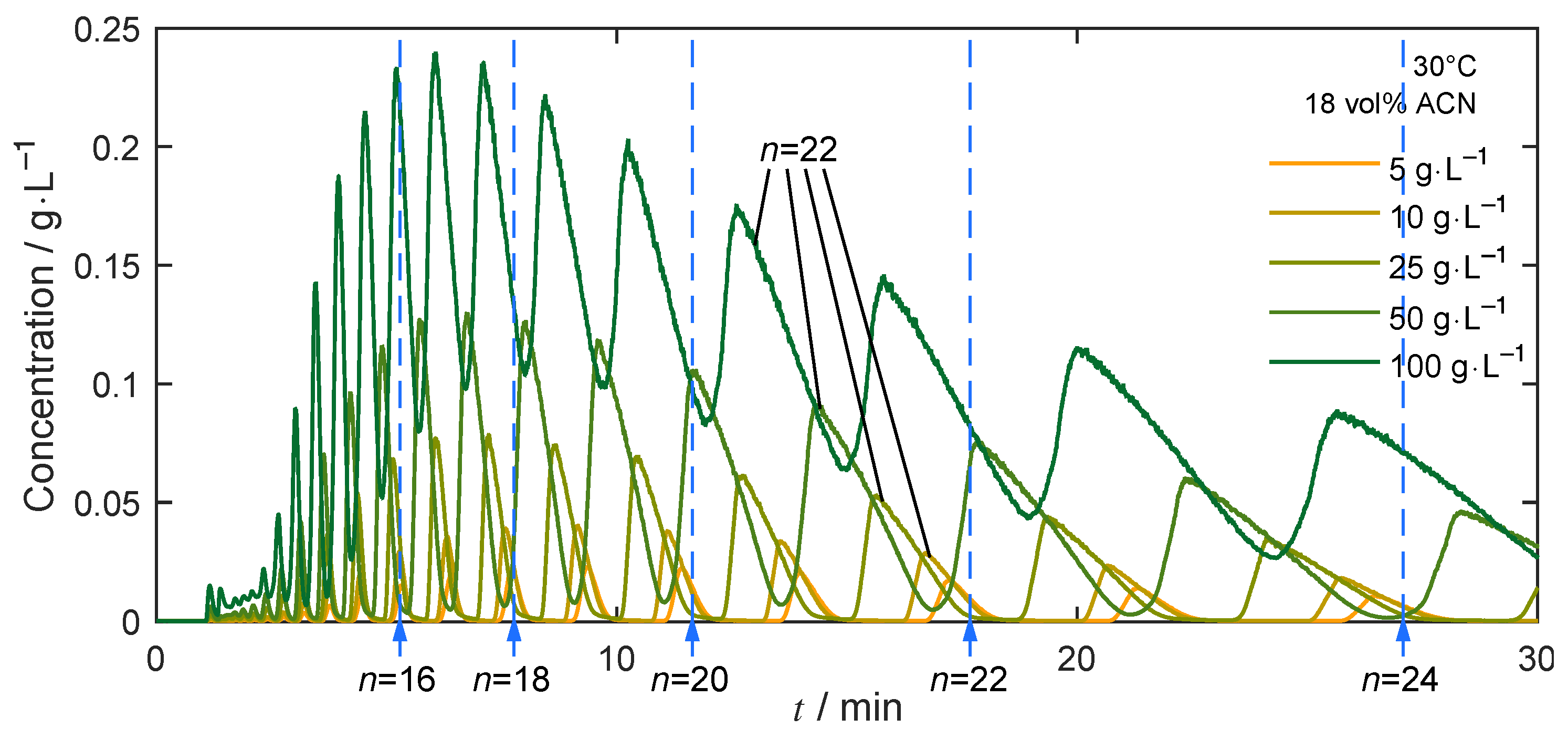
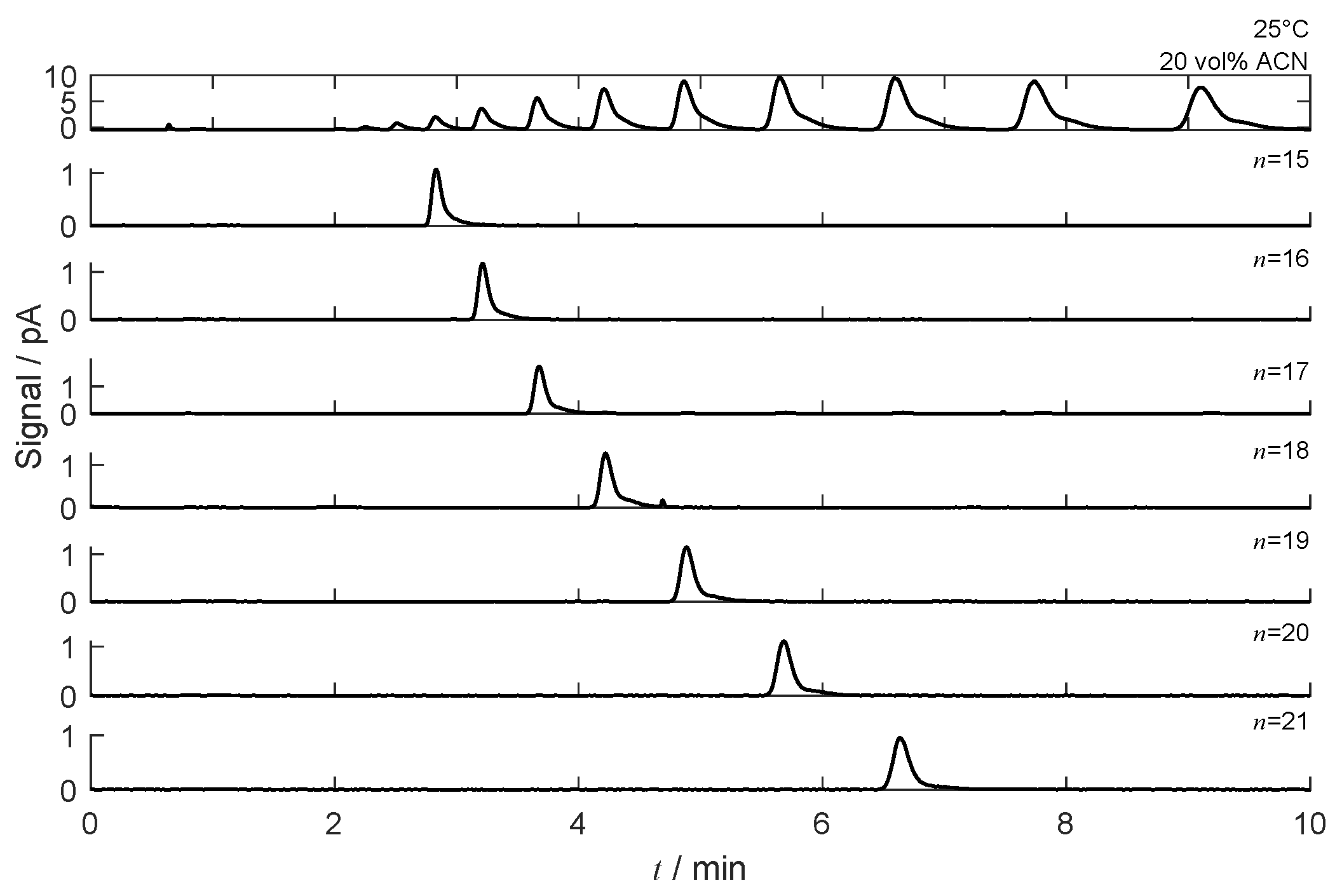
4.4. Separation under Nonlinear Conditions
4.4.1. Isocratic Operation
4.4.2. Gradient-Based Operation
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Trinh, T.T.; Laure, C.; Lutz, J.F. Synthesis of Monodisperse Sequence-Defined Polymers Using Protecting-Group-Free Iterative Strategies. Macromol. Chem. Phys. 2015, 216, 1498–1506. [Google Scholar] [CrossRef]
- Bohn, P.; Meier, M.A.R. Uniform poly(ethylene glycol): A comparative study. Polym. J. 2020, 52, 165–178. [Google Scholar] [CrossRef]
- Knop, K.; Hoogenboom, R.; Fischer, D.; Schubert, U. Poly(ethylene glycol) in Drug Delivery: Pros and Cons as Well as Potential Alternatives. Angew. Chem. Int. Ed. 2010, 49, 6288–6308. [Google Scholar] [CrossRef]
- Yu, Z.; Bo, S.; Wang, H.; Li, Y.; Yang, Z.; Huang, Y.; Jiang, Z.X. Application of Monodisperse PEGs in Pharmaceutics: Monodisperse Polidocanols. Mol. Pharm. 2017, 14, 3473–3479. [Google Scholar] [CrossRef]
- Wu, T.; Chen, K.; He, S.; Liu, X.; Zheng, X.; Jiang, Z.X. Drug Development through Modification of Small Molecular Drugs with Monodisperse Poly(ethylene glycol)s. Org. Process. Res. Dev. 2020, 24, 1364–1372. [Google Scholar] [CrossRef]
- Takahashi, K. Advanced reference materials for the characterization of molecular size and weight. J. Phys. Mater. 2020, 1193, 146–150. [Google Scholar] [CrossRef]
- Wu, W.; Supper, M.; Rausch, M.H.; Kaspereit, M.; Fröba, A.P. Mutual Diffusivities of Binary Mixtures of Water and Poly(ethylene) Glycol from Heterodyne Dynamic Light Scattering. Int. J. Thermophys. 2022, 43, 177. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Shi, Q.; Li, Y.; Xia, G.; Chen, L.; Yang, Z.; Jiang, Z.X. Highly Efficient Synthesis of Monodisperse Poly(ethylene glycols) and Derivatives through Macrocyclization of Oligo(ethylene glycols). Angew. Chem. Int. Ed. 2015, 54, 3763–3767. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Baird, M.; Simpson, J. Determination of poly(ethylene glycol)s by both normal-phase and reversed-phase modes of high-performance liquid chromatography. J. Chromatogr. A 1998, 800, 231–238. [Google Scholar] [CrossRef]
- Chang, T. Polymer characterization by interaction chromatography. J. Polym. Sci. B Polym. Phys. 2005, 43, 1591–1607. [Google Scholar] [CrossRef]
- Meyer, T.; Harms, D.; Gmehling, J. Analysis of polyethylene glycols with respect to their oligomer distribution by high-performance liquid chromatography. J. Chromatogr. A 1993, 645, 135–139. [Google Scholar] [CrossRef]
- Rissler, K. Improved separation of polyethylene glycols widely differing in molecular weight range by reversed-phase high performance liquid chromatography and evaporative light scattering detection. Chromatographia 1999, 49, 615–620. [Google Scholar] [CrossRef]
- Cho, D.; Park, S.; Hong, J.; Chang, T. Retention mechanism of poly(ethylene oxide) in reversed-phase and normal-phase liquid chromatography. J. Chromatogr. A 2003, 986, 191–198. [Google Scholar] [CrossRef]
- Trathnigg, B.; Veronik, M. A thermodynamic study of retention of poly(ethylene glycol)s in liquid adsorption chromatography on reversed phases. J. Chromatogr. A 2005, 1091, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Supper, M.; Heller, K.; Söllner, J.; Sainio, T.; Kaspereit, M. Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—Analysis and Modeling Based on Isocratic Analytical-Scale Investigations. Processes 2022, 10, 2160. [Google Scholar] [CrossRef]
- Poulton, A.M.; Poulten, R.C.; Baldaccini, A.; Gabet, A.; Mott, R.; Treacher, K.E.; Roddy, E.; Ferguson, P. Towards improved characterisation of complex polyethylene glycol excipients using supercritical fluid chromatography-evaporative light scattering detection-mass spectrometry and comparison with size exclusion chromatography-triple detection array. J. Chromatogr. A 2021, 1638, 461839. [Google Scholar] [CrossRef] [PubMed]
- Shimada, K.; Nagahata, R.; Kawabata, S.I.; Matsuyama, S.; Saito, T.; Kinugasa, S. Evaluation of the quantitativeness of matrix-assisted laser desorption/ionization time-of-flight mass spectrometry using an equimolar mixture of uniform poly(ethylene glycol) oligomers. J. Mass Spectrom. 2003, 38, 948–954. [Google Scholar] [CrossRef] [PubMed]
- Shimada, K.; Kato, H.; Saito, T.; Matsuyama, S.; Kinugasa, S. Precise measurement of the self-diffusion coefficient for poly(ethylene glycol) in aqueous solution using uniform oligomers. J. Chem. Phys. 2005, 122, 244914. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Matsuyama, S.; Saito, T.; Kato, H.; Kinugasa, S.; Yarita, T.; Maeda, T.; Kitazawa, H.; Bounoshita, M. Calibration of an evaporative light-scattering detector as a mass detector for supercritical fluid chromatography by using uniform Poly(ethylene glycol) oligomers. J. Chromatogr. A 2008, 1193, 146–150. [Google Scholar] [CrossRef]
- Takahashi, K.; Kishine, K.; Matsuyama, S.; Saito, T.; Kato, H.; Kinugasa, S. Certification and uncertainty evaluation of the certified reference materials of poly(ethylene glycol) for molecular mass fractions by using supercritical fluid chromatography. Anal. Bioanal. Chem. 2008, 391, 2079–2087. [Google Scholar] [CrossRef]
- Chester, T.L.; Coym, J.W. Effect of phase ratio on van’t Hoff analysis in reversed-phase liquid chromatography, and phase-ratio-independent estimation of transfer enthalpy. J. Chromatogr. A 2003, 1003, 101–111. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.J.P. Some Theoretical Aspects of Partition Chromatography. Symposia Biochem. Soc. 1949, 3, 4–20. [Google Scholar]
- Lochmüller, C.; Moebus, M.A.; Liu, Q.; Jiang, C.; Elomaa, M. Temperature Effect on Retention and Separation of Poly(ethylene glycol)s in Reversed-Phase Liquid Chromatography. J. Chromatogr. Sci. 1996, 34, 69–76. [Google Scholar] [CrossRef]
- Trathnigg, B.; Skvortsov, A. Determination of the accessible volume and the interaction parameter in the adsorption mode of liquid chromatography. J. Chromatogr. A 2006, 1127, 117–125. [Google Scholar] [CrossRef]
- Trathnigg, B.; Jamelnik, O. Characterization of different reversed phase systems in liquid adsorption chromatography of polymer homologous series. J. Chromatogr. A 2007, 1146, 78–84. [Google Scholar] [CrossRef] [PubMed]
- Nguyen Viet, C.; Trathnigg, B. Determination of thermodynamic parameters in reversed phase chromatography for polyethylene glycols and their methyl ethers in different mobile phases. J. Sep. Sci. 2010, 33, 464–474. [Google Scholar] [CrossRef]
- Villermaux, J. Chemical engineering approach to dynamic modelling of linear chromatography: A flexible method for representing complex phenomena from simple concepts. J. Chromatogr. A 1987, 406, 11–26. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Kaspereit, M.; Sainio, T. Intermittent recycle-integrated reactor-separator for production of well-defined non-digestible oligosaccharides from oat β-glucan. Chem. Eng. J. 2021, 410, 128352. [Google Scholar] [CrossRef]
- Nicoud, R.M. Chromatographic Processes: Modeling, Simulation, and Design; Cambridge Series in Chemical Engineering; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Guiochon, G.; Shirazi, D.G.; Felinger, A.; Katti, A.M. Fundamentals of Preparative and Nonlinear Chromatography, 2nd ed.; Academic Press: Boston, MA, USA, 2006. [Google Scholar]
- Snyder, L.R.; Dolan, J.W. High-Performance Gradient Elution: The Practical Application of the Linear-Solvent-Strength Model; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Van Middlesworth, B.J.; Dorsey, J.G. Quantifying injection solvent effects in reversed-phase liquid chromatography. J. Chromatogr. A 2012, 1236, 77–89. [Google Scholar] [CrossRef]
- Ströhlein, G.; Morbidelli, M.; Rhee, H.K.; Mazzotti, M. Modeling of modifier-solute peak interactions in chromatography. AIChE J. 2006, 52, 565–573. [Google Scholar] [CrossRef]
- Gedicke, K.; Antos, D.; Seidel-Morgenstern, A. Effect on separation of injecting samples in a solvent different from the mobile phase. J. Chromatogr. A 2007, 1162, 62–73. [Google Scholar] [CrossRef] [PubMed]
- Lei, H.; Bao, Z.; Xing, H.; Yang, Y.; Ren, Q.; Zhao, M.; Huang, H. Adsorption Behavior of Glucose, Xylose, and Arabinose on Five Different Cation Exchange Resins. J. Chem. Eng. Data 2010, 55, 735–738. [Google Scholar] [CrossRef]






| ACN | ||||||
|---|---|---|---|---|---|---|
| vol% | - | % | - | % | % | |
| 0 | 12.35 | 14,000 | 1.11 | |||
| 10 | 12.25 | −0.8 | 12,810 | −8.5 | 1.19 | 7.2 |
| 20 | 12.22 | −1.1 | 10,070 | −28.1 | 1.29 | 16.2 |
| 35 | 12.18 | −1.4 | 6170 | −55.9 | 1.36 | 22.5 |
| 50 | 12.20 | −1.2 | 6010 | −57.1 | 1.37 | 23.4 |
| ACN | ||||
|---|---|---|---|---|
| vol% | kJ/mol | kJ/mol | J/(mol K) | J/(mol K) |
| 15 | 1.185 | −4.423 | 6.401 | −29.390 |
| 17 | 1.365 | −4.773 | 6.533 | −30.131 |
| 19 | 1.485 | −5.153 | 6.551 | −30.999 |
| 21 | 1.566 | −5.488 | 6.487 | −31.548 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Supper, M.; Jost, R.; Bornschein, B.; Kaspereit, M. Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—II. Preparative Isolation of Pure Single Homologs. Processes 2023, 11, 946. https://doi.org/10.3390/pr11030946
Supper M, Jost R, Bornschein B, Kaspereit M. Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—II. Preparative Isolation of Pure Single Homologs. Processes. 2023; 11(3):946. https://doi.org/10.3390/pr11030946
Chicago/Turabian StyleSupper, Malvina, Rosanna Jost, Benedikt Bornschein, and Malte Kaspereit. 2023. "Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—II. Preparative Isolation of Pure Single Homologs" Processes 11, no. 3: 946. https://doi.org/10.3390/pr11030946
APA StyleSupper, M., Jost, R., Bornschein, B., & Kaspereit, M. (2023). Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—II. Preparative Isolation of Pure Single Homologs. Processes, 11(3), 946. https://doi.org/10.3390/pr11030946