Evolutionary Process for Engineering Optimization in Manufacturing Applications: Fine Brushworks of Single-Objective to Multi-Objective/Many-Objective Optimization
Abstract
:1. Introduction
- To the best of our knowledge, it is the first attempt to extend a proposal of interpretability on an SMO “meeting” the PFSP towards disentangling the knowledge for smart manufacturing scheduling and carbon neutrality.
- We characterize the landscapes in different gaps towards a proper guarantee of a correlation gap and an asynchronous rhythm (the second and fourth surgical knives of transfer gaps and asynchronous rhythms).
- We further discuss the gather [6] or transfer coefficient between the auxiliary tasks for boosting the core task. (The third surgical knife of the auxiliary task).
2. Materials and Methods
2.1. Test Problem: PFSP
2.2. The Framework across Tasks: ETO_PFSP or SMO
2.2.1. Four Frameworks: SOO, MOO, MFO and SMO
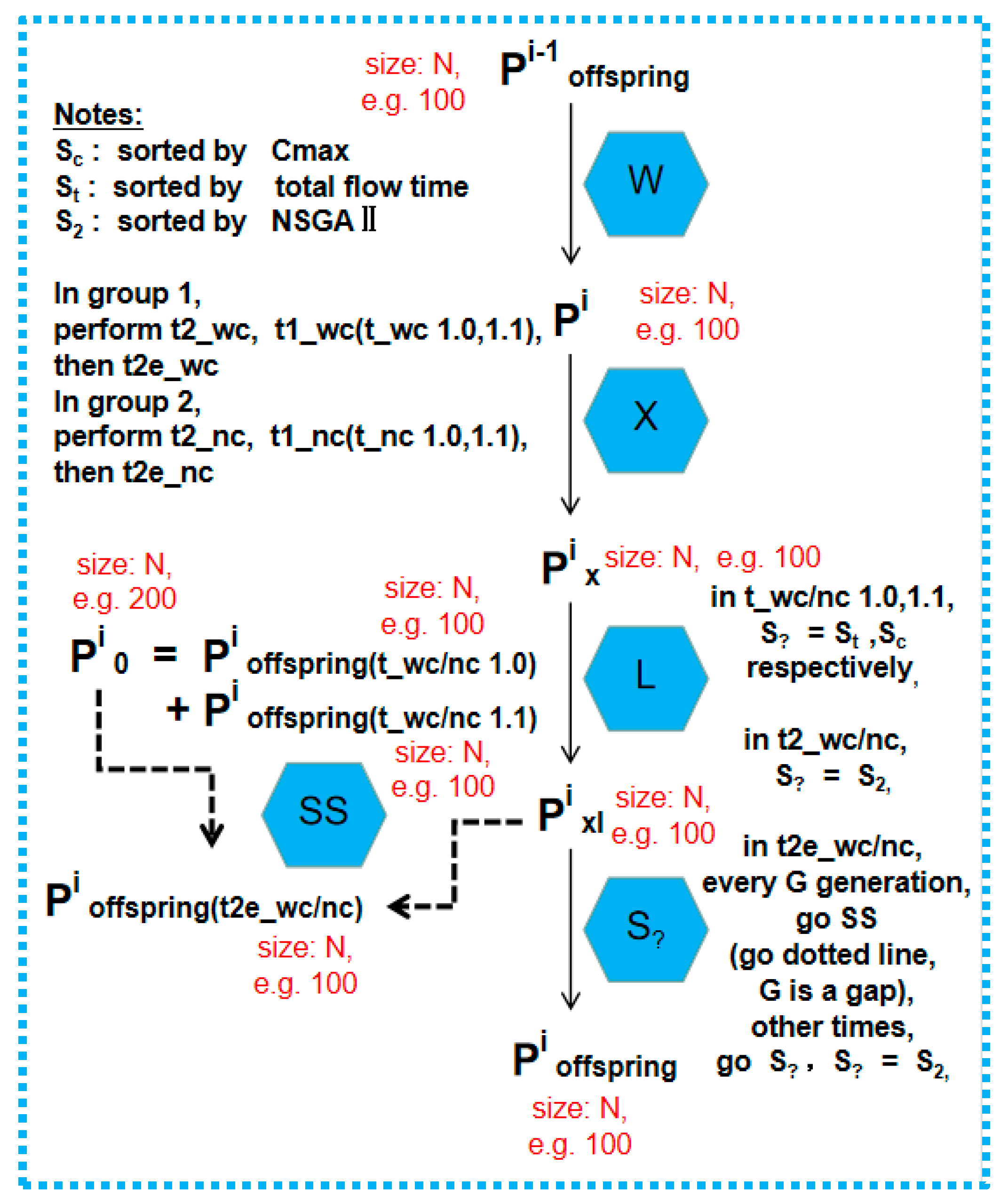
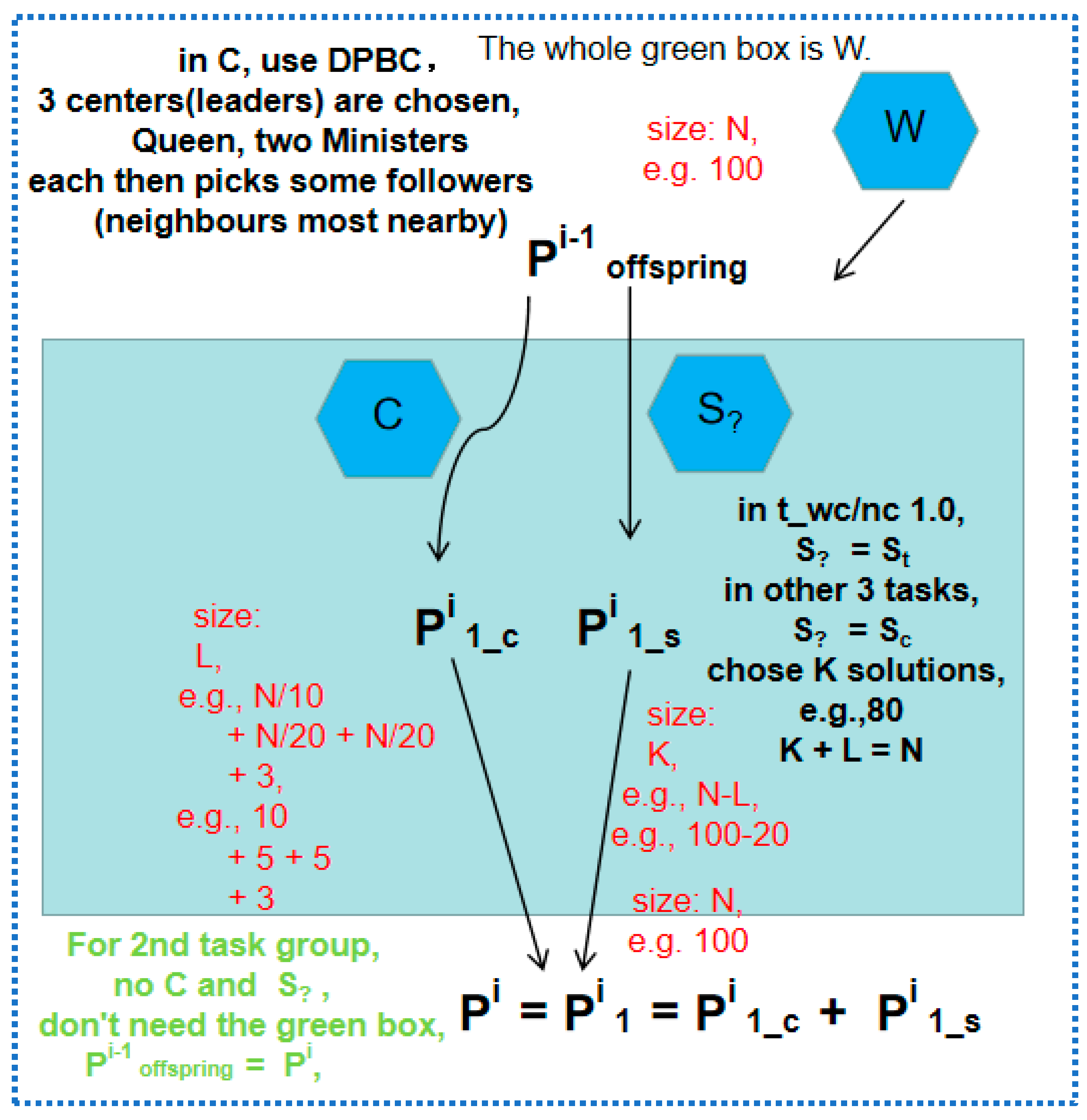
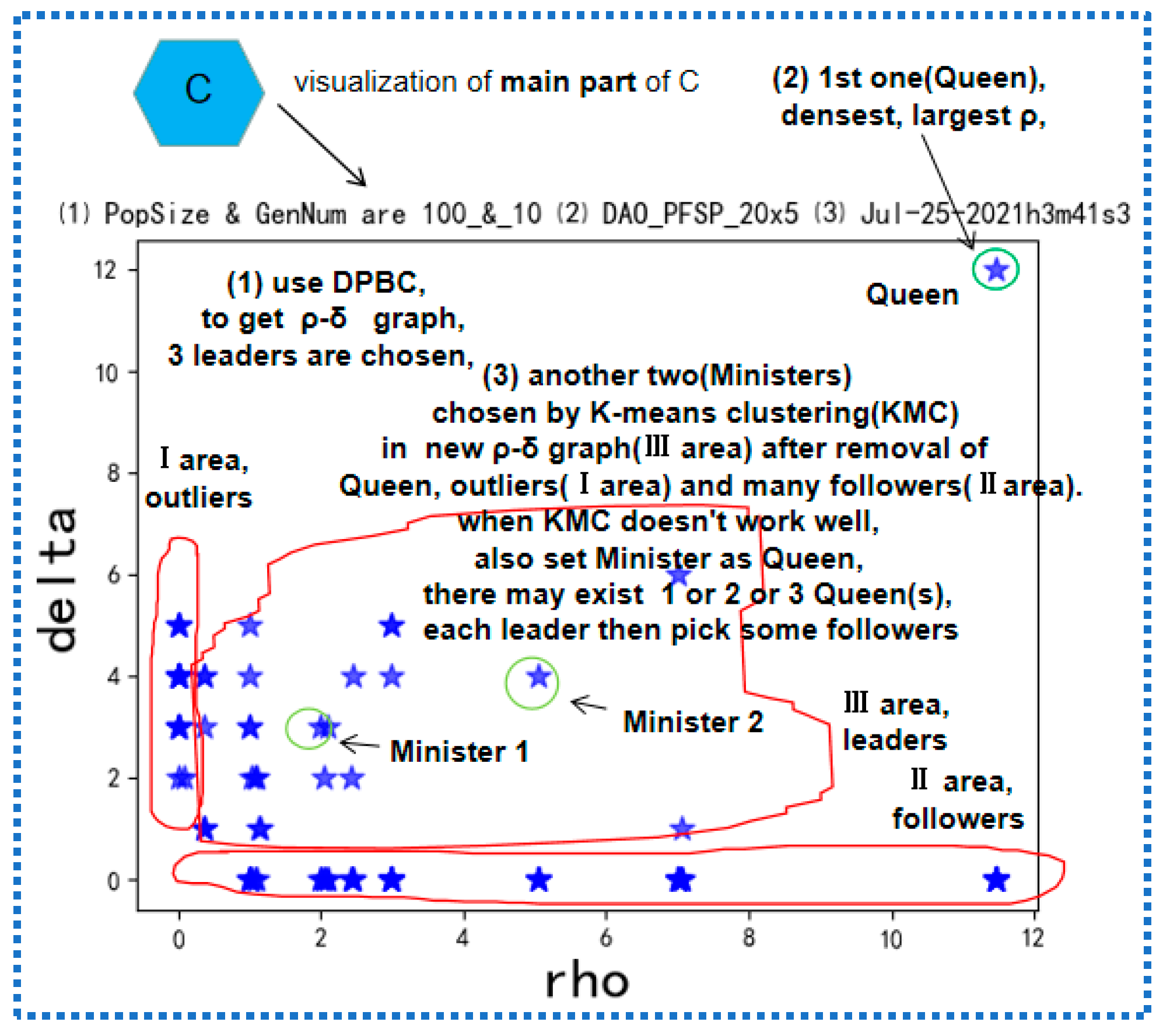
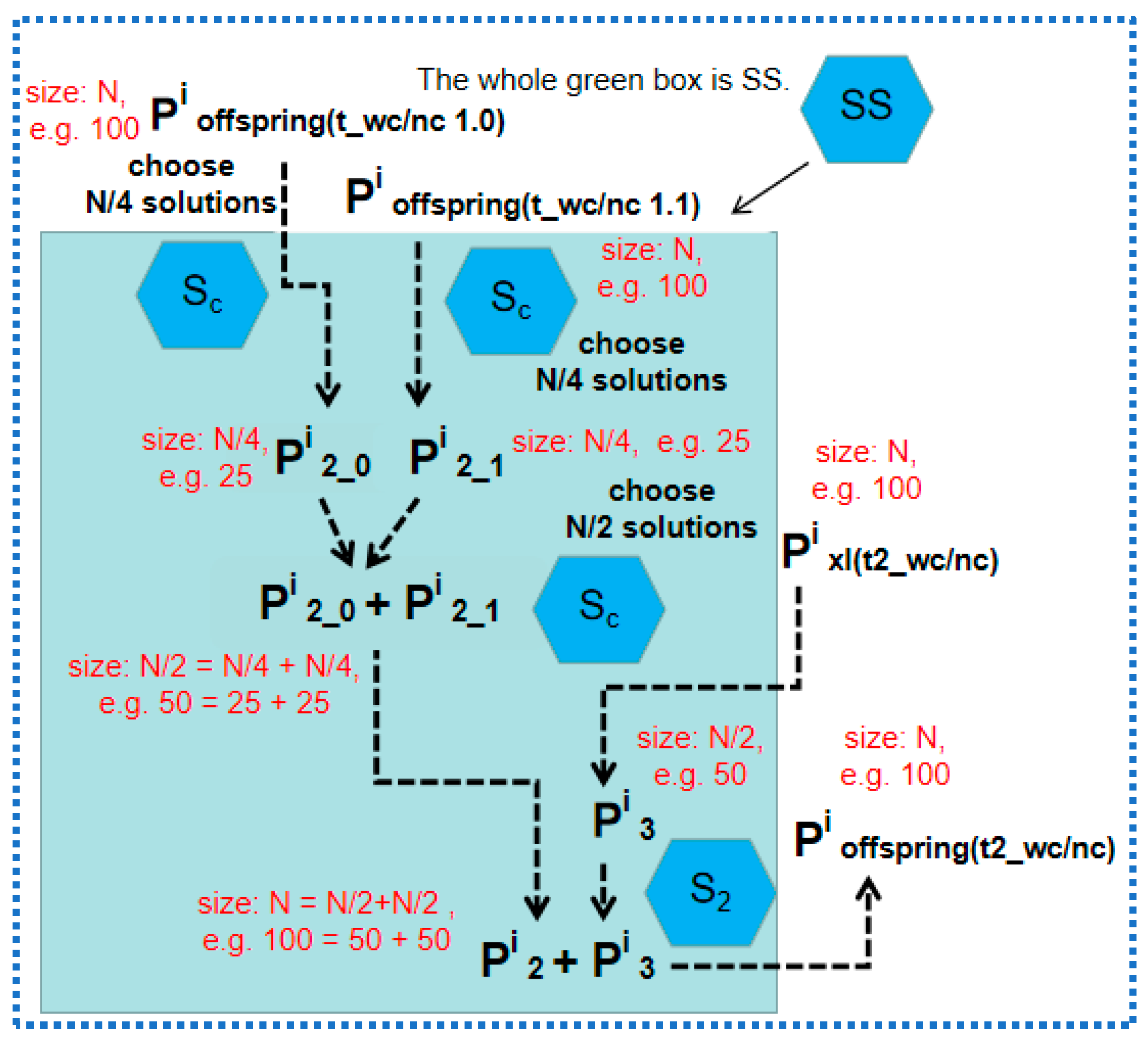
2.2.2. 4 Bags, 4 × 2 Groups, 4 × 2 × 4 tasks: e.g., Bag 0: Group 1, t1_wc(t_wc 1.0, t_wc 1.1), t2_wc and t2e_wc; Group 2, t1_nc(t_nc 1.0, t_nc 1.1), t2_nc and t2e_nc
3. Results
3.1. Experimental Setup
3.2. Simulations and Comparisons
4. Discussion
4.1. Insight into Bag 5: Building Block Distribution in Head, Middle and Tail
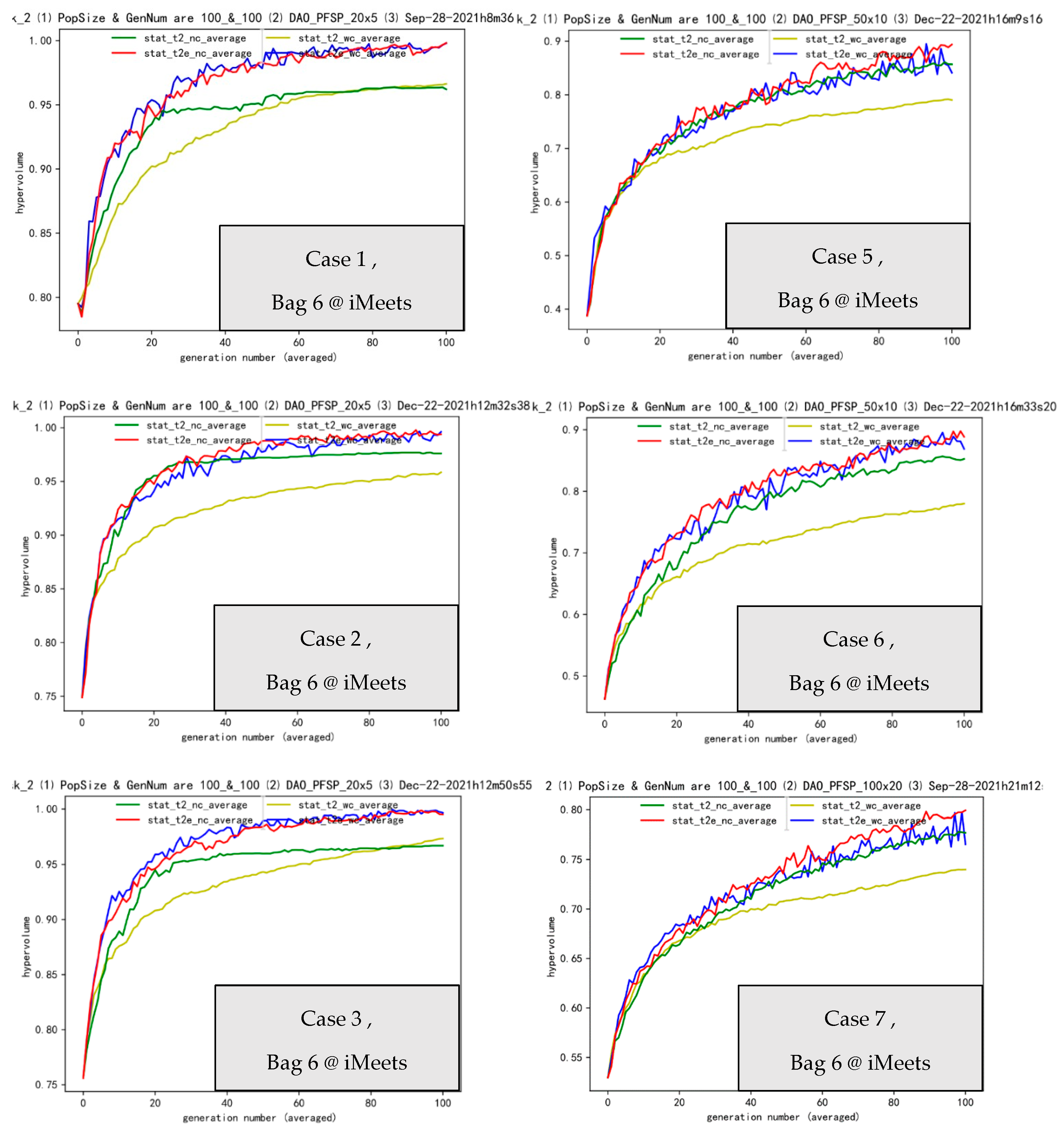
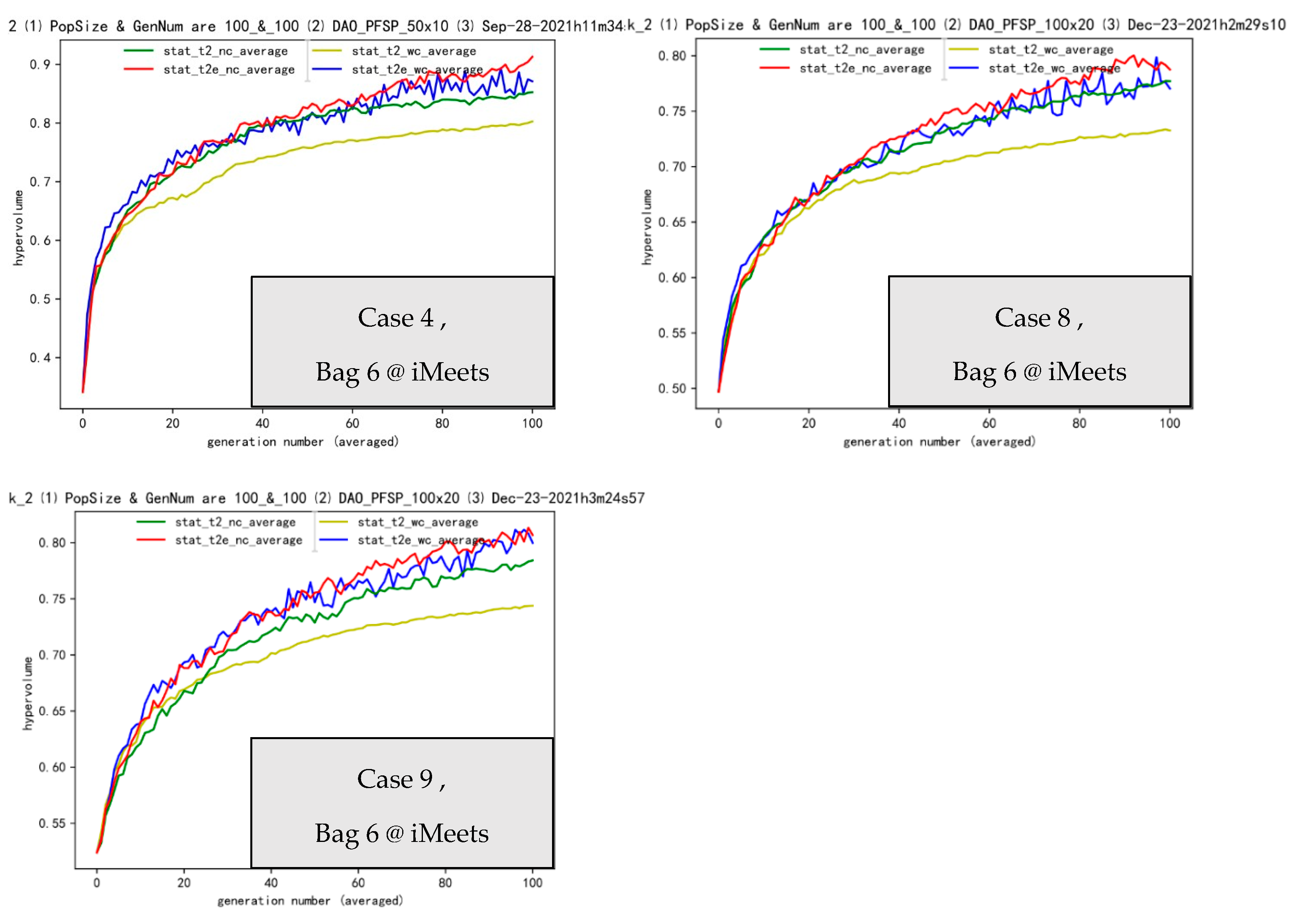
4.2. Insight into Bag 6: Fitness Landscape Analysis via Gaps 2, 4 and 1
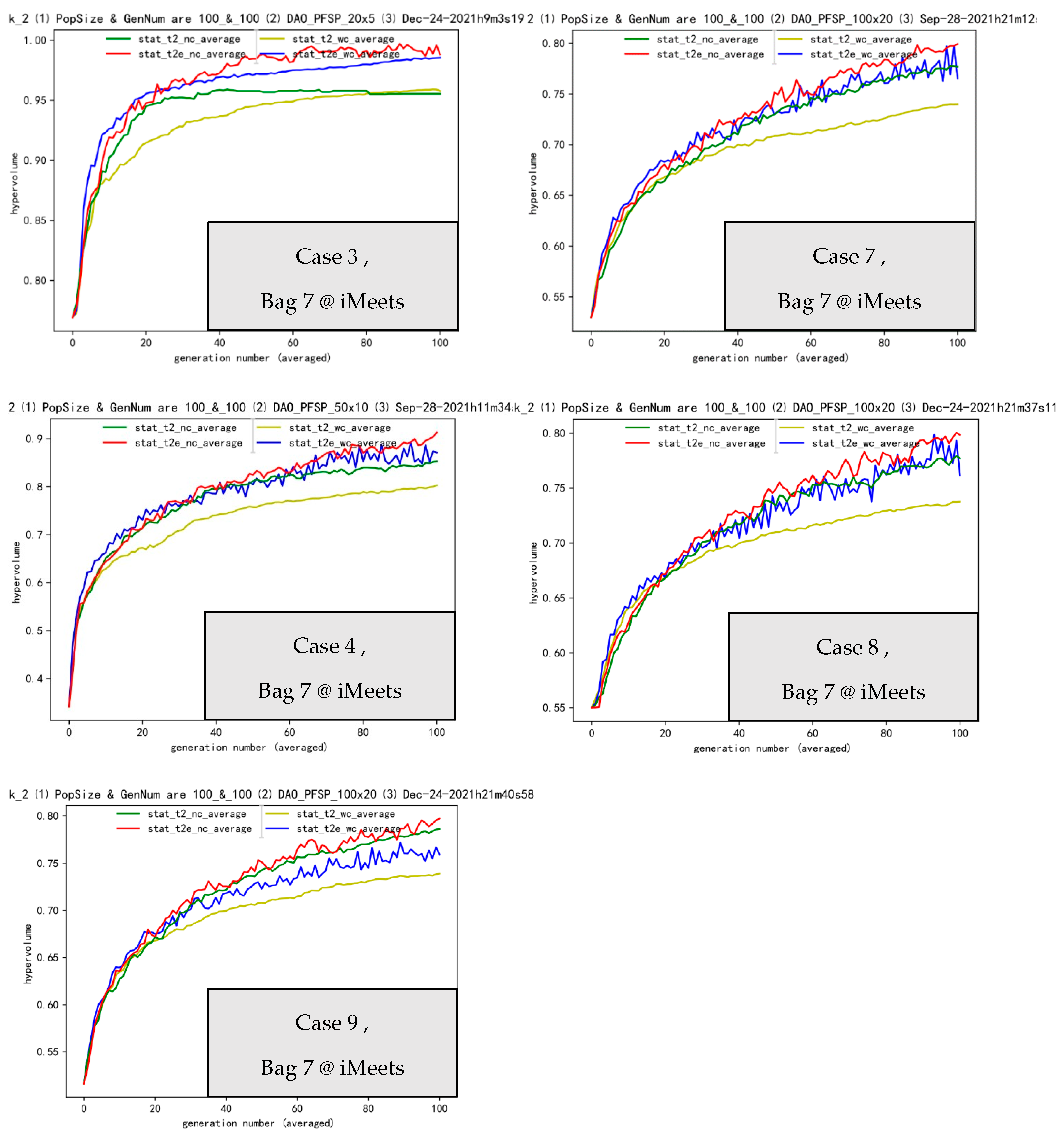
4.3. Insight into Bag 7: Auxiliary Tasks, Transfer Coefficient and Driving Forces
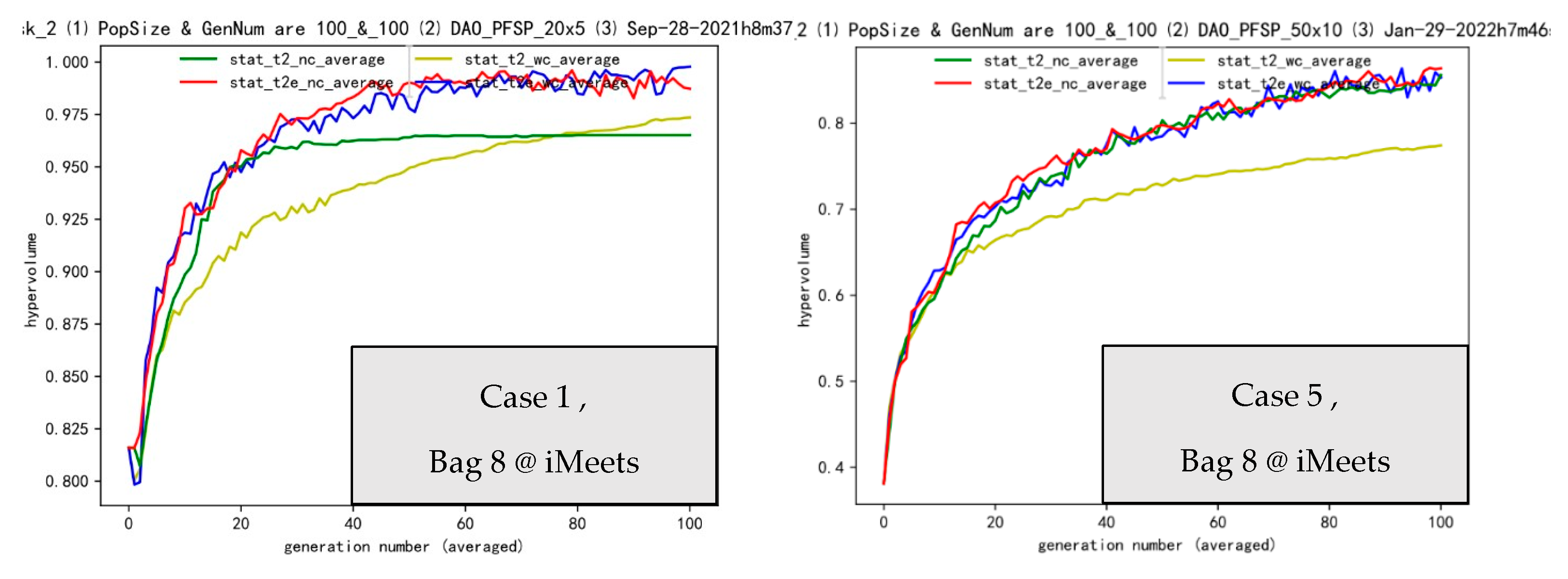
4.4. Insight into Bag 8 and the Whole Picture/Proposal Combining Bag 5,6,7,8: Asynchronous Rhythm, 3W Framework
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weinan, E. A proposal on machine learning via dynamical systems. Comm. Math Stat. 2017, 5, 1–11. [Google Scholar]
- Tang, L.; Meng, Y. Data analytics and optimization for smart industry. Front. Eng. Mana. 2021, 8, 157–171. [Google Scholar] [CrossRef]
- Tan, K.; Feng, L.; Jiang, M. Evolutionary transfer optimization—A new frontier in evolutionary computation research. IEEE Comp. Inte. Magn. 2021, 16, 22–33. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, M. Towards WARSHIP: Combining brain-inspried computing of RSH for image super resolution. In Proceedings of the 2018 5th IEEE International Conference on Cloud Computing and Intelligence Systems, Nanjing, China, 23–25 November 2018. [Google Scholar]
- Xu, W.; Wang, X.; Guo, Q.; Song, X.; Zhao, R.; Zhao, G.; Yang, Y.; Xu, T.; He, D. Towards KAB2S: Learning key knowledge from single-objective problems to multi-objective problem. arXiv 2022, arXiv:2206.12906. [Google Scholar]
- Xu, W.; Wang, X.; Guo, Q.; Song, X.; Zhao, R.; Zhao, G.; Yang, Y.; Xu, T.; He, D. Gathering strength, gathering storms: Knowledge Transfer via Selection for VRPTW. Mathematics 2022, 10, 2888. [Google Scholar] [CrossRef]
- Harik, G. Learning Gene Linkage to Efficiently Solve Problems of Bounded Difficulty Using Genetic Algorithms. Ph.D. Thesis, The University of Michigan, Ann Arbor, MI, USA, 1997. [Google Scholar]
- Chen, Y. Extending the Scalability of Linkage Learning Genetic Algorithms. In Part of the Studies in Fuzziness and Soft Computing Book Series; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Chang, P.; Huang, W.; Wu, J.; Cheng, T. A block mining and recombination enhanced genetic algorithm for the permutation flow-shop scheduling problem. Inter. J. Prod. Econ. 2013, 141, 45–55. [Google Scholar] [CrossRef]
- Huang, L.; Feng, L.; Wang, H.; Hou, Y.; Liu, K.; Chen, C. A preliminary study of improving evolutionary multi-objective optimization via knowledge transfer from single-objective problems. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020. [Google Scholar]
- Yuan, Y.; Ong, Y.; Gupta, A.; Tan, P.; Xu, H. Evolutionary multitasking in permutation-based combinatorial optimization problems: Realization with TSP, QAP, LOP, and JSP. In Proceedings of the 2016 IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016. [Google Scholar]
- Feng, L.; Ong, Y.; Lim, M.; Tsang, I. Memetic search with interdomain learning: A realization between CVRP and CARP. IEEE Trans. Evol. Comp. 2015, 19, 644–658. [Google Scholar] [CrossRef]
- Wang, X.; Tang, L. A machine-learning based memetic algorithm for the multi-objective permutation flowshop scheduling problem. Comp. Oper. Rese. 2017, 79, 60–77. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Gao, L.; Song, Y.; Li, X. An improved simulated annealing algorithm based on residual network for permutation flow shop scheduling. Comp. Inte. Sys. 2020, 7, 1173–1183. [Google Scholar] [CrossRef]
- Shi, J.; Zhao, L.; Wang, X.; Zhao, W.; Huang, M. A novel deep Q-learning-based air-assisted vehicular caching scheme for safe autonomous driving. IEEE Trans. Intelli. Transport. Sys. 2020, 22, 4348–4358. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; Wu, C. Advances in green shop scheduling. Control. Decis. 2018, 33, 385–391. [Google Scholar]
- Lei, N.; Luo, Z.; Yau, S.; Gu, D. Geometric understanding of deep learning. arXiv 2018, arXiv:1805.10451 2018. [Google Scholar] [CrossRef]
- Bronstein, M.; Bruna, J.; Cohen, T.; Velikovi, P. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv 2021, arXiv:2104.13478. [Google Scholar]
- Zhu, Y.; Gao, T.; Fan, L.; Huang, S.; Edmonds, M.; Liu, H.; Gao, F.; Zhang, C.; Qi, S.; Wu, Y.; et al. Dark, beyond deep: A paradigm shift to cognitive ai with humanlike common sense. arXiv 2020, arXiv:2004.09044 2020. [Google Scholar] [CrossRef]
- Wu, F.; Yang, C.; Lan, X.; Ding, J.; Zheng, N.; Gui, W.; Gao, W.; Chai, T.; Qian, F.; Li, D.; et al. Artificial intelligence: Review and future opportunities. Bull. Nation. Natur. Scie. Foun. China 2018, 32, 243–250. [Google Scholar]
- Li, D. Ten questions for the new generation of artificial intelligence. CAAI Trans. Intell. Sys. 2020, 15. [Google Scholar] [CrossRef]
- Littman, M.; Ajunwa, I.; Berger, G.; Boutilier, C.; Currie, M.; Velez, F.; Hadfield, G.; Horowitz, M.; Isbell, C.; Kitano, H.; et al. Gathering Strength, Gathering Storms: The One Hundred Year Study on Artificial Intelligence (AI100) Study Panel Report. Stanford University, Stanford, CA, USA, September 2021. Available online: http://ai100.stanford.edu/2021-report (accessed on 10 February 2023).
- Stone, P.; Brooks, R.; Brynjolfsson, E.; Calo, R.; Etzioni, O.; Hager, G.; Hirschberg, J.; Kalyanakrishnan, S.; Kamar, E.; Kraus, S.; et al. Artificial Intelligence and Life in 2030. Available online: http://ai100.stanford.edu/2016-report (accessed on 10 February 2023).
- Chen, Y.; Chuang, C.; Huang, Y. Inductive linkage identification on building blocks of different sizes and types. Inter. J. Syste. Scien. 2014, 43, 2202–2213. [Google Scholar] [CrossRef]
- Krasnogor, N.; Smith, J. A tutorial for competent memetic algorithms: Model, taxonomy and design issues. IEEE Trans. Evol. Comput. 2005, 9, 474–488. [Google Scholar] [CrossRef]
- Yazdani, D.; Cheng, R.; Yazdani, D.; Branke, J.; Jin, Y.; Yao, X. A survey of evolutionary continuous dynamic optimization over two decades—Part B. IEEE Trans. Evol. Comput. 2021, 49, 205–228. [Google Scholar]
- Cotta, C.; Fernández, A. Memetic Algorithms in Planning, Scheduling, and Timetabling; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Deb, K.; Agrawal, S. Understanding interactions among genetic algorithm parameters. Found. Genet. Algorithms 2002, 5, 265–286. [Google Scholar]
- Al-Sahaf, H.; Bi, Y.; Chen, Q.; Lensen, A.; Mei, Y.; Sun, Y.; Tran, B.; Xue, B.; Zhang, M. A survey on evolutionary machine learning. Journ. Royal. Soci. N. Z. 2021, 49, 205–228. [Google Scholar] [CrossRef]
- Yu, Y.; Chao, Q.; Zhou, Z. Towards analyzing recombination operators in evolutionary search. In Parallel Problem Solving from Nature, PPSN XI: 11th International Conference, Kraków, Poland, 11–15 September 2010, Proceedings; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Li, K.; Chen, R.; Fu, G.; Yao, X. Two-archive evolutionary algorithm for constrained multi-objective optimization. IEEE Trans. Evol. Comput. 2017, 99, 165–181. [Google Scholar]
- Wall, M. A Genetic Algorithm for Resource-Constrained Scheduling. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1996. [Google Scholar]
- Pinedo, M. Scheduling: Theory, Algorithms, and Systems; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Huang, G.; Huang, G.; Song, S.; You, K. Trends in extreme learning machines. Neur. Networ. 2015, 61, 32–48. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, R.; Pan, Q.; Naderi, B. Iterated greedy methods for the distributed permutation flowshop scheduling problem. Omega 2019, 83, 213–222. [Google Scholar] [CrossRef]
- Tan, K.; Lee, L.; Zhu, Q.; Ou, K. Heuristic methods for vehicle routing problem with time windows. Artif. Intelli. Engin. 2001, 15, 281–295. [Google Scholar] [CrossRef]
- Cordeau, J.; Desaulniers, G.; Desrosiers, J.; Solomon, M.; Soumis, F. The VRP with Time Windows; SIAM: Philadelpia, PA, USA, 2000. [Google Scholar]
- Watson, J.; Barbulescu, L.; Whitley, L.; Howe, A. Contrasting structured and random permutation flow-shop scheduling problems: Search-space topology and algorithm performance. INFO J. Compu. 2002, 14, 98–123. [Google Scholar] [CrossRef]
- Fieldsend, J. Computationally efficient local optima network construction. In Proceedings of the Genetic and Evolutionary Computation Conference Companion 2018, Kyoto, Japan, 15–19 July 2018. [Google Scholar]
- Zhou, Z.; Yu, Y. A new approach to estimating the expected first hitting time of evolutionary algorithms. In Proceedings of the 21st National Conference on Artificial Intelligence, Boston, MA, USA, 16–20 July 2006; Volume 172, pp. 1809–1832. [Google Scholar]
- Vérel, S.; Daolio, F.; Ochoa, G.; Tomassini, M. Local optima networks with escape edges. In Proceedings of the Artificial Evolution: 10th International Conference, Evolution Artificielle, EA 2011, Angers, France, 24–26 October 2011. [Google Scholar]
- Bandaru, S.; Ng, A.; Deb, K. Data mining methods for knowledge discovery in multi-objective optimization. Expert Syst. Appl. 2017, 70, 139–159. [Google Scholar] [CrossRef]
- Liu, X.; Xie, Y.; Li, F.; Gui, W. Admissible consensus for homogenous descriptor multiagent systems. IEEE Trans. Sys Man Cybern. Syst. 2019, 51, 965–974. [Google Scholar] [CrossRef]
- Gupta, A.; Ong, Y.; Feng, L. Multifactorial evolution: Toward evolutionary multitasking. IEEE Trans. Evolu. Compu. 2016, 20, 343–357. [Google Scholar]
- Park, J.; Mei, Y.; Nguyen, S.; Chen, G.; Zhang, M. An investigation of ensemble combination schemes for genetic programming based hyper-heuristic approaches to dynamic job shop scheduling. Appli. Soft Compu. 2017, 63, 72–86. [Google Scholar] [CrossRef]
- Miikkulainen, R.; Forrest, S. A biological perspective on evolutionary computation. Nat. Mach. Intell. 2016, 3, 9–15. [Google Scholar] [CrossRef]
- Pak, I. Random Walks on Groups: Strong Uniform Time Approach; Harvard University: Cambridge, MA, USA, 1997. [Google Scholar]
- Chen, W.; Ishibuchi, H.; Shang, K. Clustering-based subset selection in evolutionary multiobjective optimization. arXiv 2021, arXiv:2108.08453 2021. [Google Scholar]
- Xu, W.; Wang, X. ETO meets scheduling: Learning key knowledge from single-objective problems to multi-objective problem. In Chinese Automation Congress; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Pan, S.; Yang, Q. A survey on transfer learning. IEEE Trans. Know. Data Engin. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Pan, Y.; Li, X.; Yang, Y. A content-based neural reordering model for statistical machine translation. In Proceedings of the Machine Translation: 13th China Workshop, CWMT 2017, Dalian, China, 27–29 September 2017. [Google Scholar]
- Gui, W.; Zeng, Z.; Chen, X.; Xie, Y.; Sun, Y. Knowledge-driven process industry smart manufacturing. Scien. Sin. Inform. 2020. [Google Scholar] [CrossRef]
- Bengio, Y. Deep learning of representations for unsupervised and transfer learning. In Proceedings of the Workshop on Unsupervised & Transfer Learning, Bellevue, WA, USA, 2 July 2011. [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Gupta, A.; Ong, Y.; Feng, L. Insights on transfer optimization: Because experience is the best teacher. IEEE Trans. Emer. Top. Comp. Intelli. 2017, 2, 51–64. [Google Scholar] [CrossRef]
- Bai, L.; Lin, W.; Gupta, A.; Ong, Y. From multi-task gradient descent to gradient-free evolutionary multitasking: A proof of faster convergence. IEEE Trans. Cybern. 2021, 52, 8561–8573. [Google Scholar] [CrossRef]
- Liao, Q.; Poggio, T. Theory of deep learning II: Landscape of the empirical risk in deep learning. arXiv 2017, arXiv:1703.09833 2017. [Google Scholar]
- Xu, W.; Zhang, M. Theory of generative deep learning II: Proble landscape of empirical error via norm based capacity control. In Proceedings of the 2018 5th IEEE International Conference on Cloud Computing and Intelligence Systems (CCIS), Nanjing, China, 23–25 November 2018. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. arXiv 2012, arXiv:1206.5538 2012. [Google Scholar] [CrossRef]
- Sun, N. A rule in computer systems from the perspective of engineering science. China Nation. Comput. Cong. 2021. [Google Scholar]
- Zhang, P. Machine Learning Driven Computational Modeling. 2019. Available online: https://www.bilibili.com/video/av59553660/ (accessed on 10 February 2023).
- Wang, S.; Hu, Y.; Xiong, X.; Wang, S.; Zhang, W. Theories and methods research on complex management. J. Manag. Sci. China 2021. [Google Scholar]
- Tsien, H.-s.; Xu, G.; Wang, S. Technologies in Organizational Management: System Engineering; The Shanghai Mercury: Shanghai, China, 1978. [Google Scholar]
- Xu, F.; Tang, H.; Xun, Q.; Lan, H.; Liu, X.; Xing, W.; Zhu, T.; Wang, L.; Pang, S. Research on green reentrant hybrid flow shop scheduling problem based on improved moth-flame optimization algorithm. Processes 2022, 10, 2475. [Google Scholar] [CrossRef]
- Mehdi, F.; Kate, S. The impact of various carbon reduction policies on green flowshop scheduling. Appl. Energy 2019, 249, 300–315. [Google Scholar]






| Bag 5 | Operators and Transfer Effectiveness | |||
|---|---|---|---|---|
| Operators Notes: g means group e means effectiveness ee means great effectiveness. ie means ineffectiveness | t2_wc V.S. t2e_wc | t2_nc V.S. t2e_nc | ||
| case 1 | head (0~6) | total 0~19 | ee | ee |
| case 2 | middle (7~12) | total 0~19 | ee | ee |
| case 3 | tail (13~19) | total 0~19 | ee | ee |
| case 4 | head (0~16) | total 0~49 | ee | e |
| case 5 | middle (17~32) | total 0~49 | ee | e |
| case 6 | tail (33~49) | total 0~49 | ee | e |
| case 7 | head (0~33) | total 0~99 | ee | e |
| case 8 | middle (34~65) | total 0~99 | e | e |
| case 9 | tail (66~99) | total 0~99 | ee | e |
| Summary: Bag 5, head (case 147): ee, e middle (case 258): ee, e tail (case 369): ee, e | ||||
| Bag 6 | Operators and Transfer Effectiveness | ||
|---|---|---|---|
| Operators Notes: g means group e means effectiveness ee means great effectiveness. ie means ineffectiveness | t2_wc V.S. t2e_wc | t2_nc V.S. t2e_nc | |
| case 1 | transfer gap 2:2:2 | ee | ee |
| case 2 | transfer gap 4:4:4 | ee | e |
| case 3 | transfer gap 1:1:1 | ee | ee |
| case 4 | transfer gap 2:2:2 | ee | e |
| case 5 | transfer gap 4:4:4 | ee | e |
| case 6 | transfer gap 1:1:1 | ee | e |
| case 7 | transfer gap 2:2:2 | ee | e |
| case 8 | transfer gap 4:4:4 | ee | e |
| case 9 | transfer gap 1:1:1 | ee | e |
| Summary: Bag 6, baseline gap(case147): ee, e faster gap(case258): ee, e slower gap(case369): ee, e | |||
| Bag 7 | Operators and Transfer Effectiveness | |||
|---|---|---|---|---|
| Operators Notes: g means group e means effectiveness ee means great effectiveness. ie means ineffectiveness | t2_wc V.S. t2e_wc | t2_nc V.S. t2e_nc | ||
| case 1 | left tft, | right cmax | ee | ee |
| case 2 | left tft, | right tft | ee | ee |
| case 3 | left cmax | right cmax | ee | ee |
| case 4 | left tft, | right cmax | ee | e |
| case 5 | left tft, | right tft | ee | e |
| case 6 | left cmax | right cmax | e | e |
| case 7 | left tft, | right cmax | ee | e |
| case 8 | left tft, | right tft | ee | e |
| case 9 | left cmax | right cmax | e | e |
| Summary: Bag 7, tm (case147): ee, e tt (case258): ee, e mm (case369): e, e | ||||
| Bag 8 | Operators and Transfer Effectiveness | ||
|---|---|---|---|
| Operators Notes: g means group e means effectiveness ee means great effectiveness. ie means ineffectiveness | t2_wc V.S. t2e_wc | t2_nc V.S. t2e_nc | |
| case 1 | transfer gap 2:2:2 | ee | ee |
| case 2 | transfer gap 4:2:4 | e | e |
| case 3 | transfer gap 4:2:2 | ee | e |
| case 4 | transfer gap 2:2:2 | ee | e |
| case 5 | transfer gap 4:2:4 | ee | ie |
| case 6 | transfer gap 4:2:2 | ee | ie |
| case 7 | transfer gap 2:2:2 | ee | e |
| case 8 | transfer gap 4:2:4 | ee | ie |
| case 9 | transfer gap 4:2:2 | e | ie |
| Summary: Bag 8, rhythm/gap(case147): ee, e rhythm/gap(case258): ee, ie rhythm/gap(case369): ee, ie | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Wang, X.; Guo, Q.; Song, X.; Zhao, R.; Zhao, G.; Yang, Y.; Xu, T.; He, D. Evolutionary Process for Engineering Optimization in Manufacturing Applications: Fine Brushworks of Single-Objective to Multi-Objective/Many-Objective Optimization. Processes 2023, 11, 693. https://doi.org/10.3390/pr11030693
Xu W, Wang X, Guo Q, Song X, Zhao R, Zhao G, Yang Y, Xu T, He D. Evolutionary Process for Engineering Optimization in Manufacturing Applications: Fine Brushworks of Single-Objective to Multi-Objective/Many-Objective Optimization. Processes. 2023; 11(3):693. https://doi.org/10.3390/pr11030693
Chicago/Turabian StyleXu, Wendi, Xianpeng Wang, Qingxin Guo, Xiangman Song, Ren Zhao, Guodong Zhao, Yang Yang, Te Xu, and Dakuo He. 2023. "Evolutionary Process for Engineering Optimization in Manufacturing Applications: Fine Brushworks of Single-Objective to Multi-Objective/Many-Objective Optimization" Processes 11, no. 3: 693. https://doi.org/10.3390/pr11030693
APA StyleXu, W., Wang, X., Guo, Q., Song, X., Zhao, R., Zhao, G., Yang, Y., Xu, T., & He, D. (2023). Evolutionary Process for Engineering Optimization in Manufacturing Applications: Fine Brushworks of Single-Objective to Multi-Objective/Many-Objective Optimization. Processes, 11(3), 693. https://doi.org/10.3390/pr11030693









