Research on Contact Anchoring Theory and Contact Optimization of Underwater Pipeline Recovery Tools
Abstract
:1. Introduction
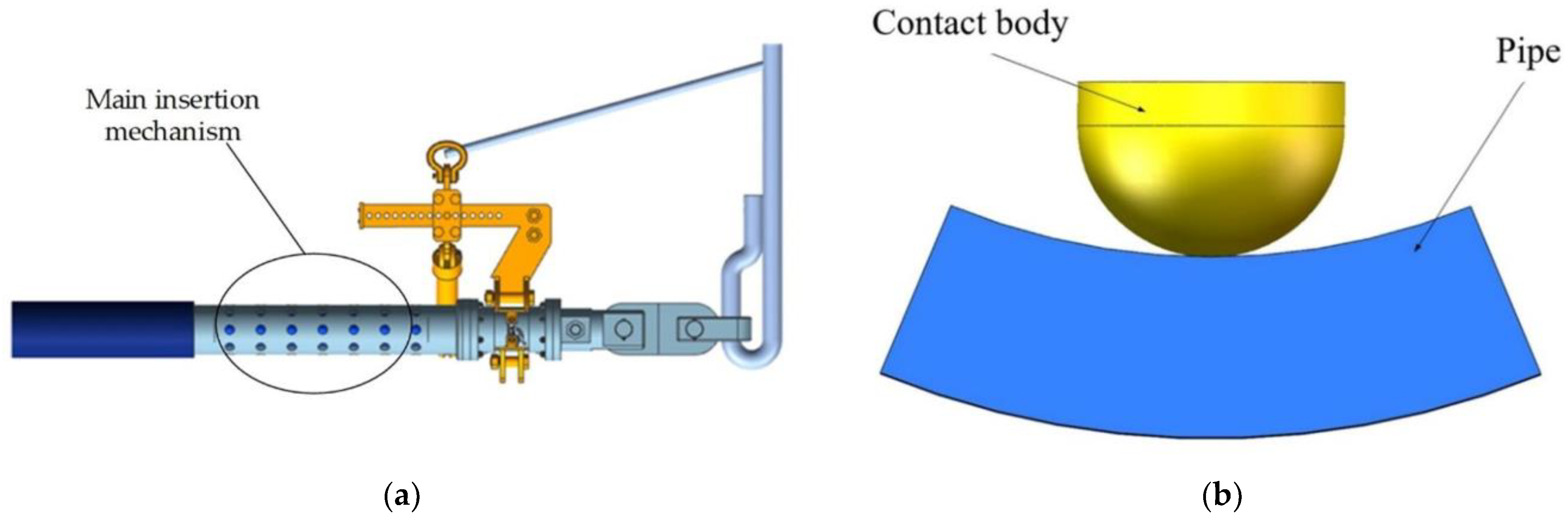
2. The Structure of the Subsea Pipeline Recovery Tool
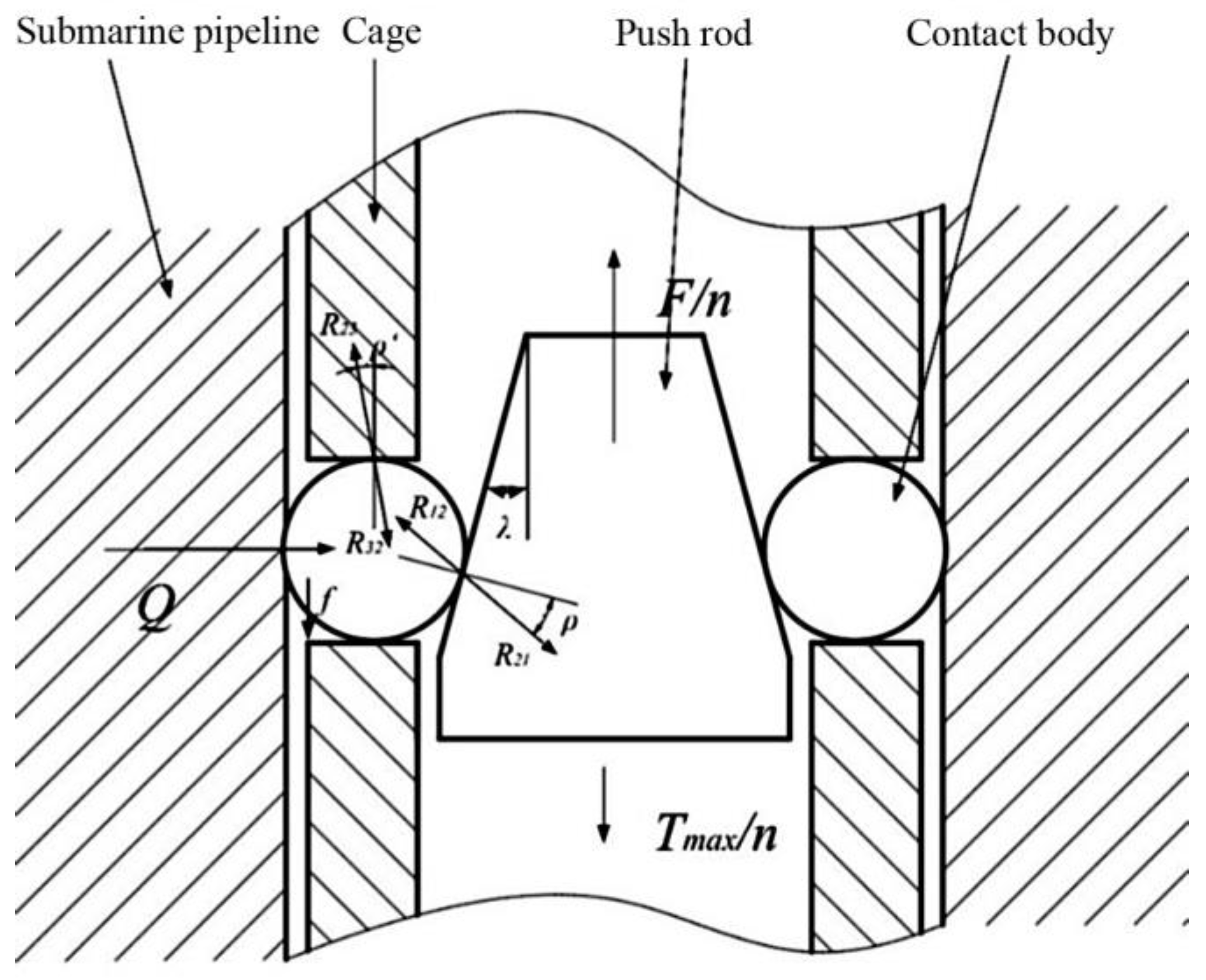
3. Contact Anchoring Theory Analysis
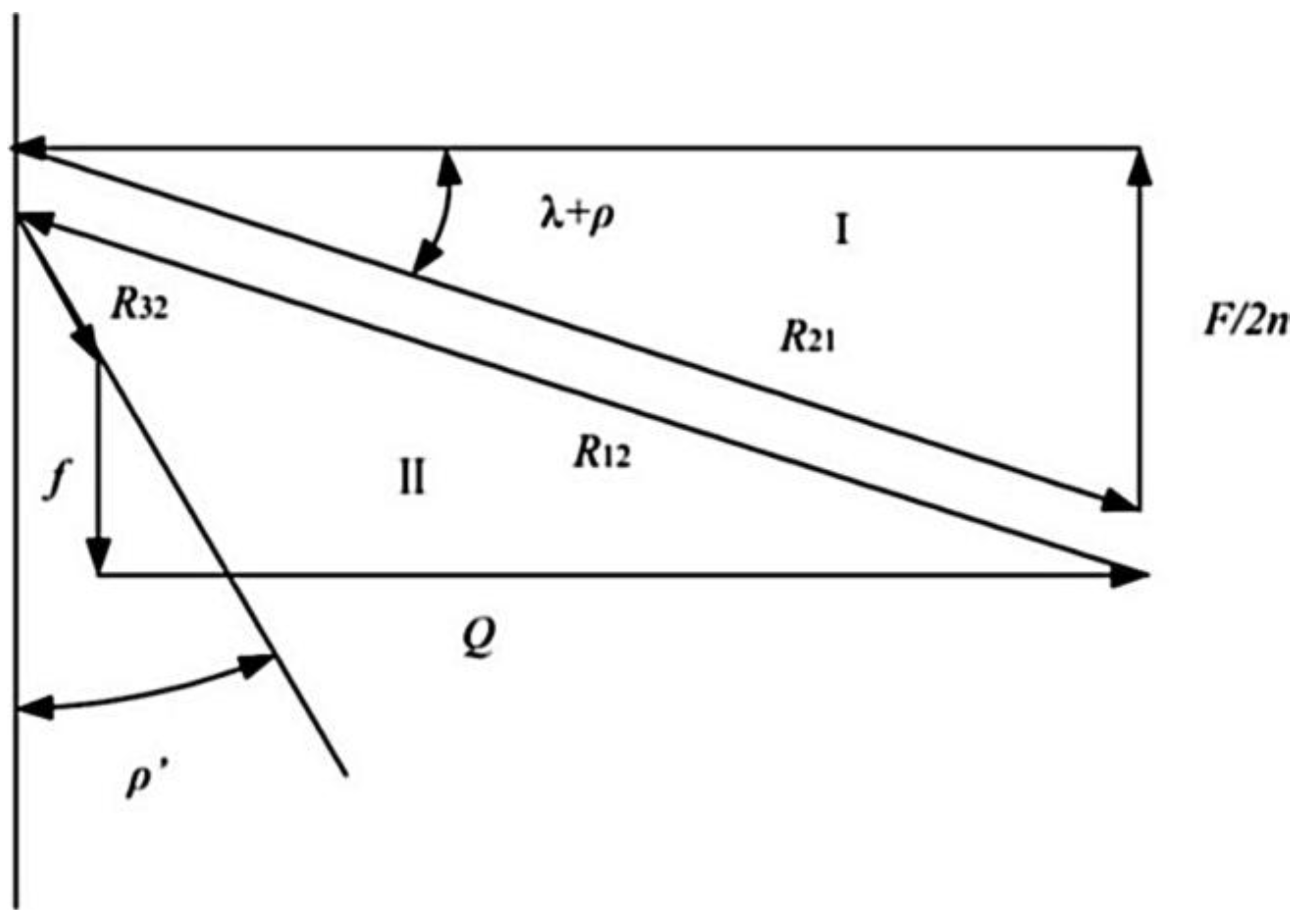
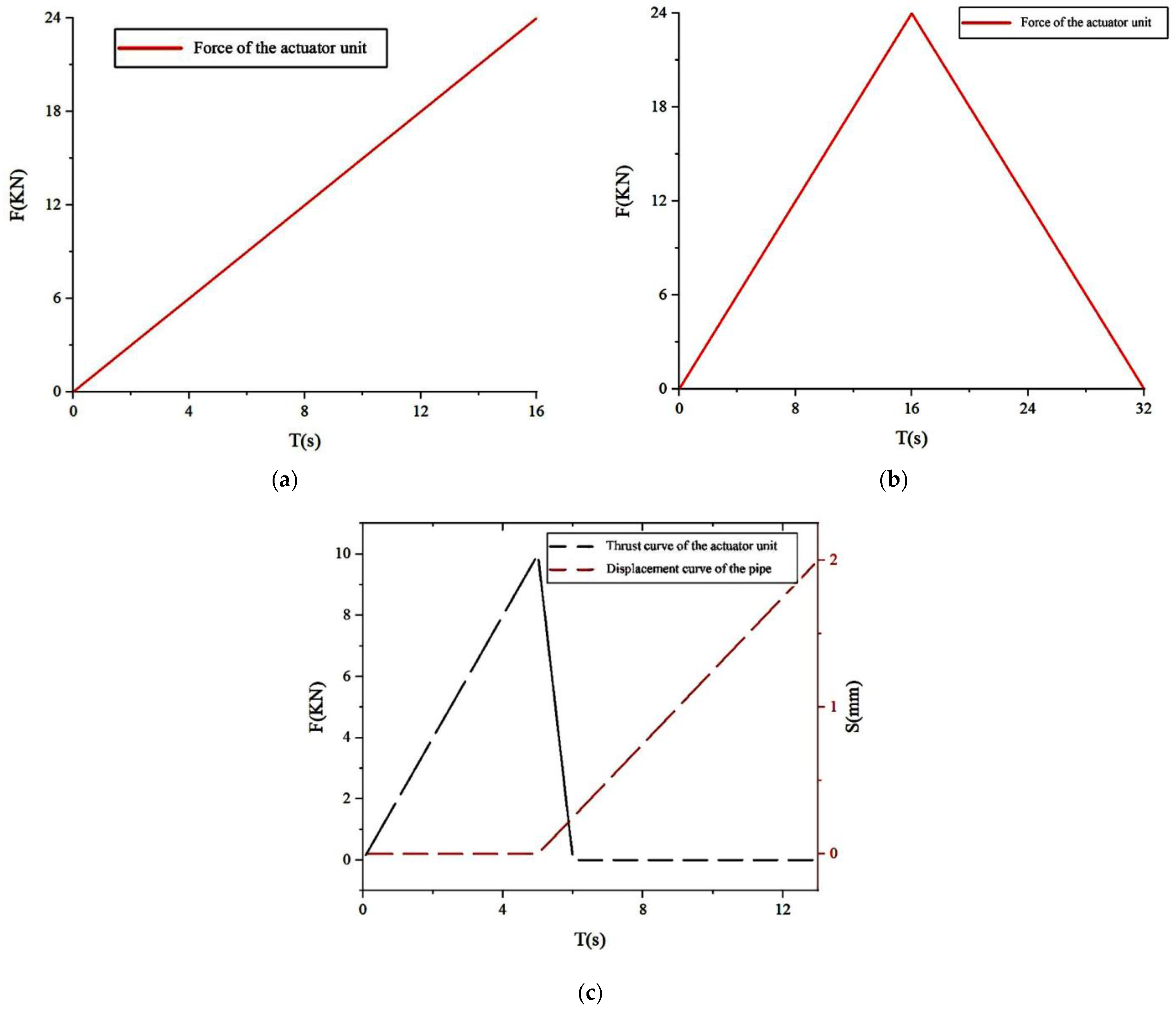
3.1. Force Analysis during Loading Stroke
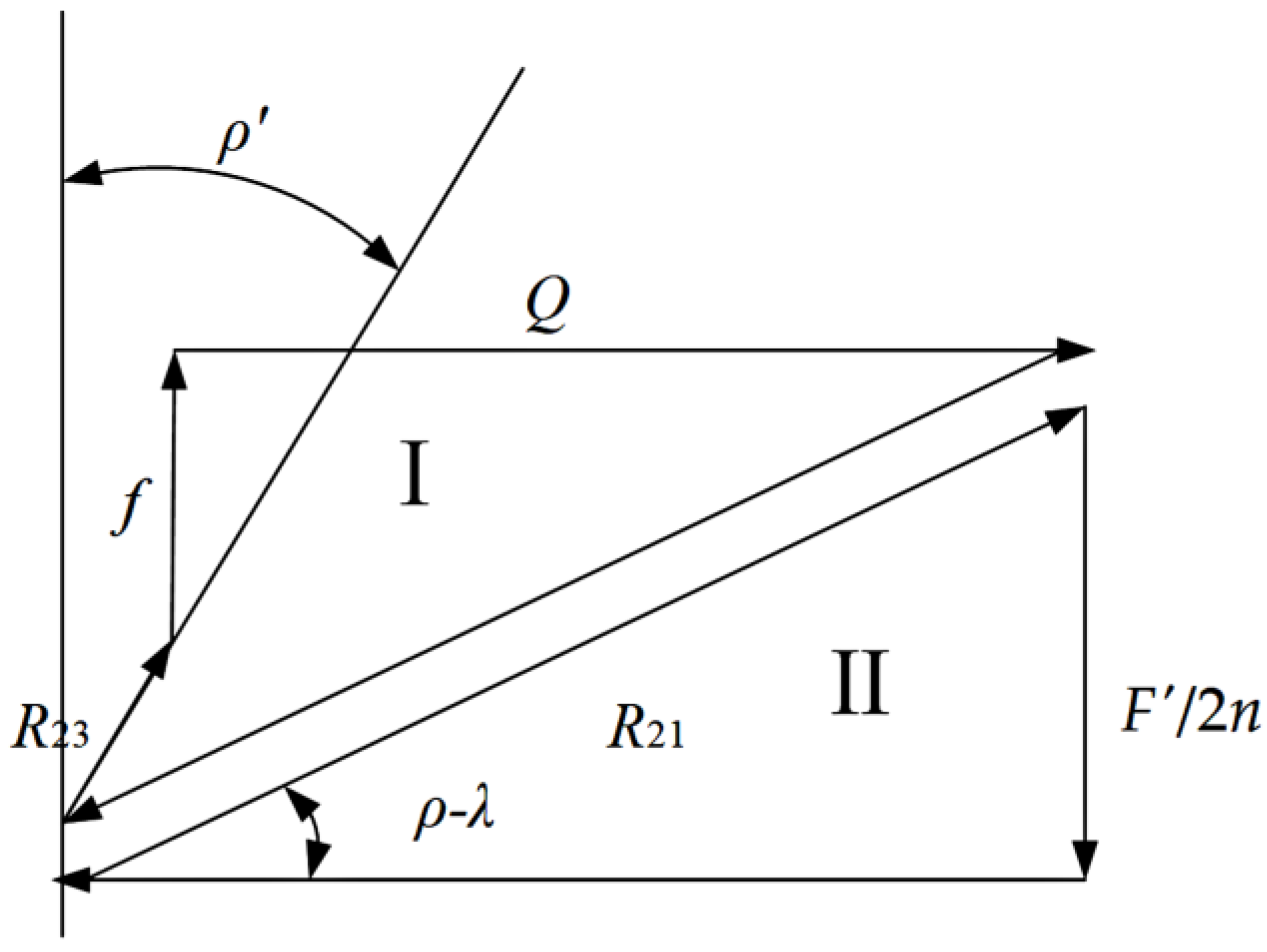
3.2. Force Analysis during Unloading
3.3. Analysis of Locking Structure
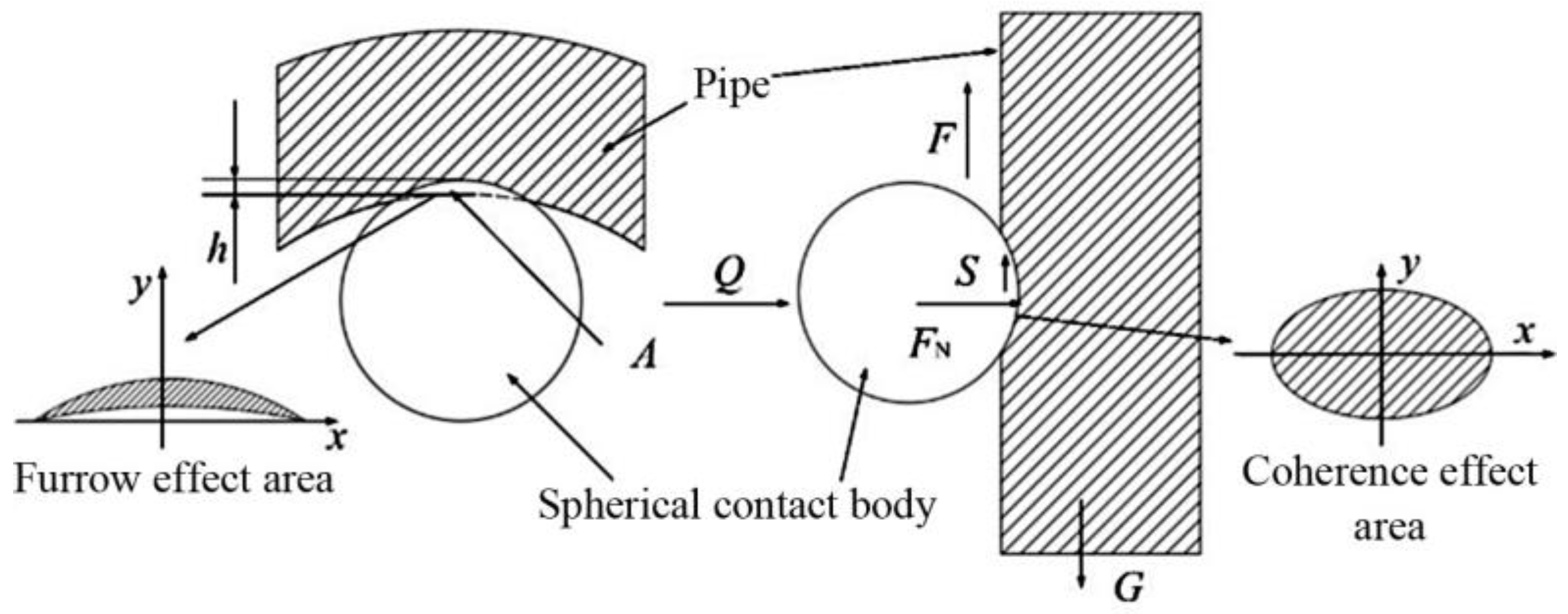
4. Damage Mechanism Analysis
5. Simulation and Experimentation
5.1. Grid Division
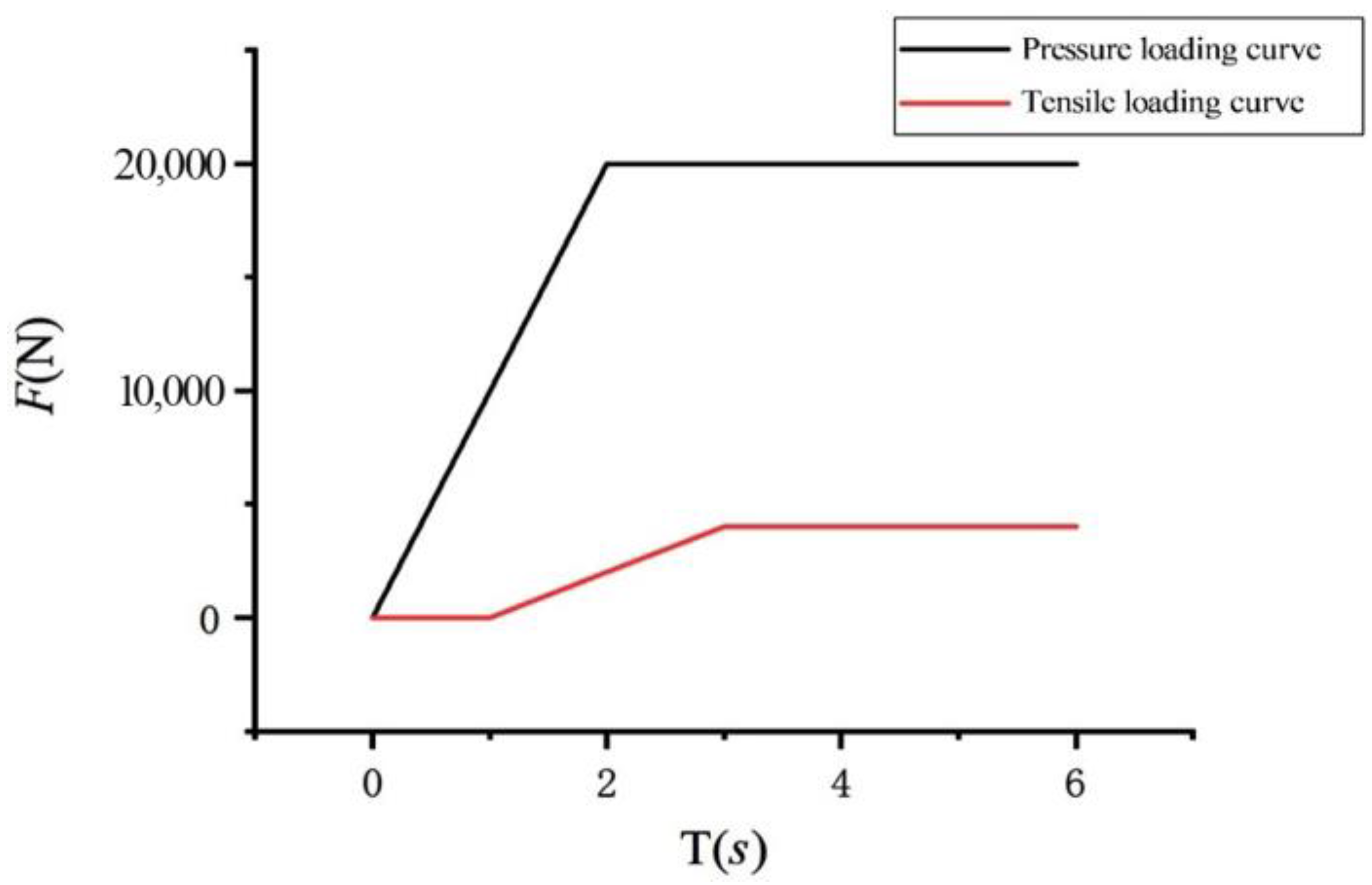
5.2. Boundary Conditions
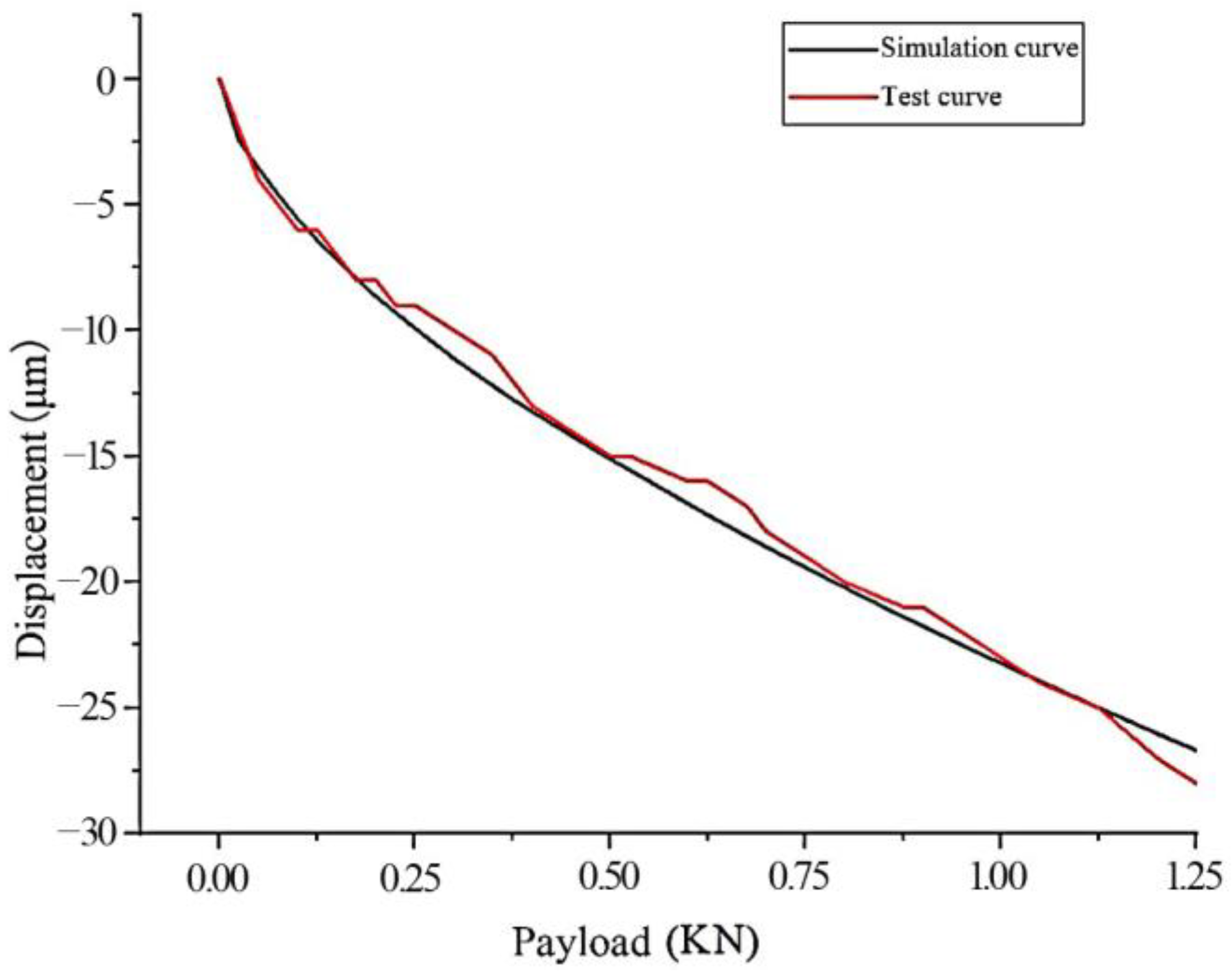
5.3. Simulation Verification Experiment
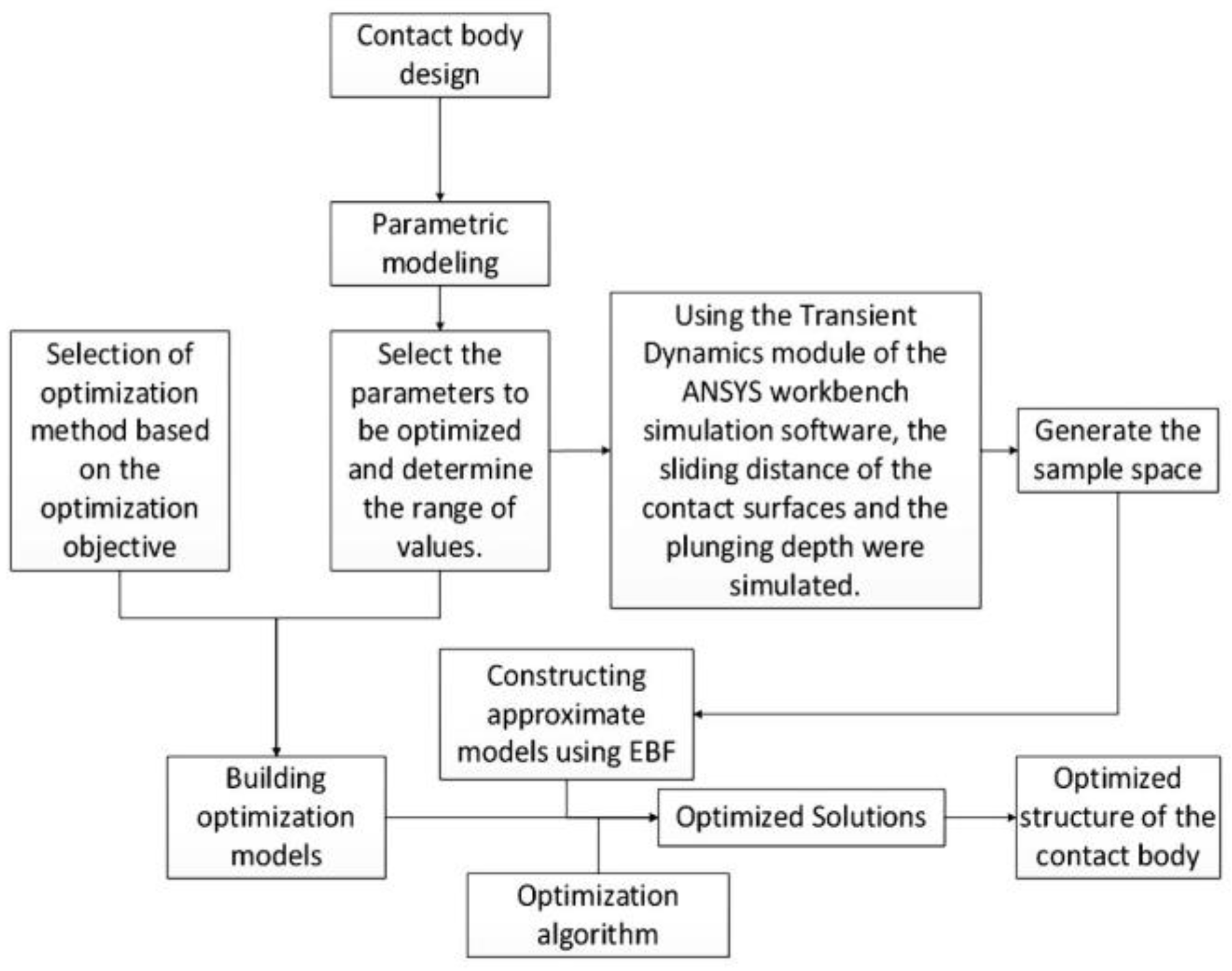
6. Multi-Objective Optimization Design
6.1. Parametric Modeling
6.2. Design of Experiment Method
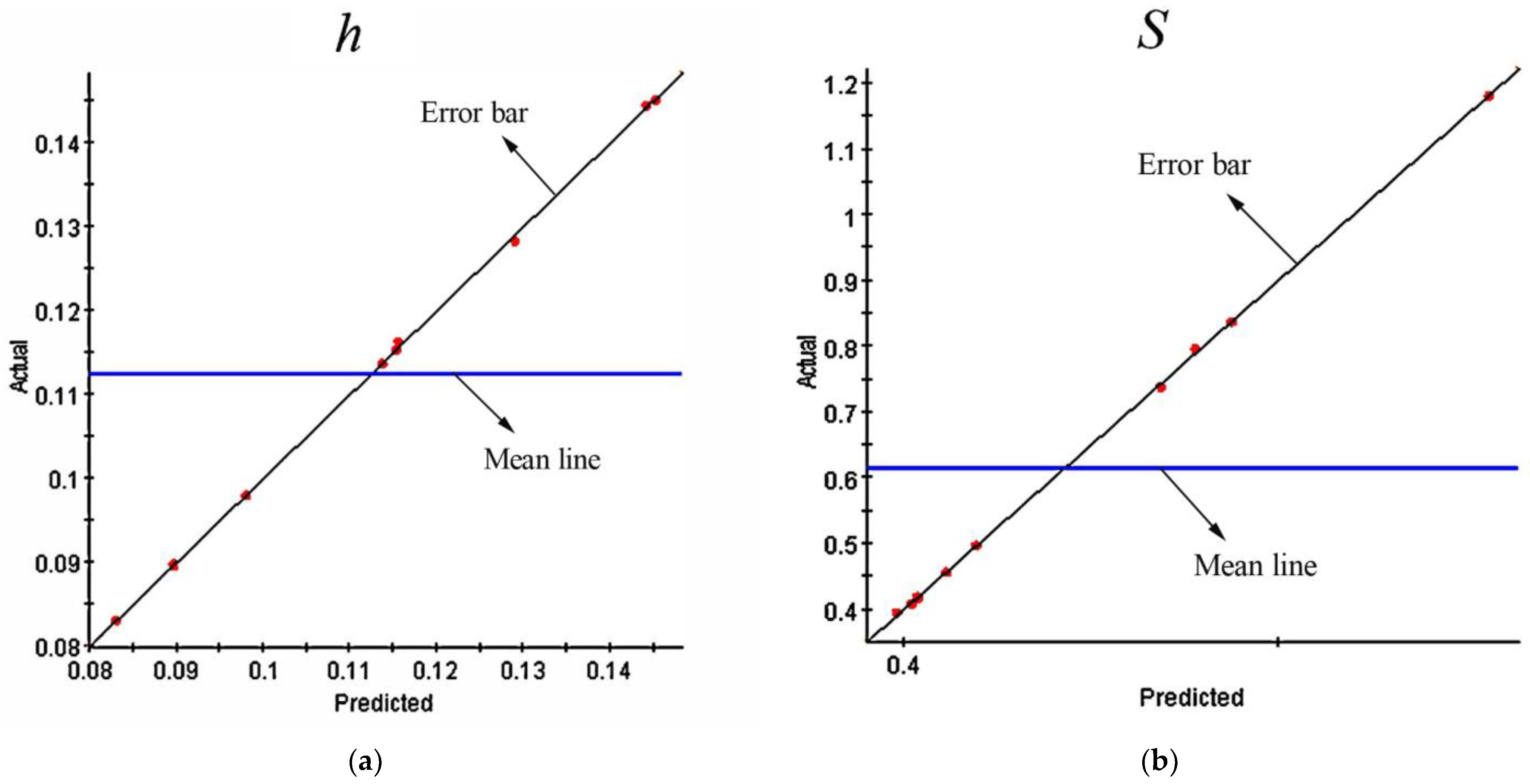
6.3. Approximation Model
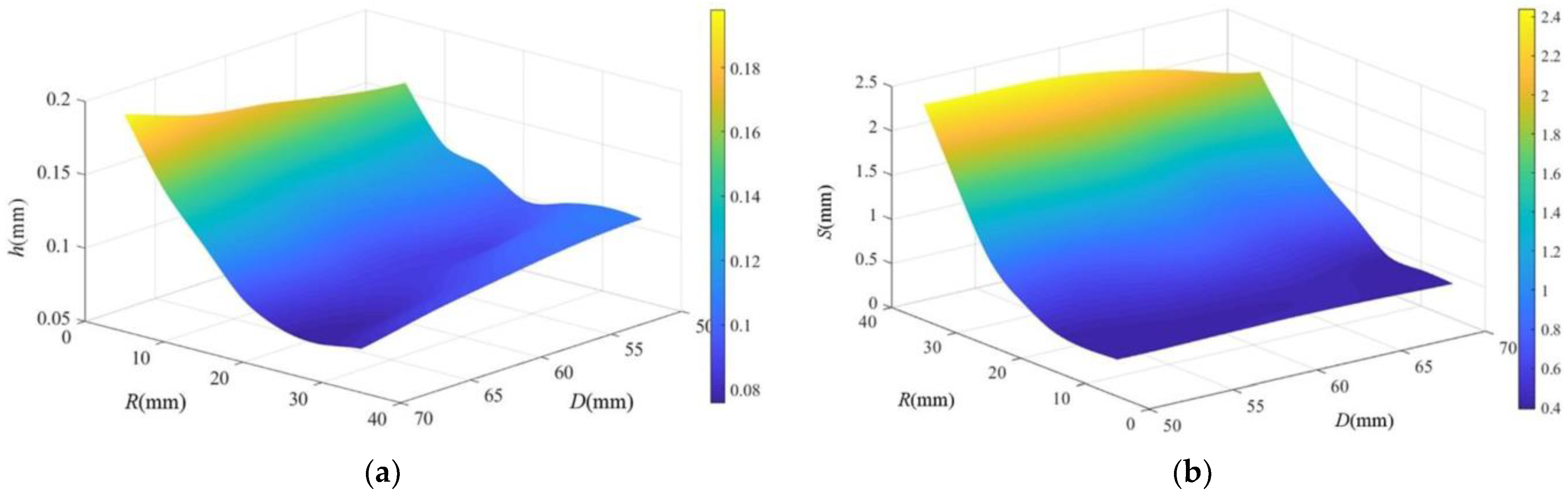
6.3.1. Sensitivity Analysis
6.3.2. Approximate Modeling
6.4. Multi-Objective Optimization Mathematical Model
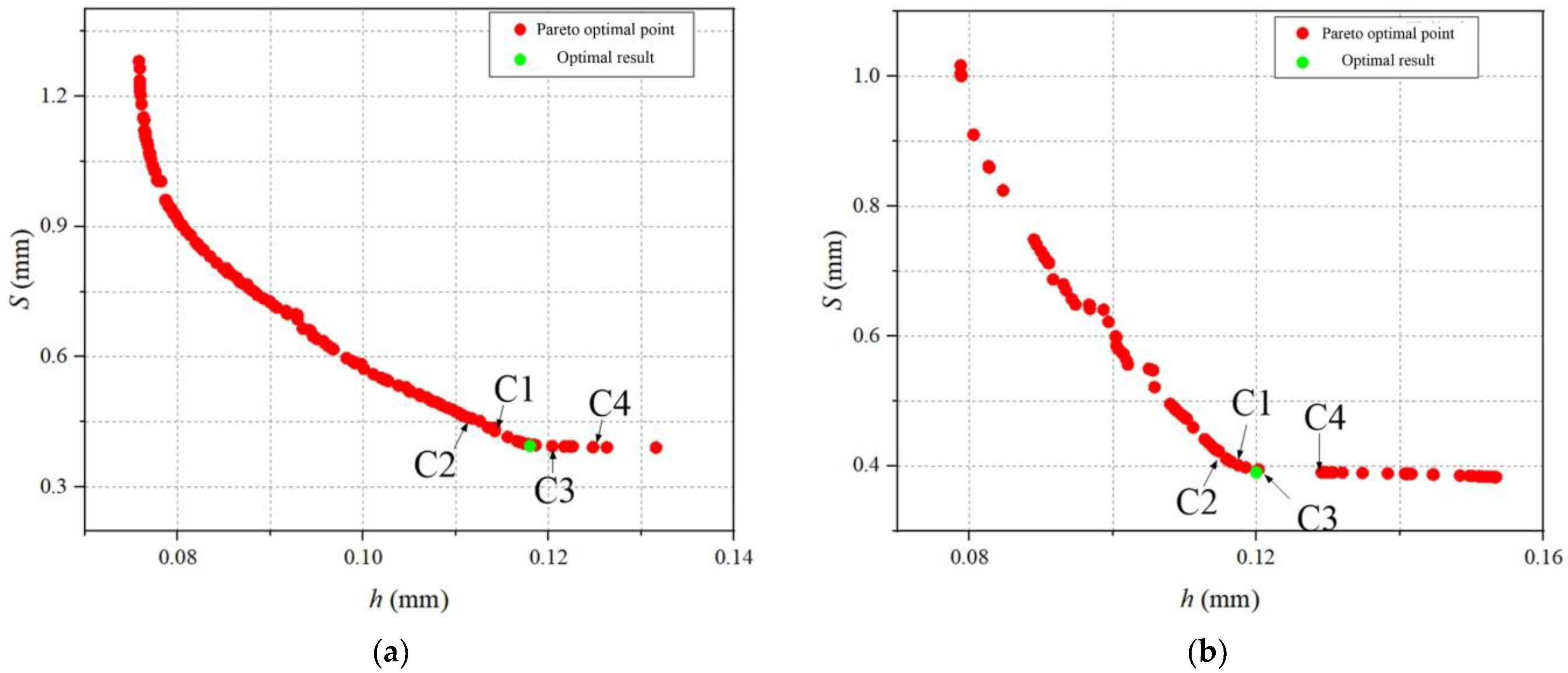
6.5. Multi-Objective Optimization Algorithm
7. Results and Discussion
7.1. Optimization Results Analysis
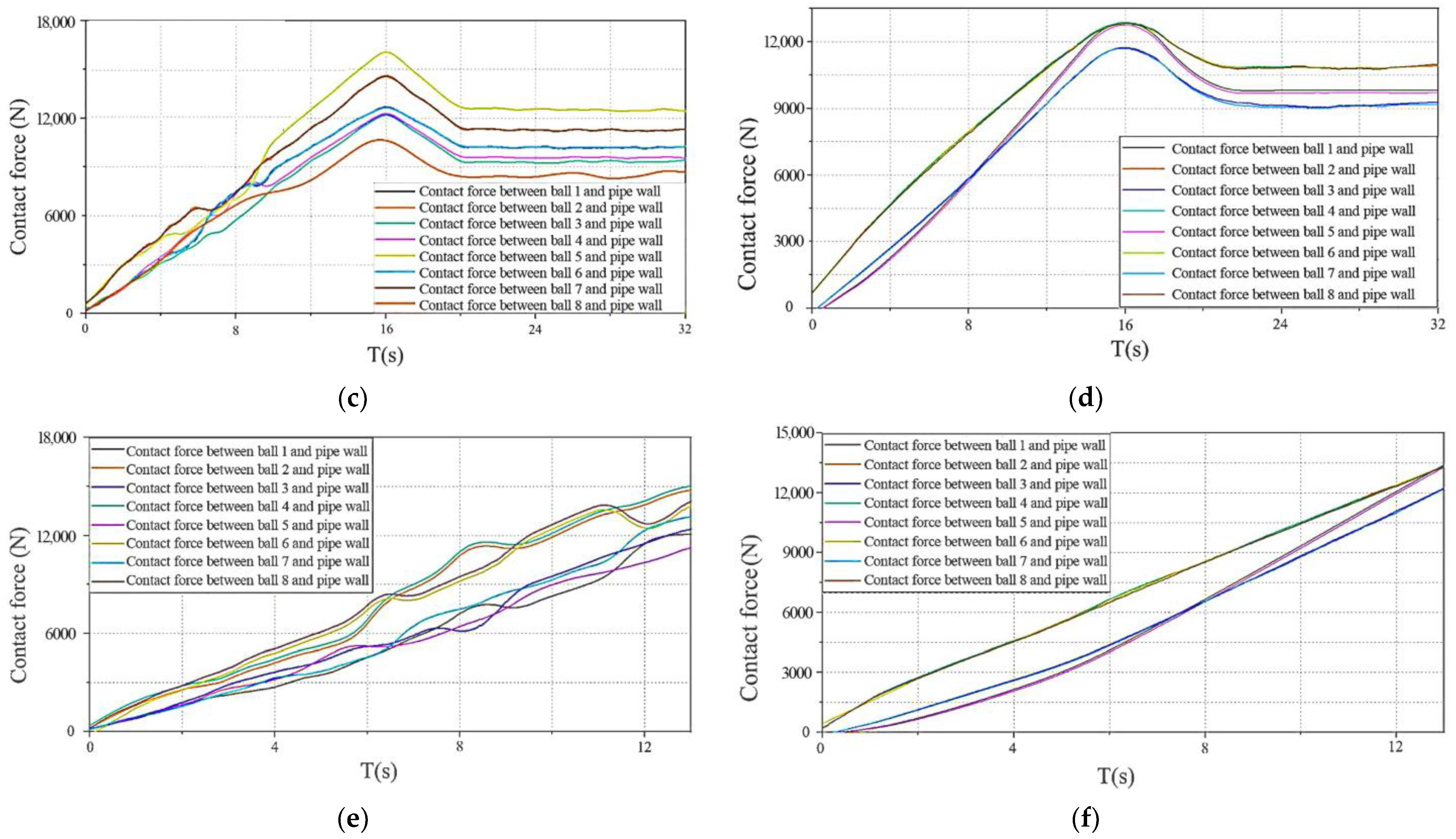
7.2. Simulation Verification
8. Conclusions
- When compared to NCGA, NSGA-II’s optimization results have greater convergence. S reduces by 49.5%, while h rises by 38.3%. The wear issue between the contact body and the inner wall of the pipe is greatly reduced by the improved contact body. The ideal design parameters are D = 57 mm and R = 11.5 mm;
- In comparison to the pre-optimization, the maximum average contact force between the optimized contact body and the pipe is low at 12,650 N. However, the improved contact body and actuator continue to fulfill the design criteria with regard to force increase capacity, making the pipe recovery operation safer;
- The minimum value of the optimal contact force between the contact body and the pipe is 9028 N, which is higher than the optimal value of 8521 N. When the pipe is expanded, the improved contact body and actuator structure remain self-locking, and the contact force between the contact body and the pipe is more consistent;
- The pipe may still be locked when it is expanded and tightened, thanks to the improved contact body and actuator construction. The contact force between the pre-optimized contact body and the pipe varies significantly during the pipe displacement stage, but the contact force between the optimized contact body and the pipe is steady. As a result, when expanding and recovering the pipe, the improved contact body and actuator construction have superior stability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, H.; Zhao, T.; You, X.; Wang, L.; Yun, F.J. Scaled model simulation and experimental verification of submarine flexible pipeline laying system. Appl. Sci. 2021, 11, 10292. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, H.; Liu, M.; Zhu, Z.; Sha, X.; Wang, L. Simulation study on mechanical wear of the diamond grain cutting pipeline steel. Part C J. Mech. Eng. Sci. 2023, 237, 3493–3506. [Google Scholar] [CrossRef]
- Javidi, A.; Salajegheh, E.; Salajegheh, J. Optimization of weight and collapse energy of space structures using the multi-objective modified crow search algorithm. Eng. Comput. 2021, 38, 2879–2896. [Google Scholar] [CrossRef]
- Guo, X.-S.; Nian, T.-K.; Fan, N.; Jia, Y.-G. Optimization design of a honeycomb-hole submarine pipeline under a hydrodynamic landslide impact. Mar. Georesour. Geotechnol. 2021, 39, 1055–1070. [Google Scholar] [CrossRef]
- Gong, H.; Li, H.; Yu, W.; Liu, S.; Yang, S.; Wang, C. Structural Design and Optimization of an Underwater Skirt Pile Gripper. Int. J. Perform. Eng. 2018, 14, 3033. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, Z.; Lian, H.; Xing, X.; Gong, H.; Xu, X. Hull shape optimization of small underwater vehicle based on Kriging-based response surface method and multi-objective optimization algorithm. Brodogradnja 2022, 73, 111–134. [Google Scholar] [CrossRef]
- Liu, F.; Hu, Y.-M.; Feng, G.-Q.; Zhao, W.-D.; Zhang, M. A study on the multi-objective optimization method of brackets in ship structures. China Ocean Eng. 2022, 36, 208–222. [Google Scholar] [CrossRef]
- Yang, H.; Wang, A.; Li, H. Multi-objective optimization for deepwater dynamic umbilical installation analysis. Sci. China Phys. Mech. Astron. 2012, 55, 1445–1453. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, C.Q.; Wang, L.Q.; Ru, C.; Zhu, Z.B. Design and Experimental Research of Expansion-Anchorage Device in Deepwater Pipeline. In Proceedings of the International Symposium on Power Electronics and Control Engineering (ISPECE), Xian, China, 28–30 December 2018. [Google Scholar]
- Li, T.; Jiang, D.P.; Xie, P. Anchoring and suspending pipe string mechanical behavior of slip ram for subsea blowout preventer. Ocean. Eng. 2022, 247, 110670. [Google Scholar] [CrossRef]
- Brach, S.; Collet, S. Criterion for critical junctions in elastic-plastic adhesive wear. Phys. Rev. Lett. 2021, 127, 185501. [Google Scholar] [CrossRef] [PubMed]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Oxford University Press: Oxford, UK, 2001; Volume 1. [Google Scholar]
- Akbarzadeh, S.; Khonsari, M. On the applicability of miner’s rule to adhesive wear. Tribol. Lett. 2016, 63, 29. [Google Scholar] [CrossRef]
- Aghababaei, R.; Warner, D.H.; Molinari, J.-F. Critical length scale controls adhesive wear mechanisms. Nat. Commun. 2016, 7, 11816. [Google Scholar] [CrossRef]
- Mishina, H.; Hase, A. Effect of the adhesion force on the equation of adhesive wear and the generation process of wear elements in adhesive wear of metals. Wear 2019, 432, 202936. [Google Scholar] [CrossRef]
- Anderson, D.; Warkentin, A.; Bauer, R. Experimental and numerical investigations of single abrasive-grain cutting. Int. J. Mach. Tools Manuf. 2011, 51, 898–910. [Google Scholar] [CrossRef]
- Godet, M. Third-bodies in tribology. Wear 1990, 136, 29–45. [Google Scholar] [CrossRef]
- Rabinowicz, E. The effect of size on the looseness of wear fragments. Wear 1958, 2, 4–8. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 2–6 September 2003; pp. 545–554. [Google Scholar]
- Zhao, M.; Cui, W.-C. Application of the optimal Latin hypercube design and radial basis function network to collaborative optimization. J. Mar. Sci. Appl. 2007, 6, 24–32. [Google Scholar] [CrossRef]
- Yu, Y.; Pan, Y.; Chen, Q.; Zeng, D.; Hu, Y.; Goh, H.-H.; Niu, S.; Zhao, Z. Cogging Torque Minimization of Surface-Mounted Permanent Magnet Synchronous Motor Based on RSM and NSGA-II. Actuators 2022, 11, 379. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sen, A. Adaptive response surface based efficient finite element model updating. Finite Elem. Anal. Des. 2014, 80, 33–40. [Google Scholar] [CrossRef]
- Guan, G.; Wang, L.; Geng, J.; Zhuang, Z.; Yang, Q. Parametric automatic optimal design of USV hull form with respect to wave resistance and seakeeping. Ocean Eng. 2021, 235, 109462. [Google Scholar] [CrossRef]
- Mao, Z.Y.; Pi, Y.B.; Li, B.; Lu, C.Y.; Tian, W.L. Parametric optimization for liquid cooling microchannels of AUV’s battery thermal management system. J. Therm. Anal. Calorim. 2022, 147, 9523–9537. [Google Scholar] [CrossRef]
- Wu, X.; Chen, C.; Hong, C.; He, Y. Flow ripple analysis and structural parametric design of a piston pump. J. Mech. Sci. Technol. 2017, 31, 4245–4254. [Google Scholar] [CrossRef]
- Bekele, E.G.; Nicklow, J.W. Multi-objective automatic calibration of SWAT using NSGA-II. J. Hydrol. 2007, 341, 165–176. [Google Scholar] [CrossRef]
- Cai, L.G.; Zhang, C.; Cheng, Q.; Gu, P.H.; Wang, H.Y. An Optimization Method for Geometric Error of Machine Tool Based on NSGA-II. Appl. Mech. Mater. 2013, 418, 180–186. [Google Scholar] [CrossRef]
- Wu, M.; Nie, Q.; Li, Y.; Chen, W.; Yue, X.; Zhang, Y. Multi-objective optimization of a new special-shaped tube for heating deicing fluid. J. Therm. Anal. Calorim. 2019, 138, 1487–1498. [Google Scholar]
- Xu, H.M.; Ma, X.B.; Liu, Q.H. Simulation and analysis of the in-pipe robot based on the software of Pro/E and ADAMS. In Proceedings of the 2014 International Symposium on Information Technology (ISIT 2014), Dalian, China, 14–16 October 2014; pp. 337–342. [Google Scholar]



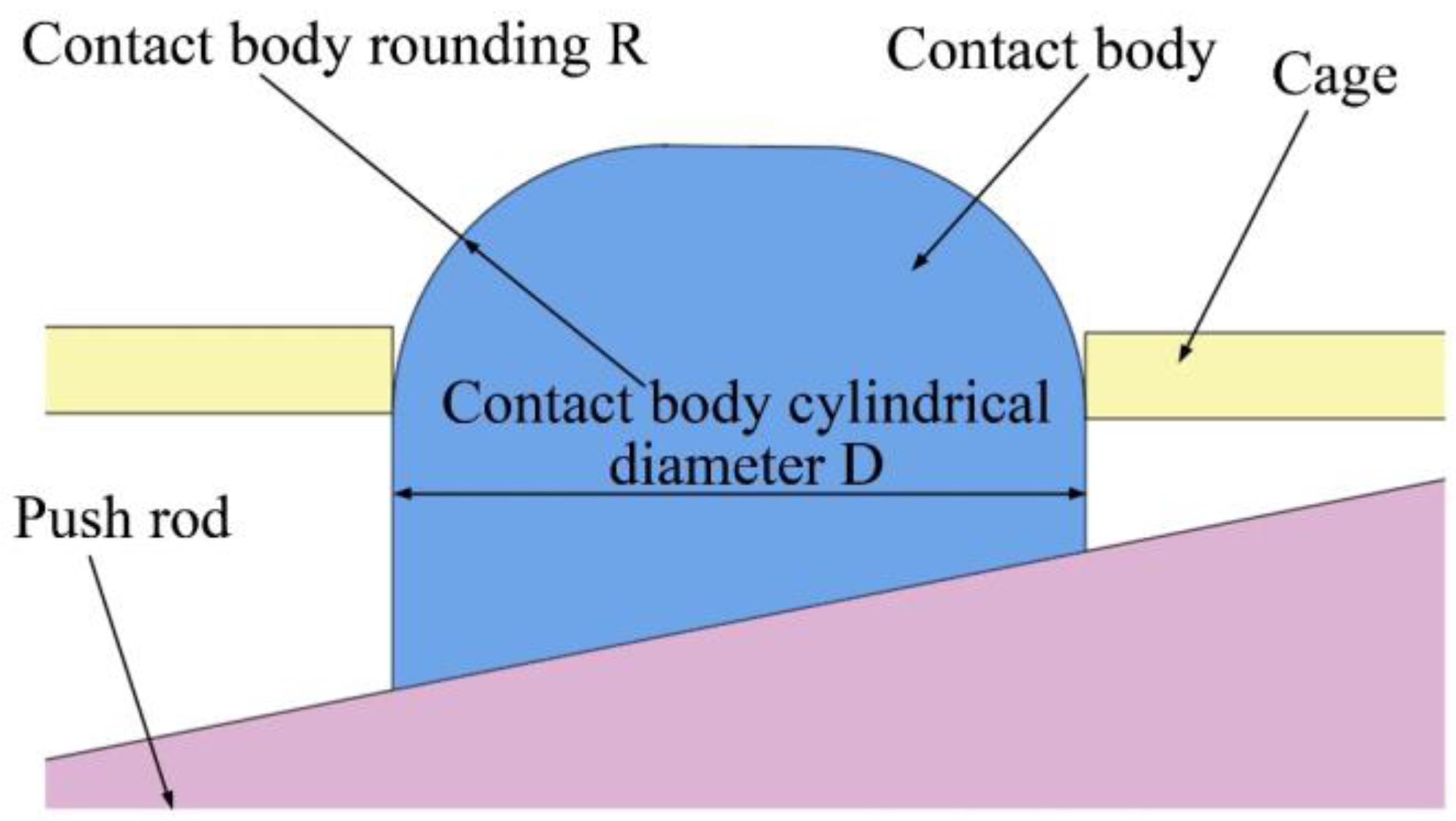


| Component | Metal Grade | Material Density (Kg/m3) | Young’s Modulus (N/m2) | Poisson’s Ratio | Compressive Yield Strength (MPa) | Tensile Yield Strength (MPa) |
|---|---|---|---|---|---|---|
| Contact Body | GCr15 | 7.85 × 103 | 2.11 × 1011 | 0.3 | 1815 | 1902 |
| Pipe | X65 | 7.85 × 103 | 2.05 × 1011 | 0.3 | 414 | 549 |
| Sports Event | Cubic Root (≥0.9) | Root Mean Square (≤0.2) | |
|---|---|---|---|
| EBF-model | h | 0.98983 | 0.028 |
| S | 0.99565 | 0.01776 | |
| Universal Kriging | h | 0.96325 | 0.05522 |
| S | 0.95476 | 0.06202 |
| NSGA-II | D (mm) | R (mm) | h (mm) | S (mm) |
|---|---|---|---|---|
| Optimal design point | 57.1 | 11.82 | 0.118 | 0.396 |
| Simulation results | 0.112 | 0.417 | ||
| Prediction error | 5.35% | 5.30% | ||
| C1 | 57.3 | 12.0 | 0.117 | 0.403 |
| Simulation results | 0.110 | 0.419 | ||
| Prediction error | 6.36% | 3.97% | ||
| C2 | 58.3 | 13.8 | 0.113 | 0.441 |
| Simulation results | 0.107 | 0.450 | ||
| Prediction error | 5.61% | 2.04% | ||
| C3 | 56.7 | 12.0 | 0.122 | 0.394 |
| Simulation results | 0.114 | 0.415 | ||
| Prediction error | 7.02% | 5.33% | ||
| C4 | 56.5 | 12.1 | 0.125 | 0.392 |
| Simulation results | 0.117 | 0.406 | ||
| Prediction error | 6.84% | 3.57% |
| NCGA | D (mm) | R (mm) | h (mm) | S (mm) |
|---|---|---|---|---|
| Optimal design point | 57 | 11.4 | 0.119 | 0.397 |
| Simulation results | 0.110 | 0.421 | ||
| Prediction error | 8.18% | 6.05% | ||
| C1 | 57.2 | 11.4 | 0.117 | 0.417 |
| Simulation results | 0.109 | 0.442 | ||
| Prediction error | 7.34% | 6.00% | ||
| C2 | 58.3 | 12.0 | 0.116 | 0.425 |
| Simulation results | 0.11 | 0.455 | ||
| Prediction error | 5.45% | 7.06% | ||
| C3 | 56.7 | 12.1 | 0.121 | 0.398 |
| Simulation results | 0.113 | 0.415 | ||
| Prediction error | 6.15% | 4.27% | ||
| C4 | 56.6 | 11.0 | 0.129 | 0.390 |
| Simulation results | 0.120 | 0.410 | ||
| Prediction error | 7.50% | 5.13% |
| Numerical Value | Original Form | NSGA-II Optimization | NCGA Optimization | |
|---|---|---|---|---|
| R (mm) | 30 | 11.72 | 11.4 | |
| D(mm) | 60 | 57.1 | 57 | |
| h | Value (mm) | 0.081 | 0.112 | 0.110 |
| Difference (%) | 38.3 | 35.8 | ||
| S | Value (mm) | 0.784 | 0.396 | 0.421 |
| Difference (%) | 49.5 | 46.3 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, H.; Ping, Z.; Zhao, T.; Hou, S.; Zu, F.; Qiu, P.; Qin, J. Research on Contact Anchoring Theory and Contact Optimization of Underwater Pipeline Recovery Tools. Processes 2023, 11, 3166. https://doi.org/10.3390/pr11113166
Gong H, Ping Z, Zhao T, Hou S, Zu F, Qiu P, Qin J. Research on Contact Anchoring Theory and Contact Optimization of Underwater Pipeline Recovery Tools. Processes. 2023; 11(11):3166. https://doi.org/10.3390/pr11113166
Chicago/Turabian StyleGong, Haixia, Zhuoran Ping, Tong Zhao, Shuping Hou, Fuqiang Zu, Pengyue Qiu, and Jianguo Qin. 2023. "Research on Contact Anchoring Theory and Contact Optimization of Underwater Pipeline Recovery Tools" Processes 11, no. 11: 3166. https://doi.org/10.3390/pr11113166
APA StyleGong, H., Ping, Z., Zhao, T., Hou, S., Zu, F., Qiu, P., & Qin, J. (2023). Research on Contact Anchoring Theory and Contact Optimization of Underwater Pipeline Recovery Tools. Processes, 11(11), 3166. https://doi.org/10.3390/pr11113166






