Computational Fluid Dynamics Modeling of HIsarna Off-Gas System—Wall Modeling and Heat Loss Prediction

Abstract

The HIsarna off-gas system wall is a cooling jacket made of cooling pipes arranged in the radial direction and in a circular pattern. Part of the off-gas system cooling pipes are isolated using a low-thermal-conductivity refractory material to protect the cooling pipe from melting and thermal stresses. During long runs and due to thermomechanical stresses, the refractory material is lost, and its thickness is reduced. It is possible to measure the thickness of the refractory layer only during shutdown, which is a disadvantage during long runs. The aim is to investigate the possibility of predicting the thickness of the refractory material by using other parameters that are possible to measure during the operation. A combination of FEM and CFD modeling is used to develop a methodology for detailed wall modeling and refractory material loss prediction. Finite element method (FEM) analysis is used to obtain the thermal properties of the wall using detailed geometries for variable refractory thickness. The obtained properties are then used to build CFD models to study the effect of refractory thickness on wall heat loss, temperature and composition profiles. The proposed procedure is validated against the plant measurement, and according to the findings, it is possible to relate the wall thickness to measured parameters such as heat loss through the walls, temperature and carbon conversion.

1. Introduction

From 2018 to 2020, approximately 1.85 tons of CO₂ were emitted from every ton of produced steel. In 2020 alone, 1860 million tons of steel were produced, which directly emitted 2.6 billion tons of CO₂. In other words, if we count the steel industry as a nation, it would rank fifth among the nations with the largest CO₂ footprint, representing 7% to 9% of global CO₂ emissions [1,2,3]. This tremendous CO₂ emission has made researchers seek alternative ways of steel production to limit pollutant emissions. Among the investigated routes, the HIsarna process has proven to be a promising alternative.

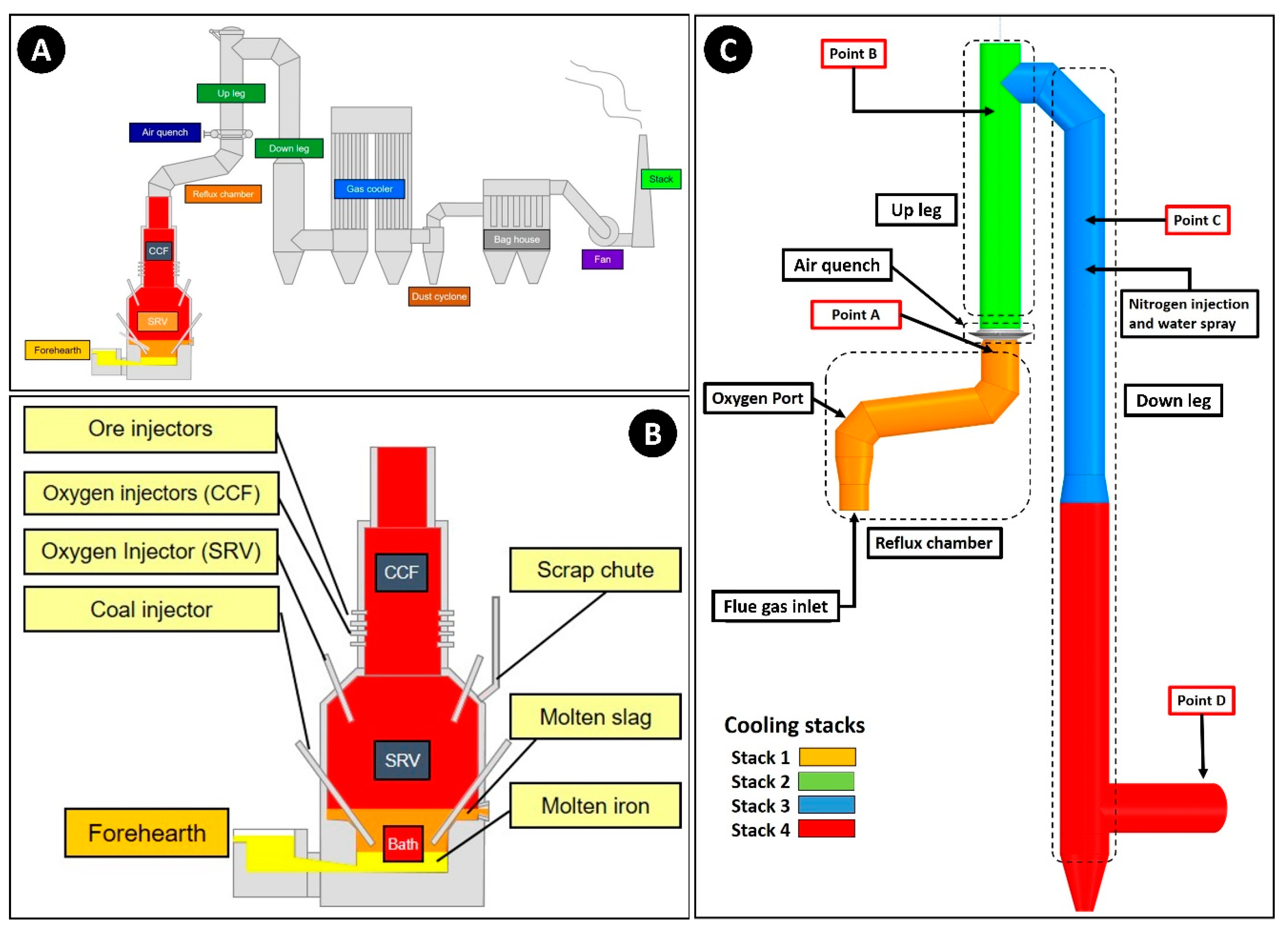
The HIsarna process is a new concept that utilizes the smelting reduction of iron ore to produce liquid hot metal. In this process, unlike the blast furnace, fine ore and coke are directly injected into the process without sintering and coking, which are responsible for 20% of the CO₂ emission. Figure 1A shows the overall scheme of the process built in pilot scale with a capacity of 8 ton/h of hot metal. Since 2010, pilot plants have been developed constantly to finalize the industrial demonstration. The main reactor is usually classified into two different regions: the cyclone converter furnace (CCF) and the smelting reduction vessel (SRV), which accommodate the “Bath” that contains molten slag and iron.

The smelting and reduction of iron ore take place inside the CCF and the SRV, and resulting off-gas from reduction reactions travels upward and enters the off-gas system, which is divided into four parts of “Reflux Chamber”, “Air Quench”, “Up Leg” and “Down Leg”.

The flue gas entering the off-gas system contains a CO₂-H₂O-N₂ mixture with a minor amount of CO, H₂, O₂, carbon and pre-reduced molten iron ore particles. Oxygen is injected to combust the remaining CO and H₂ and carbon in the gas. The flue gas is quenched via air in the air quench section immediately at the outlet of the reflux chamber. Further cooling of the flue gas is achieved via evaporative cooling by injecting water (droplets) using an atomizer in the down-leg section (using nitrogen as carrier gas). Ultimately, the flue gas is passed through a gas cooler and a set of dust-capturing units.

Figure 2 shows the wall of the reflux chamber, which is in fact a circular cooling jacket made of steel pipes. The cooling water runs through the cooling pipes to maintain a low wall temperature. Since the temperature inside the reflux chamber could locally reach 1900 °C, a refractory layer is applied on top of the cooling pipes to avoid pipe melting. On each cooling pipe, rows of anchors are welded to firmly hold the refractory material. Above the reflux chamber, the flow temperature is much lower than the melting point of the cooling pipes; therefore, no anchors and refractory layers are applied. The average thickness of fresh (as-built) refractory material is 49.5 mm, which is 10 mm above the anchor tips.

The harsh conditions inside the reflux chamber, including complex chemical attack and thermomechanical loading, as well as temperature fluctuations during the operation periods, lead to an irreversible structural response of the refractory material, such as cracking, crushing and gradual loss of material. Due to continuous thermomechanical stresses during long operating periods, the thickness of the refractory material is locally reduced. Moreover, the molten iron particles (escaped from CCF) can build up on the wall, creating a thick layer of frozen slag. These phenomena make the performance of the reflux chamber rather complicated.

In Figure 3, the reflux chamber wall near the oxygen lance is shown after a long operation for two different inspection campaigns. From the figure, the erosion pattern is obvious, and locally speaking, it could lead to a considerable material loss so that the tips of the anchors become visible. For the used wall (non-fresh) and based on the laser measurements at different cross-sections, the average thickness is between 32 and 38 mm, which is lower than the built-in average thickness of 49.5 mm. The change in refractory thickness causes thermal and structural performance changes over time. This, in turn, will lead to difficulties in process control and might negatively affect the cooling efficiency and accelerate refractory wear, limiting the operation periods.

In order to formulate precise mathematical models, the thermophysical properties of the wall must be calculated and assigned correctly. The assigned properties determine the heat loss through the walls, which has a considerable impact on temperature and composition profile predictions.

For the current case, the modeling of the walls and assigning thermophysical properties is not a straightforward task. Complexities arise since the refractory material has a very low thermal conductivity, and anchors are made of steel with relatively high thermal conductivity. Therefore, practically, the wall of the reflux chamber can be considered as a composite material of refractory and aligned steel anchors. Along with refractory thickness, the effect of embedded anchors on the calculation of density, thermal conductivity and heat capacity of the modeled wall must be considered.

The initial CFD models were set up using an original refractory thickness of 49.5 mm and a thermal conductivity of 1.15 W/(m K) (without considering the anchors’ effect). The heat loss prediction was not precise, and along with the calculated temperature profile, it was at a huge discrepancy with counterpart plant measurements. The model was then improved by tuning the thermal and physical properties of the wall to match the heat loss and correctly predict the temperature profile. 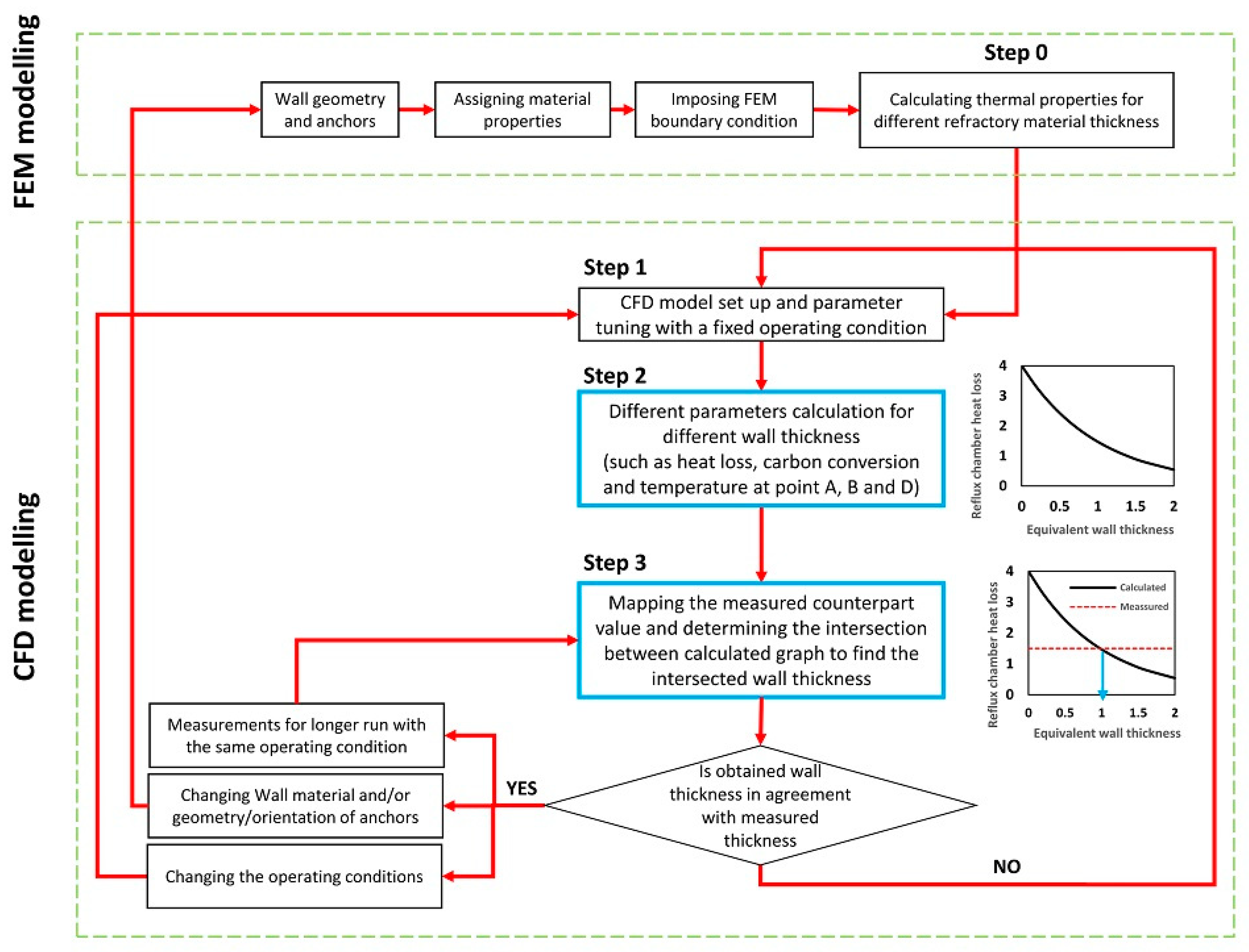The results were published and analyzed in another study by the same authors [4]. In this study, a detailed discussion on wall modeling is presented to obtain a more precise and physically sound approach for accurate wall property prediction using finite element analysis. The obtained wall properties are then used to build a CFD model without requiring complex parameter tuning for different operation periods where the refractory thickness changes. The ultimate goal is to investigate how wall thickness and parameters that can be measured during the operations are related. Achieving this will enable us to have an idea of the wall condition during a run with fixed operating conditions without direct measurement of the wall thickness, which can be achieved only during plant shutdown.

2. Wall Modeling in CFD

Three methods can be used to model a wall in CFD. The first option is directly resolving the wall by considering the wall details and its thickness in the geometry. The wall thickness can then be discretized (meshed) and assigned as a solid zone in the CFD solver. This is the most thorough approach, and heat transfer in all directions can be resolved; however, it leads to a very fine computational grid in the wall region and can become computationally expensive. For example, in the current case, considering the refractory thickness, anchor detail, cooling pipe and a reasonable cell size would lead to a total grid size of 2.5 × 10⁹ cells, which is practically impossible to model with available computational resources. In order to reduce the numerical efforts, the wall layers are often not resolved directly and are modeled using the thin-wall approach.

This leads us to consider a second option where only the fluid region is meshed, and the wall is modeled by specifying a wall thickness and assigning a specific material to it. In the setup model, the detailed wall geometry is not considered, and instead, a fixed wall thickness with assigned thermal properties is imposed. However, with this approach, conduction is considered in the normal direction only, and considering different wall layers is not possible.

If the wall is composed of different material layers and conduction in the planar direction of the wall is of importance, a third option known as the “Shell Conduction” approach can be utilized. The wall thickness is considered virtually by growing a layer of prism or hex cells in which the three-dimensional conduction heat transfer equation is solved. Figure 4 shows a visual summary of the discussed approaches for wall modeling.

There are numerous studies where the shell conduction approach has been used to model conductive heat transfer through walls. Mahmoodi et al. [5] used this approach to model heat transfer through an industrial sulfur removal unit and reported well-predicted heat loss and temperature profiles. Ghosh et al. [6] used the shell conduction model to investigate thermal convection inside a space flight sensor. Al-Abbas [7] studied heat transfer in a solar heating system and used the same approach to consider different wall layers for conductive heat transfer through a wall. Jayakumar et al. [8] modeled the walls of a coiled heat exchanger, and Popescu et al. [9] modeled the walls of a swirl combustor using the same technique.

In this study, the walls are modeled using the shell conduction approach. A schematic view of the detailed wall geometry is shown in Figure 5A with the refractory material, embedded anchors and cooling pipe thickness. In the shell conduction approach, layers are distinguished from each other in series, and only one material can be assigned to each layer. Therefore, the detailed wall is simplified to a two-layer wall, as shown in Figure 5B.

The first layer is in fact an “Equivalent Wall” with the calculated effective thermophysical properties of a composite mixture where the refractory material is a matrix and anchors are fillers. The second layer is a cooling pipe wall thickness that is made of steel with known properties. The cooling water heat transfer properties, such as average temperature and heat transfer coefficient, are imposed at the outer surface of the second layer as a boundary condition.

For the equivalent wall, the effective thermal conductivity, specific heat and density are important properties to correctly predict the heat transfer phenomena. Effective specific heat and density are calculated using mixing law by considering the mass fraction of the matrix and filler. However, among the mentioned thermophysical properties, thermal conductivity has proven to be the most important and effective parameter in thermal exchanges [10]. Different correlation and numerical approaches are available to calculate the effective thermal conductivity of composites in the literature, which will be discussed in the following section.

3. Effective Thermal Conductivity Prediction

As mentioned before, the equivalent refractory wall of the reflux chamber can be considered as a composite made of refractory material as matrix and anchor rods as fillers. A basic model for calculating the thermal conductivity of heterogeneous material is the Maxwell model. It has been used as a base model for many other models and modifications [11]. Maxwell considered the problem of the dilute dispersion of spherical particles of conductivity k_f embedded in a continuous matrix of conductivity k_m, where thermal interactions between filler particles were ignored. Maxwell’s expression is as follows:

$$\frac{k_{eff }}{k_m}=1+\frac{3\phi }{\left(\frac{k_f+2k_m}{k_f-k_m}\right)-\phi }$$

(1)

Maxwell’s formula was found to be valid only in the case of low φ (under about 25%). Different models and correlations to predict the effective thermal conductivity of such composite materials are available in the literature, which are known as effective medium approximations (EMAs). Among the available correlations, Lewis–Nielsen [12], Rayleigh [13], Bruggemann [14], Springer and Tsai [15], and Hamilton and Crosser [16,17] correlations can be mentioned. A detailed formulation of the mentioned EMA models can be found in the Appendix A. EMA models are generally unable to accurately predict the properties of heterogeneous material beyond a percolation threshold of filler volume fraction. Also, for models that consider cylindrical fillers, the alignment of fillers is regular and perpendicular to the heat transfer direction, which is not the case in the reflux chamber wall. It is also impossible to accurately predict the conductivity for complex geometries and random filler orientations.

The most reliable approach is to use the finite element method (FEM), which can handle any geometries and orientations using numerical discretization of the domain. There are quite a number of studies to model heat transfer or calculate the thermal conductivity of a composite material using FEM analysis.

Rashid et al. [18] investigated and measured the thermal conductivity of burnt clay bricks reinforced with fibers using finite element analysis. In their study, the effect of filler material, volume fraction, length and diameter on thermal conductivity is investigated, and their modeling results are validated against experimental measurements.

In another study, FEM analysis is utilized by Nagy et al. [19] to investigate the effect of different fillers on the thermal properties of steel-fiber-reinforced concrete and determine the equivalent thermal conductivity of the mentioned composite. FEM analysis can also be used to study the effect of thermal stresses on material properties and possible failures, as performed in a study by Andreev et al. [20]. In their research, the thermomechanical response of refractory material during startup and operations in the teeming ladle is investigated. With their obtained results, further analysis of lining design and material selection is presented. On the same subject, Gruber et al. [21] studied the effect of temperature on the thermomechanical behavior of the refractory lining of a blast furnace. They used FEM analysis to select the proper material for the lining by considering the complex nature of the refractories.

In this study, the FEM method is used to calculate the effective thermal conductivity of the “equivalent wall” (shown in Figure 5B) of the reflux chamber for different refractory material thicknesses, followed by a comparison with EMA correlations. Ultimately, the calculated thermal conductivities from the FEM analysis are used to perform a CFD sensitivity analysis to estimate the wall thickness.

4. Model Setup and Procedure

Figure 6 shows the methodology and procedure used in this study. The idea is to use FEM analysis to acquire the effective thermal conductivity for the equivalent wall (refractory material with embedded anchors) for different refractory material thicknesses. Then, using fixed operation conditions, a set of CFD modeling is performed for the different equivalent wall thicknesses by assigning the thermal properties obtained by the FEM analysis (Step 1). For each thickness, different parameters are calculated. The parameters are chosen so that there is an available measured counterpart at the plant such as heat loss through the walls, temperature at different points (Figure 1A,B,D), flue gas composition at different points (Figure 1A,D) and carbon conversion. A graph is obtained for the calculated parameters versus the equivalent wall thickness (Step 2). Ultimately, the measured values are mapped on corresponding graphs to see at which thickness they intersect (Step 3). The obtained thickness is then compared to the measured one. As will be discussed, this approach will lead to a fair prediction of the wall thickness inside the reflux chamber (which is impossible to measure during the operation) using other parameters that can be measured during the operation.

It is important to note that this approach is applicable for fixed operating and inlet conditions for a certain operation period. In case the inlet conditions, such as inlet temperature, composition and flow rate, or any other operating conditions are changed in a long run, Steps 1 to 3 should be repeated. This repetition is important since, during long runs, further reduction of wall thickness might occur, which can change the performance of the whole off-gas system. In case the refractory wall material is changed or the shape and orientation of the anchors are modified, the whole flowchart, including the FEM analysis, must be repeated.

4.1. FEM Analysis

To obtain the properties of the equivalent refractory wall, a steady-state thermal analysis using FEM is performed. As mentioned before, a full-scale numerical analysis of large structures may be complicated and computationally expensive. This can be overcome by considering a smaller part that can represent the whole geometry. In this approach, the refractory wall with embedded anchors can be considered as a patterned array of identical cells, often referred to as “unit cells” or representative volume elements (RVEs) [22]. In short, a unit cell is a periodic representation that repeats itself throughout a larger geometry. The geometry of the unit cell and dimensions is depicted in Figure 7.

As can be seen, the anchors are covered by the refractory material and two different thicknesses, namely “d” and “D”, are defined for the refractory material. The parameter “d” is called “tip thickness”, which refers to the thickness of the refractory material from the outer surface of the pipes. The “D” value is named “base thickness”, which refers to the refractory thickness starting from the middle of the cooling pipes where the refractory material begins. The pipes and anchors are made of steel (P235GH-TC1), and the refractory material is an alumina–silica material with the commercial name “Calde Stix 151”. The material properties for the thermal analysis are listed in

Table 1. Material properties for FEM and CFD analysis [23].

Material	ρ (kg/m3)	k (W/(m K))	Cp (J/(kg K))	Thickness (mm)
Pure Refractory (Calde Stix 151)	2200	$k=\{\begin{array}{c}0.00025\times \mathrm{T}\left[\mathrm{K}\right]+0.80175 1073\le \mathrm{T}\le 1273 \\ 0.0007\times \mathrm{T}\left[\mathrm{K}\right]+0.2289 1273<\mathrm{T}\le 2273\end{array}$	900	variable
Steel (P235GH-TC1)	7850	$k=\{\begin{array}{c}-0.0099\times \mathrm{T}\left[\mathrm{K}\right]+59.7019 273\le \mathrm{T}\le 370\\ -0.0425\times \mathrm{T}\left[\mathrm{K}\right]+71.7876 370<\mathrm{T}\le 673\end{array}$	461	5

. The thermal conductivities for both materials are considered as a function of temperature.

The temperature field is calculated using SOLIDWORKS software (2020) by solving a three-dimensional conduction heat transfer equation as stated below:

$$\frac{\partial }{\partial x}\left(k_x\left(T\right)\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k_y\left(T\right)\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left(k_z\left(T\right)\frac{\partial T}{\partial z}\right)+Q=\rho \left(T\right)Cp\left(T\right)\frac{\partial T}{\partial t}$$

(2)

Assuming an isotropic material in steady-state modeling without heat generation, Equation (2) can be simplified as Equation (3):

$$k\left(T\right)\left[\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\partial }^{2}T}{\partial z^2}\right]=0$$

(3)

where k is isotropic thermal conductivity.

Besides conductive heat transfer, heat can be transferred to the surroundings through convection, for example, the convection of heat from the flue gas to the refractory surface or heat convection from cooling pipes to the cooling water. To consider the heat transfer from the surfaces to the surroundings, convection boundary conditions are imposed according to the equation below:

$$k\left(T\right)\left(\frac{\partial T}{\partial n}\right)+h\left(T-T_0\right)=0$$

(4)

Figure 8A shows the convective boundary conditions considered for the simulations. The inner side of the unit cell is in touch with the hot flue gas with an average temperature of 1673 K and a heat transfer coefficient of 200 W/(m² K). The heat transferred through the walls of the cooling pipe is absorbed by the cooling water at an average temperature of 313 K and a high convective heat transfer coefficient of 5000 W/(m² K). The outer surface of the cooling pipe is exposed to the surrounding air at a temperature of 298 K and a heat transfer coefficient of 40 W/(m² K). The mentioned data regarding the heat transfer coefficient of the hot flue gas, cooling water and surrounding air are obtained based on the flow thermophysical properties, the calculated Re and Pr number and by using the Pak and Cho correlation [24].

The periodic boundary condition is imposed on the side walls. The computational domain consists of 750,000 tetrahedral cells (element size = 2.5 mm). The heat flux through the walls and surface temperatures are calculated and then used to estimate the effective thermal conductivity of the refractory material and anchor composite. The calculated values for effective thermal conductivity are discussed in detail in Section 5.1. The solid body is discretized with tetrahedral cells with a uniform cell size of 2 mm, as depicted in Figure 8B.

4.2. CFD Model of the Off-Gas System

A comprehensive CFD model for the current pilot-scale HIsarna off-gas system is established using the detailed geometry shown in Figure 1C. A detailed discussion on CFD model development has been published in another study by the same authors [4]. We would like to refer the readers to our previous study for detailed information; however, a brief description of the geometry, mesh, boundary condition and governing equations are mentioned in this paper.

4.2.1. Computational Grid

The generated computational grid (mesh) is composed of polyhedral cells with a total number of 1.5 million for all calculations. A representation of the computational grid is shown in Figure 9. The cell size in the reflux chamber (orange region), air quench (purple region) and up/down leg (blue region) is 40, 30 and 50 mm, respectively. The areas near the oxygen injection, nitrogen injection and also air quench pipes are meshed with 5 mm cells.

4.2.2. Governing Equations and Solution Procedure

Over the discussed computational grid, a set of conservation and transport equations is solved to describe the different phenomena in the modeled system.

Table 2. Governing equations and sub-models for CFD modeling of HIsarna off-gas system [25,26].

		Main Equation	Sub-Equations and Constants
Continuity equation	(5)	$\frac{\partial }{\partial \mathrm{t}}\left(\mathsf{\rho }\right)+\frac{\partial }{\partial x_i}\left(\mathsf{\rho }\overline{u_l}\right)=0$
Momentum equation	(6)	$\frac{\partial }{\partial \mathrm{t}}\left(\mathsf{\rho }\overline{u_l}\right)+\frac{\partial }{\partial x_j}\left(\mathsf{\rho }\overline{u_l}\overline{u_J}\right)=-\frac{\partial \mathrm{p}}{\partial x_i}+\frac{\partial }{\partial x_j}\left[\mu \left(\frac{\partial \overline{u_l}}{\partial x_j}+\frac{\partial \overline{u_J}}{\partial x_i}-\frac{2}{3}{\delta }_{ij}\frac{\partial \overline{u_l}}{\partial x_l}\right)\right]+\frac{\partial }{\partial x_j}\left(-\mathsf{\rho }\overline{u_l^{\prime }{u}_J^{\prime }}\right)$	$\frac{\partial \overline{u_l}}{\partial x_l}=\nabla .\overline{u}.IM$ $\overline{u}=u-u^{\prime }$ $\mathsf{\rho }\overline{u_l^{\prime }{u}_J^{\prime }}=-{\mu }_t(\frac{\partial \overline{u_l}}{\partial x_j}+\frac{\partial \overline{u_J}}{\partial x_i})+\frac{2}{3}(\mathsf{\rho }\mathrm{k}+{\mu }_t\frac{\partial \overline{u_l}}{\partial x_i}){\delta }_{ij}$
Turbulence models		Realizable k-ε Model	${\mu }_t=\rho C_{\mu }\frac{k^2}{\epsilon }$ ${\sigma }_k=1$ and ${\sigma }_{\epsilon }$ =1.2 $C_{1\epsilon }=$ 1.44 $C_2=1.9$
		Equation for turbulent kinetic energy (k)
	(7)	$\frac{\partial }{\partial \mathrm{t}}\left(\mathsf{\rho }\mathrm{k}\right)+\frac{\partial }{\partial x_i}\left(\mathsf{\rho }\mathrm{k}\overline{u_l}\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial \mathrm{k}}{\partial x_j}\right]+G_K+G_b-\mathsf{\rho }\mathsf{\epsilon }-Y_M+S_k$
		Equation for dissipation of turbulent kinetic energy (ε)
	(8)	$\frac{\partial }{\partial \mathrm{t}}\left(\mathsf{\rho }\mathsf{\epsilon }\right)+\frac{\partial }{\partial x_j}\left(\mathsf{\rho }\mathsf{\epsilon }\overline{u_J}\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\partial \mathsf{\epsilon }}{\partial x_j}\right]+\mathsf{\rho }{C}_{1}S\epsilon -\mathsf{\rho }{C}_2\frac{{\epsilon }^2}{k+\sqrt{\vartheta \epsilon }}+C_{1\epsilon }\frac{\epsilon }{k}{C}_{3\epsilon }{G}_b+S_{\mathsf{\epsilon }}$
Energy equation	(9)	$\frac{\partial }{\partial t}\left(\rho E\right)+\nabla .\left(\overline{u}\left(\rho E+p\right)\right)=\nabla .(k_{eff}\nabla T-{\displaystyle {\displaystyle \sum }_j}{h}_j\overrightarrow{J_J}+\left({\tau }_{eff}.\overline{u}\right))+S_h$	$\overrightarrow{J_l}=-\left(\rho D_{i,m}+\frac{{\mu }_t}{S{c}_t}\right)\nabla Y_i-D_{T,i}\frac{\nabla \mathrm{T}}{T}$
Radiation models		Discrete ordinate model (DOM)
	(10)	$\nabla ·\left(I\left(\overrightarrow{r},\overrightarrow{s}\right)\overrightarrow{s}\right)+\left(a+{\sigma }_s\right)I\left(\overrightarrow{r},\overrightarrow{s}\right)=a{n}^2\frac{\sigma T^4}{\pi }+\frac{{\sigma }_s}{4\pi }{{\displaystyle \int }}_0^{4\pi }I\left(\overrightarrow{r},\overrightarrow{s^{\prime }}\right)\varphi \left(\overrightarrow{s},\overrightarrow{s^{\prime }}\right)d{\mathsf{\Omega }}^{\prime }$
Species transport equation	(11)	$\frac{\partial }{\partial \mathrm{t}}\left(\mathsf{\rho }{Y}_i\right)+\frac{\partial }{\partial x_i}\left(\mathsf{\rho }\overline{U}{Y}_i\right)=-\nabla .\overrightarrow{J_l}+R_i+S_i$
Turbulence–chemistry interaction models		Eddy dissipation concept (EDC)	$C_{\zeta }=2.1377$ $C_{\tau }=0.4082$
	(12)	$R_i=\frac{\rho {\left({\zeta }^{*}\right)}^2}{{\tau }^{*}\left[\left(1-{\left({\zeta }^{*}\right)}^3\right)\right]}\left(Y_i^{*}-Y_i\right)$
	(13)	${\zeta }^{*}=C_{\zeta }{\left(\frac{v\epsilon }{k^2}\right)}^{0.25}$
	(14)	${\tau }^{*}=C_{\tau }{\left(\frac{v}{\epsilon }\right)}^{0.5}$
Particle force balance equation—Discrete phase model	(15)	$m_p\frac{d{\overrightarrow{u}}_p}{dt}=m_p\frac{\overrightarrow{u}-{\overrightarrow{u}}_p}{{\tau }_r}+m_p\frac{\overrightarrow{g}\left({\rho }_p-\rho \right)}{{\rho }_p}+\overrightarrow{F}$
Particle evaporation model	(16)	$\frac{d{m}_p}{dt}=k_c{A}_p\rho .Ln\left(1+\frac{Y_{i,s}-Y_{i,\infty }}{1-Y_{i,s}}\right)$
Carbon particle reaction rate	(17)	$\overline{R_{char}}=\frac{d{m}_c}{dt}=-A_p{y}_j{R}_{char,i}$
	(18)	$R_{char,i}=\frac{1}{\frac{1}{k_{diff,i}}+\frac{1}{k_{s,i}{Y}^2}+\frac{1}{k_{dash,i}}\left(\frac{1}{Y}-1\right)}\left(P_i-P_i^{*}\right)$

lists the main solved equations [25].

ANSYS FLUENT software (2019 R3) is used to set up, solve and couple the governing equations. The coupled algorithm is used for pressure–velocity coupling along with the second-order upwind scheme to discretize all of the convective terms. Simulations are performed in steady-state mode, and the solution is stopped after reaching the convergence criterion of 10⁻⁴.

4.2.3. Inlet and Wall Boundary Conditions

Table 3. Inlet boundary condition for CFD model setup [4].

	Reflux Chamber	Air Quench	Oxygen Port	Nitrogen Ports	Water Spray
Inlet Temperature (K)	2086	293	293	293	293
Actual volumetric flow rate (m3/s)	20.8	3.10	0.206		-
Average density (kg/m3)	0.208	1.19	1.31	1.25	998
Inlet mass flowrate (kg/s)	4.33	3.69	0.27	0.205	0.45
Composition—mole fraction
CO	0.0261	0	0	0	0
CO2	0.61	0.0003	0	0	0
H2	0.002	0	0	0	0
O2	0	0.21	0.995	0	0
N2	0.166	0.78	0.005	1	0
H2O	0.2	0.012	0	0	1
Post-combustion ratio (%)	96.63	-	-	-	-

reports the inlet boundary conditions that are obtained by averaging the measured transient data from the pilot plant over a fixed operating period.

For CO-H₂ mixture combustion, the kinetic mechanism proposed by Frassoldati et al. [27] is considered. Carbon particle reactions are considered through the expressions and constants proposed by Wen et al. [28].

One important factor is the number of representative particles for both carbon and water droplet particles. As mentioned before, carbon particles are carried with the inlet flue gas into the off-gas system, and water is injected at the end of the off-gas system to perform evaporative cooling. A better representation of particulate flow is achieved in the models by incorporating a higher number of particles. However, a higher number of particles leads to a higher computational cost. In order to set an appropriate number of particles, a sensitivity analysis is required to investigate how the composition and temperature profile and also carbon conversion are changed by increasing the number of particles. The details of this analysis are not mentioned in this paper for brevity; however, based on this analysis, a total of 20,000 and 2000 particles are considered to represent the carbon and water droplet flow, respectively. A further increase in the number of particles will not change the species and temperature predictions. The diameter of carbon particles is considered to be injected with a uniform size of 120 µm, which is obtained from the outlet prediction of the CFD models for the CCF reactor.

At the pilot plant, water is injected using a two-fluid atomizer. and only the measured injection flow rates are available as input data. The injection velocity and approximate diameter for the measured injection flow rate were obtained from the study of Poozesh et al. [29]. The spray injection is considered using the cone injection model with a spray angle of 30 degrees, a uniform diameter of 90 µm and an injection velocity of 25 m/s.

To reiterate, the reflux chamber wall is modeled as a two-layer wall (Figure 5). The first layer is the refractory equivalent wall, and the second layer is the cooling pipe wall thickness made of steel. The first layer has variable thermal properties that change based on the wall thickness. These values are calculated based on the FEM analysis. The second layer is considered to model the cooling pipe wall thickness (5 mm thickness) with the thermophysical properties of steel (reported in Table 1). Above the reflux chamber, the walls are modeled by considering only one layer with the same thickness and properties as the steel layer mentioned for the reflux chamber.

The outer layer of the wall for the whole off-gas system is in contact with the cooling water, and the respective heat transfer coefficients of cooling water for each cooling stack (Figure 1C) are reported in

Table 4. Wall convective heat transfer parameters for CFD model setup.

	Stack 4	Stacks 2 and 3	Stack 1
Average temperature of cooling water (K)	314.5	307	314
Heat transfer coefficient of cooling water (w/(m2 K))	4000	4500	5000

.

4.2.4. Plant Measurements for CFD Model Validation

Measurement points are shown in Figure 1C.

The temperature and gas composition are measured using high-temperature thermocouples and gas analyses in real time and are averaged over a full operating period.

These measurements are used for the validation of the CFD model and are reported in

Table 5. Measured temperature and composition.

Composition (Dry Basis Mole Fraction)
	Point A	Point B	Point D
CO	0	-	0
CO2	0.749	-	0.327
H2	0	-	0
O2	0.0542	-	0.134
N2	0.197	-	0.539
Temperature (K)	1710 *	1023 *	713 *
Heat loss (MW)
	Measured	Loss to the surrounding	Total loss
Reflux chamber (Stack 1)	3.6	0.30	3.9
Rest (Stacks 2–4)	3.5	1.9	5.4
Sum	7.1	2.2	9.3

* The values are measured with ±10% error.

. The measured heat loss through the off-gas walls is also reported in the same table. The measured values do not represent the real heat loss to the cooling water as some of the heat is lost into the surroundings. According to FEM calculations, the ratio of heat loss into the surroundings to total heat loss is 0.075 and 0.35 for the reflux chamber (Stack 1) and the rest of the wall (Stacks 2–4), respectively. The heat loss to the environment above the reflux chamber is larger due to the high thermal conductivity of pipes with no refractory coating applied. The total heat loss reported in Table 5 should be used to compare with the model prediction. The reflux chamber refractory wall thickness (used wall) is another parameter that will be used for model validation. Carbon conversion at the outlet of the reflux chamber is determined to be 50% from the pilot plant data [4], which will also be used for the model validation.

5. Results and Discussion

5.1. FEM Analysis and Estimation of the Effective Thermal Conductivity (Step 0)

Using the calculated temperature profiles and heat flow from the FEM analysis, the effective thermal conductivity is calculated as follows:

$$k_{eff=}\frac{HF}{T_h-T_c}.d_{eff}$$

(19)

where $HF$ is the calculated heat flow through the unit cell, d_eff is the average thickness of the refractory material ($\frac{d+D}{2}$), $T_h$ is the hot surface temperature and $T_{\mathrm{c}}$ is the outer surface temperature of the cooling pipes, which is equal to the average temperature of the cooling water. The measures of d and D are shown in Figure 7. The mixing law is used to calculate the effective density and heat capacity as follows:

$${\rho }_{eff}=m_f{\rho }_f+m_m{\rho }_m$$

(20)

$$C{p}_{eff}=m_{f}C{p}_f+m_{m}C{p}_m$$

(21)

The values for the effective thermal conductivity based on the FEM analysis and reviewed EMA models are shown in Figure 10 for different refractory thicknesses (and filler volume fractions). Most of the EMA models predict a similar trend and values that are in significant discrepancy with the FEM analysis results. Only the Rayleigh model has predicted values close to the FEM analysis; however, there is still a large difference between the two as Rayleigh predicts higher values than those obtained with the FEM analysis.

As can be seen, for all analyses, there is an increase in thermal conductivity with decreasing refractory thickness. The FEM analysis predicts a sharp increase in effective thermal conductivity once the tips of the anchors become visible (d = 25 mm). The effective thermal conductivity reaches a constant value close to the average conductivity of the pure refractory material (k = 1.15 W/(m K)) by increasing the refractory thickness. The predicted thermal conductivities using all of the analyzed correlations (except for the Rayleigh model) predict a value close to the pure refractory thermal conductivity. At first glance, one can conclude that these predictions are not satisfactory, and using them in the CFD models will not lead to an improved prediction. Therefore, the values obtained by the FEM analysis will be used and discussed for further analysis in the CFD models, and as will be discussed, assigning the thermal conductivity obtained by FEM will lead to much more reliable and reasonable predictions. This is due to the fact that detailed geometries, such as filler complex shape and orientation and their uneven concentration inside the matrix, can be precisely taken into account using the FEM analysis, while it is hard or impossible to consider these factors using any EMA correlations.

Figure 11 shows the temperature distribution over the unit cell volume for different “d” values. As can be seen, the highest temperature occurs at the outer surface of the refractory material, where it is in touch with the hot flue gas. However, for the cases with a lower wall thickness, the surface temperature of the refractory material reduces as more heat flows through the wall thickness due to the higher thermal conductivity of the unit cell.

One reason for the increasing effective thermal conductivity is the increase in the anchor volume fraction by reducing the refractory thickness. Since anchors are made of steel with a much higher thermal conductivity compared to the refractory material, increasing their fraction will increase the effective thermal conductivity.

The other reason is the fact that much of the heat is conducted through the anchors to the cooling pipes, as depicted in Figure 12, where directional heat flux is shown for a single anchor. It is evident that the highest heat flux in the refractory material occurs near those regions where the anchor is located. By reducing the refractory thickness, which acts as an isolation, the tips of the anchors will be closer (or imposed) to the hot flue gas, and more heat will flow through the anchors and, therefore, through the whole wall.

Another interesting finding is depicted in Figure 13A, which shows the isotherm pattern for different temperatures. There is a clear relationship between the isotherms and the erosion pattern inside the reflux chamber (Figure 13B). As can be seen from the obtained isotherms, the refractory regions close to the tips of the anchors will have a lower temperature (due to higher heat flux) with respect to faraway regions and vice versa. Thus, near the tips of the anchors, lesser thermal stress is experienced by the refractory material, which leads to a longer life cycle in those regions. Nevertheless, the thermal expansion of the anchors, which can also cause cracks and ultimately material loss on the walls, must not be ignored.

5.2. Sensitivity Analysis Using CFD Model (Steps 1–3)

The CFD analysis of the whole off-gas system is performed using different wall boundary conditions inside the reflux chamber. As mentioned before, the wall is modeled with a two-layer approach. For all layers, thermal conductivity, heat capacity, density and layer thickness must be assigned. For the equivalent wall layer (first layer), five cases are considered, as highlighted in

Table 6. Obtained values for equivalent (composite) wall from FEM analysis.

d (mm)	25 *	30	35	40	45	50	60	70	80	90	100
D (mm)	44	49	54	59	64	69	79	89	99	109	119
deff (mm)	34.5	39.5	44.5	49.5	54.5	59.5	69.5	79.5	89.5	99.5	109.5
HF (kW/m2)	115	72.5	57.3	48.3	41.9	37.1	30.2	25.5	22.1	19.5	17.5
Tc (K)	333	329	326	324	322	321	320	319	318	318	317
Th (K)	1258	1323	1387	1431	1463	1487	1522	1546	1563	1576	1586
keff (W/(m K))	4.29	2.88	2.40	2.16	2.00	1.89	1.74	1.65	1.58	1.54	1.51
ρeff (kg/m3)	3251	3136	3044	2970	2908	2855	2771	2707	2657	2616	2583
cpeff (J/kg·K)	818	827	834	840	845	849	856	861	865	868	870

* bare anchors.

. For each case, k_eff, cp_eff, ρ_eff and d_eff are assigned for the thermal conductivity, heat capacity, density and thickness of the layer, respectively.

For the simplicity of the analysis and plotting graphs, the cases are named based on the tip thickness (d). So, for example, a case with d = 40 mm corresponds to a case where the equivalent wall thickness, thermal conductivity, density and heat capacity are 49.5 mm, 2.16 W/(m K), 2970 kg/m³ and 840 J/kg·K, respectively, in the CFD model. The pipe wall thickness (second layer) is a steel material with known properties, which is similar for all studied cases. The rest of the boundary conditions and model setup are the same for all cases.

Figure 14 shows the calculated temperatures (Points A, B and D), O₂ mole fraction (Point A) and heat losses in the reflux chamber and the rest of the off-gas system for different cases (based on corresponding d values). The horizontal dot lines represent the measured values at the pilot plant, as reported in Table 5 for each parameter. For the temperature graphs, a ±10% measurement error is also shown with extra horizontal lines.

As can be seen from Figure 14A, by increasing the equivalent wall thickness in the models (and generally increasing refractory wall thickness), the amount of heat loss from the reflux chamber walls is substantially reduced. On the other hand, a lower heat loss will increase the temperature inside the reflux chamber and other parts of the off-gas system (Figure 14D–F). Due to the higher temperature within the reflux chamber, an increase in the rate of CO-H₂ and carbon particle conversion (Figure 14B), and consequently a reduction in the O₂ amount (Figure 14C) at the outlet of the reflux chamber, can be expected.

Based on Figure 14A–E, the calculated curves and measured lines intersect at a “d” value between 25 and 35 mm. This interval corresponds to an average wall thickness (d_eff) between 34.5 and 44.5 mm (see Table 6), which is in good agreement with the measured average thickness of 32 to 38 mm during the reflux chamber wall inspections. The calculated temperature graphs at Points B and D (Figure 14F,G) are also shown, and as is evident, the measured mean values fall outside the calculated range. However, the calculated graphs are still between the measured error lines.

As can be comprehended, using the mentioned methodology (summarized in Figure 6), it is possible to have an approximate average refractory thickness and, in general, an idea of the refractory condition without direct measurements, using parameters that can be measured during the operation without going into shutdown.

Using these graphs, specifically those with the least errors (heat losses, O₂ composition and carbon conversion), it seems that for the current measured data, d = 27.5 mm, which corresponds to an averaged equivalent wall thickness (d_eff) of 37 mm is a reasonable value for tuning the heat transfer for final CFD model of the current operational and wall condition.

The properties corresponding to the considered equivalent wall thickness are acquired from Figure 10 and Table 6 and summarized in

Table 7. Wall properties used in shell conduction model for tuned (used-wall) CFD calculation.

	Equivalent Refractory (First Layer)	Steel Pipe Thickness (Second Layer)
deff (mm)	37	5
keff (W/(m K))	3.65	Function of temperature (see Table 1)
ρeff (kg/m3)	3010	7850
cpeff (J/kg·K)	836	461

. One more set of CFD calculations is performed using the tuned values (hereafter called the used-wall case), and the results are compared to the fresh-wall case where d = 40 mm (d_eff = 49.5 mm). Fresh wall refers to the case with the original refractory thickness applied while constructing the reflux chamber.

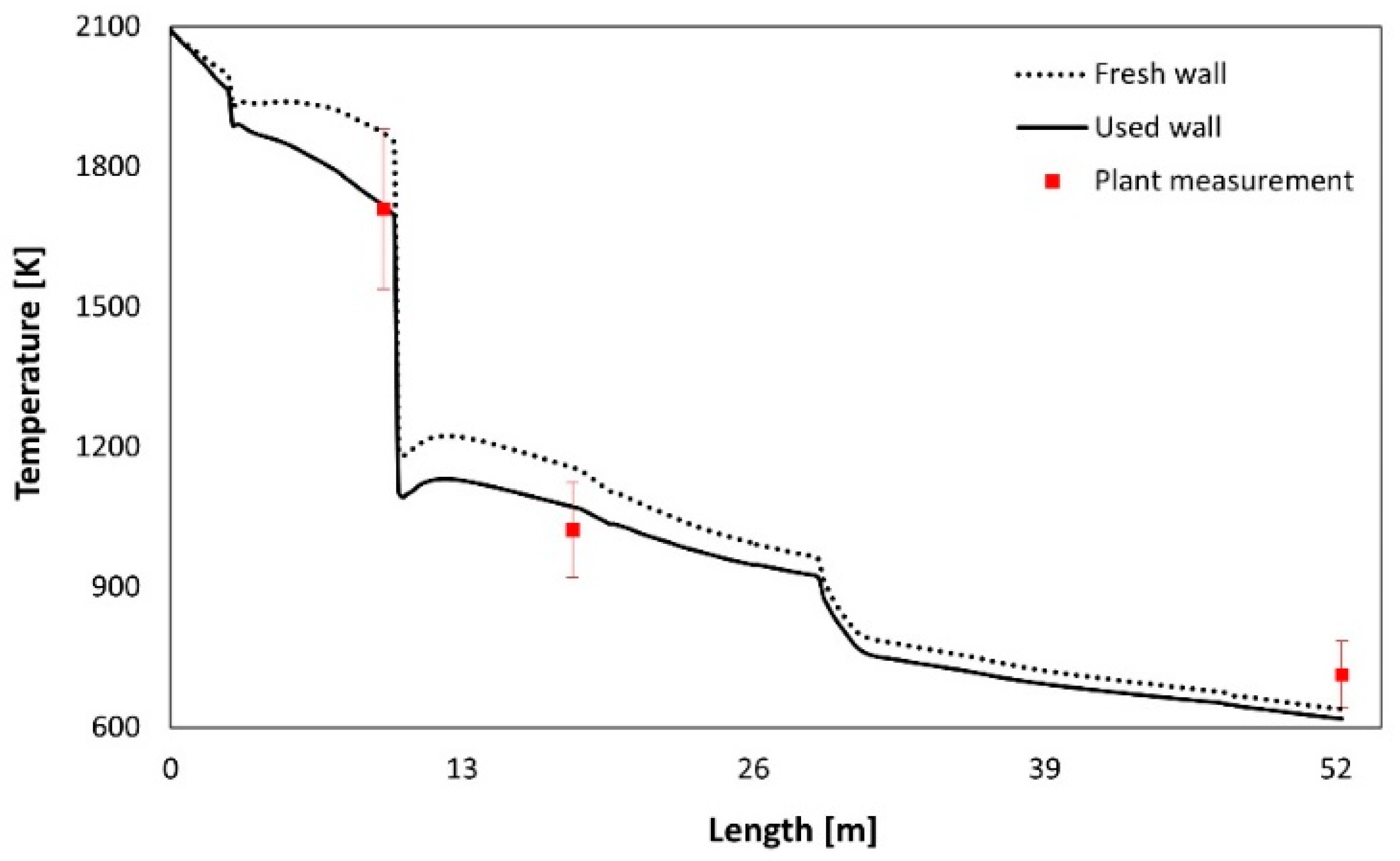
Figure 15 and Figure 16 show the predicted gas temperature and composition profile for the fresh- and used-wall cases. The calculated profiles are plotted along the centerline of the off-gas system geometry (length). As can be seen from Figure 15, there are three noticeable temperature drops along the off-gas system. The first occurs after post-combustion oxygen injection in the reflux chamber (length = 3 m), where cold oxygen is injected. A drastic temperature drop occurs at the air quench section (length = 10 m), where atmospheric air is injected in a large quantity. Ultimately, there is another temperature drop via evaporative cooling after injecting water spray in the down leg (length = 29 m). From the temperature profiles, there is a significant discrepancy between plant data and fresh-wall predictions, but a good agreement with the used-wall case. This discrepancy is not visible or is minor in the predicted gas composition profile, as depicted in Figure 16.

For more precise quantitative comparisons, Figure 17 shows the calculated and measured heat loss (at different regions), oxygen mole fraction, carbon conversion and temperature at different measurement points. Again, the same discrepancy can be seen between the plant measurements and the fresh wall, but a good agreement with the used-wall case.

The obtained results point to the fact that the state of the refractory material thickness has changed and can no longer be considered fresh. This conclusion is also confirmed by the reflux chamber wall inspection, where local erosions and material loss have been observed. The reduction in refractory material thickness will increase the thermal conductivity and thus the heat loss through the reflux chamber wall. This in turn will reduce the local temperature profile and ultimately might affect the composition of the off-gas. For example, considering the fresh-wall properties for the equivalent wall leads to a higher local temperature, a higher carbon conversion and a slightly lower oxygen molar fraction at the outlet of the reflux chamber. In general, for this specific modeled operating condition, the change in off-gas composition is minor for different equivalent wall thicknesses.

6. Conclusions

A comprehensive study is performed to demonstrate the importance of wall modeling for the proper prediction of heat losses through the walls of the HIsarna off-gas system. According to the models and also plant inspection, it turned out that the refractory wall thickness inside the reflux chamber is reduced due to the aggressive atmosphere. This change has a noticeable effect on the composition and flow temperature. Furthermore, in order to properly set up a CF model, the wall thickness and effective thermophysical properties must be properly assigned. The direct measurement of the refractory wall thickness is only possible during shutdown. Moreover, the thermophysical property calculation of the walls is not a straightforward task due to the presence of steel anchors inside the walls. Therefore, a methodology is offered and discussed in order to indirectly measure the refractory wall thickness inside the reflux chamber, and the thermal and physical properties of the off-gas system walls are calculated.

A set of FEM analyses is performed with the detailed wall geometry of the reflux chamber to obtain the effective thermal conductivity associated with refractory material with embedded anchors for different refractory thicknesses. The calculated values are then used in the CFD analysis to calculate the heat loss, temperature and gas composition for different refractory effective thicknesses. Then, the measured values for each parameter is mapped on the corresponding graph so that the calculated graph is intersected in a certain effective wall thickness (d_eff) value.

According to the measured plant temperature, composition and heat losses, as well as the comparison with calculated values, the effective wall thickness of the reflux chamber is predicted to be in the interval of 34.5 to 44.5 mm, which is in good agreement with observations and the measured average thickness of 32 to 38 mm during reflux chamber wall inspections.

The proposed methodology results are valid for a fixed operation condition and inlet boundary conditions and also a fixed anchor geometry and orientation. In case the operating condition is changed, Steps 1 to 3 of the proposed flowchart must be repeated. If the anchor geometry/orientation and refractory material are changed, the whole flowchart must be repeated; however, the methodology remains the same.

Besides the mentioned conclusions regarding the proposed methodology, the following can also be concluded based on the obtained results:

• Wall modeling and thermophysical property assignment in the CFD model have a significant effect on the prediction of temperature, composition and heat loss profiles.
• In the HIsarna off-gas system, the applied refractory at the reflux chamber has a very low thermal conductivity; however, the embedded steel anchors inside the refractory material can increase the thermal conductivity by a factor of 3.
• Refractory loss and thickness reduction increase the thermal conductivity of the wall.
• Using the original refractory thickness (thickness during the reflux chamber construction), CFD models predict much lower heat losses and much higher temperature profiles. Based on these results, the thickness of the refractory material inside the reflux chamber can no longer be the same as the original thickness. This is confirmed by the direct measurement of the walls during the shutdown period.
• FEM analysis is more reliable than the available EMA correlation for predicting the thermal conductivity of the composite walls with random-shape matrixes and fillers as in the reflux chamber wall.
• Based on the proposed methodology, on average, an effective wall thickness of 37 mm predicts heat losses, temperature and composition profiles, which is in excellent agreement with the current plant measurements. The predicted wall thickness is in good agreement with the direct thickness measurements, which was between 32 and 38 mm.
• According to the proposed methodology, it is shown that it is possible to indirectly measure the refractory thickness from other measured values during operations such as heat loss, temperature and gaseous compositions.