Abstract
Aiming to resolve the practical problem of brown rice kernels being easily broken due to overprocessing during processing (milling and polishing), brown rice kernels of Japonica rice, after hulling, were used as the research object in this study. Firstly, through a texture meter test, the discrete element bonding parameters (Kn is normal stiffness per unit area, Kτ is tangential stiffness per unit area, Cn is critical normal stiffness, Cτ is critical shear stiffness) were obtained. Secondly, a brown rice kernels’ bonding particle model was established by EDEM, and then a second orthogonal rotational combination test was carried out to calibrate the discrete bonding parameters, Kn = 4.43 × 1012 N/m3, Kτ = 6.13 × 1011 N/m3, Cn = 2.55 × 107 Pa, and Cτ = 7.92 × 107 Pa. The error of parameter calibration was within 5%, and the results were able to reflect the actual situation more realistically. Finally, analysis of the crushing process of brown rice kernels showed that their ability to withstand shear damage was not as great as their pressure-bearing capacity. The design of the relevant mechanism and the setting of parameters should be based on the critical shear stiffness of brown rice kernels, and the actual shear force Fτ* set during the processing should be smaller than the theoretical critical shear force Fτ (Fτ* < Fτ = 9.11 N). This study can provide a theoretical basis for optimizing the key structure and operating parameters of rice milling machines and polishing machines to effectively solve the practical problem of increased crushing of brown rice kernels due to overprocessing.
1. Introduction
Rice is the main grain of more than half of the world’s population [1,2]. Rice is the product of Oryza sativa processing, which requires a series of procedures such as cleaning, husking, rough separation, milling, polishing, color selection, grading, and packing [3]. The rice has been husked to form brown rice, which is then ground and polished to form finished rice [4]. More than 90% of damage to rice is generated by crushing [5], which is caused by the excessive processing of brown rice by related equipment (rice milling machine and polishing machine) [6]. Excessive wear and breakage of brown rice kernels leads to a loss of nutrients [7] and reduces the processing quality. Clarifying the mechanism of breaking brown rice kernels using mechanical force, optimizing the key structure and operating parameters of the equipment, and then improving the stress characteristics of brown rice kernels and reducing the crushing rate are effective ways to solve the problem of excessive processing by rice milling and polishing equipment.
Since the motion law and stress state of brown rice kernels in rice milling and polishing machines are difficult to observe and analyze intuitively, research on the mechanical properties of brown rice kernels is mostly based on the bench test method [8,9,10,11,12,13,14,15]. However, this method faces challenges in simulating the actual stress state of brown rice kernels in the white grinding room, and, usually, the test results differ from practical application. The discrete element method is a numerical simulation method that aims to resolve the problem of a granular medium. This method is suitable for analyzing the interaction and mechanical properties of discrete particles and has been widely used in agriculture and engineering fields [16,17,18,19,20]. A numerical study on the particle conveying in a feed screw section of a vertical rice mill based on the discrete element method was presented by Y.L. Han et al. [21]. This study described the relationship between the microscopic flow characteristics of the particles and the macro performances of screw conveying based on the method of polynomial fitting. J.W. Zhou et al. used computational fluid dynamics and discrete element coupling methods to study the pneumatic conveying of coarse coal particles under different pipeline configurations and swirling strengths. The model of coarse coal particle breakage was established by the parallel bond caking method [22]. Z.B. Tong et al. used the discrete element method to numerically study the failure of loose aggregates [23]. A numerical study of the micromechanics of the impact of a submillimeter-sized crystalline agglomerate with a target wall was carried out using granular dynamics (or discrete element) simulations by K. Kafui et al. [24]. Rackl Michael et al. described and demonstrated a methodical calibration method based on Latin hypercube sampling and Krieger. The angle of repose and bulk density of spherical glass beads were calibrated [25]. Wang Zhipeng et al. [26] calibrated the discrete element contact parameters of millet particles by simulating their angle of request with EDEM 2018 software. However, most of the existing researches focus on the motion law, stress state, parameter calibration, and other aspects, while few researches focus on the crushing mechanism of brown rice kernels.
Aiming at the actual problem that brown rice kernels are easily broken due to excessive processing (during milling and polishing), this paper adopts the original particle polymerization method (connecting by bonding) to establish the discrete element simulation model of brown rice kernels in line with the actual processing state. The bonding parameters of the simulation model (normal stiffness per unit area, shear stiffness per unit area, critical normal stiffness, critical shear stiffness) were tested and calibrated in combination with bench tests so as to clarify the crushing mechanism of brown rice kernels under the action of mechanical forces and provide a theoretical basis for optimization of the key structure and operating parameters of rice milling and polishing machines. This can effectively solve the practical problem of brown rice kernel crushing due to excessive processing and produce decreased costs and increased efficiency.
2. Materials and Methods
2.1. Particle Simulation Model
In this study, the brown rice kernels formed after hulling and dehulling of Japonica rice were used as the research object, and the hulling and dehulling processing method is shown in Figure 1. By measuring the three-axis dimensions of the brown rice seed grain, it can be seen that its average size is 5.08 mm × 2.97 mm × 2.24 mm (length × width × height). The 3D modeling software Solidworks 2019 was applied to establish a model matching the shape and size of the brown rice; this model was imported into the EDEM software, and the proto-particle polymerization method [27,28,29,30,31] was applied, which is a concept whereby dense or loose stacks of spherical particles of arbitrary sizes are combined by virtual elastic bonding at the contact points of the spherical particles, resulting in the formation of friable agglomerates, with each binder resisting, to a certain extent, tensile and shear deformation. This study carried out a large number of simulation test attempts in the early stage, when the selected sphere radius was less than 0.1 mm, and the length of the simulation time with the radius decreased and increased more. However, for the final calibration and simulation results, the size of the change of the radius became smaller. Reducing the sphere of the research results of this study had less impact on the results. Therefore, this study selected the sphere radius of 0.1 mm, at which time the number of generated bonding keys was 34,684, which streamlined its operation under the premise of guaranteeing the accuracy of the model to meet the needs of simulation and analysis in this paper, as shown in Figure 2. The spherical particles were connected by bonds, and the strength of the bonds is the key to the resistance to fragmentation of the simulation model, which mainly depends on four bonding parameters [18]: Kn is normal stiffness per unit area, Kτ is shear stiffness per unit area, Cn is critical normal stiffness, and Cτ is critical shear stiffness, which can be calculated according to the following equation [32]:

Figure 1.
Material pretreatment.
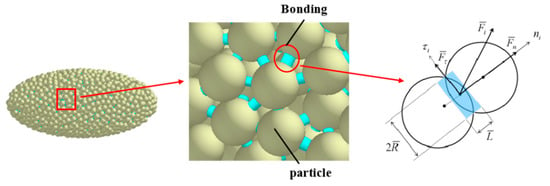
Figure 2.
Brown rice kernel simulation model.
Here, Fn and Fτ are normal extrusion force and shear force, respectively; Fnmax and Fτmax are the maximum normal extrusion pressure and maximum shear force; Δdn and Δdτ are extrusion displacement and shear displacement; Sn and Sτ are equivalent extrusion contact area and equivalent shear contact area; Snmax and Sτmax are the extrusion contact area and shear contact area under maximum stress.
2.2. Bench Test
According to Equation (1), the force, displacement, stress area, and other parameters of brown rice kernels under extrusion and shear action are needed to determine the four bonding parameters above. The extrusion pressure, shear force, and displacement can be obtained by shear and extrusion tests with a texture meter, and the force area can be estimated by image dyeing.
2.2.1. Extrusion and Shear Test
TA.XTC-18 texture apparatus was used to carry out extrusion and shear tests on brown rice kernels, as shown in Figure 3. The moisture content of the test material used was 15.5 per cent. In the extrusion and shear tests, 100 brown rice kernels with the same triaxial size were selected as the test samples, and the compression velocity of the cylinder and shear head were set as 0.1 mm/s, 0.2 mm/s, 0.3 mm/s, 0.4 mm/s, and 0.5 mm/s, respectively. The trigger force was 5 gf, the number of test cycles was one, and the speed before and after the test was 1 mm/s. The compression and shear displacements were 0.8 mm. Each group of tests was repeated 20 times. The functional relationship between shear force, extrusion pressure, and displacement can be obtained, respectively, in each test, and the measured data of each repeat group can be averaged to obtain the “Fn-Δdn” curve and “Fτ-Δdτ” curve, as shown in Figure 4. The slope of the linear stage of the above curve can be expressed as Equation (2):

Figure 3.
Bench test. (a) Squeeze test; (b) shear test.

Figure 4.
Curves of “force and displacement”. (a) The curve of “Fn-Δdn”; (b) the curve of “Fτ-Δdτ”.
Here, kn is the slope of the linear stage of the “Fn-Δdn” curve; kτ is the slope of the linear stage of the “Fτ-Δdτ” curve; Δdnmax is the displacement of an indenter under maximum extrusion pressure; and Δdτmax is the displacement of an indenter under maximum shear force.
2.2.2. Estimation of Contact Area
Estimation of equivalent crush contact area: the bottom of the cylindrical indenter (diameter was 2 mm) was coated with red coloring ink. The position of the probe was manually adjusted until it was just in contact with the brown rice kernel (no extrusion). As shown in Figure 5, the brown rice kernels were removed, Supereyes image equipment was applied to magnify and photograph the ink-impregnated area at a certain ratio, and the stained area was divided into a scale grid in Image J 1.48 software, as shown in Figure 6a, to estimate the area of the stained area for each test sample.
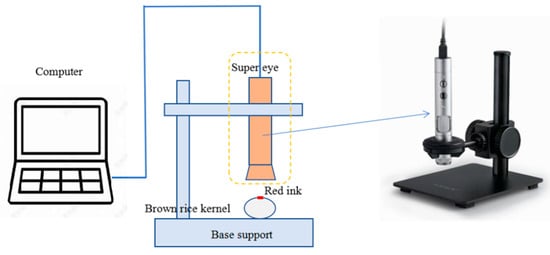
Figure 5.
Contact area measuring device.
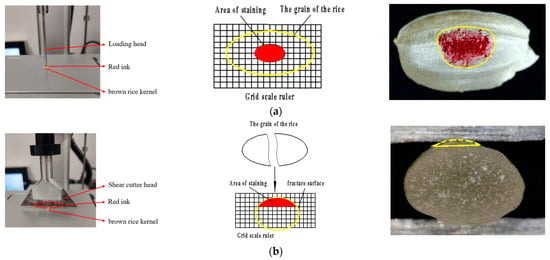
Figure 6.
Area of staining areas. (a) Extrusion staining area; (b) shear staining area.
Estimation of equivalent shear contact area: since the cutter side and the shear surface of the grains are not easily colored in the experimental process, the shear contact area can be estimated according to the “force-displacement” data in the shear test. The grains were cut into two halves, the shear surface of rice was enlarged and photographed by Supereyes image equipment at a certain ratio, and the scale grid was divided in Image J software. Only the displacement corresponding to the maximum shear force was used to estimate the shear area of each test sample, as shown in Figure 6b.
The staining areas of each group of extrusion and shear tests were recorded as {Sn1, Sn2, Sn3, Sn4, Sn5},{Sτ1, Sτ2, Sτ3, Sτ4, Sτ5}. The value range of the equivalent extrusion contact area and equivalent shear contact area of brown rice kernels is:
Calculation method of the maximum extrusion contact area: when the brown rice kernels were in the maximum extrusion state, the cylinder indenter completely contacted the brown rice kernels. Therefore, the cross-sectional area of the cylinder indenter was the maximum extrusion contact area (Snmax) at this time. Calculation method of the maximum shear contact area: the staining area corresponding to the displacement of the maximum shear force was analyzed and calculated using the same method as above. The test was repeated 20 times, and the mean value was the shear contact area at the maximum stress state (Sτmax).
2.3. EDEM Simulation Experiment
The critical normal stiffness (Cn) and critical shear stiffness (Cτ) can be calculated according to Equations (1) and (2), but the normal stiffness per unit area (Kn) and shear stiffness per unit area (Kτ) can only determine their value ranges. Therefore, we carried out EDEM simulation tests to calibrate Kn and Kτ. The simulation model shown in Figure 7 was established with EDEM software according to the actual scale. Simulation parameters are shown in Table 1 [33]. The quadratic regression orthogonal rotation combination test, with two factors and five levels, was carried out. The test levels were coded as −1.414, −1, 0, 1, and 1.414. The test index is the comprehensive error of extrusion and shear bench test and simulation test, expressed as:

Figure 7.
EDEM simulation model. (a) Extrusion simulation model; (b) shear simulation model.

Table 1.
Discrete element simulation parameters.
Here, and are, respectively, the maximum normal extrusion pressure and maximum shear force of the simulation test.
3. Results
3.1. Extrusion Test
As shown in Figure 8, the extrusion test results show that there is no significant difference between “Fn-Δdn” curves measured at different pressure rates, indicating that the pressure rate has no significant influence on the results of the extrusion test. There is no significant difference in slope kn and yield value Fnmax of the “Fn-Δdn” curve at the linear stage under different pressure rates measured, as shown in Table 2.
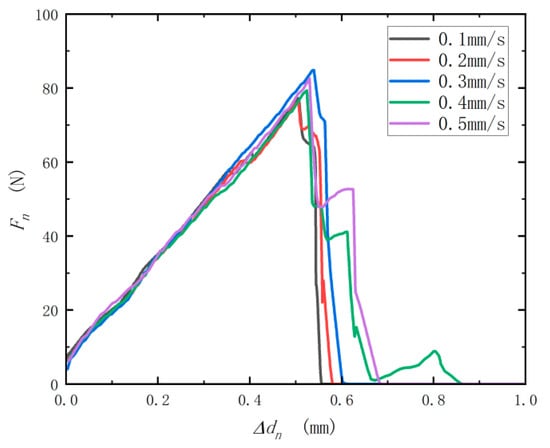
Figure 8.
Curves of “Fn-Δdn” at different pressure rates.

Table 2.
The test result of kn and Fnmax.
3.2. Shear Test
As shown in Figure 9, the shear test results show that there is no significant difference between the “Fτ-Δdτ“ curves of different shear rates, indicating that the shear rate has no significant influence on the results of the extrusion test. There is no significant difference in slope kτ and yield value Fτmax of the “Fτ-Δdτ” curve at the linear stage under different pressure rates measured, as shown in Table 3.
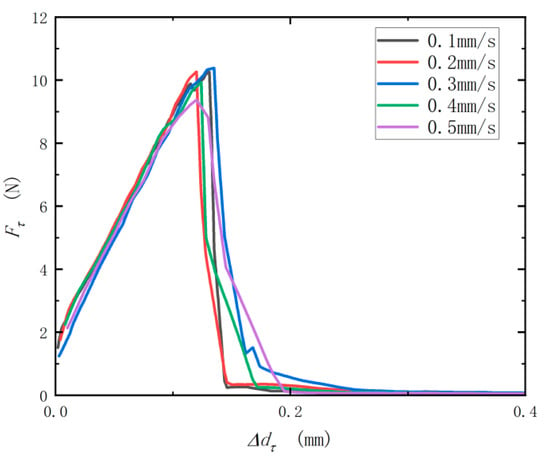
Figure 9.
Curves of “Fτ-Δdτ” at different pressure rates.

Table 3.
The test results of kτ and Fτmax.
3.3. Analysis of Test Results
The above test results show that the speed change has almost no effect on the calibration of bonding parameters within the preset speed interval. There is no significant difference between the slopes kτ and yield value Fτmax of the linear phase of the force and displacement curves of the two types of presses under different press speeds. This is because under the preset test conditions, different pressure speeds of relatively small size are used to calibrate the bonding parameters and to establish a basic simulation model. Usually, in practice, too high a speed will seriously affect the accuracy of the results, resulting in the expansion of the systematic error. From both experiments and references [12,34,35], it can be seen that when the pressure speed is less than 0.6 mm/s, it has no significant impact in determining the physical properties of the brown rice. The different pressure speeds set in the above tests are all within a small range; so, in this interval, the speed change has almost no effect on the calibration of the bonding parameters.
3.4. Calculation of Bonding Parameters
When the brown rice kernels are in the maximum extrusion state, the cylinder head contacts the brown rice kernels completely. Hence the cross-sectional area of the cylinder head Snmax is 3.14 mm2. According to the extrusion and shear staining tests at different pressure rates, the equivalent extrusion contact area, equivalent shear contact area, and shear contact area of brown rice kernels under maximum stress are shown in Table 4. According to Equation (1), the calculated mean values of critical normal stiffness and critical shear stiffness at different pressure rates were: Cn = 2.55 × 107 Pa, Cτ = 7.92 × 107 Pa.

Table 4.
Experimental results of extrusion and shear staining.
According to the extrusion and shear staining tests at different pressure rates, the average equivalent extrusion contact area Kn and equivalent shear contact area Kτ of brown rice kernels were 2.00~3.14 mm2 and 0.095~0.134 mm2, respectively. According to Table 2 and Equations (1)–(3), the normal stiffness per unit area ranges from 4.29 × 1012 N/m3 to 6.83 × 1012 N/m3. Therefore, the magnitude range of normal stiffness per unit area is estimated to be [1012, 1013]. According to Table 3 and Equations (1)–(3), the shear stiffness per unit area ranges from 5.04 × 1011 N/m3 to 7.22 × 1011 N/m3, and the magnitude range of normal stiffness per unit area is preliminarily determined as [1011, 1012].
3.5. Simulation Calibration
The normal stiffness per unit area Kn and shear stiffness per unit area Kτ were calibrated by quadratic regression orthogonal rotation combination testing. Kn and Kτ were used as the test factor, and the comprehensive error calculated by Equation (3) was used as the test index. The test level and code are shown in Table 5, and the test design and results are shown in Table 6.

Table 5.
Test factor coding.

Table 6.
Design and results of quadratic regression orthogonal rotation combination test.
The Design-Expert 13 software was used to conduct variance analysis on the test results. As shown in Table 7, the results of ANOVA show that the quadratic full model P is less than 0.0001, which means the quadratic model equation has a good fitting effect. The model determination coefficient R2 is 95.20%. The regression model fitted by quadratic multiple regression is shown in Figure 10, and the regression equation is:

Table 7.
Quadratic full model variance analysis of bonding parameter response curve.
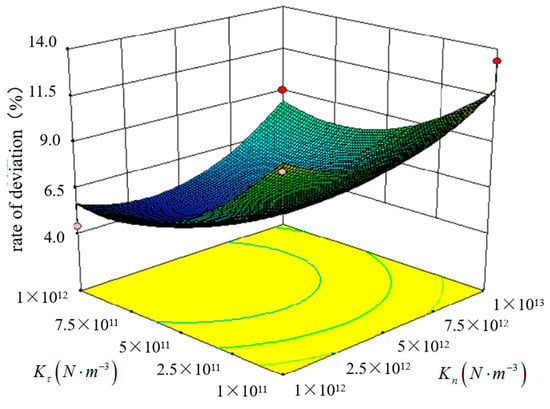
Figure 10.
Response surface diagram of regression model.
When the minimum value is 4.7%, the normal stiffness per unit area Kn is 4.43 × 1012 N/m3, and the shear stiffness per unit area Kτ is 6.13 × 1011 N/m3. At this time, the calculated value Kn and Kτ are the calibration values.
3.6. Verification of Results
To verify the feasibility and accuracy of the calibration bond parameters, a discrete element simulation model was established based on the calibrated bond parameters. The extrusion pressure, shear force, and relative errors were obtained from both the simulation test and bench test, as shown in Table 8 and Figure 11. The results show that the damage errors are all within 5%, and there is a good linear stage in the extrusion and shear simulation tests. The established model and calibrated parameters can simulate the brown rice grain breakage and overall stability of crushing force at different speeds. At the extrusion speed of 0.3 mm/s, the extrusion speed is moderate, the extrusion head and the surface of the brown rice grain fit better, the force surface is larger, the force time is long, and the corresponding crushing force will increase. At the extrusion speed of 0.1~0.2 mm/s, the extrusion speed is slower, the extrusion head and the brown rice grain surface fit slowly, the internal extrusion pressure accumulates, and some minor damage to the brown rice grain will appear with the internal extrusion process; that is, during the simulation process of the bond fracture, the brown rice grains will be broken earlier, and the corresponding crushing force will lessen. Similarly, at the extrusion speed of 0.4~0.5 mm/s, the extrusion speed is faster, the extrusion head and the surface of the brown rice grain quickly fit, the internal extrusion pressure increases rapidly within a short period of time, and some minor damage to the brown rice grain will appear with the process of internal extrusion; that is, with the simulation of the process of bond fracture, the brown rice grains will be broken earlier, and the corresponding crushing force will decrease. With an increase in shear speed, shear crushing force demonstrated a decreasing trend. When the shear speed was more than 0.3 mm/s, the shear crushing force decreased significantly. At this time, the shear speed was faster and the shear head and the surface of the brown rice grains quickly affixed to the normal shear force for a short period of time. With the dramatic increase of crushing force, internal microscopic defects were rapidly amplified, resulting in earlier breakage of the brown rice grains. Thus, at this point, the crushing force will be less.

Table 8.
Destructive force error analysis.
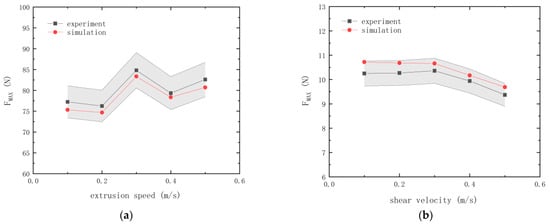
Figure 11.
(a) Squeeze crushing force error; (b) shear crushing force error.
3.7. Analysis of Brown Rice Kernels’ Crushing Process
It can be seen from the above analysis that a falling rate of indenters has no significant effect on the crushing of brown rice kernels, and the crushing process is mainly related to the stress mode (extrusion and shear). Thus, a simulation of the brown rice kernel crushing process was carried out under extrusion and shearing modes, and the compression speed of the cylindrical impress and shear speed of the cutter were both at 0.1 mm/s. The particle crushing process and the amount of bond breakage under the two stress modes are shown in Figure 12 and Figure 13.
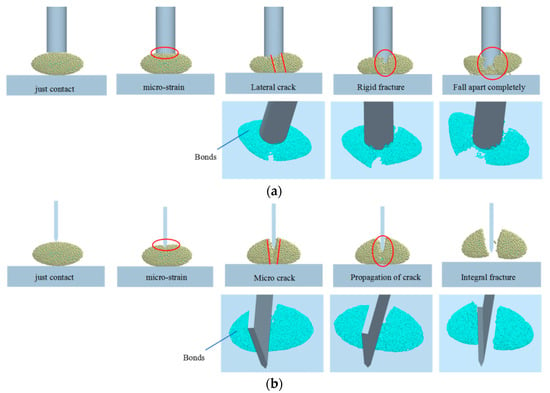
Figure 12.
(a) Simulation of brown rice kernel crushing process; (b) simulation of brown rice kernel shearing and crushing process.
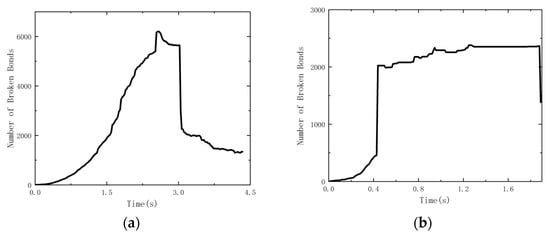
Figure 13.
(a) Simulation of the extrusion crushing process of a number of broken bonds; (b) simulation of shear crushing process of a number of broken bonds.
Since the crushing process of brown rice seed kernels occurs in a very short time when it is subjected to an extrusion test or shear test, it is difficult to analyze the process of its rupture under the action of external force. So, in this study, an observation device for the crushing process of brown rice kernels was designed, as shown in Figure 14, which consists of a texture meter, a computer, a high-speed camera, and a light source. When the texture meter performs the extrusion test or shear test according to the set parameters, the high-speed camera records the crushing process of brown rice seeds, as shown in Figure 15.
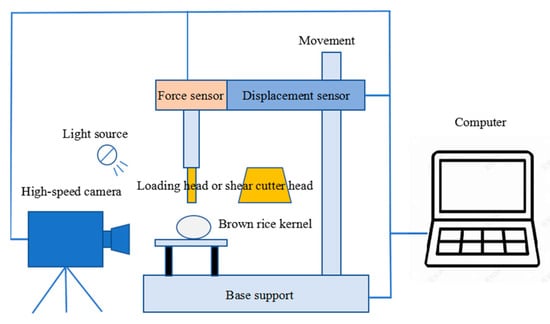
Figure 14.
Observation device for the crushing process of brown rice kernels.

Figure 15.
(a) The actual extrusion process of brown rice kernels; (b) the actual shearing process of brown rice kernels.
During the process of extruding brown rice kernels shown in Figure 12a, with the cylindrical indenter moving downward, when the range of the indenter drops by 0~0.3 mm (with the indenter contacting the brown rice kernels as the zero point), the brown rice kernels start to undergo minor deformation with the increase in extrusion pressure, and, at this time, the number of bonds destroyed is relatively small, as shown in Figure 8 and Figure 13a, and the extrusion pressure is about 40 N. With the cylindrical indenter moving further as the cylindrical indenter descends further, within the range of 0.3~0.5 mm, the internal particles of the brown rice kernels are continuously squeezed, the number of bond destructions increases significantly, cracks are generated from the side, and the squeezing pressure is about 70 N. The cylindrical indenter continues to descend, and within an indenter range of 0.5~0.6 mm, the grains of rice are rigidly broken from the cracks, and then the number of bond destructions reaches a peak. The squeezing pressure is about 80 N. When the squeezing pressure is about 80 N, the number of bond destructions reaches a peak. The squeezing force is about 80 N. When the rice grains’ fracture occurs, resulting in the range of the indenter descending to a displacement greater than 0.6 mm and accompanied by the overall separation and dispersion of some of the grains, the number of bonds destroyed decreases significantly. This is basically consistent with the actual situation, as shown in Figure 15a.
In the shear action process of the brown rice kernels, as shown in Figure 12b, as the cutter keeps moving downward, in the range of 0~0.1 mm of the cutter falling, brown rice kernels start to undergo minor deformation with the increase in shear force; at this time, the number of bond destructions is small, as shown in Figure 9 and Figure 13b, and the shear force is about 8 N. As the cutter falls further, in the range of 0.1~0.15 mm of the cutter falling, the particles in contact with the cutter are separated from the mutually bonded particles under the action of shear force, and the bond destruction number increases significantly, the shear force produces rigid fractures, and the brown rice kernels are rigidly fractured. In the range of 0.1~0.15 mm, the particles in contact with the cutter are separated from the bonded particles under the action of shear force, and the number of bond destructions increases significantly. The brown rice kernels are rigidly broken with a shear force of about 10 N. Subsequently, the cutter continues to move downward; the result of this is that in the range of the cutter dropping by more than 0.15 mm, it basically does not have any destructive effect on the grains, and the number of bond destructions increases slowly, which is consistent with the actual situation, as shown in Figure 15b.
4. Conclusions
Using brown rice grains as the research object, the bonding parameters were calibrated by the discrete element method and quadratic orthogonal rotational combination experiments to establish a model for the crushing of brown rice grains, to analyze the crushing process of brown rice grains at the microscopic level, and to verify the crushing process of brown rice grains in bench tests by recording with a high-speed camera. Regarding the particle crushing process, the current research usually uses the finite element method. The finite element method can also be used to analyze the force and crushing process, but it can only carry out static single-particle force research and cannot simulate the dynamic group of particles in the moving bodies involved in the force and crushing process. This thesis uses EDEM software to establish a discrete elemental model of brown rice which can provide a theoretical foundation for the further use of the software to simulate the dynamic process of population particles.
- (1)
- By carrying out extrusion, shear, and staining bench tests, the bond parameters of the discrete element model of brown rice kernels were tested and calculated. The critical normal stiffness Cn and the critical shear stiffness Cτ were determined to be 2.55 × 107 Pa and 7.92 × 107 Pa, respectively.
- (2)
- By using bench testing and the EDEM simulation method, the bond parameters of the discrete element model of brown rice kernels were calibrated through quadratic orthogonal rotation combination testing. The normal stiffness per unit area Kn and shear stiffness per unit area Kτ were determined to be 4.43 × 1012 N/m3 and 6.13 × 1011 N/m3, respectively.
- (3)
- The results from the bench test and the simulation test of brown rice kernels were compared. The relative error of the critical particle failure force measured by the bench test and the simulation test was less than 5%, indicating that the calibration parameters were accurate and reliable. According to the above, the calibrated critical shear stiffness optimal value and the average critical shear contact area calculation can be obtained from the theoretical critical shear Fτ = 9.11 N, using Fτ in the shear test within the range of the actual critical shear, once again, to verify that the calibrated parameters are accurate and reliable.
- (4)
- Brown rice kernels began to produce cracks when subjected to 40 N~70 N extrusion force. When subjected to 8 N~10 N shear force, the ability of brown rice kernels to withstand shear damage is nil, as is their pressure capacity. This paper determines the law of the bonding parameters of brown rice kernels. Therefore, in the design of the structure of the relevant processing and transportation machinery, the operating parameters should include the critical shear stiffness of brown rice kernels for the upper limit of the design, and the actual shear force Fτ* set during the processing should be smaller than the theoretical critical shear force Fτ (Fτ* < Fτ = 9.11 N). This will prevent structures, such as sharp bumps inside the machine, that cause the brown rice grain to be subjected to excessive shear force and breakage.
Author Contributions
Conceptualization, Y.Z. and X.L.; methodology, X.L.; software, F.D.; validation, Z.S., X.L. and J.Z.; formal analysis, Z.S.; investigation, Z.S.; resources, H.L.; data curation, Z.S.; writing—original draft preparation, Z.S.; writing—review and editing, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
The study was mainly funded by the Science and Technology Research Project of Hubei Provincial Education Department (No.2022BBA0047) and the Technological Innovation Special Program of Hubei Province (No. 2022BEC054) and the Key Research and Development Program Project of Hubei Provincial (No. 2023BBB018).
Data Availability Statement
The datasets generated and analyzed during the current study are available from the corresponding author upon reasonable request.
Acknowledgments
We express our thanks for the support of Hubei Cereals and Oils Machinery Engineering Technology Research Center in Wuhan Polytechnic University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zeng, Y.; Jia, F.G.; Meng, X.Y.; Han, Y.L.; Xiao, Y.W. The effects of friction characteristic of particle on milling process in a horizontal rice mill. Adv. Powder Technol. 2018, 29, 1280–1291. [Google Scholar] [CrossRef]
- Zhao, F.; Sun, P.; Zhang, J. Modeling the Grain Import Trade: A Cointegration Analysis of China’s Panel Data. Discret. Dyn. Nat. Soc. 2021, 2021, 3673282. [Google Scholar] [CrossRef]
- Smith, C.W.; Dilday, R.H. Rice: Origin, History, Technology, and Production; John Wiley Sons: Toronto, ON, Canada, 2003; pp. 111–113. [Google Scholar]
- Reynolds, G.K.; Fu, J.S.; Cheong, Y.S.; Hounslow, M.J.; Salman, A.D. Breakage in granulation: A review. Chem. Eng. Sci. 2005, 60, 3969–3992. [Google Scholar] [CrossRef]
- Sharma, A.D.; Kunze, O.R.; Sarker, N.N. Impact damage on rough rice. Trans. ASAE 1992, 35, 1929–1934. [Google Scholar] [CrossRef]
- Halidan, M.; Chandratilleke, G.; Dong, K.; Yu, A. Mixing performance of ribbon mixers: Effects of operational parameters. Powder Technol. 2018, 325, 92–106. [Google Scholar] [CrossRef]
- Buggenhout, J.; Brijs, K.; Celus, I.; Delcour, J. The breakage susceptibility of raw and parboiled rice: A review. J. Food Eng. 2013, 117, 304–315. [Google Scholar] [CrossRef]
- Azmir, J.; Hou, Q.; Yu, A. Discrete particle simulation of food grain drying in a fluidised bed. Powder Technol. 2018, 323, 238–249. [Google Scholar] [CrossRef]
- Wang, W.; Luo, Y.; Ji, M. Experimental Study on Tensile Mechanical Properties of Rice Hull. J. Chin. J. Cereals Oils 2019, 34, 2050070. [Google Scholar]
- Siebenmorgen, T.J.; Qin, G. Relating rice kernel breaking force distributions to milling quality. Trans. ASAE 2005, 48, 223–228. [Google Scholar] [CrossRef]
- Yang, L.; Fan, Y.; Wang, C.; Yang, T.; Chen, H.; Song, S.; Zhang, Y.; Hu, Z. Mechanical Properties of Brown Rice Grains Based on in-situ Observation. J. Chin. J. Cereals Oils 2021, 36, 1–6. [Google Scholar]
- Zhang, Q.; Yang, W.; Sun, Z. Mechanical properties of sound and fissured rice kernels and their implications for rice breakage. J. Food Eng. 2004, 68, 65–67. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, Y.; Chu, H.; Liu, Y. Experiment and analysis on mechanical properties of mechanical crushing brown rice. Trans. Chin. Soc. Agric. Eng. 2012, 28, 255–261. [Google Scholar]
- Zhao, Z.; Li, Y.; Chen, Y.; Liang, Z.; Liu, L. Impact Mechanical Characteristics Analysis of Rice Grain. Trans. Chin. Soc. Agric. Mach. 2013, 44, 88–92. [Google Scholar]
- Sadeghi, M.; Araghi, H.A.; Hemmat, A. Physico-mechanical properties of rough rice (Oryza sativa L.) grain as affected by variety and moisture content. Agric. Eng. Int. CIGR J. 2010, 12, 129–136. [Google Scholar]
- Ardi, E.G.; Dong, K.; Yu, A.; Yang, R. A combined experimental and DEM approach to determine the breakage of particles in an impact mill. Powder Technol. 2017, 318, 543–548. [Google Scholar] [CrossRef]
- Patwa, A.; Ambrose, R.K.; Casada, M. Discrete element method as an approach to model the wheat milling process. Powder Technol. 2016, 302, 350–356. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Johansson, M.; Quist, J.; Evertsson, M.; Hulthén, E. Cone crusher performance evaluation using DEM simulations and laboratory experiments for model validation. Miner. Eng. 2017, 103–104, 93–101. [Google Scholar] [CrossRef]
- Gupta, V.; Sun, X.; Xu, W.; Sarv, H.; Farzan, H. A discrete element method-based approach to predict the breakage of coal. Adv. Powder Technol. 2017, 28, 2665–2677. [Google Scholar] [CrossRef]
- Han, Y.; Jia, F.; Zeng, Y.; Jiang, L.; Zhang, Y.; Cao, B. DEM study of particle conveying in a feed screw section of vertical rice mill. Powder Technol. 2017, 311, 213–225. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Du, C.; Liu, S.; Li, J. Numerical study of coarse coal particle breakage in pneumatic conveying. Particuology 2018, 38, 204–214. [Google Scholar] [CrossRef]
- Tong, Z.B.; Yang, R.Y.; Yu, A.B.; Adi, S.; Chan, H.K. Numerical modelling of the breakage of loose agglomerates of fine particles. Powder Technol. 2009, 196, 213–221. [Google Scholar] [CrossRef]
- Kafui, K.D.; Thornton, C. Numerical simulations of impact breakage of a spherical crystalline agglomerate. Powder Technol. 2000, 109, 113–132. [Google Scholar] [CrossRef]
- Rackl, M.; Hanley, K.-J. A methodical calibration procedure for discrete element models. Powder Technol. 2017, 307, 73–83. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Xu, X. Parameter Calibration of Millet Discrete Element Based on Stacking experiment. J. Chin. J. Cereals Oils 2021, 36, 115–120. [Google Scholar]
- Schilde, C.; Burmeister, C.F.; Kwade, A. Measurement and simulation of micromechanical properties of nanostructured aggregates via nanoindentation and DEM-simulation. Powder Technol. 2014, 259, 1–13. [Google Scholar] [CrossRef]
- Dosta, M.; Dale, S.; Antonyuk, S.; Wassgren, C.; Heinrich, S.; Litster, J.D. Numerical and experimental analysis of influence of granule microstructure on its compression breakage. Powder Technol. 2016, 299, 87–97. [Google Scholar] [CrossRef]
- O’Sullivan, C.; Bray, J.D. Selecting a suitable time step for discrete element simulations that use the central difference time integration scheme. Eng. Comput. 2004, 21, 278–303. [Google Scholar] [CrossRef]
- Chehreghani, S.; Noaparast, M.; Rezai, B.; Shafaeia, S.Z. Bonded-particle model calibration using response surface methodology. Particuology 2017, 32, 141–152. [Google Scholar] [CrossRef]
- Goodman, R.E. Introduction to Rock Mechanics; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Chinese Academy of Agricultural Mechanization. Handbook of Agricultural Machinery (Part 2); Chinese Academy of Agricultural Mechanization: Beijing, China, 2007. [Google Scholar]
- Zeng, Y.; Jia, F.; Xiao, Y.; Han, Y.; Meng, X. Discrete element method modelling of impact breakage of ellipsoidal agglomerate. Powder Technol. 2019, 346, 57–69. [Google Scholar] [CrossRef]
- Tang, P.-Y.; Meng, F.-B.; Huang, D.-M.; Zheng, X.-Y.; Lin, M. Correlation between textural parameters and floral biological properties. Mod. Food Sci. Technol. 2021, 37, 294–301. [Google Scholar] [CrossRef]
- Vasseur, J.; Bimbenet, J.J.; Bonazzi, C. Effect of deformation rate and moisture content on the mechanical properties of rice grains. Trans. ASABE 2002, 45, 145. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).